前回からの続きです。
こちらを先に読んでからの方がよいかと思います。
スプライン補間について(その1)
スプライン補間について(その2)
スプライン補間について(その3)
5.空間内運動データへの適用
これまでは $y=f(x)$ と表されるグラフに対してスプライン曲線を適用する場合を考えてきました。
$y$ が目的変数、$x$が説明変数で、$y$ が $x$に従属する場合です。
これに対し、$x$と$y$が互いに独立の場合のグラフもあります。
データ点に順番があるような場合です。
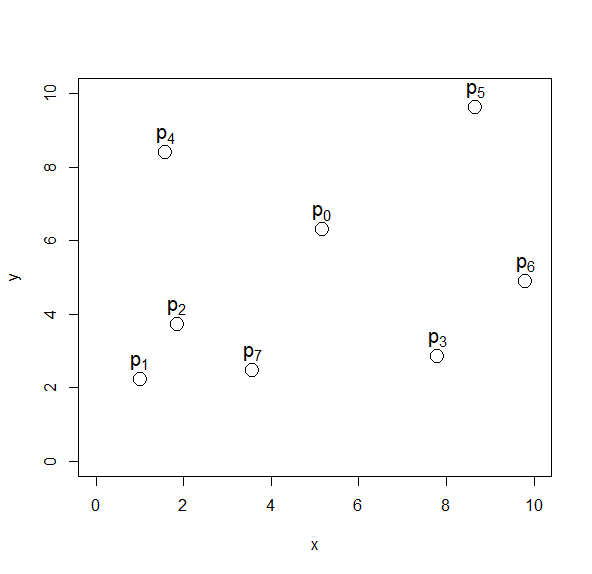
例えば以下のようなデータ点に順番があって、$x$と $y$が互いに独立変数である場合、
このように間をスプライン補間したい時があります。
さらに、三次元空間、高次元空間内のデータ点群を順番に補間したいときもあります。
これらはどうやって実現すればいいでしょうか?
2次元空間(平面)の場合
媒介変数を用いた応用
解決方法の一つは、$x,y$それぞれを共通の独立変数 $t$ の関数とみなしてやることです。
x = x(t) \\
y = y(t)
データ点に順番があるので、それを変数 $t$ の進行と捉えてやるのです。
時刻 $t$という言い方もします。
実際に、データ$(x_j,y_j)$に取得時刻が付随しているのであればその時刻を $t$として使うのがよいと思いますが、付随していないのであれば、各データ点を等間隔時刻で取得したとみなして処理することもできます。
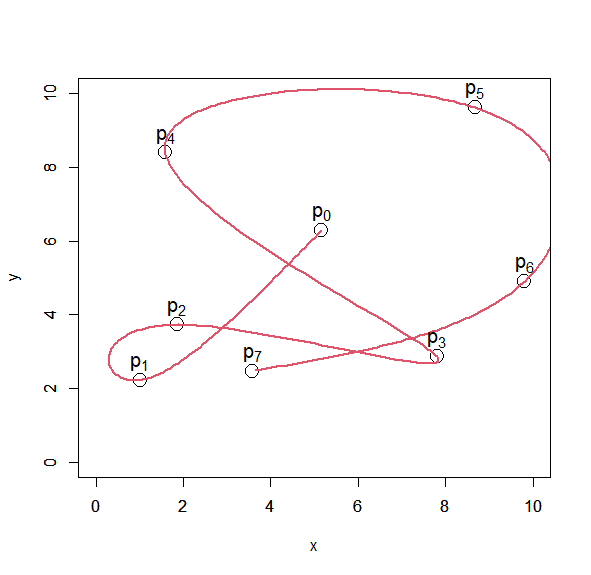
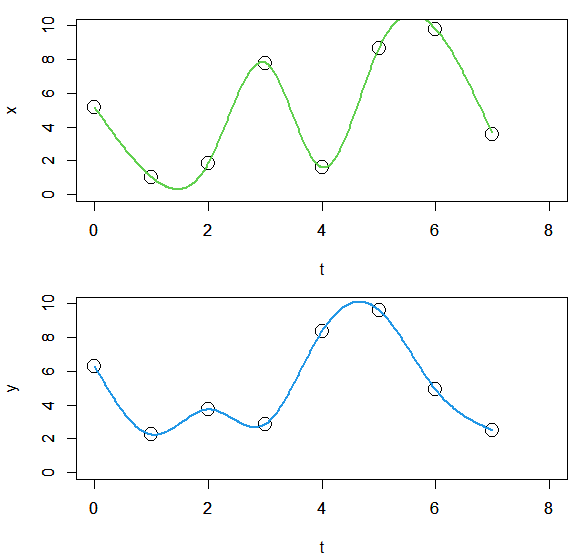
この場合、$x(t), y(t)$それぞれで $x$と$t$、$y$と$t$でスプライン補間してやって、その$x(t), y(t)$の結果を合わせてやれば$x$-$y$平面上でのスプライン補間が出来ます。
これの上から$x$、下から$y$の結果を使って合わせたグラフが以下。
この場合も先に示した方法を使えばよいのですが、媒介変数に用いた時刻 $t$ が等間隔、かつ自然数 $1,2,3,\cdots$ であるとみなすと求解が簡単になります。
\begin{eqnarray}
\begin{matrix}
x_0=x(0), & x_1 = x(1), & x_2 = x(2), & \cdots \\
y_0=y(0), & y_1 = y(1), & y_2 = y(2), & \cdots \\
z_0=z(0), & z_1 = z(1), & z_2 = z(2), & \cdots \\
\end{matrix}
\end{eqnarray}
スプライン曲線を求めるときに設定した条件式の中の差分項目がすべて1になるからです。
\Delta t_j = (t_{j+1} - t_j) = 1
そうすると、条件1の式はこうなります。
($x$の場合を書きますが、$y$の場合も同様です。$x_j$が $y_j$に変わるだけです。)
\begin{eqnarray}
\begin{matrix}
S_j(t_j) & = & a_j & + & 0 & + & 0 & + & 0 & = & x_j \\
S_j(t_{j+1}) & = & a_j & + & b_j \cdot 1 & + & c_j \cdot 1^2 & + & d_j \cdot 1^3 & = & x_{j+1}
\end{matrix}
\end{eqnarray}
よって、該当する行列の行はこう簡単になります。
\begin{bmatrix}
\ddots & \vdots & \vdots & \vdots & \vdots & \\
\cdots & 1 & 0 & 0 & 0 & \cdots \\
\cdots & 1 & 1 & 1 & 1 & \cdots \\
& \vdots & \vdots & \vdots & \vdots & \ddots \\
\end{bmatrix}
条件2の式はこうなるので
\begin{matrix}
b_j & + & 2c_j \cdot 1 & + & 3d_j \cdot 1^2 & - & b_{j+1} & = & 0 \\
\end{matrix}
該当する行列の行はこう
\begin{bmatrix}
\ddots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \\
\cdots & 0 & 1 & 2 & 3 & 0 & -1 & 0 & 0 & \cdots \\
& \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \ddots \\
\end{bmatrix}
条件3は
\begin{matrix}
c_j & + & 3d_j \cdot 1 & - & c_{j+1} & = & 0 \\
\end{matrix}
なので、
\begin{bmatrix}
\ddots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \\
\cdots & 0 & 0 & 1 & 3 & 0 & 0 & -1 & 0 & \cdots \\
& \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \ddots \\
\end{bmatrix}
条件4は
\begin{matrix}
c_0 & & & = & 0 \\
c_{n-1} & + & 3d_{n-1} \cdot 1 & = & 0
\end{matrix}
から、
\begin{bmatrix}
\ddots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \\
0 & 0 & 1 & 0 & \cdots & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & \cdots & 0 & 0 & 1 & 3 \\
\end{bmatrix}
になります。
全部合わせてみると結局、
\scriptstyle{
\begin{bmatrix}
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \cdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 \\
0 & 1 & 2 & 3 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 1 & 2 & 3 & 0 & -1 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \cdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 1 & 2 & 3 & 0 & -1 & 0 & 0 \\
0 & 0 & 1 & 3 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 & 3 & 0 & 0 & -1 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \cdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 1 & 3 & 0 & 0 & -1 & 0 \\
0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 3 \\
\end{bmatrix}
}
という、決まった簡単な形になります。
また便利なことに、$x,y$に対してこの行列は共通です。
どの区間においても、$t$の差分$\Delta t$は1だからです。
この行列を全区間に用いて計算した結果が、先に示した平面上のスプライン補間のグラフです。
$x, y$両方に同じ行列を用いることができるのは大変便利です。
検証すべきこと
さて、ここまでは他のところでも書かれていて利用されていることですが、検証しなければならないことが一つ残っています。
それは 曲率が正しく一致しているか です。
上記の方法では、あくまで$t$と$x$、$t$と$y$に対してスプライン曲線を求めています。
よって$t$-$x$平面、$t$-$y$平面各々の中のデータ点(結合点)で曲率が一致していることは保証されています。
しかし、その$x$と$y$の値を用いた$x$-$y$平面でのデータ点(結合点)での曲率が一致していることまでは保証されていません。
よって、以下これを確かめてみます。
まず、媒介変数 $t$ で表される2つの関数 $x(t), y(t)$で表される曲線の曲率は以下の式で計算されます。
\kappa = \frac{| x'y'' - y'x'' |}{(x'^2 + y'^2)^{\frac{3}{2}}}
$t$を入れてちゃんと書けば
\kappa(t) = \frac{| x'(t)y''(t) - y'(t)x''(t) |}{(x'(t)^2 + y'(t)^2)^{\frac{3}{2}}}
となります。
いましたいことは、
\kappa_{j}(t_{j+1}) = \kappa_{j+1}(t_{j+1})
です。
さて、この式の中で使われているのは、
x'(t), x''(t), y'(t), y''(t)
です。
これらすべてで、
\begin{eqnarray}
x_{j}'(t_{j+1}) &=& x_{j+1}'(t_{j+1}) \\
x_{j}''(t_{j+1}) &=& x_{j+1}''(t_{j+1}) \\
y_{j}'(t_{j+1}) &=& y_{j+1}'(t_{j+1}) \\
y_{j}''(t_{j+1}) &=& y_{j+1}''(t_{j+1}) \\
\end{eqnarray}
であれば $\kappa_{j}(t_{j+1}) = \kappa_{j+1}(t_{j+1})$ であることが言えます。
ここで大変うれしいことに、条件2と条件3を思い出せば、この条件そのものであることが分かります。
よって、$x(t), y(t)$それぞれで $t$との間でスプライン曲線を求めれば、それを合わせた$x$-$y$グラフにおいてもデータ点(曲線の結合点)で曲率が一致することが保証されることになります。
ちなみに、接線の傾きに関しては
\frac{y_{j}'(t_{j+1})}{x_{j}'(t_{j+1})} = \frac{y_{j+1}'(t_{j+1})}{x_{j+1}'(t_{j+1})}
なので、こちらも条件2で保証されます。
これで、$x$と$y$が独立な順序があるデータ点群においても、媒介変数 $t$を用いることでスプライン補間ができることが確かめられました。
いま、ここでの条件は
$x$ と $y$ が独立変数である
ということです。
$x$が説明変数で $y$が目的変数(従属変数)である $y=f(x)$のような場合はこの方法は使用できません。
いくつかのページで「 $y=f(x)$の場合に使える」と書いてあるところがありますが、使えません。
なぜ使えないかは、あとで書きますのでご覧になってください。
3次元空間の場合
3次元空間内の運動データ点においても、2次元の時と同じようにしてみましょう。
まず、
\begin{eqnarray}
x &=& x(t) \\
y &=& y(t) \\
z &=& z(t)
\end{eqnarray}
を考え、それぞれ各データ点ををスプライン補間して求めてやります。
$x_j,y_j,z_j$それぞれの全区間で使用する行列は、先の $\Delta t_j = 1$を適用した行列です。
大変便利ですね。
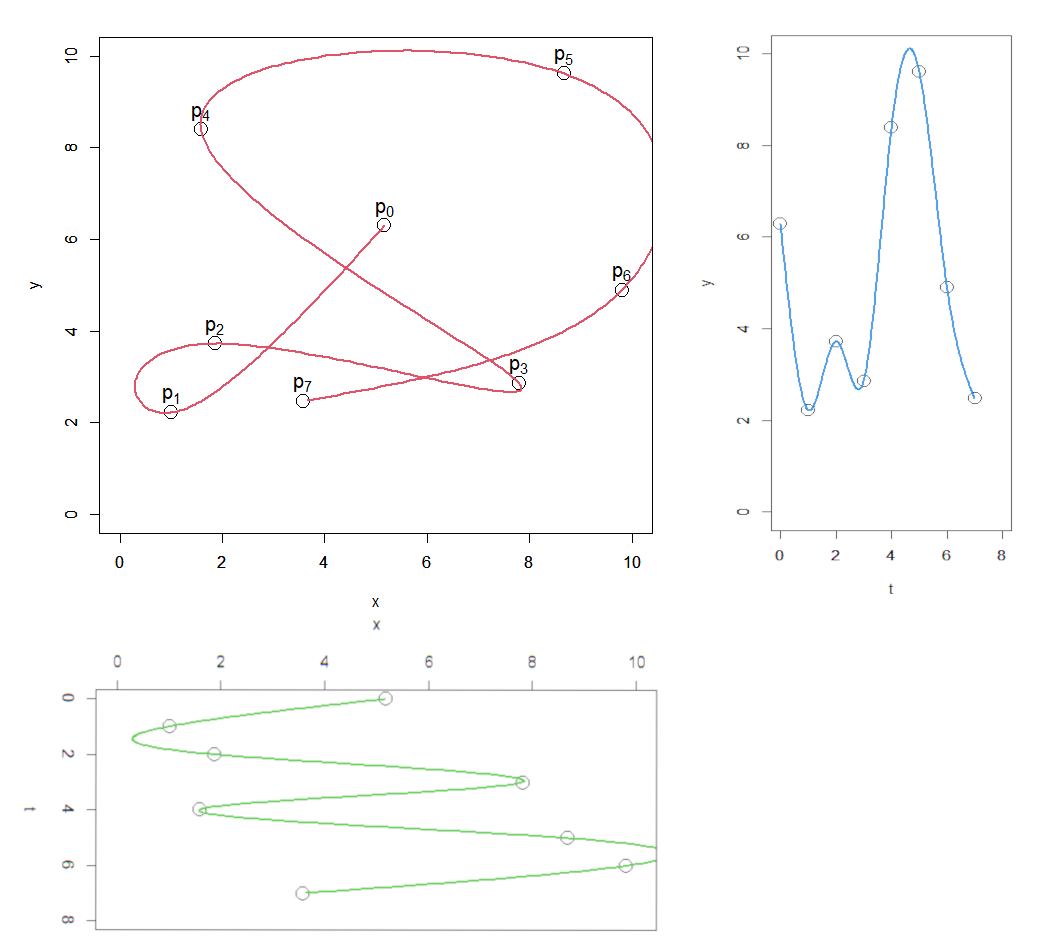
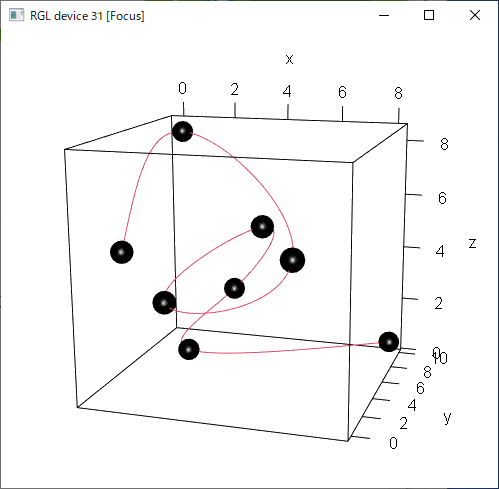
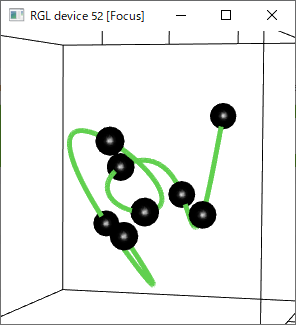
そうして求めた $x(t), y(t) ,z(t)$を座標点とした $(x(t),y(t),z(t))$をグラフ表示してやります。
以下はその一例です。
各データ点を滑らかにスプライン曲線がつないでいます。
これも2次元の時と同じように問題ない補間になっているでしょうか?
確かめてみます。
接線ベクトルの一致
3次元以上になったので、ベクトルを使って確かめていくことにします。
まず最初に、データ点で滑らかにつながっているかを確かめます。
2次元の時の接線の傾きが一致しているか、に相当します。
2次元平面の場合は接線の傾きを考えればよかったですが、今回は3次元空間内の空間曲線なので単純に接線の傾きを考えるわけにはいきません。
滑らかにつながっているためには、データ点での 接線ベクトル が同一である必要があります。
接線ベクトルは位置ベクトルの微分で求めることができます。
今、位置ベクトルは
\begin{eqnarray}
{\boldsymbol r}(t) &=& \left ( x(t), y(t), z(t) \right ) \\
\end{eqnarray}
で与えられますから、確かめるべきは
{\boldsymbol r}'_j(t_{j+1}) = {\boldsymbol r}'_{j+1}(t_{j+1})
です。
\begin{eqnarray}
{\boldsymbol r}'_{j}(t_{j+1}) &=& \left ( x'_j(t_{j+1}), y'_j(t_{j+1}), z'_j(t_{j+1}) \right ) \\
{\boldsymbol r}'_{j+1}(t_{j+1}) &=& \left ( x'_{j+1}(t_{j+1}), y'_{j+1}(t_{j+1}), z'_{j+1}(t_{j+1}) \right ) \\
\end{eqnarray}
ですので、結局、
\begin{eqnarray}
x'_j(t_{j+1}) &=& x'_{j+1}(t_{j+1}) \\
y'_{j}(t_{j+1}) &=& y'_{j+1}(t_{j+1}) \\
z'_{j}(t_{j+1}) &=& z'_{j+1}(t_{j+1}) \\
\end{eqnarray}
であれば、データ点(曲線の結合点)での接線ベクトルが一致し、滑らかに接続されていることが保証されます。
これは「条件2」そのものですから、接線ベクトルが一致、滑らかに接続される条件が満たされていることが分かります。
曲率の一致
次に曲率が一致していることを確かめます。
パラメータ $t$で表された空間曲線に対しての曲率は
\kappa (t) = \frac{\sqrt{|\boldsymbol{r}'(t)|^2 |\boldsymbol{r}''(t)|^2 - (\boldsymbol{r}'(t) \cdot \boldsymbol{r}''(t))^2}}{|\boldsymbol{r}'(t)|^3}
で計算されます。
ここに出てくるのは
\boldsymbol{r}'(t), \boldsymbol{r}''(t)
なので、これらが前後で一致していれば曲率も一致していることになります。
$\boldsymbol{r}'(t)$の方は先ほど接線ベクトルの一致を確かめたときに「条件2」から保証されることを確認したばかりです。
$\boldsymbol{r}''(t)$の方は
\begin{eqnarray}
{\boldsymbol r}''_{j}(t_{j+1}) &=& \left ( x''_j(t_{j+1}), y''_j(t_{j+1}), z''_j(t_{j+1}) \right ) \\
{\boldsymbol r}''_{j+1}(t_{j+1}) &=& \left ( x''_{j+1}(t_{j+1}), y''_{j+1}(t_{j+1}), z''_{j+1}(t_{j+1}) \right ) \\
\end{eqnarray}
なので、結局
\begin{eqnarray}
x''_{j}(t_{j+1}) &=& x''_{j+1}(t_{j+1}) \\
y''_{j}(t_{j+1}) &=& y''_{j+1}(t_{j+1}) \\
z''_{j}(t_{j+1}) &=& z''_{j+1}(t_{j+1}) \\
\end{eqnarray}
これは「条件3」そのものです。
よって、曲率も一致し連続的に接続されていることが確認できました。
捩率の一致
2次元平面であればここまででしたが、今回は3次元空間、次元が一つ上がっています。
すると、もう一つ考慮しなければならない量が増えます。
「一般化曲率」が出たときに話した 捩率 です。
接平面からの離れ方の度合い、捩じれ方を表した量でした。
3次元空間曲線なので曲線上の全点で接平面があり、捩率が存在します。
この捩率にも不連続があってはいけません。
これを確かめましょう。
パラメータ $t$で表された空間曲線に対しての捩率は
\tau(y) = \frac{\mathrm{det}\left (\boldsymbol{r}'(t), \boldsymbol{r}''(t), \boldsymbol{r}'''(t) \right )}{|\boldsymbol{r}'(t)|^2 |\boldsymbol{r}''(t)|^2 - (\boldsymbol{r}'(t) \cdot \boldsymbol{r}''(t))^2}
で計算されます。
同じように、ここで出てくるものを見てみます。
\boldsymbol{r}'(t), \boldsymbol{r}''(t), \boldsymbol{r}'''(t)
の3つの微分量が出てきています。
$\boldsymbol{r}'(t), \boldsymbol{r}''(t)$ の2つは先に見たように「条件2」「条件3」で一致することが保証されていました。
しかし今回は $\boldsymbol{r}'''(t)$ という3階微分の量が出てきてしまっています。
これを保証するものは、今までの4つの条件の中には入っていません。
これより、これまでのスプライン曲線の求解方法では「捩率」の連続性が保たれていないことが分かります。
2次元では常にゼロになるため考えなくてよかった捩率ですが、3次元になったことでゼロ以外の値を持つようになるので、不連続にならないようにスプライン曲線を構成しなければなりません。
その為には新たな条件を設定する必要があります。
上からわかるように、先の「条件2」「条件3」がある前提の上に、
{\boldsymbol r}'''_j(t_{j+1}) = {\boldsymbol r}'''_{j+1}(t_{j+1})
つまり
\begin{eqnarray}
x'''_{j}(t_{j+1}) &=& x'''_{j+1}(t_{j+1}) \\
y'''_{j}(t_{j+1}) &=& y'''_{j+1}(t_{j+1}) \\
z'''_{j}(t_{j+1}) &=& z'''_{j+1}(t_{j+1}) \\
\end{eqnarray}
という3階微分の境界での値も一致するという条件を追加しなければなりません。
次元が上がったことで2次元では考える必要のなかった捩率が出てくるため、新たな条件が必要となりました。
3次元空間でのスプライン曲線の条件
いままで、スプライン曲線は3次多項式で構成してきました。
しかし先に触れたように、3次多項式では3階微分量である上記 $\boldsymbol{r}'''(t)$ を一致させることができません。
3次多項式を三階微分すると、定数だけが出てきてしまうからです。
したがって、捩率を一致させる条件を設定するために、3次元空間でのスプライン曲線は4次以上の多項式を用いる必要があることが分かります。
一方、前回話をしたように、3次元空間では一般化曲率の4次以上の量は常にゼロになるので、5次多項式以上を用いても数学的・物理的意味はありません。
以上より 3次元空間でのスプライン補間 は、 区間多項式に4次多項式を用いて三階微分量をデータ点(曲線の接合点)で一致させる条件を追加する 必要があることが分かりました。
つまり、
【1】 区間多項式は4次
\begin{eqnarray}
S_j(t) &=& a_j + b_j(t - t_j) + c_j(t - t_j)^2 + d_j(t - t_j)^3 + e_j(t - t_j)^4 \\
\\
\end{eqnarray}
【2】 条件1~3は同じ。
\begin{eqnarray}
S_j(t_{j+1}) &=& S_{j+1}(t_{j+1}) = x_{j+1} ( \;\; or \;\; y_{j+1} \;\; or \;\; z_{j+1} )\\
\\
S_j'(t_{j+1}) &=& S_{j+1}'(t_{j+1}) \\
\\
S_j''(t_{j+1}) &=& S_{j+1}''(t_{j+1}) \\
\\
\end{eqnarray}
【3】 新しく、三階微分量も一致することを要請。
\begin{eqnarray}
S_j'''(t_{j+1}) &=& S_{j+1}'''(t_{j+1}) \\
\end{eqnarray}
【4】 両端の境界条件を考えに応じて設定。
これが3次元空間でのスプライン補間で必要な条件設定です。
比較
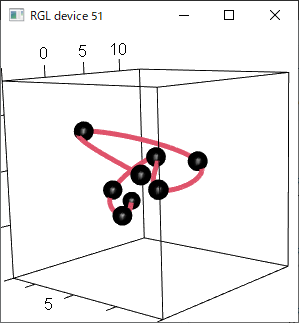
先に示した3次元空間でのスプライン補間の図は、今までと同じ3次多項式で作ったものでした。
つまり、「捩率」が不連続である空間曲線です。
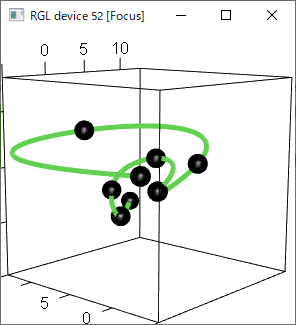
では、ここまでで分かったことを使って「捩率」も連続であるようなスプライン曲線を求めて比べてみましょう。
赤が従来の3次多項式でのスプライン補間、緑が4次多項式でのスプライン補間です。
こうして一方方向からの画像にしてしまうと分かりにくいですが、4次多項式でのスプライン補間のほうが、緩やかにカーブして連続的に変化していることが分かります。
3次スプライン補間したほうは、データ点で急に旋回する印象があります。
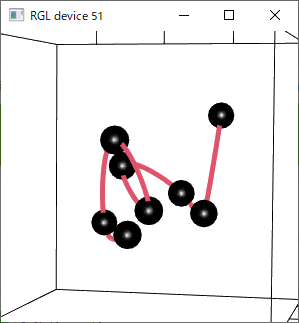
角度を変えて見てみると3次多項式で補間した方は、データ点で捩率、つまり平面への入力と出力が変わっていることが分かるところがあります。
一方、4次多項式で補間した方は連続的に滑らかにつながっていることがわかります。
ぜひ、実際に描画してみて確かめてみることをお勧めします。
4次以上の高次元の場合
ここまでの話から、スプライン補間では n次元の空間の場合は $n+1$次多項式を使用する必要があることが分かります。
n次元空間内の曲線には曲線の形を決定するn階微分量があるため、その一つ上の次数の多項式が必要になるわけです。
そして、各データ点でのn階微分の値を前後の多項式で一致させる必要があることがわかります。
4次元以上の場合において、実際に一般化曲率を合わせる為にはn階微分の値を一致させればよいかどうか、確かめてみるのも面白いかと思います。
高次元空間内のデータ点をスプライン補間する場合、以上のことに気を付けて補間をするようにしてください。
誰かの作ったライブラリを使う場合においても、以上のことを満たすように適切に使用するようお勧めいたします。
つづく
次はスプライン補間を使う際に注意することを書いていきます。
その5につづく。