前回からの続きです。
こちらを先に読んでからの方がよいかもしれません。
スプライン補間について（その１）
スプライン補間について（その２）
４．なんで３次スプライン曲線なのか
「スプライン補間」と検索するとなぜか３次スプライン曲線のものばかり出てきて、任意の次数のものが出てきません。
なんでか疑問に思った方はいないでしょうか？
それを解説しているサイトが見つけられなかったので、自分がここで書いてみようと思います。
その理由は、３次スプライン曲線が最も適切だからなのですが、その理由を見ていきたいと思います。
１次、２次の場合
まず３次より下の１次、２次のスプライン曲線がどうなるのか見てみます。
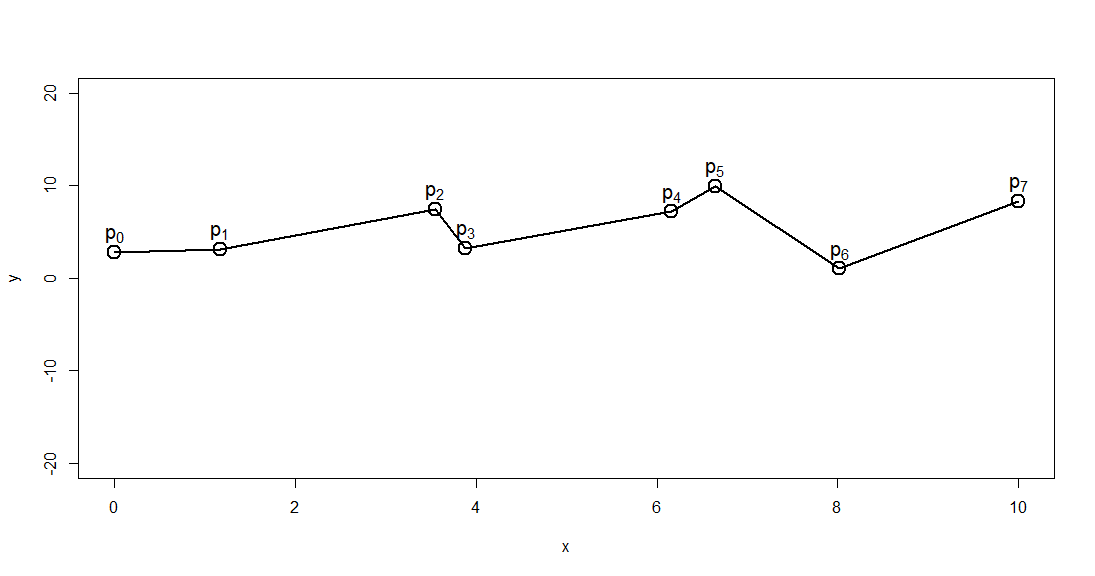
１次スプライン曲線はデータ点を直線で結んだ折れ線に他なりません。
考えてみれば、これも各データ点の間は、傾きも切片もそれぞれ異なる直線の式ですね。
次に２次スプライン曲線はこうなります。
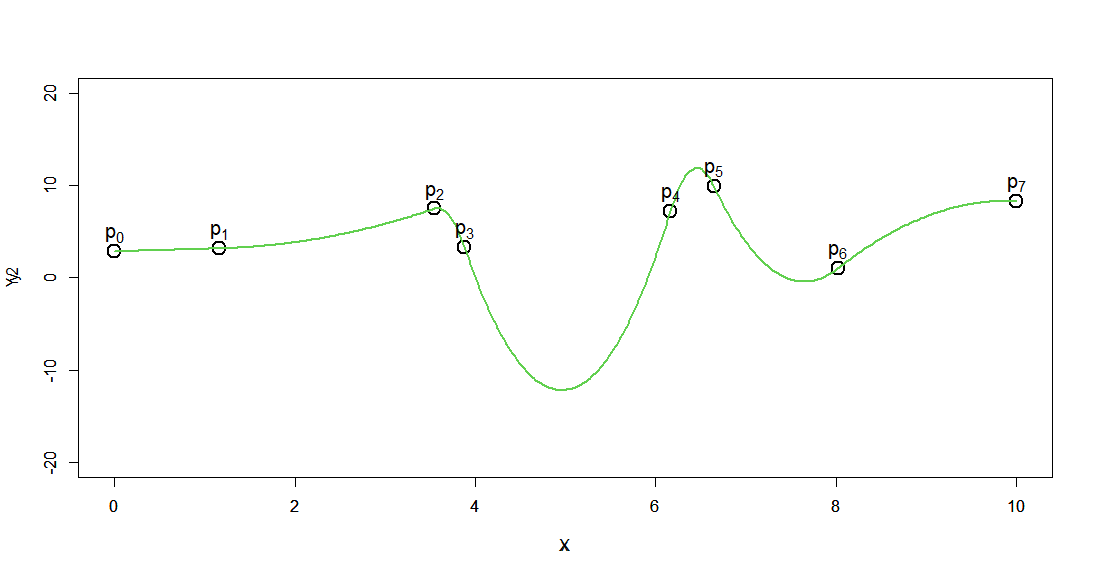
１次と違い、滑らかにデータ点をつなげられています。
ただ気にするポイントもあります。
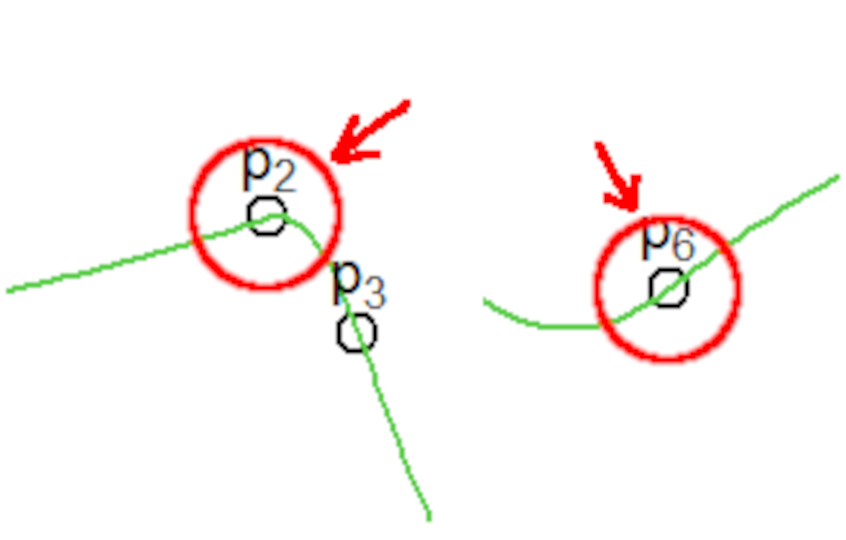
データ点 $p_2$ や $p_6$ の前後をみると、滑らかに繋がってはいますが曲がり方が急に変わっているのが分かるかと思います。
これは（その１）で条件３を説明したところで書きましたが、曲率が不連続だから起きています。
すべてのデータ点 $p_1$～$p_6$ で曲率が不連続になっているので、わかりづらいですが全部の点の前後で曲がり方が変わっています。
これが妥当なのか、ということが問題です。
実際の物理現象を考えたとき、このような急激な変化が毎回起きているとは考えづらいです。
物理現象は常に連続的に変化し、不連続な変化はおきないというのが物理の基本です。
（量子力学などを除く）
なので、このような不連続がある補間はあまりよい補間とはいえません。
３次のスプライン曲線と比べてみるとこうなります。
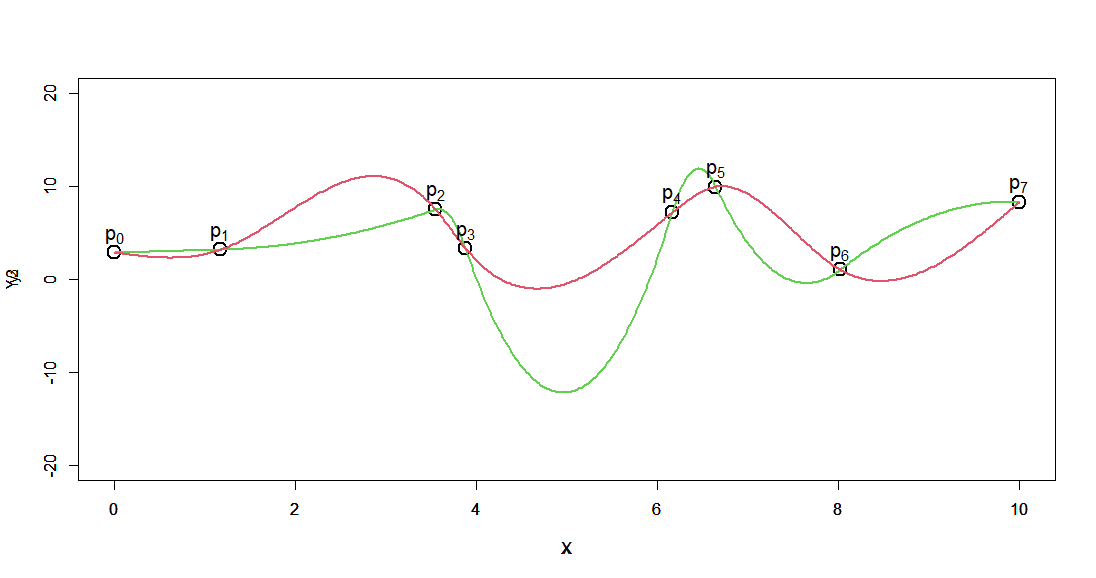
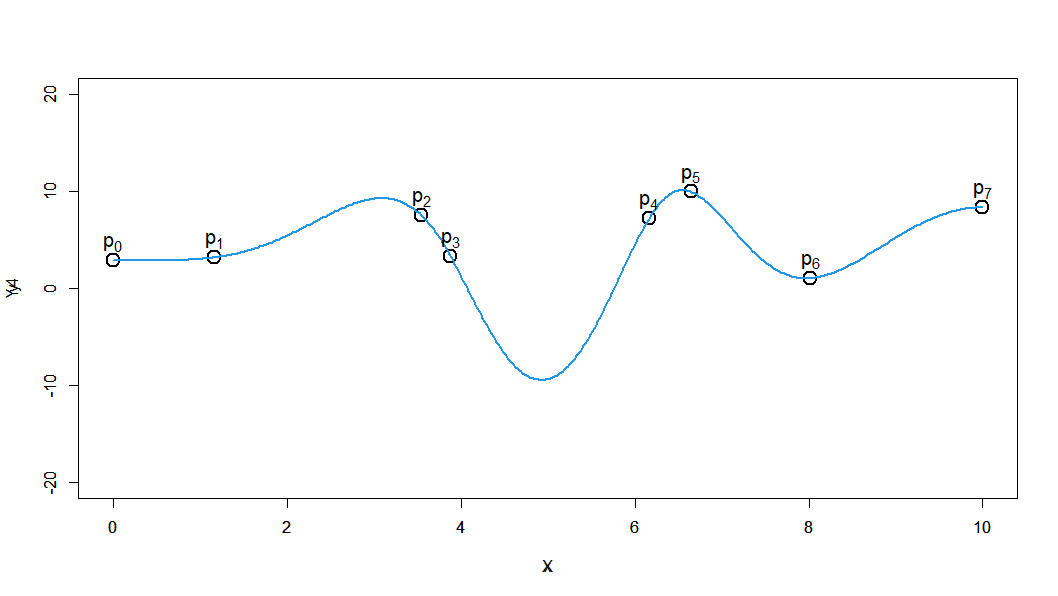
赤で示した３次スプライン曲線を見てみると、各データ点で急激に曲がり方が変化することもなく、滑らかに全データ点をつなげられています。
物理現象として考えると、２次の時より自然に間を補間できているように思えます。
では、２次スプライン曲線で曲率を合わせることが出来るかですが、これはできません。
曲率は二階微分に依存する量だからです。
二次方程式を二階微分すると定数が出てきてしまいます。
これは二次の項の係数が全区分多項式で固定されることを意味します。
そのため $x,y$ の値に合わせた曲率にすることが出来ません。
１次での直線近似の時に全データ点の前後で傾きを一緒にできるか、を考えると分かるのではないかと思います。
一次方程式を一階微分すると$x$の係数である定数が出てきます。
まさに直線の傾きを決める値です。
接線の傾きは一階微分に依存する量でした。
この$x$にかかる係数を全部の区分多項式で同一にすれば確かに傾きは同じになりますが、すべてのデータ点が直線上に並んでいない限り、すべてのデータ点を結ぶことが出来なくなることは明らかです。
これと同じく、２次スプライン曲線においてすべての区分多項式で境界の曲率を同じにすることは、全データ点がある二次関数上に並んでいない限り不可能です。
以上のことより、２次までのスプライン曲線ではデータ間を補間するには問題があることが分かります。
４次以上の場合
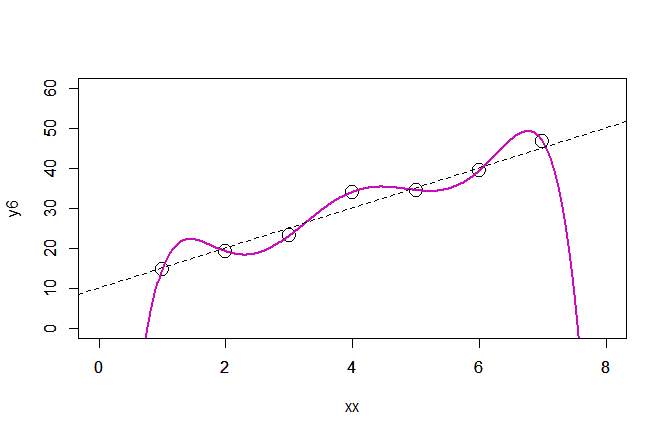
では４次以上の場合はどうでしょうか。
-
４次スプライン
-
５次スプライン
-
６次スプライン
-
７次スプライン
-
３次から７次を重ねたもの
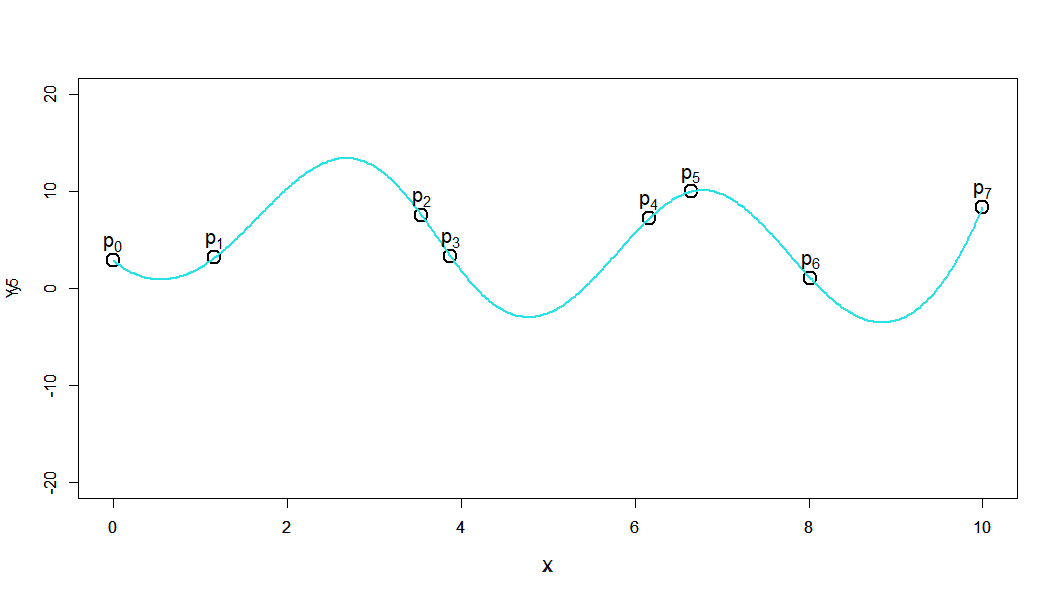
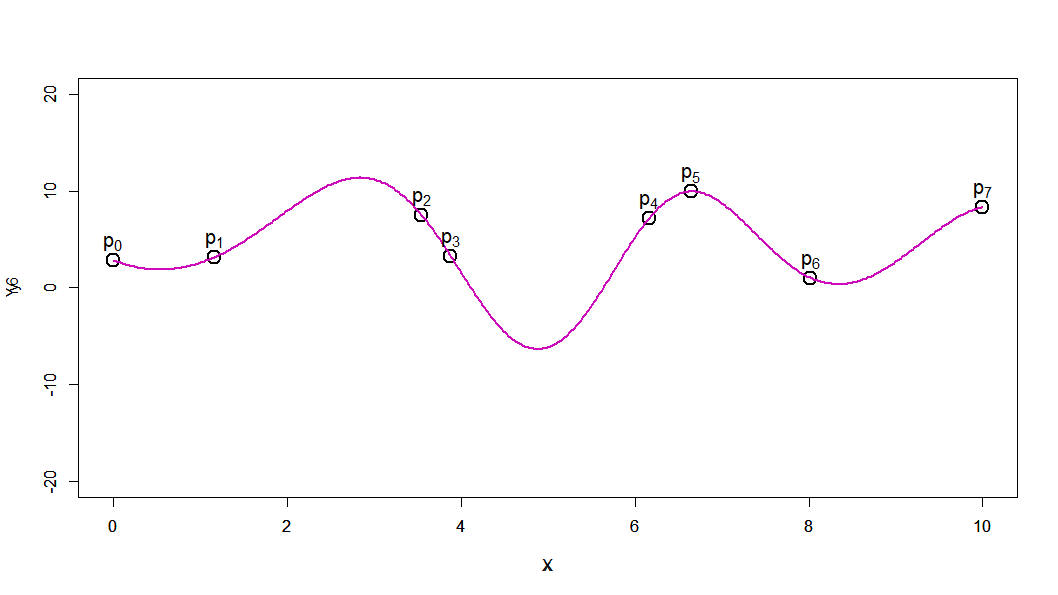
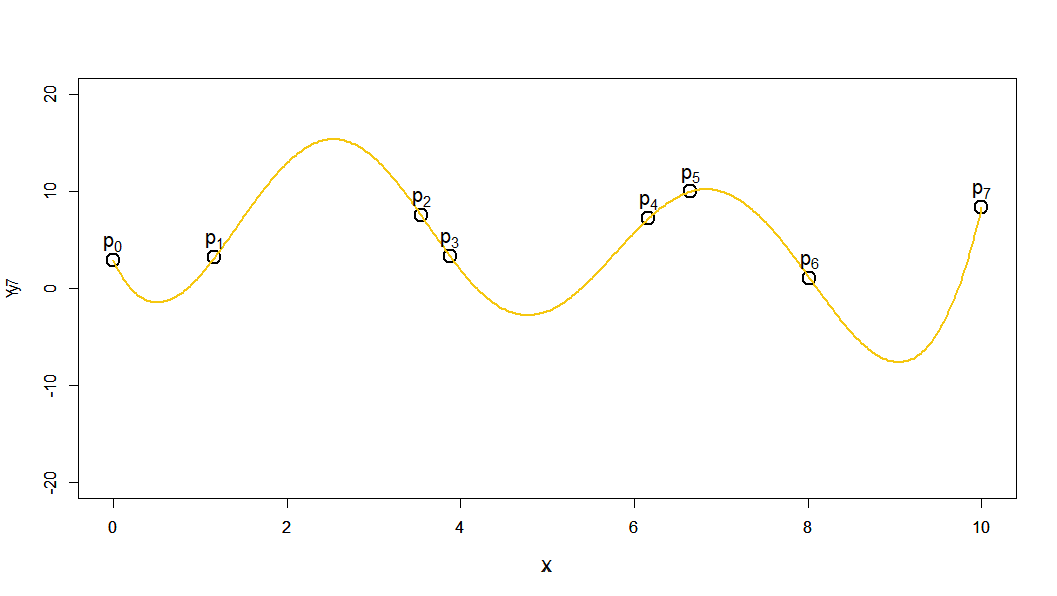
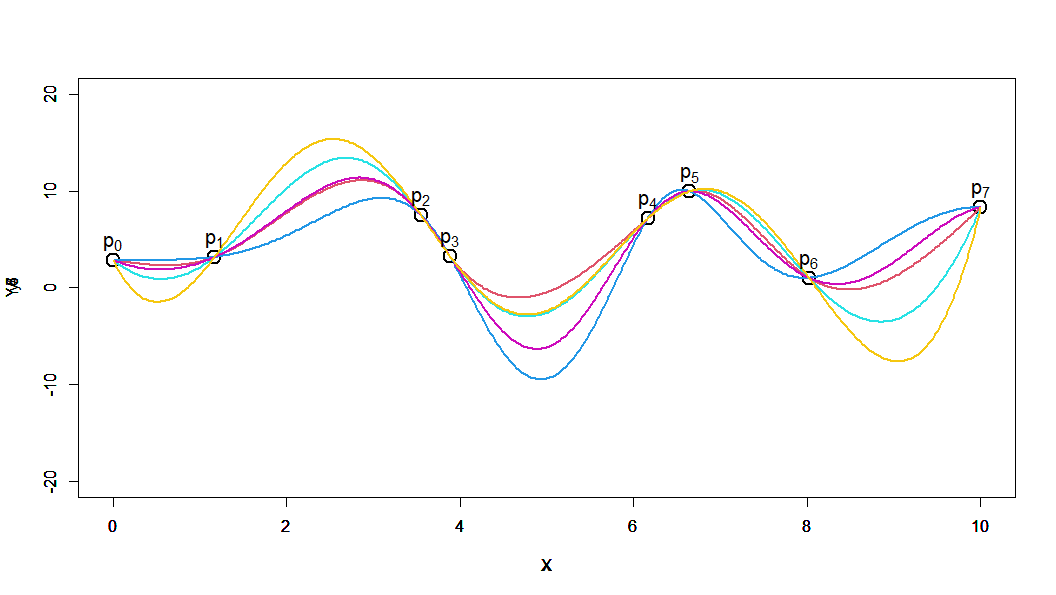
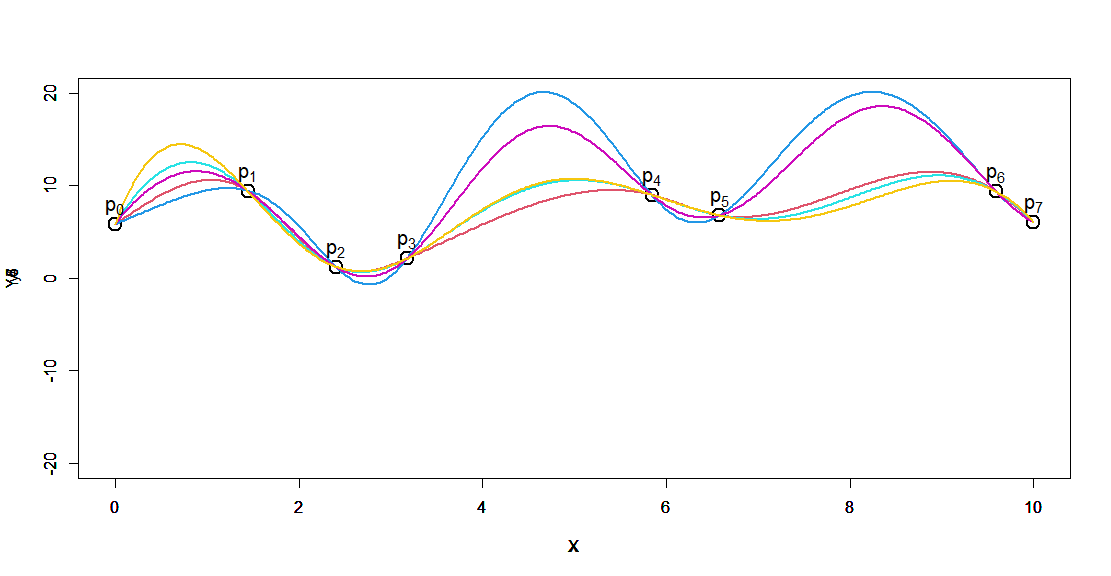
それぞれがどう見えるかは人によるかと思いますが、おおむねどれもそれなりによさそうに見えます。
ちなみに、このデータの場合はよかったですが、偶数次の曲線はデータによっては結構バタつきます。
赤：３次 青：４次 水色：５次 紫色：６次 橙色：７次
青と紫の４次と６次が上下に大きくうねっているのが見えます。
偶関数で補完しようとするので、間が膨らみやすくなるのだろうと思います。
どれを採用するかは使う人の考えで選んでよいとは思いますが、以下の理由により私は３次を使うべきだと思います。
１．次数が大きいと過剰適合を起こしやすい
２．数学的、物理的に４次以上は意味がない
次数が大きいと不要な振動を起こす
近似なり補間なり、観測データを数式で表す場合においては不必要に高次の関数を用いると補間や近似に適さない振動を起こしやすくなります。
分かりやすく、補間ではなく近似での例を示します。
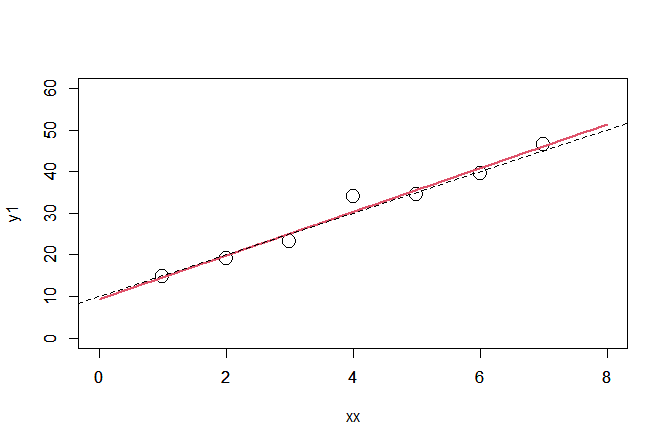
以下のグラフを見てください。
これの〇で表されている点は
y=5x+10
で表される $y$ の値に正規分布に従うノイズ（平均：0、分散3）を加えて作ったデータ点です。
黒い点線が本当のこのグラフのモデルの線、$y=5x+10$ の線です。
赤い線は、最小二乗法を用いてデータ点から推測したモデル式の値をグラフに書き加えたものです。
y = 5.25712 x + 9.249918
になりました。
なかなか良い推測になっており、他の値を推測するのに大変よいモデルになっています。
さて、ここで不必要に高次の多項式でこのデータ点群のモデルを推測したらどうなるでしょうか？
以下は6次の多項式で推測した結果です。
〇と点線は先ほどの通り、データ点と正解のモデルによる線です。
紫の曲線が6次の多項式によって推測したモデルから得られる推測値です。
見ての通り、すべてのデータ点を通過し曲線が波打っています。
このデータにはノイズが加えられている為全部のデータ点を通過してはダメなのですが、見事に通過しています。
（データ点を通過するということは、その点でノイズがゼロということ）
また、両端は正解のモデルから大きく乖離し下降してしまっているため、このモデル式を未来予測に使うことは不適切であることが分かります。
これが不要な振動を起こした一例になります。
これは不必要に高次関数を用いてモデルを推測した結果です。
データ点通過しても、モデル式としては全く役に立ちません。
また、別の補間方法である「ラグランジュ補間」においても同じようなことが起きます。
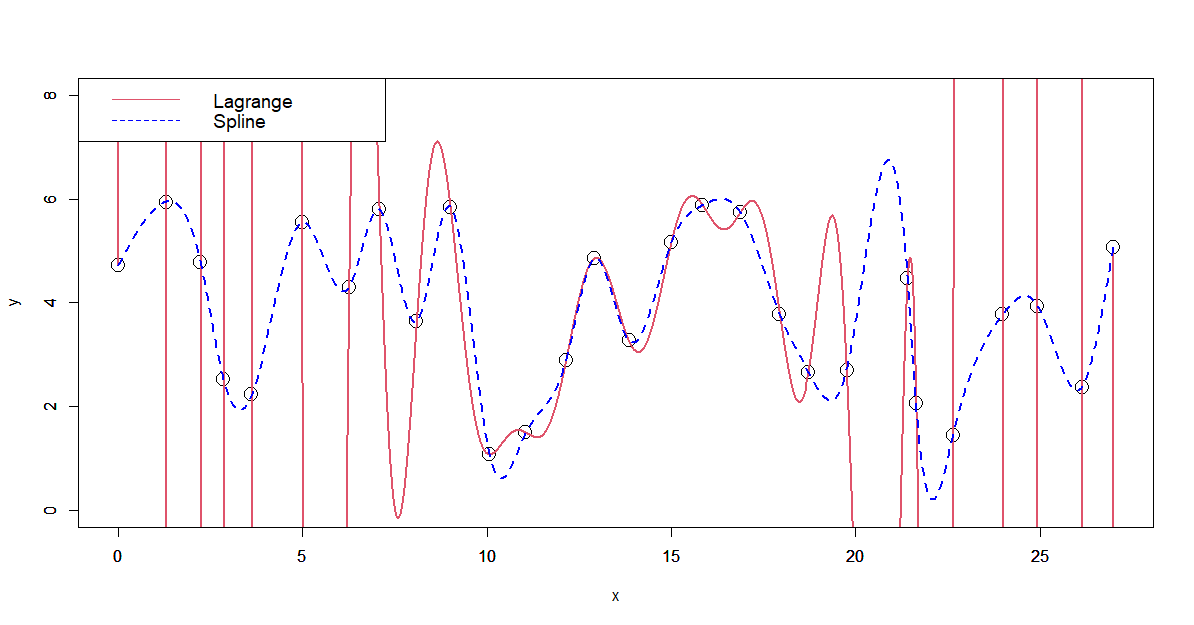
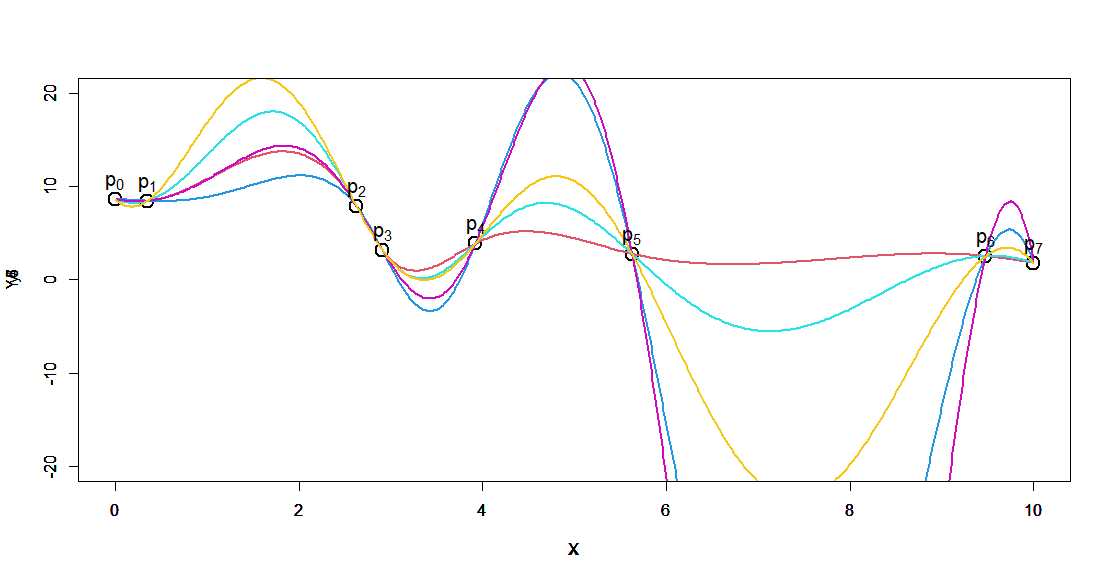
これはラグランジュ補間とスプライン補間を比較したグラフです。
ラグランジュ補間の方は、両端に行くほど大きく振動してしまっています。
ラグランジュ補間は 「（データ点数 － １）次多項式」を用いることになるため、データ点が増えると次数が高次に上がっていきます。
それによって振動が起きてきてしまっています。
高次多項式を使用した際の分かりやすい結果です。
このように、不必要に高次多項式を用いると良くない結果が返ってきます。
何も考えず、ただ手法を適用するだけでは結果を誤ります。
背景にある数学的、物理的意味をできる限り考慮して、最適な次数の関数を選ばなければなりません。
数学的推測方法が不必要な高次項の係数を自動でゼロに推測してくるわけではありません。
データから現象を読み取り、最適なモデルを選択する責任は人間の方にあります。
モデルに放り込めば正しい結果が出てくるわけではないのです。
数学的、物理的に４次以上は意味がない
条件を設定する時、多項式の境界で微分量が一致するように条件設定をしてきました。
これは境界で不連続な事が起きないようにするためでした。
そして既にみてきたように、
・ 一階微分量は接線の傾き
・ 二階微分量は曲率
という数学的、物理的な意味に関係がありました。
では三階以上の微分量はどんな数学的、物理的意味に関係があるでしょうか？
まず、三回微分量は 「捩率」 という曲線の捩れを表す量に関係します。
さらに高次の微分量は、一般に 「一般化曲率（generalized curvature）」 という量と関係します。
いわば曲率は2次曲率、捩率は3次曲率と言うわけです。
これは一般化された高次ユークリッド空間における フレネ・セレの公式 に現れる量です。
さて、一般化曲率が何を表しているかを考えます。
まず曲率ですが、これは曲線の曲り具合を表していました。
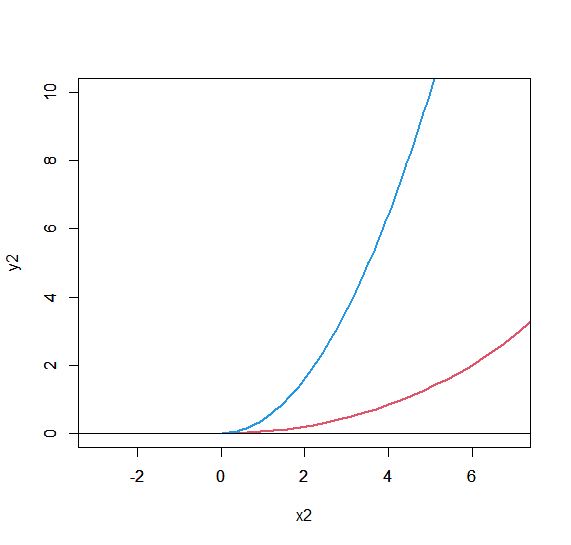
この「曲り具合」というものがどういう事なのかをよく考えてみると、接線からの離れ方 と捉えられる事がわかります。
このグラフは、曲率が小さい曲線と大きい曲線を描いています。
$y=0$の直線からの離れ方がゆっくり（赤）なのか、急（青）なのかが見えます。
離れ方が急な方が曲率が大きいわけです。
同じように一つ上の「3次曲率＝捩率」を考えてみます。
捩率は曲線の「捩じれ具合」を表す量です。
曲線の捩じれ具合とはなにか、と考えるときによく出る例は「螺旋」です。
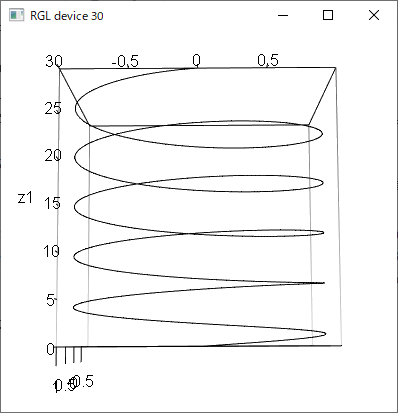
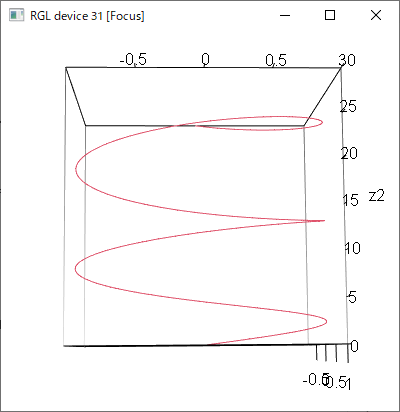
平面上の円運動を$z$軸方向に伸ばしていくと螺旋が出来ます。
この時、どのくらい早く$z$軸方向に動くかによって螺旋の形、伸ばされ具合が変わります。
これを平面からの離れ方と考えると、曲率の時と同じように曲線の捩じれ具合という量を捉えることが出来ます。
平面からの離れ方が急な方が捩率が大きいわけです。
ちなみに、今回の図にある一番下の平面ですが、この螺旋の接平面の一つになります。
三次元空間内の曲線においては、接線と同時に接平面が存在します。
接線の平面版です。
定義等は微分幾何の教科書等にゆずります。
この接平面からの離れ方の度合いが捩率になります。
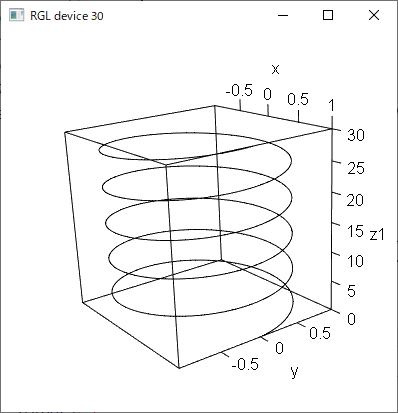
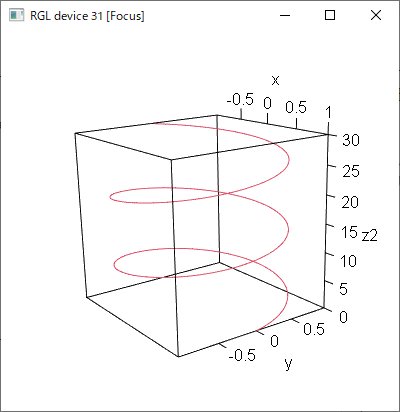
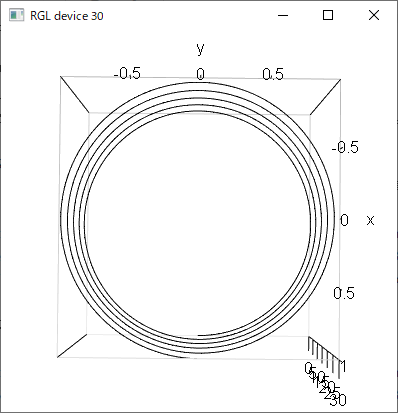
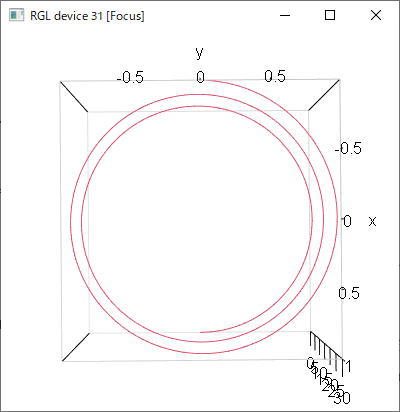
尚、この曲線の“曲率”はというと、円の半径の逆数になります。
この図は両方とも同じ半径の円で作図しているので、曲率は同一になります。
接線からの曲線の離れ方は両方とも同一です。
（半径が同じなので当然です）
しかし見て分かる通り、平面からの離れ方は違うので、捩率は異なります。
曲率は同じで捩率が違う2つの螺旋、ということです。
以上から。
曲率は接線からの離れ方の度合いでした。
捩率は接平面からの離れ方の度合いでした。
ここから、一般化曲率は “n次元超接平面からの離れ方の度合い” ということが分かります。
これを踏まえて、高次多項式でスプライン曲線を求めることの是非を考えてみます。
いま扱っているのは、$x$の値によって$y$の値が決まる、$(x_j, y_j)=(x_j, f(x_j))$の2次元グラフに表されるデータのスプライン曲線です。
つまり、2次元平面上の曲線を扱っているわけです。
そうすると、接平面からの離れ方の度合いを表す捩率は常にゼロになります。
曲線が平面内に留まり、離れていかないからです。
当然、それより高次の一般化曲率もゼロになります。
区分多項式の境界で微分量を一致させるようにしてきました。
しかし今言及したように、平面上のグラフにおいて捩率以上の一般化曲率はゼロです。
3次微分以上の量を一致させたとしても、これらの曲線の形を決める量とは無関係ということです。
平面上のグラフにおいて、一致させて意味があるのは曲率に関係する2次微分量まで。
つまり、2次微分量までを合わせる3次多項式が意味ある最大次数の多項式ということになります。
（3次多項式において3次微分量を合わせることはできません）
4次以上の多項式においては合わせる3次以上の高次微分量は曲線の形に対して意味を持ちません。
逆に2次と1次多項式は曲率を合わせることが出来ないので曲線の形に対して不連続を許すことになり適切ではありません。
結局、
3次多項式でスプライン曲線を求めることが最も適切である
ということになります。
物理的エネルギーを最小にする曲線
各データ点を通る曲線が、物理的な連続体であるとみなした場合。
たとえば、曲がる金属の板や棒のようなもので点をつないでいくと考えた時、その板や棒はなるべく元のまっすぐな状態に戻ろうとします。
なるべく曲がりがないまっすぐな状態になろうとする、物理的に言えば、曲げの弾性エネルギーが最小になる状態で止まります。
この 曲げの弾性エネルギーを最小にする曲線 が３次元スプライン曲線になります。
このグラフを物理現象ととらえた場合、実際に実現される形を表しているわけです。
その導出はこちらに記載したので興味がある方は読んでみてください。
まとめ
・高次式は不要な振動を起こしやすい（発散しやすい）
・1次2次では不連続が、4次以上では曲線に対する数学的物理的意味がない
・弾性連続体でデータ点をつないでいくとみなした場合の物理現象の形が３次スプライン曲線になる
以上が3次スプライン曲線がスプライン補間に用いられる理由になります。
もちろん利用する人によって、任意の次数のスプライン曲線を使うのはいいと思います。
しかし、曲線の形に意味をなさない3次以外の次数のスプライン曲線を使う場合は、その理由をしっかり認識して使うようにすることをお勧めします。
つづく
（その４）に続きます。