時系列逐次スプライン補間の実践（後編）

前回からの続きです。

４次多項式を使うことで逐次でデータ点を補間していくことができました。
しかし、３次スプライン曲線と大きく違う軌跡を描いてしまい、本当に意味のある補間になっているか、使い物になるか疑問です。

別のもっとよい逐次補間の方法はないでしょうか？

よいと思われる方法がありましたので、こちらを導出していきます。

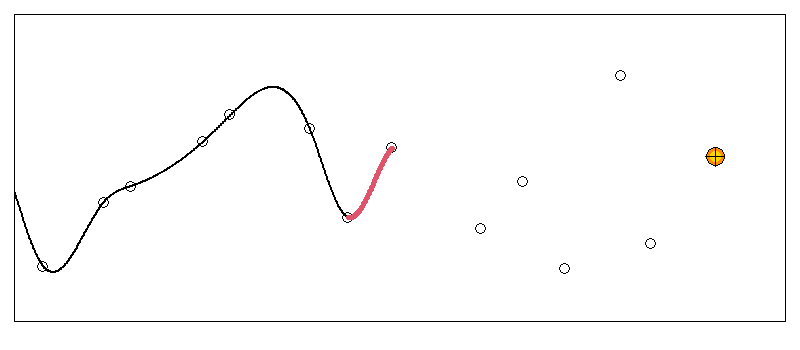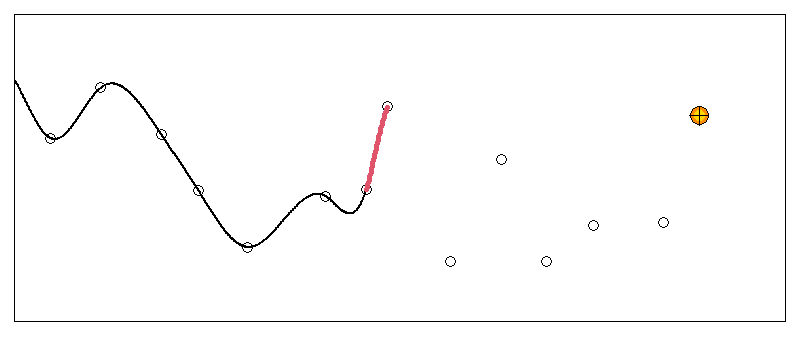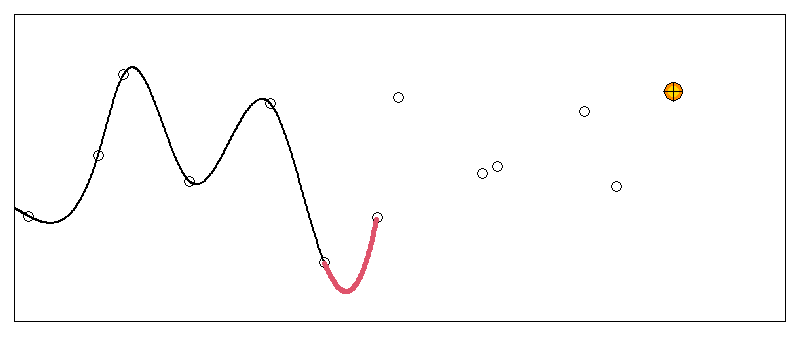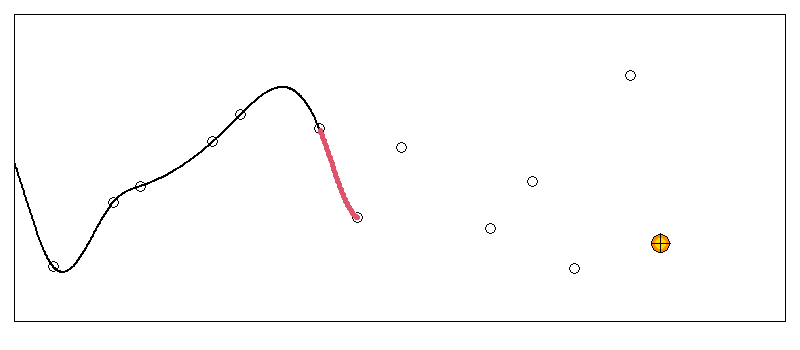
逐次スプライン補間方法の検討

データ点増加による区分曲線の変化

ひとつ疑問を解消しておきたいと思います。
データ点増加によって区分曲線がどう変化するのか、です。
逐次で補間曲線を求める場合、一回求めた過去の曲線を後で変更するわけにはいきません。
逐次補間していく場合、全体としてみれば求める対象の区分が次々と増えて大きくなっていくことを意味します。
全区間の連立方程式で求めるスプライン曲線において、逐次で対象範囲が広がっていく（連立させる方程式が増えていく）中で、過去の曲線はどう変化していくでしょうか？
それとも、曲線が変化するのは先頭の方だけで、そのうち変化はしなくなるのでしょうか？

曲線の形を決定しているのは各区間４つの係数なので、この係数がどう変化していくかを見れば、進んでいく先頭の影響度合いが分かります。
もし、先頭が進み曲線が長くなるにつれて、ある区間の各係数がある値に収束していくならば、その区間の曲線はある曲線に収束していくことになります。

ある区分 $j$ の係数が

\begin{eqnarray}
\lim_{n \rightarrow \infty} a_{n} &=& a \\
\lim_{n \rightarrow \infty} b_{n} &=& b \\
\lim_{n \rightarrow \infty} c_{n} &=& c \\
\lim_{n \rightarrow \infty} d_{n} &=& d \\
\end{eqnarray}

と収束するならば、区分 $j$ の区分曲線は

S_j(x) = a + b(x-x_j) + c(x-x_j)^2 + d(x-x_j)^3

に収束する。

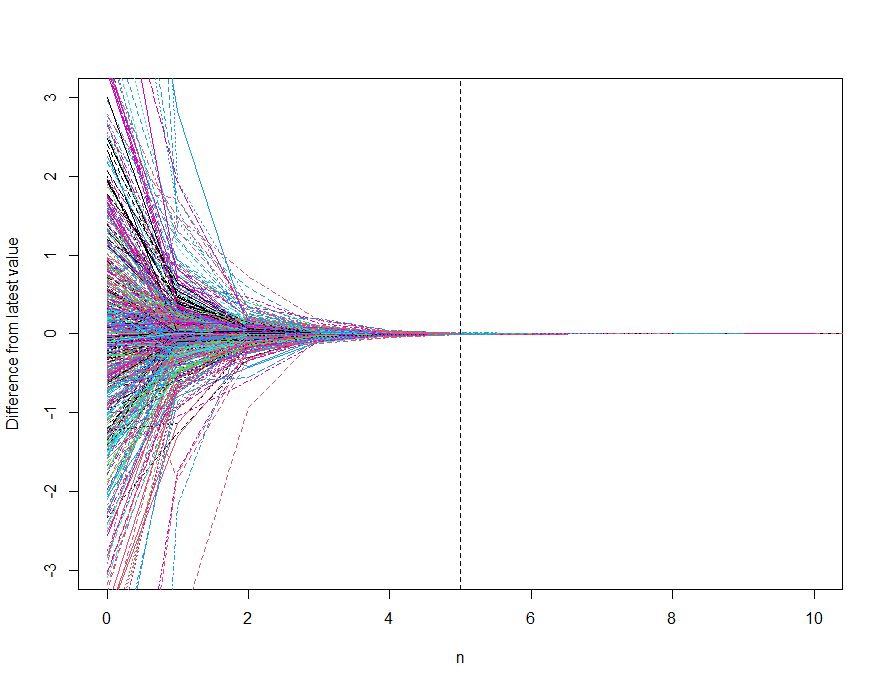
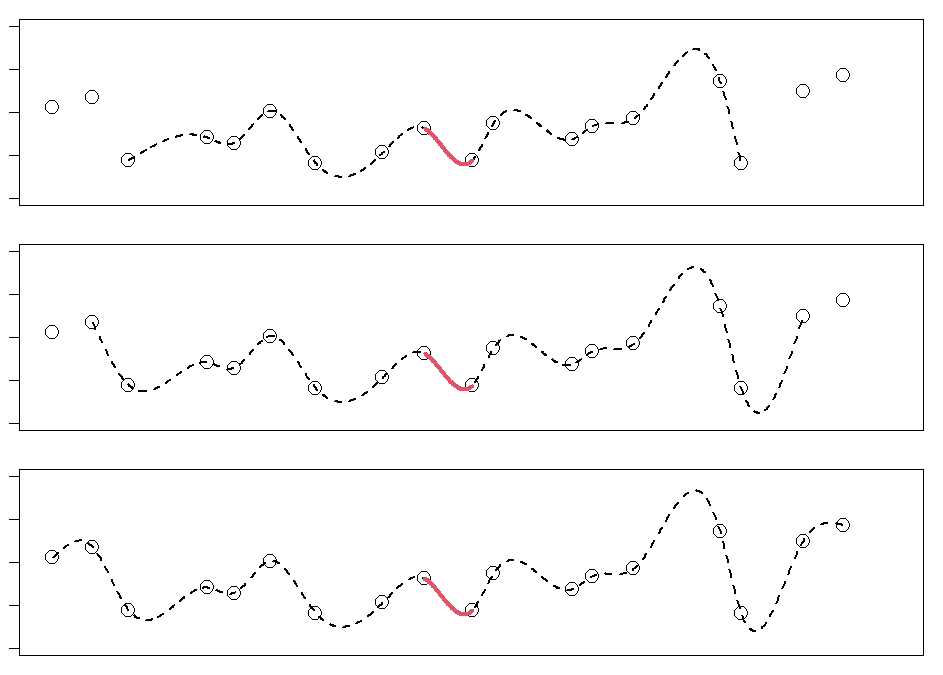
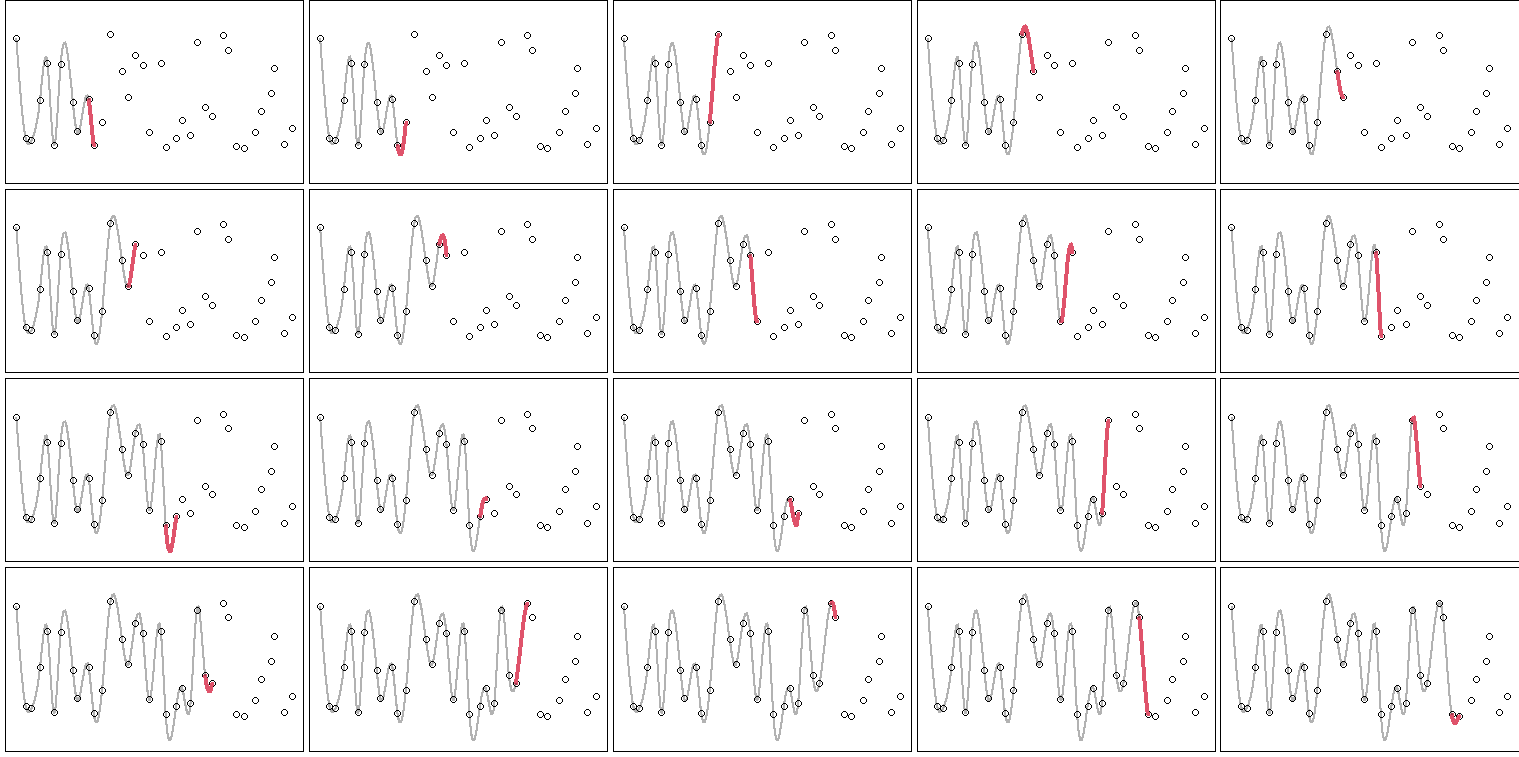
以下のグラフは、ある区間 $j$ の係数が、先頭が進むにつれ（先頭が区間 $j$ から離れるにつれ）収束するのか検証したグラフです。
先頭が進む（補間対象区間が増える）たびに係数の値を更新し、最新の係数値と過去の係数値との差を計算して、それをプロットしています。

a_n - a_{\textrm{latest}} \qquad (n=1,2,3,\cdots) \\
b_n - b_{\textrm{latest}} \qquad (n=1,2,3,\cdots) \\
c_n - c_{\textrm{latest}} \qquad (n=1,2,3,\cdots) \\
d_n - d_{\textrm{latest}} \qquad (n=1,2,3,\cdots)

サンプル数は係数 1000個 程度です。

この結果を見てみると、対象区間 $j$ が先頭から５点～６点離れると、係数がある値に収束し安定する様子が分かります。

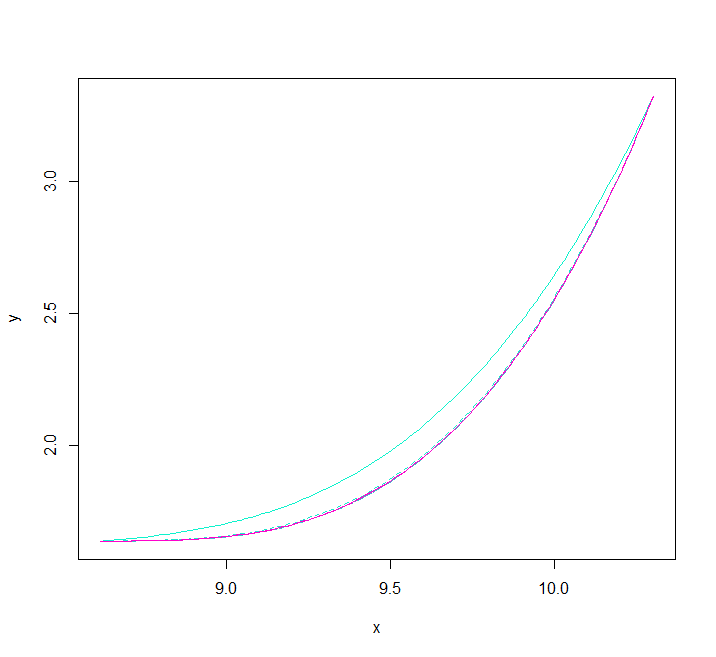
こちらは実際にある区間の曲線がどう変化していくか試してみた例です。
先頭から５，６点離れるまでの間に一つの曲線に収束しているのが分かります。

以上より、

　先頭から５，６点離れれば、以後その区分曲線はほとんど変化しない

と言えそうです。

本当は数式を用いてちゃんと証明するべきですが、$c_j$ の具体的な形があまりに複雑になりすぎて計算しきれませんでした。
上の説明でご容赦ください。

この区間を使った移動ウィンドウ法での継ぎ足し

区間が先頭から５，６点離れれば曲線が以後ほぼ変化しないことが分かりました。
これは進行方向に関して対称なので、先頭が左から右へ進んでいこうが右から左に進んでいこうが同じです。
ということは、始点終点両方から６点以上離れた区間の曲線はほぼ変化しないということが分かります。
結局、

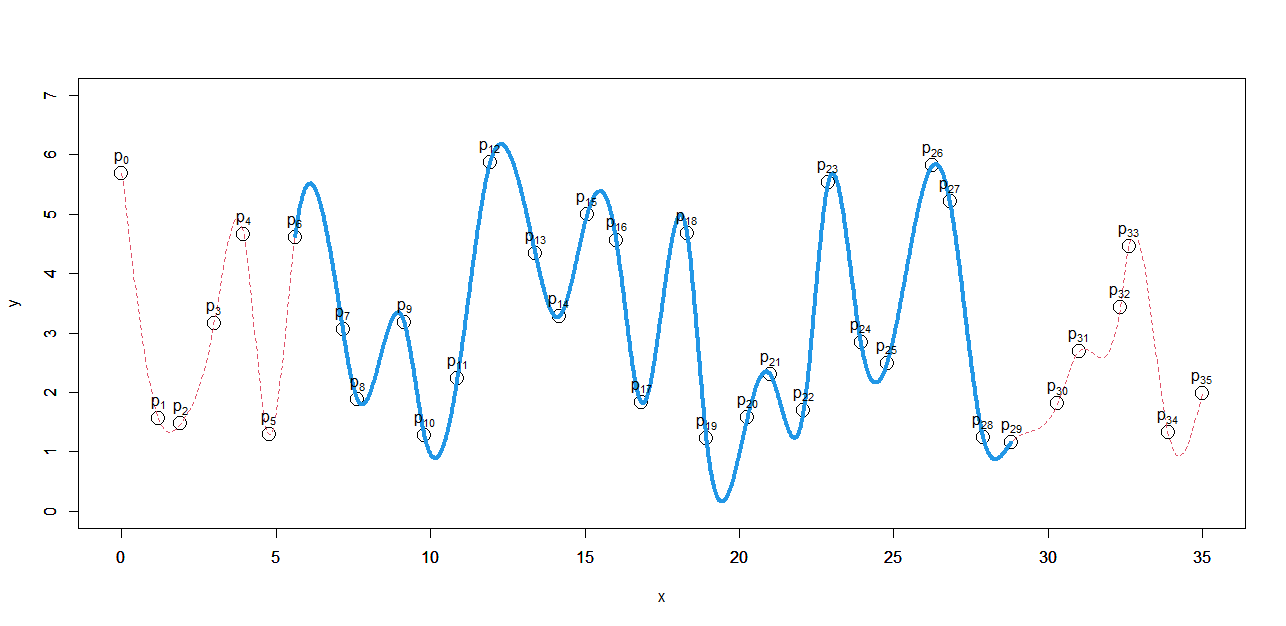
　データ点 $p_0 \sim p_{13}$ の14点からなるスプライン曲線の場合、区間 $p_6, p_7$ の曲線は、両端が伸びていったとしてもほぼ変わらない

ということになります。

それならば、このほぼ曲線が変わらない区間を継ぎ足していけばよいのでは ということを思いつきます。
この区分曲線が変わらないのであれば、その両端の１階、２階微分の値も変化しないからです。

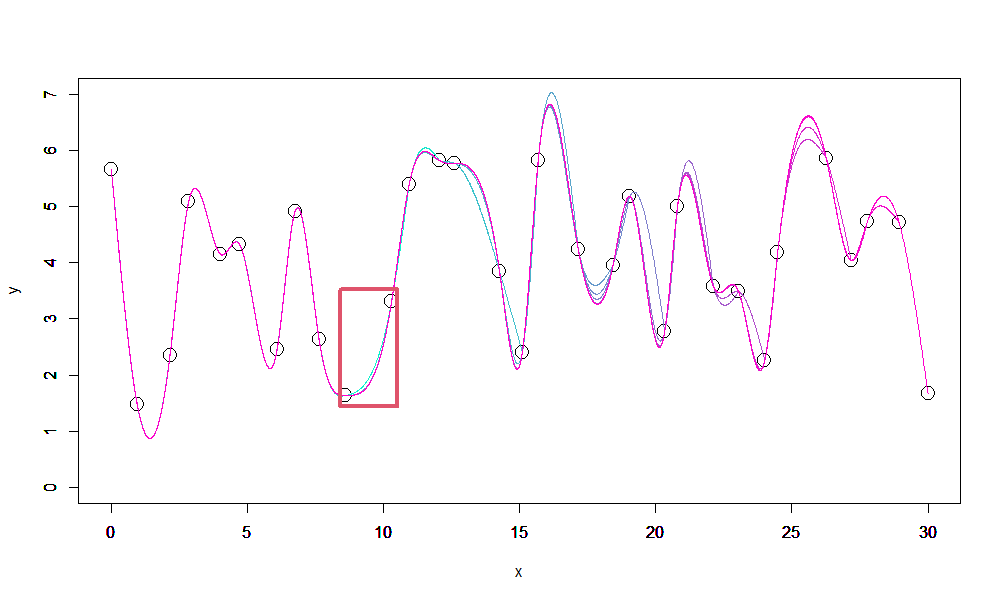
この考えを実践した結果が以下になります。

６点以上離れている場所を継ぎ足していっているので、境界も一致してなめらかにつながっているように見えます。
前回みたような進むにつれて発散することもなく、４次式での補間のように過度に振動もせず、正解の赤の点線（本来のスプライン曲線）ともよく一致していて良さそうです。

では実際の境界の微分値の結果を見てみると、以下になります。

	$\rightarrow p_7$	$p_7 \leftarrow$	$\rightarrow p_8$	$p_8 \leftarrow$	$\rightarrow p_9$	$p_9 \leftarrow$	$\rightarrow p_{10}$	$p_{10} \leftarrow$	$\rightarrow p_{11}$	$p_{11} \leftarrow$	$\rightarrow p_{12}$	$p_{12} \leftarrow$	$\rightarrow p_{13}$	$p_{13} \leftarrow$	$\rightarrow p_{14}$	$p_{14} \leftarrow$	$\cdots$
$S'$	-3.2867110	-3.2862700	-1.1449827	-1.1445190	-1.6879267	-1.6882950	-2.2944354	-2.2956519	3.3674375	3.3692887	1.8420173	1.8396776	-2.3568091	-2.3559635	0.3478689	0.3484986	$\cdots$
$S''$	0.5446150	0.5431533	8.5968471	8.5983871	-9.3130559	-9.3155097	7.4661166	7.4676293	3.2080283	3.2068739	-6.0860355	-6.0903801	0.3605590	0.3637246	6.7563737	6.7518267	$\cdots$

前後で値がほぼ近い値になっていますが、完全に一致はしていません。
残念ながら比較的小さいですが、データ点において不連続が発生していることになります。

非常におしいです。
このくらいの差は「誤差だ」と割り切ってしまうのも手かもしれませんが、ここはもう少し頑張ってみます。

あとひと手間です。

区分と区分の間にある区分曲線の求め方

前回、始点と終点の境界条件を設定しなければ、曲線が振動して値が発散していってしまうことを見ました。
では、始点と終点の境界条件が分かっている時、その間の区分曲線をどうやって求めたらいいでしょうか？
ここでそれを考えてみます。

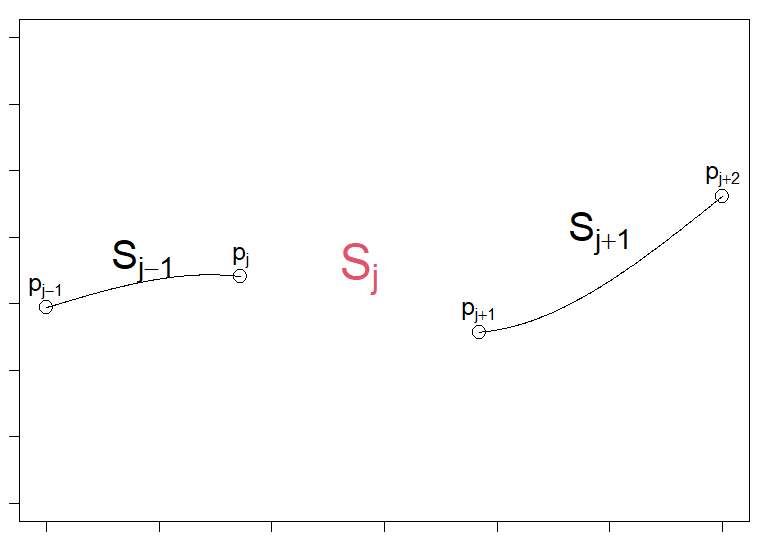
ある区分と区分の間にある区分曲線を求める方法について考えます。
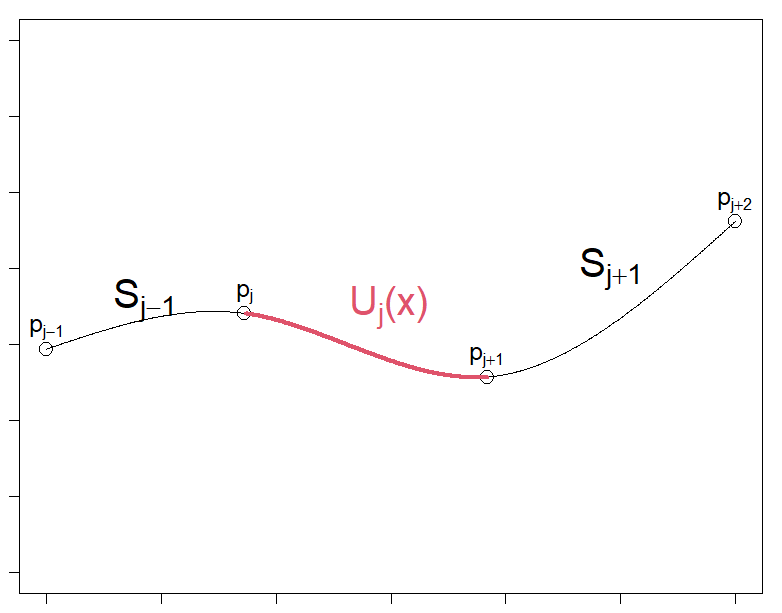
$S_{j-1}(x), S_j(x), S_{j+1}(x)$ と区分曲線があったとき、$S_j(x)$ を求める方法。
つまり、ある区分における始点と終点の１階、２階微分値が分かっている場合において、その区分の区分多項式 $S_j(x)$ をどう求めるかということです。

まず全区間一括でスプライン曲線を求めておきます。
区間 $j$ の区分多項式 $S_j(x)$ に着目し、この $S_j(x)$ を左右の $S_{j-1}(x), S_{j+1}(x)$ を使って復元することを考えます。

左右の　$S_{j-1}(x), S_{j+1}(x)$ が分かっているので、左右の $p_{j}, p_{j+1}$ における１階微分と２階微分の値が分かります。
その合計４つの微分値はそのまま境界条件になり、さらに両端の座標の条件を加えた合計６つの条件

\begin{eqnarray}
S_j(x_j) &=& y_j \\
S_j(x_{j+1}) &=& y_{j+1} \\
S_j'(x_j) &=& b_{j-1} + 2c_{j-1}(x_j - x_{j-1}) + 3d_{j-1}(x_j - x_{j-1})^2 \\
S_j'(x_{j+1}) &=& b_{j+1} \\
S_j''(x_j) &=& 2c_{j-1} + 6d_{j-1}(x_j - x_{j-1}) \\
S_j''(x_{j+1}) &=& 2c_{j+1} \\

\end{eqnarray}

これを満たす３次多項式を見つけることになります。
しかし、条件式が６つに対して３次多項式の求める係数（未知変数）の数は４つ。
削ることのできる条件式もないため、これは求解不能となります。

では、条件式６つに対して求解可能な多項式はというと、５次多項式になります。
５次多項式の係数は６つだからです。

では一旦３次多項式のことは忘れて、この６つの条件を満たす５次多項式を求めてみることにします。

U_j(x) = \alpha_j + \beta_j(x-x_j) + \gamma_j(x-x_j)^2 + \delta_j(x-x_j)^3 + \epsilon_j(x-x_j)^4 + \zeta_j(x-x_j)^5

として係数を求めることを考えると、

\begin{bmatrix}
1 & 0 & 0 & 0 & 0 & 0 \\
1 & \Delta x_{j} & {\Delta x_{j}}^2 & {\Delta x_{j}}^3 & {\Delta x_{j}}^4 & {\Delta x_{j}}^5 \\
0 & 1 & 0 & 0 & 0 & 0 \\
0 & 1 & 2{\Delta x_{j}} & 3{\Delta x_{j}}^2 & 4{\Delta x_{j}}^3 & 5{\Delta x_{j}}^4 \\
0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 2 & 6{\Delta x_j} & 12{\Delta x_j}^2 & 20{\Delta x_j}^3
\end{bmatrix}
\begin{bmatrix}
\alpha_j \\ \beta_j \\ \gamma_j \\ \delta_j \\ \epsilon_j \\ \zeta_j
\end{bmatrix}
=
\begin{bmatrix}
y_j \\
y_{j+1} \\
b_{j-1} + 2c_{j-1}{\Delta x_{j-1}} + 3d_{j-1}{\Delta x_{j-1}}^2 \\
b_{j+1} \\
2c_{j-1} + 6d_{j-1}{\Delta x_{j-1}} \\
2c_{j+1}
\end{bmatrix}

これを $XA=Y$として、

A = X^{-1}Y

とすれば解けます。
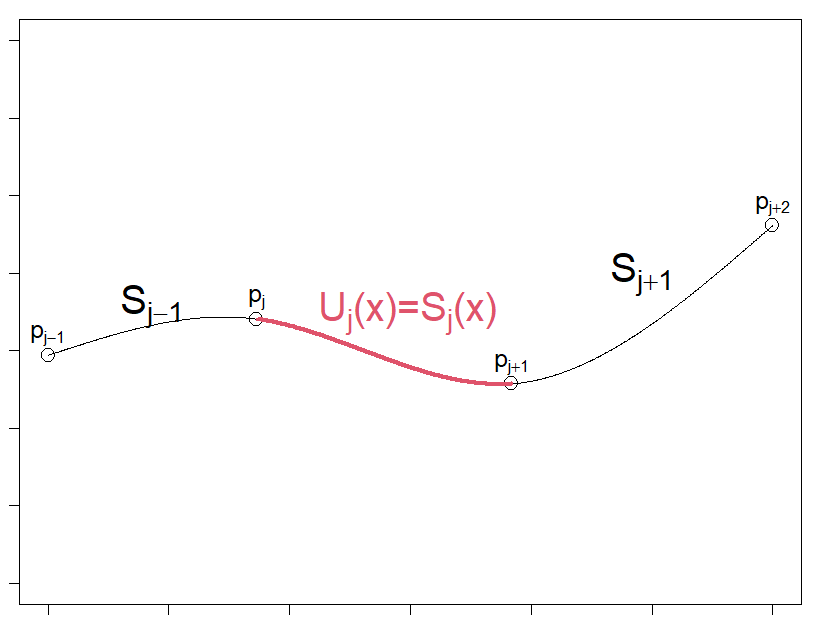
こうして求めた５次多項式 $U_j(x)$ は $S_{j-1}(x)$ と $S_{j+1}(x)$ の間に連続的にピッタリ接合して収まります。
両端の接合点において微分値も一致しています（そのように求めたので当然です）。
これで不連続はなくなりました。

では次にこの５次多項式 $U_j(x)$ と、本来ここにあるはずの３次多項式 $S_j(x)$ との関係がどうなっているかを調べます。

\begin{eqnarray}
S_j(x) &=& a_j + b_j(x - x_j) + c_j(x - x_j)^2 + d_j(x - x_j)^3 \\ 
U_j(x) &=& \alpha_j + \beta_j(x-x_j) + \gamma_j(x-x_j)^2 + \delta_j(x-x_j)^3 + \epsilon_j(x-x_j)^4 + \zeta_j(x-x_j)^5
\end{eqnarray}

$U_j(x)$ を求めるときに使用した６つの条件式は、当然そのまま $S_j(x)$ にも当てはまります。
なので、両端での境界条件の元では $U_j(x)$ と $S_j(x)$ をイコールで結ぶことができます。

\begin{align}
U_j(x_j) &=& S_j(x_j) \tag{1} \\
U_j'(x_j) &=& S_j'(x_j) \tag{2} \\
U_j''(x_j) &=& S_j''(x_j) \tag{3} \\
U_j(x_{j+1}) &=& S_j(x_{j+1}) \tag{4} \\
U_j'(x_{j+1}) &=& S_j'(x_{j+1}) \tag{5} \\
U_j''(x_{j+1}) &=& S_j''(x_{j+1}) \tag{6} \\
\end{align}

これをもとに２つの式の関係を求めます。
式(1)から(3)によって、

\begin{eqnarray}
\alpha_j &=& a_j \\
\beta_j &=& b_j \\
\gamma_j &=& c_j
\end{eqnarray}

が分かります。
次にこの結果と(4)から、

\small{
\begin{eqnarray}
\alpha_j + \beta_j{\Delta x_j} + \gamma_j{\Delta x_j}^2 + \delta_j{\Delta x_j}^3 + \epsilon_j{\Delta x_j}^4 + \zeta_j{\Delta x_j}^5 &=& a_j + b_j{\Delta x_j} + c_j{\Delta x_j}^2 + d_j{\Delta x_j}^3 \\
\delta_j + \epsilon_j{\Delta x_j} + \zeta_j{\Delta x_j}^2 &=& d_j \\
\\
\therefore \qquad (\delta_j - d_j) + \epsilon_j{\Delta x_j} + \zeta_j{\Delta x_j}^2 &=& 0 \\
\end{eqnarray}
}

同じく(5)(6)から、

\begin{eqnarray}
\beta_j + 2\gamma_j{\Delta x_j} + 3\delta_j{\Delta x_j}^2 + 4\epsilon_j{\Delta x_j}^3 + 5\zeta_j{\Delta x_j}^4 &=& b_j + 2c_j{\Delta x_j} + 3d_j{\Delta x_j}^2 \\
3\delta_j + 4\epsilon_j{\Delta x_j} + 5\zeta_j{\Delta x_j}^2 &=& 3d_j \\
\\
\therefore \qquad 3(\delta_j - d_j) + 4\epsilon_j{\Delta x_j} + 5\zeta_j{\Delta x_j}^2 &=& 0 \\
\end{eqnarray}

\begin{eqnarray}
2\gamma_j + 6\delta_j{\Delta x_j} + 12\epsilon_j{\Delta x_j}^2 + 20\zeta_j{\Delta x_j}^3 &=& 2c_j + 6d_j{\Delta x_j} \\
3\delta_j + 6\epsilon_j{\Delta x_j} + 10\zeta_j{\Delta x_j}^2 &=& 3d_j \\
\\
\therefore \qquad 3(\delta_j - d_j) + 6\epsilon_j{\Delta x_j} + 10\zeta_j{\Delta x_j}^2 &=& 0 \\
\end{eqnarray}

まとめると、

\begin{bmatrix}
1 & \Delta x_j & {\Delta x_j}^2 \\
3 & 4{\Delta x_j} & 5{\Delta x_j}^2 \\
3 & 6{\Delta x_j} & 10{\Delta x_j}^2
\end{bmatrix}
\begin{bmatrix}
\delta_j - d_j \\
\epsilon_j \\
\zeta_j
\end{bmatrix}
=
\begin{bmatrix}
0 \\ 0 \\ 0
\end{bmatrix}

これを解くと、

\begin{bmatrix}
\delta_j - d_j \\
\epsilon_j \\
\zeta_j
\end{bmatrix}
=
\begin{bmatrix}
0 \\ 0 \\ 0
\end{bmatrix}

となります。

結局、境界条件により導かれたのは、

\begin{eqnarray}
\alpha_j &=& a_j \\
\beta_j &=& b_j \\
\gamma_j &=& c_j \\
\delta_j &=& d_j \\
\epsilon_j &=& 0 \\
\zeta_j &=& 0
\end{eqnarray}

これら係数の関係は x に依存しないので $p_j, p_{j+1}$の区間中変わりません。
したがって、

\begin{eqnarray}
U_j(x) &=& \alpha_j + \beta_j(x-x_j) + \gamma_j(x-x_j)^2 + \delta_j(x-x_j)^3 + 0 + 0 \\
     &=& a_j + b_j(x - x_j) + c_j(x - x_j)^2 + d_j(x - x_j)^3 \\
     &=& S_j(x) \\
\\
\therefore \quad U_j(x) &=& S_j(x)
\end{eqnarray}

となります。

この結果から、区間両端の境界条件を満たす５次多項式を求めると、４乗、5乗の項の係数がゼロになり3次多項式が導かれるということが分かりました。
しかもこの導かれた３次多項式が $S_j(x)$ と一致します。

以上により、左右の区分多項式から、区間 $j$ の区分多項式を求める方法がわかりました。

３次元以上の空間へ適用する場合は一致させる微分量が増えるので、それに合わせて使用する多項式は５次より高次になります。
例えば３次元空間内の運動データに対する適用ならば、７次多項式を用いて４次区分多項式を求めることになります。
応用させてみてください。

Uj(x) と Sj(x) の一致度合い検証

$U_j(x)$ と $S_j(x)$ の関係に関しては上で導いた通りです。
しかし実際の数値計算上でもちゃんと一致するかは気になるところです。
確認しておきます。

まず、数値計算で求めた係数が上の理論通り

\begin{eqnarray}
\alpha_j &=& a_j \\
\beta_j &=& b_j \\
\gamma_j &=& c_j \\
\delta_j &=& d_j \\
\epsilon_j &=& 0 \\
\zeta_j &=& 0
\end{eqnarray}

となるのか確認します。

こちらは、実際に $S_j(x)$ と $U_j(x)$ を計算して比較してみた結果です。

	a	b	c	d	e	f
3次	5.4024785	0.9422687	0.2362082	-0.7563243	0.0000000	0.0000000
5次	5.4024785	0.9422687	0.2362082	-0.7563243	-4.440892e-16	1.998401e-15
3次	5.732618	-1.231726	-2.233502	1.474195	0.000000	0.000000
5次	5.732618e+00	-1.231726e+00	-2.233502e+00	1.474195e+00	-2.042810e-14	4.440892e-15
3次	4.1579827	3.2664245	0.1534735	-1.8144030	0.0000000	0.0000000
5次	4.157983e+00	3.266424e+00	1.534735e-01	-1.814403e+00	1.776357e-15	1.243450e-14
3次	1.600560	-1.724067	6.274893	-2.707002	0.000000	0.000000
5次	1.600560e+00	-1.724067e+00	6.274893e+00	-2.707002e+00	2.309264e-14	-4.662937e-15

理論通り、$a,b,c,d$ は一致していて、$\epsilon, \zeta$ はほぼゼロになっているのが分かります。
数値計算で行う関係上、丸め誤差などの影響で本当はゼロなのに数値的にゼロにならないことは当たり前に起こるので、これは理論通りゼロになっているとみなしてよいです。

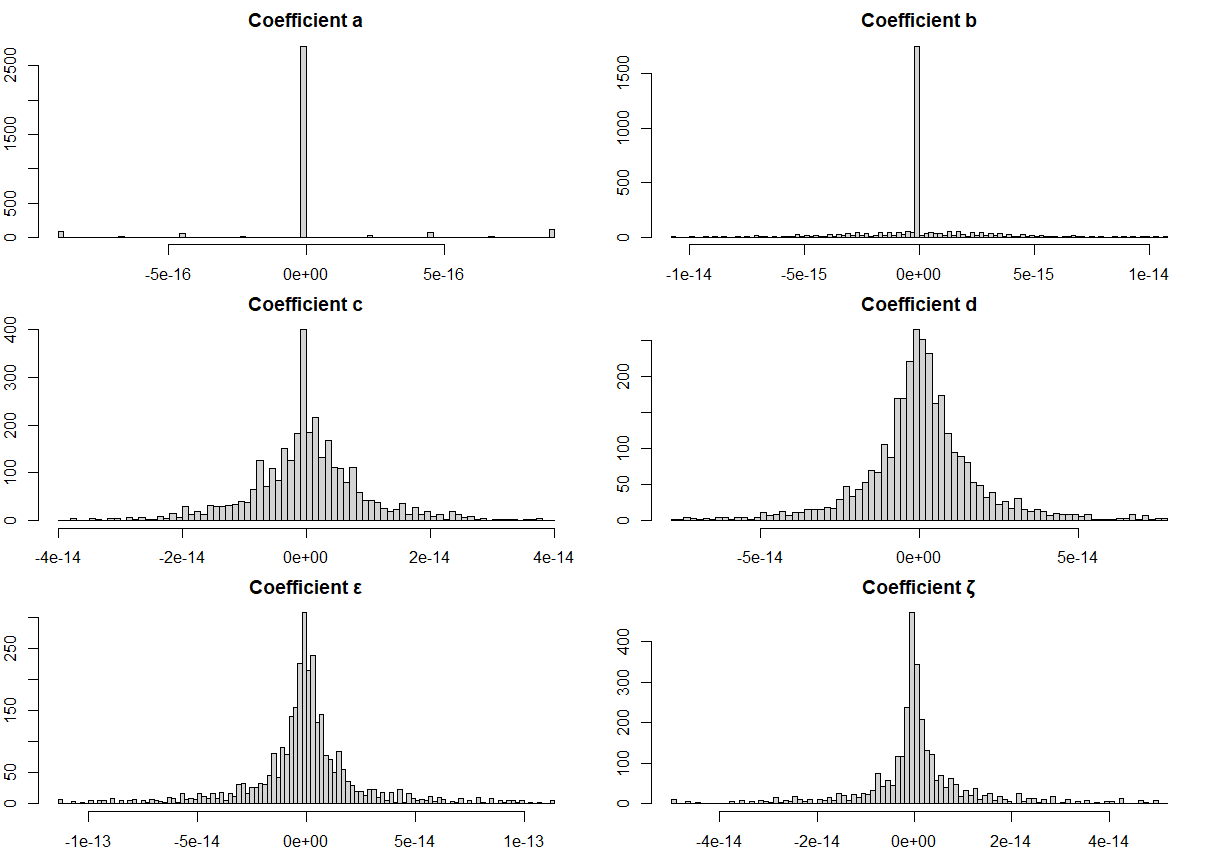
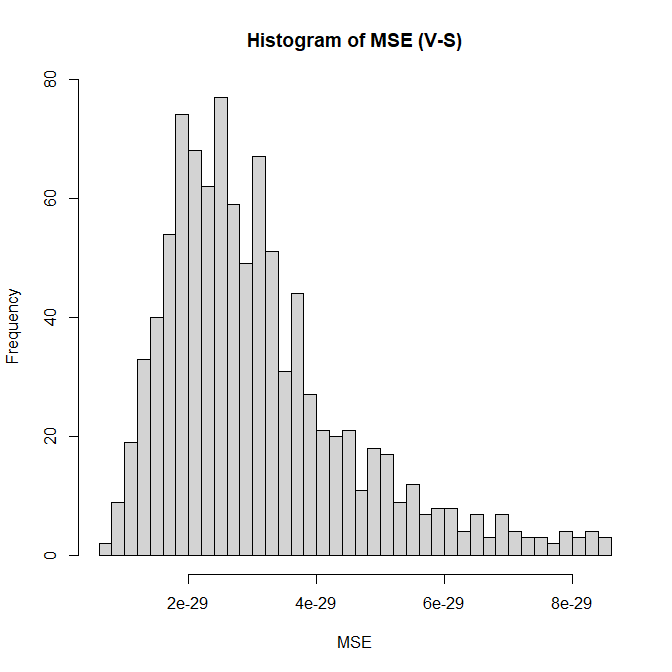
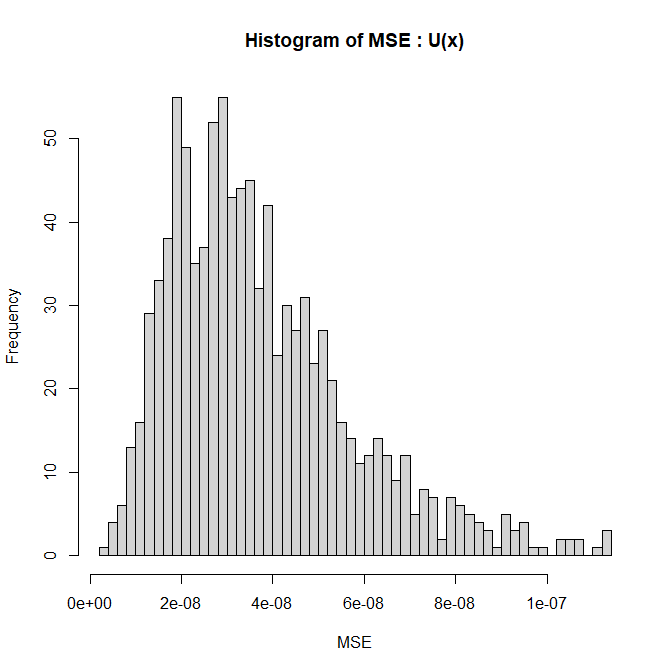
こちらのヒストグラムは、$U_j(x)$ と $S_j(x)$ を 3300組 求めて係数同士の差を計算した結果の分布です。
係数 $\epsilon$ と $\zeta$ は３次多項式では該当する係数がないので、ゼロと比較しています（つまり、$\epsilon, \zeta$ の係数値そのもの）。

見ての通り、一番大きくてもせいぜい $10^{-13} = 0.0000000000001$ のオーダーです。
$U_j(x)$ と $S_j(x)$ の係数が $10^{-13}$ の精度で一致していることが分かります。

次に曲線としてどれだけ一致しているか確認しましょう。

　１．　本来の区分多項式を $S_j(x)$
　２．　境界条件から求めた５次多項式を $U_j(x)$
　３．　$U_j(x)$ の下位４つの係数から作った３次多項式を $V_j(x)$

とします。

\begin{eqnarray}
S_j(x) &=& a_j + b_j(x - x_j) + c_j(x - x_j)^2 + d_j(x - x_j)^3 \\ 
U_j(x) &=& \alpha_j + \beta_j(x-x_j) + \gamma_j(x-x_j)^2 + \delta_j(x-x_j)^3 + \epsilon_j(x-x_j)^4 + \zeta_j(x-x_j)^5 \\
V_j(x) &=& \alpha_j + \beta_j(x-x_j) + \gamma_j(x-x_j)^2 + \delta_j(x-x_j)^3
\end{eqnarray}

この３つの曲線の一致度合いがどの程度かをみる為に以下を計算してみます。

\begin{eqnarray}
E_{US} &=& \frac{1}{x_b - x_a} \int_{x_a}^{x_b} (U_j(x) - S_j(x))^2 dx \\
E_{VS} &=& \frac{1}{x_b - x_a} \int_{x_a}^{x_b} (V_j(x) - S_j(x))^2 dx \\
\end{eqnarray}

関数の差の二乗をある範囲で積分して、その範囲の x の長さで割ります。
よく使われる平均二乗誤差（MSE）です。
数値計算で検証するので、実際の計算式はこっちでやります。

\begin{eqnarray}
E_{US} &=& \frac{1}{n} \sum_{i=0}^{n} \left ( U(x_i) - S(x_i) \right ) ^2 \\
E_{VS} &=& \frac{1}{n} \sum_{i=0}^{n} \left ( V(x_i) - S(x_i) \right ) ^2
\end{eqnarray}

結果は以下の通りです。

〇　$U_j(x) - S_j(x)$ のMSE結果

〇　$V_j(x) - S_j(x)$ のMSE結果

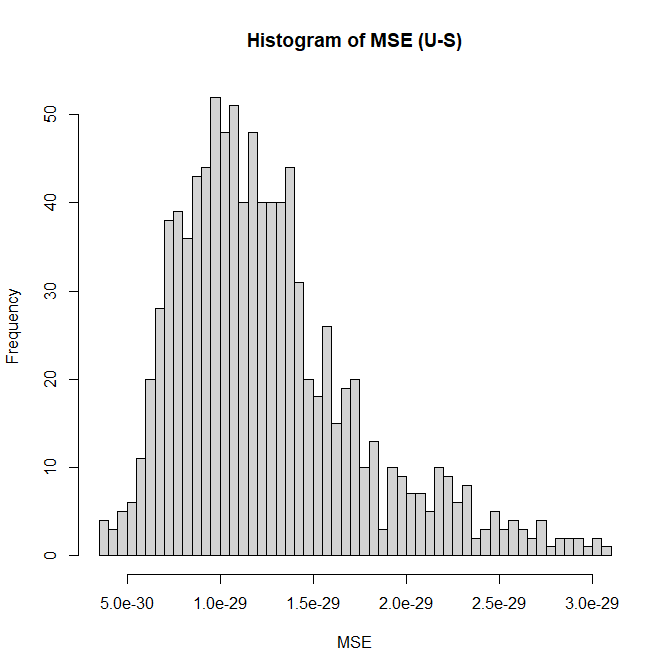
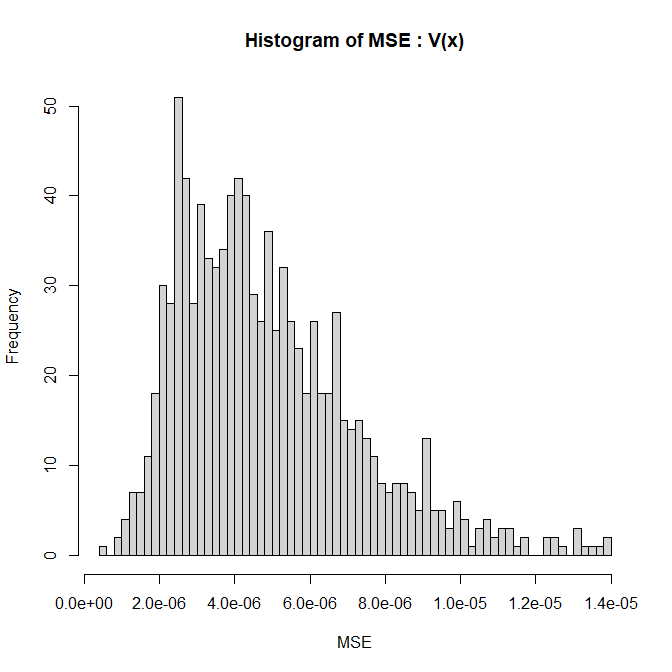
今度は補間点 1000点 の $S_j(x), U_j(x), V_j(x)$ を 33000組 求めて平均二乗誤差（MSE）を計算し、ヒストグラムにしています。

どちらもせいぜい $10^{-15}$ オーダーで一致していることが分かります。
$\sqrt{10^{-29}} \approx 10^{-15}$

若干 $U_j(x)$ の方が一致精度が高いようですが、どちらでも問題なさそうです。
数値誤差が気になる場合は、５次多項式の $U_j(x)$ で補間するとよいと思います。
その場合でも、理論的には３次多項式と同一なので問題ありません。

これで、５次多項式を用いて３次の区分多項式を求める前述の方法の妥当性を確かめることができました。

逐次スプライン曲線の求め方

以上で準備は終わりました。
分かったことを組み合わせることで、逐次スプライン曲線を求めていくことができます。

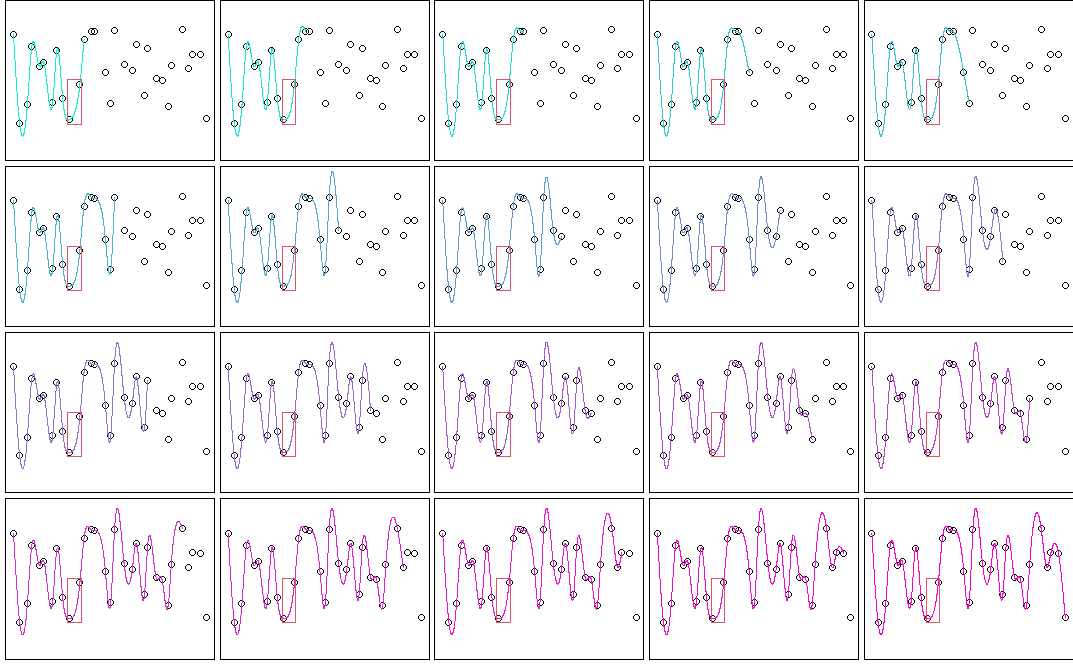
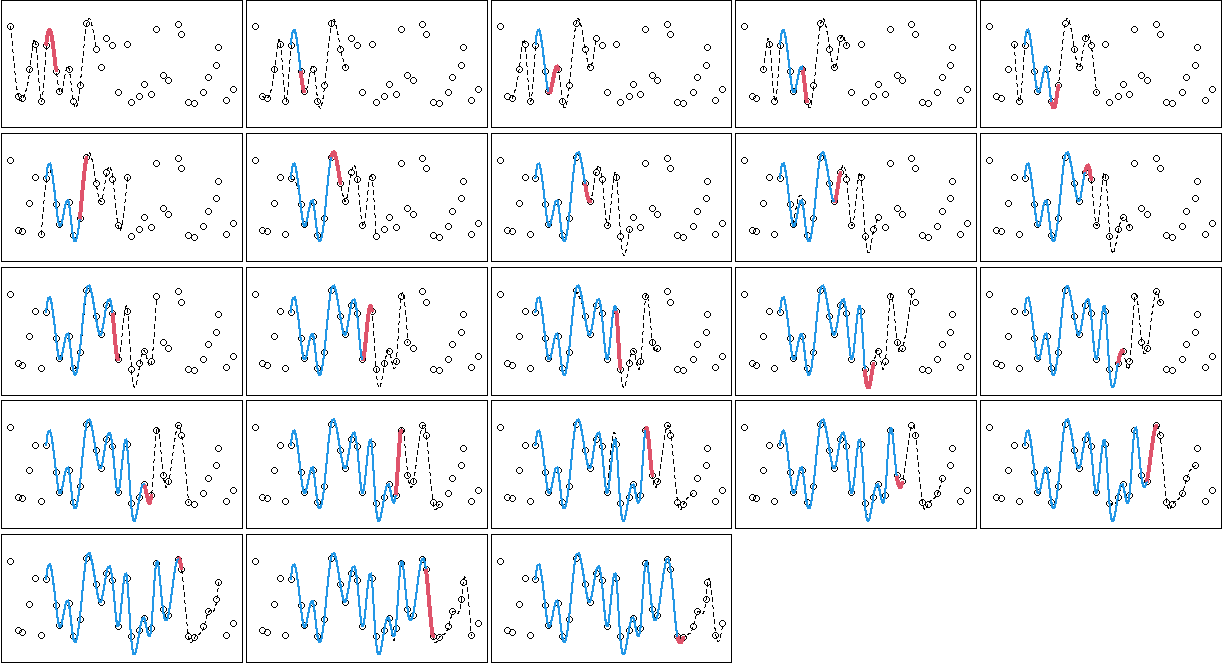
Step. 1

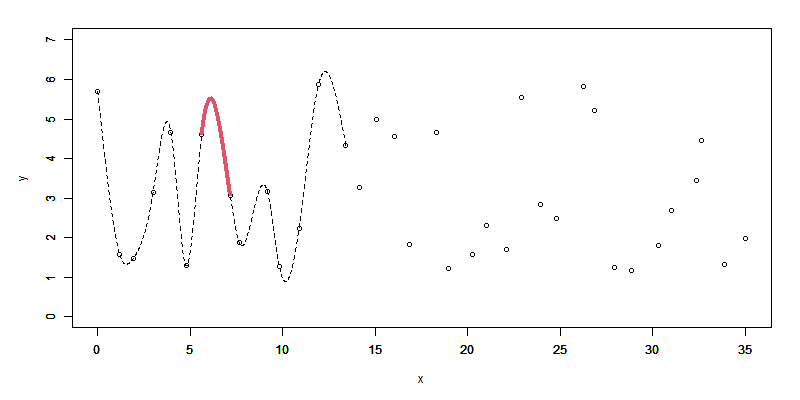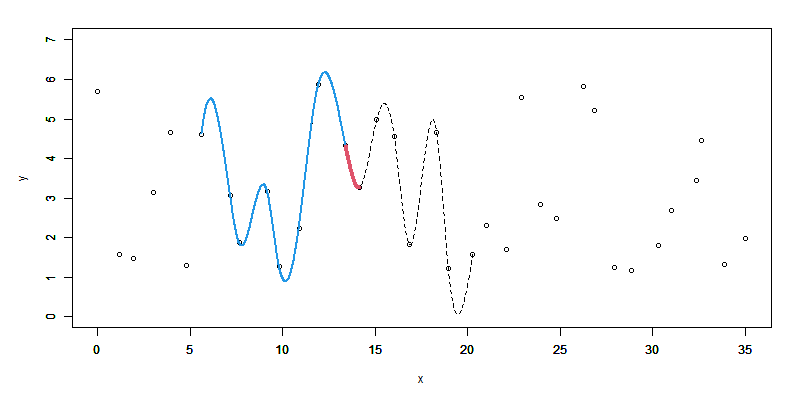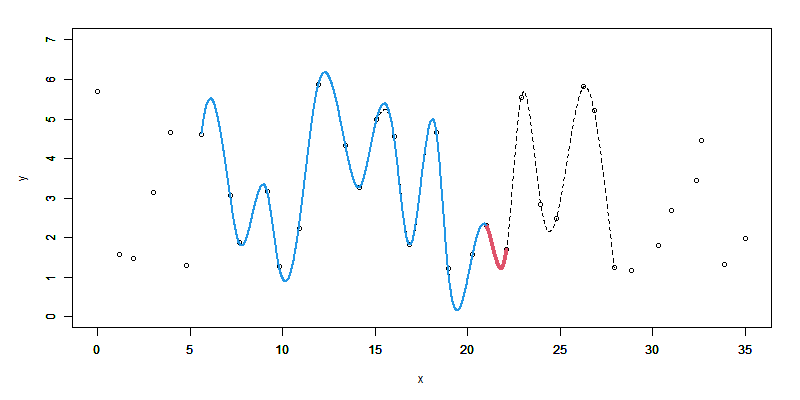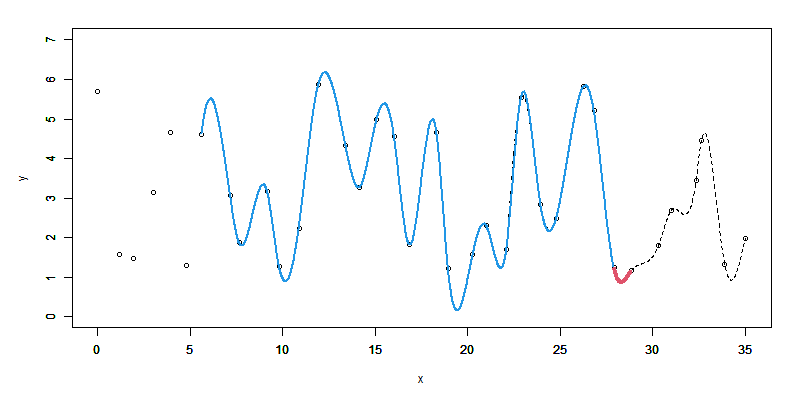
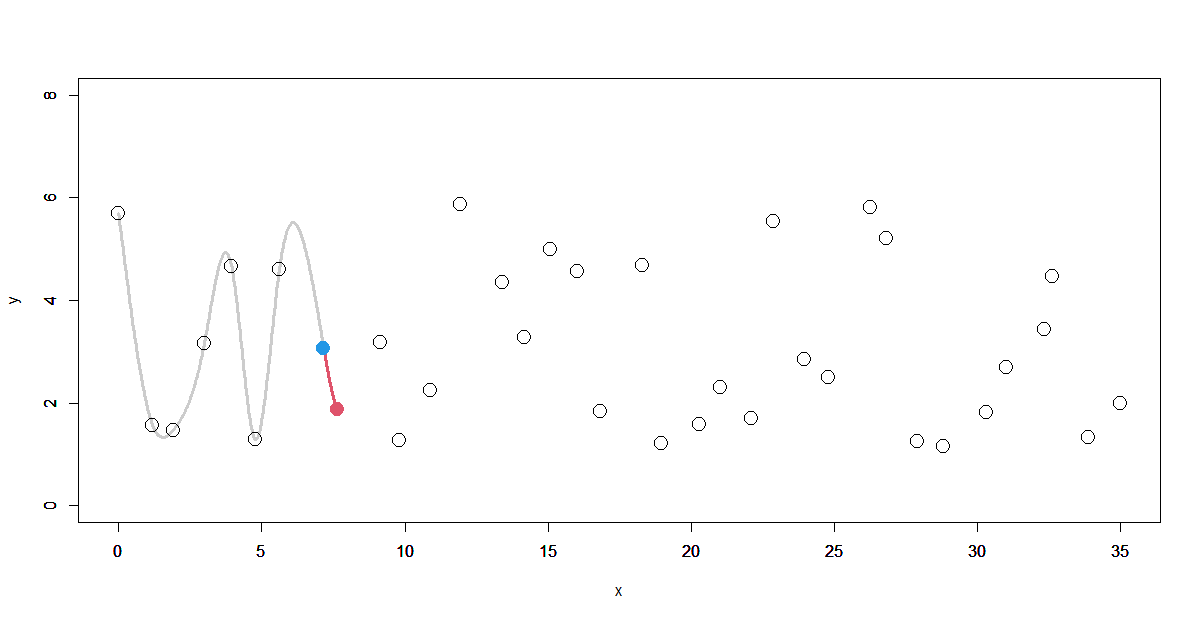
まず先頭から12点以上のデータ点でスプライン曲線を求めます。

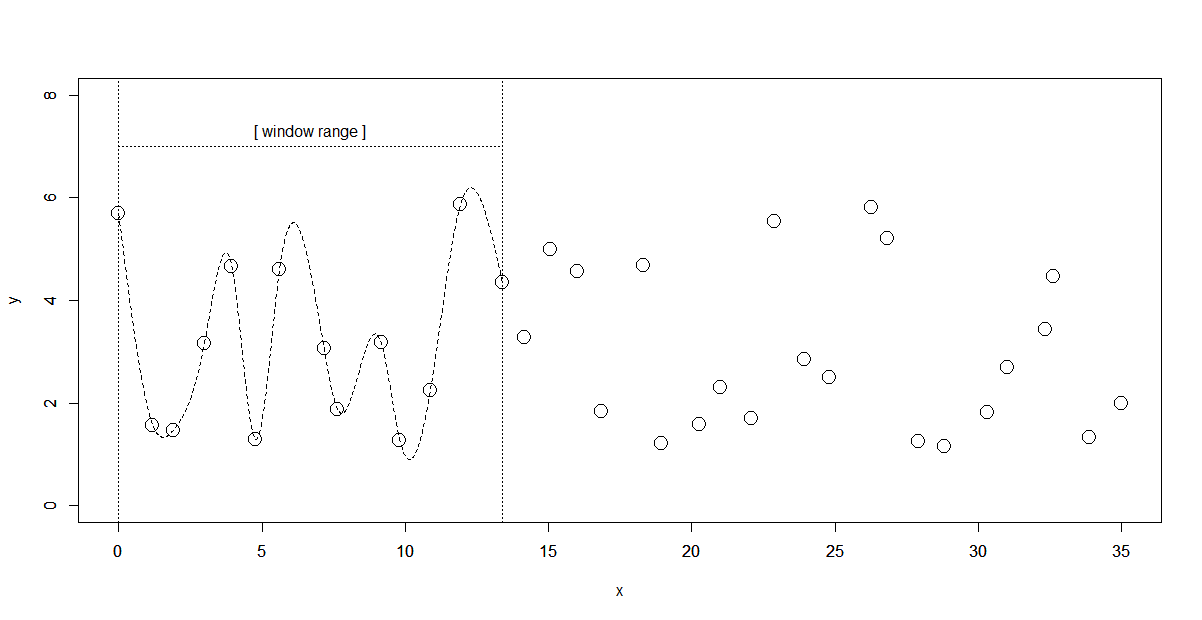
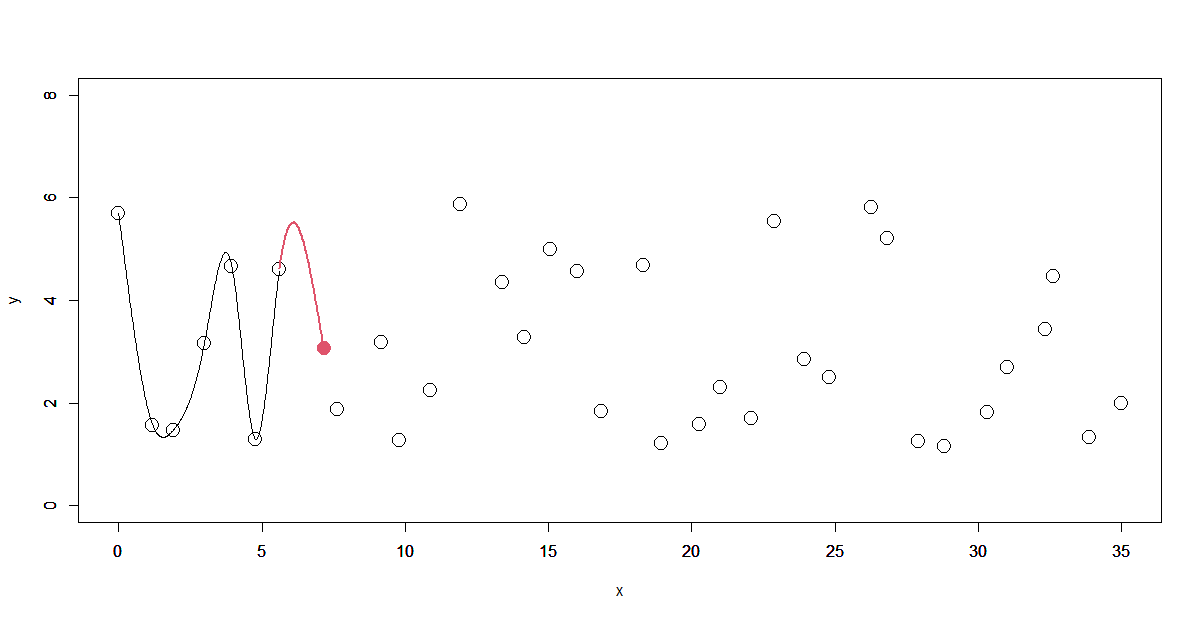
ここでは前半をそのまま使うことにします。
先頭から６区間以上離れた区間を逐次で継ぎ足す最初の区間と定めて（赤線の区間）、その区間終点の１階、２階微分値を求めます（赤のデータ点）。

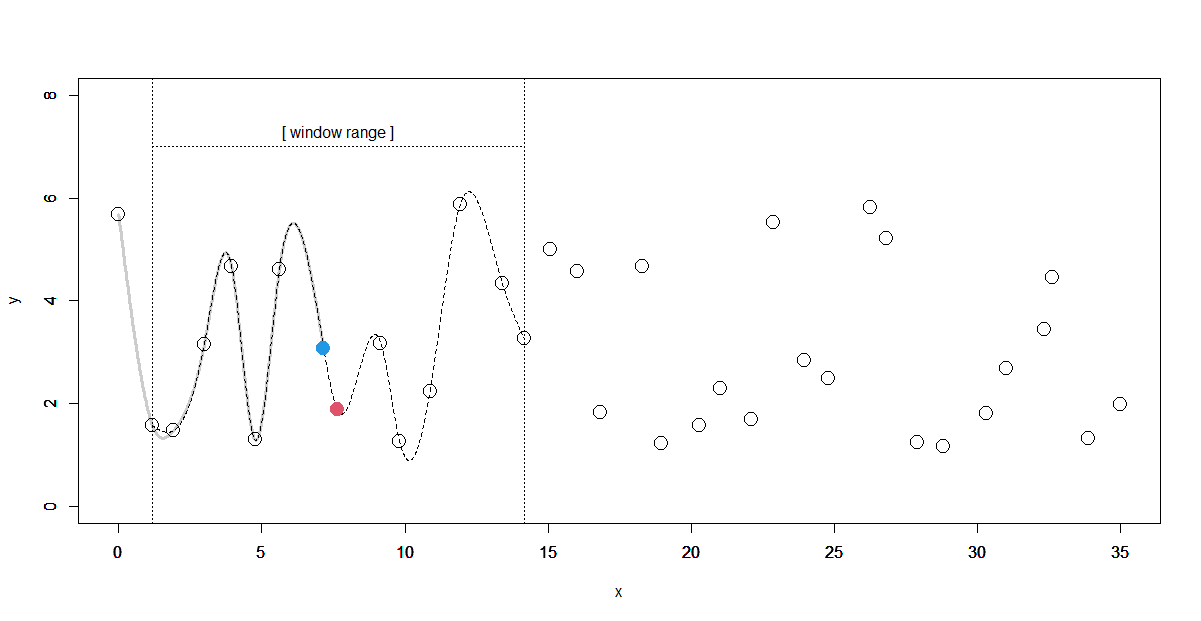
Step. 2

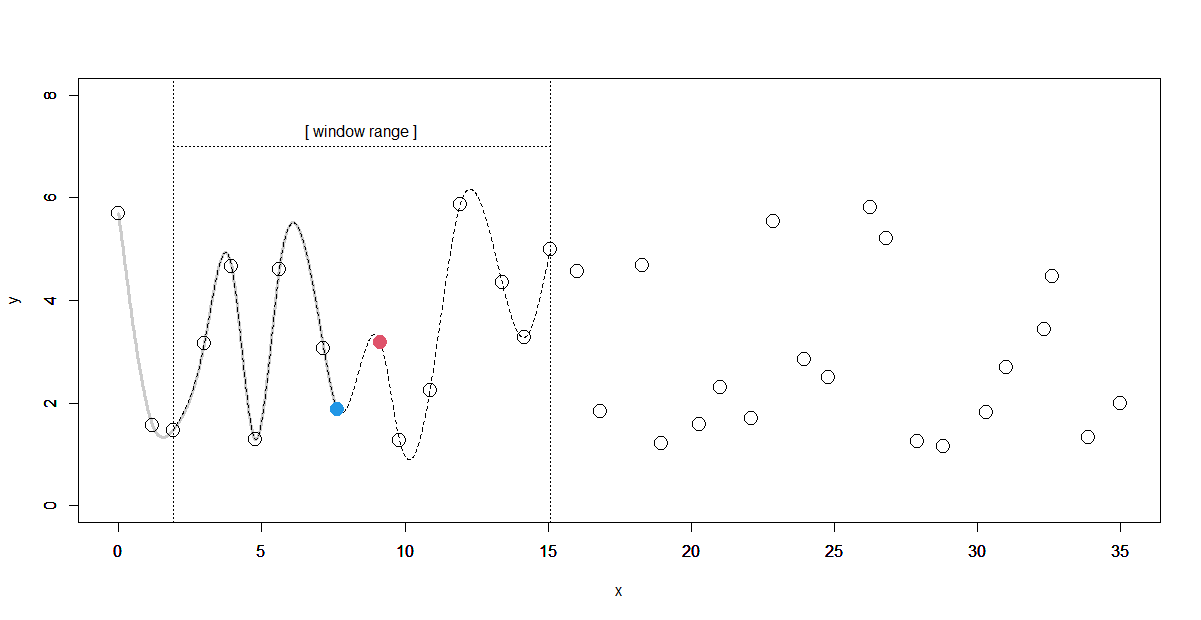
ウィンドウ区間（ここでは14点）を１つずらして、スプライン曲線を求めます。
そして、次に継ぎ足す区間の終点の１階、２階微分値を求めます。
（１回前に求めたデータ点が青、今回求めるデータ点は赤）

Step. 3

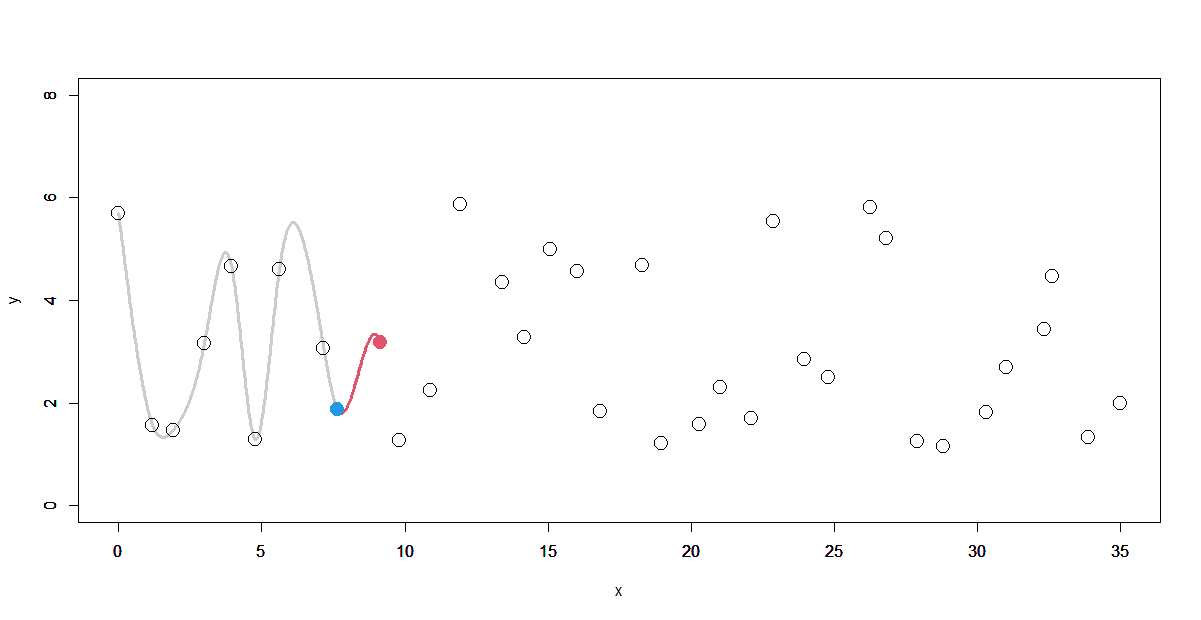
求めた区間前後の微分値（青と赤のデータ点の４つの微分値）と２点の y の値を使って５次多項式の係数を求めます。

\scriptstyle{
\begin{bmatrix}
1 & 0 & 0 & 0 & 0 & 0 \\
1 & \Delta x_{j} & {\Delta x_{j}}^2 & {\Delta x_{j}}^3 & {\Delta x_{j}}^4 & {\Delta x_{j}}^5 \\
0 & 1 & 0 & 0 & 0 & 0 \\
0 & 1 & 2{\Delta x_{j}} & 3{\Delta x_{j}}^2 & 4{\Delta x_{j}}^3 & 5{\Delta x_{j}}^4 \\
0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 2 & 6{\Delta x_j} & 12{\Delta x_j}^2 & 20{\Delta x_j}^3
\end{bmatrix}
\begin{bmatrix}
\alpha \\ \beta \\ \gamma \\ \delta \\ \epsilon \\ \zeta
\end{bmatrix}
=
\begin{bmatrix}
y_j \\
y_{j+1} \\
b_{j-1} + 2c_{j-1}{\Delta x_{j-1}} + 3d_{j-1}{\Delta x_{j-1}}^2 \\
b_{j+1} \\
2c_{j-1} + 6d_{j-1}{\Delta x_{j-1}} \\
2c_{j+1}
\end{bmatrix}
}

係数 $\alpha, \beta, \gamma, \delta$ を使って、区分多項式 $S(x)$ を作り、継ぎ足し区間を補間します。

S_j(x) = \alpha + \beta(x-x_j) + \gamma(x-x_j)^2 + \delta(x-x_j)^3

求めた係数すべてを使って５次多項式で区間を補間してもよいです。
$\epsilon=0, \zeta=0$ のはずなので、同じ結果が出るはずです。

実際の計算には５次式の

U_j(x) = \alpha + \beta(x-x_j) + \gamma(x-x_j)^2 + \delta(x-x_j)^3 + \epsilon(x-x_j)^4 + \zeta(x-x_j)^5

を使った方が全体の精度は良くなります。
詳しくはこの先に書きました。

Step. 4 以降

以後、同じことの繰り返しです。

　〇　ウィンドウ区間をひとつずらしてスプライン曲線を求め
　〇　次の継ぎ足し区間の終点の微分値を求め
　〇　区分多項式を求めて補間する

です。

続き

これで、逐次でスプライン曲線を求めることができるようになりました。
目的を達成することができました。

逐次で求めたスプライン曲線の妥当性

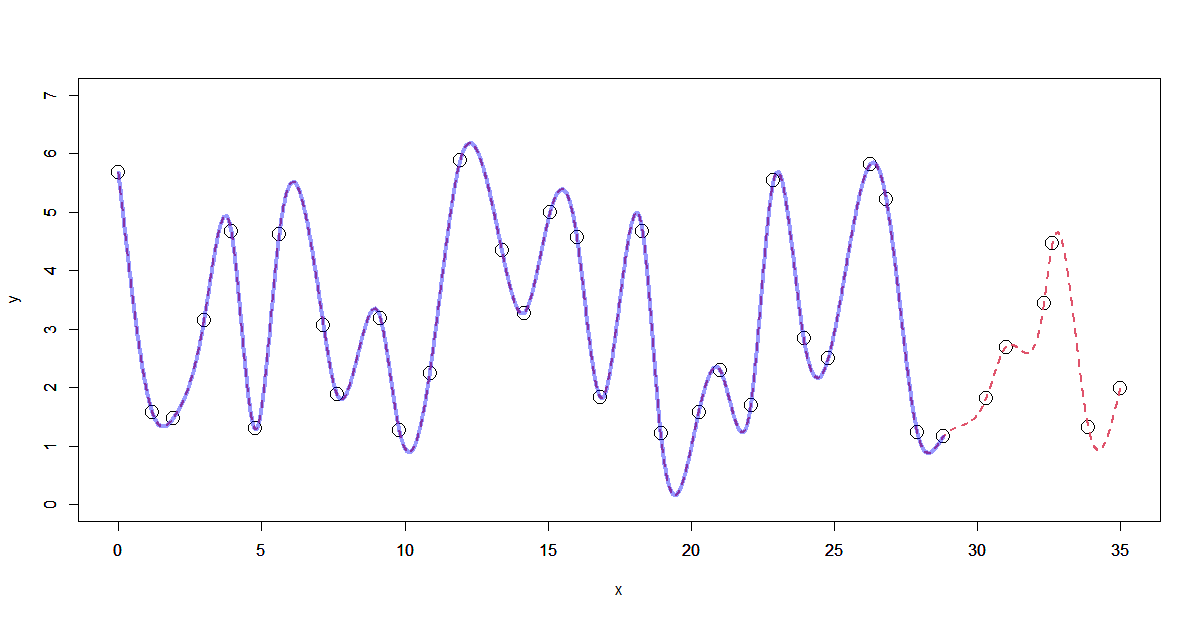
この方法で求めた逐次のスプライン曲線と、全体を一括で求めた本来のスプライン曲線との違いを確認してみます。

先ほどの例において比べたグラフが以下です。

赤い点線が本来の一括で求めたスプライン曲線、青い線が上の方法で逐次で求めたスプライン曲線です。
目視では完全に一致しているように見えます。

ここで改めて、

　青の逐次のスプライン曲線を $U(x)$
　赤の本来のスプライン曲線を $S(x)$

とおきます。
今度は区分多項式ではなく、つなぎ合わせた全体を $U(x), S(x)$ としています。
そして、どのくらい一致しているのかをみる為に以下を計算してみます。

E = \frac{1}{x_b - x_a} \int_{x_a}^{x_b} (U(x) - S(x))^2 dx

区分多項式の検証の時に使った平均二乗誤差（MSE）です。
先とおなじく実際の数値計算の式はこちらです。

E = \frac{1}{n} \sum_{i=0}^{n} \left ( U(x_i) - S(x_i) \right ) ^2

これでわかることは、逐次で求める事による影響の度合いです。
厳密には先頭が進むたびに過去の曲線もそれに従い変化します。
$S(x)$ は常に最新の正しい曲線であり、$U(x)$ は過去分の変化がない履歴の積み重ねの曲線です。
先頭が進むことによって過去分含め全体の曲線が大きく変わるようなことがあれば、$S(x)$ と $U(x)$ の乖離は大きくなりMSEの値が大きくなります。
逆に過去分の曲線に大きな変化がなければ、MSEの値は小さくなります。
過去分を変更できない（過去の曲線が変わってしまっては困る）時系列逐次処理に使う場合には非常に重要な確認事項です。

結果はこうなりました。

これは 31点 のデータ点に対して、補間点 1000点 の $U(x)$ と $S(x)$ を 1000組 求め、上の式のMSEを計算し、ヒストグラムにしたものです。

　平均値：3.732669e-08
　中央値：3.305561e-08

でした。
大きくても $10^{-4} = 0.0001$ の範囲で一致しました。

上の方法を用いて逐次で求めたとしても、更新された最新の範囲で一括して求める本来のスプライン曲線との差はほぼない、つまり $U(x)$ と $S(x)$ はほぼ一致しているということが示されました。

この結果を見る限り、この逐次スプライン曲線を求める方法は、全体一括でスプライン曲線を求める本来の方法と ほとんど同一の曲線を得ることができる と言っていいかと思います。

この方法の妥当性が示されたと思ってよさそうです。

尚、この結果は５次多項式での補間をつなぎ合わせた $U(x)$ で行いました。
５次多項式の下位４係数を使ってつくる３次多項式 $V_j(x)$ をつなぎ合わせた $V(x)$ との比較に関しては以下になりました。

　平均値：4.882871e-06
　中央値：4.387751e-06
　一致の程度：0.001 (1.0e-3)

と $U(x)$ の時より若干成績が悪くなりました。
これは丸め誤差などの数値計算によるズレが積み重なった結果だと思われます。

なるべく本来のスプライン曲線に近づけたいなら、計算上は高次係数は捨てずに５次多項式で補間を行った方がよさそうです。

おわり

以上が、逐次でのスプライン補間実施の検討結果と実施手法です。
今回の手法で逐次補完した一例がこちらです。

どうだったでしょうか？
時系列解析などで、逐次データ処理などに役立てて頂ければ幸いです。

間違いなどありましたらご指摘下さればありがたく思います。
また、感想など頂けたら励みになります。

読んで頂きありがとうございました。

また次の話題でお会いできればと思います。