本題
これは、ResNetについて考察した4本立て(序、破、Q、:||)の一記事です。
というわけで、前回の続きなのですが、前回は、
第一回で定義した疑問
- 研究者がどうやってこの残差ブロックのアイディアに至ったのか
- そもそもなぜ残差を学習するのか
- なぜResNetが(数学的に)高精度を達成できるのか
の疑問とは少し離れて、ResNetと勾配ブースティングのアンサンブル学習との相関についてより詳しく考察しました。
今回は、
- THE LOSS SURFACE OF RESIDUAL NETWORKS: ENSEMBLES & THE ROLE OF BATCH NORMALIZATION
-
Functional Gradient Boosting based on Residual Network Perception (ラスボス)
を読み込んでいきます。ただし、この2つは正直自分のキャパオーバーや勉強がまだ足りないこともあり、
うまく説明できないことも多いと思います。ただ、自分が理解した範囲で、できるだけわかりやすく説明できるようにがんばります。
そもそもこの一連の勉強は、ResNetと勾配ブースティングってどちらも残差学習だよなぁ、なにか関連性でもあるのかな
と考えたことがきっかけでした。
それを調べていった際、最後の核心とも言える論文が2018年に出ている -
Functional Gradient Boosting based on Residual Network Perception (ラスボス)
であり、著者が日本人の研究者だったということがなんとも嬉しかったです。私の理解はまだまだですが、少しでもこの人たちに近づけるように頑張りたいです!!
まず、LittwinさんらによるTHE LOSS SURFACE OF RESIDUAL NETWORKS: ENSEMBLES & THE ROLE OF BATCH NORMALIZATIONですが、一番驚いたことは理論物理(自分のバックグラウンド)でよく出てくるハミルトニアンが出てきたことです。スピングラスモデルの物理系がまさか機械学習の論文で出てくるとは思いませんでした。もっと勉強しようと思います。

この論文で議論されているのは、ResNetモデルのロス関数がアンサンブル学習という側面からどういう挙動をしているのか、ということです。
この際にスピングラスモデルのハミルトニアンを導入することによって、ResNetモデルの物理系を記述しています。
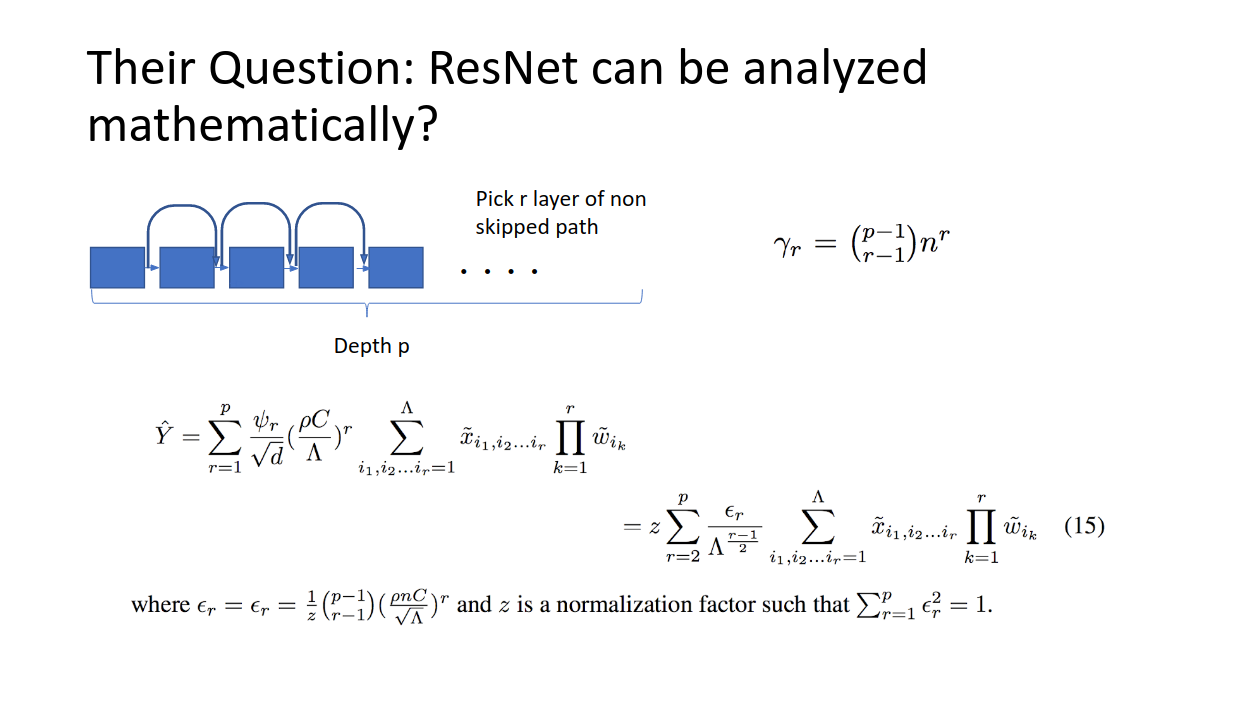
たとえば、残差ブロックp−1個の積み重ねでできたResNetがあったとして、物理系の経路を考えます。p−1個のネットワークから、r−1回だけショートカットしない、という選択を取ったとき、その系のとる経路の長さがgammaで書かれています。これから(15)までの導出は完全には追えませんが、結論を言うとYはResNetの推論値です。
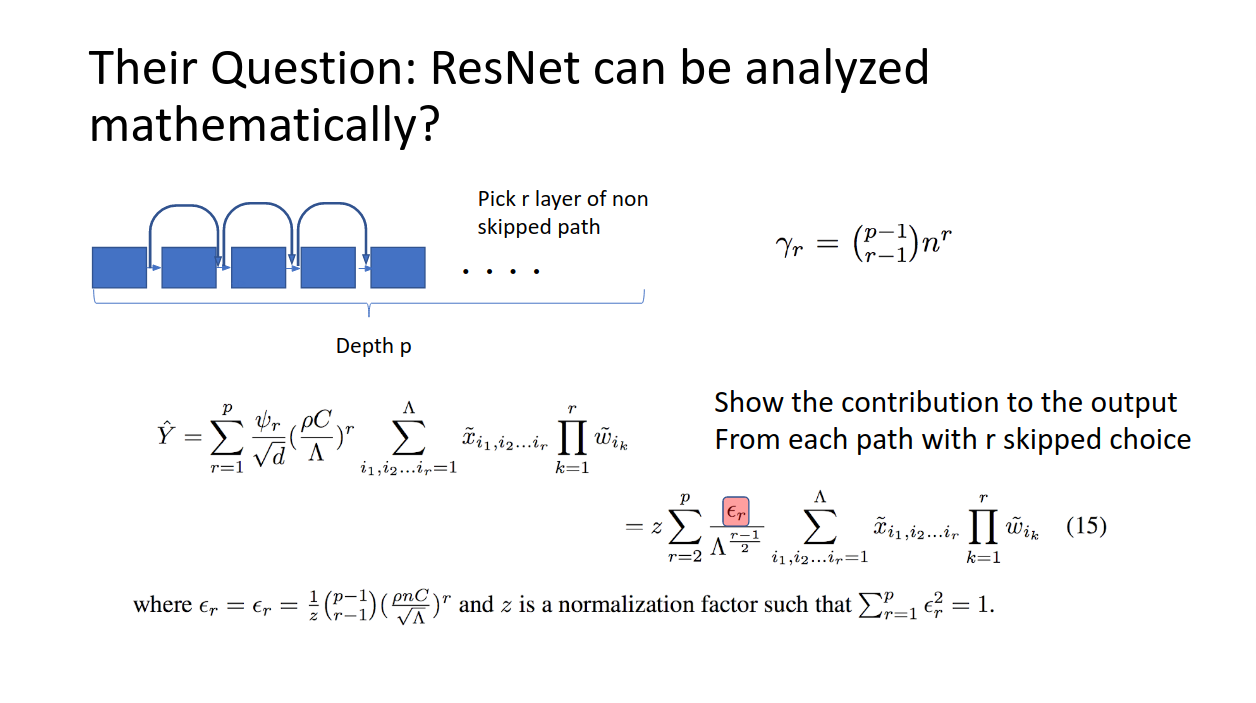
ここでe_rが右辺に現れていますが、これはベクトルで、r回スキップしなかった経路の、推論への寄与度を表しています。
ここが大事なので付け加えると、例えばe_0がめちゃくちゃ大きいとすると、一回もスキップしなかった経路長の長いネットワークが、出力にめちゃくちゃ寄与している。逆にe_100が大きいと、スキップをしまくった経路長の短いネットワークが最後の推論に大きく寄与している。ということです。

先程出てきた、経路長の違うネットワーク毎の推論への寄与ですが、(18)式のパラメータに左右されることがわかります。nはここでは残差ブロックの幅の大きさなのですが、p(つまり全体のネットワークの深さ)が定数であるとき、幅nが大きくなれば、e_rはr=pで最大となります。
つまり、この条件下では推論、及びロス関数は最大経路長のネットワークに支配され、スキップを行った残差接続されたネットワークの寄与が殆どないということです。

しかしながら、betaが定数で、大きなp(つまり全体のネットワークが非常に深いとき)では、e_rはr<pで最大値を取ります。つまり、ショートカットしたネットワークの寄与が大きくなるということです。

このbetaやpによって、どの経路長のネットワークがアンサンブルにおいてロス関数に寄与するのかが変動する。ということが驚きですね。。
また、よく見てみるとbetaにでてくるCによってbetaが変わる、つまり支配的経路長も変わるなあ、ということが見て取れます。
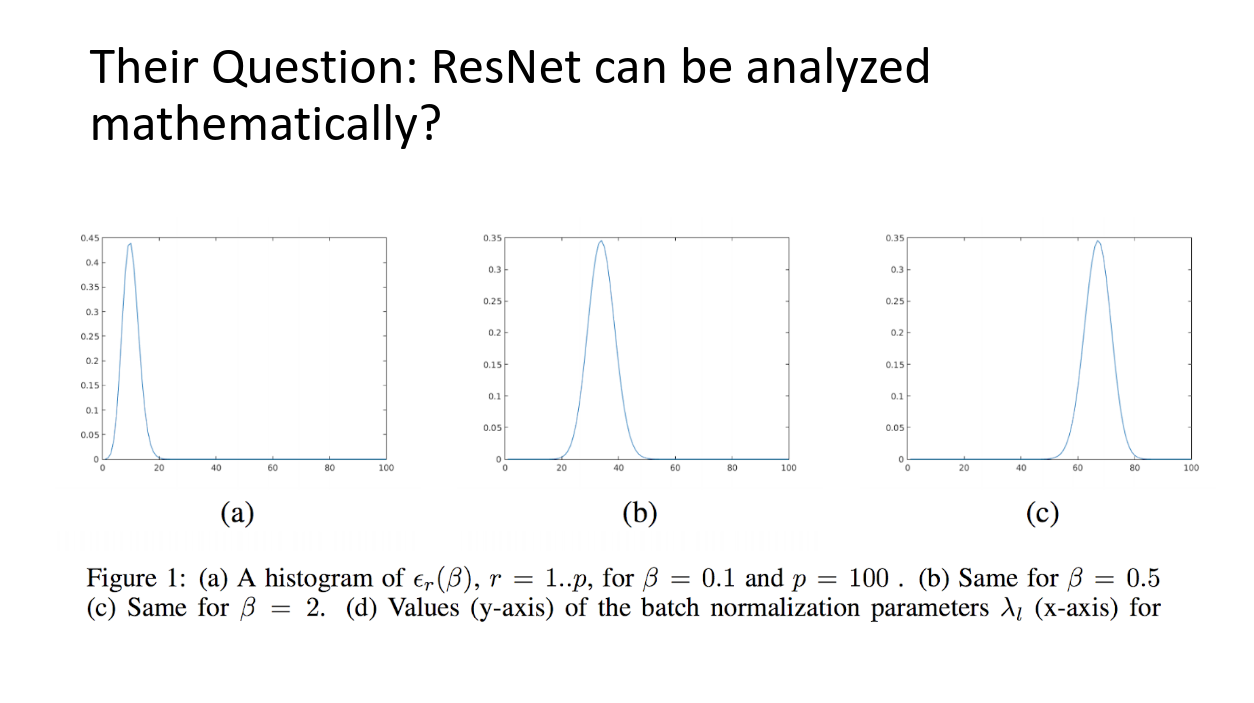
この表はe_rの分布を、様々なbetaで描画しています。betaが大きくなるに連れて、経路長の長いネットワークがロス関数に寄与していることが見て取れます。
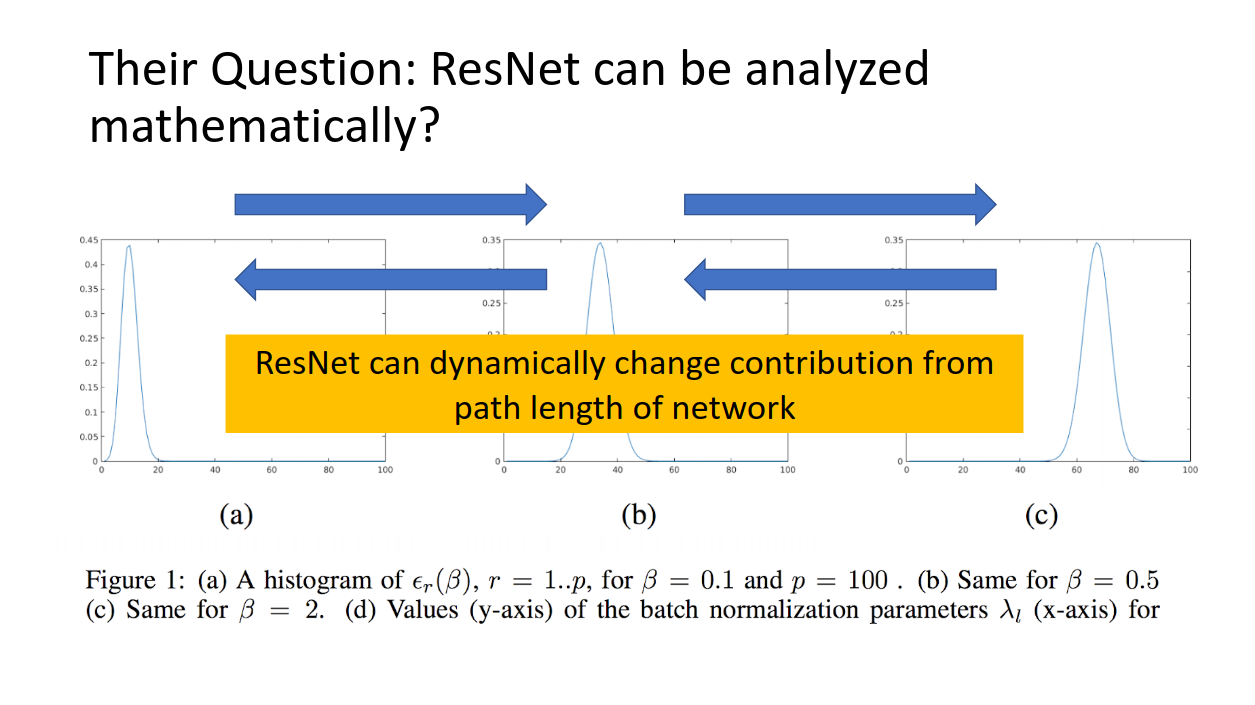
つまり、(ここ大事!!)ResNetはダイナミックに支配的な経路長を変えることのできるアンサンブル学習なのです!!
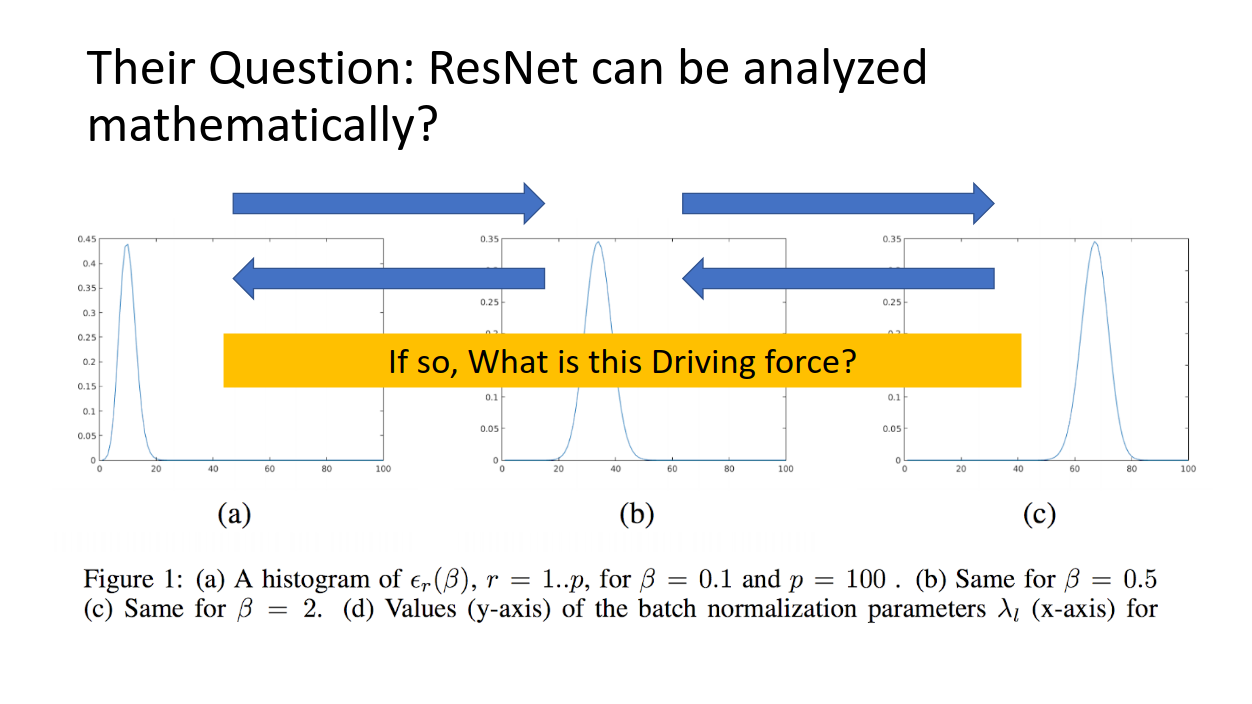
であるとすれば、これらをダイナミックに変える原動力となるものがあるはずですが、ResNetでそれに対応するのは何なのでしょうか??
なんと答えは、、、、、
**バッチノーマライゼーション(BN)**なのです。
- アンサンブルされる弱学習器のネットワーク経路長はResNetで様々であるが、それらの支配力分布は、パラメータにより動的である。
- 学習時には、パラメータCが変動し、この支配力を浅いネットワークから深いネットワークへと変動させる。これがResNetの大きなキャパシティに繋がっている。
- バッチノーマライゼーションをもつネットワークにおいて、CはBNで定義されるlambdaになる。lambda=1で学習を始めることで、最初はとても浅いネットワークの支配力を上げた状態でスタートし、学習が進むに連れて深いネットワークの支配力が上がる。

上の赤字の式は、ロス関数をショートカットした経路ネットワークの寄与係数(lambda_m)と、していない経路ネットワークの寄与係数(lambda_p)を明示して書き出したものです。

(25)の条件がマッチしたとき、(物理的にはこの条件は、浅いネットワークがローカルミニマに近づいていっているということらしいです。申し訳ないですがこの辺が完全に理解しきれていません。。。)上の赤字の式で行くと、lambda_pが大きくなり、lambda_mが変わらないので、先程の支配勢力が、深いネットワークにシフトすることになります。これが起こっていることが、実験的にも示されている、と論文に書かれています。
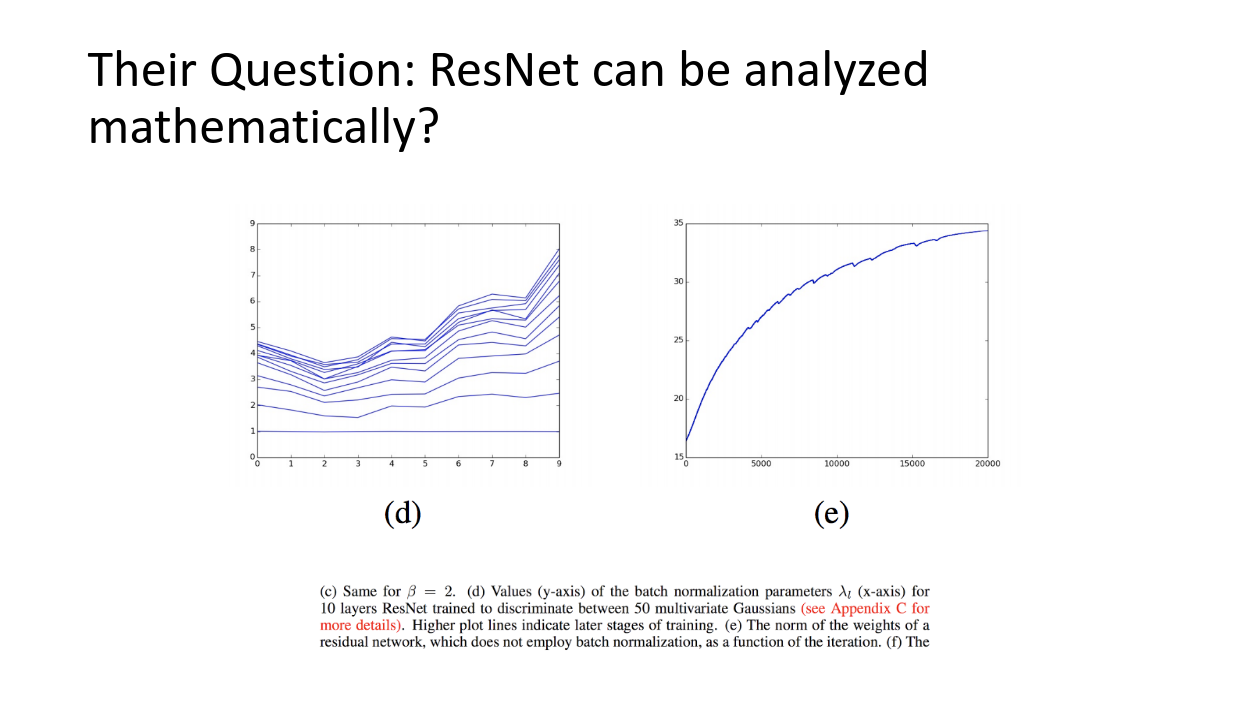
左の図(d)はBNのパラメータlambdaが学習が進むに連れて大きくなっていることを示したプロットです。
更に、右図(e)はBNを行わなかったときの重みのノルムの増加です。
つまり、学習が進むに連れてBNのパラメータlambdaが上昇し、アンサンブルにおける支配要素は、深いネットワークの弱学習器(あまりショートカットを行わなかったもの)に「動的に」変化しているということです。
おもしれえ!
また、スピングラスモデルを用いることで、ロス関数の極値について考察しているのが論文後半部分に書かれているのですが、ここがまたおもしろい!!
まず、言葉の整理をすると、
- critical point: 極値を与える場所と考えて問題ないと思う
- critical point with high index: 極値なんだけど、落ちる先(次元)がたくさんある極値。したがってここにハマることはあんまりなく、もっといいところに落ちてくれる。
- critical point with low index: 極値なんだけど、落ちる先が少ない物。つまりここにハマるとスタックしやすい。
Littwinさんによると、深いネットワークを作ると、critical point with low indexがたくさんある、つまり局所的な極値(でさらにハマりやすい厄介なもの)にモデルがスタックしやすくなるという欠点があるのに対し、ResNetだとまず支配的な項が浅いネットワークのため、critical point with low indexが少なく、局所的な極値にスタックする可能性が低くなるということ。その後、ネットワークの支配勢力が深いネットワークのものにシフトするので、いいとこ取りやな!みたいなことが書いて有ります。
- スピングラスモデルを考えると、pだけ相互作用を考えたモデル(つまり深いネットワークだけアンサンブルした学習器)よりも、いろいろな数の相互作用を考えることのできるモデル(つまり浅いネットワークが支配し、後に深いネットワークが支配するようなアンサンブル学習、ResNet)のほうが、少ないcritical point を持っている。
- 深さpのResNetで得られるロス関数と、VGGとかで同じ深さpを持つモデルで得られるロス関数には、critical point がそれぞれあるが、ResNetでのそれはVGGのそれより少ない。
これすごくないですか??
かなり根幹にたどり着いた気がしますよね?
あと少しだけがんばりましょう。
ラスボスにたどり着きました。私はこの論文が日本人の書いたものというのがなんとも誇らしいです。
Functional Gradient Boosting based on Residual Network Perception (ラスボス)
この論文は、以上すべてのことを踏まえた上で、
勾配ブースティングの上位概念の「関数勾配ブースティング」というアルゴリズムを発表したものです。
発想はタイトルにもあるとおりResNetの考察から来ています。なんとも感慨深い。。。。
ただ、書いてある数式を追うのがかなり難しかったので、簡単にまとめることしか自分にはできませんでした。これからもっと読めるように頑張るので今回は許してください。

ここの記述が興味深いのですが、簡単に言うと関数勾配は、普通の勾配の上位互換だよね!すごいね!!と言っています。すごく面白いと思うのですが、関数で勾配を取ったときのstationary point(停留値)は、普通の勾配を使ってもそれ以上良くならないよね?ってことです。

言い換えると、普通の勾配法を用いてロス関数を下っていくのに失敗したとしても、関数勾配を用いるとそれを越えられる、ということです。
とぅげえ!!!

関数勾配を用いた特徴量のアップデートは上のように書けます。もともとのやりたいことは、ロス関数のリスク(全学習データでの期待値)の最小化でした。ここで、rは最後の層、つまり残差ブロックと最後の推論次元に特徴量をマッピングする変換です。
この目的ロス関数の関数微分を記述すると、見ての通り、idは恒等変換ですから、関数微分の項がほしいわけです。これは、関数微分をロス関数に施したときに出てくる値にほかならないわけです。
これをT回繰り返したもの(最後の行です)は、ResNetの構造そのものを表しています!!

Nitandaさんが提案したResFGBというアルゴリズムの最初の部分です。
結局、学習時にはアップデートしたい特徴空間に学習データが飛び込んでくるわけですが、それをどのようにアップデートすればいいかを記述してあげる必要が有ります。それを、彼らはカーネル関数を使い、畳込みを行うことでどのようにアップデートすればいいかを計算しており、それがきちんと収束すること、また、どのようにカーネルを選ぶか、最後にこのアルゴリズムの優位性についてまとめています。自分はまだきちんと終えるほど知識がありませんが、素晴らしいアイディアだと思いました!!
:||のまとめ
複数の論文(ここに書いた2つだけではありません)で、ResNetを数学的に精査し、なぜ優位なアキュラシーがあるのか、という研究が行われている。
おそらく、Kaiming He さんの始祖論文時には、彼は機械学習のこれまでの問題点と、総合的な洞察からResNetの構造を思いついたが、精査は行われていなかった。
その後、ResNetが実際は関数勾配ブースティングを特徴空間に行っているアンサンブル学習であることは、たくさんの研究者たちによって分析され、少しずつResNetの「最深部」が見えるようになってきた。
まとめ
以上、4本立て(序、破、Q、:||)でResNetについて考察してみましたが、なかなか面白かったです。知識のなさに萎えることも有りましたが、とりあえず最後まで書けてよかったです。機械学習ガチ勢の方ぜひご指導ください。いいねやコメントお待ちしております。




