サポートベクターマシンの考え方
- 参考にしたもの:機械学習のエッセンスの第05章「機械学習アルゴリズム」
- 回帰、ロジスティック回帰分析は別ページ
サポートベクターマシンとは
- 2つのデータ群を分ける境界を引く方法。境界の形は直線・平面・超平面や曲線・曲面・超曲面
- 略称SVM (Support Vector Machine)
分け方(=境界の作り方)
- 直線・平面・超平面(完全に分離できる場合)(=このページ)
- 直線・平面・超平面(完全に分離できない場合)
- 曲線・曲面・超曲面
特徴、考え方
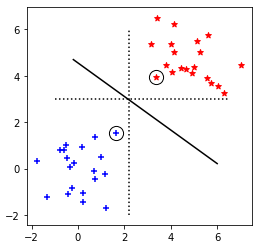
基本の考え方:「境界から一番近くなる点」との距離が最大になるように、境界を作る
- ↓の例だと、点線でも境界にはなるが、ギリギリを攻めすぎているため「新しく点が増えたとき、どちらになるか?」という判別が不正確になる。
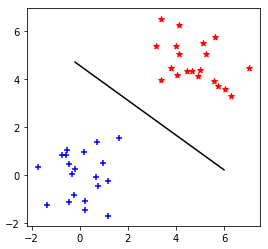
- SVMでは、実線のように両方の点群のちょうど間を通るように境界を作る。
- ↓では「境界(実線)から一番近い点」に丸がついており、コレをサポートベクタと呼ぶ。サポートベクタによって境界が決まる。
**考え方はココまでで終わり。**コレ以降は数学・数値計算問題としての解き方。
図作ったときのコード置き場
解き方
- n個の点(↑の赤、青)に$i(=1, 2, \cdots, n)$と番号をつける。それぞれの点の位置は$\mathbf{x_i}=(x_1, x_2, \cdots, x_d)_i$と表す。
- 境界線を$w_0+\mathbf{w}\mathbf{x}=0$と置く。$\mathbf{w}=(w_1, w_2, \cdots, w_d)$
- $w_0$と$\mathbf{w}$で境界の形が決まる。
- ある点iがどちらのグループになるかは、$w_0+\mathbf{w}\mathbf{x_i}$の符号(±)によって判別される
- 全部の点に$y_i=1,-1$を設定する。「$w_0+\mathbf{w}\mathbf{x_i}>0$になる点は$y_i=1$」「$w_0+\mathbf{w}\mathbf{x_i}<0$になる点は$y_i=-1$」とする。(=↑で同じ色は$y_i$が同じになる)
- 点i ($\mathbf{x_i}$)の、直線$w_0+\mathbf{w}\mathbf{x}=0$からの距離を$l_i$とすると、↓のように表される
$$
l_i = \frac{|w_0+\mathbf{w}\mathbf{x_i}|}{|\mathbf{w}|} = \frac{y_i(w_0+\mathbf{w}\mathbf{x_i})}{|\mathbf{w}|}
$$
- 1つ目の式は、「点と直線の距離公式をベクトルを使って導く」を参照
- 2つ目の式は、↑3での$y_i$の設定の仕方より、こう書くと絶対値と同じ(必ず+)になる
- 全て(n個)の点で最小の$l_i$を以下のように表すと、↓が最大(=「境界から一番近くなる点」との距離が最大)となるような$w_0, \mathbf{w}$を設定したい
$$
min_i(l_i) = min_i(\frac{y_i(w_0+\mathbf{w}\mathbf{x_i})}{|\mathbf{w}|}) = \frac{1}{|\mathbf{w}|}min_i(y_i(w_0+\mathbf{w}\mathbf{x_i}))
$$ - ココで、$min_i(y_i(w_0+\mathbf{w}\mathbf{x_i}))=m$とすると、$w_0, \mathbf{w}$を両方$1/m$倍すると$min_i(y_i(w_0+\mathbf{w}\mathbf{x_i}))=1$と変形できる。(この操作は、$w_0+\mathbf{w}\mathbf{x}=0$にも$min_i(l_i)$にも影響を与えない)
- よって、5は「↓を最大にする$w_0, \mathbf{w}$を求める」という問題とできる
$$
\frac{1}{|\mathbf{w}|}
$$ - また、計算しやすくするため変形(逆数をとり、二乗し、$1/2$をかける)すると、「↓を最小にする$w_0, \mathbf{w}$を求める」という最適化問題となる
$$
\frac{1}{2}|\mathbf{w}|^2
$$
- 6で$min_i(y_i(w_0+\mathbf{w}\mathbf{x_i}))=1$としたことにより、拘束条件は全てのiで↓となる
- 境界から一番近くなる点(=サポートベクタ)で等号が成り立つ
$$
y_i(w_0+\mathbf{w}\mathbf{x_i})\geq1
$$
w0, wの求め方
↑より、↓を満たす$w_0, \mathbf{w}$を求める。
\begin{align}
Minimize \; &\frac{1}{2}|\mathbf{w}|^2 \\
Subject \; to \; &y_i(w_0+\mathbf{w}\mathbf{x_i})\geq1 \; (i=1, 2, \cdots, n) \\
&\Leftrightarrow -\bigl(y_i(w_0+\mathbf{w}\mathbf{x_i})-1\bigr) \leq 0
\end{align}
コレをラグランジュの未定乗数法(Wikipedia)、カルーシュ・クーン・タッカー条件(Wikipedia)で解く。
制約式がn個なので、$\mathbf{a}=(a_1, a_2, \cdots, a_n)$を導入すると、ラグランジュ関数は
L(w_0, \mathbf{w}, \mathbf{a}) = \frac{1}{2}|\mathbf{w}|^2 - \sum_{i=1}^{n} a_i \bigl(y_i(w_0+\mathbf{w}\mathbf{x_i})-1 \bigr) \; ・・・(i)
と表され、↓を満たす$w_0, \mathbf{w}, \mathbf{a}$を求めれば良い。
\begin{align}
\frac{\partial L}{\partial w_0} &= 0 \; ・・・(ii)\\
\frac{\partial L}{\partial w_j} &= 0 \; ・・・(iii)\\
\end{align}
\begin{align}
a_i &\geq 0 \; ・・・(iv)\\
y_i(w_0+\mathbf{w}\mathbf{x_i})-1 &\geq 0 \; ・・・(v)\\
a_i \bigl(y_i(w_0+\mathbf{w}\mathbf{x_i})-1 \bigr) &= 0 \; ・・・(vi)\\
\end{align}
$(ii), (iii)$より
\begin{align}
\frac{\partial L}{\partial w_0} = - \sum_{i=1}^{n} a_i y_i &= 0 \\
\Leftrightarrow \sum_{i=1}^{n} a_i y_i &= 0 \; ・・・(ii)'\\
\end{align}
\begin{align}
\frac{\partial L}{\partial w_j} &= w_j - \sum_{i=1}^{n} a_i y_i x_{ij} = 0 \\
\Leftrightarrow w_j &= \sum_{i=1}^{n} a_i y_i x_{ij} \; ・・・(iii)'\\
\end{align}
ここで$x_{ij}$は、$\mathbf{x_i}=(x_1, x_2, \cdots, x_j, \cdots, x_n)_i$の$x_j$
$(ii)', (iii)'$を$(i)$に代入すると
L(w_0, \mathbf{w}, \mathbf{a}) = \sum_{k=1}^{n} a_k - \frac{1}{2} \sum_{k=1}^{n} \sum_{l=1}^{n} a_k a_l y_k y_l \mathbf{x_k} \mathbf{x_l}\; ・・・(i)'
となり$w_0, \mathbf{w}$が消えるため、「$w_0, \mathbf{w}, \mathbf{a}$についての最適化」から「$\mathbf{a}$についての最適化(二次計画法(Wikipedia))」となる。
$\mathbf{a}$を求めたら、
w_j = \sum_{i=1}^{n} a_i y_i x_{ij} \; ・・・(iii)'\\
より$\mathbf{w}$を求め、$(vi)$より$a_i \neq 0$となる$i$で
\begin{align}
y_i(w_0+\mathbf{w}\mathbf{x_i})-1 &= 0 \; ・・・(vi)'\\
w_0 &= y_i - \mathbf{w}\mathbf{x_i}
\end{align}
を使って$w_0$を求めればよい。(式変形には${y_1}^2 = 1$を利用した)
aの求め方
↑より$L(w_0, \mathbf{w}, \mathbf{a}) = f(\mathbf{a})$とおくと、↓を満たす$\mathbf{a}$を求める。
\begin{align}
Minimize \; &f(\mathbf{a}) = \sum_{k=1}^{n} a_k - \frac{1}{2} \sum_{k=1}^{n} \sum_{l=1}^{n} a_k a_l y_k y_l \mathbf{x_k} \mathbf{x_l}\; ・・・(i)' \\
Subject \; to \; &\sum_{i=1}^{n} a_i y_i = 0 \; ・・・(ii)'\\
&a_i \geq 0 \; ・・・(iv)\\
&a_i \bigl(y_i(w_0+\mathbf{w}\mathbf{x_i})-1 \bigr) = 0 \; ・・・(vi)\\
\end{align}
- ほとんどの$a_i$は0となるので、プログラムで解く際は「汎用の2次計画問題ソルバ」で解くよりも、「Platによるアルゴリズム」で解くのが効率が良い。(機械学習のエッセンスより)
- ↓の例だと、丸がついている2点(サポートベクタ)以外は$y_i(w_0+\mathbf{w}\mathbf{x_i})-1 \neq 0$なので、$(vi)$より$a_i=0$となる
Platによるアルゴリズム
- 最初に初期値$\mathbf{a^0}$を設定する。今回は$\mathbf{a^0}=(0, 0, \cdots, 0)$
- n個の点から、適当な$i, j$を選ぶ。(選び方は後述)
- $Minimize ; f(\mathbf{a})$となるよう$a_i, a_j$だけ変更する。
- 収束条件を満たすまで、2, 3を繰り返す。(収束条件は後述)
↑の3.「a_i, a_jだけ変更」について
f(\mathbf{a}) = \sum_{k=1}^{n} a_k - \frac{1}{2} \sum_{k=1}^{n} \sum_{l=1}^{n} a_k a_l y_k y_l \mathbf{x_k} \mathbf{x_l}\; ・・・(i)' \\
で、$\sum$から$k, l=i, j$の部分だけ取り出す。まず、$(i)'$第二項の$\sum \sum$部分だけ考えると
\begin{align}
&\sum_{k=1}^{n} \sum_{l=1}^{n} a_k a_l y_k y_l \mathbf{x_k} \mathbf{x_l} \\
= &(\sum_{k=1}^{n} a_k y_k \mathbf{x_k}) (\sum_{l=1}^{n} a_l y_l \mathbf{x_l}) \\
= &(a_i y_i \mathbf{x_i} + a_j y_j \mathbf{x_j} + \sum_{k \neq i,j} a_k y_k \mathbf{x_k}) (a_i y_i \mathbf{x_i} + a_j y_j \mathbf{x_j} + \sum_{l \neq i,j} a_l y_l \mathbf{x_l}) \\
= &a_i^2 y_i^2 \mathbf{x_i} \mathbf{x_i} + a_j^2 y_j^2 \mathbf{x_j} \mathbf{x_j} + 2 a_i a_j y_i y_j \mathbf{x_i} \mathbf{x_j} \\
&+ \sum_{k \neq i,j} a_i a_k y_i y_k \mathbf{x_i} \mathbf{x_k} + \sum_{l \neq i,j} a_i a_l y_i y_l \mathbf{x_i} \mathbf{x_l} \\
&+ \sum_{k \neq i,j} a_j a_k y_j y_k \mathbf{x_j} \mathbf{x_k} + \sum_{l \neq i,j} a_j a_l y_j y_l \mathbf{x_j} \mathbf{x_l} \\
&+ \sum_{k \neq i,j} \sum_{l \neq i,j} a_k a_l y_k y_l \mathbf{x_k} \mathbf{x_l} \\
\end{align}
ここで、↓を適用すると
- $y_{i, j} = 1, -1$より、$y_i^2 =1$、$y_j^2 =1$
- 2行目(第4, 5項)、3行目(第6, 7項)は$k, l$で$\sum$が独立しているため、$\sum_{l \neq i,j}$を$\sum_{k \neq i,j}$とすると、それぞれまとめられる
\begin{align}
&\sum_{k=1}^{n} \sum_{l=1}^{n} a_k a_l y_k y_l \mathbf{x_k} \mathbf{x_l} \\
= &a_i^2 \mathbf{x_i} \mathbf{x_i} + a_j^2 \mathbf{x_j} \mathbf{x_j} + 2 a_i a_j y_i y_j \mathbf{x_i} \mathbf{x_j} \\
&+ 2 \sum_{k \neq i,j} a_i a_k y_i y_k \mathbf{x_i} \mathbf{x_k} \\
&+ 2 \sum_{k \neq i,j} a_j a_k y_j y_k \mathbf{x_j} \mathbf{x_k} \\
&+ \sum_{k \neq i,j} \sum_{l \neq i,j} a_k a_l y_k y_l \mathbf{x_k} \mathbf{x_l} \\
\end{align}
となる。コレを$(i)'$に代入すると
\begin{align}
f(\mathbf{a}) = &\sum_{k=1}^{n} a_k - \frac{1}{2} \sum_{k=1}^{n} \sum_{l=1}^{n} a_k a_l y_k y_l \mathbf{x_k} \mathbf{x_l} \\
= &(a_i + a_j + \sum_{k \neq i, j} a_k) - \frac{1}{2} \sum_{k=1}^{n} \sum_{l=1}^{n} a_k a_l y_k y_l \mathbf{x_k} \mathbf{x_l} \\
= &- \frac{1}{2} a_i^2 \mathbf{x_i} \mathbf{x_i} - \frac{1}{2} a_j^2 \mathbf{x_j} \mathbf{x_j} - a_i a_j y_i y_j \mathbf{x_i} \mathbf{x_j} \\
&+ a_i (1 - y_i \mathbf{x_i} \sum_{k \neq i,j} a_k y_k \mathbf{x_k}) \\
&+ a_j (1 - y_j \mathbf{x_j} \sum_{k \neq i,j} a_k y_k \mathbf{x_k}) \\
&+ \sum_{k \neq i, j} a_k - \frac{1}{2} \sum_{k \neq i,j} \sum_{l \neq i,j} a_k a_l y_k y_l \mathbf{x_k} \mathbf{x_l} \\
\end{align}
となる、ここで
\begin{align}
A &= - \frac{1}{2} \mathbf{x_i} \mathbf{x_i} \\
B &= - \frac{1}{2} \mathbf{x_j} \mathbf{x_j} \\
C &= - y_i y_j \mathbf{x_i} \mathbf{x_j} \\
D &= 1 - y_i \mathbf{x_i} \sum_{k \neq i,j} a_k y_k \mathbf{x_k} \\
E &= 1 - y_j \mathbf{x_j} \sum_{k \neq i,j} a_k y_k \mathbf{x_k}\\
F &= \sum_{k \neq i, j} a_k - \frac{1}{2} \sum_{k \neq i,j} \sum_{l \neq i,j} a_k a_l y_k y_l \mathbf{x_k} \mathbf{x_l} \\
\end{align}
とおくと、
f(\mathbf{a}) = A a_i^2 + B a_j^2 + C a_i a_j + D a_i + E a_j + F \; ・・・(i)'' \\
と表せる。
また、拘束条件$(ii)'$で$\sum$のiをkに変更し、i,jを取り出すと
\begin{align}
& a_i y_i + a_j y_j + \sum_{k \neq i, j}^{n} a_k y_k = 0 \\
\Leftrightarrow & a_j = \frac {1}{y_j} (- a_i y_i - \sum_{k \neq i, j}^{n} a_k y_k) \\
\end{align}
となり「$y_j^2 = 1$より$\frac {1}{y_j} = y_j$」と「$G = \sum_{k \neq i, j}^{n} a_k y_k$」とおくと
\begin{align}
a_j =& y_j (- a_i y_i - \sum_{k \neq i, j}^{n} a_k y_k) \; ・・・(ii)'' \\
=& y_j (- a_i y_i - G) \\
\end{align}
となる。コレを$(i)''$に代入すると
\begin{align}
f(\mathbf{a}) = &A a_i^2 + B (y_j (- a_i y_i - G))^2 \\
&+ C a_i y_j (- a_i y_i - G) + D a_i \\
&+ E y_j (- a_i y_i - G) + F \\
= & a_i^2 (A + B y_j^2 y_i^2 - C y_j y_i) \\
&+ a_i \bigl(B y_j^2 (2 y_i G) - C y_j G + D - E y_j y_i \bigr) \\
&+ Const \\
= & a_i^2 (A + B - y_i y_j C) \\
&+ a_i (2 y_i B G - y_j C G + D - y_i y_j E) \\
&+ Const
\end{align}
$a_i$の二次関数と考えると、頂点となる$a_i$は(このへん参照)
a_ i = - \frac {2 y_i B G - y_j C G + D - y_i y_j E}{2 (A + B - y_i y_j C)}
分子、分母をそれぞれ計算すると
\begin{align}
2 y_i B G - y_j C G + D - y_i y_j E = & 2 y_i (- \frac{1}{2} \mathbf{x_j} \mathbf{x_j}) G - y_j (- y_i y_j \mathbf{x_i} \mathbf{x_j}) G \\
& + (1 - y_i \mathbf{x_i} \sum_{k \neq i,j} a_k y_k \mathbf{x_k}) - y_i y_j (1 - y_j \mathbf{x_j} \sum_{k \neq i,j} a_k y_k \mathbf{x_k}) \\
= & 1 - y_i y_j + y_i (\mathbf{x_i} - \mathbf{x_j}) (\mathbf{x_j} G - \sum_{k \neq i,j} a_k y_k \mathbf{x_k}) \\
= & 1 - y_i y_j + y_i (\mathbf{x_i} - \mathbf{x_j}) (\mathbf{x_j} \sum_{k \neq i, j}^{n} a_k y_k - \sum_{k \neq i,j} a_k y_k \mathbf{x_k})
\end{align}
\begin{align}
2 (A + B - y_i y_j C) = & 2 \bigl(- \frac{1}{2} \mathbf{x_i} \mathbf{x_i} - \frac{1}{2} \mathbf{x_j} \mathbf{x_j} - y_i y_j (- y_i y_j \mathbf{x_i} \mathbf{x_j}) \bigr) \\
= & - \mathbf{x_i} \mathbf{x_i} - \mathbf{x_j} \mathbf{x_j} + 2 \mathbf{x_i} \mathbf{x_j} \\
= & -|\mathbf{x_i} - \mathbf{x_i}|^2
\end{align}
よって、$f(\mathbf{a})$が頂点をとる$a_i$は
a_ i = \frac {1}{|\mathbf{x_i} - \mathbf{x_i}|^2} \bigl(1 - y_i y_j + y_i (\mathbf{x_i} - \mathbf{x_j}) (\mathbf{x_j} \sum_{k \neq i, j}^{n} a_k y_k - \sum_{k \neq i,j} a_k y_k \mathbf{x_k}) \bigr) \; ・・・(vii)
となる。$a_i$を求めたら、
a_j = y_j (- a_i y_i - \sum_{k \neq i, j}^{n} a_k y_k) \; ・・・(ii)'' \\
で$a_j$を求める。
最後に、$(iv)$より$a_{i, j} \geq 0$という拘束条件があるので、
- $(vii)$より$a_i$を求める。ただし、$a_i \leq 0$となったら$a_i = 0$とする。
- $(ii)''$より$a_j$を求める。ただし、$a_j \leq 0$となったら$a_j = 0$とする。
- 2で$a_j = 0$となったら、$a_i$を計算しなおす。(計算式は$a_i = y_i (- a_j y_j - \sum_{k \neq i, j}^{n} a_k y_k)$)
↑の2.「i, jを選ぶ」, 4.「収束条件」について
\begin{align}
Minimize \; &f(\mathbf{a}) = \sum_{k=1}^{n} a_k - \frac{1}{2} \sum_{k=1}^{n} \sum_{l=1}^{n} a_k a_l y_k y_l \mathbf{x_k} \mathbf{x_l}\; ・・・(i)' \\
Subject \; to \; &\sum_{i=1}^{n} a_i y_i = 0 \; ・・・(ii)'\\
&a_i \geq 0 \; ・・・(iv)\\
&a_i \bigl(y_i(w_0+\mathbf{w}\mathbf{x_i})-1 \bigr) = 0 \; ・・・(vi)\\
\end{align}
にもう一度ラグランジュの未定乗数法(Wikipedia)、カルーシュ・クーン・タッカー条件(Wikipedia)を適用すると、ラグランジュ関数$L'$は
L'(\mathbf{a}, \lambda, \mathbf{\mu}) = f(\mathbf{a}) - \lambda \sum_{i=1}^{n} a_i y_i - \mathbf{\mu} \mathbf{a}
となり、拘束条件は
\begin{align}
Subject \; to \; &\mu_j a_j = 0 \\
&\mu_j \leq 0 \\
\end{align}
ここで
\nabla_a L' = \nabla_a f(\mathbf{a}) + \lambda \mathbf{y} - \mathbf{\mu} = 0
の、ある成分$t$だけに注目すると
\begin{align}
&\nabla_a f(\mathbf{a})_t + \lambda y_t - \mu_t = 0 \\
&\nabla_a f(\mathbf{a})_t + \lambda y_t = \mu_t \leq 0 \\
\end{align}
となる。
拘束条件$\mu_j a_j = 0$より、$a_t = 0$(サポートベクタ以外の点)のとき$\mu_t \leq 0$より
\nabla_a f(\mathbf{a})_t \leq - \lambda y_t \\
y_t \nabla_a f(\mathbf{a})_t \left\{
\begin{array}{ll}
\geq - \lambda & (y = -1) \\
\leq - \lambda & (y = 1) \\
\end{array}
\right.
(両辺に$y_t$をかけて、$y_t^2 = 1$を適用した)
また、$a_t > 0$(サポートベクタ)のとき$\mu_t = 0$より
y_t \nabla_a f(\mathbf{a})_t = - \lambda \\
以上をまとめると
y_t \nabla_a f(\mathbf{a})_t \left\{
\begin{array}{ll}
\geq - \lambda & (y = -1 \; or \; a_t > 0) \\
\leq - \lambda & (y = 1 \; or \; a_t > 0) \\
\end{array}
\right.
{y_t \nabla_a f(\mathbf{a})_t}_{(y = 1 \; or \; a_t > 0)} \leq - \lambda \leq {y_t \nabla_a f(\mathbf{a})_t}_{(y = -1 \; or \; a_t > 0)}
コレは全部の点$t$について考えているが、
- $y = -1 ; or ; a_t > 0$で、$y_t \nabla_a f(\mathbf{a})_t$が最小値をとる$t$を$i$
- $y = 1 ; or ; a_t > 0$で、$y_t \nabla_a f(\mathbf{a})_t$が最大値をとる$t$を$j$
のように$i, j$を選ぶと
y_j \nabla_a f(\mathbf{a})_j \leq y_i \nabla_a f(\mathbf{a})_i
と表せる。
これらが「2. n個の点から、適当な$i, j$を選ぶ」の選び方、「4. 収束条件を満たすまで、2, 3を繰り返す」の収束条件となる。