線形回帰、リッジ回帰、ラッソ回帰の考え方
- 参考にしたもの:機械学習のエッセンスの第05章「機械学習アルゴリズム」
- ロジスティック回帰分析、サポートベクターマシンは別ページ
内容
対象:第05章「機械学習アルゴリズム」で出てくる以下の項目
中身:それぞれの意味・ロジック(何をしているのか)・どういう特徴があるのかについて
- 回帰
- 線形回帰
- 汎化(汎化誤差)・バイアス・バリアンス
- リッジ回帰
- ラッソ回帰
回帰とは
- 与えられた情報から、ある値を予測すること。
- 例
- 「身長、年齢、性別」から、体重を予測する
- 「築年数、家の大きさ、駅からの距離」から、「住宅の価格」を予測する
- 回帰分析(wikipedia)
- 超入門!リッジ回帰・Lasso回帰・Elastic Netの基本と特徴をサクッと理解!
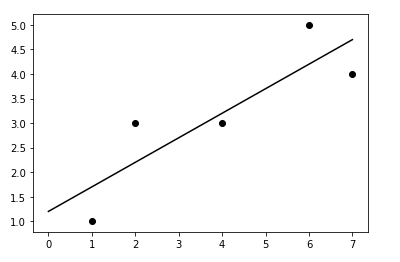
線形回帰
$f(\mathbf{x})$を↓のように表し、できるだけ正確に予測できるよう$w=(w_0, w_1, w_2, \cdots, w_n)$を求める
f(\mathbf{x}) = w_0 + w_1x_1 + w_2x_2 + \cdots + w_nx_n = w_0 + \sum_{i=1}^{n} w_ix_i
- $y$:真の値。コレを予測したい(=目的変数)
- $\mathbf{x}=(x_1, x_2, \cdots, x_n)$:コレを使って$y$を予測したい(=説明変数)。
- $f(\mathbf{x})$:予測値
説明変数が1つだと「単回帰分析」、複数だと「重回帰分析」と呼ばれる
ロジック
直線を引いたときに「予測と真の値の平均二乗誤差↓」が最小になるよう、パラメータ(係数)を求める。細かい計算についてはコッチ参照。
\sum{(y - f(x))^2}
特徴
回帰の基本。特に無し。(特徴が無いことが特徴?)
汎化(汎化誤差)・バイアス・バリアンス
「リッジ回帰」「ラッソ回帰」がなぜ必要なのか、という話
汎化誤差
- まだ手に入れていないデータを予測した時の誤差。期待損失 (expected risk)とも言う
- 機械学習では、コレを小さくしたい
- 汎化誤差 = バイアス + バリアンス + ノイズ
バイアス
- コレが大きい = 予測値と真の値が合ってない。学習不足。もっと学びましょう。
バリアンス
- コレが大きい = 過学習。学習データに合わせに行き過ぎてモデルが複雑になり、未知データからの予測がうまくできない。
- よくマンガとかで、データ作戦が得意な敵が過去のデータに頼りすぎて「馬鹿な。これまでのデータではこんなはずでは・・・」ってなるやつ。
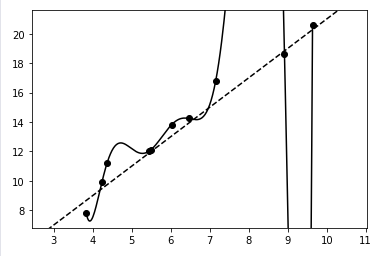
- 過学習の原因としては、$w=(w_0, w_1, w_2, \cdots, w_n)$が極端に大きい(or小さい)値となることが挙げられる。
- 例としては↓こういうの
ノイズ
- 削減不能な誤差
主な検証方法
-
ホールド・アウト検証
- データを訓練データ・テストデータに分割してモデルを作って、モデルがイケてるか確認する。
- 1パターンでハイパーパラメータを調整しすぎると、ハイパーパラメータが過学習することがあるので注意。
-
交差検証(クロスバリデーション)
- ハイパーパラメータの過学習を防止する方法
- データを複数個に分割し、1つをテストデータ・他を訓練データとして全パターンでモデルを作り、評価する。
リッジ回帰
ロジック
「↓**(予測と真の値の平均二乗誤差)+(ハイパーパラメータ)×(パラメータのL2ノルム)**」が最小になるよう、パラメータ(係数)を求める(=L2正則化)。細かい計算についてはコッチ参照
\sum{(y - f(x))^2}+\lambda \sum_{i=0}^{n} w_i^2
単語
- ハイパーパラメータ:学習前に設定しておく。コレで学習によるパラメータ(係数)が変わってくる。いくつかのパラメータを試して、一番良さそうなものを選ぶ
- L2ノルム:$\sqrt{\sum_{i=0}^{n} w_i^2} = \sqrt{w_0^2 + w_1^2 + w_2^2 + \cdots + w_n^2}$
- 正則化:過学習を防ぐテクニックの一つ
特徴
- ○なめらかなモデルが得られる(=ハズレ値やノイズの影響を受けにくい)
- ×説明変数が多い時にはモデルの解釈が複雑になる(係数は完全に0にはならないため)
- ※バランスタイプ = 「まぁ、バランスよくパラメータ割り振りましょう」
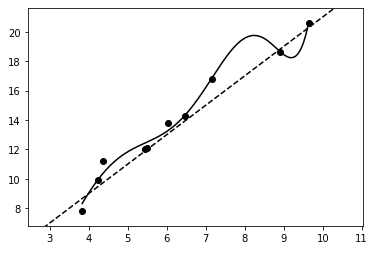
- ↑で過学習してたやつに、リッジ回帰使うと↓こうなる
ラッソ回帰
ロジック
「↓**(予測と真の値の平均二乗誤差)+(ハイパーパラメータ×パラメータのL1ノルム)**」が最小になるよう、パラメータ(係数)を求める(=L1正則化)。細かい計算についてはコッチ参照
\sum{(y - f(x))^2}+\lambda \sum_{i=0}^{n} |w_i|
(単語)
- L1ノルム:$\sum_{i=0}^{n} |w_i| = |w_0| + |w_1| + |w_2| + \cdots + |w_n|$
特徴
- ○不要と判断されるパラメータが0になる = いくつかの特徴量(説明変数)が完全に無視される = モデルを解釈がしやすくなる
- ×複数の相関が強い説明変数が存在する場合、その中で一つの変数だけ選択される
- ※極振りタイプ = 「意味がなさそうなパラメータは、容赦なく切り捨てる(0にする)」
- ※ハイパーパラメータが大きいほど、スパーシティが上がる(係数が0になりやすい)
- ※スパーシティ:行列の、全体に対するゼロ要素の割合
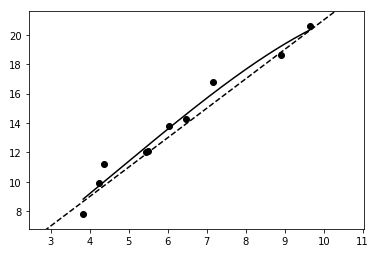
- ↑で過学習してたやつに、ラッソ回帰使うと↓こうなる