サポートベクターマシン(曲線・曲面・超曲面)の考え方
- 参考にしたもの:機械学習のエッセンスの第05章「機械学習アルゴリズム」
- 基本的な考え方は「サポートベクターマシン」について参照
分け方(=境界の作り方)
- 直線・平面・超平面(完全に分離できる場合)(「サポートベクターマシン」について参照)
- 直線・平面・超平面(完全に分離できない場合)
- 曲線・曲面・超曲面(=このページ)
考え方
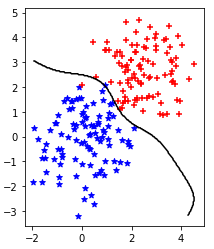
これまでは超平面で境界線を作ったが、超曲面での境界線を作る。(↓こんな感じ)
- 使うのはカーネル法という手法。
- 超平面では境界線を$w_0+\mathbf{w}\mathbf{x}=0$とおいていたが、ここでは$w_0+\mathbf{w} \phi(\mathbf{x})=0$とおく。
- (超平面のときは次数がdのとき$\mathbf{x}=(x_1, \cdots, x_d)$のため$\mathbf{w}=(w_1, \cdots, w_d)$であったが、超曲面の場合は$\phi, \mathbf{w}$は特に次元数には縛られないため膨大に大きな数を設定できる)
- こうすると、直線・平面・超平面(完全に分離できない場合)の最適化問題は↓になる
\begin{align}
Minimize \; &C \sum_{i=1}^{n}\xi_i + \frac{1}{2}|\mathbf{w}|^2 \\
Subject \; to \; &y_i\bigl(w_0+\mathbf{w}\phi(\mathbf{x_i})\bigr) \geq 1 - \xi_i \; (i=1, 2, \cdots, n) \\
&\xi_i \geq 0 \\
\end{align}
図作ったときのコード置き場
解き方
ラグランジュの未定乗数法(Wikipedia)、カルーシュ・クーン・タッカー条件(Wikipedia)を適用すると、ラグランジュ関数は
L(w_0, \mathbf{w}, \mathbf{\xi}, \mathbf{a}) = C \sum_{i=1}^{n}\xi_i + \frac{1}{2}|\mathbf{w}|^2 - \sum_{i=1}^{n} a_i \Bigl(y_i \bigl(w_0+\mathbf{w}\phi(\mathbf{x_i}) \bigr) - 1 + \xi_i \Bigr) - \sum_{i=1}^{n}\eta_i \xi_i
となり、KKT条件は次のようになる。
\begin{align}
a_i &\geq 0 \\
y_i \bigl(w_0+\mathbf{w}\phi(\mathbf{x_i}) \bigr) - 1 + \xi_i &\geq 0 \\
a_i \Bigl(y_i \bigl(w_0+\mathbf{w}\phi(\mathbf{x_i}) \bigr) - 1 + \xi_i \Bigr) &= 0 \; \cdots (i)\\
\eta_i &\geq 0 \\
\xi_i &\geq 0 \\
\eta_i \xi_i &= 0 \\
\end{align}
直線・平面・超平面(完全に分離できる場合)、直線・平面・超平面(完全に分離できない場合)と同様に計算すると
\begin{align}
\frac{\partial L}{\partial w_0} = - \sum_{i=1}^{n} a_i y_i &= 0 \\
\Leftrightarrow \sum_{i=1}^{n} a_i y_i &= 0 \\
\end{align}
\begin{align}
\frac{\partial L}{\partial \mathbf{w}} &= \mathbf{w} - \sum_{i=1}^{n} a_i y_i \phi(\mathbf{x_i}) = 0 \\
\Leftrightarrow \mathbf{w} &= \sum_{i=1}^{n} a_i y_i \phi(\mathbf{x_i}) \\
\Leftrightarrow \mathbf{w} \phi(\mathbf{x}) &= \sum_{i=1}^{n} a_i y_i \phi(\mathbf{x_i}) \phi(\mathbf{x}) \\
&= \sum_{i=1}^{n} a_i y_i K(\mathbf{x_i}, \mathbf{x}) \; \cdots (ii)\\
\end{align}
ここで、$\phi(\mathbf{x_k}) \phi(\mathbf{x_l}) = K(\mathbf{x_k}, \mathbf{x_l})$とおいた。これ以下の計算では、$\phi$の値を計算しなくても、$K$だけの評価で考えることができ、この$K$をカーネル関数という。
ここから、直線・平面・超平面(完全に分離できる場合)、直線・平面・超平面(完全に分離できない場合)と同様に以下を最小にする$\mathbf{a}$を求め、$(i), (ii)$より$w_0, \mathbf{w} \phi(\mathbf{x})$を求めればよい
\begin{align}
Minimize \; f(\mathbf{a}) &= \sum_{k=1}^{n} a_k - \frac{1}{2} \sum_{k=1}^{n} \sum_{l=1}^{n} a_k a_l y_k y_l \phi(\mathbf{x_k}) \phi(\mathbf{x_l}) \\
&= \sum_{k=1}^{n} a_k - \frac{1}{2} \sum_{k=1}^{n} \sum_{l=1}^{n} a_k a_l y_k y_l K(\mathbf{x_k}, \mathbf{x_l}) \\
Subject \; to \; &\sum_{i=1}^{n} a_i y_i = 0 \\
&0 \leq a_i \leq C\\
\end{align}
f(\mathbf{a}) = \sum_{k=1}^{n} a_k - \frac{1}{2} \sum_{k=1}^{n} \sum_{l=1}^{n} a_k a_l y_k y_l K(\mathbf{x_k}, \mathbf{x_l}) \\
Platによるアルゴリズム
直線・平面・超平面(完全に分離できる場合)、直線・平面・超平面(完全に分離できない場合)と同様に、以下の流れで解いていく
- 最初に初期値$\mathbf{a^0}$を設定する。今回は$\mathbf{a^0}=(0, 0, \cdots, 0)$
- n個の点から、適当な$i, j$を選ぶ。(選び方は後述)
- $Minimize ; f(\mathbf{a})$となるよう$a_i, a_j$だけ変更する。
- 収束条件を満たすまで、2, 3を繰り返す。(収束条件は後述)
↑の3.「a_i, a_jだけ変更」について
基本の流れは直線・平面・超平面(完全に分離できる場合)では、$f(\mathbf{a})$が頂点をとる$a_i$は
a_ i = \frac {1}{|\mathbf{x_i} - \mathbf{x_i}|^2} \bigl(1 - y_i y_j + y_i (\mathbf{x_i} - \mathbf{x_j}) (\mathbf{x_j} \sum_{k \neq i, j}^{n} a_k y_k - \sum_{k \neq i,j} a_k y_k \mathbf{x_k}) \bigr)
であったが、今回はカーネル関数が入っているので、
\begin{align}
a_ i = \frac {1}{K(\mathbf{x_i}, \mathbf{x_i}) + K(\mathbf{x_j}, \mathbf{x_j}) - 2 K(\mathbf{x_i}, \mathbf{x_j})} \biggl( &1 - y_i y_j + y_i \Bigl( \bigl(K(\mathbf{x_i}, \mathbf{x_j}) - K(\mathbf{x_j}, \mathbf{x_j}) \bigr) \sum_{k \neq i, j}^{n} a_k y_k \\
&- \sum_{k \neq i,j} a_k y_k \bigl(K(\mathbf{x_i}, \mathbf{x_k}) - K(\mathbf{x_j}, \mathbf{x_k}) \bigr) \Bigr) \biggr) \\
\end{align}
あとは直線・平面・超平面(完全に分離できない場合)と同様に$0 \leq a_{i, j} \leq C$なので、以下のようになる。
- $a_i$を求める。ただし、$a_i \leq 0$となったら$a_i = 0$、$a_i \geq C$となったら$a_i = C$とする。
- $a_j$を求める。ただし、$a_j \leq 0$となったら$a_j = 0$、$a_j \geq C$となったら$a_j = C$とする。
- 2で$a_j = 0 ; or ; C$となったら、$a_i$を計算しなおす。
↑の2.「i, jを選ぶ」, 4.「収束条件」について
直線・平面・超平面(完全に分離できない場合)と同様に考えればよく
- $(a_t > 0 ; and ; y = 1) ; or ; (a_t < C \; and \; y = -1)$で、$y_t \nabla_a f(\mathbf{a})_t$が最小値をとる$t$を$i$
- $(a_t > 0 ; and ; y = -1) ; or ; (a_t < C \; and \; y = 1)$で、$y_t \nabla_a f(\mathbf{a})_t$が最大値をとる$t$を$j$
のように$i, j$を選ぶと
y_j \nabla_a f(\mathbf{a})_j \leq y_i \nabla_a f(\mathbf{a})_i
と表せる。
これらが「2. n個の点から、適当な$i, j$を選ぶ」の選び方、「4. 収束条件を満たすまで、2, 3を繰り返す」の収束条件となる。
カーネル関数が入っているので、$f(\mathbf{a})$の$\mathbf{a}$についての勾配のt番目の成分は次のようになる。
\nabla_a {f(\mathbf{a})}_t = 1 - \sum_{l=1}^{n} a_l y_t y_l K(\mathbf{x_t}, \mathbf{x_l}) \\
「使用するカーネル関数K」 + 「aを求めた後の処理」
ここで(機械学習のエッセンスより)カーネル関数を
K(\mathbf{u}, \mathbf{v}) = \exp(- \frac {||\mathbf{u} - \mathbf{v}||^2}{2 \sigma^2}) \\
とおき、↑によって$\mathbf{a}$を求めると$(i), (ii)$より$w_0, \mathbf{w} \phi(\mathbf{x})$を求められる。
\mathbf{w} \phi(\mathbf{x}) = \sum_{i=1}^{n} a_i y_i K(\mathbf{x_i}, \mathbf{x}) \; \cdots (ii)\\
\begin{align}
a_i \Bigl(y_i &\bigl(w_0+\mathbf{w}\phi(\mathbf{x_i}) \bigr) - 1 + \xi_i \Bigr) = 0 \; \cdots (i)\\
\Leftrightarrow y_i \bigl( &w_0+\mathbf{w}\phi(\mathbf{x_i}) \bigr) - 1 + \xi_i = 0 \; (for \; a_i \neq 0) \\
\Leftrightarrow y_i \bigl( &w_0+\mathbf{w}\phi(\mathbf{x_i}) \bigr) = 1 \; (for \; a_i \neq 0) \\
\Leftrightarrow w_0 &= y_i - \mathbf{w}\phi(\mathbf{x_i}) \; (for \; a_i \neq 0) \\
&= y_i - \sum_{l=1}^{n} a_l y_l K(\mathbf{x_l}, \mathbf{x_i}) \; (for \; a_i \neq 0) \\
\end{align}
新しい点$\mathbf{x}$が与えられたときに$w_0+\mathbf{w} \phi(\mathbf{x})$を計算し、その符号(±)によってその点がどちらの集団に属するか判別する。
カーネル関数Kについて
「なんでカーネル関数を↓のようにおくの?そうすると何でうまくいくの?」という話
K(\mathbf{u}, \mathbf{v}) = \exp(- \frac {||\mathbf{u} - \mathbf{v}||^2}{2 \sigma^2}) \\
特徴ベクトルΦから考える
$\phi(\mathbf{x})$は特徴ベクトルと呼ばれ$\phi(\mathbf{x}) = (\phi_1(\mathbf{x}), \cdots, \phi_r(\mathbf{x}) \cdots, \phi_M(\mathbf{x}))$とおくと、
K(\mathbf{x}, \mathbf{y}) = \phi(\mathbf{x}) \phi(\mathbf{y}) = \sum_{r=1}^{M} \phi_r(\mathbf{x}) \phi_r(\mathbf{y})
と表せる。$\phi_r(\mathbf{x})$一つ一つは、例えば$\phi_1(\mathbf{x}) = x_1^2$や$\phi_2(\mathbf{x}) = x_1 x_2$といったように、$\mathbf{x}$の成分を組み合わせたような形となる。
このままだと$\mathbf{x}$の次数が増えるにつれて$\phi(\mathbf{x})$の次数$M$は急激に増えてき、$K(\mathbf{x}, \mathbf{y})$計算量が膨大になり大変なことになる。
ここで
\phi_r(\mathbf{x}) = C e^{-2a(x-r)^2}
と設定し、「$r$が実数全体を動ける」=「$\phi(\mathbf{x})$は(連続無限個成分があるような)無限次元ベクトル」とすると$\sum$が$\int$となり
\begin{align}
K(\mathbf{x}, \mathbf{y}) = &\phi(\mathbf{x}) \phi(\mathbf{y}) \\
= &\int_{-\infty}^{\infty} \phi_r(\mathbf{x}) \phi_r(\mathbf{y}) dr \\
&\vdots \\
= & \exp(-a ||\mathbf{x} - \mathbf{y}||^2) \\
= & \exp(- \frac{||\mathbf{x} - \mathbf{y}||^2}{2 \sigma^2}) \\
\end{align}
と表せ、無限個の特徴量の積分が、簡単な関数であらわせるようになった!(←ココが凄い)。($a=\frac{1}{2 \sigma^2}$とした)
このとき、$K(\mathbf{x}, \mathbf{y})$は無限個の特徴量$\phi_r$を含んでいるので、「無限個の特徴量を含んでいれば、役に立つ特徴量も入ってるよね」という考え方。
解説と途中計算は、「機械学習におけるカーネル法について」と、そこから参照されている「ガウスカーネルとその特徴ベクトル」がわかりやすかったです。
Introduction to Kernel Methodsと、コレで紹介されている本読んだらわかるかも
w0+wΦ(x)の式をそのまま見てみる
数学的には↑の考えだけど、完全には理解できてないので$w_0+\mathbf{w} \phi(\mathbf{x})$をそのまま考えてみる。
$(ii)$より
\begin{align}
w_0 + \mathbf{w} \phi(\mathbf{x}) &= w_0 + \sum_{i=1}^{n} a_i y_i K(\mathbf{x_i}, \mathbf{x})\\
K(\mathbf{x_i}, \mathbf{x}) &= \exp(- \frac {||\mathbf{x_i} - \mathbf{x}||^2}{2 \sigma^2}) \\
\end{align}
となる。ここで
- $||\mathbf{x_i} - \mathbf{x}||^2$は、既存の点$x_i$と新しい点$x$の距離(の二乗)
- ↑より、$$K(\mathbf{x_i}, \mathbf{x}) = \exp(- \frac {||\mathbf{x_i} - \mathbf{x}||^2}{2 \sigma^2})$$は、既存の点$x_i$と新しい点$x$が近いほど大きく、遠いほど小さくなる。(完全に重なると1になる)
- ↑より$$\mathbf{w} \phi(\mathbf{x}) = \sum_{i=1}^{n} a_i y_i K(\mathbf{x_i}, \mathbf{x})$$は、新しい点$x$の全ての既存の点$x_i$からの距離をもとに、$y = 1 ; or ; -1$どちら寄りなのかを表したもの。($a_i$によって点の影響度に重みがつけられている。)
- ↑を全体的なズレ(切片)$w_0$と足し合わせ、それの符号(±)によって$y = 1 ; or ; -1$のどちらの集団に属するか判定する。($w_0+\mathbf{w} \phi(\mathbf{x}) = 0$が境界線)