サポートベクターマシン(完全に分離できない場合)の考え方
- 参考にしたもの:機械学習のエッセンスの第05章「機械学習アルゴリズム」
- 基本的な考え方は「サポートベクターマシン」について参照
分け方(=境界の作り方)
- 直線・平面・超平面(完全に分離できる場合)(「サポートベクターマシン」について参照)
- 直線・平面・超平面(完全に分離できない場合)(=このページ)
- 曲線・曲面・超曲面
考え方
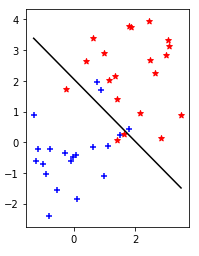
今回は、直線・平面・超平面ではキレイに分離できない場合の、境界として適した直線・平面・超平面の作り方を考える。
(↓こういう場合)
直線・平面・超平面(完全に分離できる場合)を参照すると、境界線を$w_0+\mathbf{w}\mathbf{x}=0$と置いたとき、
\begin{align}
Minimize \; &\frac{1}{2}|\mathbf{w}|^2 \\
Subject \; to \; &y_i(w_0+\mathbf{w}\mathbf{x_i}) \geq 1 \; (i=1, 2, \cdots, n) \\
\end{align}
という最適化問題を解いた。しかし$y_i(w_0+\mathbf{w}\mathbf{x_i})\geq1$は
「サポートベクタ(=境界に一番近い点)だと等号、サポートベクタ以外だと不等号となる」
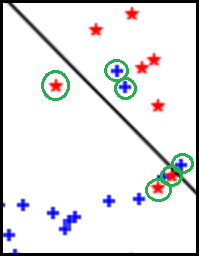
という意味の拘束条件だが、今回は反対側になるものも出てくる。(↓で緑丸に囲まれたもの)
コレらも考えるため、スラック変数と呼ばれる間違いの度合いを表す変数$\xi_i \geq 0 ; (i = 1, \cdots, n)$を考え、
- 判別が誤っている点(緑丸で囲まれた点)で$\xi_i > 0$
- 判別が正しい点(↑以外)で$\xi_i = 0$
と設定し、最適化問題を
\begin{align}
Minimize \; &C \sum_{i=1}^{n}\xi_i + \frac{1}{2}|\mathbf{w}|^2 \\
Subject \; to \; &y_i(w_0+\mathbf{w}\mathbf{x_i}) \geq 1 - \xi_i \; (i=1, 2, \cdots, n) \\
&\xi_i \geq 0 \\
\end{align}
のように表す。
- これは「境界に一番近い点との距離も小さくするけど、$\xi_i$(間違い度合い)の合計も小さくしよう」という意味。
- Cは調整のための定数で、Cが大きくなるほど$\sum_{i=1}^{n}\xi_i$の影響が大きくなるので、$\xi_i$を小さくしようとする力が強く働く。
**考え方はココまでで終わり。**コレ以降は数学・数値計算問題としての解き方。
図作ったときのコード置き場
解き方
これにラグランジュの未定乗数法(Wikipedia)、カルーシュ・クーン・タッカー条件(Wikipedia)を適用すると、ラグランジュ関数は
L(w_0, \mathbf{w}, \mathbf{\xi}, \mathbf{a}) = C \sum_{i=1}^{n}\xi_i + \frac{1}{2}|\mathbf{w}|^2 - \sum_{i=1}^{n} a_i \bigl(y_i(w_0+\mathbf{w}\mathbf{x_i}) - 1 + \xi_i \bigr) - \sum_{i=1}^{n}\eta_i \xi_i
となり、KKT条件は次のようになる。
\begin{align}
a_i &\geq 0 \\
y_i(w_0+\mathbf{w}\mathbf{x_i})-1 + \xi_i &\geq 0 \\
a_i \bigl(y_i(w_0+\mathbf{w}\mathbf{x_i})-1 + \xi_i \bigr) &= 0 \; \cdots (i)\\
\eta_i &\geq 0 \\
\xi_i &\geq 0 \\
\eta_i \xi_i &= 0 \\
\end{align}
\begin{align}
\frac{\partial L}{\partial w_0} = - \sum_{i=1}^{n} a_i y_i &= 0 \\
\Leftrightarrow \sum_{i=1}^{n} a_i y_i &= 0 \\
\end{align}
\begin{align}
\frac{\partial L}{\partial w_j} &= w_j - \sum_{i=1}^{n} a_i y_i x_{ij} = 0 \\
\Leftrightarrow w_j &= \sum_{i=1}^{n} a_i y_i x_{ij} \; \cdots (ii)\\
\end{align}
となるので、直線・平面・超平面(完全に分離できる場合)と同様に以下を最小にする$\mathbf{a}$を求め、$(i), (ii)$より$w_0, \mathbf{w}$を求めればよい
腑に落ちない点:
- $C \sum_{i=1}^{n}\xi_i$と$- \sum_{i=1}^{n} a_i \xi_i$の項どこ行った・・・?
- 機械学習のエッセンス内のPythonでの実装時、$(i)$から$w_0$求めるとき、$\xi_i$を無視してる(微小だから無視して良いって事?)
L(w_0, \mathbf{w}, \mathbf{\xi}, \mathbf{a}) = f(\mathbf{a}) = \sum_{k=1}^{n} a_k - \frac{1}{2} \sum_{k=1}^{n} \sum_{l=1}^{n} a_k a_l y_k y_l \mathbf{x_k} \mathbf{x_l}
ここで、
\begin{align}
\frac{\partial L}{\partial \xi_i} = C - a_i - \eta_i &= 0 \\
C - a_i &= \eta_i \geq 0 \\
a_i &\leq C \\
\end{align}
となるので、解くべき最適化問題は次のようになる。
\begin{align}
Minimize \; &f(\mathbf{a}) = \sum_{k=1}^{n} a_k - \frac{1}{2} \sum_{k=1}^{n} \sum_{l=1}^{n} a_k a_l y_k y_l \mathbf{x_k} \mathbf{x_l} \\
Subject \; to \; &\sum_{i=1}^{n} a_i y_i = 0 \\
&0 \leq a_i \leq C\\
\end{align}
Platによるアルゴリズム
直線・平面・超平面(完全に分離できる場合)と同様に、以下の流れで解いていく
- 最初に初期値$\mathbf{a^0}$を設定する。今回は$\mathbf{a^0}=(0, 0, \cdots, 0)$
- n個の点から、適当な$i, j$を選ぶ。(選び方は後述)
- $Minimize ; f(\mathbf{a})$となるよう$a_i, a_j$だけ変更する。
- 収束条件を満たすまで、2, 3を繰り返す。(収束条件は後述)
↑の3.「a_i, a_jだけ変更」について
基本の流れは直線・平面・超平面(完全に分離できる場合)参照
ただし、最後の拘束条件による修正は$0 \leq a_{i, j} \leq C$となるので、以下のようになる。
- $a_i$を求める。ただし、$a_i \leq 0$となったら$a_i = 0$、$a_i \geq C$となったら$a_i = C$とする。
- $a_j$を求める。ただし、$a_j \leq 0$となったら$a_j = 0$、$a_j \geq C$となったら$a_j = C$とする。
- 2で$a_j = 0 ; or ; C$となったら、$a_i$を計算しなおす。
↑の2.「i, jを選ぶ」, 4.「収束条件」について
\begin{align}
Minimize \; &f(\mathbf{a}) = \sum_{k=1}^{n} a_k - \frac{1}{2} \sum_{k=1}^{n} \sum_{l=1}^{n} a_k a_l y_k y_l \mathbf{x_k} \mathbf{x_l} \\
Subject \; to \; &\sum_{i=1}^{n} a_i y_i = 0 \\
&0 \leq a_i \leq C\\
\end{align}
にもう一度ラグランジュの未定乗数法(Wikipedia)、カルーシュ・クーン・タッカー条件(Wikipedia)を適用すると、ラグランジュ関数とKKT条件は次のようになる。($\mathbf{e}=(1, \cdots, 1)$)
f(\mathbf{a}) + \lambda \sum_{i=1}^{n} a_i y_i - \mathbf{\mu} \mathbf{a} - \mathbf{\nu} (C \mathbf{e} - \mathbf{a}) \\
\mu_k a_k = 0, \; \mu_k \leq 0, \; \nu_k (C - a_k) = 0, \; \nu_k \leq 0 \\
分離できる場合と同様にラグランジュ関数の$\mathbf{a}$についての勾配のt番目の成分を考えると、
\begin{align}
\nabla_a {f(\mathbf{a})}_t + \lambda y_t - \mu_t + \nu_t &= 0 \\
\nabla_a {f(\mathbf{a})}_t + \lambda y_t &= \mu_t - \nu_t \\
\end{align}
ここで、
\mu_t \left\{
\begin{array}{ll}
\leq 0 & (a_t = 0) \\
= 0 & (a_t > 0)
\end{array}
\right.
\nu_t \left\{
\begin{array}{ll}
\leq 0 & (a_t < C) \\
= 0 & (a_t = C)
\end{array}
\right.
より、
\nabla_a {f(\mathbf{a})}_t + \lambda y_t = \mu_t - \nu_t \left\{
\begin{array}{ll}
\geq 0 & (a_t > 0) \\
\leq 0 & (a_t < C)
\end{array}
\right.
\nabla_a {f(\mathbf{a})}_t \left\{
\begin{array}{ll}
\geq - \lambda y_t & (a_t > 0) \\
\leq - \lambda y_t & (a_t < C)
\end{array}
\right.
$y_t = 1 ; or ; -1$なので、両辺に$y_t$をかけると
y_t \nabla_a {f(\mathbf{a})}_t \left\{
\begin{array}{ll}
\geq - \lambda & (a_t > 0 \; and \; y = 1) \\
\leq - \lambda & (a_t < C \; and \; y = 1) \\
\leq - \lambda & (a_t > 0 \; and \; y = -1) \\
\geq - \lambda & (a_t < C \; and \; y = -1) \\
\end{array}
\right.
y_t \nabla_a {f(\mathbf{a})}_t \left\{
\begin{array}{ll}
\geq - \lambda & (a_t > 0 \; and \; y = 1) \; or \; (a_t < C \; and \; y = -1) \\
\leq - \lambda & (a_t > 0 \; and \; y = -1) \; or \; (a_t < C \; and \; y = 1) \\
\end{array}
\right.
ここからは分離できる場合と同様に考えると
- $(a_t > 0 ; and ; y = 1) ; or ; (a_t < C \; and \; y = -1)$で、$y_t \nabla_a f(\mathbf{a})_t$が最小値をとる$t$を$i$
- $(a_t > 0 ; and ; y = -1) ; or ; (a_t < C \; and \; y = 1)$で、$y_t \nabla_a f(\mathbf{a})_t$が最大値をとる$t$を$j$
のように$i, j$を選ぶと
y_j \nabla_a f(\mathbf{a})_j \leq y_i \nabla_a f(\mathbf{a})_i
と表せる。
これらが「2. n個の点から、適当な$i, j$を選ぶ」の選び方、「4. 収束条件を満たすまで、2, 3を繰り返す」の収束条件となる。