教師あり学習 ~入門者のメモ~ (scikit-learn)

本記事の内容

「東京大学のデータサイエンティスト育成講座」を読んで、scikit-learn の各モデルについての概要が掴めたので、忘れないうちにメモ。
書籍で言うと：Chapter 8 機械学習の基礎（教師あり学習）

初心者の自分にとっては、機械学習モデルの種類が多く感じてしまうので、シンプルに整理してみた。
実装サンプルのパラメータは、本の中で使ったもののみ。

scikit learn の機械学習モデル全体像

チートシート
ここでのポイントは、ザックリ、上が教師あり学習、下が教師なし学習。
今回は上の部分の説明。

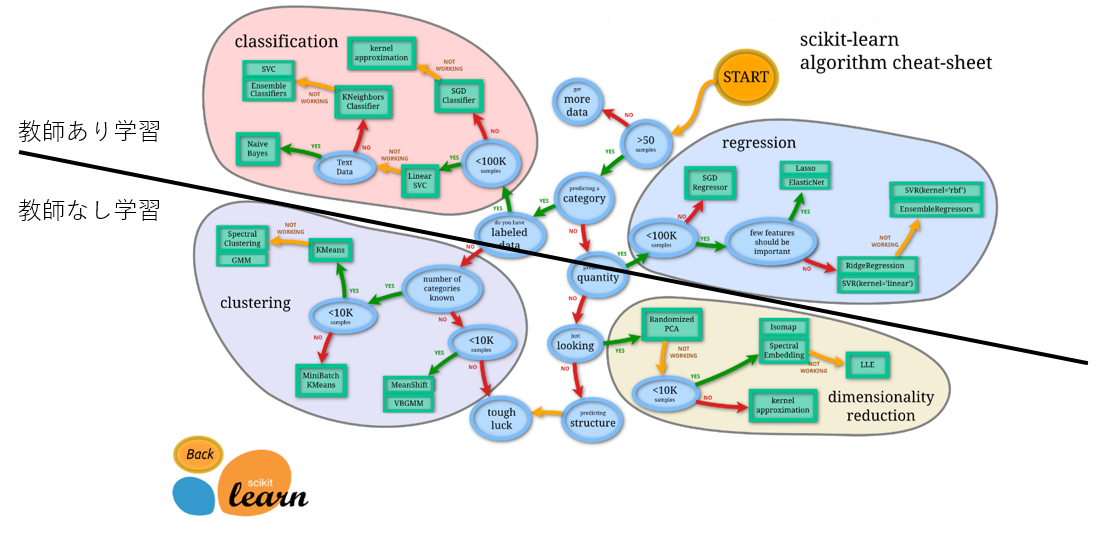
教師あり学習

• classification: 分類＝予測したい変数がクラス　（例：「合格／不合格」、「晴れ／曇り／雨／雪」）
• regression: 回帰＝予測したい変数が値　（例：体重「66.6kg, 32.3kg, ...」）

教師なし学習

• clustering: クラスタリング　（似ているデータのグループ化）
• dimensionality reduction: 次元削減　（多数の特徴=>少数の本質的な特徴に減らす、主成分分析とも）

教師あり学習

説明変数（または特徴量：Ｘ）から目的変数（y）を予測するモデルを求める手法。

教師あり学習モデルの全体像（例の本の８章）

雑に言えば、以下４つ。

1. 線形モデル
2. 決定木
3. kNN (k近傍法)
4. SVM (サポートベクターマシン)

それぞれに分類と回帰のモデルがある。

右側の図がポイント。

各論

モデルの詳細や数学的背景は他の記事が沢山あるので割愛（←まだ上手く説明できないだけ）

1. 線形モデル（linear model）

イメージ

線形なので、一次多項式（y=ax+by+cz）のイメージ
本当はこうみたい。

y = w_0x_0+w_1x_1+w_2x_2+\cdots

基本的なものだけでも複数のモデルがある。
正則化項のある回帰とか、名前がかっこよすぎて、どっちがどっちかいつも忘れる。

単回帰、重回帰

単回帰：説明変数が１つ。

y = ax+b

重回帰：説明変数が複数。

y = w_0x_0+w_1x_1+w_2x_2+\cdots

最小二乗法（「正解-予測値」の2乗の総和=正解からどれぐらいかけ離れているかというペナルティを最小にする方法）で各項の最適な係数(重み)を求める。
以下の損失関数（loss function）が最小になれば勝ち。

loss = \sum_{i=1}^n(y_i-f(x_i))^2

モデル作成

from sklearn.linear_model import LinearRegression
model = LinearRegression()

パラメータ：あれ、何も設定しなかったや。。

ラッソ回帰、リッジ回帰

正則化の話。
正則化とは、ザックリ言うと、モデルが複雑になり過ぎるのを防ぐ手法。
訓練データに適応し過ぎるが故に未知のデータをいい感じに予測できない現象（=過学習）を防ぎたい。ほんで、汎化性能（テストデータのような未知のデータに対する予測精度）を高めたい。
ペナルティに正則化項（モデルが複雑になると大きくなる）を加えることで、複雑になることを防ぐ。

loss = \sum_{i=1}^n(y_i-f(x_i))^2+\lambda\sum_{j=1}^m|w_j|^q

ラッソ(Lasso): q=1: 正則化項（L1ノルム）=重みの(1乗の)総和を加える
リッジ(Ridge): q=2: 正則化項（L2ノルム）=重みの2乗の総和
ルンバ(roomba):ロボット掃除機
思わず「あいうえお作文」したくなる。

ついでに、本の内容超えるけど、以下のポイントを風の噂で聞きました。知らんけど。

Lasso は、不要な説明変数（特徴量）の係数を0にしてくれるので、不要なパラメータを削りたい時に便利らしい（スパース推定だってさ）。おや、教師なし学習の次元削減と、どう使い分けるのだろう・・・？？？
Ridge は、多重共線性（相関の高い特徴量が含まれるため、それらの係数がいい感じに決まらない）により通常の線形回帰では上手くいかない場面でも、いい感じに推定できるようにしてくれるらしい。

因みに、L1ノルムとL2ノルムを合体させると Elastic Net ！だってさ。知らんけど。

ついでに、正則化項（Lpノルム）をグラフにしたら**こんな感じらしいっす。
ついでに、ここ**の「Ridge回帰」のとこにある図が気に入った。（って、おい、上からｗ）

ついでのついでに、なんで、Lasso の場合だけ係数（パラメータ）を0にできるかと言うと・・・パラメーターの値を変える意味合いが違うんだって。
Ridge の場合、パラメーターの二乗がペナルティ＝大きい値のパラメータを小さくするほうが、元々小さい値のパラメータをさらに小さくするより効果ある（そりゃそうだね）。だから、特定のパラメータを0に近づけるより、別の大きなパラメータを減らす方向に動く。なので、係数が0になりにくいとのこと。
Lasso の場合、パラメーターの絶対値なので、元々の値の大きさに関わらず、係数を1小さくしたら、ペナルティが1減る。なので、簡単に0まで減らせる。だってさ。（そうだよね）

モデル作成（Lasso）

from sklearn.linear_model import Lasso
model = Lasso(alpha=1.0, random_state=0)

パラメータ：alpha（上の loss にある「λ（ラムダ）」の値、default=1）

モデル作成（Ridge）

from sklearn.linear_model import Ridge
model = Ridge(random_state=0)

パラメータ：random_state

ロジスティック回帰（Logistic Regression）

線形モデルで分類問題を解くにはコイツ。
シグモイド(sigmoid)関数とか使うと、二値分類ができる。多クラス分類は、それを「１対その他」に拡張するだけ。グラフだと分かりやすいが、以下の x の部分にさっきの一次多項式が入る予定。

何となく、yが50%以上の奴らは上、それ以外は下って分類すればよさそうだけど、この閾値（50%）をどこに設定するかというのも重要。

モデル学習の過程では、予測値が正解に近づくように、正解から遠い予測値が出されるとペナルティが大きくなるように定義された損失関数を使う。ペナルティが最小になるようにモデルを構築できれば（=いい感じの係数を見つけられれば）勝ち。
ペナルティ（交差エントロピー誤差）はこんな感じ。

関数にするなら、
(教えて！google先生「y=- log x graph」)

-log(予測値)

0が正解の場合は、関数を左右反転。
(教えて！google先生「- log -(x-1) graph」)

-log(-(予測値-1))

モデル作成

from sklearn.linear_model import LogisticRegression
model = LogisticRegression()

パラメータ：あれ、何も設定しなかったや。。

2. 決定木（Decision Tree）

前処理が楽。（今回、前処理とか詳細割愛）
スケーリングが不要（分岐条件が値の大小関係なので影響がない）
何なら欠損値処理も不要（欠損値を特別な値として処理してくれる）

コンペでよく使われる xgboost とか LightGBM とかのベースになるやつやから、頑張って勉強しとこ。表面ツラだけ

てか、**ここ**見たらええよ、マジで。

分類

リンクの「分類木」参照、マジで。

モデル作成

from sklearn.tree import DecisionTreeClassifier
model = DecisionTreeClassifier(criterion='entropy', max_depth=5, random_state=0)

パラメータ：

• criterion : {“gini”, “entropy”}, default=”gini”
• max_depth : 木の最大深さ

回帰

リンクの「回帰木」参照、マジで。

モデル作成

from sklearn.tree import DecisionTreeRegressor
model = DecisionTreeRegressor()

パラメータ：あれ、何も設定しなかったや。。

3. kNN (k-Nearest Neighbor: k近傍法)

属性が近いk個による多数決

てか、**ここ**見たらええよ。マジで。（キノコの話、おもろ）

分類

キノコの種類、教えて～（リンク先PDF参照）

モデル作成

from sklearn.neighbors import KNeighborsClassifier
model = KNeighborsClassifier(n_neighbors=5)

パラメータ：n_neighbors : k個の数

回帰

キノコの直径、教えて～（リンク先PDF参照）

モデル作成

from sklearn.neighbors import KNeighborsRegressor
model = KNeighborsRegressor(n_neighbors=5)

パラメータ：n_neighbors : k個の数

4. SVM (Support Vector Machine: サポートベクターマシン)

カテゴリを識別する境界線を、マージンが最大になるように引く手法。
図で言うと、左でも右でもなく、真ん中。

てか、**ここ**見たらええよ。マジで。

分類

上の記事そのまんまやな。

モデル作成1

from sklearn.svm import LinearSVC
model = LinearSVC()

パラメータ：あれ、何も・・・(ry

モデル作成2

from sklearn.svm import SVC
model = SVC(probability=True)

パラメータ：

• probability : 予測の結果として、最終的に判断された分類クラスではなく、各分類クラスに該当する確率を取得できる関数 predict_proba を使うには True にする必要がある。

回帰

だから**ここ**見たらええって。マジで。

モデル作成

from sklearn.svm import SVR
model = SVR()

パラメータ：あれ、何も・・・(ry

実装

処理の流れ

1. モデル作成（上の各論参照）
2. モデルの訓練
3. モデルの評価

# モデルは何でもいいよ。ここでは重回帰。
model = LinearRegression()
# 訓練
model.fit(X_train, y_train)
# 評価
print('train:', model.score(X_train, y_train))
print('test:', model.score(X_test, y_test))

model.score について

0 ～ 1 の値で、実際は以下を計算している。
分類の場合、accuracy
回帰の場合、決定係数: R^2

もっと全体像

import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression

# データロード
iris = load_iris()

# テストデータを分割
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=0)

# モデルの構築～評価
model = LogisticRegression()
model.fit(X_train, y_train)
print('train:', model.score(X_train, y_train))
print('test:', model.score(X_test, y_test))

結果：
train: 0.9821428571428571
test: 0.9736842105263158

モデル比較

import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC

iris = load_iris()

X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=0)

models = {
    'linear': LogisticRegression(),
    'tree': DecisionTreeClassifier(),
    'knn': KNeighborsClassifier(n_neighbors=3),
    'svm': SVC()
}

scores = {}

for name, model in models.items():
  # モデルの構築～評価
  model.fit(X_train, y_train)
  scores[(name, 'train')] = model.score(X_train, y_train)
  scores[(name, 'test')] = model.score(X_test, y_test)

pd.Series(scores).unstack()

結果：

モデルの評価

ここにきて、モデルの評価について。
書籍では10章だが、教師あり学習について語っているので、こちらで。

モデルの評価指標

分類と回帰で、それぞれの評価指標がある。

分類

分類問題の指標として、混同行列とAUCがある。

混同行列

下の表の通り。これをベースに関連指標がある。

	Predict:Positive	Predict:Negative
Actual:Positive	True Positive	False Negative
Actual:Negative	False Positive	True Negative

実装

from sklearn.metrics import confusion_matrix
y_pred = model.predict(X_test)
confusion_matrix(y_test, y_pred)

結果（例）：
array([[49, 4],
[ 9, 81]])

関連指標

• 正解率（accuracy）：全体に対する正答の割合
  accuracy = (TP + TN) / (TP + FP + FN + TN)

• 適合性（precision）：１と予測した中で、実際に１であった割合
  precision = TP / (TP + FP)

• 再現性（recall）：実際に１であった中で、１と予測した割合
  recall = TP / (TP + FN)

• F1スコア（f1 score）：適合性と再現性の調和平均
  調和平均：逆数の算術平均の逆数（詳細はこちら）

F1 score = \frac{2}{\frac{1}{precision} + \frac{1}{recall}}

以上、図にしてみた。

AUC

各クラスに属する予測確率（0.0 ～ 1.0）と観測値（実際の値：0 or 1）との関係からモデルの性能を評価する。

不均衡データに対するモデルの評価に耐えられる指標。
例えば、病気の予測などにおいて、圧倒的に正例が少ない場合、accuracy だと True Negative のせいで正解率>90%となってしまい、正しく評価できない。そんな時に有効。

各クラスに属する予測確率は、svmの分類のところで言及した probability。
svm以外は特に事前のプロパティ指定は不要で、predict_proba を使えば求められる。

# y_pred: 各クラスに属する予測確率（0.0 ～ 1.0）
y_pred = model.predict_proba(X_test)

ROC 曲線（Receiver Operating Characteristic curve）
x軸に偽陽性率、y軸に真陽性率をとったグラフ。
図にした方が分かりやすい。

AUC (Area Under the Curve)は、ROC 曲線とx軸で囲まれた部分の面積。
ランダムな予測を y=x となる直線とすると、AUC=0.5。
完璧な予測で、AUC=1.0。

from sklearn.metrics import roc_curve, auc

# load_breast_cancer データの場合、
# model.predict_proba で 0, 1 のそれぞれのクラスに属する確率が返されるため、
# shape が (143,2)となる。
# ここでは、1に属する確率を見たいため、[:,1]とする。
y_pred = model.predict_proba(X_test_data)[:,1]

fpr, tpr, thresholds = roc_curve(y_test, y_pred)
roc_auc = auc(fpr, tpr)

# 作図
plt.plot(fpr, tpr)

回帰

• 平均二乗誤差：Mean Squared Error (MSE)
  MSE = 予測値と正解の差（残差）の二乗の総和：残差平方和（SSE）／サンプル数
  二乗しているので、スケールを戻すためにRootをとる： RMSE

• 平均絶対誤差：Mean Absolute Error (MAE)
  MAE = 残差の絶対値の総和／サンプル数
  二乗していないので、外れ値の影響を受けにくい。

• Median Absolute Error (MedAE)
  残差の絶対値の中央値。
  MAE よりもさらに外れ値に対して堅牢（ロバスト）。

• 決定係数：R2
  回帰モデルの score(y_test, y_pred) で計算される値。
  検証データの（答えの）平均値を（全検証データに対する）予測値とした場合に比べて、どれだけ誤差を削れたか。
  完全正解で1.0、平均値予測と同等で0.0、単純な平均値予測よりも外していると負の値。
  SSE(Sum of Squared Error): モデルの残差平方和
  SST(Sum of Squared Total): 検証データの平均値を予測値とした場合の残差平方和（二乗誤差）

R^2 = 1 - SSE/SST

実装

from sklearn.metrics import mean_absolute_error, mean_squared_error, median_absolute_error, r2_score

mean_absolute_error(y_test, y_pred)
mean_squared_error(y_test, y_pred)
median_absolute_error(y_test, y_pred)
r2_score(y_test, y_pred)

モデルの検証方法

未知のデータに対する予測精度（汎化性能）を評価するのに、トレーニングデータの一部をテストデータとして用いる。
予め、一部を別にとっておき、残りのデータで訓練・モデル構築した上で、別にしたデータを使って予測させ、未知のデータを正しく予測できているか、確認する。

	train - 高スコア	train - 低スコア
test - 高スコア	理想（ここを目指す）	-（汎化性能は担保されない）
test - 低スコア	過学習(overfitting)	学習不足(underfitting)

トレーニングデータのみスコアが高い場合は、過学習(over fitting)。この場合、未知のデータに対する汎化性能がよくないので、正規化や次元削減（特徴選択／特徴抽出）で、トレーニングデータとテストデータのスコアの差が小さくなるようにする。
トレーニングデータもテストデータもスコアが低い場合は、学習不足(under fitting)。この場合、新しくデータを収集する、データを水増しする、新しい特徴量を追加する、特徴量同士の比率などで特徴量を増やす、などがある。いずれにせよ、訓練データの行・列を増やす必要がある。

ホールドアウト法

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y)

これで、訓練データとテストデータを分ける方法。

分割結果の偏り、例えば患者データを２つに分けた時、１つ目のグループには癌患者のデータがほとんどで、２つ目のグループには健康な人のデータばかり、のようになってしまうことを防ぐために、stratify パラメータで偏りを防ぐことができる。
例：train_test_split(X, y, stratify = y)

random_state でランダムシードを指定することで、分割に再現性を持たせることができる。
例：train_test_split(X, y, random_state = 0)

欠点

1. 分割がランダムであるがゆえ、特定の分割によっては、たまたまテストデータがハイスコアとなってしまうことがある。
2. トレーニングデータを減らしてテストデータを準備しているため、学習が十分に進まない。

交差検証 (Cross Validation)

上記の欠点を補完するため、検証を繰り返すことによって、限られたデータを最大限活用する手法。
これはデータの役割を学習用と検証用に交差（交換）させる手法。

k分割交差検証（k-fold法）

データをk個に分割し、そのうち１つをテストデータ、残りをトレーニングデータとして学習させる・・・というのを分割された各データセットに繰り返し、テストデータのk個のスコアの平均を、そのモデルの評価値とする。（図で表した方がいいけど、なぜか今は割愛）

from sklearn.model_selection import cross_val_score
scores = cross_val_score(model, X_train, y_train, cv=5)
scores.mean()

１個抜き交差検証（leave-one-out）

ラベル付きデータのうち、1つだけを検証データとし、残りで学習する。
これを全データについて繰り返す。
データがかなり少ない場合、この手法。

from sklearn.model_selection import cross_val_score, LeaveOneOut
scores = cross_val_score(model, X_train, y_train, cv=LeaveOneOut())
scores.mean()

cvに設定するだけでいいんだ・・・

パフォーマンスチューニング

パフォーマンスチューニングでは、ハイパーパラメータチューニングと特徴量の扱いが記載されていた。
特徴量の扱いについては、上の「モデルの検証方法」にて記載済みなので割愛。
ここでは、ハイパーパラメータチューニングのグリッドサーチについて記載。

Grid Search

指定したパラメータの全ての組み合わせについて、モデルの構築、検証を行う。
書籍ではCとgamma について、チューニングを行っている。
Cとgamma の意味についてはこちら。

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split

from sklearn.datasets import load_breast_cancer
from sklearn.preprocessing import StandardScaler

cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, stratify = cancer.target, random_state=0)

# ここから
from sklearn.metrics import GridSearchCV
from sklearn.svm import SVC

param_grid = {
    'C': np.logspace(-3, 2, num=6),
    'gamma': np.logspace(-3, 2, num=6),
}

gs = GridSearchCV(estimator=SVC(), param_grid=param_grid, cv=5)
gs.fit(X_train, y_train)

print('Best score:', gs.best_score_)
print('Best params:', gs.best_params_)
print('test score:', gs.score(X_test, y_test))

Optuna (番外編)

書籍には無かったが、上と同様の内容を便利な「ハイパーパラメータ自動最適化フレームワーク」なるもので実装してみる。本家はこちら。

まずはパッケージのインストール。

!pip install optuna
import optuna

そして、いざ、最適化！

import optuna
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.svm import SVC

# 目的関数を定義
def objective(trial):
  cancer = load_breast_cancer()
  X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, stratify = cancer.target, random_state=0)
  
  # パラメータ振ってる
  trial.suggest_categorical('kernel', ['linear', 'rbf', 'poly', 'sigmoid', 'poly'])
  trial.suggest_float('C', 1e-3, 1e2, log=True)
  trial.suggest_float('gamma', 1e-3, 1e2, log=True)
  trial.suggest_int('degree', 2, 10)

  scores = cross_val_score(SVC(), X_train, y_train, cv=5)

  return scores.mean()

# 目的関数を最大化する方向
study = optuna.create_study(direction='maximize')
# 最適化
study.optimize(objective, n_trials=100)
# 最適なトライアルを表示
print(study.best_trial)

・・・結果、変わらんかった orz
kernel と degree も変えてみたけど、best trial は常に最初の１回目。
scikit-learn の他の dataset （分類／回帰）で SVM モデル試したけど、簡単なパラメータではすべて同様で面白い結果は得られなかった。

アンサンブル学習

バギング、ブースティング、スタッキングの３つでＯＫ。
決定木の話はこちらのスライドが面白かった。

バギング

Bootstrap Aggregat ing
データからランダムサンプリング（復元抽出）したブートストラップ標本から学習したモデルを平均するだけ。
高分散、低バイアスの手法に対して有効。
sklearn.ensemble の RandomForest (Regressor/Classifier)とか、既に実装されている。

ブースティング

バギングは平均化、ブースティングは最適化。
モデル生成＝＞これまでのモデルで説明できない部分を説明するモデルを生成
を繰り返す。
sklearn.ensemble の GradientBoosting (Regressor/Classifier)とか、既に実装されている。

スタッキング（番外編）

ここが激しく分かりやすいので、丸投げ。
実際のコンペでは、みんなスタッキングしてるんだろーなと。

まとめ

今回学んだ教師あり学習のモデルは以下４つ。

1. 線形モデル
2. 決定木
3. kNN (k近傍法)
4. SVM (サポートベクターマシン)

それぞれに、回帰と分類のためのモデルがあるよ。

今回学んだモデルの評価は以下だよ。

• 回帰
  • MSE
  • MAE
  • MedAE
  • 決定係数
• 分類
  • 混同行列（正解率・適合率・再現率・F1スコア）
  • AUC

感想

こうやって整理してみると、モデルの概要は結構シンプル。
説明書いたのほぼ線形モデルのみで、あとはリンク集（苦笑）。
今後、気が向いたら深堀していけばいいと思うけど、理論の詳細を追いかけるより、xgboost とか LightGBM とか使ってスコア改善する方が楽しそう。
近いうちに9章の教師なし学習についてもメモしたい。
メモしたので、こちら
(2020.1.30) - 10章：モデルの評価を追記した。