教師なし学習 ~入門者のメモ~ (scikit-learn)

本記事の内容

「東京大学のデータサイエンティスト育成講座」を読んで、Chapter 9 機械学習の基礎（教師なし学習）のメモ。

scikit learn の機械学習モデル全体像

チートシート
ここでのポイントは、ザックリ、上が教師あり学習、下が教師なし学習。
今回は下の部分の説明。

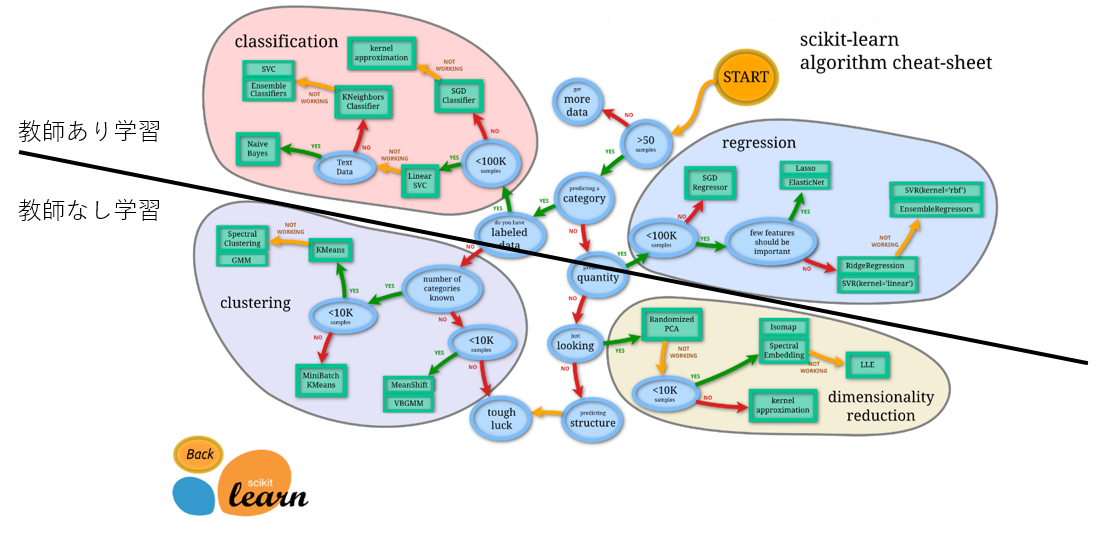
この記事の続き。

教師なし学習

目的変数がない学習モデル。
データに潜む構造やインサイトの発見のための探索的分析(Exploratory Data Analysis)として活用。
教師あり学習の特徴量を検討するため、前段階のEDAで使われるなど。

種類

書籍では、以下の３つを取り上げていた。

1. クラスタリング
2. 次元削減（主成分分析）
3. マーケットバスケット分析

マーケットバスケット分析については、ビジネス的に意味のある割合を専門用語で定義付けしているだけに見えたので、割愛。

クラスタリング

データをいくつかの類似グループに分類する手法。
今回、k-means法しか詳細説明がなかったものの、手法がいくつかあるらしい。

まずは、階層的かどうか。

• 階層的手法
  各データを１つのクラスタとみなし、距離が近いクラスタを段階的に結合する手法。
  下のトーナメント表のようなもの（デンドログラム）を作成するイメージ（各色の線の長さが距離を表してたりする）。
  

• 非階層的手法
  決められたクラスタ数でデータを分割し、最適となる分割方法を探索する手法。
  

続いて、ハードかソフトか。

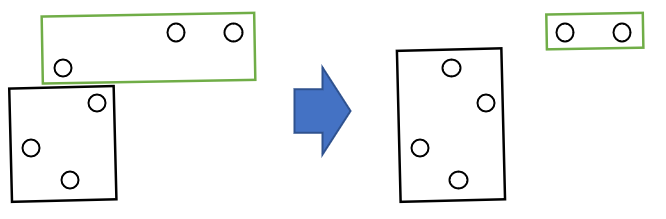
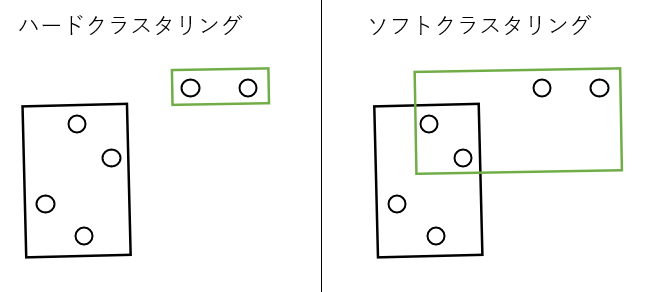
• ハードクラスタリング
  各データは１つのクラスタにのみ属する。
  属するクラスタを予測。

• ソフトクラスタリング
  各データが複数のクラスタに属することを許容。
  各クラスタに属する確率を予測。

今回学習した k-means法は以下の通り。

	ハードクラスタリング	ソフトクラスタリング
階層的手法
非階層的手法	k-means法

他の手法は、おいおいということで・・・

k-means法

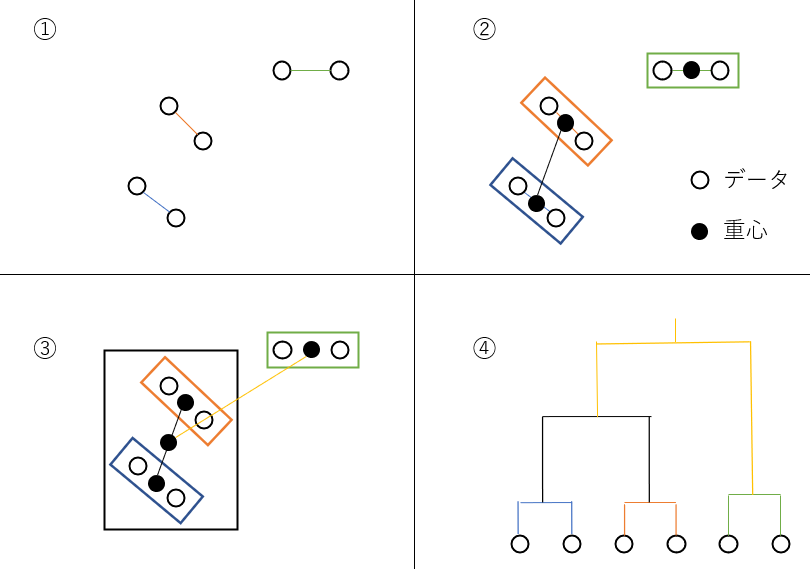
クラスタリングと重心計算による中心移動を繰り返し、所与のクラスタ数に分割する手法。

1. ランダムにk個のクラスタ中心をプロット
2. データと各クラスタ中心の距離を計算し、最も距離の短いクラスタに属すると仮定
3. 全データに繰り返す
4. 仮定したクラスタに属するデータ群の重心を求める
5. 求めた重心にクラスタ中心を移動
6. クラスタ中心の位置が変わったので、データとの距離も変更となり、再度、上記2.から繰り返す
   

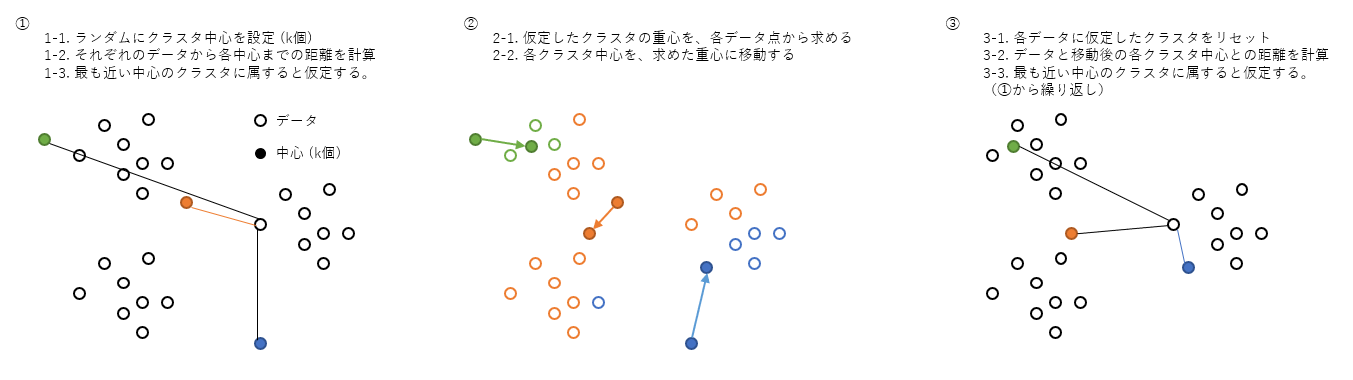
そもそも k個って明確に言えないことも多そう。。。
=> クラスタ数の推定へ

実装

from sklearn.cluster import KMeans

# モデル作成
model = KMeans(init='random', n_clusters=3)
# 重心計算
model.fit(X_train)
# 各データの所属クラスタを予測
y_pred = model.predict(X_train)

パラメータ：
init: 中心の初期化方法
n_clusters: クラスタの数

クラスタ数の推定

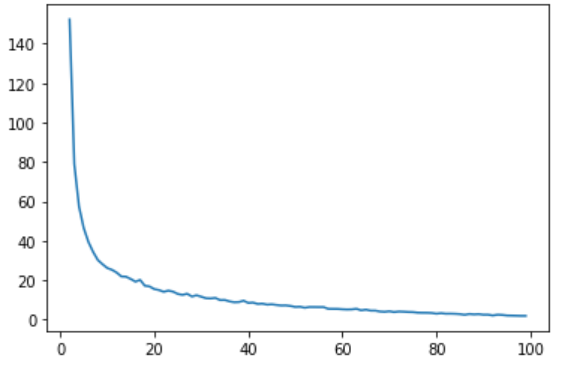
１つの手法として、エルボー法の紹介。

クラスタ中心と各データとの距離の総和を指標として、クラスタ数を増やしていくと、どれだけ距離の総和が減っていくかを確認する。
ある程度増やすと、減りが悪くなるので、そのあたりがいい感じのクラスタ数。

距離の総和は KMeans.inertia_ で取得可能。

試しに、おなじみ iris のデータで、クラスタ数100ぐらいまでプロットしてみた。

import pandas as pd
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans

iris = load_iris()

distortion = {}

for i in range(2, 100):
  kmeans = KMeans(init='random',n_clusters=i)
  kmeans.fit(iris.data)
  distortion[i] = kmeans.inertia_

pd.Series(distortion).plot.line()

クラスタ数 10 ぐらいまでの減り方が顕著。
本当は3だけど・・・

次元削減（主成分分析）

説明変数の種類を減らす方法。
主成分分析(Principle Component Analysis)という手法がよく使われる。

数学的詳細に立ち入るには、固有ベクトルの話をしなきゃなんだろうけど、小難しい話は一気に端折って、２変数を１変数に次元削減するイメージは以下の通り。

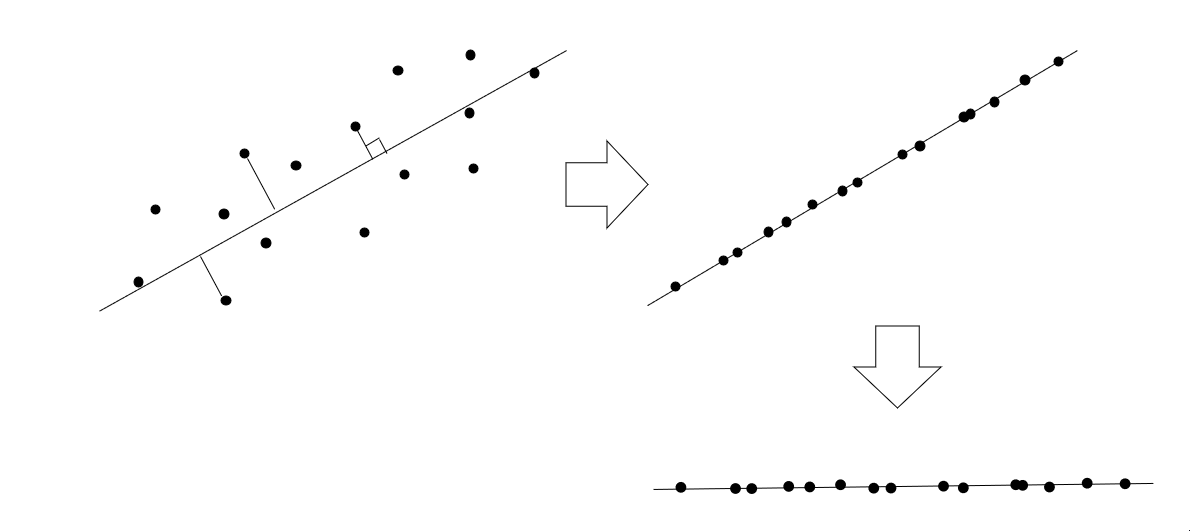
分散が最大の方向に新たな軸をとって、そこに射影していくイメージ。
３次元＝＞１次元ぐらいまでならイメージできそうだけど、それ以上は直感的には無理。
次元削減するからには、全体の情報量としては減少しているはずで、それがどの程度なのかを表すのに、やっぱり分散を使うらしい。
PCAクラスの属性で各主成分の分散やその比率が確認できる。

• explained_variance_
• explained_variance_ratio_

教科書では、乳がんデータで例示しているが、素のデータのままだと明確な線引きができそうもないように見えるのだが、主成分分析すると、かなり明確に線引きできるようになる。恐るべし・・・

多重共線性の対策になるのかな、とか、読んで字のごとく、最も特徴を表しているパラメータを抽出できるんだろうな、とか、色々思う。

余談として、主成分分析の前にスケーリングをした方がいいのか、必ずしも標準偏差で割ることがベストではないという記事もあったような・・・

実装

# 標準化
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_std = sc.fit_transform(cancer.data)

# PCA
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
# 固有ベクトルの計算
pca.fit(X_std)
# 主成分を求める
X_pca = pca.transform(X_std)

# variance 確認したり、plot とか

• n_components: 固有ベクトル（主成分）の数を指定

総合演習

最後に、総合演習問題(4)で、ハイブリッドアプローチなる、「教師なし学習（クラスタリング＋次元削減）」からの「教師あり学習」の流れの説明があり、なかなか良いなと思ったのでメモ。
ついでだから、パイプラインを使ってハイパーパラメータチューニングしてみた。
パイプラインも、ハイパーパラメータチューニングで使うには大変便利。
（Kaggle のコースでは imputer と scaler / encoder を組み合わせた前処理に使ってたけど、あまり便利さを実感できなかった・・・数値・カテゴリそれぞれでやれば２回じゃん的な・・・）

import warnings
# 警告非表示
warnings.simplefilter('ignore')

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split

from sklearn.datasets import load_breast_cancer
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression

# データロード
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, stratify = cancer.target, random_state=0)

# 標準化
sc = StandardScaler()
sc.fit(X_train)
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)

# 単純な教師あり学習
model = LogisticRegression()
clf = model.fit(X_train_std,y_train)
print('================== Simple Logistic Regression ==================')
print("train:",clf.__class__.__name__ ,clf.score(X_train_std,y_train))
print("test:",clf.__class__.__name__ , clf.score(X_test_std,y_test))


# 教師なし学習 - クラスタリング: k-means
from sklearn.cluster import KMeans
# クラスタ数: 5
kmeans_pp = KMeans(n_clusters=5)
kmeans_pp.fit(X_train_std)
y_train_cl = kmeans_pp.predict(X_train_std)
y_test_cl = kmeans_pp.predict(X_test_std)

# ダミー変数化
cl_train_data_dummy = pd.get_dummies(pd.DataFrame(y_train_cl, columns=['cl_nm']).astype('str'))
cl_test_data_dummy = pd.get_dummies(pd.DataFrame(y_test_cl, columns=['cl_nm']).astype('str'))

# 元々の説明変数のテーブルに結合：元々の説明変数＋クラスタ数の特徴量
X_train_data = pd.concat([pd.DataFrame(X_train_std), cl_train_data_dummy], axis=1)
X_test_data = pd.concat([pd.DataFrame(X_test_std), cl_test_data_dummy], axis=1)

y_train_data = pd.DataFrame(y_train, columns=['flg'])
y_test_data = pd.DataFrame(y_test, columns=['flg'])

# 教師なし学習 - 次元削減: PCA
from sklearn.decomposition import PCA
from sklearn.pipeline import Pipeline
from sklearn.model_selection import GridSearchCV

# パイプライン作成
p = Pipeline([['pca', PCA()],
              ['linear', LogisticRegression()]])

# ハイパーパラメータチューニング
params = {
    'pca__n_components': range(1, 12),
    'linear__C': np.logspace(-3, 2, 6)
}

# Grid Search による Cross Validation
gs = GridSearchCV(p, params, cv=3)
gs.fit(X_train_data, y_train_data)

print('\n================== Hybrid approach ==================')

print('Best score:', gs.best_score_)
print('Best param:', gs.best_params_)

print('test score:', gs.score(X_test_data, y_test_data))

実行結果

================== Simple Logistic Regression ==================
train: LogisticRegression 0.9906103286384976
test: LogisticRegression 0.958041958041958

================== Hybrid approach ==================
Best score: 0.9812206572769954
Best param: {'linear__C': 1.0, 'pca__n_components': 8}
test score: 0.9790209790209791