概要
SVM(Support Vector Machine)は分類精度の高い機械学習の手法として知られています.
SVMでより高い分類精度を得るには, ハイパーパラメータを訓練データから決定する必要があります.
この記事では, RBFカーネル(Gaussian カーネル)を用いたSVMのハイパーパラメータを調整することで, 決定境界がどのように変化するのかを解説します.
決めるべきハイパーパラメータ
RBFカーネルを用いたSVMでは, 以下の2つのハイパーパラメータを調整します.
- コストパラメータ: $C$
- RBFカーネルのパラメータ: $\gamma$
コストパラメータについて
SVMは特徴空間に写像されたデータ点集合を分離する超平面を決定する手法です.
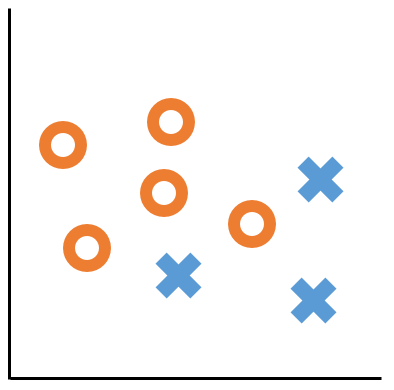
しかし, 特徴空間上の点集合がいつも分離可能とは限りません.
例えば, 以下の図では二種類の記号を完璧に分割するような直線を引くことはできません.
ここで, 誤分類を許容して直線を引き, 点集合を分割することを考えます.
例えば, 先ほどの図に以下のように直線を引いて二種類の記号を分割してみます.
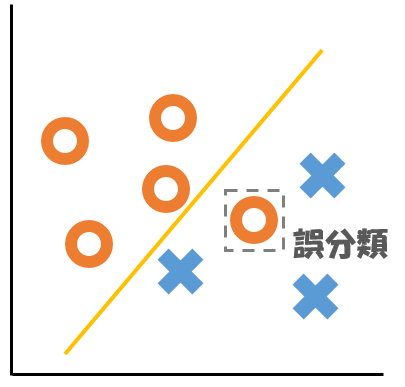
コストパラメータ$C$は, 誤分類をどの程度許容するかを決めるパラメータです.
$C$はSVMが解く2次計画問題の式に現れます.
\min_{\beta}\frac{1}{2}\|\beta\|^2+C\sum_{i=1}^{N}\xi_i
$C$が小さいほど誤分類を許容するように, 大きいほど誤分類を許容しないように超平面を決定します.
RBFカーネルのパラメータについて
RBFカーネルのパラメータ: $\gamma$は, 以下のRBFカーネルの式の中で現れます.
K(x, x')=\exp(-\gamma\|x-x'\|^2)
後述の実験で示しますが, $\gamma$の値が小さいほど単純な決定境界となり, 大きいほど複雑な決定境界となります.
実験
$C$と$\gamma$を極端な値に設定したときの決定境界を描いてみます.
$C$は$2^{-5}$と$2^{15}$に, $\gamma$は$2^{-15}$と$2^3$にそれぞれ設定しました.
SVMはscikit-learn(0.15)で実装されているものを使います.(内部ではLIBSVMが使われています.)
データセットはirisを使います.
irisは3つのクラスラベル, 4つの特徴量が含まれるデータセットです. 今回はその中から2つのクラスラベル, 2つの特徴量だけを使います.
問題を難しくするために, 2つの特徴量それぞれにノイズを加えます.
ソースコード
# -*- coding: utf-8 -*-
import numpy as np
from sklearn import svm, datasets
import matplotlib.pyplot as plt
from itertools import product
if __name__ == '__main__':
iris = datasets.load_iris()
#特徴量は最初の2つ, クラスラベルも最初の2つを使う
X = iris.data[:100, :2]
#特徴量にノイズを加える
E = np.random.uniform(0, 1.0, size=np.shape(X))
X += E
y = iris.target[:100]
#meshのステップサイズ
h = 0.02
#コストパラメータ
Cs = [2 ** -5, 2 ** 15]
#RBFカーネルのパラメータ
gammas = [2 ** -15, 2 ** 3]
svms = [svm.SVC(C=C, gamma=gamma).fit(X, y) for C, gamma in product(Cs, gammas)]
titles = ["C: small, gamma: small", "C: small, gamma: large",
"C: large, gamma: small", "C: large, gamma: large"]
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
for i, clf in enumerate(svms):
plt.subplot(2, 2, i + 1)
plt.subplots_adjust(wspace=0.4, hspace=0.4)
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.Paired, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired)
plt.xlabel("Sepal length")
plt.ylabel("Sepal width")
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.xticks(())
plt.yticks(())
plt.title(titles[i])
plt.show()
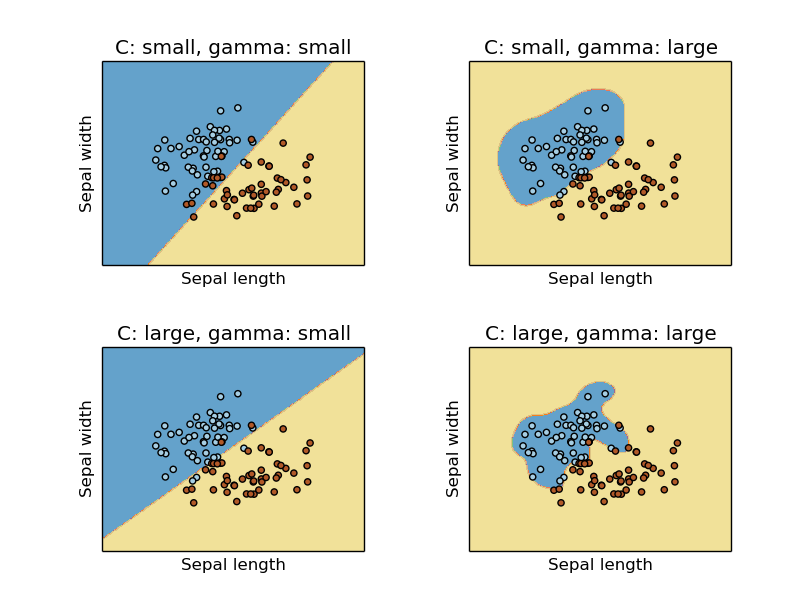
実行結果
横軸と縦軸はそれぞれ2つの特徴量を表しています.
$C$が小さいときは決定領域の中に多くの誤分類点を含んでいる一方で, $C$が大きいときは決定領域内の誤分類点が少なくなっています.
$\gamma$が小さいときの決定境界は単純な決定境界(直線)である一方で, $\gamma$が大きいときの決定境界は複雑な形をしています.
その他
$C$と$\gamma$を調整すると, 線形カーネルを使ったときの決定境界と似たようなものが得られるみたいです.
カーネル選択に迷ったらRBFカーネルを使っておけばオッケーという感じですが, どうしてもパラメータチューニングに時間がかかってしまいます.(´・ω・`)