為替レートを対象とするトレードは金融市場の中でももっとも成功する確率が低く、特に期間の短い取引は厳禁です。その難しさは参加者と情報の発信等、市場の構造にあります。国籍、年齢、業種、目的等、多様な参加者と国別の会計制度、経済指標の基準の違い、公表の方法、中央銀行・公的機関の立場など、同じ情報であっても、その立場によって全く解釈が違ってしまいます。客観的な分析が難しく、主観的なものの見方が市場を左右しています。特に、レバレッジ(借入)を用いた外国為替市場での売買は破綻の可能性が高く気を付けましょう。
ブレドンウッズシステムが崩壊し、固定相場から変動相場に移行して以来、多くの為替レートのモデルが発表されてきました。
- 物価
- 金利、
- 株価
- 貿易統計
等さまざまです。
しかし、万人が納得するモデルはできていません。また、実務家の間では、理論構造モデルが機能しないために、チャート分析、テクニカル分析のようなものが多く用いられています。特に移動平均はトレーディングの主要な道具のひとつです。
予測モデルを考える場合には2つのタイプのモデルを考えます。1つは確定的、または決定論的モデルというものです。この場合、予測はほぼ確実に実現します。もう一つは確率的モデルです。この場合には、ピンポイントの予測はできませんが、分布としての予測は可能です。リスクマネジメントには、確率的モデルが使われます。実はもう1つのタイプのモデルがあります。過去のデータをベースにモデルを作っていきます。説明が難しい部分は確率的なモデルに任せてしまいます。このタイプのモデル化では過去のパターンの組み合わせの数が勝負となります。予測について(翻訳) を参考にしてください。
データのダウンロード
そこでまずはFREDからデータをダウンロードします。経済データのダウンロード
またはエクセルで世界の経済データをダウンロード
# 初期化
%matplotlib inline
import pandas_datareader.data as web
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
import pandas as pd
from pandas.plotting import register_matplotlib_converters
# データの取得
start="1949/5/16"
dgs10 = web.DataReader("DGS10", 'fred',start).dropna()
dgs5 = web.DataReader("DGS5", 'fred',start).dropna()
dgs2 = web.DataReader("DGS2", 'fred',start).dropna()
dgs1 = web.DataReader("DGS1", 'fred',start).dropna()
j10 = web.DataReader("INTGSBJPM193N", 'fred',start).dropna()
j1 = web.DataReader("JPY12MD156N", 'fred',start).dropna()
fx = web.DataReader("DEXJPUS", 'fred',start).dropna()
n100 = web.DataReader("NASDAQ100", 'fred','1990/1/1').dropna()#
sp500 = web.DataReader("SP500", 'fred',start)#S&P 500© (SP500)
n225 = web.DataReader("NIKKEI225","fred",'1990/1/1').dropna()#nikkei225
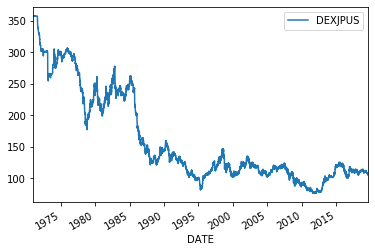
fx.plot()
長期のチャートでは対数を取らないと為替レートの桁違いの影響で、パターンの解釈を間違う可能性があります。システムトレードにおける対数の役割 を参照してください。
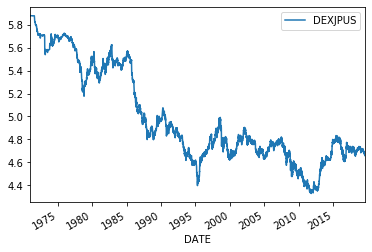
np.log(fx).plot()
少しイメージが変わりましたか?動きの偏りが全体に均一になりました。つぎは価格の変動性を見てみましょう。
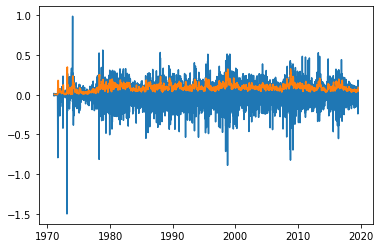
plt.plot((np.log(fx).diff()*np.sqrt(250)))
plt.plot(((np.log(fx).diff().dropna()).rolling(20).std()*np.sqrt(250)))
短期の動きと長期のボラティリティでは大分動きが違います。
ランダムウォーク
もしも為替レートがランダムウォークにしたがうのであれば、タイミングを計って取引をしても収益を上げることはできません。ランダムということは予測が的中しないということだからです。また、このランダムウォークという概念は経済学や計量経済学の分野でも注目されています。もしも為替レートがランダムウォークにしたがうとトレンドはたまたま発生した見せかけのトレンドである可能性があります。また、経済指標との関係を見るために相関をとったとしてもそれはたまたま発生した見せかけの相関を見ているかもしれません。ですから為替レートとランダムウォークの関係を把握しておくことは重要なことなのです。
期間を1994年8月まで、1994年9月―2007年12月と2008年以降の3つ期間に分けて分析します。統計的仮説検定を用いるとランダムウォークであるかどうかを判定できます。その手法をディッキー‐フラー検定といいます。帰無仮説はランダムウォークなので、仮説が棄却されれば確定的トレンドがある可能性があります。
y=np.log(fx.loc[:'1994/12/31'])
y.columns=['close']
rw=sm.tsa.adfuller(y.close,regression='nc')[1]
rwc=sm.tsa.adfuller(y.close,regression='c')[1]
rwct=sm.tsa.adfuller(y.close,regression='ct')[1]
rwctt=sm.tsa.adfuller(y.close,regression='ctt')[1]
print(rw,rwc,rwct,rwctt)
# 0.022684554184513497 0.904123882900183 0.5807982505339062 0.5779940716742864
統計的仮説検定では、まず帰無仮説を立てます。この場合は時系列の価格がランダムウォークにしたがうです。
出力の一番左はドリフト無しランダムウォークのp値です。この値が有意水準(0.05 または 0.1)以下であると、ドリフト無しランダムウォークであるという帰無仮説は棄却されますが。ドリフト無しランダムウォークが棄却されてもAR(1)である可能性が高く、それはほぼランダムウォークと同じと解釈できます。ですのであまり意味がありません。その右がドリフト付きランダムウォークです。価格差はドリフトを持ちます。これでは帰無仮説を棄却するには十分ではありません。その右はドリフト付き時間トレンドですが、p値は58%です。有意水準の10%よりもかなり大きいですが、この場合は棄却できる可能性もあると考えることができます。一番右はドリフト付き時間の2乗トレンドモデルですが、これも同じように解釈できます。別の期間も見てみましょう。
['1995/1/1':'2007/12/31']
print(rw,rwc,rwct,rwctt)
#0.7472257538180412 0.15680945162895915 0.4517869884620361 0.6268713605010524
結果は同じように解釈できます。
['2007/12/31':]
print(rw,rwc,rwct,rwctt)
# 0.6308957787993135 0.5696997804733883 0.37876955015093083 0.7959612941999099
結果は同じように解釈できます。つぎにそれぞれの期間について、より短い間隔をローリングして調べてみましょう。
def adfcheck(y,n):
prw=0
prwc=0
prwct=0
prwctt=0
prww=0
trial=len(y)
for i in range(0,len(y)-n,n):
y0=y.iloc[i:i+n]
rw=sm.tsa.adfuller(y0.close,regression='nc')[1]
rwc=sm.tsa.adfuller(y0.close,regression='c')[1]
rwct=sm.tsa.adfuller(y0.close,regression='ct')[1]
rwctt=sm.tsa.adfuller(y0.close,regression='ctt')[1]
if rw<0.1:
prw+=1
if rwc<0.1:
prwc+=1
if rwct<0.1:
prwct+=1
if rwctt<0.1:
prwctt+=1
if rwctt<0.1 or rw<0.1 or rwc<0.1 or rwct<0.1:
prww+=1
print(prw/trial,prwc/trial,prwct/trial,prwctt/trial,prww/trial)
print(prw,prwc,prwct,prwctt,prww)
y=np.log(fx)
y.columns=['close']
adfcheck(y,10)
# 0.0 0.028592197722316453 0.027299895000403845 0.02988450044422906 0.06243437525240288
# 0 354 338 370 773
結果の解釈はさらに難しくなります。帰無仮説を棄却できる期間は全体の数パーセントにすぎません。一番右の結果はそれぞれの判断をORで結合した結果です。大まかに言って全体の10%ぐらいが帰無仮説のランダムウォークを棄却できるということでしょうか?他の期間についても結果はほぼ同じです。
つまり、為替レートの動きはランダムウォークにしたがう可能性が高いということです。
大まかなトレンド
大まかなトレンドを主要な経済指標について見ておきましょう。ここで注意が必要なのは経済指標と為替レートの動きに関係がありそうに見えても見せかけの関係である可能性があるということです。まずは経済指標がランダムウォークにしたがうかどうかは気にせずに、見た感じの関係だけを見てみましょう。
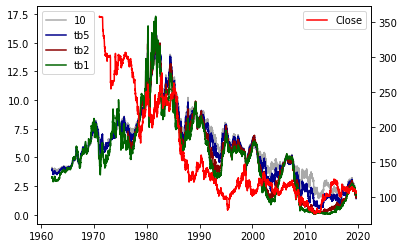
米金利と為替
fig, ax1 = plt.subplots()
ax2=ax1.twinx()
ax1.plot(dgs10,label='10',color="darkgray")
ax1.plot(dgs5,label='tb5',color="darkblue")
ax1.plot(dgs2,label='tb2',color="darkred")
ax1.plot(dgs1,label='tb1',color="darkgreen")
ax2.plot(fx,label='Close',color="red")
ax1.legend(loc='upper left')
ax2.legend()
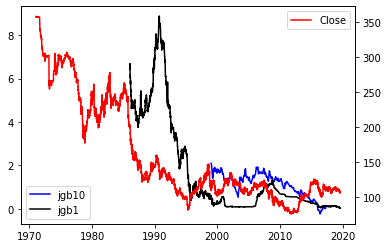
日本の金利と為替
fig, ax1 = plt.subplots()
ax2=ax1.twinx()
ax1.plot(j10,label='jgb10',color="blue")
ax1.plot(j1,label='jgb1',color="black")
ax2.plot(fx,label='Close',color="red")
ax1.legend(loc='lower left')
ax2.legend()
j10.count()
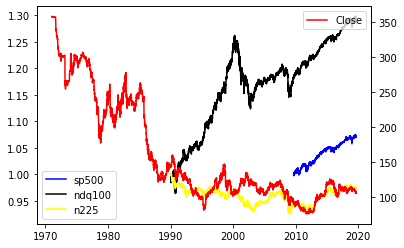
株価と為替
fig, ax1 = plt.subplots()
ax2=ax1.twinx()
ax1.plot(np.log(sp500)/np.log(sp500.iloc[0]),label='sp500',color="blue")
ax1.plot(np.log(n100)/np.log(n100.iloc[0]),label='ndq100',color="black")
ax1.plot(np.log(n225)/np.log(n225.iloc[0]),label='n225',color="yellow")
ax2.plot(fx,label='Close',color="red")
ax1.legend(loc='lower left')
ax2.legend()
米国金利、日本金利、株価とドル円の為替レートを見てきましたが、どうでしょうか?
そこで統計学を使ってみましょう。
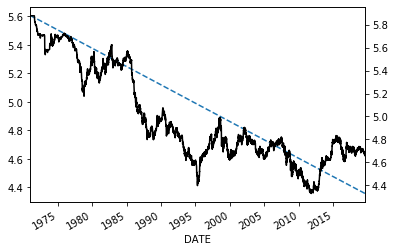
時間トレンドはあるのか?
cl=np.log(fx)
x=range(len(cl))
x=sm.add_constant(x)
model=sm.OLS(cl,x)
results=(model.fit())
print(results.summary())
fig, ax1 = plt.subplots()
ax2=ax1.twinx()
ax2.plot(cl,label='Close',color="black")
results.fittedvalues.plot(label='prediction',style='--',ax=ax1)
OLS Regression Results
==============================================================================
Dep. Variable: DEXJPUS R-squared: 0.765
Model: OLS Adj. R-squared: 0.765
Method: Least Squares F-statistic: 3.976e+04
Date: Thu, 22 Aug 2019 Prob (F-statistic): 0.00
Time: 18:10:52 Log-Likelihood: 2331.7
No. Observations: 12194 AIC: -4659.
Df Residuals: 12192 BIC: -4644.
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 5.6070 0.004 1548.969 0.000 5.600 5.614
x1 -0.0001 5.14e-07 -199.392 0.000 -0.000 -0.000
==============================================================================
Omnibus: 761.616 Durbin-Watson: 0.001
Prob(Omnibus): 0.000 Jarque-Bera (JB): 316.887
Skew: -0.161 Prob(JB): 1.55e-69
Kurtosis: 2.279 Cond. No. 1.41e+04
==============================================================================
長期の時間トレンドはありそうにありません。見た感じは予測トレンドを中心に実際の為替レートが上振れたり下振れたりしているのでトレンドがありそうですが、統計学でいう時間トレンドではありません。それはサマリーレポートの一番下のグループを見るとわかります。ここでは予測値と実際の値の誤差を分析しています。ここでの結果はモデルが正しくないと示唆しています。
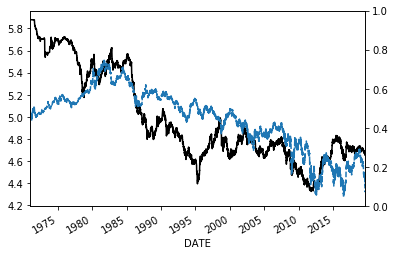
米国金利とドル円レートの関係
f=np.log(dgs10.DGS10)
lnfx=np.log(fx)
fm=pd.concat([f,lnfx],axis=1).dropna()
fm.columns=['f','fx']
x=fm.f
x=sm.add_constant(x)
#x['t']=range(len(fm))
model=sm.OLS(fm.fx,x)
results=(model.fit())
print(results.summary())
fig, ax1 = plt.subplots()
ax2=ax1.twinx()
ax1.plot(fm.fx,label='Close',color="black")
results.fittedvalues.plot(label='prediction',style='--',ax=ax1)
OLS Regression Results
==============================================================================
Dep. Variable: fx R-squared: 0.441
Model: OLS Adj. R-squared: 0.441
Method: Least Squares F-statistic: 9566.
Date: Thu, 22 Aug 2019 Prob (F-statistic): 0.00
Time: 18:10:52 Log-Likelihood: -2943.2
No. Observations: 12129 AIC: 5890.
Df Residuals: 12127 BIC: 5905.
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 4.1126 0.009 441.441 0.000 4.094 4.131
f 0.5069 0.005 97.804 0.000 0.497 0.517
==============================================================================
Omnibus: 814.532 Durbin-Watson: 0.001
Prob(Omnibus): 0.000 Jarque-Bera (JB): 990.630
Skew: 0.700 Prob(JB): 7.72e-216
Kurtosis: 2.998 Cond. No. 7.70
==============================================================================
とりあえずは長い期間の適合は無理そうです。
株価指数とドル円レートの関係
そこで株価指数を用いますが、期間を短くしてみましょう。
f1=n100
f2=sp500
f3=n225
f4=np.log(dgs2)
lnfx=np.log(fx)
fm=pd.concat([f1,f2,f3,f4,lnfx],axis=1).dropna()
fm.columns=['f1','f2','f3','f4','fx']
fm=fm[-120:] #ここで終わりから120個のデータを抽出しています。
x=fm.f1
x=sm.add_constant(x)
#x['f2']=fm.f2
x['f3']=fm.f3
#x['f4']=fm.f4
model=sm.OLS(fm.fx,x)
results=(model.fit())
print(results.summary())
fig, ax1 = plt.subplots()
ax2=ax1.twinx()
ax1.plot(fm.fx,label='Close',color="black")
results.fittedvalues.plot(label='prediction',style='--',ax=ax1)
OLS Regression Results
==============================================================================
Dep. Variable: fx R-squared: 0.817
Model: OLS Adj. R-squared: 0.814
Method: Least Squares F-statistic: 261.0
Date: Thu, 22 Aug 2019 Prob (F-statistic): 7.41e-44
Time: 20:49:55 Log-Likelihood: 427.02
No. Observations: 120 AIC: -848.0
Df Residuals: 117 BIC: -839.7
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 0.5285 0.316 1.674 0.097 -0.097 1.154
f1 -0.3094 0.018 -16.726 0.000 -0.346 -0.273
f3 0.6949 0.034 20.605 0.000 0.628 0.762
==============================================================================
Omnibus: 2.716 Durbin-Watson: 1.114
Prob(Omnibus): 0.257 Jarque-Bera (JB): 1.835
Skew: -0.069 Prob(JB): 0.399
Kurtosis: 2.410 Cond. No. 6.68e+03
==============================================================================
見た感じ大分よくなってきましたが、まだ不十分です。モデルとしては仕様はただしくありません。
このように為替レートのモデル化は大変に難しものです。統計学を用いる方法はいろいろな意味で制限があります。この制限をなくせばモデルはより柔軟になり、モデルの当てはまりはよくなります。しかし、その場合には過学習に陥る可能性があります。機械学習、人工知能等を用いると、確かに当てはまりはよくなります。しかし、実際の予測能力が向上するかどうかは不確かです。ここで、注意が必要なことはだからと言ってこれらの方法を否定することにはなりません。パターンの組み合わせの数が勝負なので、最善の注意を払いながら、うまく利用することが求められます。
購買力平価について見てみよう
長期の為替レートのモデルを考えるときに注目されるのが購買力平価と経常収支を基にしたモデルです。まずは購買力平価について見てみましょう。購買力平価とは国内のものの価格とある特定の外国の国の価格がどれくらい違うかを示したものです。または、双方の価格が同じになるためには為替レートがいくらでなければならないかを示しています。それで平価という名前が付いています。
購買力平価=日本の物価水準/外国の物価水準
一般に物価水準は消費者物価指数と生産者物価指数に分かれています。そこで両方について調べてみましょう。
start="1949/5/16"
billus =web.DataReader("TB1YR", 'fred',start).dropna() #1-Year Treasury Bill: Secondary Market Rate
billjp = web.DataReader("INTGSTJPM193N","fred",start)# Treasury Bills for Japan
fx = web.DataReader("EXJPUS","fred",start)# usdjpy
cpius =web.DataReader("CPIAUCSL", 'fred',start).dropna() #us consumer price index
ppius =web.DataReader("PPIACO", 'fred',start).dropna() #us producer price index
cpijp =web.DataReader("JPNCPIALLMINMEI", 'fred',start).dropna() #Japan consumer price index
ppijp =web.DataReader("PITGCG01JPM661N", 'fred',start).dropna() #Japan producer price index
X=pd.concat([fx,cpius,ppius,cpijp,ppijp],axis=1,join="outer").fillna(method='ffill')
#X=X.fillna(method='bfill',axis=0)
X.columns=['fx','cus','pus','cjp','pjp']
X=X.dropna()
X['cfx']=X.cjp/X.cus
X['pfx']=X.pjp/X.pus
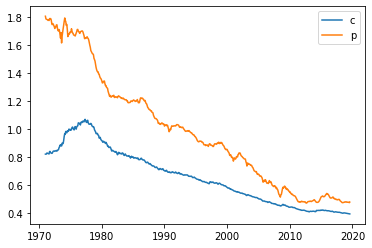
plt.plot(X.cfx,label='c')
#plt.plot(X.fx,label='fx')
plt.plot(X.pfx,label='p')
plt.legend()
第2次世界大戦後の日本の経済がいかに発展してきたかが分かります。戦後は米国の経済と圧倒的な差があったことが分かります。その状況はオイルショックまで続いていたと考えることができます。上述の計算は絶対的購買力平価と呼ばれるもので、これに基準となる為替レートを掛けると相対的購買力平価になります。しかし問題はどこを為替レートの基準値としたらよいのだろうかという点です。
経常収支(フローアプローチ)
ex = web.DataReader("XTEXVA01JPM667S", 'fred',start)#Exports: Value Goods for Japan
im = web.DataReader("XTIMVA01JPM667S", 'fred',start)#Imports: Value Goods for Japan
X=pd.concat([fx,ex,im],axis=1,join="outer").fillna(method='ffill')
#X=X.fillna(method='bfill',axis=0)
X.columns=['fx','ex','im']
X=X.dropna()
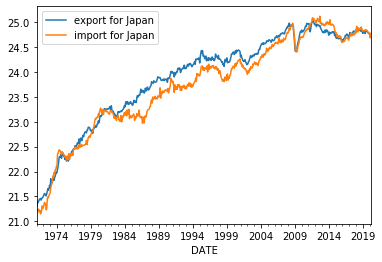
X.ex.plot(label='export for Japan')
X.im.plot(label='import for Japan')
plt.legend()
本当に日本が輸出に力を発揮したのはオイルショック以降であることが分かります。そして、
リーマンショック以降はじめてその傾向に変化が出たことが分かります。
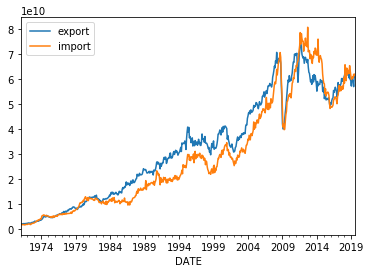
実は、このような場合は対数を取ったほうが良いです。
np.log(X.ex).plot(label='export for Japan')
np.log(X.im).plot(label='import for Japan')
plt.legend()
GDP
# annual
gdpus = web.DataReader("GDPCA","fred",start)*1000# Real Gross Domestic Product
gdpjp = web.DataReader("RGDPNAJPA666NRUG","fred",start)# Real GDP at Constant National Prices for Japan usd
X=pd.concat([gdpus,gdpjp],axis=1,join="outer").fillna(method='ffill')
#X=X.fillna(method='bfill',axis=0)
X.columns=['us','jp']
X=X.dropna()
X['us']=X.us#/X.us.iloc[0]
X['jp']=X.jp#/X.jp.iloc[0]
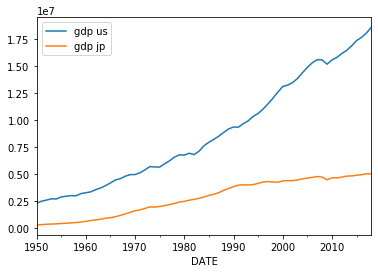
X.us.plot(label='gdp us')
X.jp.plot(label='gdp jp')
plt.legend()
国力の違いは鮮明です。バブル崩壊以後、その差はさらに開いています。
対数を取ってみましょう。
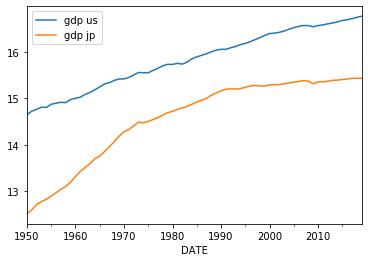
np.log(X.us).plot(label='gdp us')
np.log(X.jp).plot(label='gdp jp')
plt.legend()
どちらも対数の役割が明確です。
Python3ではじめるシステムトレード: システムトレードにおける対数の役割参照
よくある誤解
ニクソンショック以降、変動相場制に移行するとさまざまな為替レートのモデルが発表されました。しかし、1983年にはメーシーとロゴフ(1983)が論文を発表し各種経済時系列モデルでは為替レートの予測は難しいことを実証しました。それ以来、大した進展はありません。一方で為替レートは予測可能という論文も多数報告されています。その中でお粗末なものは為替レートの平均値を使ったモデルです。メーシーとロゴフの論文の中にも平均値を使うよりも、点で得られたデータを使わないと自己相関があり、そのようなデータを使ったとしても予測ができることにはならないとあります。このような誤解を招くような報告は結構あるので、実際に試してみましょう。
FREDから月次のデータをダウンロードします。これを四半期の平均値のデータに変換します。月次のデータはもともと月間の為替レートの終値の平均値です。つぎに用いるデータの期間は論文にしたがいます。
index = web.DataReader("EXJPUS","fred",'1970/1/1')# usdjpy
index=index.resample('Q').mean()
index=np.log(index).diff()
index.iloc[0]=0
index0=index.loc['1975/9/30':'2009/12/31']
つぎにアウトオブサンプルのバックテストを行いましょう。
pred=[]
y=[]
for i in range(len(index0)-110):
data=index0.iloc[i:i+110]
model = sm.tsa.ARMA(data, order=(0,1))
res = model.fit(disp=0)
pred.append(res.forecast(steps=1)[0])
y.append(data.iloc[-1].values)
あとは実際の結果の評価をするだけです。
pred=pd.DataFrame(pred)
y=pd.DataFrame(y)
pred=pd.DataFrame(pred)
yy=pd.concat([y,pred],axis=1)
yy['dy']=yy.iloc[:,0].diff()
yy.iloc[:,1]=yy.iloc[:,1].shift(1)
yy['dpred']=yy.iloc[:,0]-yy.iloc[:,1]
yy=yy.dropna()
(yy.dy**2).mean(),(yy.dpred**2).mean()
(0.002573298762845856, 0.001384787245332085)
結果はもちろんMAモデルの方がよくなります。それは系列相関を利用して予測をしているからです。しかし、将来の平均値の予測をしてそれがどのような用途に有効なのでしょうか?もちろんトレーディングには使えませんし、ヘッジにも使えません。したがって、為替レートの予測ができ、それが何かに役に立ちそうだというためには点と点の予測を行う必要があるのです。為替レートが簡単に予測できるという主張が認められシステムトレードで簡単に儲けることができるのだということに用いられると最悪です。特にレバレッジを掛けるトレードにこのような主張が使われると大きな損失を被る恐れがあります。レバレッジはトレードに破綻を招くということはいろいろな方法で証明されているので、よくよく気を付ける必要があります。
このような誤解を与える予測ができるという主張はトレードの勧誘にもよく使われるので注意が必要です。また、間抜けなヘッジファンドはこのような主張をマーケティングに使っています。気を付けましょう。(計算に間違いがあり修正しました。2019/10/18)
汎化性能、インサンプル、アウトオブサンプル
予測モデルのパラメータを、与えられたデータを用いて最適化した後に、未知のデータを与えてどれだけの予測ができるかを汎化性能といいます。パラメータの調整に使うデータを訓練データ、汎化性能の評価に使うデータをテストデータといいます。時系列分析ではこれはインサンプルとアウトオブサンプルに相当します。平均はこの汎化性能の獲得に一躍買いそうに思います。しかし、実際に時系列がランダムウォーク、またはそれに近い場合にはその限りではありません。ドル円で試してみましょう。
まず、FREDからダウンロードしたEXJPUSはその月の終値の平均値なので、それを月末の日の終値と入れ替えます。
#月次のデータを作ります。EXJPUSは月次の平均の価格なので月末のデータに入れ替えます。
fx0=fx.resample('BM').last().iloc[:-1].copy()
fxm= web.DataReader("EXJPUS","fred",start)# usdjpy
dindex=fxm.index
fx0=pd.DataFrame(fx0.values,index=dindex)
fx0.columns=['fx']
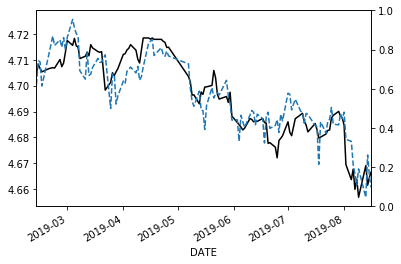
つぎに、平均として、移動平均を使って一年先の為替レートが予測できるかどうかをテストします。$i=0$のときは終値そのものです。$i=1$のときはデータを2つ使った移動平均です。その移動平均値と12か月先の為替レートを比べます。そしてどれが最も良い予測値になっているかを見ます。評価には平均2乗誤差を用います。結果の最初の列は、移動平均の日数です。2番目の列は移動平均と1年先の為替レートの平均2乗誤差です。3番目の列は月末の為替レートと1年後の為替レートの平均2乗誤差です。これをベンチマークとします。そうすると実際に各移動平均が月末の為替レートよりも1年後の為替レートをうまく予測しているという結果は得られませんでした。
# 1 year prediction
XX=fx0.copy()
for i in range(12):
tmp=XX.copy()
tmp['pred']=tmp.fx.rolling(i+1).mean().shift(12)
tmp['dif']=(tmp.fx-tmp.pred)
tmp['fx12']=tmp.fx.shift(12)
tmp['dfx']=tmp.fx-tmp.fx12
tmp=tmp.dropna()
print(i+1,(tmp.dif**2).mean(),(tmp.dfx**2).mean(),len(tmp))
tmp.head(1).index.date,tmp.tail(1).index.date
1 488.62180052356337 488.62180052356024 573
2 505.5650941433602 485.5878078671327 572
3 521.9983614127221 481.3010866900174 571
4 538.321656710524 477.19879035087735 570
5 554.7354239015796 473.1897365553604 569
6 570.7233146077892 469.13136619718335 568
7 584.9027658064279 464.3346650793652 567
8 598.598032265903 459.6144083038867 566
9 612.0979539888533 457.7716238938051 565
10 625.5735536631216 456.5045920212764 564
11 638.5964589433806 455.88383268206013 563
12 651.4197476003362 455.4614393238432 562
(array([datetime.date(1972, 12, 1)], dtype=object),
array([datetime.date(2019, 9, 1)], dtype=object))
少なくとも移動平均には汎化性能はありません。
過去一か月の為替レートの変化は未来を予測するか?
過去一か月の為替レートの対数価格差をとって12か月先の為替レートが予測できるかどうかを見てみましょう。
yyy='1970'
X0=XX.loc[yyy:].copy()
X0['dlnfx']=X0.lnfx.diff().shift(-1)
X0['dlnfx12']=(X0.lnfx.diff(12)-X0.lnfx.diff(1).shift(11)).shift(-12)
X0=X0.dropna()
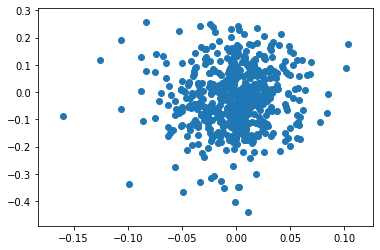
plt.scatter(X0.dlnfx,X0.dlnfx12)
X0.head()
ほぼ丸なので予測は不可能です。つぎにプラザ合意以降に絞ってみてみましょう。
yyy='1988'
X0=XX.loc[yyy:].copy()
X0['dlnfx']=X0.lnfx.diff().shift(-1)
X0['dlnfx12']=(X0.lnfx.diff(12)-X0.lnfx.diff(1).shift(11)).shift(-12)
X0=X0.dropna()
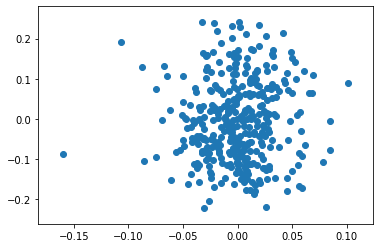
plt.scatter(X0.dlnfx,X0.dlnfx12)
X0.head()
まん丸さは少しなくなっていますが、これはデータの数が減ったからだと見たほうが良いと思います。つまり、過去一か月の価格レートの差には汎化性能はありません。しかし、これは月末のレートだけを使っていることに注意をしましょう。
(注) 為替市場のメカニズム
1990年以前の為替市場は先物市場が中心でした。インターバンク市場を大きく凌いでいました。しかし、それ以降は圧倒的にインターバンク市場が成長しました。当時は今のようにコンピュータによる自動発注もなく、すべてが手信号と電話の市場でした。したがって、3角アービトラージが可能でした。しかし、このようなことをする行為はインターバンク市場では禁止されていました。それはアービトラージフリーにする市場を構築するのが不可能だったからです。実は、それはコンピューターによる自動売買が進んだ今においても実は変わりがありません。その理由は注文処理の能力だけではなく、冒頭に説明した異質の人達が市場で取引をしていることによります。ですから今でも3角アービトラージを狙うヘッジファンドがいますし、そのような人たちは成功していると認識されるや否や市場から強制的に退場させられます。もちろん個人も同様です。さて、なぜ先物市場よりもインターバンク市場が発達したのでしょうか?その理由の1つが何度も説明している、市場の価格形成の難しさにあります。あまりにも価格形成の舞台裏が明らかになってしまうと、効率的市場の概念が壊れてしまいますし、たとえば売買スプレッドの上昇は流動性を減らす強い力があります。グロスマン・ミラーモデル(翻訳)
ですので、為替市場の取引にはよくよく注意が必要なのです。
為替レートの予測に使われるモデル
2つのモデルが重要な役割を果たします。1つはカルマンフィルターまたは状態方程式です。もう1つはベクトル誤差修正モデル(VECM)です。
カルマンフィルター
VECM
為替レートの予測に使われる構造モデル
カバー無し金利平価
相対的購買力平価
実質金利平価
粘着性マネタリーモデル
粘着性マネタリーモデル+リスク要因+流動性要因
イールドカーブの傾き
システムトレードってなに?
参考文献
「為替オーバーレイ―CFA Institute(CFA協会)コンフェレンス議事録」(パンローリング)

Python3ではじめるシステムトレード【第2版】環境構築と売買戦略

「画像をクリックしていただくとpanrollingのホームページから書籍を購入していただけます。