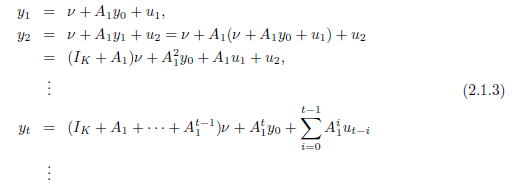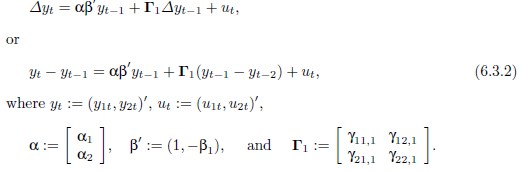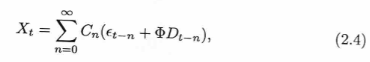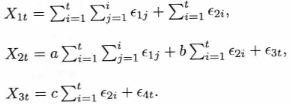ECM (wiki簡易翻訳)
誤差修正モデル(ECM)は、基になる複数の変数が共和分と呼ばれる長期的な確率的トレンドを持つデータに使用される多重時系列モデルである。ECMは、ある時系列が別の時系列に及ぼす短期的および長期的影響の推定に役立ち、理論的に裏付けされている。誤差修正は、長期の均衡からの前期の誤差が、短期のダイナミクスに影響を与えるという事実を捉えている。したがって、ECMでは、他の変数の変化後に従属変数が均衡に戻る速度を直接推定できる。
歴史
Yule(1936)とGranger and Newbold(1974)は、見せかけの相関の問題点に最初に着目し、時系列分析における解決策を見出した。2つの完全に無関係な和分(非定常)過程では、一方が他方に関し回帰分析により統計的に有意な関係を示す傾向がある。そのため、これらの変数間に真の関係があると誤る可能性がある。通常の最小二乗法では一致性がなく、一般的に使用される検定統計量は有効ではない。特に、モンテカルロシミュレーションでは、非常に高い$R^2$、個々に非常に高いt統計量、および低いダービンワトソン統計量が得られることが示されている。技術的に言えば、フィリップス(1986)は、標本数が増加するにつれて、パラメーター推定値が確率的に収束せず、切片が発散し、勾配が非退化分布になることを証明している。これらは変数間の長期的な関係を反映し、研究者が真に興味を持っている両方の時系列に共通の確率的トレンドがある可能性がある。
トレンドの確率的性質のため、和分過程を決定論的(予測可能)トレンドとトレンドからの偏差を含む定常時系列に分割することはできない。決定論的なトレンドを除去されたランダムウォークでも、見せかけの相関が最終的に現れる。したがって、トレンド除去では推定の問題の解決にはならない。Box-Jenkins法では、多くの時系列(経済学など)が一般的に、1次の差分で定常になると考えられ、時系列データの差分を取り、ARIMAなどのモデルを推定する。そのようなモデルからの予測は、データの周期性と季節性を反映するが、ただし、レベル(原系列、価格)のもつ長期的な調整に関する情報は失われ、長期予測は信頼できなくなる。これにより、Sargan(1964)はレベルに含まれる情報を保持するECM方法論を開発した。
推定
上記のように洗練された動学モデルを推定するためのいくつかの方法が知られている。これらの中には、Engle and Grangerの2ステップアプローチと、1ステップでECMを推定するJohansenの方法を使用したベクトルベースのVECMがある。
Engle and Grangerの2ステップアプローチ
最初のステップで、使用する個々の時系列が非定常であるかどうかを事前に検定する。標準の単位根のDF検定およびADF検定(系列相関誤差の問題を解決するため)を用いる。2つの異なる時系列$x_ {t}$と$y_ {t}$の場合を考える。 両方がI(0)の場合、標準回帰分析は有効である。異なる次数の和分では、たとえば 一方がI(1)で、もう1方がI(0)の場合では、モデルを変換する必要がある。両方が同じ次数(通常はI(1))の和分の場合、次の形式のECMモデルを推定できる。
$A(L)\Delta y_{t}=\gamma +B(L)\Delta x_{t}+\alpha (y_{t-1}-\beta_{0}-\beta_{1}x_{t-1})+\nu_{t}$
両方が和分で、このECMが存在する場合、それらはEngle–Grangerの表現定理によって共和分であるという。次に、通常の最小二乗法を使用してモデル$y_ {t} = \beta_{0} + \beta_{1} x_{t} + \varepsilon_{t}$を推定する。上記の検定基準で決定されたように回帰が見せかけでない場合、通常の最小二乗法が有効であるだけでなく、実際には超一致性がある(Stock、1987)。次に、この回帰からの予測残差$\hat{\varepsilon_{t}} = y_{t}-\beta_{0}-\beta_{1} x_{t}$ を保存し、差分変数と遅延誤差項の回帰に用いる。
$A(L)\Delta y_{t}=\gamma +B(L)\Delta x_{t}+\alpha {\hat {\varepsilon }}_{t-1}+\nu _{t}$
その後、$\alpha$の標準t統計を使用して、共和分を検定する。この方法は簡単だが、多数の問題点がある。
‐ 最初の段階で使用される単変量単位根検定の統計的検出力は低い。
- 最初の段階の従属変数の選択が検定結果に影響する。つまり、グレンジャーの因果関係によって決定される$x_ {t}$は弱い外生性をもつ。
- 潜在的に小さなサンプルバイアスを持つ可能性がある。
- $\alpha$の共和分検定は標準分布に従わない。
- 共和分ベクトルのOLS推定量の分布は非常に複雑で正規分布ではない。したがって、残差を取得する最初の回帰での長期パラメーターの妥当性は検証できない。
- 1つの共和分関係しか調べることができない。
VECM
上記のEngle-Grangerアプローチには、多くの弱点がある。つまり、1つの変数が従属変数として指定された単一の方程式のみに制限される。この変数は、目的のパラメーターに対して弱い外生性があると想定される別の変数によって説明される。また、時系列が事前検定によりI(0)またはI(1)であるかどうかを調べる。これらの弱点は、ヨハンセンの方法で対処できる。その利点は、事前検定が不要であり、多数の共和分関係があっても問題なく、すべてが内生変数として扱われ、長期パラメータに関連する検定が可能だということだ。結果、モデルは、ベクトル自己回帰(VAR)として知られる外生的モデルに誤差修正機能を追加し、ベクトル誤差修正モデル(VECM)として知られている。手順は次のように行われる。
ステップ1:非定常変数を含む可能性のある制約のないVARを推定する
ステップ2:ヨハンセンの検定を使用した共和分検定
ステップ3:VECMを作成して分析。
ECMの例
共和分の考え方は、単純なマクロ経済の例で示せる。消費$C_ {t}$および可処分所得$Y_{t}$は、長期的な関係のあるマクロ経済時系列だと仮定する。具体的には、平均的な消費傾向を90%にする。つまり、長期的には$C_{t} = 0.9Y_{t}$が成り立つ。計量経済学者の観点から、回帰からの誤差$\varepsilon_{t}(=C_{t} - \beta Y_{t} )$が定常時系列で、$Y_{t}$および$C_{t}$が非定常な場合、この長期的な関係(別名共和分)が存在する。 また、$Y_{t}$が突然 $\Delta Y_{t}$だけ変化した場合、 $C_{t}$が変化すると仮定する。$\Delta C_{t} = 0.5 \Delta Y_{t}$で、つまり限界消費傾向は50%になる。最後の仮定は、現在の消費と均衡消費のギャップが各期間で20%減少するとする。
この設定では、消費レベルの変更
$\Delta C_{t} = C_{t} - C_{t-1}$
を
$\Delta C_{t} = 0.5 \Delta Y_{t} -0.2(C_{t-1} -0.9Y_ {t-1})+ \varepsilon_{t}$
とする。
右辺の最初の項は$C_{t}$に対する$Y_{t}$の変化の短期的な影響を説明し、2番目の項は変数が均衡に向かう長期的な関係を説明し、3番目の項は、系が受けるランダムなショック、例えば消費に影響を与える消費者の信頼のショックなどを反映する。
モデルがどのように機能するかを確認するには、恒久的および一時的な2種類のショックを検討する。簡単にするために、すべてのtに対して$\varepsilon_{t}$をゼロにする。
期間t − 1で系が均衡状態にあると仮定する。つまり、$C_{t-1} = 0.9Y_{t-1}$である。
期間tで$Y_{t}$が10増加するが、それは一時的でその後に前のレベルに戻ったとする。その場合、$C_{t}$は最初(期間t)に5(10の半分)増加するが、2番目以降の期間では、$C_{t}$は減少し始め、初期レベルに収束する。
対照的に、$Y_{t}$への衝撃が恒久的である場合、$C_{t}$はゆっくりと初期の$C_{{t-1}}$を9超える値に収束する。
より具体的に理解するために、
$C_{t-1} = 0.9Y_{t-1}$
で考えてみる。こちらの結果は明確だ。単純にするために
$y_0 = 0$とする。
- $y_t$の増加が一時的な場合:
| $t$ | $Y_t$ | $\Delta C_t$ | $C_t$ |
|---|---|---|---|
| 0 | 0 | 0 | |
| 1 | 10 | 9 | 9 |
| 2 | 0 | 0 | 0 |
| 3 | 0 | 0 | 0 |
- $y_t$の増加が恒久的な場合:
| $t$ | $Y_t$ | $\Delta C_t$ | $C_t$ |
|---|---|---|---|
| 0 | 0 | 0 | |
| 1 | 10 | 9 | 9 |
| 2 | 10 | 0 | 9 |
| 3 | 10 | 0 | 9 |
つぎに$\Delta C_{t} = 0.5 \Delta Y_{t} -0.2(C_{t-1} -0.9Y_ {t-1})+ \varepsilon_{t}$とする。
- $y_t$の増加が一時的な場合:
| $t$ | $Y_t$ | $\Delta Y_t$ | $u_t$ | $0.2u_t$ | $0.5Y_t$ | $\Delta C_t$ | $C_t$ |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | ||
| 1 | 10 | 10 | 0 | 0 | 5 | 5 | 5 |
| 2 | 0 | -10 | 14 | 2.8 | 0 | -2.8 | 2.2 |
| 3 | 0 | 0 | 2.2 | 0.44 | 0 | -0.44 | 1.56 |
- $y_t$の増加が恒久的な場合:
| $t$ | $Y_t$ | $\Delta Y_t$ | $u_t$ | $0.2u_t$ | $0.5Y_t$ | $\Delta C_t$ | $C_t$ |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | ||
| 1 | 10 | 10 | 0 | 0 | 5 | 5 | 5.8 |
| 2 | 10 | 0 | -4 | -0.8 | 0 | 0.8 | 6.6 |
| 3 | 10 | 0 | -3.8 | -0.76 | 0 | 0.76 | 7.36 |
ベクトル誤差修正モデルを学ぶ前に
新しい課題を学ぶときはまずはいろいろなもの読まずに1つの教科書に絞って学んだ方が方が良いとよく言われる。statsmodelsでは参考文献としてつぎの2つを紹介している。
Lütkepohl, H. 2005. New Introduction to Multiple Time Series Analysis. Springer.
Johansen, S. 1995. Likelihood-Based Inference in Cointegrated * *Vector Autoregressive Models. Oxford University Press.
Lütkepohlは厚くてすべてを読むのは不可能である。ヨハンセンは薄いのだが、内容が濃すぎるところとやさしいところが混在している。良くない方法と分かっていながら、両方をかじって学習の時間を短縮したい。
Lütkepohl, H. 2005. New Introduction to Multiple Time Series Analysisから学ぶ
確率過程の基礎知識 (1.2の部分翻訳)
特定の経済変数の値は、ある時の確率変数の実現値であり、時系列は確率過程から生成されると考える。基礎的な概念を明確にするために、いくつかの基本的な定義と表現を簡単に確認する。
Ωはすべての基本事象(標本空間)の集合で、 Fは事象のシグマ代数、またはΩの補集合、PrはFで定義される確率測度で,(Ω、F、Pr)は確率空間である。ランダム変数yは、各実数cに対してΩで定義される実数値関数$A_c$ = {ω∈Ω| y(ω)≤c}∈Fであり、$A_c$は、確率がPrで定義される事象である。関数F:R→[0、1]は、$F(c)= Pr(A_c)$で定義され、$y$の分布関数である。
K次元の確率ベクトルまたは確率変数のK次元ベクトルは、ΩからyへのK次元ユークリッド空間$R^K$への関数である。すなわち、yは$y(ω)=(y_1(ω)、...、y_K(ω))^\prime$ をω∈Ωに写像し、それぞれの$c =(c_1、...、c_K)∈R_K$に対して、$A_c={ω| y_1(ω)≤c_1,\cdots,y_K(ω)≤c_K}∈F$である。関数F:RK→[0、1]は$F(c)= Pr(A_c)$で定義され、yの関数の同時分布である。
Zが最大で数え切れないほど多くの要素を持つ添字集合(時間など)であり、例えば、すべての整数またはすべての正の整数の集合であるとする。 (離散)確率過程はy:Z×Ω→Rの実数値関数で、t∈Zごとに確定され、y(t、ω)は確率変数である。tに対応する確率変数は、$y_t$として示し、もととなる確率空間については言及しない。その場合、確率過程のすべてのメンバー$y_t$は同じ確率空間で定義されると考える。通常、シンボルの意味が文脈から明らかな場合、確率過程も$y_t$で示される。
確率過程は、t∈S⊂Zのとき、$y_t$のすべての有限な部分集合族の同時分布関数として記述される。実際には、分布の完全な系はしばしば未知であるので、多くの場合、分布の1次と2次のモーメントを用いる。つまり、平均$E(y_t)=\mu_t$、分散$E[(y_t-\mu_t)^2]$および共分散$E[(y_t-\mu_t)(y_s-\mu_s)]$を用いる。
K次元ベクトル確率過程または多変量確率過程はy:Z×Ω→$R^K$の関数で、確定した各t∈Zに対して、y(t、ω)はK次元の確率ベクトルである。確定したt∈Zに対応する確率ベクトルに$y_t$を使用する。また、完全な確率過程を$y_t$で表すこともある。この特定の意味は、文脈から明確になる。確率的特性に関しては、単変量過程と同じである。つまり、確率的特性は、確率ベクトル$y_t$のすべての有限な補集合族の同時分布関数として要約される。 実際には、関連するすべての確率変数から求められる1次と2次のモーメントが用いられる。
(ベクトル)確率過程の実現値は、t∈Zで固定されたωに対する(ベクトルの)数列集合$y_t(\omega)$である。言い換えれば、確率過程の実現値は、t→$y_t$(ω)の関数Z→$R^K$である。(複数の)時系列は、そのような実現値または場合によってはそのような実現値の有限部分と見なされる。つまり、たとえば、(ベクトル)$y_1(\omega),\dots,y_T(\omega)$で構成される。もととなる確率過程が(複数の)時系列を生成したと考えられ、それは時系列の生成または生成プロセス、またはデータ生成プロセス(DGP)と呼ばれる。時系列$y_1(\omega),\cdots,y_T(\omega)$は通常、$y_1,\cdots,y_T$、または混乱が生じない場合には単にもととなる確率過程$y_t$によって示される。観測値の数Tは、標本の大きさまたは時系列の長さと呼ぶ。
VAR過程(1.3の部分翻訳)
線形関数は扱いやすいので、過去の観測値を用いた線形関数による予測から始める。 単変量の時系列$y_t$と$h = 1$期先の将来予測を考える。 f(・)を線形関数とすると、
$\hat{y_{T+1}}=\nu+\alpha_1 y_T+\alpha_2 y_{T-1}+\cdots$
となる。予測式は有限なp個の過去の値yを用いて、
$\hat{y_{T+1}} = \nu + \alpha_1y_{T}+\alpha_2y_{T-1} +\cdots+\alpha_p y_{T-p} + 1$
となる。もちろん、真の値$y_{T +1}$と予測$\hat{y_{T +1}}$は全く同じではないので、予測誤差を$u_{T +1}= \hat{y_{T +1}} − y_{ T +1}$とすると、
$y_{T +1} = y_{ T +1} + u_{T +1} =\nu + \alpha_1 y_T+\cdots+\alpha_p y_{T-p + 1} + u_{T +1}$
となる。ここで、数値が確率変数の実現値であると仮定し、データ生成には自己回帰プロセス
$y_t =\nu + \alpha_1 y{t−1} +\cdots+ \alpha_p y_{t−p} + u_t$
を各期間Tで適用する。ここで、$y_t$、$y_{t−1},\cdots,y_{t−p}$、および$u_t$は確率変数である。 自己回帰(AR)過程では、異なる期間の予測誤差$u_t$は無相関、つまり$u_t$と$u_s$は$s=t$で無相関であると仮定する。つまり、すべての有用な過去の情報$y_t$を予測に用いるので、系統的な予測誤差は無い。
複数の時系列を考えると、まずは
$\hat{y_{k,T +1}} =\nu + \alpha_{k1,1}y_{1,T} +\alpha_{k2,1}y_{2,T} +
\cdots+\alpha_{kK,1}y_{K,T}+\cdots+\alpha_{k1,p}y_{1,T-p+1} +\cdots+\alpha_{kK,p}y_{K,T-p+1}$
$k = 1,\cdots K$と拡張するのが自然である。
表記を簡単にするために、
$y_t=(y_{1t},\cdots,y_{Kt}),$
$\hat{y_t}:=(\hat{y_{1t}},\cdots,\hat{y_{Kt}}),$
$\nu =(\nu_1,\cdots,\nu_K)$および
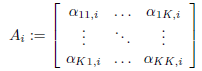
とすると、上述のベクトルの式は、次のようにコンパクトに記述できる。
$y_{T+1}=\nu+ A_1y_T +\cdots+ A_py_{T −p + 1}$
$y_t$が確率変数のベクトルであるので、この予測子は次の形式のベクトル自己回帰モデルから取得された最適な予測となる。
$y_t =\nu+ A1y_{t−1} +\cdots+ A_py_{t−p} + u_t$
ここで、$u_t=(u_{1t},\cdots,u_{Kt})$は、ベクトルの平均がゼロで独立同一に分布するK次確率ベクトルの連続時系列である。
VAR(p)の安定過程(2.1.1の簡易部分翻訳)
VAR(p)モデル(次数pのVARモデル)
$y_t =\nu + A_1y_{t−1} +\cdots+ A_py_{t−p} + u_t、t = 0、±1、±2、...、(2.1.1)$
について考える。$y_t =(y_{1t},\cdots,y_{Kt})^\prime$は確率変数の(K×1)ベクトル、$A_i$は(K×K)係数行列で固定されていて、$\nu =(\nu_1,\cdots,\nu_K)^\prime$は、(K×K)係数行列で固定され、非ゼロの平均$E(y_t)$となる切片をもつ。したがって、$u_t =(u_{1t},\cdots,u_{Kt})^\prime$はK次元のホワイトノイズまたはイノベーション過程となる。つまり、$s \ne t$で、$E(u_t)= 0, E(u_tu_t^\prime)=\sum_u, E(u_tu_s^\prime)= 0$である。特に明記しない限り、共分散行列Σuは非特異行列である。
(2.1.1)の過程についてもう少し考えてみる。モデルの意味を理解するるために、VAR(1)モデルを考える。
$y_t =\nu + A_1y_{t−1} + u_t \cdots (2.1.2)$
この生成メカニズムを$t = 1$から繰り返すと
したがって、ベクトル$y_1,\cdots,y_t$は、$y_0,u_1,\cdots,u_t$によって一意に決まる。また、$y_1,\cdots,y_t$の同時分布は、$y_0,u_1,\cdots,u_t$の同時分布によって決定される。
特定の期間に始まる過程を想定することもあるが、無限の過去から開始したほうが便利なこともある。実際には(2.1.1)がこれに相当する。その場合、(2.1.1)のメカニズムと一致性のある過程はどのようなものだろうか?この問題を考えるために、(2.1.2)のVAR(1)過程を再度検討する。(2.1.3)から
$y_t =\nu+ A_1y_{t−1} + u_t$
$\ \ =(I_K + A_1 +\cdots+ A_j^1)\nu+ A_1^{j + 1} y_{t−j−1} +\sum_{i=0}^j A_1^i u_{t-i}$
$A_1$のすべての固有値の係数が1未満の場合、$A^i_1$の過程、$i = 0,1,\cdots$は、絶対加算可能となる。したがって、無限和
$\sum_{i=1}^\infty A=1^j u_{t−i}$
には二乗平均がある。 また、
$(I_K + A_1 +\cdots+ A_1^j)\nu \rightarrow_{j→\infty}(I_K − A_1)^{−1}\nu$
さらに、$A_1^{j + 1} $は$j→\infty$として急速にゼロに収束するため、極限で$A_1^{j + 1} y_{t−j−1}$の項は無視される。したがって、$A_1$のすべての固有値の係数が1より小さい場合、$y_t$は(2.1.2)のVAR(1)過程であり、$y_t$は明確に定義された確率過程
$y_t = µ +\sum_{t=0}^\infty A_1^i u_{t−i}、t = 0,±1,±2,\cdots, (2.1.4)$
である。ここで$µ=(I_K − A_1)^{−1}\nu$。
$y_t$の分布と同時分布は、$u_t$の分布によって一意に決まる。$y_t$の過程の1次と2次のモーメントは、すべての$t$に対して
$E(y_t)= \mu \ \ \ \ \ (2.1.5)$
であることがわかる。そして
$\Gamma y(h)= E(y_t −\mu)(y_t−h −\mu)^\prime$
$\ \ \ \ \ \ = \lim_{n→\infty}\sum_{i=0}^n \sum_{i = 0}^n A_1^i E(u_{t-i}u_{t-h-j}^\prime)(A_1^j )^\prime \ (2.1.6)$
$\ \ \ \ \ = \lim_{ n = 0}^n A_1^{h + i} \sum_u A_1^i=\sum_{i=0}^\infty A_1^{h+i}\sum_u A^{i\prime}_1$、
なぜなら、$s \ne t$の場合は$E(u_tu_s^\prime)= 0$であり、すべての$t$で$E(u_t u_t)=\sum_u$である。
行列$A_1$のすべての固有値の係数が1未満という条件は重要であり、この条件を満たすVAR(1)過程を安定という。この条件は$|z|\le1$に対して
$ det(I_K − A_1z) \ne 0 \ \ \ \ \ (2.1.7)$
と等価である。安定条件(2.1.7)が満たされない場合にも、t = 0、±1、±2、...の過程$y_t$も定義することができるが、ここではそれをしないで、すべてのt∈Zに対して定義された過程の過程の安定性を常に仮定する。
これまでの説明は、VAR(p)過程をVAR(1)形式で記述しているため、$p>1$のVAR(p)過程に簡単に拡張できる。より正確には、$ y_t $が(2.1.1)のようにVAR(p)である場合、対応するKp次元のVAR(1)を
$ Y_t =ν+ AY_{t−1} + U_t $ (2.1.8)
と定義することができる。
ここで
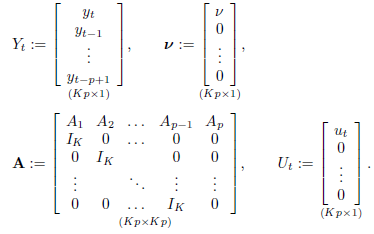
である。
前述の説明に従って
$ det(I_{Kp} − Az)\ne 0 for | z | ≤1 $。 (2.1.9)
の場合、$Y_t$は安定する。その平均ベクトルは
$ µ:= E(Y_t)=(I_ {Kp} − A)^ {− 1}ν$
で自己共分散は
$\Gamma_Y(h)=\sum_{i=0}^\infty A^{h+i}\sum_U(A^i)^{'}$、(2.1.10)
となる。ここで、$\sum_U:= E(U_t U_t)$である。(K×Kp)行列を用いて、
$ J:= [I_K:0:・・・:0] $、(2.1.11)
となる。この過程$ y_t $は$ y_t = JY_t $として取得される。$ Y_t $は明確に定義された確率過程であるため、$ y_t $についても同じことが言える。その平均は$ E(y_t)= Jµ $であり、すべての$ t $に対して一定であり、自己共分散$Γ_y(h)=JΓ_Y(h)J^{'} $も時不変である。
$ det(I_ {Kp}-Az)= det(I_K-A_1 z-・・・-A_pz ^ p)$
は理解しやすい(問題2.1を参照)。行列の特性多項式の定義を前提として、この多項式をVAR(p)過程の逆特性多項式と呼ぶ。したがって、過程(2.1.1)は、その逆特性多項式が複素単位円内および上に根を持たない場合、安定する。正式には$ y_t $は
$ det(I_K − A_1 z −・・・− A_pz^p)\ne 0 for | z | ≤1 $(2.1.12)
の場合に安定する。この状態を安定状態という。
要約すると、(2.1.12)が成り立ち、
$ y_t = JY_t = Jµ + J\sum_{i=0}^\infty A^iU_{t-i} $ (2.1.13)
である場合、$y_t$は安定したVAR(p)過程であるという。$ U_t:=(u_t、0,\cdots,0)$にはホワイトノイズプロセス$ u_t $が含まれるため、$ y_t $はホワイトノイズまたはイノベーションプロセスによって決定される。多くの場合、$u_t$に関する特定の仮定がなされ、前述の規則によって$ y_t $が決定される。重要な例は、$ u_t $がガウスホワイトノイズであるという仮定である。つまり、すべての$t$および$u_t$について$ u_t〜N(0,\sum_u)$であり、$ s \ne t $については独立している。その場合、$y_t$がガウス過程、つまり補集合$ y_t,..., y_t + h $はすべてのtとhに対して多変量正規分布であることを示すことができる。
条件(2.1.12)は、VAR過程の安定性を確認するための簡単な道具である。たとえば、3次元のVAR(1)過程を考える。

この過程では、逆特性多項式は
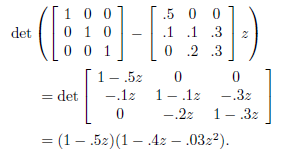
である。この多項式の根は、
$z_1 = 2,\ z_2=2.1525,\ z_3=-15.4858$
である。それらはすべて、絶対値が1より大きいことは明らかだ。したがって(2.1.14)の過程は安定である。
この多項式の根は、
$ z_1 = 1.3、z_2 = 3.55 4.26i $、および$ z_3 = 3.55 − 4.26i $
である。ここで$ i:= \sqrt{−1} $は虚数単位である。$ z_2 $および$ z_3 $の係数は$ | z2 |= | z3 | = \sqrt {3.552 ^ 2 4.262 ^ 2} = 5.545 $であることに注意してほしい。したがって、すべての根が単位円の外側にあるため、(2.1.15)の過程は安定条件(2.1.12)を満たしている。高次元で高次の過程の根を手作業で計算することは難しい場合が多いが、効率的なコンピュータープログラムが存在する。
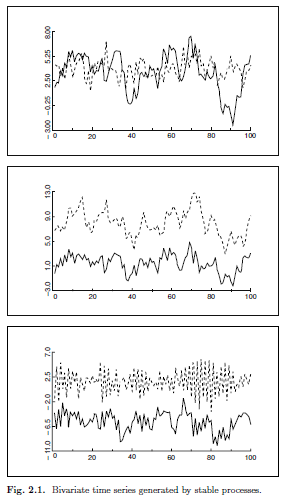
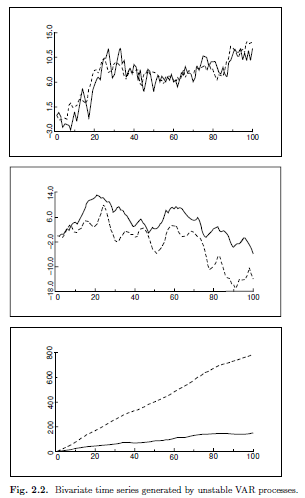
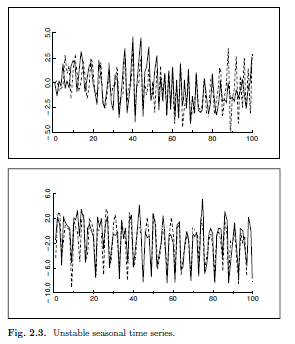
安定性の仮定の影響を理解するには、安定過程によって生成された時系列を視覚化し、それらを不安定なVAR過程からの実現値と対比すると役立つ場合がある。図2.1には、3つの異なる安定した2変量(2次元)VAR過程によって生成された3組の時系列が示されている。それらはかなり異なるが、共通の特徴は、それらが一定の平均値の周りで変動し、その変動性(分散)が移動しても変化しないことである。対照的に、図2.2および2.3に描かれた一対の時系列は、不安定な2変量VAR過程によって生成される。図2.2の時系列にはトレンドがあり、図2.3の時系列は非常に顕著な季節変動を示している。どちらの形状も特定の典型的な不安定性を示すが、実際には非常に一般的である。したがって、安定性の仮定は、実際に興味が抱かれているような多くの時系列を除外している。
(注)
一致性:標本の大きさを無限としたときに推定量が母数と一致すること。
超一致性:共和分の関係があるときに通常よりも早く推定量が母数と一致すること。
共和分過程、一般的な確率的トレンド、およびベクトル誤差補正モデル(6.3の簡易部分翻訳)
家計収入や支出、そして異なる市場での同じ商品の価格など、多くの経済変数の間での均衡は本当に成り立つのだろうか。対象となる変数をベクトル$y_t =(y_{1t}、...、y_{Kt})^\prime$とし、それらの長期均衡関係が、$\beta y_t =(\beta_1y_{1t}+···+\beta_Ky_{Kt}= 0)^\prime$で表されるとする。ここで、$\beta=(\beta_1、...、\beta_K)^\prime$である。ある期間で、この関係が正確には満たされない可能性がある。$z_t$を均衡からの乖離を表す確率変数とし、$\beta y_t = z_t$が成り立つとする。均衡が、実際に成立していれば、変数$y_t$はそれぞれが互いに変化し、$z_t$は安定であると考えられる。ただし、この設定では、変数$y_t$がグループとして広範囲にさまよう可能性がある。それは、共通の確率的トレンドによって動かされる可能性だ。言い換えると、各変数が和分であり、定常となる変数の線形結合が存在するということだ。この特性を持つ和分変数を、共和分という。
一般に、K次元$y_t$過程のすべての構成要素が$I(d)$で、$\beta=(\beta_1,\cdots,\beta_K)^\prime \ne 0$のもとで、$z_t=\beta^\prime y_t$の線形結合が存在し、$z_t$が$I(d − b)$であるような場合、変数$y_t$は、次数$(d,b)$の共和分と呼ばれ、$y_t〜CI(d,b)$で表現する。たとえば、$y_t$のすべての構成要素がI(1)であり、$\beta y_t$が定常(I(0))である場合、$y_t〜CI(1,1)$となる。ベクトル$\beta$は、共和分ベクトルと呼ばれる。 共和分となる変数で構成される過程は、共和分過程と呼ばれる。この過程は、Granger(1981)およびEngle&Granger(1987)によって導入された。
用語を簡略化するために、わずかに異なる共和分の定義を用いる。$\Delta^d y_t$が安定で、$\Delta^{d−1}y_t$が安定でないとき、K次元$y_t$過程を次数$d$の和分といい、簡単に$y_t〜I(d)$と書く。$y_t$のI(d)過程は、$d$より小さい次数で和分であり、$\beta \ne 0$の線形結合$\beta y_t$がある場合、それを共和分という。この定義はEngle&Granger(1987)のものとは異なり、和分の次数がdより小さい$y_t$の構成要素を除外しない。$y_t$にI(d)構成要素が1つだけあり、他のすべての構成要素が安定している場合(I(0))、$\Delta^d y_t$が安定で、$\Delta^{d−1}y_t$が安定でないとき、ベクトル$y_t$は定義に従ってI(d)となる。このような場合、定常成分のみを含む関係$\beta y_t$が、私たちの用語では共和分関係となる。明らかに、私たちの定義のこの側面は、共通の確率的トレンドを持つ和分変数間の特別な関係を共和分ととらえる元の考えと一致しないが、次数の異なる変数からなる和分を区別しないで、用語を簡素化しているだけであり、定義は依然として有効である。読者は、特定の関係の解釈に関しては、共和分の基本的な考え方をもっていてほしい.
明らかに、共和分ベクトルは一意ではない。ゼロ以外の定数を乗算すると、共和分ベクトルが得られてしまう。また、線形に独立したさまざまな共和分ベクトルが存在する場合がある。 たとえば、系に4つの変数がある場合、最初の2つが長期的な均衡関係にあり、最後の2つも同様であるとする。したがって、最後の2つの位置がゼロで、最初の2つのうちのひとつがゼロを持つ共和分ベクトルが存在する場合がある。さらに、4つの変数すべてに共和分関係がある場合がある。
共和分の概念が導入される前は、非常に近い誤差修正モデルが計量経済学の分野で議論されていた。一般に、誤差修正モデルでは、変数の変化は均衡関係からの乖離としてとらえる。たとえば、$y_{1t}$が特定の市場の商品の価格を表し、$y_{2t}$が別の市場の同じ商品の価格に対応するとする。さらに、2つの変数間の均衡関係が$y_{1t} =\beta_1 y_{2t}$で与えられ、$y_{1t}$の変化は期間t − 1のこの均衡からの偏差に依存すると仮定する。
$\Delta y_{1t} =\alpha_1(y_{1,t−1} −\beta_1y_{2,t−1})+ u_{1t}$
同様の関係が$y_{2t}$にも当てはまる場合がある
$\Delta y_{2t} =\alpha_2(y_{1t−1} −\beta_1y_{2,t−1})+ u_{2t}$
より一般的な誤差修正モデルでは、$\Delta y_{it}$はさらに両方の変数の前の変化に依存する場合がある、例えば、次のモデル:
$\Delta y_{1t} =\alpha_1(y_{1,t−1} −\beta_1y_{2,t−1})+ \gamma_{11,1}\Delta y_{1,t−1} + \gamma_{12,1}\Delta y_{2,t−1} + u_{1t}$、
$\Delta y_{2t} =\alpha_2(y_{1,t−1} −\beta_1y_{2,t−1})+ \gamma_{21,1}\Delta y_{1t}−1 + \gamma_{22,1}\Delta y_{2,t−1} + u_{2t} / / (6.3.1)$
$\Delta y_{it}$のさらに前のラグも含まれる場合がある。
誤差修正モデルと共和分の概念の近い関係を確認するには、$y_{1t}$と$y_{2t}$の両方がともにI(1)変数であると仮定する。その場合、$\Delta y_{it}$を含む(6.3.1)のすべての項は(仮定により)安定している。さらに、$u_{1t}$および$u_{2t}$はホワイトノイズの誤差であり、これも安定している。 不安定な項は安定した過程と同等ではないため、
$\alpha_i(y_{1,t−1} −\beta_1y_{2,t−1})= \Delta y_{it} − \gamma_{i1,1}\Delta y_{1,t−1} − \gamma_{i2,1}\Delta y_{2,t−1} − u_{it}$
も安定している必要がある。したがって、$\alpha_1\ne 0$または$\alpha_2\ne 0$の場合、$y_{1t}-\beta_1 y_{2t}$は安定し、共和分関係となる。
となる。
ウィキの例にもどる
消費$C_ {t}$および可処分所得$Y_{t}$の関係
$$ \Delta C_t= 0.5 \Delta Y_{t} -0.2(C_{t-1} -0.9Y_ {t-1})$$
を表現しなおしてみよう。
ベクトルとマトリックスを用いた表現
\begin{bmatrix}
\Delta C_t \\
\Delta Y_t
\end{bmatrix}
=
\Gamma_1
\begin{bmatrix}
\Delta C_t \\
\Delta Y_t
\end{bmatrix}
+\alpha\beta^{'}
\begin{bmatrix}
C_{t-1} \\
Y_{t-1}
\end{bmatrix}
\begin{matrix}
\end{matrix}
=
\begin{bmatrix}
0 & 0.5
\end{bmatrix}
\begin{bmatrix}
\Delta C_t \\
\Delta Y_t
\end{bmatrix}
+
\begin{bmatrix}
0.2\\
0
\end{bmatrix}
\begin{bmatrix}
1 & -0.9
\end{bmatrix}
\begin{bmatrix}
C_{t-1} \\
Y_{t-1}
\end{bmatrix}
\begin{matrix}
\end{matrix}
=
0.5 \Delta Y_t
+
\begin{bmatrix}
0.2 & -0.2 \cdot 0.9\\
0 & 0
\end{bmatrix}
\begin{bmatrix}
C_{t-1} \\
Y_{t-1}
\end{bmatrix}
$$ \Delta C_t= 0.5 \Delta Y_{t} -0.2(C_{t-1} -0.9Y_ {t-1})$$
Johansen, S. 1995. Likelihood-Based Inference in Cointegrated Vector Autoregressive Modelsからまなぶ
ランダムウォークと自己回帰モデルの基礎 (2.1参考)
ランダムウォークは
$X_t=X_{t-1}+\varepsilon_t$
と記述できる。これを書き換えると
$X_t=X_{t-1}+\varepsilon_t$
$X_{t-1}=X_{t-2}+\varepsilon_{t-1}$
$X_{t-2}=X_{t-2}+\varepsilon_{t-2}$
$\vdots$
$X_{2}=X_{1}+\varepsilon_{2}$
$X_{1}=X_{0}+\varepsilon_{1}$
と書ける。これを足し合わせると、斜め下のXが相殺されるので、結局
$X_t=X_0+\sum \varepsilon_t$
と記述できる。ランダムウォークは乱数の和である。
つぎにAR(1)について同じことを行う。ただしそれぞれの行に$C_{t-j}(=\Pi^j$)を掛けて斜め下のXが左辺と相殺されるようにする。
$X_t=\Pi X_{t-1}+\varepsilon_t$
と記述できる。これを書き換えると
$X_t=\Pi X_{t-1}+\varepsilon_t$
$X_{t-1}=\Pi X_{t-2}+\varepsilon_{t-1}$
$X_{t-2}=\Pi X_{t-2}+\varepsilon_{t-2}$
$\vdots$
$X_{2}=\Pi X_{1}+\varepsilon_{2}$
$X_{1}=\Pi X_{0}+\varepsilon_{1}$
と書ける。これを足し合わせると、斜め下のXが相殺されるので、結局
$X_t=C_{t-1} \Pi X_0 +\sum_{i=0}^{t-1} C_i \varepsilon_{t-j}$
と記述できる。ふたたび乱数の和であるが、
$X_t=\Pi^t X_0 +\sum_{i=0}^{t-1} \Pi^t \varepsilon_{t-j}$
であるので、$\Pi<1$であれば
$X_t^*=\sum_{i=0}^{\infty}\Pi^i\varepsilon_t$
に収束する。
基本的な定義と概念(3,3.1参考)
和分、共和分、および共通トレンドを定義する。定義は基本的にEngle and Granger(1987)のものだが、ここでの使用に適するように単純なフレームワークに変更されている。ベクトル過程の構成要素が異なる次数の和分であることを可能としている。これは、経済データを分析する際に、変数が統計的特性ではなく経済的重要性により選択されているためである。したがって、長期的な関係や短期的な関係を記述するために、同じモデルでたとえば定常変数と非定常変数を分析できる。
共和分と共通トレンド
多くの経済変数は定常ではないが、差分によって非定常性を取り除くことができるタイプを議論する。この現象をモデル化する場合、経済の2つの側面に焦点を当てる。つまり、元の変数よりも変動性が低い変数間の「安定した」関係、または誤差が累積して非定常性となる場合である。本節の目的は、これらの概念を統計モデルとして詳細に議論できるように正確に統計的に定義することにある。望ましくない特性を持つ過程を含めずに和分の概念の一般的な定義を与えることは困難であるので、必要な過程を正確に表現する定義を与える。$ \epsilon_t $を、平均ゼロと分散行列$ \Omega $を持つ独立同一に分布したp次元確率過程とする。
定義3.1 線形過程、$Y_t = \sum_{i = 0}^\infty C_ie_{t-i}、t = 0、1、...$によって定義される。ここで、$C(z)= \sum_{i = 0}^\infty C_iz^i$ は ある $\delta>0$で$| z | <1+ \delta$ に収束する。
係数は急激に減少する。
定義3.2 $Y_t-E(Y_t)= \sum C_i \epsilon_{t-1}$を満たす確率過程$Y_t$は、$C = \sum_{i = 0}^\infty C_i \ne 0$の場合、$I(0)$と呼ばれる。
Cは特異行列である可能性がある。実際、この特性は共和分の原因となる。単変量線形過程の簡単な例として、| p | <1のAR(1)過程を考える。
$X_{1t} = \sum_{i = 0}^\infty \rho^i \epsilon_{1t-i}$
係数の和は$\sum_{i = 0}^\infty \rho_i = 1 /(1- \rho)$であり、I(0)過程である。
過程
$X_ {2t} = \epsilon_{2t} — \theta \epsilon_{2t-1}$
すべての$\theta$に対して定常だが、$\theta \ne 1$の場合はI(0)過程である。$X_t =(X_{1t}、X_{2t})^{'}$の過程は、C行列が次のようになっているため、$\theta = 1$であってもI(0)過程と呼ばれる。
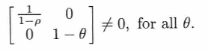
で指定された$X_t$過程には、次の特性がある。$X_t — E(X_t)$はI(0)過程である。これは、$C(1)= A(1)^{-1}$が非ゼロであり、実際にフルランクであるためである。
定義3.3 確率過程$X_t$は、$\Delta^d(X_t、— E(X_t))$がI(0)の場合、次数dの和分I(d)、d = 0、1、2、...と呼ぶ。
和分の特性は、定義で期待値を差し引いるので確率的部分と関連している。I(0)の概念は、平均やトレンドなどの決定論的な項に関係なく定義される。和分過程のレベルに制限はなく、差のみがあることにも注意。定義のもう1つの側面は、ランダムウォークと定常過程の2つの次元で構成される過程として表現できる。これにより、I(1)過程のように異なる次数から構成される過程を統合できる。
共和分の意味を直感的に理解する例 3.1 Johansen, S. 1995. Likelihood-Based Inference in Cointegrated Vector Autoregressive Models p.37
#初期化
%matplotlib inline
import matplotlib.pyplot as plt
from statsmodels.tsa.api import VECM
import statsmodels.api as sm
from statsmodels.tsa.base.datetools import dates_from_str
import pandas as pd
import numpy as np
from numpy import linalg as LA
from statsmodels.tsa.vector_ar.vecm import coint_johansen
from statsmodels.tsa.vector_ar.vecm import select_coint_rank
from statsmodels.tsa.vector_ar.vecm import select_order
2次元の過程$X_t$を
$X_{1t}=\sum_{i=1}^t \epsilon_{1i}+\epsilon_{2t}$,
$X_{2t}=\sum_{i=1}^t \epsilon_{1i}+\epsilon_{3t}$,
と定義すれば、これらは$\beta^`=(a,-1)$の共和分ベクトルのもとで共和分となる。線形関係$\beta^`X_t=aX_{1t}-X_{2t}=a\epsilon_{2t}-\epsilon_{3t}$は定常であるので、それをチェックしてみよう。
\beta^{'}X_t=
\begin{bmatrix}
a & -1
\end{bmatrix}
\begin{bmatrix}
X_{1t} \\
X_{2t}
\end{bmatrix}
=aX_{1t}-X_{2t}=a\epsilon_{2t}-\epsilon_{3t}
は定常である。それをチェックしてみよう。
Oxford University Press.
n=10000
a=0.3
e1=np.random.normal(0,1,n)#.reshape([n,1])
e2=np.random.normal(0,1,n)#.reshape([n,1])
e3=np.random.normal(0,1,n)#.reshape([n,1])
X1=np.cumsum(e1)+e2
X2=a*np.cumsum(e1)+e3
X=np.concatenate([X1.reshape([n,1]),X2.reshape([n,1])],1)
plt.plot(X)
グラフからどちらも和分過程であり、共通トレンドを持つことが分かる。
betaX=a*X1-X2
plt.plot(betaX)
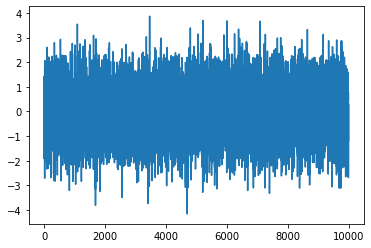
定常性が確認できる。
つぎに、
$X_{3t}=\epsilon_{4t}$を追加する。$X_t^{'}=(X_{1t},X_{2t},X_{3t})$は$I(1)$で、3変数の線形結合が$I(0)$になる場合は幾つかある。このベクトル過程では共和分ベクトルは(a,-1,0)と(0,0,1)の2つある。
共和分の意味を直感的に理解する例 3.2 Johansen, S. 1995. Likelihood-Based Inference in Cointegrated Vector Autoregressive Models p.37
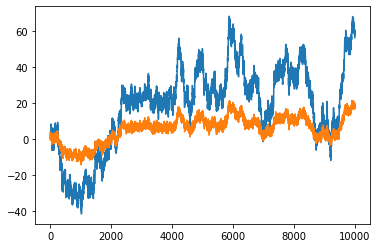
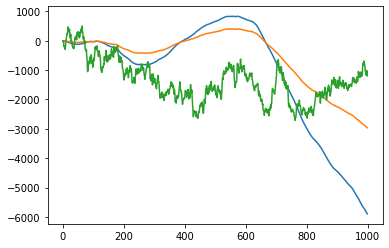
X1,X2、X3についてはどうも今一歩本当に定常になるかどうかが定かでないので、実際に乱数を作ってみる。a,b,cについては適当にグラフが見やすいように調整した。
n=1000
e1=np.random.normal(0,1,n)#.reshape([n,1])
e2=np.random.normal(0,1,n)#.reshape([n,1])
e3=np.random.normal(0,1,n)#.reshape([n,1])
e4=np.random.normal(0,1,n)#.reshape([n,1])
cs_e1=np.cumsum(e1)
cs_cs_e1=np.cumsum(cs_e1)
cs_e2=np.cumsum(e2)
X1=cs_cs_e1+cs_e2
a=0.5
b=2
X2=a*cs_cs_e1+b*cs_e2+e3
c=100
X3=c*cs_e2+e4
plt.plot(X1)
plt.plot(X2)
plt.plot(X3)
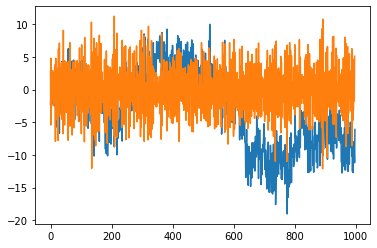
つぎに実際の差分を取って定常性を調べてみよう。
plt.plot(np.diff(X1))
plt.plot(np.diff(np.diff(X1)))
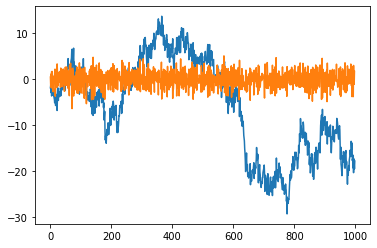
なるほど一階の差分では定常にならないのは分かるが2階とると定常になっている。
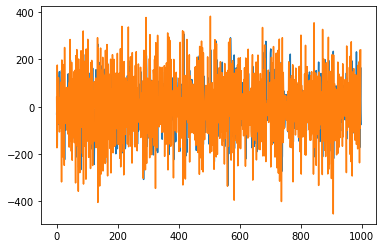
plt.plot(np.diff(X2))
plt.plot(np.diff(np.diff(X2)))
plt.plot(np.diff(X3))
plt.plot(np.diff(np.diff(X3)))
ベクトル誤差修正モデル(VECM)statsmodels マニュアル
ベクトル誤差修正モデルは、目的変数のもつ恒久的な確率的トレンド(単位根)とそれとの短期的な乖離の関係を研究するために用いられる。 VECMは、複数の確率的トレンドがあるという仮定の下で、ベクトルの階差系列をモデル化し、これらのモデルを特定・推定するために使用される。VECM($k_{ar}-1)$は
$\Delta y_t= \Pi y_{t−1} + \Gamma_1\Delta y_{t−1} +\dots + \Gamma_{k_{ar}-1}\Delta y_{t−k_{ar} + 1} + u_t$
の形式をとる。また、$\Pi=\alpha \beta^`$である。この$\alpha$と$\beta^`$は最小二乗法では推定できないので、誤差修正モデルを最尤推定することで$\Pi$の固有値、固有ベクトルを求め、共和分検定で$\Pi$のランクを決定し、固有値に対応する固有ベクトルを求める。[1]の7章参照。また、$ \Pi y_{t−1}$に定数項やトレンド項などの決定論的な項を含めることも可能である。[3]参照。
決定論的項を持つVECM($k_{ar}−1$)は
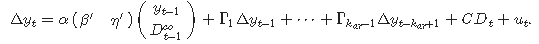
となる。$D_{t-1}^\infty$は、共和分ベクトル内に(または共和分ベクトルを制約する)決定論的な項があることを示している。 $\eta$は関連する推定量である。共和分ベクトル内に決定論的な項を渡すには、引数のexog_cointを用いる。定数項と線形トレンドの2つの特殊なケースでは、これらの項を用いるよりも簡単な方法がある。"ci"と"li"のそれぞれを引数のdeterministicに渡せばよい。したがって、共和分ベクトル内の定数項については、引数のdeterministicに"ci"を、またはnp.ones(len(data))をexog_cointに渡せばよい。この場合には、すべての$t$で$D_{t-1}^\infty = 1$となる。
また、共和分ベクトル外の決定論的な項を使用することもできる。これらは、上記の式の$D_t$で行列$C$に関する推定量とともに定義される。これらの項を、引数のexogに渡すことで指定する。定数項および/または線形トレンドの場合、引数のdeterministicを代わりに使用することもできる。定数項の場合は"co"を渡し、線形トレンドの場合は"lo"を渡す。"o"は外部を表す。次の表は、[2]で考慮される5つのケースを示している。最後の列は、これらの各ケースの引数のdeterministicに渡す文字列を示している。
-
class statsmodels.tsa.vector_ar.vecm.VECM(endog, exog=None, exog_coint=None, dates=None, freq=None, missing='none', k_ar_diff=1, coint_rank=1, deterministic='nc', seasons=0, first_season=0)
-
Class representing a Vector Error Correction Model (VECM).
-
パラメーター
endog array-like(nobs_tot x neqs)
2次元の内生的応答変数。
exog:ndarray(nobs_tot x neqs)またはNone
共和分ベクトル外の決定論的項。
exog_coint:ndarray(nobs_tot x neqs)またはNone
共和分ベクトル内の決定論的項。
date array-like datetime、オプション.
詳細については、statsmodels.tsa.base.tsa_model.TimeSeriesModelを参照.
freqstr、オプション
詳細については、statsmodels.tsa.base.tsa_model.TimeSeriesModelを参照.
missing str、オプション、
詳細については、statsmodels.base.model.Modelを参照.
k_ar_diff int
モデル内の階差の次数。上記の式でkar-1と等しい.
coint_rank int
共和分ランクは、行列のランクΠおよびαとβの列数に等しい.
deterministic str {"nc"、 "co"、 "ci"、 "lo"、 "li"}
"nc"-決定論的項なし
"co"-共和分ベクトル外の定数
"ci"-共和分ベクトル内の定数
"lo"-共和分ベクトル外の線形トレンド
"li"-共和分ベクトル内の線形トレンド
組み合わせが可能(例:定数項付き線形トレンドの場合は"cili”または”colo”)。定数項を使用する場合、それを共和分関係に制限する(つまり”ci”)か、無制限のままにする(つまり”co”)かを選択する必要がある。 “ci”と”co”の両方を使用しない。線形項を使用する場合、”li”と”lo”にも同じことが当てはまる。詳細については、注を参照。
seasons int、デフォルト:0
季節サイクルの期間の数。 0は季節がないことを意味する.
first_season int、デフォルト:0
最初の観測値の季節。
-
VECMResults.predict(steps=5, alpha=None, exog_fc=None, exog_coint_fc=None)[source]
時系列の将来の値を計算 -
パラメータ
steps int
予測期間。
alpha float, 0 < alpha < 1 or None
Noneの場合、ポイント予測のみを計算。 floatの場合、信頼区間も計算。 この場合、引数は信頼レベルを表す。
exog ndarray (steps x self.exog.shape[1])
self.exogがNoneでない場合、exogの将来の値に関する情報をこのパラメーターから渡します。 ndarrayは、最初の次元でより大きくなる場合があります。 この場合、最初のステップの行のみが考慮されます。
- Returns
forecast - ndarray (steps x neqs) or three ndarrays
ポイント予測の場合:返されるndarrayの各行は、特定の期間のneqs変数の予測を表します。 最初の行(index[0])は次の期間の予測であり、最後の行(index[steps-1])はsteps-periods-ahead-予測です。
References
[1] Lütkepohl, H. 2005. New Introduction to Multiple Time Series Analysis. Springer.
[2] Johansen, S. 1995. Likelihood-Based Inference in Cointegrated Vector Autoregressive Models. Oxford University Press.
[3] Johansen, S. and K Jusellus 1990. Likelihood-Based Estimation and Inference on Cointegration with application to the demand for money. 0xford Bullretin of Economics and Statisitics,52,169-210
実データを分析する前に
実際のデータを分析する前に人工データを生成し、そのデータを用いてモデルの特性を理解することは最も有効な武器である。
そこで、$x$と$y$という2つの非定常時系列を生成して、それをVECMで分析してみよう。その際にdeterministic='nc'、K_ar_diff=0とする。これはモデルの変数を$\alpha$と$\beta$のみに絞ってみようという試みである。その際に、$x$と$y$を単回帰してベータを求め、その誤差を用いてアルファを推計する。データの数は$n=10000$である。収束するには十分である。
n=10000
y=pd.DataFrame(np.random.normal(0,1,n).reshape([n,1]),columns=['y'])
x=pd.DataFrame(np.random.normal(0,1,n).reshape([n,1]),columns=['x'])
data=pd.concat([y.cumsum(),x.cumsum()],axis=1)
data.columns=['y','x']
model=VECM(data,k_ar_diff=0,deterministic='na')
res=model.fit()
print(res.summary())
xx=sm.add_constant(x.cumsum())
res= sm.OLS(y.cumsum(), xx).fit()
print(res.summary())
Loading coefficients (alpha) for equation y
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ec1 -0.0005 0.000 -1.671 0.095 -0.001 8.89e-05
Loading coefficients (alpha) for equation x
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ec1 -3.723e-05 0.000 -0.121 0.904 -0.001 0.001
Cointegration relations for loading-coefficients-column 1
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
beta.1 1.0000 0 0 0.000 1.000 1.000
beta.2 -0.2731 0.382 -0.716 0.474 -1.021 0.475
==============================================================================
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.126
Model: OLS Adj. R-squared: 0.126
Method: Least Squares F-statistic: 1443.
Date: Sun, 01 Mar 2020 Prob (F-statistic): 4.92e-295
Time: 02:27:15 Log-Likelihood: -43187.
No. Observations: 10000 AIC: 8.638e+04
Df Residuals: 9998 BIC: 8.639e+04
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const -29.8591 0.210 -142.406 0.000 -30.270 -29.448
x -0.1572 0.004 -37.984 0.000 -0.165 -0.149
==============================================================================
Omnibus: 414.693 Durbin-Watson: 0.003
Prob(Omnibus): 0.000 Jarque-Bera (JB): 401.515
Skew: -0.447 Prob(JB): 6.49e-88
Kurtosis: 2.593 Cond. No. 58.5
==============================================================================
u=res.resid
#x1=pd.concat([x,u],axis=1)
#x1=sm.add_constant(x1)
res= sm.OLS(y, u).fit()
print(res.summary())
OLS Regression Results
=======================================================================================
Dep. Variable: y R-squared (uncentered): 0.000
Model: OLS Adj. R-squared (uncentered): -0.000
Method: Least Squares F-statistic: 0.2729
Date: Sun, 01 Mar 2020 Prob (F-statistic): 0.601
Time: 02:57:55 Log-Likelihood: -14187.
No. Observations: 10000 AIC: 2.838e+04
Df Residuals: 9999 BIC: 2.838e+04
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
x1 0.0001 0.000 0.522 0.601 -0.000 0.001
==============================================================================
Omnibus: 0.070 Durbin-Watson: 2.013
Prob(Omnibus): 0.966 Jarque-Bera (JB): 0.053
Skew: -0.002 Prob(JB): 0.974
Kurtosis: 3.011 Cond. No. 1.00
==============================================================================
これをなんども繰り返し動かすこで、モデルの意味と使い方が見えてくるはずである。忘れてはいけないのはデータはランダムウォークということである。
例:米国マクロデータ
year 期間 - 1959q1 - 2009q3
quarter: 四半期 - 1-4
realgdp: 実質国内総生産 - (Bil. of chained 2005 USD,季節調整済年率)
realcons: 実質個人消費 - (Bil. of chained 2005 USD, 季節調整済年率)
realinv: 実質民間総国内投資(Bil. of chained 2005 USD, 季節調整済年率)
from statsmodels.tsa.api import VECM
import statsmodels.api as sm
from statsmodels.tsa.base.datetools import dates_from_str
import pandas as pd
import numpy as np
mdata = sm.datasets.macrodata.load_pandas().data
dates = mdata[['year', 'quarter']].astype(int).astype(str)
quarterly = dates["year"] + "Q" + dates["quarter"]
quarterly = dates_from_str(quarterly)
mdata = mdata[['realgdp','realcons','realinv']]
mdata.index = pd.DatetimeIndex(quarterly)
data = np.log(mdata).diff().dropna()
model = VECM(data)
results = model.fit()
print(results.summary())
Det. terms outside the coint. relation & lagged endog. parameters for equation realgdp
===============================================================================
coef std err z P>|z| [0.025 0.975]
-------------------------------------------------------------------------------
L1.realgdp -0.0101 0.147 -0.068 0.945 -0.298 0.278
L1.realcons -0.4094 0.133 -3.081 0.002 -0.670 -0.149
L1.realinv 0.0039 0.020 0.197 0.843 -0.035 0.043
Det. terms outside the coint. relation & lagged endog. parameters for equation realcons
===============================================================================
coef std err z P>|z| [0.025 0.975]
-------------------------------------------------------------------------------
L1.realgdp 0.0039 0.140 0.028 0.978 -0.270 0.277
L1.realcons -0.4813 0.126 -3.818 0.000 -0.728 -0.234
L1.realinv -0.0083 0.019 -0.443 0.658 -0.045 0.028
Det. terms outside the coint. relation & lagged endog. parameters for equation realinv
===============================================================================
coef std err z P>|z| [0.025 0.975]
-------------------------------------------------------------------------------
L1.realgdp 2.3752 0.825 2.879 0.004 0.758 3.992
L1.realcons -1.4317 0.745 -1.922 0.055 -2.892 0.028
L1.realinv -0.3738 0.110 -3.383 0.001 -0.590 -0.157
Loading coefficients (alpha) for equation realgdp
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ec1 -1.2524 0.141 -8.875 0.000 -1.529 -0.976
Loading coefficients (alpha) for equation realcons
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ec1 0.0673 0.134 0.503 0.615 -0.195 0.330
Loading coefficients (alpha) for equation realinv
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ec1 -7.3749 0.791 -9.322 0.000 -8.926 -5.824
Cointegration relations for loading-coefficients-column 1
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
beta.1 1.0000 0 0 0.000 1.000 1.000
beta.2 -0.9514 0.037 -25.704 0.000 -1.024 -0.879
beta.3 -0.0204 0.010 -1.967 0.049 -0.041 -6.88e-05
==============================================================================
為替レートの分析
import matplotlib.pyplot as plt
start="1949/5/16"
fx = web.DataReader("DEXJPUS","fred",start)# usdjpy
rf = web.DataReader("USD12MD156N", 'fred',start)
rd = web.DataReader("JPY12MD156N", 'fred',start)
data=pd.concat([fx,rf,rd],axis=1).ffill().dropna()
data.tail()
DEXJPUS USD12MD156N JPY12MD156N
DATE
2019-12-02 109.09 1.96250 0.10283
2019-12-03 108.53 1.93663 0.10367
2019-12-04 108.87 1.91700 0.10567
2019-12-05 108.69 1.92263 0.09833
2019-12-06 108.66 1.92313 0.10833
model = VECM(data)
results = model.fit()
print(results.summary())
Det. terms outside the coint. relation & lagged endog. parameters for equation DEXJPUS
==================================================================================
coef std err z P>|z| [0.025 0.975]
----------------------------------------------------------------------------------
L1.DEXJPUS 0.0179 0.011 1.681 0.093 -0.003 0.039
L1.USD12MD156N 0.2679 0.155 1.729 0.084 -0.036 0.572
L1.JPY12MD156N -0.1119 0.272 -0.412 0.681 -0.645 0.421
Det. terms outside the coint. relation & lagged endog. parameters for equation USD12MD156N
==================================================================================
coef std err z P>|z| [0.025 0.975]
----------------------------------------------------------------------------------
L1.DEXJPUS 0.0042 0.001 5.762 0.000 0.003 0.006
L1.USD12MD156N 0.0529 0.011 4.931 0.000 0.032 0.074
L1.JPY12MD156N 0.0111 0.019 0.590 0.555 -0.026 0.048
Det. terms outside the coint. relation & lagged endog. parameters for equation JPY12MD156N
==================================================================================
coef std err z P>|z| [0.025 0.975]
----------------------------------------------------------------------------------
L1.DEXJPUS 0.0041 0.000 9.923 0.000 0.003 0.005
L1.USD12MD156N 0.0337 0.006 5.562 0.000 0.022 0.046
L1.JPY12MD156N -0.0922 0.011 -8.665 0.000 -0.113 -0.071
Loading coefficients (alpha) for equation DEXJPUS
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ec1 -0.0002 7.46e-05 -3.277 0.001 -0.000 -9.82e-05
Loading coefficients (alpha) for equation USD12MD156N
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ec1 -8.487e-06 5.16e-06 -1.645 0.100 -1.86e-05 1.63e-06
Loading coefficients (alpha) for equation JPY12MD156N
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ec1 -1.177e-05 2.92e-06 -4.034 0.000 -1.75e-05 -6.05e-06
Cointegration relations for loading-coefficients-column 1
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
beta.1 1.0000 0 0 0.000 1.000 1.000
beta.2 -34.4981 7.117 -4.847 0.000 -48.447 -20.549
beta.3 52.7028 12.677 4.157 0.000 27.857 77.549
==============================================================================
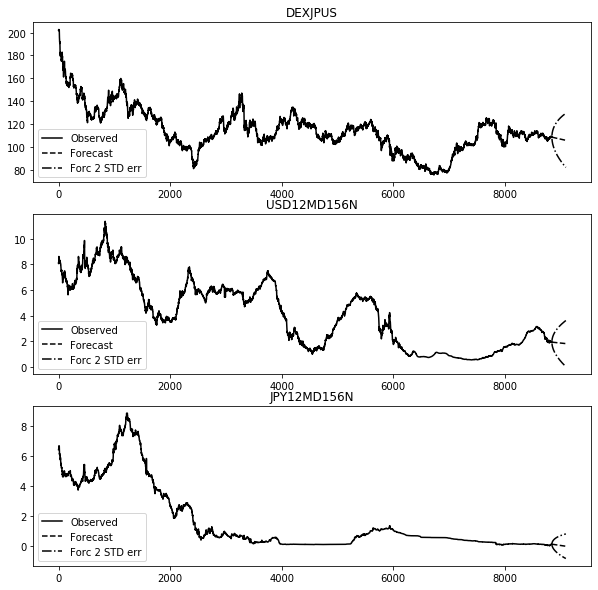
為替レート、12カ月LIBORと250データの予測
from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()
results.plot_forecast(250)
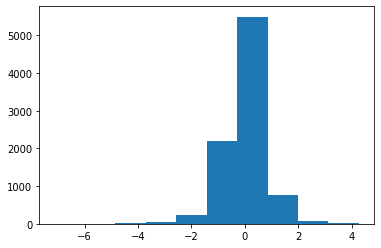
為替レートの予測誤差
plt.hist(results.resid[:,0])
株価の分析
n225 = web.DataReader("NIKKEI225", 'fred',start)
sp500 = web.DataReader("SP500", 'fred',start)
data=pd.concat([fx,n225,sp500],axis=1).ffill().dropna()
data.tail()
DEXJPUS NIKKEI225 SP500
DATE
2019-12-09 108.66 23430.70 3135.96
2019-12-10 108.66 23410.19 3132.52
2019-12-11 108.66 23391.86 3141.63
2019-12-12 108.66 23424.81 3168.57
2019-12-13 108.66 24023.10 3168.80
model = VECM(data)
results = model.fit()
print(results.summary())
Det. terms outside the coint. relation & lagged endog. parameters for equation DEXJPUS
================================================================================
coef std err z P>|z| [0.025 0.975]
--------------------------------------------------------------------------------
L1.DEXJPUS -0.0278 0.021 -1.308 0.191 -0.069 0.014
L1.NIKKEI225 0.0001 6.14e-05 2.016 0.044 3.45e-06 0.000
L1.SP500 0.0019 0.001 2.823 0.005 0.001 0.003
Det. terms outside the coint. relation & lagged endog. parameters for equation NIKKEI225
================================================================================
coef std err z P>|z| [0.025 0.975]
--------------------------------------------------------------------------------
L1.DEXJPUS 63.7228 6.161 10.342 0.000 51.647 75.799
L1.NIKKEI225 -0.1888 0.018 -10.592 0.000 -0.224 -0.154
L1.SP500 5.1709 0.200 25.879 0.000 4.779 5.562
Det. terms outside the coint. relation & lagged endog. parameters for equation SP500
================================================================================
coef std err z P>|z| [0.025 0.975]
--------------------------------------------------------------------------------
L1.DEXJPUS -0.5797 0.631 -0.919 0.358 -1.816 0.656
L1.NIKKEI225 0.0020 0.002 1.097 0.273 -0.002 0.006
L1.SP500 -0.0170 0.020 -0.830 0.406 -0.057 0.023
Loading coefficients (alpha) for equation DEXJPUS
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ec1 0.0003 0.000 1.906 0.057 -8.9e-06 0.001
Loading coefficients (alpha) for equation NIKKEI225
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ec1 0.1447 0.048 3.023 0.003 0.051 0.238
Loading coefficients (alpha) for equation SP500
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ec1 0.0109 0.005 2.231 0.026 0.001 0.021
Cointegration relations for loading-coefficients-column 1
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
beta.1 1.0000 0 0 0.000 1.000 1.000
beta.2 -0.0469 0.014 -3.367 0.001 -0.074 -0.020
beta.3 0.3437 0.113 3.050 0.002 0.123 0.564
==============================================================================
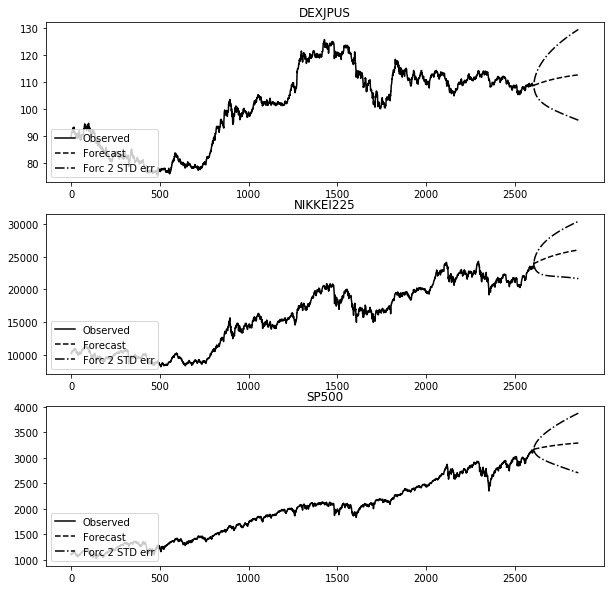
register_matplotlib_converters()
results.plot_forecast(250)
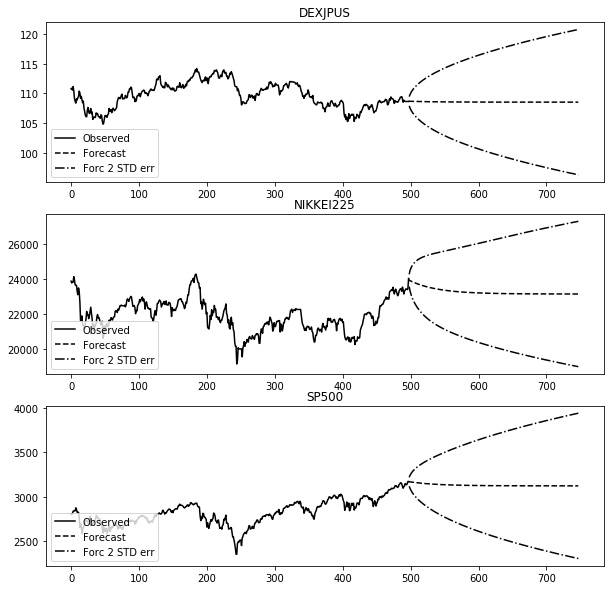
model = VECM(data.iloc[-500:])
results = model.fit()
print(results.summary())
register_matplotlib_converters()
results.plot_forecast(250)
Det. terms outside the coint. relation & lagged endog. parameters for equation DEXJPUS
================================================================================
coef std err z P>|z| [0.025 0.975]
--------------------------------------------------------------------------------
L1.DEXJPUS 0.0021 0.048 0.043 0.966 -0.092 0.096
L1.NIKKEI225 6.633e-05 8.34e-05 0.795 0.427 -9.72e-05 0.000
L1.SP500 -0.0004 0.001 -0.499 0.618 -0.002 0.001
Det. terms outside the coint. relation & lagged endog. parameters for equation NIKKEI225
================================================================================
coef std err z P>|z| [0.025 0.975]
--------------------------------------------------------------------------------
L1.DEXJPUS 74.0915 21.467 3.451 0.001 32.017 116.166
L1.NIKKEI225 -0.1603 0.037 -4.298 0.000 -0.233 -0.087
L1.SP500 4.7485 0.332 14.311 0.000 4.098 5.399
Det. terms outside the coint. relation & lagged endog. parameters for equation SP500
================================================================================
coef std err z P>|z| [0.025 0.975]
--------------------------------------------------------------------------------
L1.DEXJPUS -2.4372 3.102 -0.786 0.432 -8.517 3.642
L1.NIKKEI225 -0.0029 0.005 -0.545 0.586 -0.014 0.008
L1.SP500 0.0160 0.048 0.333 0.739 -0.078 0.110
Loading coefficients (alpha) for equation DEXJPUS
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ec1 0.0004 0.002 0.215 0.830 -0.003 0.004
Loading coefficients (alpha) for equation NIKKEI225
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ec1 2.4929 0.866 2.880 0.004 0.796 4.190
Loading coefficients (alpha) for equation SP500
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ec1 0.1778 0.125 1.421 0.155 -0.067 0.423
Cointegration relations for loading-coefficients-column 1
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
beta.1 1.0000 0 0 0.000 1.000 1.000
beta.2 -0.0117 0.003 -4.390 0.000 -0.017 -0.006
beta.3 0.0521 0.021 2.510 0.012 0.011 0.093
==============================================================================
参考:
statsmodels リファレンス
error correction model wiki
VARモデルにおける共和分、ECM、因果関係の分析
Python3ではじめるシステムトレード【第2版】環境構築と売買戦略

「画像をクリックしていただくとpanrollingのホームページから書籍を購入していただけます。