分析の対象となる時系列データがランダムウォークにしたがうかどうかを知ることはつぎの2つの点から重要です。
- 発生したトレンドがたまたま生じたものなのか、
- 2つの時系列の相関は見せかけの相関なのか、たまたま発生したものではないのか、
という点です。
多くの経済時系列や株価のレベル(原系列)はランダムウォークにしたがいます。ランダムウォークにしたがう時系列は時間の経過にともない平均や分散が以前のものと異なってしまう非定常時系列です。ランダムウォークでは時間の経過とともに平均は変化し、分散は時間の経過の平方根に比例して増大します。非定常時系列にもいろいろあります。時間の経過とともに確実に平均値が上昇したり下落するトレンド定常性もその1つです。ランダムウォークであるかどうかを判定するにはその時系列が単位根を持つかどうかで判断します。その方法としてディッキーフラー検定があります。しかし、検出力が低いとよく指摘されています。そこで少し調べてみようと思います。
DF検定に移る前に
まず1次の自己回帰モデル(AR(1))を
$y_t=\rho y_{t-1}+u_t$
とします。$\rho$が1であればこのAR(1)は単位根をもつといいます。$y_t$はランダムウォークです。$\Delta y_t=y_t-y_{t-1}$が時間の経過に対して平均値と分散が一定の定常過程であるとき、それを1次の和分といいます。この単位根過程は
$y_1=y_0+e_1$
$y_2=y_1+e_2$
$y_3=y_2+e_3$
...
となり、t=2とt=3のときの$y$を書き換えると
$y_2=(y_0+e_1)+e2=x_0+e1+e2$
$y_3=(y_0+e_1+e_2)+e_3=y_0+e_1+e_2+e_3$
...
となります。一般化すると
$y_t=y_0+\sum_{i=1}^te_i$
となり$y_t$は初期値と乱数の和になります。
$\rho>1$では時系列は発散してしまうので、$\rho<1$とします。そうするとAR(1)モデルも同様に
$y_1=ρ\cdot y_0+e_1$
$y_2=ρ\cdot y_1+e_2$
$y_3=ρ\cdot y_2+e_3$
...
となり、$y_2$と$y_3$を書き換えると
$y_2=ρ\cdot (ρ\cdot y_0+e_1)+e2=ρ^2\cdot y_0+ρ\cdot e_1+e2$
$y_3=ρ\cdot (ρ^2\cdot y_0 +ρ\cdot e_1+e_2)+e_3$
$=ρ^3y_0+ρ^2\cdot (e_1)+ρ\cdot (e_2)+e_3$
$=ρ^3y_0+\sum_{i=1}^3ρ^{3-i}\cdot (e_i)$
となります。一般化すると
$y_t=ρ^ty_0+\sum_{i=1}^tρ^{t-i}\cdot (e_i)$
となります。
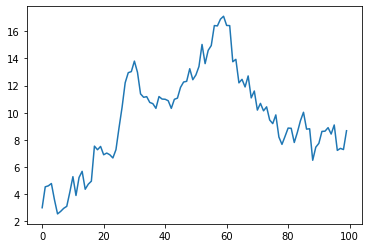
ここまでをpythonを使って確かめましょう。つぎのコードは乱数を発生させ、それを利用してランダムウォーク、またはAR(1)の時系列データを生成する関数です。まず、rho=1, sigma=1としてランダムウォークとなるデータを生成します。
import numpy as np
import matplotlib.pyplot as plt
def generate(y0,rho,sigma,nsample):
e = np.random.normal(size=nsample)
y=[]
y.append(rho*y0+e[0])
for i,u in enumerate(e[1:]):
y.append(rho*y[i]+u)
plt.plot(y)
generate(1,1,1,100)
酔っ払いの千鳥足のようにどこに行くかわかません。価格の動きは時間の経過とともに初期値から離れていくことができます。もちろん、初期値に戻ることも可能です。
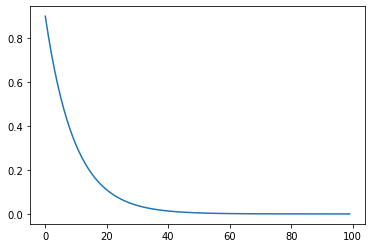
つぎに$rho=0.9$にしてみます。
generate(1,0.9,1,100)
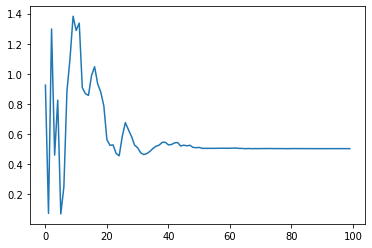
ある値に収束していくことが分かります。これはAR(1)の特徴です。
つぎにsigma=0にしてみましょう。これは時系列が確率過程ではなく、確定的過程としたらどうなるかを見るものです。まずはランダムウォークの場合です。
generate(1,1,0,100)
つぎに、rho=0.9の場合についてみてみましょう。
generate(1,0.9,0,100)
ランダムウォークでは1のままでしたが、AR(1)ではゼロに収束していきます。これはrhoを1よりも小さくした場合の特徴です。
これでは不便なので、AR(1)モデルをつぎのように書き換えます。
$y_t=c+\rho y_{t-1}+u_t$
とします。つぎにこの系列を足し合わせます。
$\sum_{t=2}^n y_t=\sum_{t=2}^n c+\sum_{t=2}^n\rho y_{t-1}+\sum_{t=2}^nu_t$
$y_t$の平均値を$\mu$とすると、nが十分に大きければ、$\sum_{t=2}^nu_t=0$なので
$\mu=c+\rho \mu$となります。したがって
$c=\mu(1-\rho)$
となります。これを使って関数generateを書き換えましょう。そして回帰係数0.9のAR(1)を生成してみます。
def generate(y0,rho,c,sigma,nsample):
e = np.random.normal(size=nsample)
y=[]
y.append(rho*y0+e[0]*sigma+c)
for i,u in enumerate(e[1:]):
y.append(rho*y[i]+u*sigma+c)
plt.plot(y)
generate(1,0.9,0.1,0,100)
となりました。これでAR(1)は時間が経過しても平均値は一定です。sigmaを小さくして確認してみましょう。
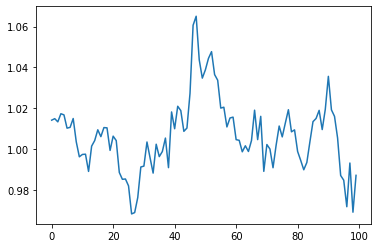
generate(1,0.9,0.1,0.01,100)
何となく、平均回帰しているのが分かると思います。AR(1)モデルはある条件を満たせば定常(弱定常)になります。平均回帰しているようですが、ここに明確な周期があるわけではなく、平均に回帰してくるタイミングはランダムです。それは上限に到達する時間、下限に到達する時間にも言えることです。つまりrhoが1に近ければ、限りなくランダムウォークに近い動きをするということです。
トレンド定常
トレンド定常過程$y_t$は、$y_t = f(t)+ u_t$に従います。ここで、tは時間、fは決定論的関数、$u_t$は長期的な平均値がゼロとなる定常確率変数です。この非確率的ドリフトは、tで$y_t$を回帰し、定常な残差がえられれば、データから差し引いて求めることができます。もっとも簡単なトレンド定常過程は$y_t=d \cdot t +u_t$です。$d$は定数です。
階差定常
単位根(定常)過程は、$y_t = y_ {t-1} + c + u_t$に従います。$u_t$は長期的にはゼロとなる平均値をもつ定常確率変数です。ここでcは非確率的ドリフトパラメーターです。ランダムショック$u_t$がなくても、yの平均は期間ごとにcだけ変化します。この非定常性は1次の階差を取ることでデータから削除できます。階差された変数$z_t = y_t-y_{t-1}=c+u_t$はcの長期的に一定となる平均値を持ち、したがってこの平均値にドリフトはありません。つぎにc = 0として考えてみます。この単位根過程は、$y_t = y_ {t-1} + c + u_t$です。$u_t$は定常過程ですが、その確率的なショック$u_t$の存在により、ドリフト、特に確率的ドリフトが$y_t$に生じます。一度発生したゼロ以外の値uは同じ期間のyに組み込まれます。これは、1期間後にyの1期間遅れの値になり、次の期のy値にも影響します。 yは次々に新しいy値に影響を与えます。したがって、最初のショックがyに影響した後、その値はyの平均に永久に組み込まれるため、確率的なドリフトが生じるのです。ですからこのドリフトも、最初にyを差分してドリフトしないzを取得することで除くことができます。この確率的ドリフトは$c\ne0$でも生じます。ですから$y_t = y_ {t-1} + c + u_t$でも生じます。cは非確率的ドリフトパラメーターです。なぜ確定的なドリフトではないのでしょうか?実は、$c+u_t$から生じるドリフトは確率過程の一部と考えます。
numpy.random.normal
numpyのリファレンスから
numpy.random.normal(loc=0.0, scale=1.0, size=None)
loc float or array_like of floats: 分布の平均値
scalefloat or array_like of floats:分布の標準偏差
です。ここでlocの意味を考えてみます。この分布から生成される標本の平均値は$N(μ,σ^2/n)$に近似的に従います。その仕組みをみてみましょう。あえてloc=1,scale=1.0とします。n=2としてその標本平均と標準偏差を求めてみました。ただし、計算方法は2つです。1つは
$z_t$の平均と標準偏差を求めます。
もう1つは
それぞれの観測値$z_t$から1を引きその標本の平均と標準偏差を求めます。そしてその標本平均に1を足します。
import numpy as np
import matplotlib.pyplot as plt
s = np.random.normal(1, 1, 2)
print(np.mean(s),np.std(s))
o=np.ones(len(s))
Print(np.mean(s-o)+1,np.std(s-o))
# 0.9255104221128653 0.5256849930003175
# 0.9255104221128653 0.5256849930003175 # 標本から1を引いて、その平均値に1を足した。
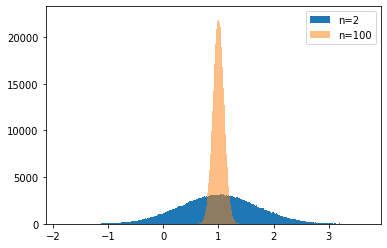
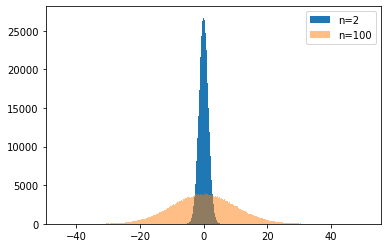
結果は同じになりました。これはnp.random.normal(1,1,n)が1/n+np.random.normal(0,1,n)で乱数を生成していることが分かります。しかし、これはコンピュータの中での話です。実際にはどちらが確率的ドリフトを作り出しているかは判別不能なはずです。そこでn=2とn=100の場合について1000000回データを生成してその結果がどうなるかを見てみましょう。
階差定常過程の標本の算術平均の分布
階差された変数$z_t = y_t-y_{t-1}=c+u_t$はcの長期的に一定となる平均値を持ちます。その標本平均はnが大きければ、$N(μ,σ^2/n)$に近似的に従います。したがって、平均値は一定ではありません。しかし、この場合には平均値にドリフトはありません。長期的に一定となる平均値をもちます。
m1=[]
trial=1000000
for i in range(trial):
s = np.random.normal(1, 1, 2)
m1.append(np.mean(s))
m2=[]
for i in range(trial):
s = np.random.normal(1, 1, 100)
m2.append(np.mean(s))
bins=np.linspace(np.min(s),np.max(s),1000)
plt.hist(m1,bins=bins,label='n=2')
plt.hist(m2,bins=bins,label='n=100',alpha=0.5)
plt.legend()
plt.show()
標本平均も標準偏差も分布を形成し、一意には定まりません。一意に定まるためにはnはもっともっと大きくする必要があります。したがって、時系列の特性を、トレンド成分、周期成分、および確率的な成分(確率的ドリフト)に分解して概念化しますが、確率的ドリフトとドリフト率の扱いには注意が必要です。
単位根過程では確率的ドリフトが発生します。もし、確定的なドリフト率があったとしてもそれは識別が不可能です。
最終日の単位根をもつyの分布
単位根過程では標本の数が増えるにつれて標準偏差は大きくなっていきます。標本の大きさがnのyの平均値はc=0ではゼロですが、標準偏差$\sqrt{n \cdot \sigma^2}$が大きくなった分だけ、その分布は広がります。
m1=[]
trial=1000000
for i in range(trial):
s = np.cumsum(np.random.normal(0, 1, 2))
m1.append(s[-1])
m2=[]
for i in range(trial):
s = np.cumsum(np.random.normal(0, 1, 100))
m2.append(s[-1])
bins=np.linspace(np.min(m2),np.max(m2),1000)
plt.hist(m1,bins=bins,label='n=2')
plt.hist(m2,bins=bins,label='n=100',alpha=0.5)
plt.legend()
plt.show()
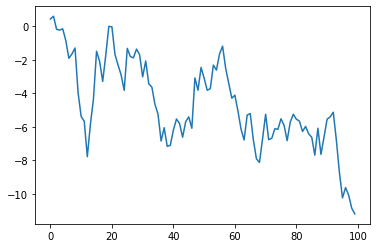
先ほどとは異なる分布になりました。標本の大きさが大きいほうの分布の広がりが大きくなります。ためしに1つのsの系列をプロットして見ましょう。
plt.plot(s)
この場合、階段的にそれぞれの標本のレベルが変化していきます。この変化は確率的なショック$u_t$によるものです。それが加算されていったものがプロットされています。確率的ドリフトの系列がプロットされています。これが大きなトレンドを形成することがあります。それはn=100の分布図でいえば両端の領域に相当します。どの範囲かはトレンドの定義によります。そのトレンドは確率的トレンドです。これはトレンド定常性がつくる確定的トレンドと明確に区別されます。
1次の自己回帰過程
1次の自己回帰過程はつぎに様に書き換えることができます。
$x_1=ρ\cdot x_0+y_1+e_1$
$x_2=ρ\cdot x_1+y_2+e_2$
$x_3=ρ\cdot x_2+y_3+e_3$
$x_2=ρ\cdot (ρ\cdot x_0+y_1+e_1)+e2=ρ^2\cdot x_0+ρ\cdot (y_1+e1)+y_2+e2$
$x_3=ρ\cdot (ρ\cdot ρ\cdot x_0+ρ\cdot (y_1+e_1)+y_2+e_2)+y_3+e_3$
$=ρ^3x_0+ρ^2\cdot (y_1+e_1)+ρ\cdot (y_2+e_2)+y_3+e_3$
$=ρ^3x_0+\sum_{i=1}^n\rho^{n-i}(y_i+e_i)$
ここで$y_i=c+d\cdot i$
$\rho=1$のときランダムウォーク過程となります。
# 初期化
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
from scipy.stats import norm
from statsmodels.tsa.stattools import adfuller
#np.random.seed(0)
# AR(1)過程の生成
# x0は価格の初期値
# nsampleは1回の試行の期間の数
# rho=1: random walk
## c=c1-rho はドリフト、c1=1のときはドリフト無しランダムウォーク dは確定的トレンド
# rho<1で1次の自己回帰モデル
## x0とcとdの効果は時間の経過とともに消滅
def ar1(rho,x0,c1,d,sigma,nsample):
e = np.random.normal(size=nsample)#random variable
rhoo=np.array([rho ** num for num in range(nsample)]) #effects of rho
rhoo_0=np.array([rho**(num+1) for num in range(nsample)]) #effects of rho
t=np.arange(nsample) #deterministic trend
one=np.ones(nsample) #effect of x0
x00=x0*one*rhoo_0 #effect of rho to x0
c=c1-rho # constant of autoregressive mdoel
c0=np.cumsum(c*one*rhoo) #effect of rho to c
d0=(d*t*rhoo) # effect of rho to determinist trend
y=np.cumsum(rhoo*e*sigma)+x00+c0+d0
return y
AR(1)過程の最終日のyの分布
m1=[]
trial=1000000
nsample=250
x0=1
for i in range(trial):
s = np.cumsum(np.random.normal(0, 1, nsample))
m1.append(s[-1]+x0)
def generate(rho,x0,c1,sigma,nsample,trial):
m=[]
for i in range(trial):
e = np.random.normal(0, 1, nsample)
rhoo=np.array([rho ** num for num in range(nsample)]) #effects of rho
rhoo_0=np.array([rho**(num+1) for num in range(nsample)]) #effects of rho
one=np.ones(nsample) #effect of x0
x00=x0*one*rhoo_0 #effect of rho to x0
c=c1-rho # constant of autoregressive mdoel
c0=np.cumsum(c*one*rhoo) #effect of rho to c
s=np.cumsum(rhoo*e*sigma)+x00+c0
m.append(s[-1])
return m
c1=1
x0=1
rho=0.99
sigma=1
m2=generate(rho,x0,c1,sigma,nsample,trial)
rho=0.9
m3=generate(rho,x0,c1,sigma,nsample,trial)
rho=0.5
m4=generate(rho,x0,c1,sigma,nsample,trial)
bins=np.linspace(np.min(m1),np.max(m1),1000)
plt.hist(m1,bins=bins,label='rw')
plt.hist(m2,bins=bins,label='ar1 rho=0.99',alpha=0.5)
plt.hist(m3,bins=bins,label='ar1 rho=0.9',alpha=0.5)
plt.hist(m4,bins=bins,label='ar1 rho=0.5',alpha=0.5)
plt.legend()
plt.show()
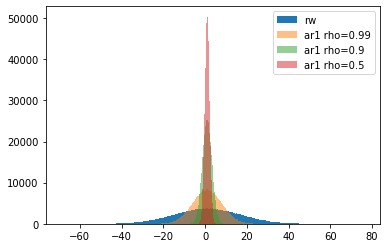
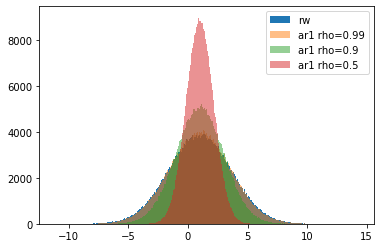
1次の自己回帰モデルでは$\rho$が1より小さくなるにしたがい、初期値の周りをうろうろするのが分かります。$\rho$が1に近づくとランダムウォークとの区別はつきにくくなります。つぎの図はn=7とした場合です。7日程度ですとどの$\rho$でも広がり具合は似たり寄ったりです。
検出力(statsmodelsによる統計的仮説検定 入門)
仮説検定では帰無仮説と対立仮説を立てます。帰無仮説は母数で構成します。標本はこの母集団から抽出されたものとして扱います。つぎの図では、その母集団の分布を青い点線で示しています。標本からはその統計量の標本分布が得られます。それを橙の線で示しています。この2つを比べます。2つの分布が近ければ、この2つの分布を違うと判断するのが難しく、離れていれば違うと判断できます。
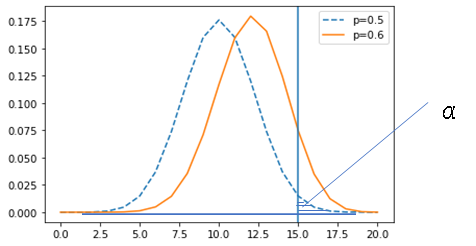
この判断を有意水準を用いて行うことができます。有意水準$\alpha$は母集団の右端の面積のことです。10%,5%などが用いられます。青い分布の青い垂直の線の右側の面積です。青い垂直の線は帰無仮説が棄却される境界を示しています。この線よりも内側を採択域、外側を棄却域といいます。
標本が得られると平均、分散などの統計量を計算することができます。p値は、その統計量を下限として帰無仮説を棄却した場合の棄却される確率を母集団の分布から算出したものです。つぎに図でいうと赤い垂直の線から右の部分の面積です。この値が判断基準である有意水準より小さければ、標本(統計量)は母集団(母数)とは異なる分布から得られたと判断します。図では赤い垂直の線は青い垂直の線の左側にありますが、橙色の標本分布の平均値が青い垂直の線の右側にくれば、そのp値は有意水準よりも小さくなることは明確です。
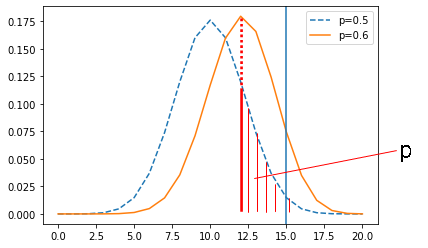
誤った帰無仮説を正しく棄却できる力を検出力といいます。検出力$1-\beta$は青い垂直の線の橙の分布の右側の面積に相当します。$1-\beta$の部分が大きければ帰無仮説を棄却した時に対立仮説が正しい確率が大きくなります。
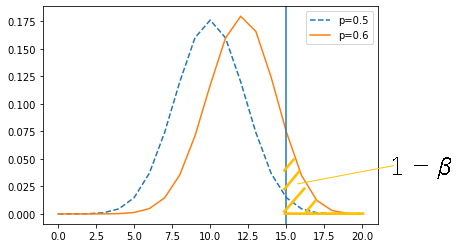
この$1-\beta$を大きくするためには2つの分布が大きく離れている、または分布の中心の位置が大きく異なることが考えられます。もう1つは標本の大きさが大きいことです。そうすれば分布の形状は狭くなり、標本の大きさが分布を線とみなせるほど大きくなれば、2つの直線を比べることになります。
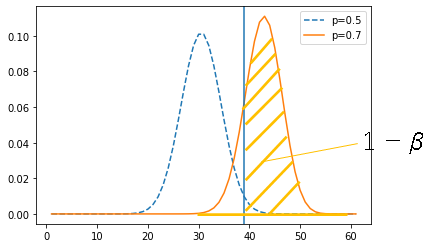
Dicky-fuller検定
単純なAR(1)過程を
$ y_t= \rho y_{t-1}+u_t$
とし、両辺から$y_{t-1}$を差し引いて
$y_t-y_{t-1}=(\rho-1)y_{t-1}+u_t$
とします。$\delta=\rho-1$として、帰無仮説はARモデルに単位根が存在するとします。
$H_0$:$\delta=0$
$H_1$: $\delta<0$
となります。
3つのタイプがあります。
1)ドリフト無しランダムウォーク
$\Delta y_t=\delta y_{t-1}+u_t$
2) ドリフト付きランダムウォーク
$\Delta y_t=c+\delta y_{t-1}+u_t$
3) ドリフト付きランダムウォーク+時間トレンド
$\Delta y_t=c+c\cdot t+\delta y_{t-1}+u_t$
これらは左辺が一次の差分なので、差分がドリフトを持つ、または時間トレンドをもつという意味です。
# Dicky-Fuller検定のテスト
def adfcheck(a0,mu,sigma,nsample,trial):
prw=0
prwc=0
prwct=0
for i in range(trial):
y=ar1(a0,1,mu,sigma,nsample)
rw=sm.tsa.adfuller(y,maxlag=0,regression='nc')[1]
rwc=sm.tsa.adfuller(y,maxlag=0,regression='c')[1]
rwct=sm.tsa.adfuller(y,maxlag=0,regression='ct')[1]
if rw>0.05:
prw+=1
if rwc>0.05:
prwc+=1
if rwct>0.05:
prwct+=1
print('nsample',nsample,prw/trial,prwc/trial,prwct/trial)
単位根の検定
ドリフト無しランダムウォーク
rho=1
c1=1
c1=(c1-1)/250+1
d=0
d=d/250
sigma=0.4/np.sqrt(250)
trial=10000
for i in [7,20,250]:
adfcheck(rho,x0,c1,d,sigma,i,trial)
# nsample 7 0.9448 0.8878 0.8528
# nsample 20 0.9635 0.9309 0.921
# nsample 250 0.9562 0.9509 0.9485
ドリフト付きランダムウォーク
rho=1
c1=1.1
c1=(c1-1)/250+1
d=0
d=d/250
sigma=0.4/np.sqrt(250)
trial=10000
for i in [7,20,250]:
adfcheck(rho,x0,c1,d,sigma,i,trial)
# nsample 7 0.9489 0.8889 0.8524
# nsample 20 0.9649 0.9312 0.921
# nsample 250 0.9727 0.9447 0.9454
ランダムウォーク+ドリフト+確定的トレンド
rho=1
c1=1.1
c1=(c1-1)/250+1
d=0.9
d=d/250
sigma=0.4/np.sqrt(250)
trial=10000
for i in [7,20,250]:
adfcheck(rho,x0,c1,d,sigma,i,trial)
# nsample 7 0.9971 0.948 0.8581
# nsample 20 1.0 1.0 0.983
# nsample 250 1.0 1.0 0.9998
ランダムウォークが棄却されるべき場合
ドリフト無しAR(1)モデル
rho=0.99
c1=rho
#c1=(c1-1)/250+1
d=0
d=d/250
sigma=0.4/np.sqrt(250)
trial=10000
for i in [7,20,250]:
adfcheck(rho,x0,c1,d,sigma,i,trial)
# nsample 7 0.7797 0.9012 0.8573
# nsample 20 0.6188 0.9473 0.9225
# nsample 250 0.0144 0.7876 0.944
ドリフト付きAR(1)モデル
rho=0.90
c1=1.1
c1=(c1-1)/250+1
d=0
d=d/250
sigma=0.4/np.sqrt(250)
trial=10000
for i in [7,20,250]:
adfcheck(rho,x0,c1,d,sigma,i,trial)
# nsample 7 0.9715 0.8868 0.8539
# nsample 20 0.9989 0.9123 0.912
# nsample 250 1.0 0.0306 0.1622
AR(1)モデル+ドリフト+確定的トレンド
rho=0.90
c1=1.1
c1=(c1-1)/250+1
d=1
d=d/250
sigma=0.4/np.sqrt(250)
trial=10000
for i in [7,20,250]:
adfcheck(rho,x0,c1,d,sigma,i,trial)
# nsample 7 0.999 0.9404 0.8576
# nsample 20 1.0 1.0 0.918
# nsample 250 1.0 1.0 0.0044
正しい仕様のモデルを使うこと、標本の大きさは大きいほうが良いこと、そして帰無仮説を棄却するときにはρは1から離れていたほうが良いことが分かります。
ノイズの影響について
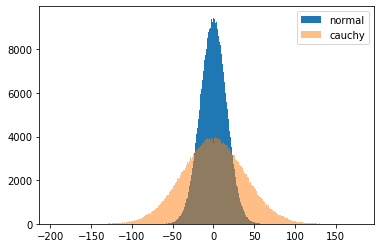
コーシー分布を使ってファットテイルのノイズを発生させそれを使って時系列を生成した時にどのような影響が出るかを調べてみます。
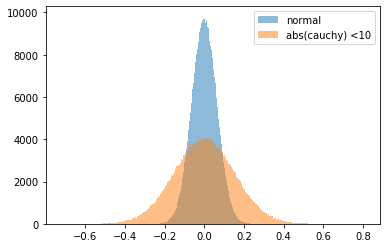
まずコーシー分布の分布をみます。
from scipy.stats import cauchy
trial=1000000
m1=[]
for i in range(trial):
s = np.random.normal(0, 1, 250)
m1.append(np.mean(s))
m2=[]
for i in range(trial):
s=[]
i=1
while i<=250:
s0 = (cauchy.rvs(0,1,1))
if abs(s0)<10:
s.append(s0)
i+=1
m2.append(np.mean(s))
bins=np.linspace(np.min(m2),np.max(m2),1000)
plt.hist(m1,bins=bins,label='normal')
plt.hist(m2,bins=bins,label='abs(cauchy) <10',alpha=0.5)
plt.legend()
plt.show()
ファットテイルが強いことが分かります。これをノイズに見立てます。
つぎにコーシ分布から乱数の和を形成し、その最後の値の分布をみます。
from scipy.stats import cauchy
m1=[]
trial=1000000
for i in range(trial):
s = np.cumsum(np.random.normal(0, 1, 250))
m1.append(s[-1])
m2=[]
for i in range(trial):
s=[]
i=1
while i<=250:
s0 = (cauchy.rvs(0,1,1))
if abs(s0)<10:
s.append(s0)
i+=1
m2.append(np.cumsum(s)[-1])
bins=np.linspace(np.min(m2),np.max(m2),1000)
plt.hist(m1,bins=bins,label='normal')
plt.hist(m2,bins=bins,label='cauchy',alpha=0.5)
plt.legend()
plt.show()
つぎにコーシー分布を使ったAR1関数を作ってみます。
def ar1_c(rho,x0,c1,d,sigma,nsample):
e = cauchy.rvs(loc=0,scale=1,size=nsample)
c=c1-rho # constant of autoregressive mdoel
y=[]
y.append(e[0]+x0*rho+c+d)
for i,ee in enumerate(e[1:]):
y.append(rho*y[i]+ee+c+d*(i+1))
return y
できた1次の自己回帰時系列を用いてDF検定を行います。
def adfcheck_c(rho,x0,c1,d,sigma,nsample,trial):
prw=0
prwc=0
prwct=0
for i in range(trial):
y=ar1_c(rho,x0,c1,d,sigma,nsample)
rw=sm.tsa.adfuller(y,maxlag=0,regression='nc')[1]
rwc=sm.tsa.adfuller(y,maxlag=0,regression='c')[1]
rwct=sm.tsa.adfuller(y,maxlag=0,regression='ct')[1]
if rw>0.05:
prw+=1
if rwc>0.05:
prwc+=1
if rwct>0.05:
prwct+=1
print('nsample',nsample,prw/trial,prwc/trial,prwct/trial)
rho=0.90
c1=1.1
c1=(c1-1)/250+1
d=1
d=d/250
sigma=0.4/np.sqrt(250)
trial=10000
for i in [7,20,250]:
adfcheck_c(rho,x0,c1,d,sigma,i,trial)
# nsample 7 0.973 0.8775 0.8377
# nsample 20 0.9873 0.9588 0.9143
# nsample 250 0.8816 0.8425 0.0897
ファットテイルの影響で、この場合はドリフト付き時間トレンドなのですが、標本の大きさが250のときに5%有意水準で帰無仮説を棄却できません。rho=0.85ではつぎの結果です。
nsample 7 0.9717 0.8801 0.8499
nsample 20 0.987 0.9507 0.903
nsample 250 0.8203 0.7057 0.0079
標本の大きさが250のときに5%有意水準で帰無仮説を棄却できています。
つぎにコーシー分布のファットテイルの部分を少し削ってみましょう。
def cau(cut,nsample):
s=[]
i=1
while i<=nsample:
s0 = cauchy.rvs(0,1,1)
if abs(s0)<cut:
s.append(s0[0])
i+=1
return s
def ar1_c2(rho,x0,c1,d,sigma,nsample):
e = cau(10,nsample)
c=c1-rho # constant of autoregressive mdoel
y=[]
y.append(e[0]*sigma+x0*rho+c+d)
for i,ee in enumerate(e[1:]):
y.append(rho*y[i]+ee*sigma+c+d*(i+1))
return y
def adfcheck_c2(rho,x0,c1,d,sigma,nsample,trial):
prw=0
prwc=0
prwct=0
for i in range(trial):
y=ar1_c2(rho,x0,c1,d,sigma,nsample)
rw=sm.tsa.adfuller(y,maxlag=0,regression='nc')[1]
rwc=sm.tsa.adfuller(y,maxlag=0,regression='c')[1]
rwct=sm.tsa.adfuller(y,maxlag=0,regression='ct')[1]
if rw>0.05:
prw+=1
if rwc>0.05:
prwc+=1
if rwct>0.05:
prwct+=1
print('nsample',nsample,prw/trial,prwc/trial,prwct/trial)
rho=0.90
c1=1.1
c1=(c1-1)/250+1
d=1
d=d/250
sigma=0.4/np.sqrt(250)
trial=10000
for i in [7,20,250]:
adfcheck_c2(rho,x0,c1,d,sigma,i,trial)
# nsample 7 0.9969 0.9005 0.8462
# nsample 20 1.0 0.9912 0.9182
# nsample 250 1.0 1.0 0.0931
先ほどとは違った結果になりました。帰無仮説を棄却できるのはドリフト付き時間トレンドだけになりましたが、有意水準は10%です。rho=0.85にすると
nsample 7 0.9967 0.9012 0.8466
nsample 20 1.0 0.9833 0.9121
nsample 250 1.0 1.0 0.0028
という結果になります。
つぎに拡張ディッキーフラー検定を試してみます。
$\Delta y_t=c+c\cdot t+\delta y_{t-1}+\delta_1\Delta y_{t-1}+,\cdots,+\delta_{p-1}\Delta y_{t-p+1}+u_t$
で遅延の1階差分を増やすことで自己相関などの構造的な効果を取り除いています。
def adfcheck_c3(rho,x0,c1,d,sigma,nsample,trial):
prw=0
prwc=0
prwct=0
for i in range(trial):
y=ar1_c2(rho,x0,c1,d,sigma,nsample)
rw=sm.tsa.adfuller(y,regression='nc')[1]
rwc=sm.tsa.adfuller(y,regression='c')[1]
rwct=sm.tsa.adfuller(y,regression='ct')[1]
if rw>0.05:
prw+=1
if rwc>0.05:
prwc+=1
if rwct>0.05:
prwct+=1
print('nsample',nsample,prw/trial,prwc/trial,prwct/trial)
rho=0.90
c1=1.1
c1=(c1-1)/250+1
d=1
d=d/250
sigma=0.4/np.sqrt(250)
trial=10000
for i in [7,20,250]:
adfcheck_c3(rho,x0,c1,d,sigma,i,trial)
# nsample 7 0.94 0.8187 0.8469
# nsample 20 1.0 0.873 0.7969
# nsample 250 1.0 1.0 0.1253
rho=0.90では正しく判断できません。rho=0.85にすると結果は
nsample 7 0.9321 0.8109 0.8429
nsample 20 1.0 0.8512 0.7942
nsample 250 1.0 1.0 0.0252
となりドリフト+時間トレンドを棄却できています。
標準偏差がゼロまたは小さい時のドリフト、時間トレンドの検出
# driftのみ、標準偏差はゼロ
rho=0
c1=1.1
c1=(c1-1)/250+1
d=0
d=d/250
sigma=0#.4/np.sqrt(250)
trial=1#0000
for i in [7,20,250]:
adfcheck(rho,x0,c1,d,sigma,i,trial)
nsample 7 0.0 0.0 0.0
nsample 20 0.0 0.0 0.0
nsample 250 0.0 0.0 0.0
ドリフトだけがあるときにはすべてで帰無仮説は棄却されます。
# driftと時間トレンド、標準偏差はゼロ
rho=0
c1=1.1
c1=(c1-1)/250+1
d=1
d=d/250
sigma=0#.4/np.sqrt(250)
trial=1#0000
for i in [7,20,250]:
adfcheck(rho,x0,c1,d,sigma,i,trial)
nsample 7 1.0 1.0 0.0
nsample 20 1.0 1.0 0.0
nsample 250 1.0 1.0 0.0
AR(1)+ドリフト+時間トレンドが標本の大きさに関係なく帰無仮説を棄却
つぎはドリフトつきに若干の標準偏差を加えます。
# drift+ very small sigma
rho=0
c1=1.1
c1=(c1-1)/250+1
d=0
d=d/250
sigma=0.004#.4/np.sqrt(250)
trial=10000
for i in [7,20,250]:
adfcheck(rho,x0,c1,d,sigma,i,trial)
nsample 7 0.9986 0.6379 0.7223
nsample 20 1.0 0.0396 0.1234
nsample 250 1.0 0.0 0.0
つぎはドリフト+時間トレンドに若干の標準偏差を加えます。
# drift+ very small sigma
rho=0
c1=1.1
c1=(c1-1)/250+1
d=1
d=d/250
sigma=0.004#.4/np.sqrt(250)
trial=10000
for i in [7,20,250]:
adfcheck(rho,x0,c1,d,sigma,i,trial)
nsample 7 1.0 0.9947 0.6877
nsample 20 1.0 1.0 0.1095
nsample 250 1.0 1.0 0.0
参考
statsmodels.tsa.stattools.adfuller
Python3ではじめるシステムトレード【第2版】環境構築と売買戦略

「画像をクリックしていただくとpanrollingのホームページから書籍を購入していただけます。