ニューラルネットワークや機械学習を始めて学んだときに、大きな障害になるのが学習という概念です。よく耳にするのが「気持ち悪くて使えない」という声です。なぜそのように感じる人がいるのでしょうか?そのような人の多くは学生時代にまじめに数学を学んだ人が多いのです。また、数式を解いて解を得るということに厳しく訓練された人に多いのです。このような方法を解析解を得るといいます。しかし、どのような問題に対しても解析解が得られるわけではありません。問題が複雑になればなるほど解析解は得にくくなります。そこでニューラルネットでは探索法を用いて解を得ています。まずは非常に簡単な例で説明してみましょう。
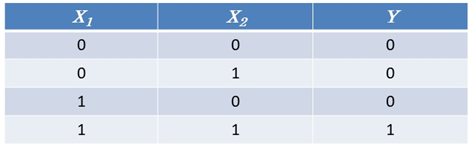
この表は掛け算の結果を表しています。
$X_1$と$X_2$は2つの変数で、0と1を取ります。$Y$は$X_1$と$X_2$の掛け算の結果です。最初に、$X_1$と$X_2$を入力データとして与えて、つぎに$Y$を正解として与えて、$X$と$Y$の関係を見つけてくださいといったら、一般には結構大変なことをしなければなりません。たとえばこれが掛け算の入力と出力であるとわかっていたとしても、実際にプログラムを組むのは大変です。しかし、ニューラルネットワークでは入力を与えて、つぎに正解データを与えて、学習をさせるとつぎからはちゃんとした答えを返してくれます。その仕組みは探索法にあります。
探索法
実際には
$$Y=f(W_1 X_1+W_2 X_2+B)$$
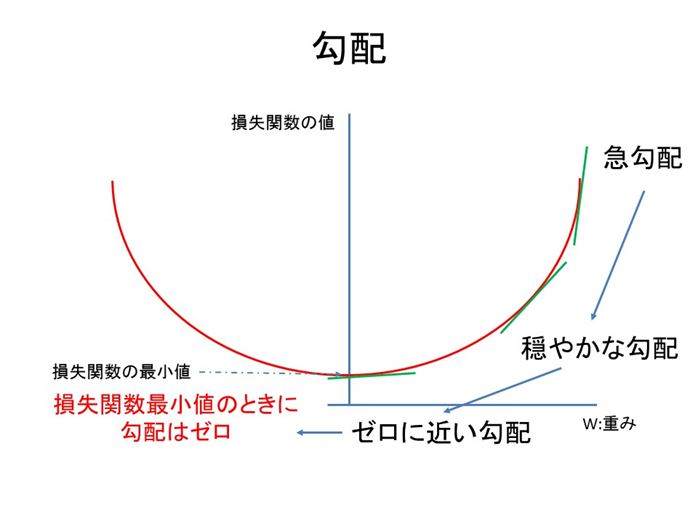
という方程式の$W_1$と$W_2$と$B$を得ることになります。$f$は活性化関数で事前に指定します。探索法ではこれを探索的に探していくのです。$W_1$と$W_2$に乱数を与えて最も良いと思えるものを得るというのでも可能です。その際には確かに探索のイメージそのものです。しかし、実際にはそれでは問題が複雑になればなるほど結果を得るのにかかる時間が長くなってしまいます。そこで勾配降下法という計算アルゴリズムを用います。アルゴリズムとか言われると難しく感じますが、そうでもありません。勾配というのは階段の上り下り、山登りなどで経験するあの勾配のことです。道の傾斜のことです。これは道の傾きの度合いと言ったらいいでしょうか?では学習の勾配とはどのようなものでしょうか?正直言うと学習の勾配というよりも、学習が定めた目的関数の勾配ということになります。
目的関数と誤差平方和
では目的関数とは何でしょうか?それはこの場合には$Y$と$Y$の推定値$\hat{Y}$の誤差を測定する関数となります。
$$ E=\frac{1}{2}\sum_{k=1}^K(Y_k-\hat{Y_k})^2$$
と表されます。この関数は誤差平方和と呼ばれます。この関数を最小にする$W_1$と$W_2$を見つけるのです。
勾配と微分
山登りの勾配ですが、これは歩いた距離と高さの変化の割合で決まります。関数の場合も同様です。先ほどの例ですと、歩いた距離は$W_1$と$W_2$の変化に相当します。$\Delta W_1$、$\Delta W_2$と書きます。つまりこの場合の勾配は
$$\frac{(W_1+\Delta W_1)X_1+W_2 X_2}{\Delta W_1}$$
$$\frac{W_1 X_1+(W_2+\Delta W_2) X_2}{\Delta W_2}$$
で表されます。$\Delta W_1$を限りなくゼロに近づけると微分になります。この場合には変数が2つあるので偏微分になります。
この勾配が大きければ、または急勾配であれば重み$W$は最適解から遠く、ゼロであれば傾き、勾配がなく最適解になります。
損失関数の微分は
$$\frac{\partial}{\partial W_1}\frac{1}{2}\sum_{k=1}^K(Y_k-\hat{Y_k})^2=\sum (Y_k-\hat{Y_k})X_{1,k} $$
$$\frac{\partial}{\partial W_2}\frac{1}{2}\sum_{k=1}^K(Y_k-\hat{Y_k})^2=\sum (Y_k-\hat{Y_k})X_{2,k} $$
となります。
勾配法
したがって、勾配法では
$$ 新しい重み=古い重み- 学習率×勾配$$
という形式で更新していきます。
別の書き方をすると
$$ W=W-\eta f(\frac{\partial g}{\partial W})$$
となります。さらに書き換えると
$$W_1=W_1-\eta \sum (Y_k-\hat{Y_k})X_{1,k} $$
$$W_2=W_2-\eta \sum (Y_k-\hat{Y_k})X_{2,k} $$
となります。
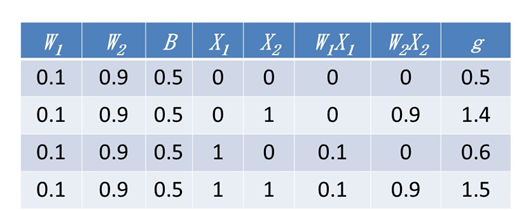
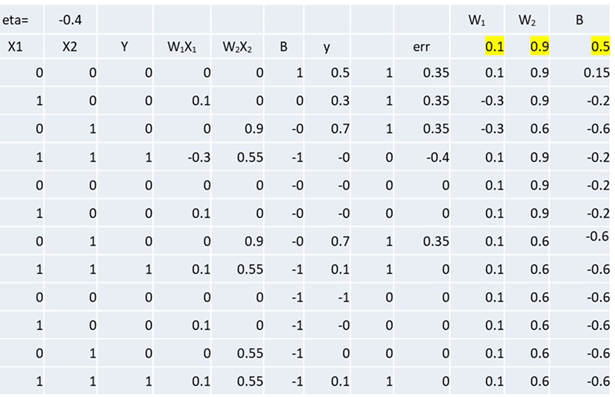
$W_1$と$W_2$と$B$の初期値は乱数で決めるのですが、ここでは$W_1=0.1$と$W_2=0.9$と$B=0.5$とします。計算をすると
0.1×0+0.9×0 + 0.5 = 0.5
0.1×0+0.9×1 + 0.5 = 1.4
0.1×1+0.9×0 + 0.5 = 0.6
0.1×1+0.9×1 + 0.5 = 1.5
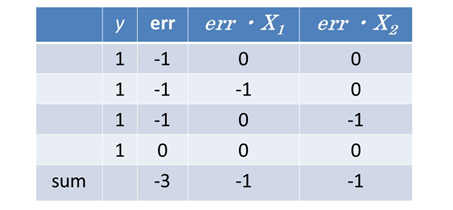
となります。手計算でもできます。脳のために良いのでやってみてください。まとめると
そうすると新しい変数は
W1 = 0.1 - 1×(- 1) = 1.1
W2 = 0.9 - 1×(- 1) = 1.9
B = 0.5 - 1×(- 3) = 3.5
となります。
反復法
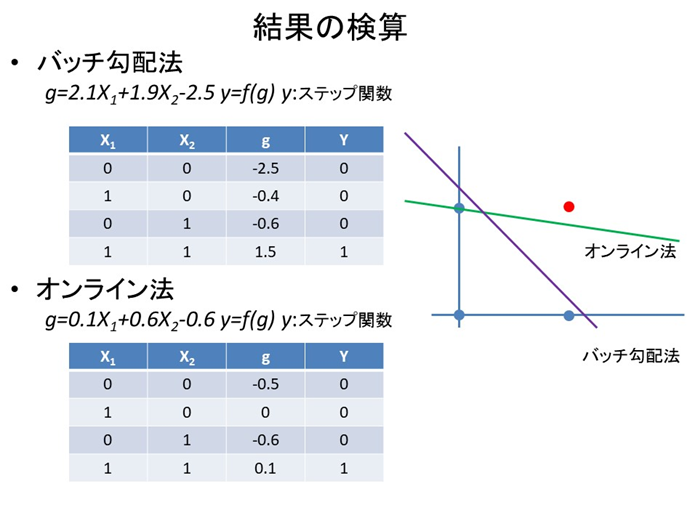
誤差を十分に小さくするためにはこの計算を24回程度行えばよいことになります。最終的な重みはW1 = 2.1、W2 = 1.9、B = -2.5となります。この方法は1バッチごとに重みの再計算をしているのでバッチ法と呼ばれます。
さてこの方法のどこが気持ち悪いのでしょうか?それは解がいくつも得られてしまうことです。
確率的勾配降下法
バッチ勾配降下法ではまとまったデータに対して重みの更新をしていきます。しかし、損失関数が最小値に近づいているようなときにはたくさんのデータを用いて損失関数の値を求める必要はないかもしれません。それではときには非効率的です。1つ1つのデータについて重みを更新するのではいけないのでしょうか。損失関数が重みの変化に対してなめらかに減少していくのではなく凹凸がある場合には、そのくぼみから出てこられなくなってしまうかもしれません。よく局所解におちいるというのはこのことです。では、局所解におちいる原因はなんでしょうか?いろいろ考えられますが、1つはデータの偏りです。したがって、データの偏りを減らすために乱数を用いて、データの順番を入れ替える方法が考えられました。このような方法を確率的勾配降下法といいます。順番の入れ替えはエポックごとに行われます。またつぎからつぎへと入ってくるデータを用いてそのまま重みを調整するような場合はオンライン学習と呼ばれます。オンライン学習を試してみましょう。
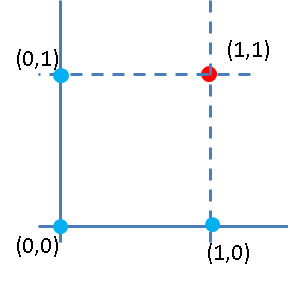
結果をチェックしてみましょう。データを2次元平面で書いてみます。
$X_1$がx軸、$X_2$がy軸です。(1,1)の点が赤くなっていて、残りの点は青になっています。この点に疑問を抱く人は鋭いところをついています。誰でもわかるニューラルネットワーク:分類の仕組みも併せて見てみてください。
解が2つ得られましたが、どちらも正解です。
気持ち悪いを気持ちよいに変える
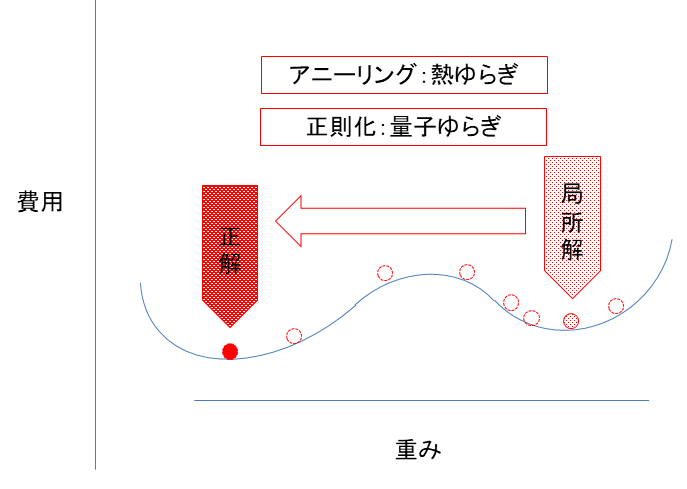
ここまでで、何となく気持ち悪いという人の気持ちが分かったのではないでしょうか?単純パーセプトロンの欠点は複数の解が得られてしまう点です。また、勾配降下法に相当する自然界の仕組みはありません。そのような点も気持ち悪いに直結するのです。確率勾配降下法ですが、これは勾配降下法に乱数を用いて計算の効率を改善させただけで、やはりこの仕組みは自然界にはありません。しかし、反復法の欠点に思える気持ち悪い点ですが、実は強みでもあるのです。確率勾配降下法の説明の中で局所解におちいるという説明をしました。
これを解決してくれ方法の1つがシミュレーテッドアニーリングという手法です。これは熱力学的ゆらぎを利用しています。焼きなまし法ともいわれます。重みを最適化する際に、目的関数に乱数を加えてあげます。これは熱力学的ゆらぎを利用しています。また、正則化を利用する方法もあります。その場合には量子ゆらぎを利用していることになります。重みの関数を目的関数に加えます。このような背後に何らかの原理がある柔軟性のある最適化を用いることができることがニューラルネットワークの強みなのです。これは機械学習についても言えます。そして、このような方法は汎化性能という、未知のデータに対しても有効にモデルが機能する能力を向上させる可能性があるのです。
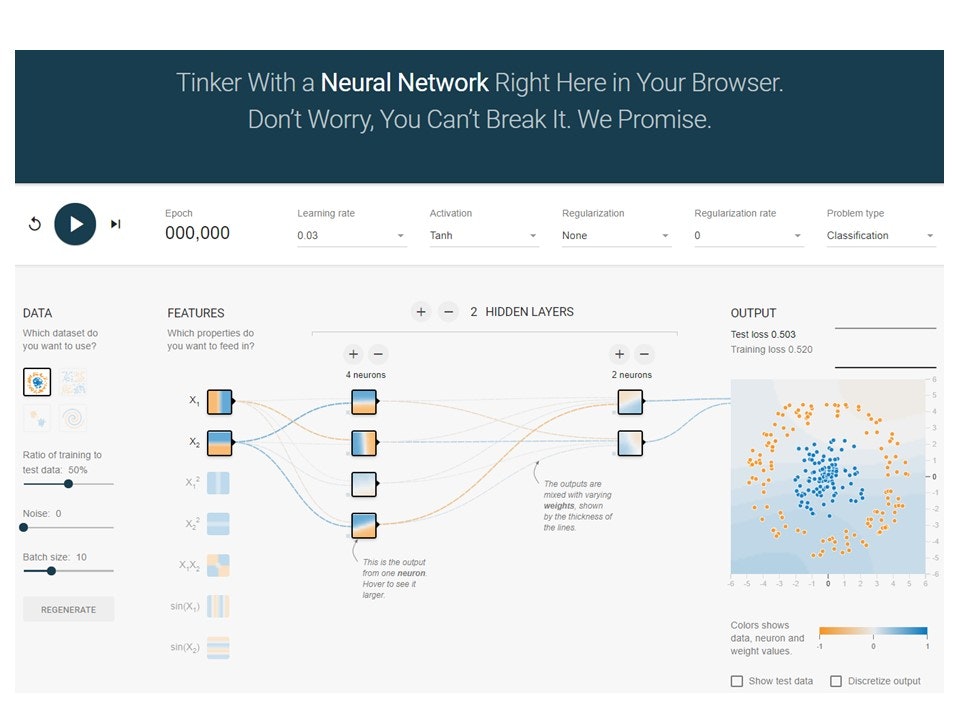
深層学習とかニューラルネットワークはいとも簡単にデータを分類します。その分類の仕組みをテンソルフロープレイグラウンドというブラウザー上で動くニューラルネットワーク学習アプリを動かしながら説明していきます。テンソルフロープレイグラウンドが初めての方は誰でもわかるニューラルネットワーク:アプリのように動かす人工知能ーテンソルフロープレイグラウンドを参照してください。
まず、テンソルフロープレイグラウンドをクリックするとA Neural Network Playgroundが立ち上がります。
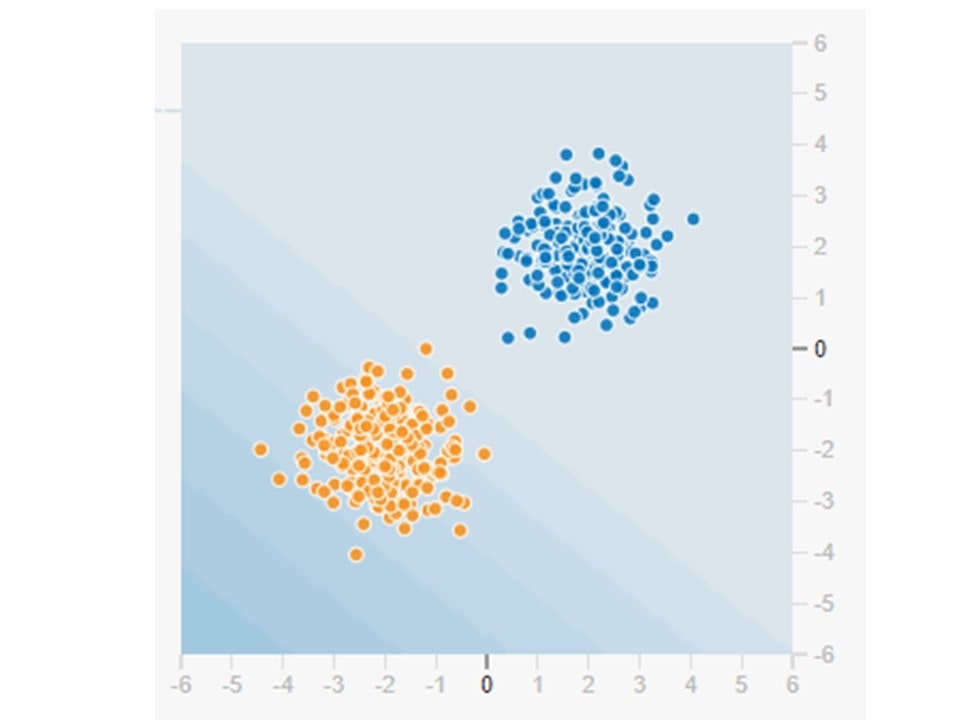
左端の4つのボックスから出力の画像を選びます。今回は正規分布といわれる青の点が第一象限に赤の点が第三象限にあるものを選びます。
分類の仕組み
この画像の赤と青の点を分類したいのです。
この赤と青を分離するためには単純パーセプトロンで十分です。単純パーセプトロンは一般には入力が2つで隠れ層の数が1つ、ユニットの数も1つです。したがって入力には
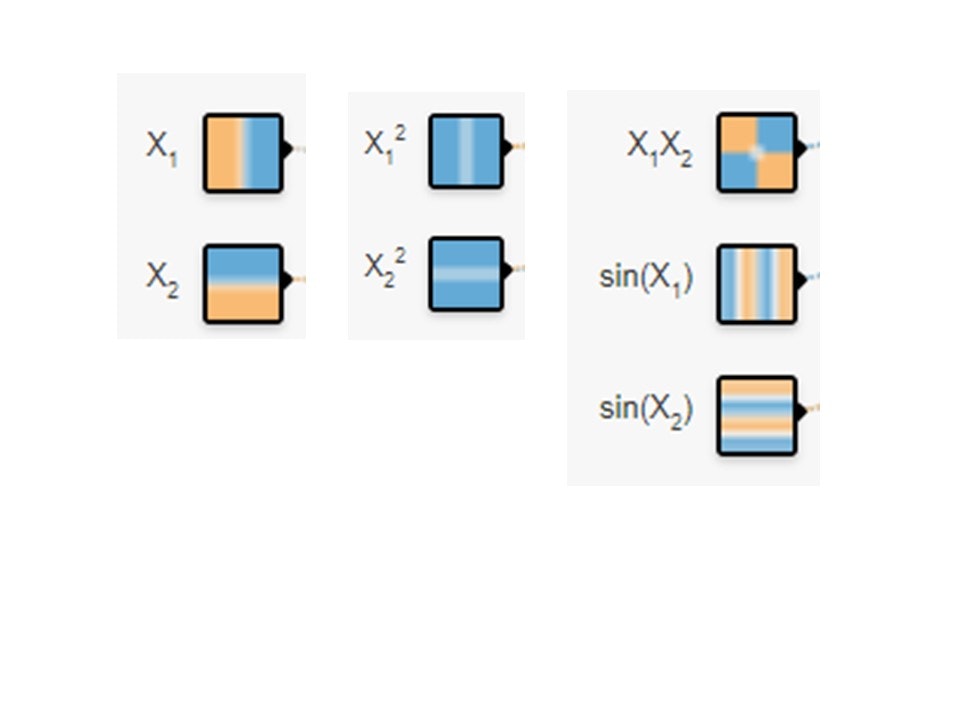
の中から$X_1$と$X_2$を選びます。そうしてつぎのようなニューラルネットワークを作ります。
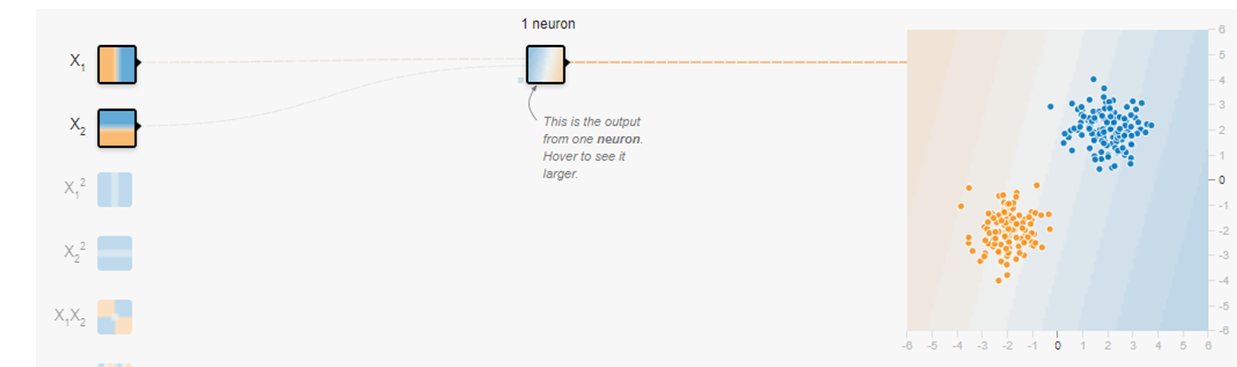
実行ボタンを押して少し経つと画面が動いて、2つの赤と青の点が分離されます。
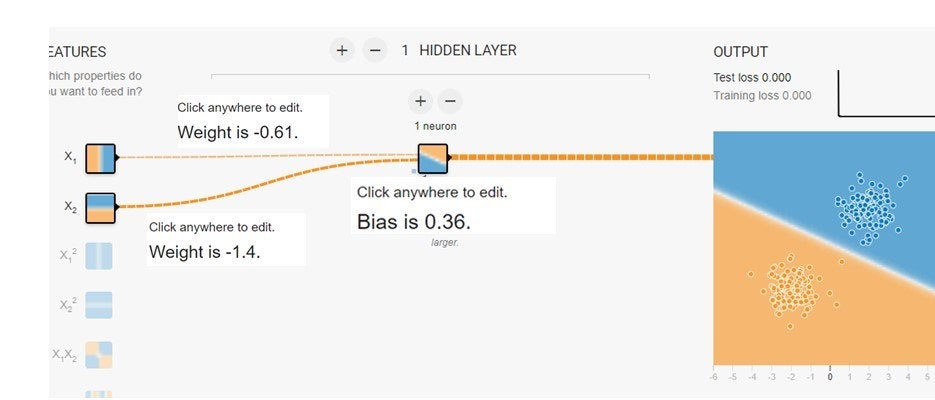
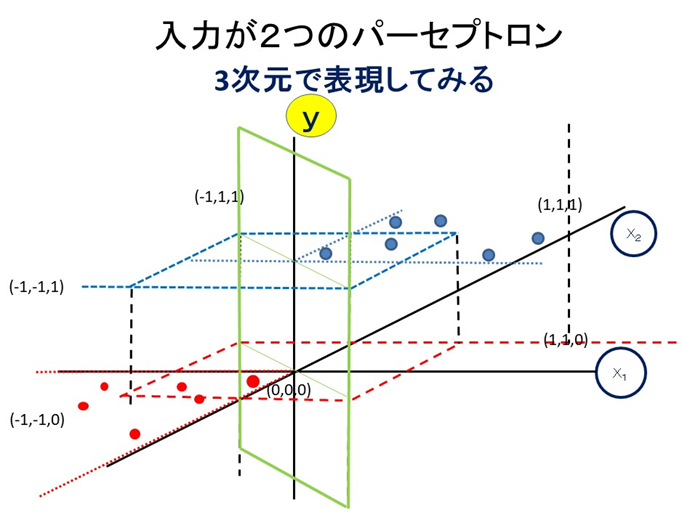
見た感じ2次元平面上に散らばった赤と青の点を分類したように感じます。しかし、実際には$x_1$軸と$x_2$軸の他にy軸を使った3次元空間で分類を実行しています。y軸には色情報が入っていると考えればよいのです。多くの人は3次元空間といわれると戸惑ってしまうでしょう。3次元空間よりも2次元空間で考えたいものです。そこで、$x_1$軸とy軸だけで考えることにします。青と赤の点の散らばり具合をよく見てみると$x_1$軸だけで見ても分類ができてしまうのです。
そこで入力データを$X_1$だけにしてみましょう。
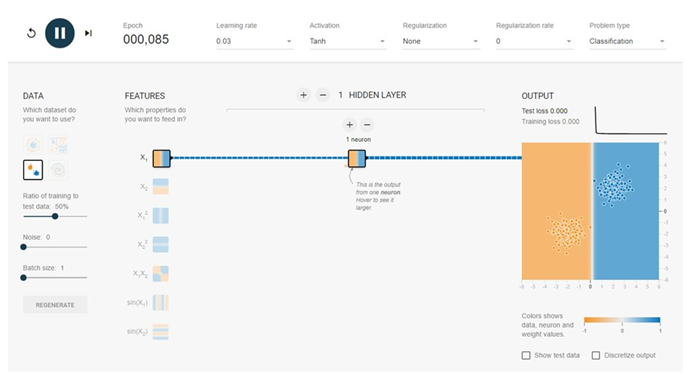
見事に分類ができていますね。これを2次元平面で表してみましょう。
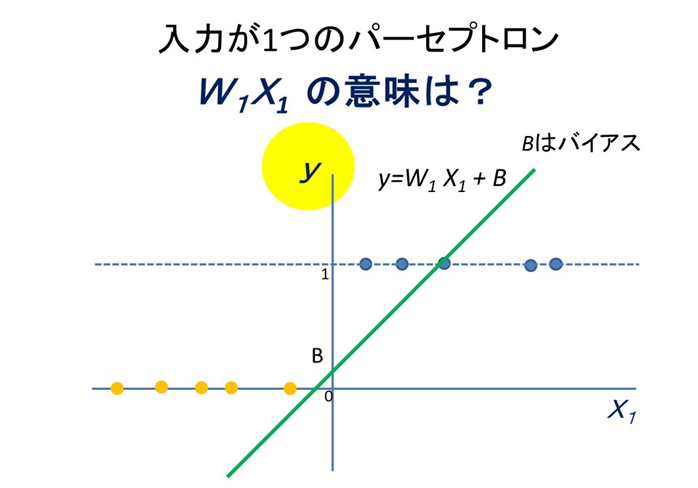
図にはグリーンの直線が描かれています。この直線は赤と青の点を分類できていません。数式で表現すると
$g=B+W_1 X_1$
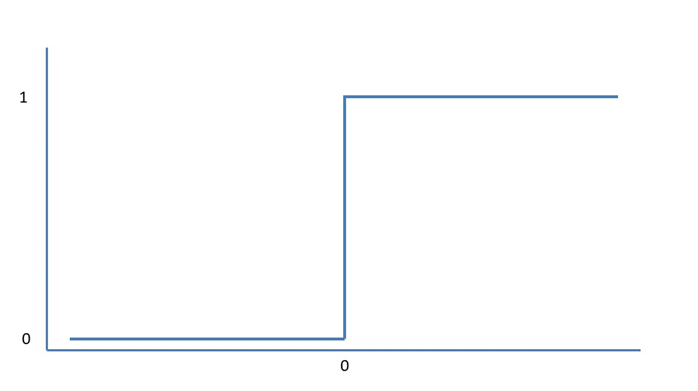
となります。y軸上では青の点は1、赤の点は0で表現されています。数式には$g$が出てきて$y$は出てきません。上述の式では赤と青の1と0を表現できません。そこで活性化関数を用いるのです。活性化関数をステップ関数として、$g$が0より大きければ1、小さければ0とするのです。
y=1 : W1X1 + B > 0
y= 0 : W1X1 + B ≦ 0
といった感じです。ステップ関数は
で表せます。この関数を使えば、先ほどの緑の直線がy軸上で0と1の値に変換されるのです。これでニューラルネットワークの分類の仕組みが分かったのではないでしょうか?
あとは変数の数が増えるだけなので、ここまでが分かっていれば理解しやすいはずです。
最初の図に戻って考えてみましょう。
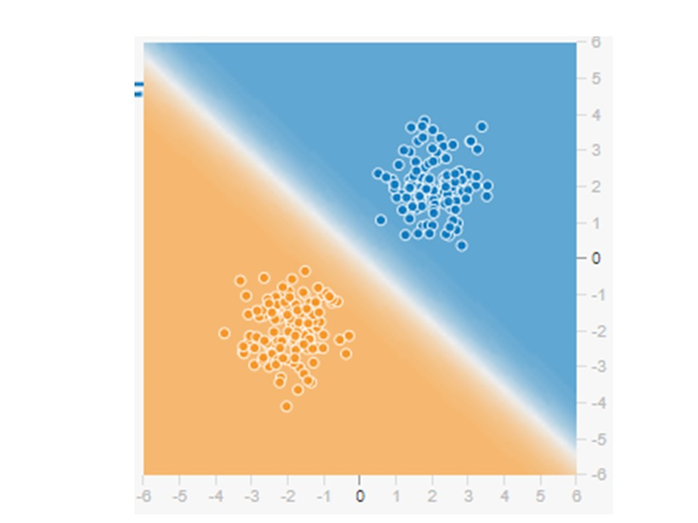
横軸は$X_1$を縦軸は$X_2$を表しています。この場合には
$$ y= f(W_1 X_1+W_2 X_2+B)$$
という形式で表現します。ここで$f$は活性化関数です。この次元平面には色を表してる3つ目の次元がありますが、軸はややこしいので表されていません。しかし、それを色で表現しています。3次元目は青と赤の色を表していると考えればよいのです。先ほどの2次元で考えたときと同じです。ですからfの活性化関数は青と赤の区別に使われているのです。
今回はこの活性化関数の中
$$ g= W_1 X_1+W_2 X_2+B$$
に着目します。$g=0$と置くと
$$ 0= W_1 X_1+W_2 X_2+B$$
となります。さらに変形すると
$$X_2=-\frac{W_1}{W_2}X_1-\frac{B}{W_2}$$
となります。これは1次関数の最も簡単なものと同じ形式です。
線形代数
先ほどの式は
$$ y= aX +b $$
と同じ形式です。$a$は回帰係数、$b$は切片です。図で表すと、
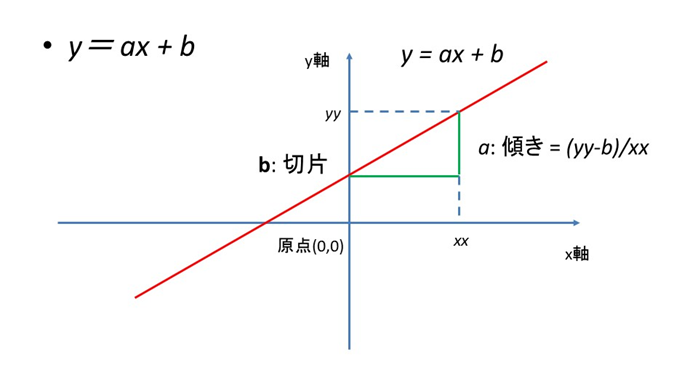
というような形になります。この赤い線の周りにデータが点在すると回帰分析になり、この線が2つの種類のデータの境界になると分類になります。イメージ的には
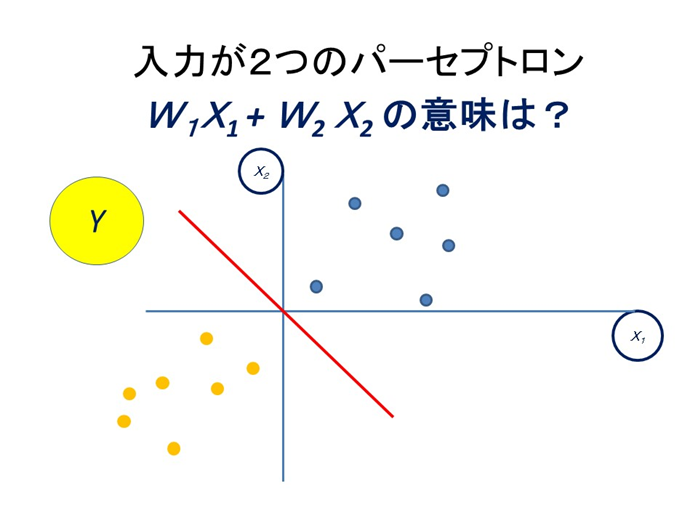
という感じです。繰り返しになりますが、まさに

出所:playground.tensorflow.org
と同じ形です。白い線で青い点と赤い点が分離されました。
ちなみに3次元空間で表現すると
といった感じです。
では層の数が増えるとどうなるでしょうか?そうなるとより複雑なことができそうなことは想像がつきます。しかし、どのようにでしょうか?それは線形回帰ではなく、非線形回帰の分析となるのです。それでも多くの問題は4層程度あれば十分だと考えられています。では最近はやりの層の数が膨大に多い、深層学習の場合はどうでしょうか?より複雑な構造をネットワークに持たせ、かつ層の数をふやすと、人の目や鼻、耳、ビルの角の特徴、窓の様子など、より特徴的な細かな部分を分析できるようなるのです。そして、このような能力に将来の期待が寄せられているのです。
線形代数の重要性
実はニューラルネットワークの複雑な仕組みの最適化には線形代数が大きな活躍をしています。連立方程式の解を求めるだけではなく、微分もできてしまいます。パラメータの最適化には微分が不可欠ですが、それも線形代数でできてしまうのです。
参考:
「シミュレーターでまなぶニューラルネットワーク」(アマゾンkindle出版)
「脳・心・人工知能 数理で脳を解き明かす」(ブルーバックス)
「圧縮センシングにもとづくスパースモデリングへのアプローチ」