LoginSignup
16
11

More than 3 years have passed since last update.

OpenCVAdvent Calendar 2020Day 21
@fukushima1981(福嶋 慶繁)

OpenCVのK-meansを高速化する

Last updated at Posted at 2020-12-20

はじめに

この記事はOpenCV Advent Calendar 2020の21日目の記事です．

教師なし学習でとりあえず何も考えずに最初に使ってみるのがK-meansだと思います．
（異論は認める．）

割と簡単に実装できるので世の中にはたくさんK-meansの実装であふれかえっています．
その中でも，みんなPython使ってますね．
ただこの記事はC++です．
私はPythonで高速化するとかPython速いという記事は一切信用しません．
なお，DeepなPythonはTVMなDSLの別言語ということで．

メンテナンスされているK-means実装だと以下のものがあります．

なお，DAAIは，インテルコンパイラが新しくなって新登場した関係で名前が変わっており，Intel® oneAPI Data Analytics Library (oneDAL)になっています．

また，オープンソースもあるみたいです．oneDAL
新しいコンパイラも発注したので，Threadripper3990X vs Core i9 10980XEの頂上対決画像処理編でもいつかやりたいところです．
高速化の某☆社さんも代理店にだった用ですが，すでに直で頼んだ後でした．

今のところ，お値段的にAMDの高級スリッパ3990Xがインテルのコンシューマ最上位の5倍くらいのお値段がするので，勝負にならないかもしれません．

高速化のモチベーション

初手で選ぶKmeansが速く動くと世の中多くの人が幸せになれます．
本記事では，速い気がするOpenCVのK-means実装をさらに速くすることを試みます．

なお，でっかいデータは，実装で高速化せずにアルゴリズムから頑張っているものを使いましょう．
松井先生のPQk-meansとか．

高速化のモチベーション（2回目，実態）

下記論文のバイラテラルフィルタを速くするために，Kmeansが必要だった私は，OpenCVのKmeans関数を使っていた．
T. Miyamura, N. Fukushima, M. Waqas, K. Sugimoto, and S. Kamata, "Image Tiling for Clustering to Improve Stability of Constant-time Color Bilateral Filtering," in Proc. International Conference on Image Processing (ICIP), Oct. 2020. link

最初はそれでよかったのだが，K-means以外のコードを限界まで最適化した結果，議論したい話よりもK-meansの処理時間が支配的になってしまった．

Kmeansへの入力をサブサンプルとかを駆使してごまかしたが，精度などで限界が．．．

そして．．．

「そうだ，ライブラリなんて投げ捨てて全部自分で書けばいいじゃない．」

で出来た記事がこれです．
なお，上記論文はOpenCVのKmeans使ってます．
（注意：OpenCVのコードもちゃんとベクトル化されるように書かれてます）

高速化のモチベーション（3回目，真）

某某→投稿数集めるために原稿出して！→現在に至る．

K-meansの実装

OpenCVのKmeansは通常のK-meansとK-meansの初期化を少し頑張ったK-means++が実装されてます．
アルゴリズムの詳細は下記記事等に任せます．

．．．が，それだけだと，理解しづらいと思いますので概略だけ書きます．

Lloyd-Forgy1965のK-means

よく使われるLloydさんやForgyさんが提案したK-means実装です．

  1. 分割数Kを決める
  2. ランダムに各特徴ベクトルにラベルを割り当て
    • Lloydは各ベクトルにラベルをランダムに割り当て
    • Forgyは各ベクトルをランダムにK個を選びそれをセントロイドにする（初回は下記2のプロセスがカット可能）
    • K-means++は初期セントロイドができるだけはなれるように選択
    • その他いろいろ初期化を頑張る方法が提案されてます．
  3. 各ラベルのセントロイドを計算
  4. 各ベクトルとすべてのラベルのセントロイドとの距離を計算し，最も距離の近いラベルに置き換え
    • 距離はユークリッド距離，マンハッタン距離，チェビシェフ距離，コサイン距離など
  5. 終了条件チェック（距離が小さいとか繰り返し回数が一定値以上とか．
  6. 3に戻る

MacQueen1967のK-means

MacQueen1967のK-meansは，ベクトル1つづつにセントロイドの更新を行っていきます．
はじめにこのアルゴリズムをK-meansと名付けたのはMacQueenです．
ベクトル１つごとに全データ更新するので遅いです．本記事の実装は，Lloyd-Forgy1965ベースです．
本記事の実装はOpenCVの実装を元にしており，OpenCVの実装もLloyd-Forgy1965ベースです．

実装のボトルネック

K-meansが最も計算時間を消費するのは，ループのど真ん中である上記2つ，特徴ベクトルとセントロイドとの距離の計算で，特に特に距離計算がボトルネックです．
この距離計算をSIMDでベクトル化していくことで高速化します．

まず，入力データがd次元，サイズN，設定クラスタ数がKとします．
この時，入力データはだいたい次元のところをインタリーブして並びます．
例えばカラー画像だったらBGRBGR...と並びます．
これをArray of Structure (AoS)配置と呼びます．
OpenCVの実装もAoSが入力されることを前提にコードがかかれています．

AoS

このAoS配置はだいたいベクトル化に向きません．
同時に計算できるSIMD演算器（AVXやAVX512とかNEON）のベクトル長は，8とか16といった長さなのに関わらず，RGBのデータは3チャネルなど短くなっています．
K-meansだともう少し対象のデータのチャネル数が増えてきますが，８の倍数でないとデータの読み込み時に余りの部分が発生するためベクトル演算の設定が難しくなります．

以下に距離計算の疑似コードを貼ります．
入力データ（data）はAoSなため，最内ループにdがくる構造です．
入力のコードと，ベクトル化候補の疑似コードを示しています．

ベクトル化のコードでは，余り部分をベクトル化せずに書いています．
余りとは例えばカラー画像など3次元データだった場合，8チャネルベクトル化できますが，8チャネルには足りないためそこは非ベクトル演算で処理するなどの形です．
なので8チャネル以下だとまったくベクトル化されません．

また，2点X-Yの間の距離計算は，たとえ次元数が8の倍数であっても水平演算が必要です．
差分と二乗は垂直演算（普通のSIMD演算）が可能ですが，チャネル間の総和のところでベクトル要素同士の和（水平演算）が必要になります．

(x_0-y_0)^2+(x_1-y_1)^2+\cdots+(x_n-y_n)^2

この水平演算はだいぶ遅いため高速化の邪魔をします．
水平演算の詳細については@tomoaki_teshimaさんのadd (2) -水平加算系-を参考に．
MacもARMになったことだし，みんなでひとりNEON Advent Calendar 2020を応援しよう！

なお，OpenCVでは，AoSの形でベクトル化をしています．
下記のhal::normL2Sqrを使って距離計算を高速化しています．
チャネルが短いと，#ifdefの外側のスカラーだけが実行されます．

//halモジュールのコード
float normL2Sqr_(const float* a, const float* b, const int n)
    {
        int j = 0; float d = 0.f;
#if CV_SIMD
        v_float32 v_d0 = vx_setzero_f32(), v_d1 = vx_setzero_f32();
        v_float32 v_d2 = vx_setzero_f32(), v_d3 = vx_setzero_f32();
        for (; j <= n - 4 * v_float32::nlanes; j += 4 * v_float32::nlanes)
        {
            v_float32 t0 = vx_load(a + j) - vx_load(b + j);
            v_float32 t1 = vx_load(a + j + v_float32::nlanes) - vx_load(b + j + v_float32::nlanes);
            v_float32 t2 = vx_load(a + j + 2 * v_float32::nlanes) - vx_load(b + j + 2 * v_float32::nlanes);
            v_float32 t3 = vx_load(a + j + 3 * v_float32::nlanes) - vx_load(b + j + 3 * v_float32::nlanes);
            v_d0 = v_muladd(t0, t0, v_d0);
            v_d1 = v_muladd(t1, t1, v_d1);
            v_d2 = v_muladd(t2, t2, v_d2);
            v_d3 = v_muladd(t3, t3, v_d3);
        }
        d = v_reduce_sum(v_d0 + v_d1 + v_d2 + v_d3);
#endif
        for (; j < n; j++)
        {
            float t = a[j] - b[j];
            d += t * t;
        }
        return d;
    }

inline float floorTo(float, int) {}
void AoS() {
//AoSでの距離計算疑似コード
    const int d = 3;//number of channels/dimensions
    const int N = 1024;//data size
    const int K = 8;//number of clusters
    float centroid[K][d];
    float data[N][d];
    float label[N];
    for (int n = 0; n < N; n++)
    {
        float Dxn = FLT_MAX;
        for (int k = 0; k < K; k++)
        {
            float Dk = 0.f;
            for (int i = 0; i < d; i++)
            {
                float diff = (data[n][i] - centroid[k][i]);
                Dk += diff * diff;
            }
            if (Dk < Dxn)
            {
                Dxn = Dk;
                label[n] = k;
            }
        }
    }

    //AoS SIMD
    for (int n = 0; n < N; n++)
    {
        float Dxn = FLT_MAX;
        for (int k = 0; k < K; k++)
        {
            float Dk = 0.f;
            int dsimd = floorTo(d, 4);//floor function for 2nd argment
            for (int i = 0; i < dsimd; i += 4)
            {
                //__m128 diff = _mm_sub_ps(&data[n],&centroid[k]);
                float diff0 = (data[n][i + 0] - centroid[k][i + 0]);
                float diff1 = (data[n][i + 1] - centroid[k][i + 1]);
                float diff2 = (data[n][i + 2] - centroid[k][i + 2]);
                float diff3 = (data[n][i + 3] - centroid[k][i + 3]);
                // diff = _mm_mul_ps(diff,diff);
                diff0 = diff0 * diff0;
                diff1 = diff1 * diff1;
                diff2 = diff2 * diff2;
                diff3 = diff3 * diff3;
                // horizontal add: 
                //diff = _mm_hadd_ps(diff,diff);
                //diff = _mm_hadd_ps(diff,diff);
                //Dk = diff[0];
                Dk = diff0 + diff1 + diff2 + diff3;
            }
            for (int i = dsimd; i < d; i++)//radidual processing
            {
                float diff = (data[n][i] - centroid[k][i]);
                Dk += diff * diff;
            }
            if (Dk < Dxn)
            {
                Dxn = Dk;
                label[n] = k;
            }
        }
    }

SoA

ベクトル化のためには，データ構造を Structure of Array(AoS)配置にすると適切なことが多いです．
これは，AoSのデータ配置のループ順序を入れ替えたものです．
AoS,SoAのデータ構造変換は，使ってるライブラリにある転置関数を呼べば入れ替えられます．
RGBRGBRGBをRRRBBBGGGに入れ替える専用関数などもありますが，データがNｘdの行列だと思えばdxNの行列に転置してしまえばデータ構造変換ができます．
ライブラリの転置関数は最適化されていることが多いので自分でやらずに，ライブラリのコードを呼びましょう．

下記にSoAで距離計算した疑似コードを示します．
非ベクトル化のコードは見た目あまり変わりませんが，配列の添え字の位置が変わっています．
なお，非ベクトル化で動かす場合，SoAはデータアクセス的にAoSよりも遅くなりがちです．
ベクトル化したほうのコードでは，通常最内ループでベクトル化するところを最外ループでベクトル化しています．これにより，次元ではなくデータのサイズでベクトル演算を発行することができるようになります．
データの次元数＜＜＜＜データサイズであり，通常データサイズが8とか16とかそんな小さなデータを扱うことがないため，余りのことはほぼ無視できる状態になります．

また，水平演算がすべてなくなります．
（あとついでに計算結果をベクトルストアできたりします．）
こうすると上記に比べて圧倒的にベクトル化効率が上がります．

なお，Kmeansに限らず，多くの画像処理コードでAoSよりもSoAのほうが速く動くように書けます．

void SoA()
{
    const int d = 3;//number of channels/dimensions
    const int N = 1024;//data size
    const int K = 8;//number of clusters
    float centroid[d][K];
    float data[d][N];
    float label[N];
    for (int n = 0; n < N; n++)
    {
        float Dxn = FLT_MAX;
        for (int k = 0; k < K; k++)
        {
            float Dk = 0.f;
            for (int i = 0; i < d; i++)
            {
                float diff = (data[i][n] - centroid[i][k]);
                Dk += diff * diff;
            }
            if (Dk < Dxn)
            {
                Dxn = Dk;
                label[n] = k;
            }
        }
    }


    //AoS SIMD
    int Nsimd = floorTo(N, 4);//floor function for 2nd argment
    for (int n = 0; n < Nsimd; n += 4)
    {
        float Dxn0 = FLT_MAX;
        float Dxn1 = FLT_MAX;
        float Dxn2 = FLT_MAX;
        float Dxn3 = FLT_MAX;
        for (int k = 0; k < K; k++)
        {
            float Dk0 = 0.f;
            float Dk1 = 0.f;
            float Dk2 = 0.f;
            float Dk3 = 0.f;
            for (int i = 0; i < d; i++)
            {
                //__m128 diff = _mm_sub_ps(&data[i],&centroid[i]);
                float diff0 = (data[i][n + 0] - centroid[i][k]);
                float diff1 = (data[i][n + 1] - centroid[i][k]);
                float diff2 = (data[i][n + 2] - centroid[i][k]);
                float diff3 = (data[i][n + 3] - centroid[i][k]);
                // diff = _mm_mul_ps(diff,diff);
                Dk0 += diff0 * diff0;
                Dk1 += diff1 * diff1;
                Dk2 += diff2 * diff2;
                Dk3 += diff3 * diff3;
            }

            if (Dk0 < Dxn0) { Dxn0 = Dk0; label[n + 0] = k; }
            if (Dk1 < Dxn1) { Dxn1 = Dk1; label[n + 1] = k; }
            if (Dk2 < Dxn2) { Dxn2 = Dk2; label[n + 2] = k; }
            if (Dk3 < Dxn3) { Dxn3 = Dk3; label[n + 3] = k; }

        }
    }
    //radidual processig...
}

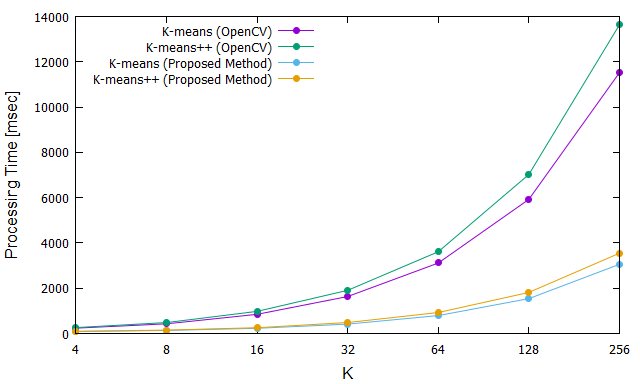
結果

結果を下記に示します．
3チャネル画像をKmeansしたときの結果です．
OpenCVにはKmeansとKmeans++があるのですが，どちらも上記のようなベクトル化を施しました．
3~4倍のゲインが出ています．
たぶん8チャネルとかのデータでやればこんなに差は出ないと思います．

kmeansres.png

まとめ

K-meansのコードを最適化しました．

結論
「OpenCVのコードは，本気を出した最適化コードよりも遅いので書き直そう！」（暴言）

今のところ，私がOpenCVのコード（というかIPP）に勝てないものとして，アップサンプルがあります．
どうやって書いてるんだろう．．．

作ったコードは以下にあります．

コードを見ればわかる通り可読性はだいぶ悪いです．（記事のコードを疑似コードにした理由）
なお，個人的な需要により，3チャネル以外テストしていません．

参考文献

  • よく使われているほうのK-means
    • Forgy, E. W. 1965. Cluster analysis of multivariate data: efficiency vs interpretability of classifications. Biometrics. Volume 21. 768-769.
    • Lloyd, S. P. 1982. Technical Note: Least squares quantization in PCM. IEEE Transactions on Information Theory. Bell Laboratories. Volume 28. 128-137.
  • K-meansと名前を付けた論文のほうのK-means（ちょっと遅い）
    • MacQueen, J. 1967. Some methods for classification and analysis of multivariate observations. Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability. Berkeley, CA: University of California Press. (eds L. M. Le Cam & J. Neyman) Volume 1. pp. 281-297.
  • K-means++
    • Arthur, D., and Vassilvitskii, S., "k-means++: The Advantages of Careful Seeding.," Technical Report, Stanford (2006)
16
11
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
16
11