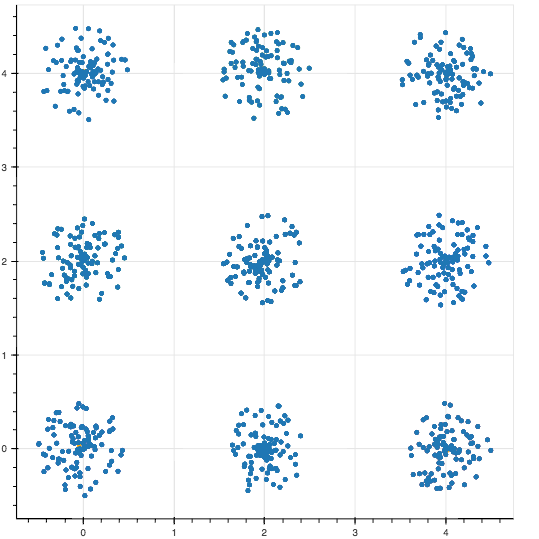
本記事では,以下のような特徴を持ったデータを分けることを行いたいと思います.
k-meansをはじめとするクラスタリングでは教師なしの学習(分類)なので,事前にデータの形を見れるということは想定していません.
ですから現実ではクラスタの数を変えていきながら,関数f最小化するを分類を目指してクラスタ数を変更するということになると思います.
※今回はクラスタ数(セントロイド数)を9個としています。
k-menas法を表すと以下のようになります.
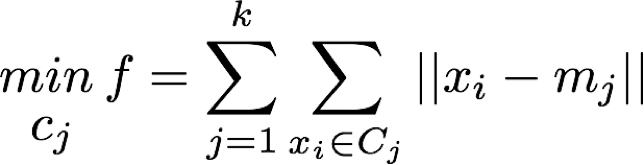
それぞれ,Cjがクラスタ,xiがベクトル(データ),mjがセントロイド(クラスタ重心)を表しています.
この場合fがクラスタ中心からデータの差を意味することになりますが,そのfの最小を求めることをがk-means法および,k-means++法における基本プロセスとなります.
普通のk-meansでやると以下のような感じで見るからに無様な結果になっています.
これは初期セントロイドを乱数で割り当ててるために,近い位置にセントロイドが置かれた場合にこういう感じになってしまいます.
これを解決する簡単な手法の一つにk-means++という方法があります.
簡単に言えば.複数のセントロイドが近くの位置にならないように初期化するというだけです.
詳しい説明はwikipediaに書いております.
以下のようになってます.
データ点からランダムに1つ選びそれをクラスタ中心とする。
$while$ $k$個のクラスタ中心が選ばれるまで $do$
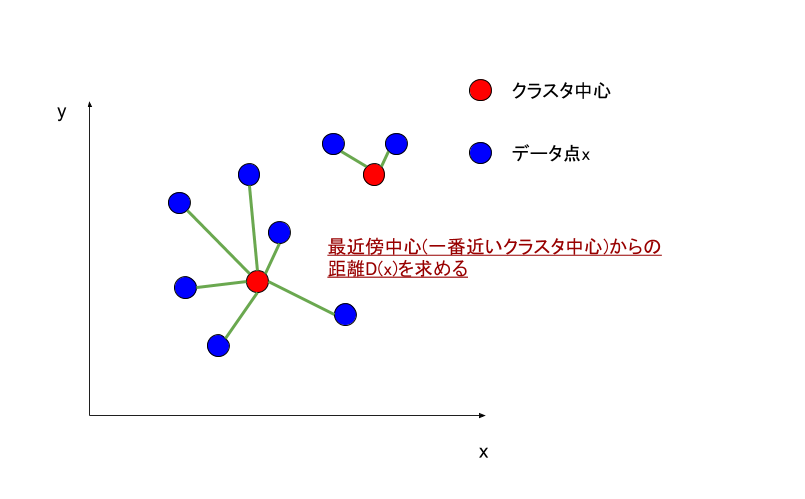
それぞれのデータ点$x$に関して、その点の最近傍中心との距離$D(x)$を計算する。
データ点$x$に関して重みつき確率分布$\frac{D(x)^2}{\sum D(x)^2}$を用いて、データ点の中から新しいクラスタ中心をランダムに選ぶ。
選ばれたクラスタ中心を初期値として標準的なk-means法を行う。
(wikipedia: k-means++法より引用)
以下k-means++法の解説
解説としては最初のデータ点からランダムに1つ選びそれをクラスタ中心とすることから微妙にk-means法と異なりますね.k-meansはデータ点ではなくランダムに重心を決定します.
それぞれのデータ点に$x$に関して, その点の最近傍中心との距離$D(x)$を計算する.
最近傍中心というのは一番近いクラスタ中心との距離という意味です.以下に図を作って見ました.
ここまではk-means法と同じですね.次の重み付き確率分布がk-means++法の新しく取り入れた部分です.
重み付き確率分布 = \frac{D(x)^2}{\sum D(x)^2}
この重み付き確率分布を用いてデータ点xから新しいクラスタ中心をランダムにk個選ぶことを繰り返します.この作業によってクラスタ中心の初期値依存をうまく解決します.
普通のk-meansは最初だけランダムにクラスタ中心を選びますが,それ以降はデータ$x_i$とクラスタの中心とのばらつきを最小にしているだけなので、そう考えると結構違うとも言えますが…
このような確率分布を取り入れることによって精度がwikipediaの説明では以下のようになるらしいです.
"だいたい収束スピードに関しては2倍、あるデータセットでは誤差が1000分の1となったことを報告している。"
こんな簡単な違いなのに凄いですよね...
以下にscikit-learnを用いてかいたk-means++法のコードを示します.
ソースコード
from sklearn.cluster import KMeans
from bokeh.plotting import figure, show #グラフの描画には注目されてるbokehを使う.
from bokeh.io import output_notebook
import numpy as np
data = np.loadtxt('./data.txt', delimiter=' ')
# クラスタ, kmeans++で初期化, k-means++で初期クラスタを設定,異なるセントロイドを用いたアルゴリズムの実行回数,最大イテレーション数, 相対許容誤差, 乱数生成器の状態
km = KMeans(n_clusters=9, init='k-means++', n_init=10, max_iter=300, tol=1e-04, random_state=0)
# 初期クラスタをランダムで設定する普通のk-means法は以下のようにする.
# km = KMeans(n_clusters=9, init='random', n_init=10, max_iter=300, tol=1e-04, random_state=0)
y_km = km.fit_predict(data)
# jupyter notebook内にグラフを表示する
output_notebook()
# グラフの設定
p=figure()
p.scatter(data[y_km==0, 0], data[y_km==0, 1], color='red')
p.scatter(data[y_km==1, 0], data[y_km==1, 1], color='blue')
p.scatter(data[y_km==2, 0], data[y_km==2, 1], color='green')
p.scatter(data[y_km==3, 0], data[y_km==3, 1], color='pink')
p.scatter(data[y_km==4, 0], data[y_km==4, 1], color='gray')
p.scatter(data[y_km==5, 0], data[y_km==5, 1], color='purple')
p.scatter(data[y_km==6, 0], data[y_km==6, 1], color='yellow')
p.scatter(data[y_km==7, 0], data[y_km==7, 1], color="#8f5555")
p.scatter(data[y_km==8, 0], data[y_km==8, 1], color='black')
p.scatter(km.cluster_centers_[:, 0], km.cluster_centers_[: ,1], color='orange', marker="square")
# 図の出力
show(p)
data.txtは以下のURLからダウンロードしてください.
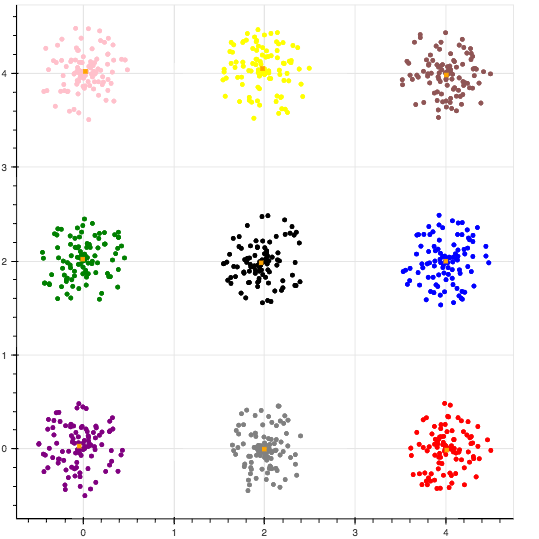
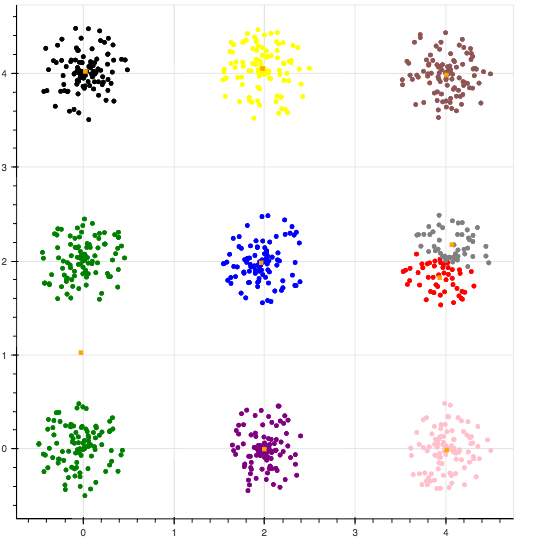
k-means++でセントロイドを初期化した結果
綺麗に分類されました.
おまけ
最近話題のJuliaでも実装してみました.
function input_data()
parse_data1= Float64[]
parse_data2 = Float64[]
open("./dataset/data_4.txt","r") do fp
data = readlines(fp)
for i in 1:length(data)
push!(parse_data1,parse(Float64,split(data[i], " ")[1]))
push!(parse_data2 ,parse(Float64,split(data[i], " ")[2]))
end
end
X = [parse_data1 parse_data2]
return X
end
X = input_data()
n = length(X[:,1])
using Plots
gr()
function dist(μx, μy, xx, xy)
return sqrt.((xx.-μx).^2 .+(μy.-xy).^2)
end
# 重心の数
k = 9
# 重心の変数.
μx_old = Float64[]
μy_old = Float64[]
DX = Float64[]
probs = []
function centroid()
# データ点からランダムに選びそれを重心とする.
z1 = rand(1:1:length(X[:,1]))
push!(μx_old, X[z1,1])
push!(μy_old, X[z1,2])
for i in 1:k
DX = Float64[]
for j in 1:n
# 最近傍距離を計算
Dx = minimum([dist(X[j,1], X[j,2], μx_old[m], μy_old[m]).^2 for m in 1:length(μx_old)])
push!(DX, Dx)
end
probs = DX ./ sum(DX)
cum_probs = cumsum(probs)
r = rand()
#println(r)
push!(μx_old, X[findall(cum_probs -> cum_probs >= r, cum_probs)[1],1])
push!(μy_old, X[findall(cum_probs -> cum_probs >= r, cum_probs)[1],2])
end
end
centroid()
print(μx_old)
# 以下は全てk-meansと同じ.
min = 1000000.0
cluster = 0
center_of_gravity_x = Float64[]
center_of_gravity_y = Float64[]
clusters = Int64[]
n = length(X[:,1])
μx_new = Float64[]
μy_new = Float64[]
# 収束判定用の変数
error = 100.0
error_arr = Float64[]
# 誤差関数が収束すれば終わり.
while error != 0.0
clusters = Int64[]
for i in 1:n
# 重心割り当て
# どの重心に一番近いかを決める.その距離の計算をしている.
# iには全データが入る.
min = 100000.0
for j in 1:k
distance = dist(μx_old[j], μy_old[j], X[i,1], X[i,2])
if min > distance
min = distance
cluster = j
end
end
push!(clusters, cluster)
end
plotdata = [X [string(i) for i=clusters];]
# 主に重心の計算
for i in 1:k
cluster_len = length(findin(plotdata[:,3],["$i"]))
for j in findin(plotdata[:,3],["$i"])
# 下二行が重心の計算
push!(center_of_gravity_x,((X[j,1]) / cluster_len))
push!(center_of_gravity_y,((X[j,2]) / cluster_len))
end
push!(μx_new, sum(center_of_gravity_x))
push!(μy_new, sum(center_of_gravity_y))
center_of_gravity_x = Float64[]
center_of_gravity_y = Float64[]
error = dist(μx_new[i], μy_new[i], μx_old[i], μy_old[i])
push!(error_arr, error)
end
μx_old = μx_new
μy_old = μy_new
μx_new = Float64[]
μy_new = Float64[]
end
tmp_x = Float64[]
tmp_y = Float64[]
x_arr = []
y_arr = []
function result(cluster_num)
tmp_x = Float64[]
tmp_y = Float64[]
for p in 1:cluster_num
result = findin(plotdata[:,3],["$p"])
# 割り振られたデータをx座標をx_arr, y座標をy_arrにそれぞれ代入する.
# 重心数が3だったら三つの配列で帰ってくる.
for i in result
push!(tmp_x, plotdata[i,1])
push!(tmp_y, plotdata[i,2])
end
push!(x_arr, tmp_x)
push!(y_arr, tmp_y)
tmp_x = Float64[]
tmp_y = Float64[]
end
end
plotdata = [X [string(i) for i=clusters];]
result(k)
# 誤差のプロット
plot(error_arr)
# 結果のプロット
scatter(x_arr, y_arr,legend=false)
scatter!(μx_old, μy_old,label="center",legend=false)