こんにちは、大学 1 年になったばかりの E869120 です。
私は競技プログラミングが趣味で、AtCoder や日本情報オリンピックなどに出場しています。ちなみに、2021 年 5 月 15 日現在、AtCoder では赤(レッドコーダー)です。
本記事では、アルゴリズムが実生活と結びつくトピックについて紹介したいと思います。
【シリーズ】
- 実生活に学ぶアルゴリズム【第 1 回:セブンイレブンでは 500 円で何カロリー得られるか?】
- 実生活に学ぶアルゴリズム【第 2 回:3 つのアルゴリズムで最適なソーシャルディスタンスを求める】
- 実生活に学ぶアルゴリズム【最終回:1000 個の六角形ピースをたった 45 回の切断で作る方法、そしてアルゴリズムを学ぶ意義】
1. はじめに
21 世紀となった今、生活の中にはたくさんの問題があふれており、そのうちいくつかは、皆さんも考えたことや悩んだことがあると思います。
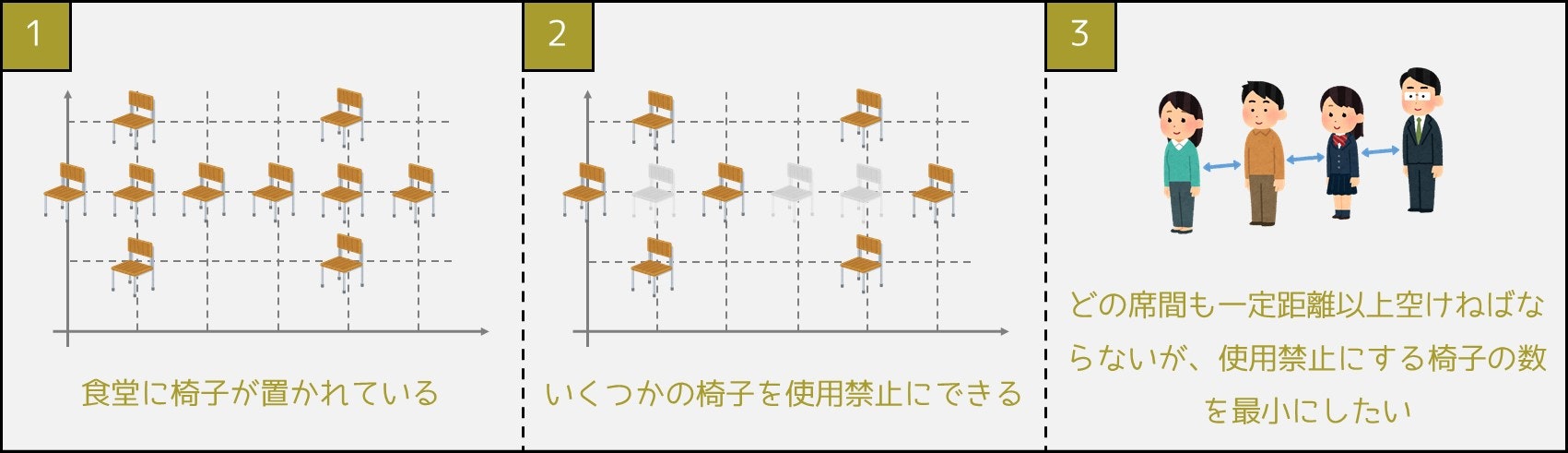
しかし、それらすべてが解けない問題というわけではなく、下図に書かれているもののように、「アルゴリズム(計算の手順)の効率化」によって解ける問題もあるのです。

そこで本シリーズでは、このようなトピックを紹介することで、「あの実生活の問題はこうやって解けるのか!!!」という感動を伝えること、そしてアルゴリズムの面白さを伝えることを最大の目標にします。1
3 記事にわたる連載を予定していますが、各記事で独立したトピックを扱うオムニバス形式であり、それぞれの内容を楽しめる構成となっています。皆さん是非お読みください。
なお、読者によっては知らないアルゴリズムが出てくることもありますが、必要となるアルゴリズムの解説も本記事に記していますので、ご安心ください。
目次
| 章 | タイトル | 備考 |
|---|---|---|
| 1. | はじめに | |
| 2. | 第 2 回で扱う問題 | |
| 3. | ケース A|カウンター席の場合 | 比較的簡単な内容です |
| 4. | ケース B|1.4m 以上離す場合 | |
| 5. | 予備知識:グラフ理論・ネットワークフローの導入 | |
| 6. | ケース B で最適解を出す方法 | 本記事のメインです |
| 7. | ケース C|10m 以上離す場合 | 6 章より易しいかもしれません |
| 8. | おわりに | |
| 9. | 次回予告・参考資料 |
2. 第 2 回で扱う問題
2020 年以降 COVID-19 の感染拡大により、ソーシャルディスタンスが重要になっています。それに関連して、今回は以下の問題を扱いたいと思います。
食堂に座席が並べられている。できるだけ少ない数の席を使用禁止にすることで、どの席間も一定以上(例:2 メートル)の間隔を空けるようにしたい。どの席を使用禁止にすべきか求めよ。
また、座席の並びや条件にはいろいろなケースがあるので、本記事では特に、
- 座席が一直線上に並んでいる、カウンター席の場合(3 章)
- 格子点上に座席があり、1.4m 以上の間隔を空ける必要がある場合(4 章~6 章)
- 格子点上に座席があり、10m 以上の間隔を空ける必要がある場合(7 章)
3. ケース A|カウンター席の場合
最初に、ラーメン屋のカウンター席のように、一直線上に座席が並んでいるケースを考えてみましょう。厳密に述べると以下の通りです。
$N$ 個の座席がある。$i$ 個目の座席は左端から $X_i$ $[\rm{m}]$ の位置にある。
できるだけ少ない数の席を使用禁止にすることで、どの席間も $K$ $[\rm{m}]$ 以上の間隔を空けるようにしたい。その方法を求めよ。(ただし椅子の大きさは無視してよいとする)
これはどうやって解けば良いのでしょうか。
3-1. 方法 1: 全通り調べ上げる
まず、「どの座席を使用禁止にするか」を全通り列挙する方法が考えられます。
例えば座席が 3 個の場合、以下の $2^3 = 8$ 通りのパターンそれぞれについて、「席間距離が $K$ $[\rm{m}]$ 未満となっている座席の組が存在しないか」チェックするということです。
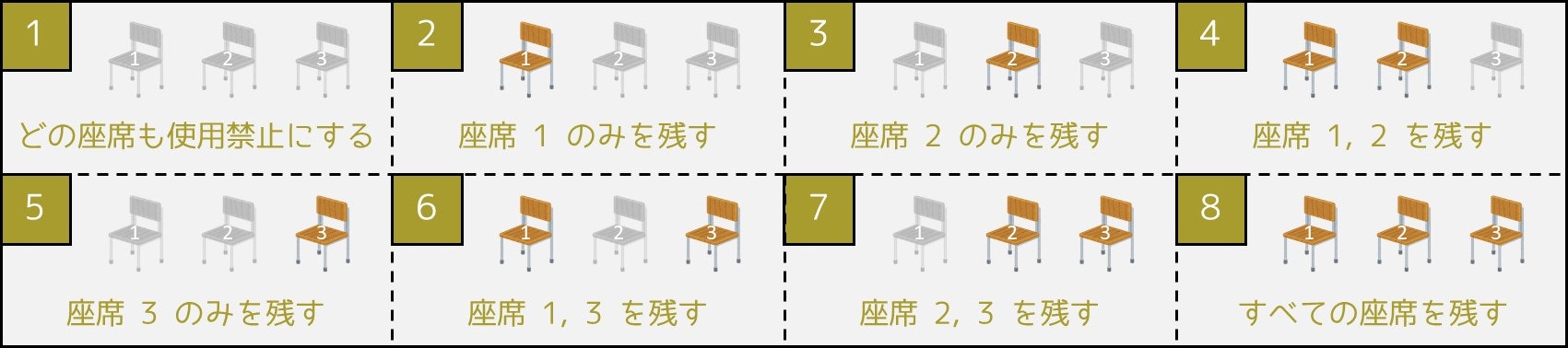
しかし、座席の数が増えるにつれ、パターン数が急激に増大してしまいます。例えば、
- 座席が 10 個の場合 $2^{10} = 1 \ 024$ 通り
- 座席が 20 個の場合 $2^{20} = 1 \ 048 \ 576$ 通り
- 座席が 30 個の場合 $2^{30} = 1 \ 073 \ 741 \ 824$ 通り
- 座席が 40 個の場合 $2^{40} = 1 \ 099 \ 511 \ 627 \ 776$ 通り
- 座席が 100 個の場合 $2^{100} = 1 \ 267 \ 650 \ 600 \ 228 \ 229 \ 401 \ 496 \ 703 \ 205 \ 376$ 通り
となります。残念ながら、一般的なコンピュータでは 1 秒当たり $10^9$ 回程度の計算しかできないため、座席が 100 個の場合、この方法で解くのは絶望的なのです。2
3-2. 方法 2: 貪欲法を使った解法
そこで、以下のような「貪欲法アルゴリズム3」を考えてみましょう。
左から順番に、残す席を 1 つずつ決めていく方針です。
以下の操作を、席が選べなくなるまで繰り返す。
操作
次の条件を両方満たす席のうち、最も左にあるものを選び、残すと決める。
- 直前に選んだ席より右側にある。
- 直前に選んだ席から $K \ [\rm{m}]$ 以上離れている。
最終的に、一度も選ばれなかった席を使用禁止にする。
例えば、$N = 6, K = 3, X = (1, 3, 4, 6, 8, 9)$ の場合、下図の手順により 3 個の席 $\{1, 3, 5\}$ が選ばれ、残りの席 $\{2, 4, 6\}$ が使用禁止になります。
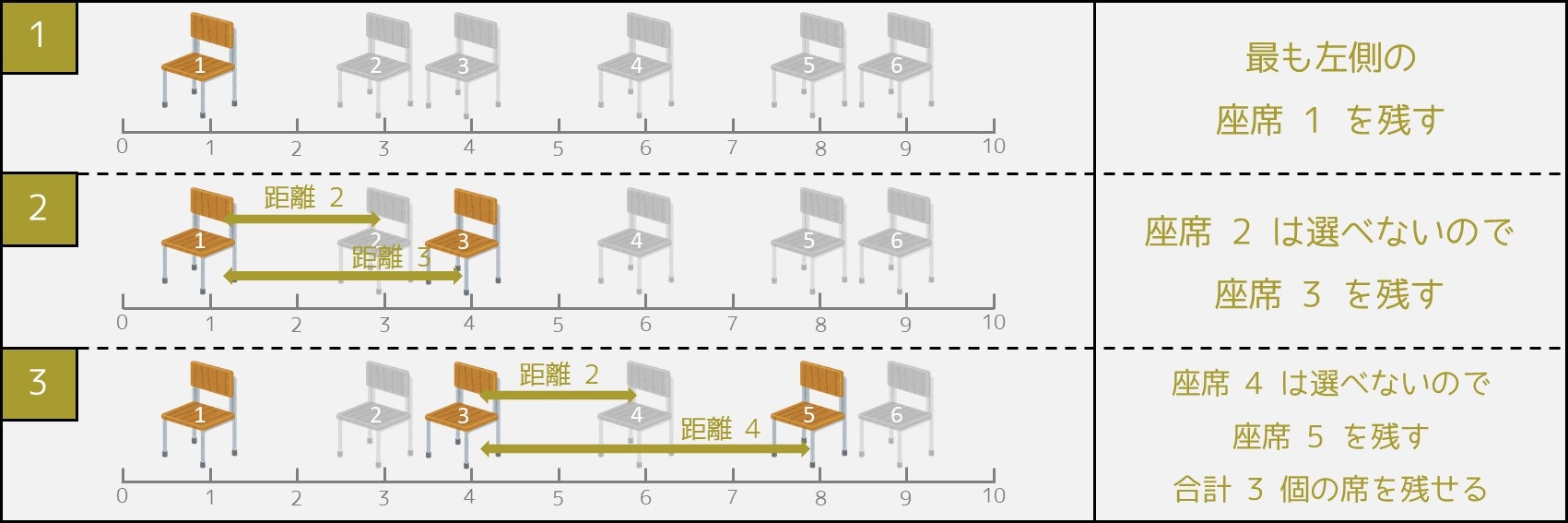
さて、このアルゴリズムで得られた答えはどの程度「良い」のでしょうか。**実は最適解なのです。**実際に上の具体例において、いろいろなパターンを手元で試しても、4 個以上残せないことが分かると思います。
しかし、なぜこれが最適なのでしょうか。理由を考えてみましょう。
3-3. 最適性の証明 ~今が良ければ未来も良い~
背理法を用いて、次のように証明することができます。
仮定
最適解の 1 つで選ばれた席の座標を $opt_1, opt_2, \cdots, opt_a \ (opt_1 < \cdots < opt_a)$ とする。また、貪欲法アルゴリズムで選ばれた席の座標を $g_1, g_2, \cdots, g_b \ (g_1 < \cdots < g_b)$ とし、それが最適ではない(すなわち $a > b$ である)と仮定する。仮定が成り立たないことの証明
まず、仮定が成り立てば、以下の 2 つの性質が必ず成り立つ。
- $opt_1 \geq g_1$(貪欲法アルゴリズムで最初に選ばれる席は一番左であるため)
- $opt_b < g_b$(そうでなければ貪欲法アルゴリズムで $b+1$ 個目の席が選べてしまう)
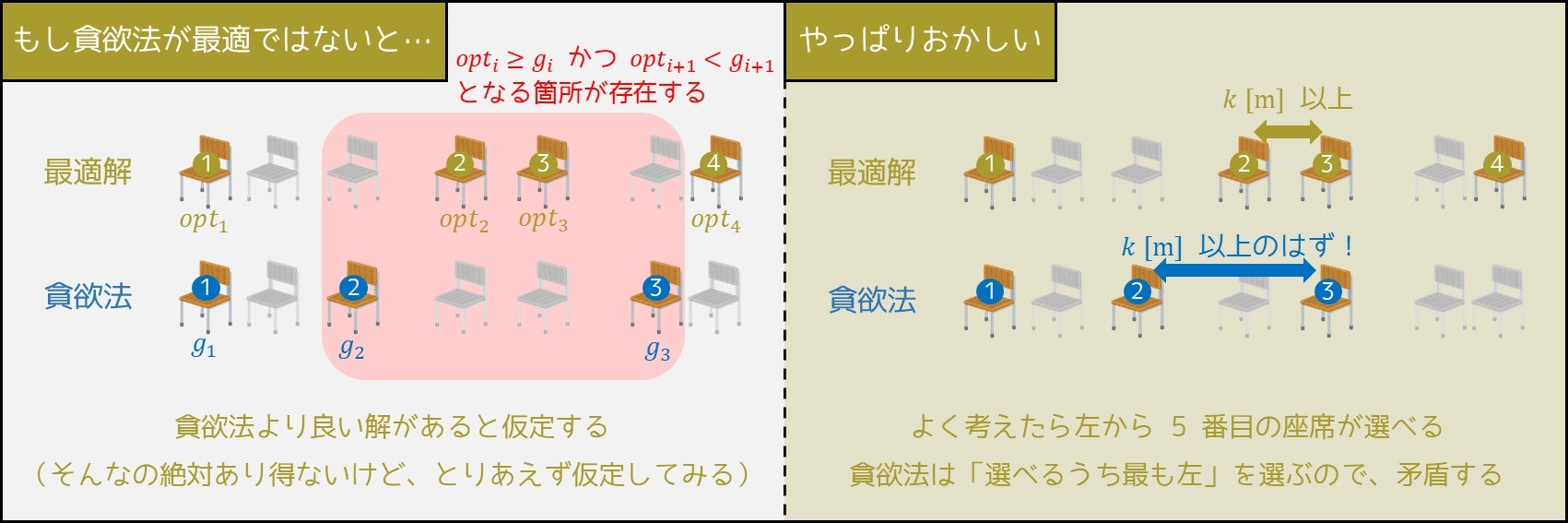
したがって、「$opt_r \geq g_r$ かつ $opt_{r+1} < g_{r+1}$」が成り立つ位置 $r \ (1 \leq r \leq b-1)$ が少なくとも 1 つ存在する。しかしその場合、貪欲法アルゴリズムでは $r+1$ 個目に(座標 $g_{r+1}$ ではなく)座標 $opt_{r+1}$ の席を選ぶことができるため4、「選べる最も左のものを選ぶこと5」に矛盾する。
文章の説明だけでは分かりにくいと思うので、イメージ図も載せておきます。
「今選んだものの座標が小さければ、次選ぶものの座標も小さい」、つまり**「今が良ければ未来も良い」**というアイデアを考えると、直感的に理解しやすいと思います。
3-4. 計算量・サンプルコード
最後に、サンプルコードを載せておきます。
まず、貪欲法を 3-2. 節に書かれた通りにそのまま実装すると、次のようになります。
// 入力・出力部分は省略(Answer が答え)
// 制約は 0 ≦ X[i] ≦ 1000000 程度を想定しています
// pre は前に選んだ席の座標です(存在しない場合 -∞)
// nex は次の操作で選ぶべき席の番号です(存在しない場合 -1)
int pre = -1000000000;
vector<int> Answer;
while (true) {
int nex = -1;
for (int i = 1; i <= N; i++) {
if (X[i] < pre + K) continue;
if (nex == -1 || X[nex] > X[i]) nex = i;
}
if (nex == -1) break;
Answer.push_back(nex);
pre = X[nex];
}
しかし、すべての席を残せるようなケースでは、計算量が $\Theta(N^2)$ となり遅いです。例えば席が $N=10^5$ 個あるとき、$10^{10}$ 回程度の計算が必要となってしまいます。
そこで、std::sort などを用いて、座標を小さい順にソートすることを考えます。(ソートについて詳しく知りたい方は、こちらの記事を読むことを推奨します。)
そうすると、例えば以下のアルゴリズムが通用します。
$i = 1, 2, \cdots, N$ の順に、次の操作を行う。
操作 左から $i$ 番目の席(座標 $X[i]$)が、直前に選んだ席と $K$ $[\rm{m}]$ 以上離れていれば、それを選ぶ。※なお、これは 3-2. 節のアルゴリズムを言い換えただけである。
実装例は次の通りです。計算量は std::sort がボトルネックとなり $O(N \log N)$ です。
// 入力・出力部分は省略(Answer が答え)
// 制約は 0 ≦ X[i] ≦ 1000000 程度を想定しています
// pre は前に選んだ席の座標です(存在しない場合 -∞)
int pre = -1000000000;
vector<int> Answer;
sort(X + 1, X + N + 1);
for (int i = 1; i <= N; i++) {
if (X[i] - pre >= K) {
Answer.push_back(i);
pre = X[i];
}
}
4. ケース B|1.4m 以上離す場合
3 章では、席が一直線上に並んだカウンター席でのケースを考えましたが、本章では少しレベルを上げた「二次元の問題」を考えてみましょう。厳密に述べると以下の通りです。
二次元平面上に $N$ 個の座席がある。$i$ 個目の席の座標は $(X_i, Y_i)$ であり、**$X_i, Y_i$ は整数である。**できるだけ少ない数の席を使用禁止にすることで、どの席間も 1.4m 以上の間隔が空くようにしたい。その方法を求めよ。
これはどうやって解けば良いのでしょうか。
4-1. 方法 1: 市松模様のように、X+Y の偶奇を考える
まず、次のようなアルゴリズムを考えます。
- $X_i + Y_i$ の値が奇数である座席の数を $A$ 個とする
- $X_i + Y_i$ の値が偶数である座席の数を $B$ 個とする
- そこで、$A \geq B$ の場合「$X_i + Y_i$ の値が奇数」である座席をすべて残し、$A < B$ の場合「$X_i + Y_i$ の値が偶数」である座席をすべて残す。
そのとき $A+B=N$ であることから、少なくとも $\lceil N \div 2 \rceil$ 個以上の座席を残せることが証明できます。分かりやすくするため、具体例も載せておきます。
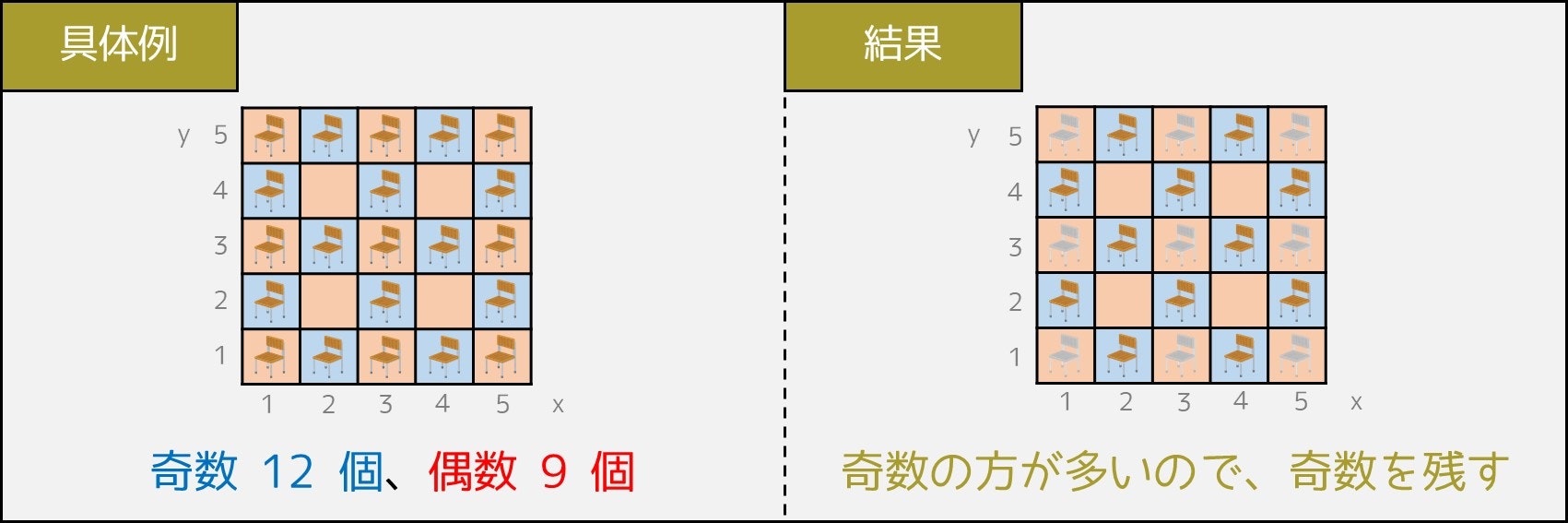
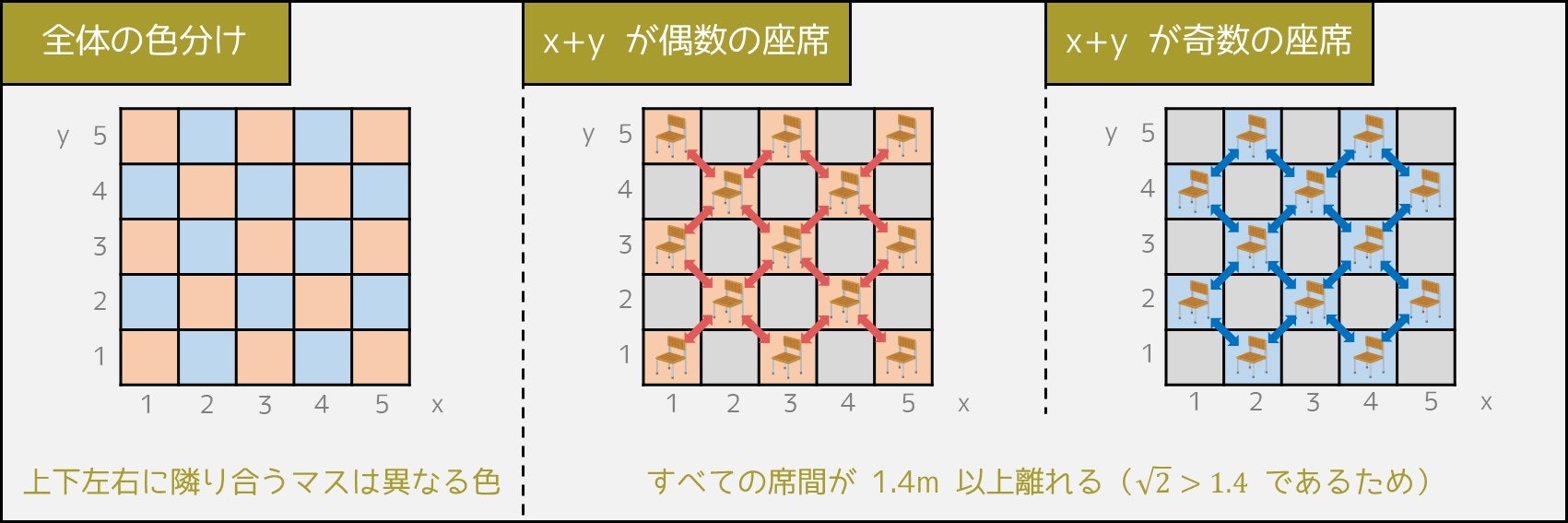
なお、この方法で残す席を決めた場合、どの席間も 1.4m 以上の間隔が空いています。なぜなら、
- $x+y$ が奇数の座席を青色
- $x+y$ が偶数の座席を赤色
で塗ると、上下左右に距離 1 で隣り合う座席6が異なる色で塗られているため、間隔 1m の席を同時に残すことはあり得ないからです。また、$\sqrt{2} > 1.4$ であるからです。
4-2. 本当にそれが最適か?
さて、4-1. 節で述べた方法を使うと、半分以上の座席を残すことができます。だが本当にそれが最適なのでしょうか。例えば次のケースを考えてみましょう。
$N=10, (X_i, Y_i) = (2, 1), (5, 1), (2, 3), (5, 3), (1, 2), (2, 2), (3, 2), (4, 2), (5, 2), (6, 2)$
このとき、$X_i + Y_i$ の偶奇で 2 つのグループに分け、数が多い方を選ぶと、下図の通り 5 個の座席を残すことができます。
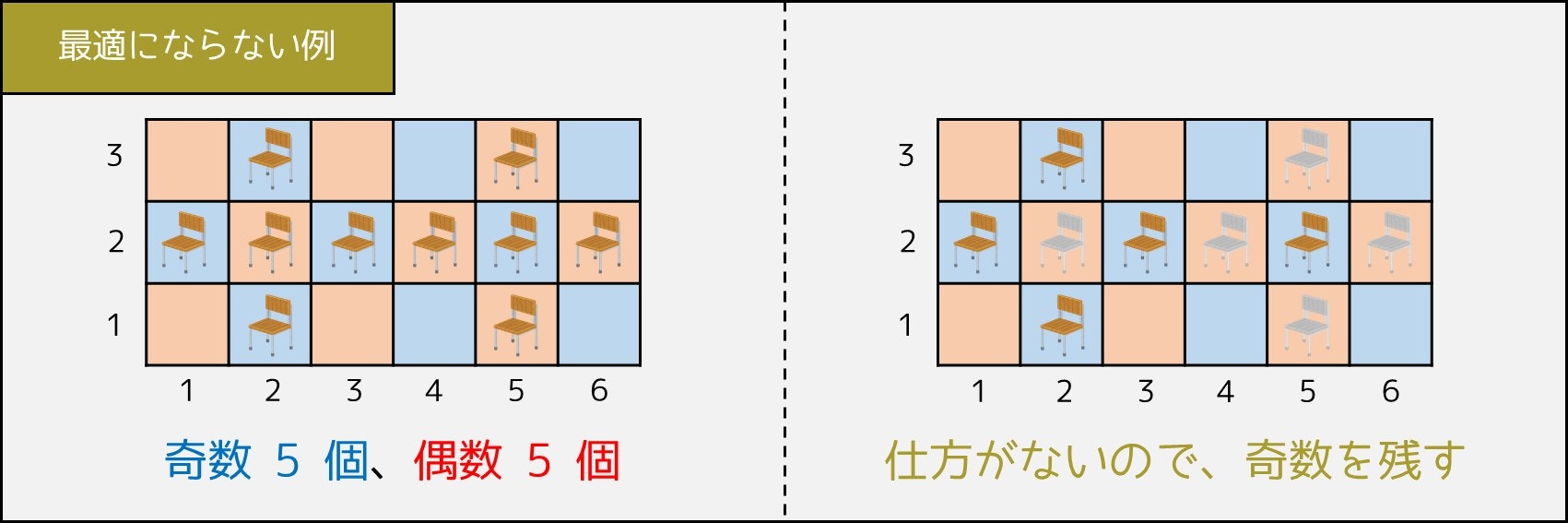
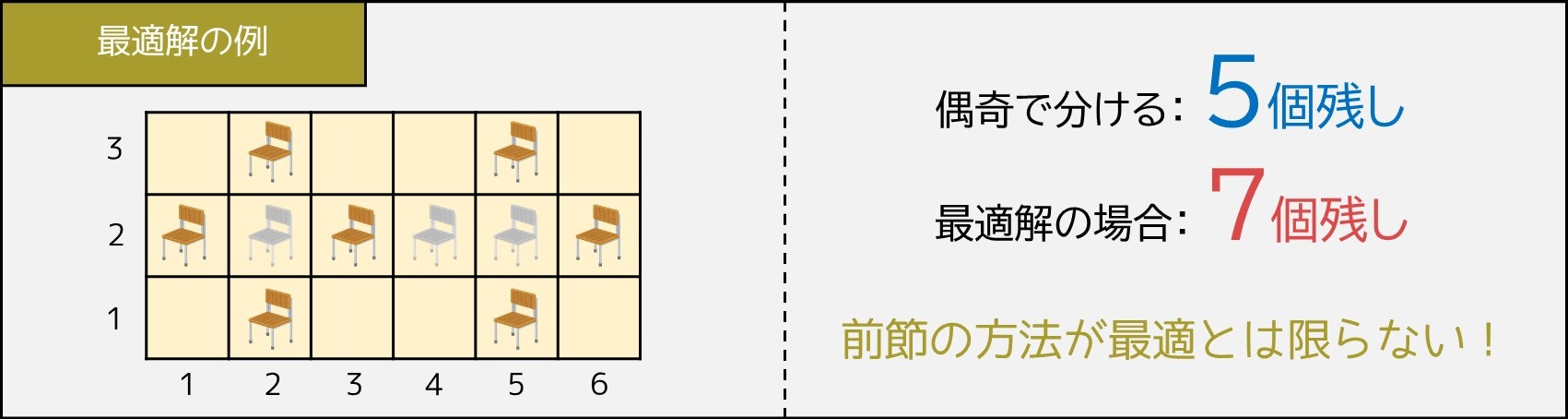
しかし、例えば座標 $(2, 1), (5, 1), (2, 3), (5, 3), (1, 2), (3, 2), (6, 2)$ の席を残すことで、最大 7 個残すことができます。したがって、市松模様のように偶奇で分ける方法は、最適とは限らないのです。
4-3. 最適解を出すための方針
では、どうやったら最適な答えを導けるのでしょうか。
大まかな方針を書いておくと、
- 「座席」を頂点(丸のようなもの)
- 「両方残してはいけない座席同士の関係」を辺(線分のようなもの)
で表した上で、アルゴリズムを工夫すると解けます。(注:このような構造をグラフといいます)
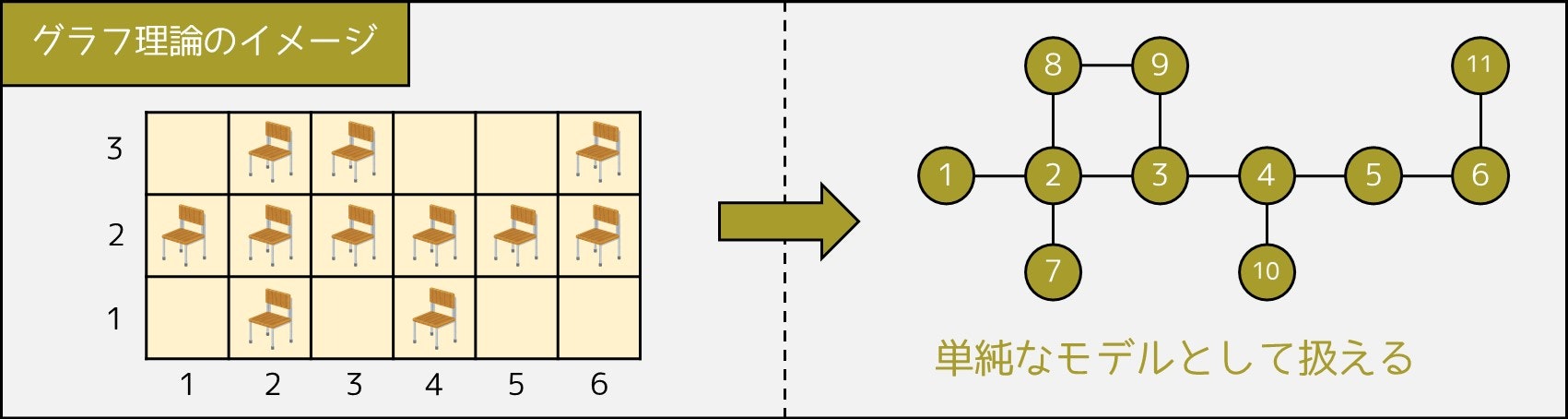
なお、この問題を解くためには、グラフ理論・グラフ探索・ネットワークフローなどの知識が必要になりますが、これらについては
で解説しますので、ご安心ください。
5. 予備知識 ~グラフ理論・ネットワークフローの導入~
5-1. グラフとは
まず、「グラフ」という言葉に対して、皆さんはどのようなイメージを思い浮かべますか?
円グラフ・折れ線グラフなどの表現の仕方。
$y = f(x)$ といった関数のグラフ。
などと答える方が多いのではないかと思います。
しかし、アルゴリズムを勉強していくうえでは違うのです。アルゴリズムの世界において、グラフとは「モノとモノとの関係性」を単純なモデルに表したものなのです。
もう少し詳しく説明しましょう。グラフは、**頂点(Vertex)と辺(Edge)**からなるものであり、辺は 2 つの頂点の間を繋ぎます。辺の向きの有無によってグラフの種類が異なり、
- 辺の向きがない場合は**「無向グラフ」**
- 辺の向きがある場合は**「有向グラフ」**
と呼ばれます。
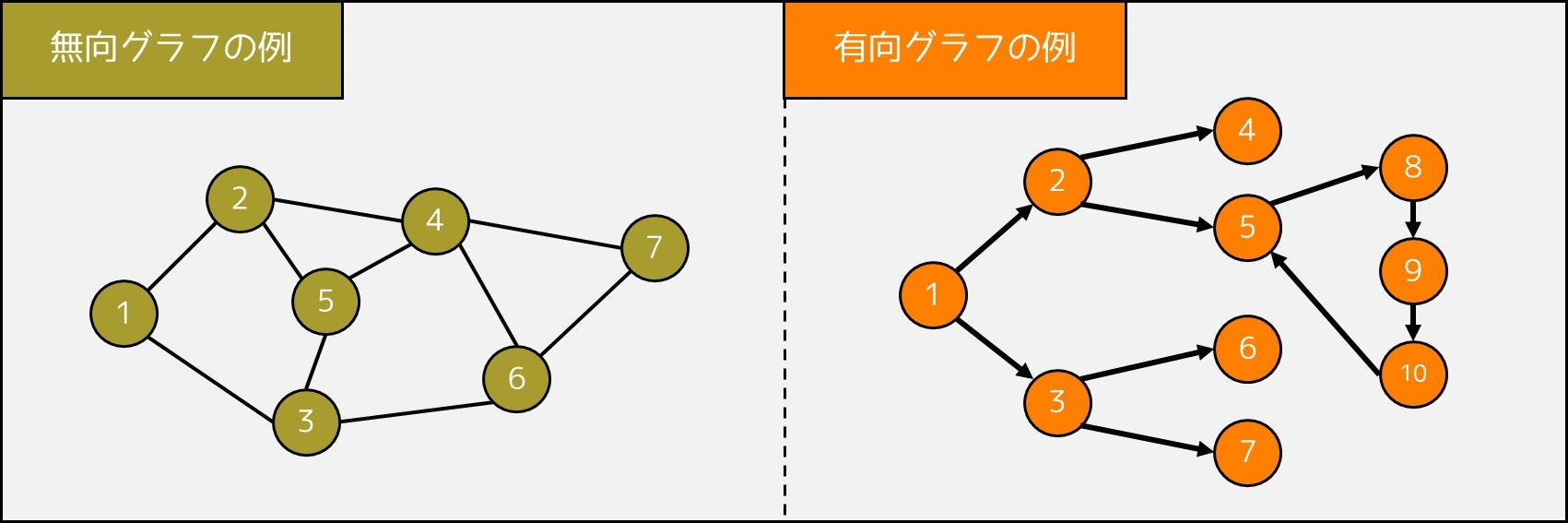
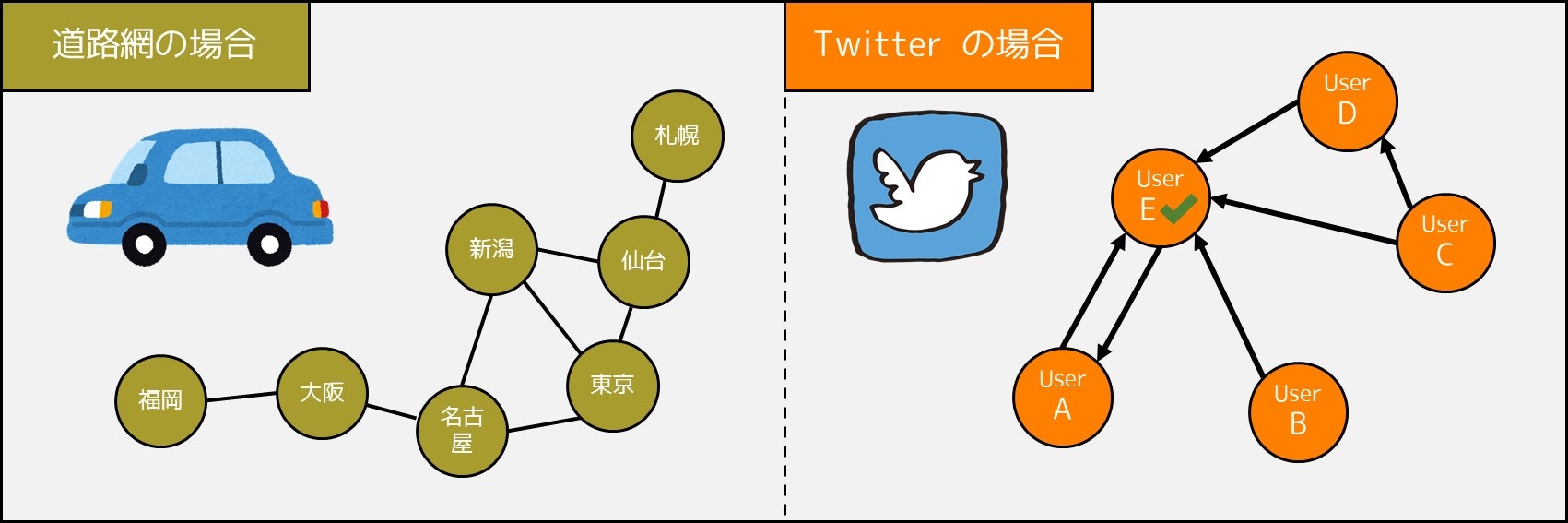
なお、「グラフ」は適用範囲がとても広く便利です。例えば
- 日本の道路網ネットワーク
- Twitter のフォロー/フォロワー関係
など、世の中のたくさんのものは、グラフとして表すことができます!!!
5-2. 二部グラフとは
次に、グラフの中でも特別なものである**「二部グラフ」**について紹介します。
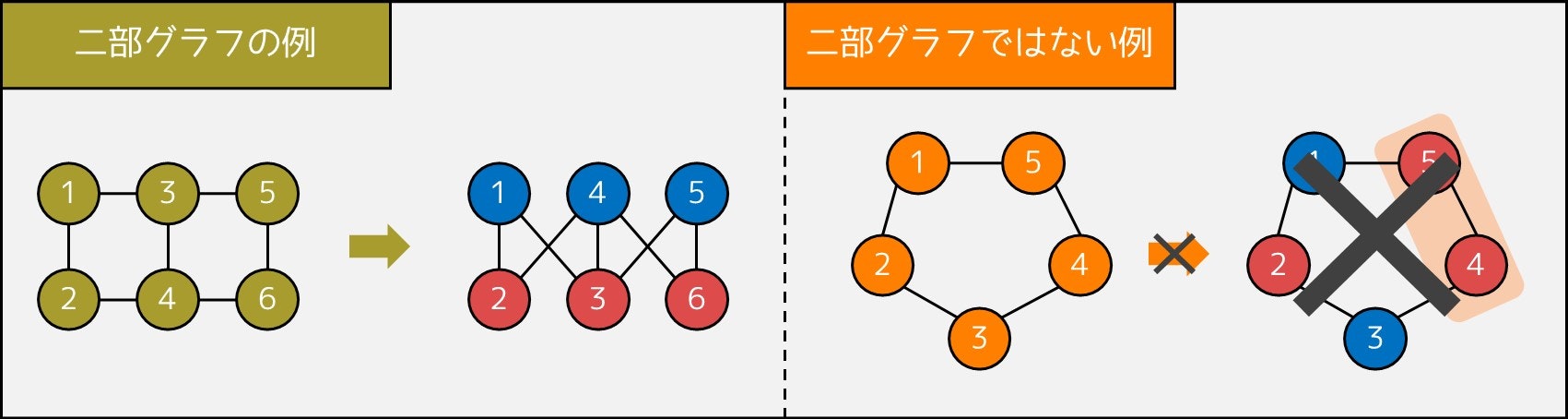
二部グラフとは、以下の条件を満たすグラフのことを指します。
辺で隣接する頂点同士が同じ色にならないように、各頂点を青か赤で塗ることができる。
例えば、図の左側は二部グラフですが、右側は二部グラフではありません。
二部グラフには、他にも「奇数長の閉路がない」などの様々な性質があります。
5-3. 最大マッチング問題とその解法
次に、以下のような**「二部グラフの最大マッチング問題」**について紹介します。
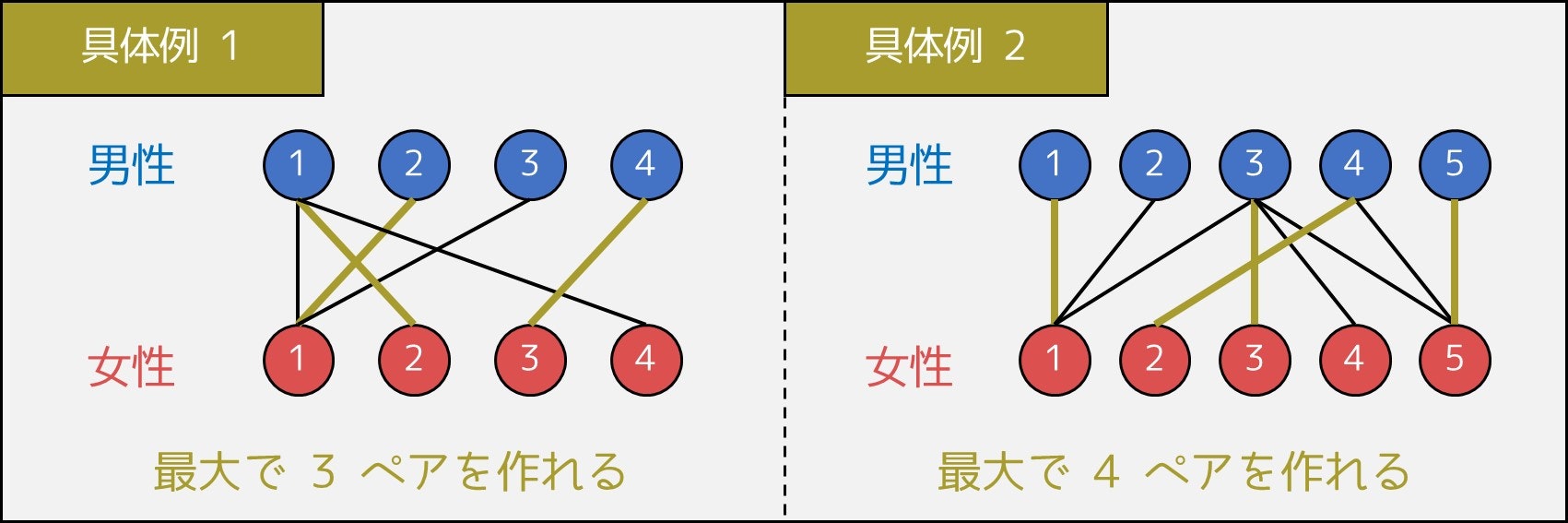
男性と女性が何人かいて、「ペアになっても良い」という男女 2 人の間には線が引かれている。最大で何組のペアを作れるか?
厳密に述べると、次の通りになります。
入力
男性の数 $A$、女性の数 $B$、ペアの情報 $M, (a_1, b_1), (a_2, b_2), \cdots, (a_M, b_M)$出力
$A$ 人の男性と $B$ 人の女性がいる。男性には $1$ から $A$ の番号が、女性には $1$ から $B$ までの番号が付けられている。「男性 $a_1$ と女性 $b_1$」「男性 $a_2$ と女性 $b_2$」$\cdots$「男性 $a_M$ と女性 $b_M$」はペアになっても良いが、同じ人が複数のペアに属すことはできない。作れるペアの数の最大値を出力せよ。
例えば下図の「具体例 1」の場合、(男性1, 女性2)・(男性2, 女性1)・(男性4, 女性4)をペアにすることで、3 つのペアを作ることができます。
4 つのペアを作ることは不可能であるため、答えは 3 です。
この問題では二部グラフ(5-2. 節参照)を扱うため、**「二部グラフの最大マッチング問題」**と呼ばれています。では、どうやって解けば良いのでしょうか。
5-3-1. 解法(ステップ 1)
まず、二部グラフを以下のように変形することを考えます。ただし、男性を青色頂点、女性を赤色頂点として表すものとします。
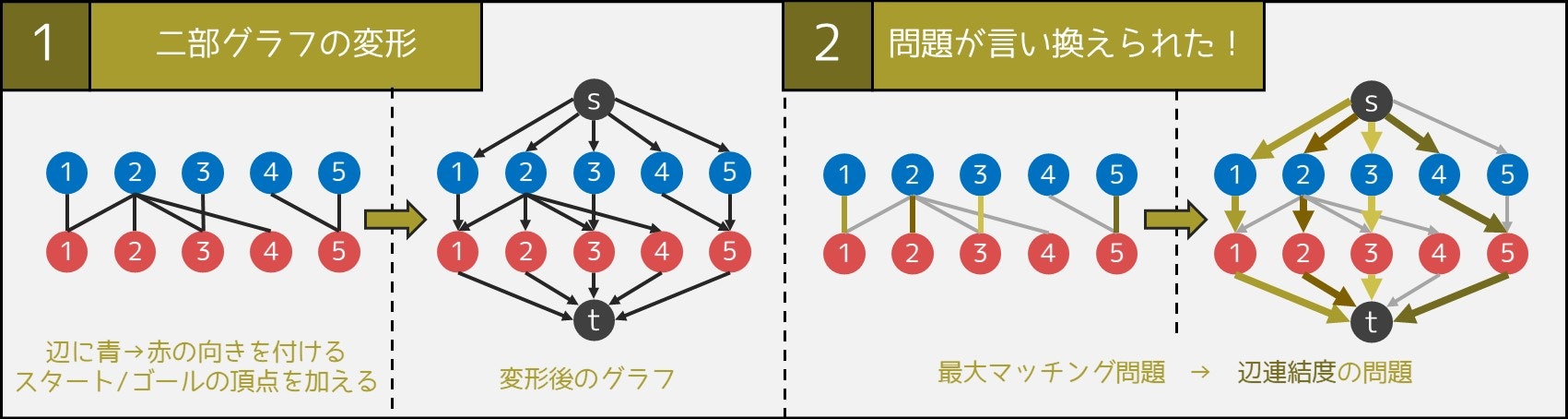
変形1 すべてのペア(辺)に対して、青色→赤色の方向になるように向きを設定する。
変形2 スタートの頂点 $s$ とゴールの頂点 $t$ を新たに用意する。
変形3 スタートから青色頂点へ、赤色頂点からゴールへ向かう辺を追加する。
そうすると、以下の**「グラフの辺連結度を求める問題」**と同値になります。
頂点 $s$ から頂点 $t$ まで、互いに辺を共有しない(=辺素な) $s-t$ パス(頂点 $s$ から頂点 $t$ へ向かう経路)は何本選べるか?
より分かりやすく説明するため、イメージ図も載せておきます。
「選んだ $s-t$ パスに含まれる辺(黄色の辺)のうち、青色頂点と赤色頂点を結んでいるもの」が最大マッチングだと考えると、イメージしやすいと思います。
5-3-2. 解法(ステップ 2)
次に、辺連結度はどうやって求めるのでしょうか。
実は次のようなアルゴリズムで最適解を出すことができます7。なお、ここでは黄色の辺を「選んだ $s-t$ パスに含まれている辺」、灰色の辺を「そうでない辺」とします。
次の操作を、操作が行えなくなるまで繰り返す。
操作
頂点 $s$ から頂点 $t$ に向かう増加パスを 1 つ見つけ、増加パス上の状態を反転させる(黄色の辺を灰色の辺、灰色の辺を黄色の辺にする)
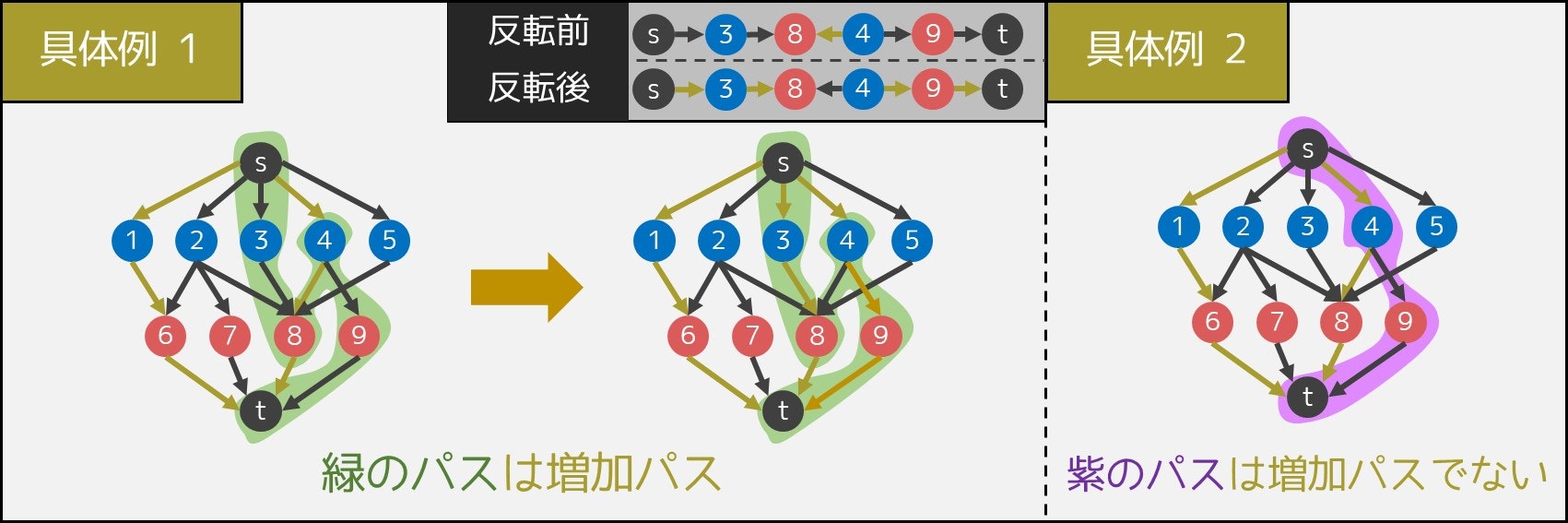
ただし、増加パスとは、次の条件の通りに頂点 $s$ から $t$ まで行く経路のことを指します。
- 灰色の辺を正しい向きで通る。
- 黄色の辺を間違った向きで通る。
より分かりやすく説明するため、いくつか例を載せておきます。具体例 1($s \to 3 \to 8 \to 4 \to 9 \to t$)は増加パスである一方、具体例 2($s \to 4 \to 9 \to t$)は「黄色の辺を間違った向きで通る」を満たしていないため、増加パスではありません。
5-3-3. アルゴリズムの実演
次に、アルゴリズムへの理解をさらに深めるため、実際に辺の状態がどう動いているかを GIF 画像で実演したいと思います。1 回操作を行うごとに、「互いに辺を共有しない $s-t$ パスの個数」が 1 個ずつ増えていることが分かります。
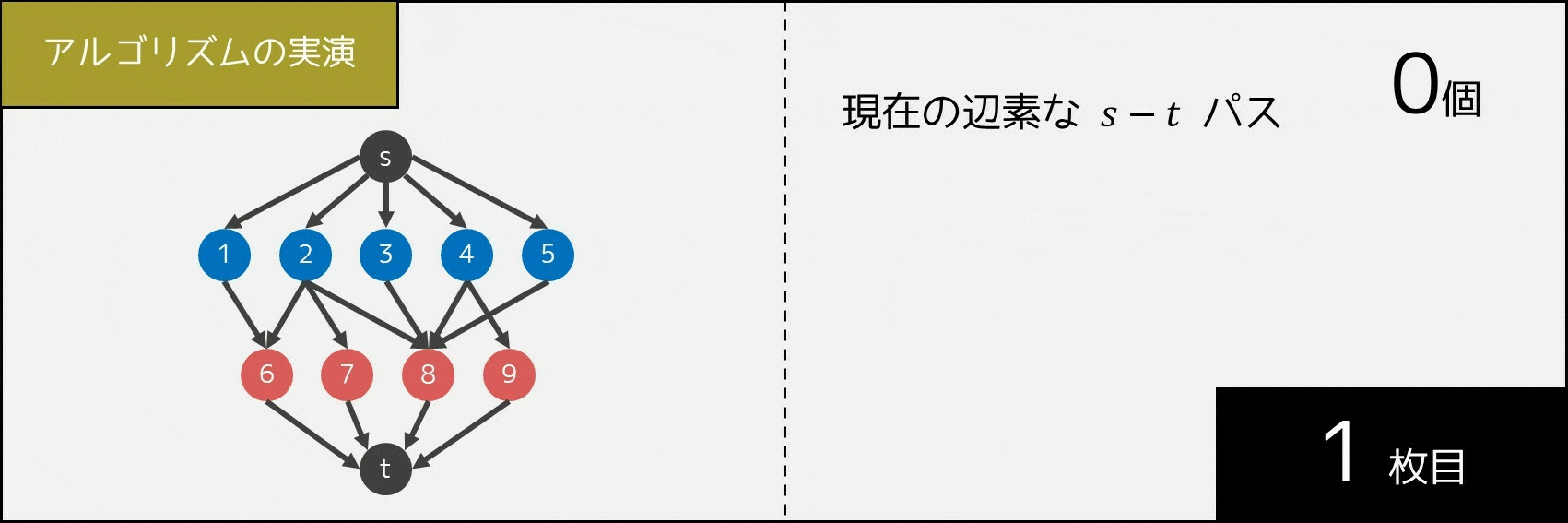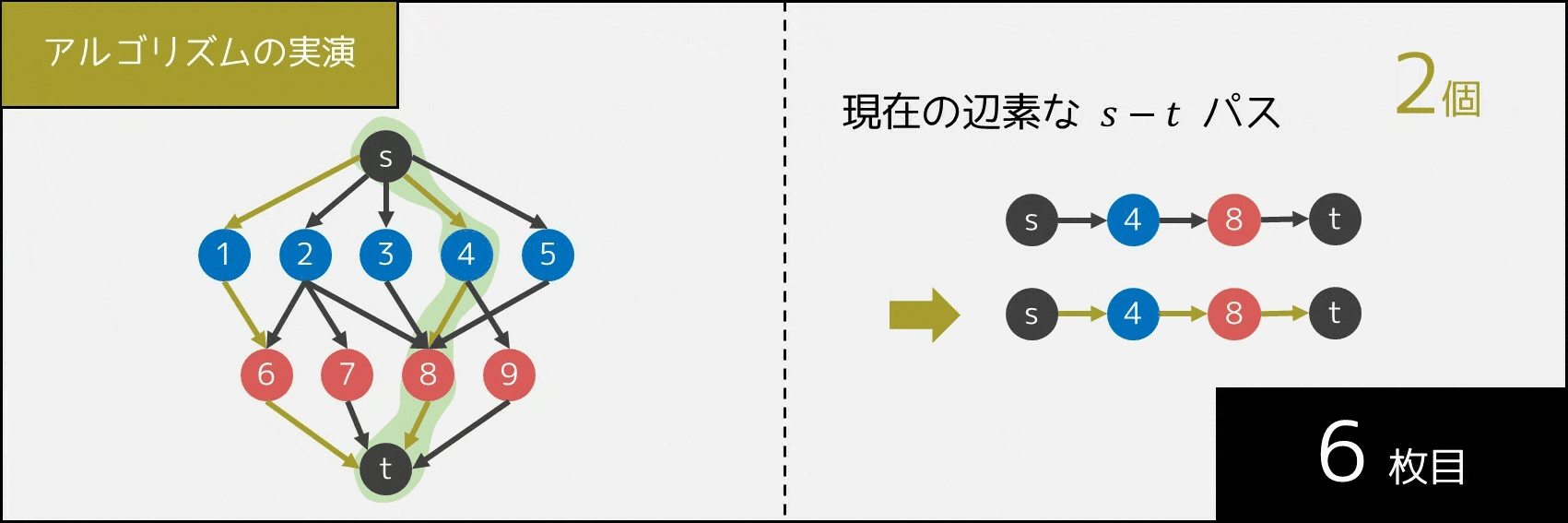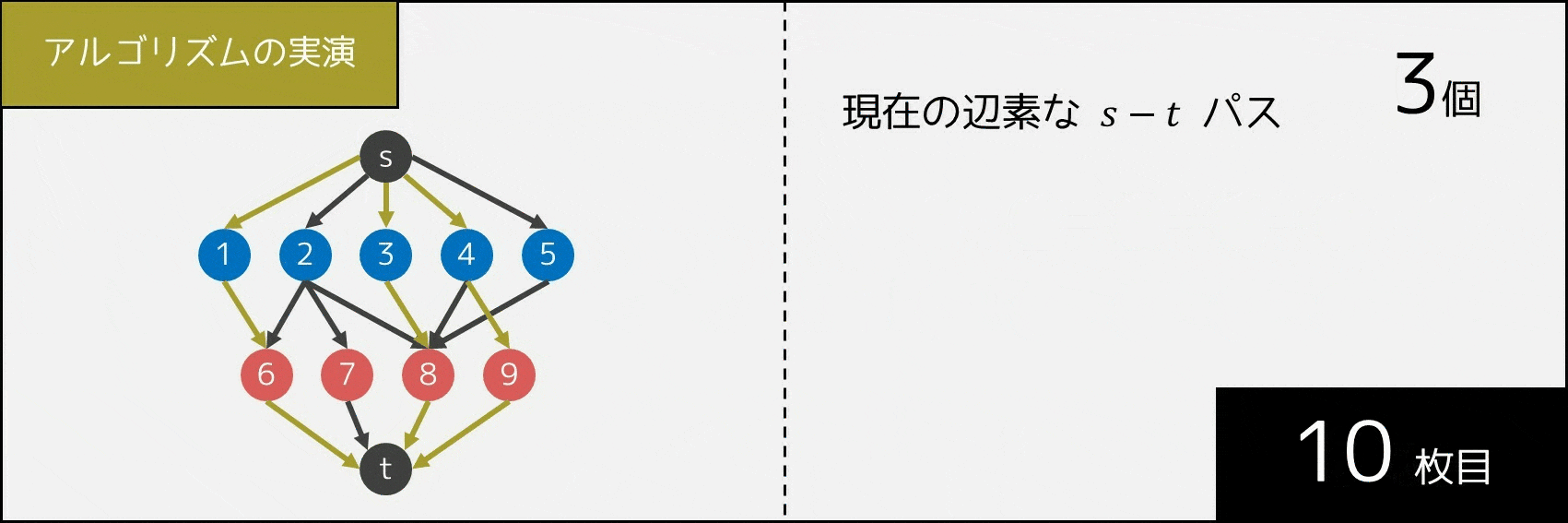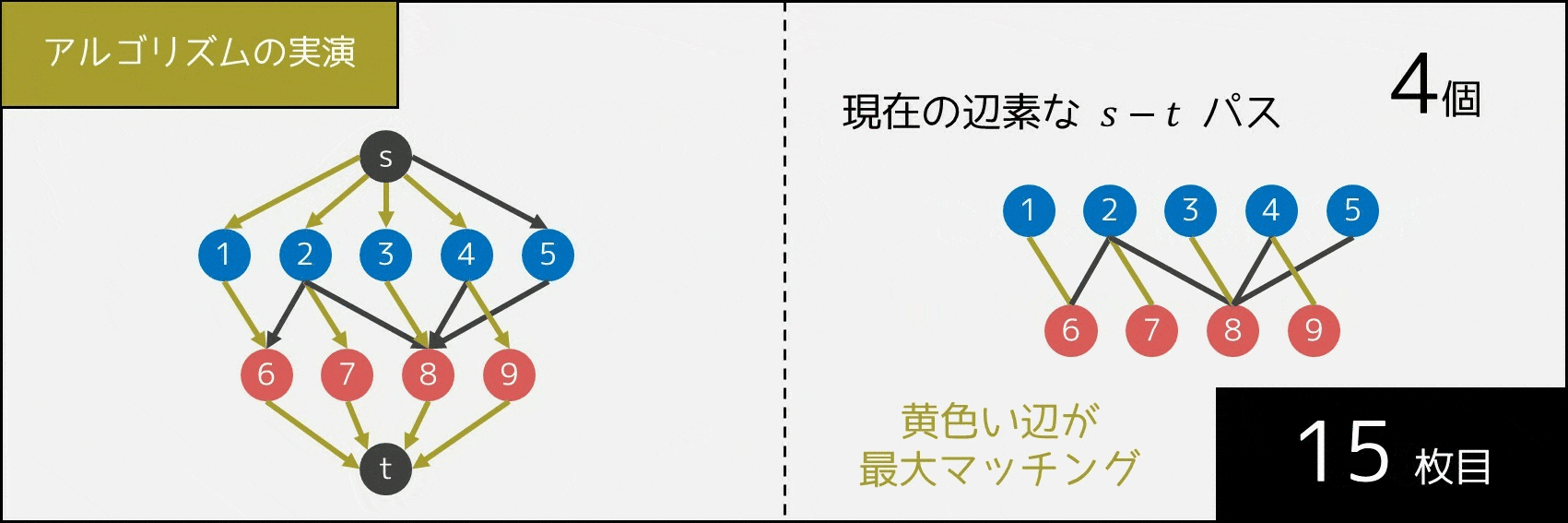
5-3-4. 計算量・実装・サンプルコード
まず、増加パスは**深さ優先探索(DFS)**を使うことで見つけられます。DFS については、
を読んでいただけたらと思います。
次に、計算量を見積もってみましょう。
- 1 回増加パスを見つけるのに $M$ 回程度の計算が必要である
- 増加パスを見つける操作を、最大 $\rm{min}$$(A, B)$ 回行う
ことから、全体計算量は $O(\rm{min}$$(A, B) \times M)$ となります。したがって、$A, B, M = 2000$ 程度の比較的大きなデータでも、数秒以内に実行が終了します。
最後に、実装例としては以下のようなものが考えられます。(難しいですが、コードの内容を理解できなくても 6 章で扱う「座席の問題」を解くことができます。ご安心ください。)
# include <iostream>
# include <vector>
using namespace std;
struct Edge {
int to, rev;
bool isvalid;
};
class Maximum_Matching {
public:
vector<Edge> G[5009];
bool used[5009];
// グラフに辺を追加する
void add_edge(int u, int v) {
G[u].push_back(Edge{ v, (int)G[v].size(), true });
G[v].push_back(Edge{ u, (int)G[u].size() - 1, false });
}
// 増加道を見つける
bool dfs(int pos, int to) {
if (pos == to) return true;
used[pos] = true;
for (int i = 0; i < G[pos].size(); i++) {
if (used[G[pos][i].to] == true) continue;
if (G[pos][i].isvalid == false) continue;
bool ret = dfs(G[pos][i].to, to);
if (ret == true) {
G[pos][i].isvalid = false;
G[G[pos][i].to][G[pos][i].rev].isvalid = true;
return true;
}
}
return false;
}
// 最大マッチングを求める
int getans(int u, int v) {
int cnt = 0;
while (true) {
for (int i = 0; i < 5009; i++) used[i] = false;
bool zouka_path = dfs(u, v);
if (zouka_path == false) break;
cnt++;
}
return cnt;
}
};
5-4. <参考>最大流問題・最小カット問題
本章の最後に、関連する話題として「最大流問題(Maximum Flow)」を紹介します。
なお、6 章の内容とは関係ないので、読み飛ばしていただいても構いません。
最大流問題とは、次のような問題のことを指します。
入力
頂点数 $N$、辺数 $M$、グラフの情報 $(a_1, b_1, c_1), \cdots, (a_M, b_M, c_M)$出力
$N$ 頂点 $M$ 辺のグラフがあり、$i$ 個目の辺は頂点 $a_i$ から $b_i$ まで毎分 $c_i$ $\rm{[L]}$ の水を流すことができる。頂点 $1$ に十分な量の水を出す水源があるとき、頂点 $N$ には最大で毎分何 $\rm{[L]}$ の水を届けることができるか、出力せよ。
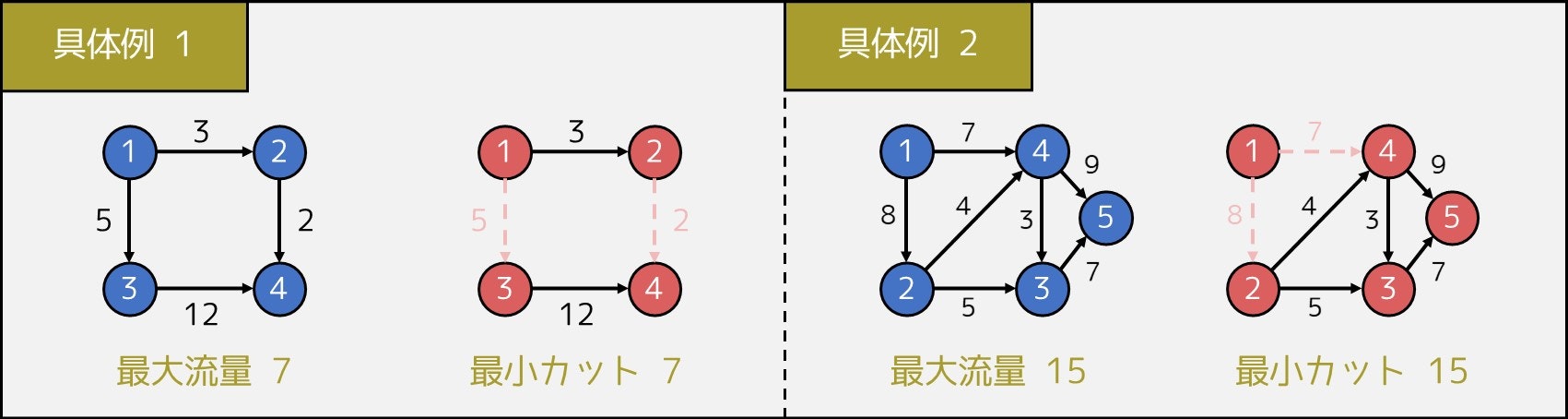
例えば、$N = 4, M = 4, (a_i, b_i, c_i) = (1, 2, 3), (1, 3, 5), (2, 4, 2), (3, 4, 12)$ の場合、下図のような流し方をすると、毎分 7 L の水を頂点 4 に届けることができます。
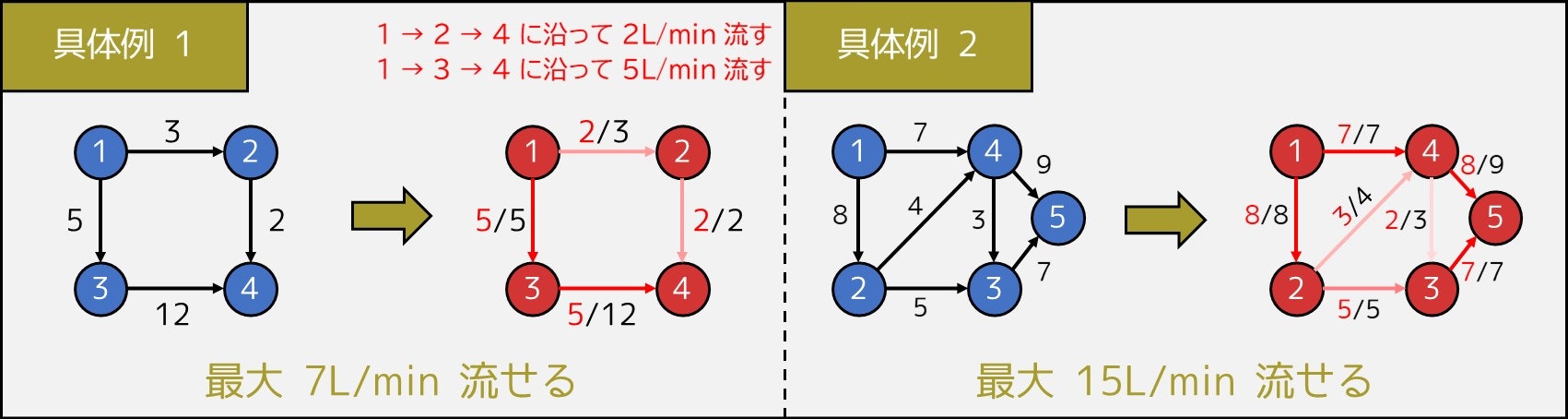
本記事では、紙面の都合上詳細を割愛させていただきますが、この問題は
を使うことで、計算量 $O(FM)$ で解くことができます。($F$ を問題の答えとする)
それに関連して、次のような問題を最小カット問題といいます。
入力
頂点数 $N$、辺数 $M$、グラフの情報 $(a_1, b_1, c_1), \cdots, (a_M, b_M, c_M)$出力
$N$ 頂点 $M$ 辺のグラフがあり、$i$ 個目の辺は頂点 $a_i$ から $b_i$ へ結び、この辺を消すのに $c_i$ 円かかる。頂点 $1$ から頂点 $N$ まで行けないようにしたい。最小何円必要か。
そこで、以下の定理が成り立ちます。(最大フロー最小カット定理といいます)
- (最大フローの答え) = (最小カットの答え)
したがって、最大流問題とまったく同じプログラムで解くことができるのです。
6. ケース B で最適解を出す方法
5 章では、問題を解くために必要な知識の解説を行いました。
さて、本題に移りたいところですが、いきなり最適な答えを構成するのは難しいので、まずは**「最大で何個の席を残せるか」を求める問題**から考えたいと思います。本記事では、
- 6-1. 節|ステップ 1: 最大独立集合問題に帰着させる
- 6-2. 節|ステップ 2: 二部グラフであることに気づく
- 6-3. 節|ステップ 3: 最大マッチング問題に帰着させる
- 6-4. 節|ステップ 4: 計算量とサンプルコード
といった順序で解説します。そして、本章の最後に、答えを 1 つ構成する方法を記します。
6-1. ステップ 1: 最大独立集合問題に帰着させる
まず、次のようなグラフを作ることを考えましょう。
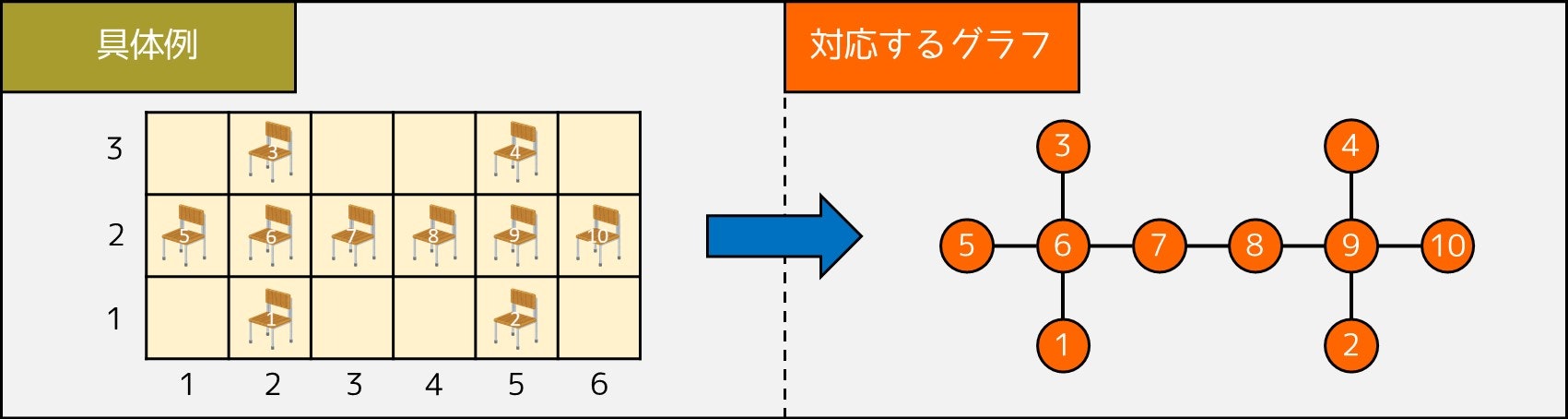
**頂点:**それぞれの座席(頂点番号 $i$ は、$i$ 個目の座席に対応する)
**辺:**距離が 1.4m 未満である座席の組を辺で結ぶ
例えば、$N = 10$ で座標 $(2, 1), (5, 1), (2, 3), (5, 3), (1, 2), (2, 2), (3, 2), (4, 2), (5, 2), (6, 2)$ に席があった場合、グラフは下図のようになります。
そのとき、今回解くべき問題は、以下の最大独立集合問題に言い換えることができます。
次の条件を満たすように頂点の集合を選ぶとき、集合の要素数の最大値はいくつか?
条件 隣接した 2 つの頂点が両方選ばれることはない
例えば上の例の場合、頂点 $\{1, 2, 3, 4, 5, 7, 10\}$ が最大独立集合の 1 つであり、7 個の席を残すことができます。
6-2. ステップ 2: 二部グラフであることに気づく
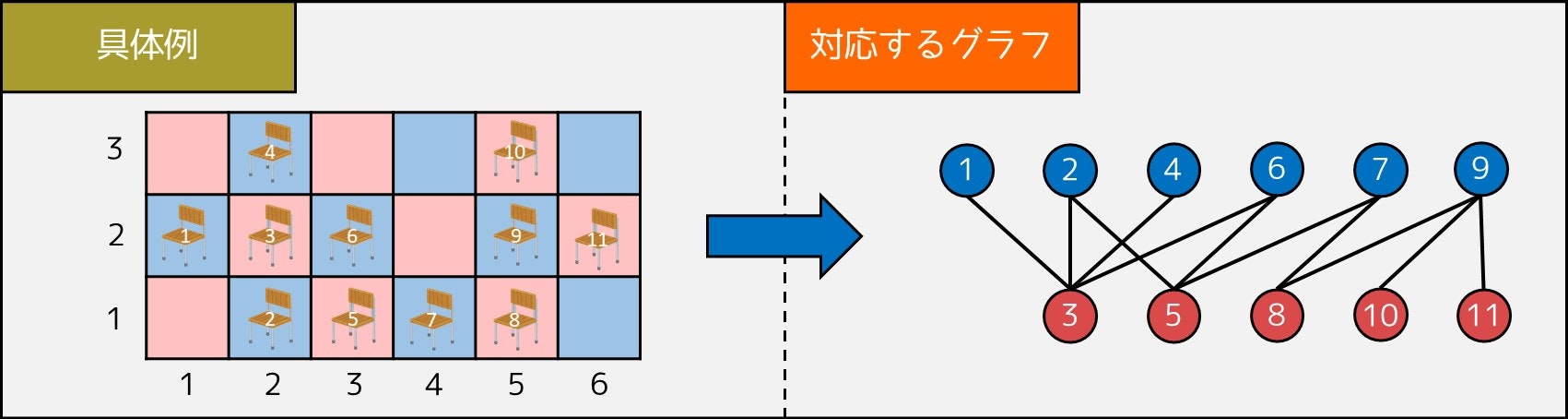
さて、6-1. 節の方法で作られるグラフはどんな性質を持つのでしょうか。実は二部グラフになっています。(二部グラフについては 5-2. 節参照)
なぜなら、以下のように頂点を塗ると、どの隣接する 2 頂点も異なる色になるからです。
- $X_i + Y_i$ が奇数である座席に対応する頂点を青色で塗る
- $X_i + Y_i$ が偶数である座席に対応する頂点を赤色で塗る
下図の例でも、二部グラフであることが容易に確認できると思います。
したがって、二部グラフの最大独立集合問題を解けば良いことになります。
6-3. ステップ 3: 最大マッチングに帰着させる
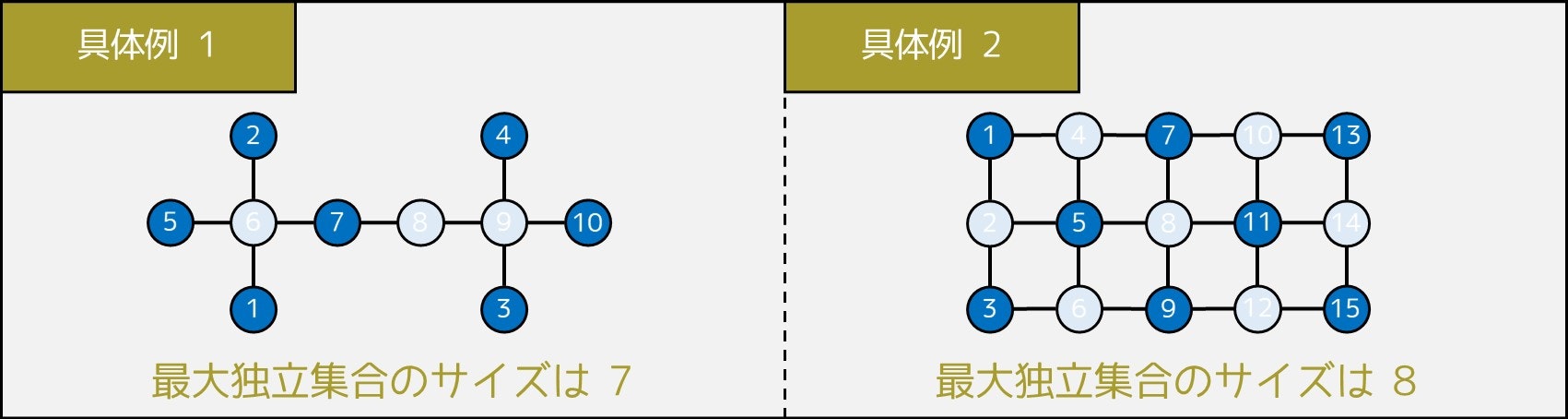
次に、二部グラフの最大独立集合問題はどうやって解くのでしょうか。実は次の重要な性質が成り立つため、最大マッチングの個数が求まれば、答えが分かってしまうのです。
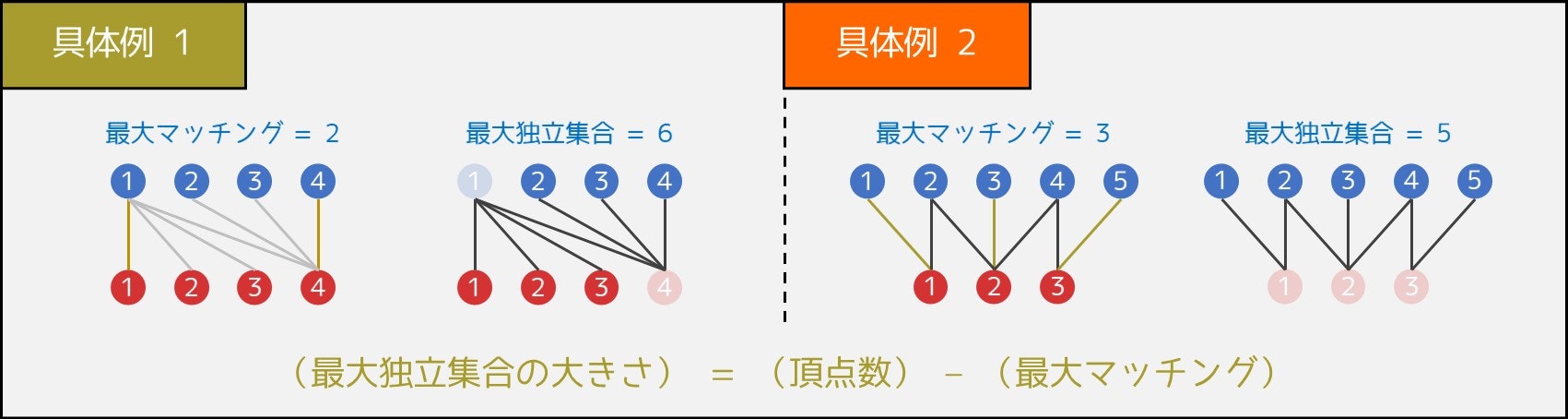
(二部グラフの最大独立集合のサイズ) = (頂点数 $N$) - (二部グラフの最大マッチングの個数 $P$)
具体例を 2 つ挙げておきますが、いずれの場合も上の式が成り立っています。他にもいろいろなケースを試してみてください。反例は 1 つも見つからないはずです。
6-4. ステップ 4: 計算量とサンプルコード
ここまでの考察を使うと、次の手順により「座席の問題」を解くことができます。
手順1 6-1. 節の通りに、グラフを構成する。
手順2 5-3. 節の通りに、二部グラフの最大マッチングを求める。
手順3 6-3. 節の式にしたがって、最大独立集合のサイズ(答え)を求める。
さて、計算量を見積もると、以下の通りになります。
- まず手順2について考える。作られるグラフの頂点数と辺数をそれぞれ $N, M$ とするとき、$M \leq 2N$ であることが証明できるため、計算量は $O(N^2)$ である8
- 次に手順1について考える。グラフを構成するにあたって、すべての $(i, j)$ の組に対して「座席 $i$ と座席 $j$ の間の距離が 1.4m 未満かどうか」調べれば良いので、計算量は $O(N^2)$ である
したがって、全体の計算量は $O(N^2) + O(N^2) = O(N^2)$ となり、$N = 5000$ 程度のデータでも数秒以内で実行が終わります。実装例は次の通りです。
# include <iostream>
# include <vector>
using namespace std;
// Maximum_Matching クラスは省略(5-3. 節参照)
int N, X[1 << 18], Y[1 << 18];
Maximum_Matching H;
int main() {
// Step #1. 入力
cin >> N;
for (int i = 1; i <= N; i++) {
cin >> X[i] >> Y[i];
}
// Step #2. グラフを構成(グラフの辺は [青色の座席] → [赤色の座席] の向き)
for (int i = 1; i <= N; i++) {
if ((X[i] + Y[i]) % 2 != 1) continue;
for (int j = 1; j <= N; j++) {
if ((X[j] + Y[j]) % 2 != 0) continue;
H.add_edge(i, j);
}
}
// Step #3. 最大マッチングを求めるために追加で辺を作る
for (int i = 1; i <= N; i++) {
if ((X[i] + Y[i]) % 2 == 1) H.add_edge(N + 1, i);
if ((X[i] + Y[i]) % 2 == 0) H.add_edge(i, N + 2);
}
// Step #4. 最大マッチングと答えを求める
int max_matching = H.getans(N + 1, N + 2);
int independent_set = N - max_matching;
cout << independent_set << endl;
return 0;
}
6-5. <発展>ステップ 5: 最適な構成を 1 つ求める
前節の手法を使うことによって、「最大で何個の座席を残せるか?」という疑問を解消することができました。しかしそこまで来ると、
どのような席の残し方をすれば、最適になるのか…?
と、新たな疑問が生まれます。
そこで本章の最後に、二部グラフの最大独立集合を構成する方法を 1 つ紹介します。
最適解を求める手順
答えを先に書いてしまいます。最大マッチングが求まった後、以下の手順の通りに計算を行うと、最大独立集合が分かります。ただし、二部グラフは青色と赤色で塗られているとします。
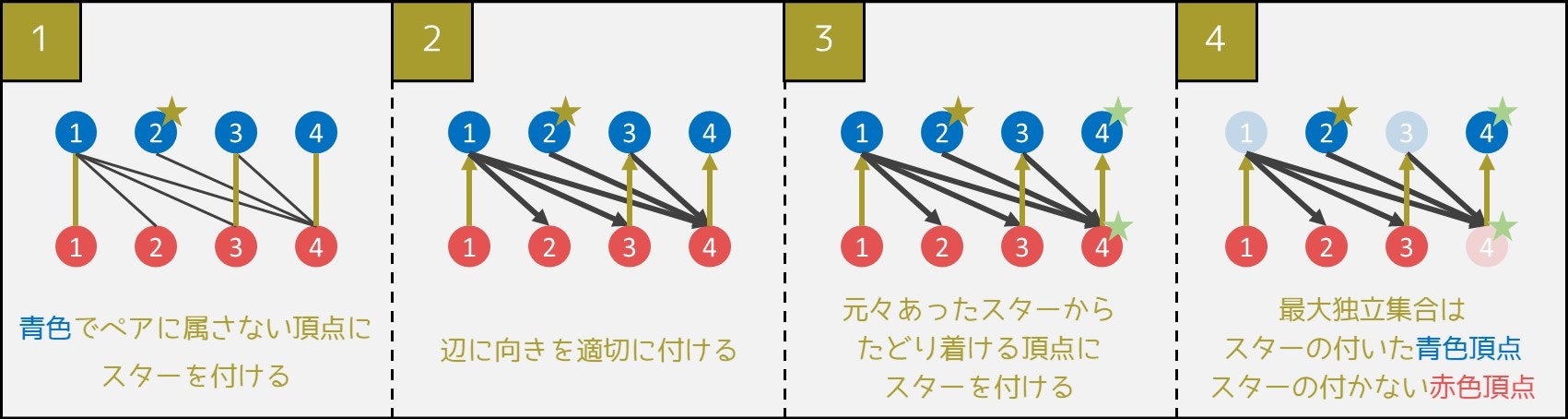
手順1
青色頂点のうち、どのペアにも含まれない(孤独な)頂点すべてにを付ける
手順2
二部グラフの各辺に、次のように向きを付ける。
マッチングに使われる辺:赤色頂点から青色頂点に向かう
マッチングに使われない辺:青色頂点から赤色頂点に向かう手順3
グラフの辺を(手順2で決めた)正しい向きで何本か通ることで、の付いた頂点からたどり着ける頂点に、新たに
を付ける
手順4
最大独立集合は、の付いた青色頂点と
の付いていない赤色頂点である
手順3で深さ優先探索(DFS)などを用いた場合、計算量は $O(N+M)$ になります。
具体例
例えば青色頂点と赤色頂点が 4 つずつあり、辺が以下の通りであるとします。
(青1 - 赤1)、(青1 - 赤2)、(青1 - 赤3)、(青1 - 赤4)、(青2 - 赤4)、(青3 - 赤3)、(青3 - 赤4)、(青4 - 赤4)
そのとき、下図のような手順により、最大独立集合が求まります。
証明など
かなり難しいので、本記事では割愛させていただきますが、知りたい方は
を読んでいただけたらと思います。
7. ケース C|10m 以上離す場合
最後に、席の間隔制限が「1.4m 以上」から**「10m 以上」**にグレードアップした問題を考えてみましょう。これはどうやって解けば良いのでしょうか。
7-1. 最適解を出すのは難しい ~NP困難~
6 章で述べた通り、この問題は「最大独立集合問題」に帰着することができます。例えば、
$N = 5, K=10 [\rm{m}]$
$(X_i, Y_i) = (1, 1), (10, 1), (1, 10), (10, 10), (9, 8)$
の場合、下図のグラフにおける最大独立集合を求めれば、最適な席の残し方が分かります。
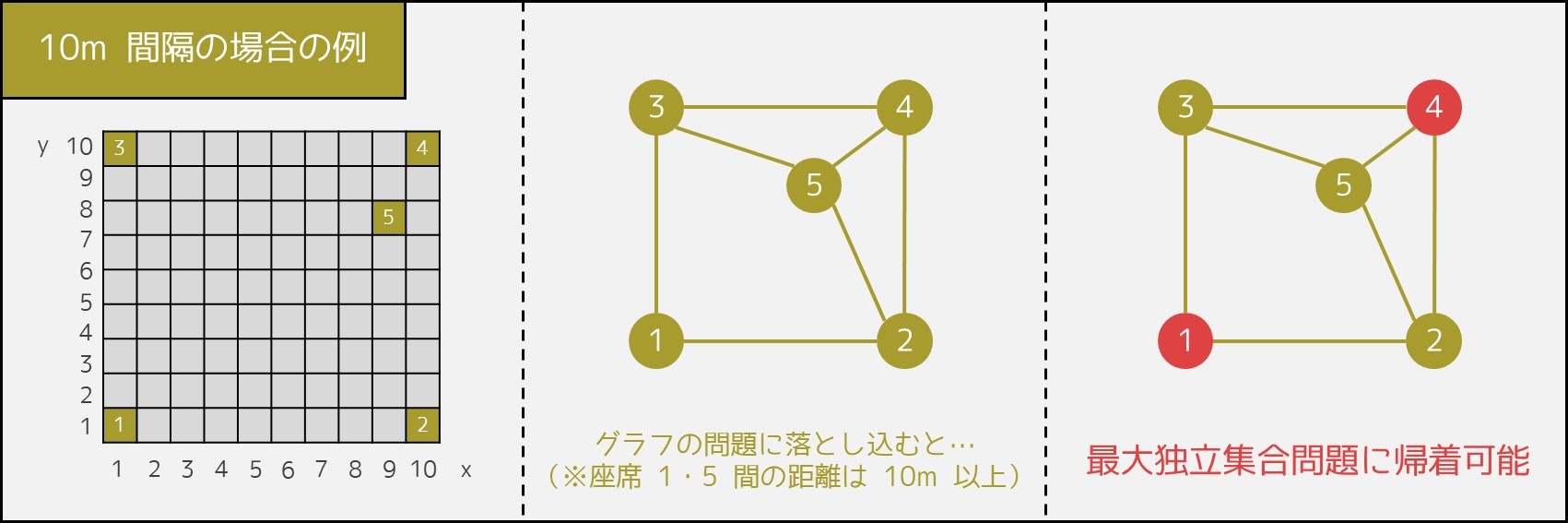
しかし、最大独立集合問題は NP困難9であり、$N$ が大きいケースで解くのは絶望的とされています。
など、特殊なケースでは効率的に解くことができますが、本章で扱う「10m の問題」では上図の例のように、扱うグラフが二部グラフでない場合もあるのです。
したがって、「10m の問題」における最適解を効率的に求めるのには無理があります。
ですが、諦めるのはまだ早いです。「$N \div 100$ 個以上の席を残す」など、できるだけ良い「近似解」を出すことには、まだ希望が残っています。次節以降では、それらについて解説したいと思います。
7-2. 近似解 1 ~N/100 個の座席を残す~
まず、次のようなアルゴリズムが思いつきやすいでしょう。
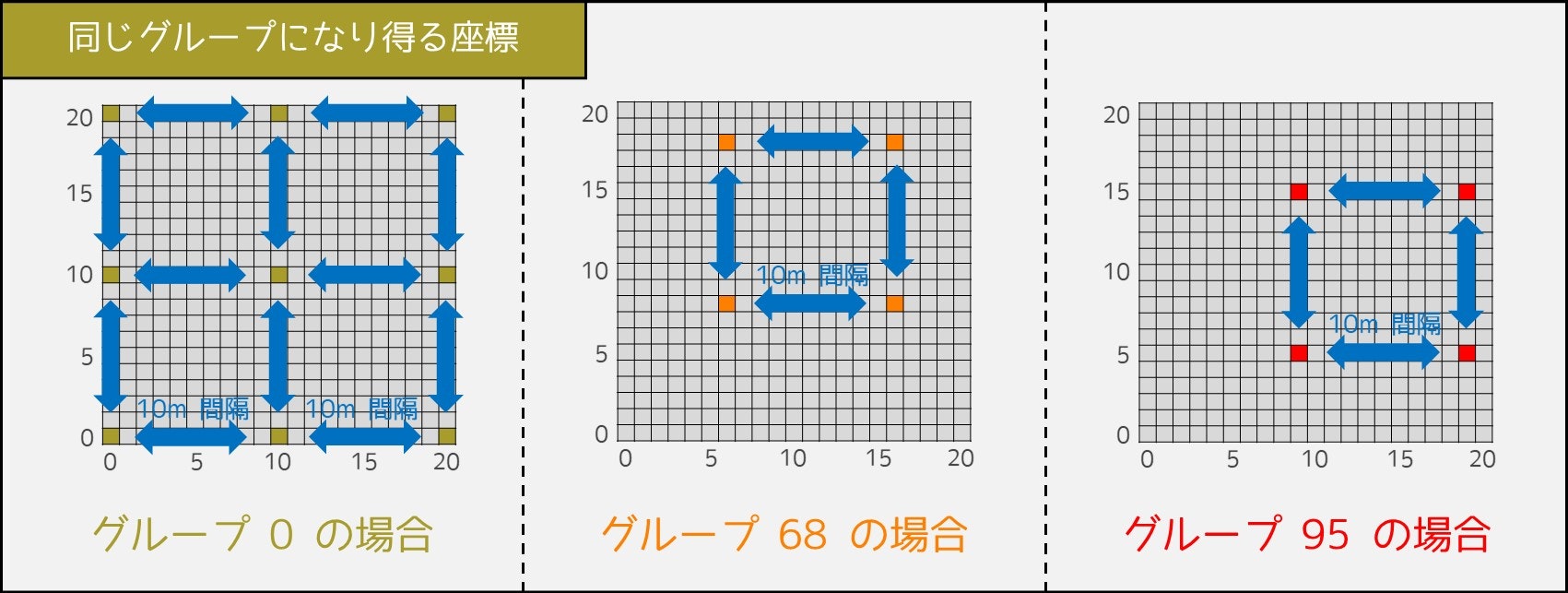
座席を $100$ 個のグループに分け、$0, 1, 2, \cdots, 99$ と番号を付ける。
座標 $(X_i, Y_i)$ にある席は、グループ $10 \times (X_i \bmod 10) + (Y_i \bmod 10)$ に入れる。最後に、$100$ 個のグループの中で最も多くの座席があるものを選び、そのグループに属する座席のみを残す。
そこで得られた答えは、以下の 2 つの性質を必ず満たします。
性質1 $N \div 100$ 個以上の席を残せている。
性質2 どの「残す席」の間も 10m 以上の間隔が空く。
性質 1 は「もしどのグループも $N \div 100$ 個未満の座席からなっていた場合、グループの大きさの合計が $N$ にならずおかしい」ことを考えると、証明できます。
また、性質 2 は「同じグループになる可能性のある座標が下図のようになっていること」を考えれば、理解しやすいと思います。
実装例は次のようになります。
ここでは変数 group[i] で、グループ $i$ に属す座席の番号を管理しています。
# include <iostream>
# include <vector>
using namespace std;
int N, X[1 << 18], Y[1 << 18];
vector<int> group[100];
int main() {
cin >> N;
for (int i = 1; i <= N; i++) {
cin >> X[i] >> Y[i];
group[10 * (X[i] % 10) + (Y[i] % 10)].push_back(i);
}
int maxn = 0, maxid = 0;
for (int i = 0; i < 100; i++) {
if (maxn < (int)group[i].size()) { maxn = group[i].size(); maxid = i; }
}
cout << "Number of seats = " << maxn << endl;
for (int i = 0; i < maxn; i++) { if (i) cout << " "; cout << group[maxid][i]; }
cout << endl;
return 0;
}
7-3. 特殊なパターンに着目する
さらに良い近似解を出すためには、どうすれば良いのでしょうか。
いきなり解法を思いつくのは難しいので、まずは問題設定を簡単にした、以下のケースを考えてみましょう。
大きさ $70 \times 70$ の正方形の部屋の中に、できるだけ多くの人を入れたい。
しかし、どの人の間も 10m 以上の間隔を保つ必要がある。
そのような方法を 1 つ求めよ。
7-2. 節のアプローチをそのまま使って、人を正方形状に整然と並べると、$8 \times 8 = 64$ 人しか入れることができません。
一方、三角形をなすように人を並べると、$8 + 7 + 8 + 7 + 8 + 7 + 8 + 7 + 8 = 68$ 人を入れることができ、効率的なのです。

7-4. 近似解 2 ~N/90 個の座席を残す~
最後に、座席の問題に戻りましょう。
まず、「同じグループ内のどの 2 つも 10m 以上の間隔が空くようにする」という条件のもとで、整数座標をできる限り少ないグループに分けることを考えます。
7-2. 節では、正方形状に整然と並べることで 100 個のグループに分割しました。
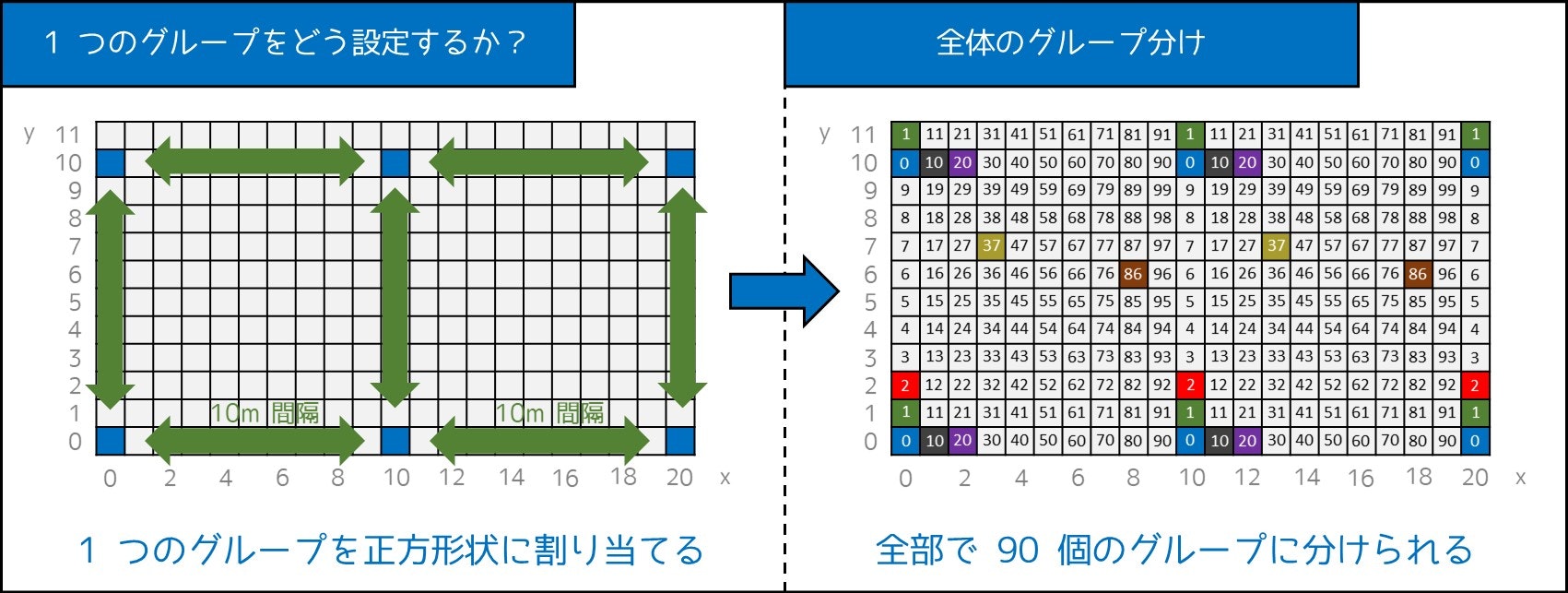
一方、7-3. 節で紹介したアイデアを使って、各グループを三角形状に並べると、下図のように縦 10 × 横 9 = 90 個のグループに分けられるのです。
実際、青色矢印で描かれている、どの 2 つの座標間の距離も、$\sqrt{9^2 + 5^2} = \sqrt{106} \fallingdotseq 10.3 > 10$ であるため、条件を満たしていることが分かります。
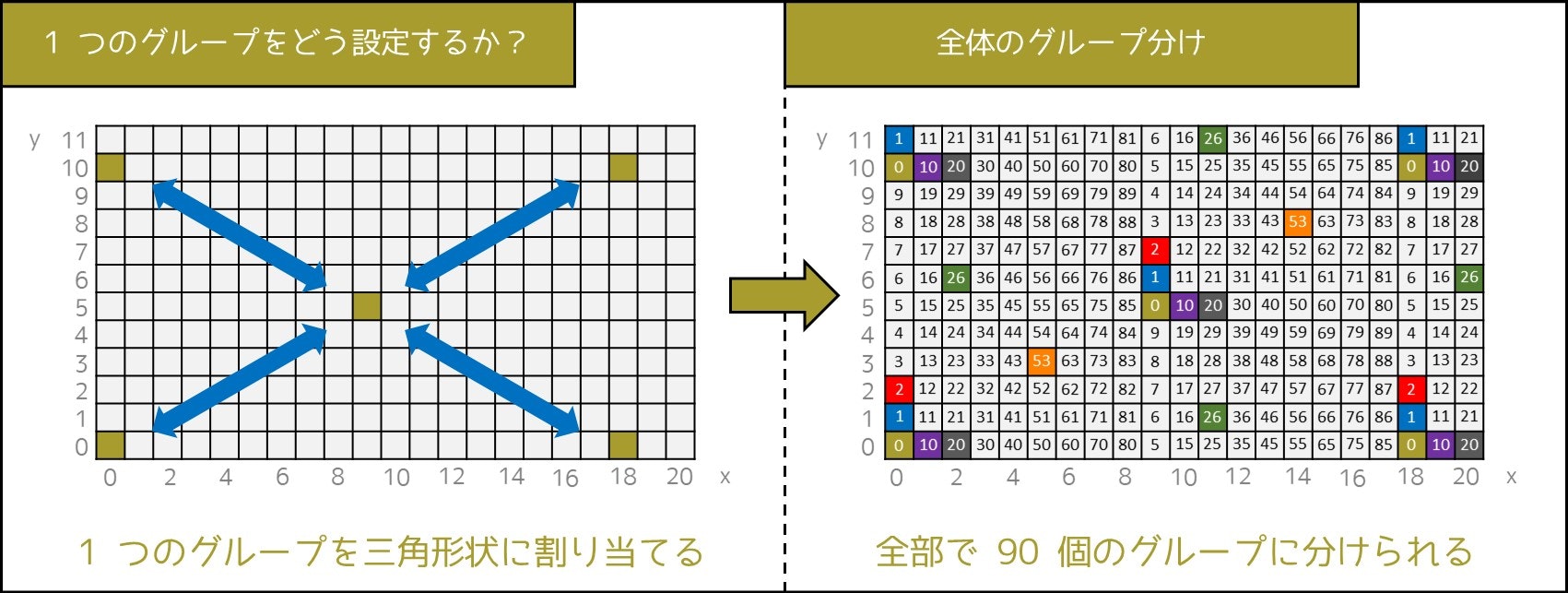
厳密に述べると、以下のようなアルゴリズムを使うことで、$N \div 90$ 個以上の席を残せます。
座席を $90$ 個のグループに分け、$0, 1, \cdots, 89$ と番号を付ける。
座標 $(X_i, Y_i)$ にある席は、次の規則によってグループが決められる。規則
$0 \leq (X_i \bmod 18) < 9$ のとき:グループ $10 \times (X_i \bmod 9) + (Y_i \bmod 10)$
$9 \leq (X_i \bmod 18) < 18$ のとき:グループ $10 \times (X_i \bmod 9) + ((Y_i + 5) \bmod 10)$最後に、$90$ 個のグループの中で最も大きいものを選び、そのグループに属する座席のみを残す。
このように、現実的な実行時間で最適解を出すのが不可能とされる「NP 困難」に分類される問題でも、アルゴリズムの改善によって、より良い近似解を出せる場合もあるのです。
7-5. サンプルコード
7-4. 節で述べた手法は、例えば次のように実装することができます。
# include <iostream>
# include <vector>
using namespace std;
int N, X[1 << 18], Y[1 << 18];
vector<int> group[90];
int main() {
cin >> N;
for (int i = 1; i <= N; i++) {
cin >> X[i] >> Y[i];
if (X[i] % 18 < 9) group[10 * (X[i] % 9) + (Y[i] % 10)].push_back(i);
else group[10 * (X[i] % 9) + ((Y[i] + 5) % 10)].push_back(i);
}
int maxn = 0, maxid = 0;
for (int i = 0; i < 90; i++) {
if (maxn < (int)group[i].size()) { maxn = group[i].size(); maxid = i; }
}
cout << "Number of seats = " << maxn << endl;
for (int i = 0; i < maxn; i++) { if (i) cout << " "; cout << group[maxid][i]; }
cout << endl;
return 0;
}
7-6. <参考>鳩ノ巣原理について
最後に、関連する話題として「鳩ノ巣原理11」を紹介して、本記事を締めたいと思います。
まず、鳩ノ巣原理とは、以下のような定理です。
$M$ 個の箱に $M+1$ 個のモノを入れると、必ず 2 個以上のモノが入る箱が存在する。
それを使うと、例えば「5 人いれば同じ血液型の人が必ずいる」「367 人いれば同じ誕生日の人が必ずいる」ことなどが証明できます。

また、それを拡張させると、次のことも正しいといえます。($\lceil x \rceil$ のような記号についてはこちらをご覧ください)
$M$ 個の箱に $N$ 個のモノを入れると、必ず $\lceil N \div M \rceil$ 個以上のモノが入る箱が存在する。
このような「鳩ノ巣原理の拡張」を使うと、例えば
- $N$ 個の座席を 100 個のグループに分けると、必ず $\lceil N \div 100 \rceil$ 個以上の座席からなるグループが、少なくとも 1 つ存在する(7-2. 節)
- $N$ 個の座席を 90 個のグループに分けると、必ず $\lceil N \div 90 \rceil$ 個以上の座席からなるグループが、少なくとも 1 つ存在する(7-4. 節)
といったことも、楽に証明できるのです。
8. おわりに
今回の記事では、ソーシャルディスタンスと食堂の席数を両立させる問題について扱いました。3-1. 節で紹介した「全探索アルゴリズム」では、N=40 程度の比較的小さいデータでも、答えを出すために相当な時間が必要でしたが、座席数が多くても、
- 3 章で紹介した貪欲法を使うことで、カウンター席(1 次元)の場合に対応する
- 5 章で紹介した二部マッチングを使うことで、2 次元の場合に対応する
- 7 章で紹介した鳩ノ巣原理を使うことで、制限距離が長いケースにも対応する
ことができました。
このように、社会にあふれている問題や、実生活でふと考えたことのあるような問題も、アルゴリズムの改善によって解決できることがあるのです。このような理由で、アルゴリズムを学んでいくことは大切だと私は考えています。
本記事によって、「アルゴリズムって面白い!」と感じる人が増え、一人でも多くの方の役に立つことができれば、とても嬉しい気持ちです。
最後に、これは大学 1 年生が書いた記事なので、文章の分かりにくい部分があったかと思いますが、最後までお読みいただきありがとうございました。
9. 次回予告・参考資料
「実生活に学ぶアルゴリズム」最終回は、第 1・2 回よりもさらに身近な話題について触れたいと思います。2021 年 5 月 19 日公開予定ですので、楽しみにお待ちください。
なお、これが私にとって 2021 年最後の Qiita 記事となるので、次回記事ではアルゴリズムの面白さ、そしてアルゴリズムを学ぶ意義についても熱く語りたいと思います。
また、本記事で扱ったトピックと似た問題がプログラミングコンテストに出題されていますので、こちらも是非解いてみてください。
- JOIG 2021 D - 展覧会 2
- SoundHound Inc. Programming Contest 2018(春)C - 広告
- yukicoder No.1121 - Social Distancing in Cinema
追記(2021/5/19)
最終回記事を公開しました!!!
-
筆者自身も、Google Map のナビゲーションと最短経路問題が繋がったときは感動し、アルゴリズムを本格的に勉強する 1 つのきっかけとなりました。これは今でも鮮明に覚えています。 ↩
-
宇宙の年齢である $138$ 億年 $\fallingdotseq 4 \times 10^17$ 秒をかけても、$10^{26}$ 回程度しか計算を行えません。$2^{100} \fallingdotseq 10^{30}$ 回はそれより大きいと考えると、相当な時間が必要だと分かります。 ↩
-
「次の 1 手だけを考えたときに最善な選択」をし続けることによって、良い解を得る方法のことを指します。他の具体例としては、オセロで「次の手で得られるスコア」を最大にする選択を繰り返すような感じです。 ↩
-
$K \leq |opt_{r+1}-opt_r| \leq |opt_{r+1}-g_r|$ であるためです。 ↩
-
貪欲法の各ステップでは「直前に選んだ席の右側にあり、距離 $K$ 以上離れているもの」=「選べるもの」の中で最も左のものが選ばれます。(詳しくは 3-2. 節 参照) ↩
-
座標 $(x, y)$ に対して、座標 $(x+1, y), (x-1, y), (x, y+1), (x, y-1)$ のことを指します。 ↩
-
一見 $O(N^2)$ 辺だと思われがちですが、座標 $(x, y)$ から 1.4m 未満の位置にある座席は $(x, y+1), (x, y-1), (x+1, y), (x-1, y)$ の 4 つしかないので、高々 $4N$ 辺であることが証明できます。実際は、各辺が 2 度数えられているので $2N$ 辺以内です。 ↩
-
多項式時間($O(N^2)$ や $O(N^3)$ など)で解くアルゴリズムが存在しないとされている問題のグループ。詳しくはこちらの記事を参照。 ↩
-
$N$ 頂点 $N-1$ 辺の連結なグラフのことを指します。他にも「閉路が存在しない」「二部グラフである」などの特徴があります。 ↩
-
競技プログラミングでも頻出で、例えば ABC100D - Happy Birthday!・JSC2019FINAL_A - Equal Weight・AtCoder Beginner Contest 200 D - Happy Birthday! 2などの問題は、鳩ノ巣原理により解くことができます。 ↩