こんにちは、大学 1 年になったばかりの E869120 です。
私は競技プログラミングが趣味で、AtCoder や日本情報オリンピックなどに出場しています。ちなみに、2021 年 5 月 9 日現在、AtCoder では赤（レッドコーダー）です。

本記事では、アルゴリズムが実生活と結びつくトピックについて紹介したいと思います。

【シリーズ】

1. はじめに

21 世紀となった今、世の中には様々な問題があふれていて、そのうちいくつかは皆さんの生活の中で考えたことがあると思います。例えば、

どのような経路を選べば、駅から学校まで最短ルートで行けるか？
どのような買い物をすれば、500 円以内で嬉しさが最大になるか？
どのように株の投資をすれば、1 年後の利益が最大になるか？
これからどんな勉強をすれば、1 週間後のテストの点数の期待値が最大になるか？

などは、読者の大半が人生で一度は悩んだことがある問題だと思います。

その中には「解けない問題」もたくさんあります。仮に全部の問題が解けてしまったら、世界に悩みの種は完全に消えてしまい、現実と矛盾してしまうので当然です。

しかし世の中には、一見解けないように感じても、「アルゴリズム（計算の手順）の効率化」によって解くことができる問題がたくさんあるのです。実際、アルゴリズムを学習していくと、

1 つ目の問題はダイクストラ法
2 つ目の問題は動的計画法
4 つ目の問題は貪欲法アルゴリズム

を使って解けるのだ、ということが徐々に分かってきます。

このように、「生活で悩んでいた問題の解決策が分かる」といった体験をすると、

これまで僕が考えていた問題は、こういうアルゴリズムを使えば解けるのか！！！
実社会のああいう場面にアルゴリズムが使われていたのね、面白い！！！

と感動することがあるかもしれません。実際、私も Google Maps のナビゲーションと最短経路問題が繋がったときは感動し、アルゴリズムを本格的に勉強する 1 つのきっかけになったことは、今でも鮮明に覚えています。

そこで本シリーズでは、アルゴリズムと実生活が関わるトピックをいくつか紹介し、皆さんにアルゴリズムの本当の面白さを体感してもらうことを最大の目標にします。

3 記事にわたる連載を予定していますが、各記事で独立したトピックを扱うオムニバス形式であるため、それぞれの内容を楽しめる構成となっています。また、基本的な内容・発展的な内容両方を扱うため、アルゴリズム初心者から競プロ経験者まで、幅広い層にとって面白いと思います。皆さん是非お読みください。¹

なお、読者によっては知らないアルゴリズムが出てくることもありますが、必要となるアルゴリズムの解説も本記事に記していますので、ご安心ください。

2. 第 1 回で扱う問題

まず、次の問題を考えてみましょう。これはナップザック問題と呼ばれる有名問題であり、一度は買い物中にふと思ったことのある方もいるかもしれません。

コンビニには $N$ 個の商品があり、あなたはカロリーと値段の表を見ることができます。（$i \ [1 \leq i \leq N]$ 番目の商品は $V_i$ kcal であり、値段は $W_i$ 円です。）
同じ商品をたくさん買うと飽きるので、$1$ つの商品は $1$ 個までしか買えません。$500$ 円以内の買い物で、最大何 kcal を得ることができますか。（また、どのような買い方が最適ですか？）

そこで、いきなり現実のコンビニの場合を解くのは難しいので、本記事では、

N=3 の場合のアルゴリズム（商品が 3 個しかない）
N=5 の場合のアルゴリズム（商品が 5 個しかない）
N=20 の場合のアルゴリズム（商品が 20 個しかない）
N=46 の場合のアルゴリズム（実際のセブンイレブン）

といった順序で解説します。記事の後半では、さらに良い買い物計画を実現させるアルゴリズムについても記したいと思います。

章	タイトル	備考
1.	はじめに
2.	第 1 回で扱う問題
3.	レベル A｜小型のコンビニの場合	ここからサポートします
4.	レベル B｜現実のコンビニの場合	本記事のメインです
5.	レベル C｜さらに食事の質を上げる	発展的なトピックです
6.	まとめ
7.	次回予告・関連資料

3. レベル A｜小型のコンビニの場合

まず、コンビニにある商品の数が非常に少ない場合を考えてみましょう。本章では、

の順に解説していきたいと思います。

3-1. N = 3 の場合

コンビニには 3 つの商品しかありません。つまり、例えば次の問題を解くことになります。

少し考えてみると、買い物の仕方は以下の 8 通りしか存在しないことが分かると思います。

買い方	合計 kcal の式	合計値段 (円) の式	kcal	値段
何も買わない	$0$	$0$	0	0
「りんご」のみを買う	$V_1$	$W_1$	80	260
「みかん」のみを買う	$V_2$	$W_2$	40	120
「りんご」「みかん」を買う	$V_1 + V_2$	$W_1 + W_2$	120	380
「ぶどう」のみを買う	$V_3$	$W_3$	100	230
「りんご」「ぶどう」を買う	$V_1 + V_3$	$W_1 + W_3$	180	490
「みかん」「ぶどう」を買う	$V_2 + V_3$	$W_2 + W_3$	140	350
全部を買う	$V_1 + V_2 + V_3$	$W_1 + W_2 + W_3$	220	610 (アウト)

そこで、以下のように 7 個の条件分岐を書くことで、簡単に解けます。例えば、

という入力をすると「180」という出力が得られ、最適解が 180 kcal（りんごとぶどうを買う場合）であることが簡単に分かります。他の入力でも是非試してみましょう。

#include <iostream>
#include <algorithm>
using namespace std;

int main() {
    int N, V[4], W[4], Answer = 0;
    cin >> N;
    for (int i = 1; i <= N; i++) cin >> V[i] >> W[i];

    if (W[1] <= 500) Answer = max(Answer, V[1]);
    if (W[2] <= 500) Answer = max(Answer, V[2]);
    if (W[1] + W[2] <= 500) Answer = max(Answer, V[1] + V[2]);
    if (W[3] <= 500) Answer = max(Answer, V[3]);
    if (W[1] + W[3] <= 500) Answer = max(Answer, V[1] + V[3]);
    if (W[2] + W[3] <= 500) Answer = max(Answer, V[2] + V[3]);
    if (W[1] + W[2] + W[3] <= 500) Answer = max(Answer, V[1] + V[2] + V[3]);
    cout << Answer << endl;
    return 0;
}

3-2. N = 5 の場合

今度は、コンビニにある商品の数が 5 個に増えました。

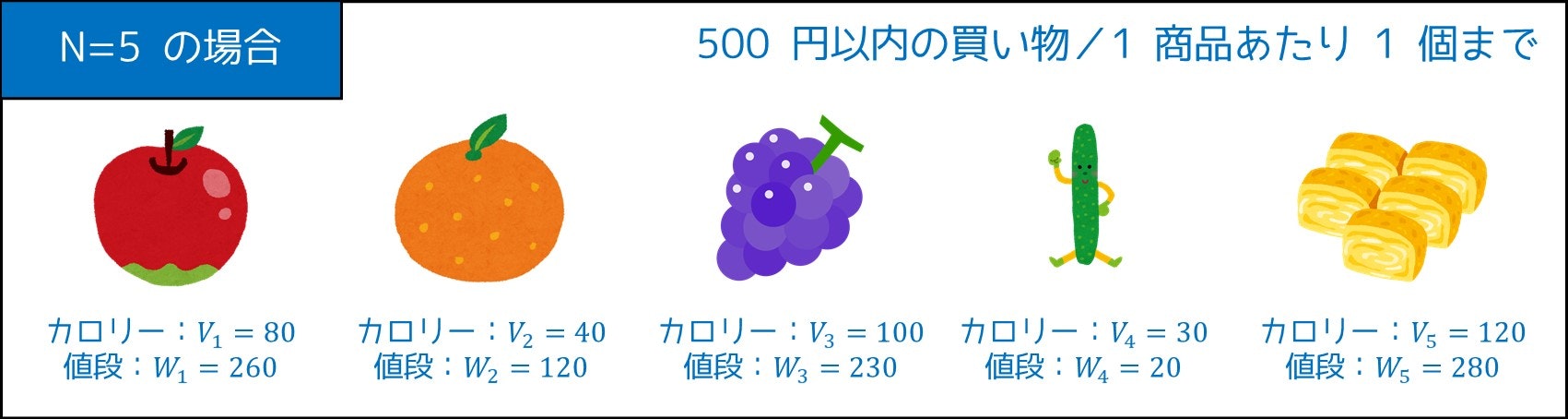
この場合、何通りの「商品の選び方」があるのでしょうか。

商品 1（りんご）の状態は、選ぶか選ばないかの $2$ 通り
商品 2（みかん）の状態は、選ぶか選ばないかの $2$ 通り
商品 3（ぶどう）の状態は、選ぶか選ばないかの $2$ 通り
商品 4（きゅうり）の状態は、選ぶか選ばないかの $2$ 通り
商品 5（玉子焼き）の状態は、選ぶか選ばないかの $2$ 通り

であるため、選び方の数は $2 \times 2 \times 2 \times 2 \times 2 = 2^5 = 32$ 通りです。考えるべき場合の数が少し多いですが、家庭用コンピュータの計算速度は 1 秒当たり $10^8 \sim 10^9$ 回程度なので、一瞬のうちにプログラムの実行が終わってしまいます。（補足：$2^5$ のような表記はべき乗といいます。）

そこで、頑張って 32 通り全部調べ上げると、上の画像の例であれば、

みかん・きゅうり・玉子焼きの $3$ つを選ぶ。
合計値段 $120 + 20 + 280 = 420$ 円、合計カロリー $40 + 30 + 120 = 190$ kcal

が最適であると分かります。$500$ 円以内で $191$ kcal 以上にする方法はありません。

しかし、3-1. 節のように全パターンを列挙し、それぞれ if 文を使って調べ上げると以下のようなプログラムになり、実装が無駄に長くなってしまいます。$N=5$ であればギリギリ書けますが、$N = 6, 7, 8, \cdots$ と増えていけばプログラムを書く気力もなくなると思います。

#include <iostream>
#include <algorithm>
using namespace std;

int main() {
    int N, V[6], W[6], Answer = 0;
    cin >> N;
    for (int i = 1; i <= N; i++) cin >> V[i] >> W[i];

    if (W[1] <= 500) Answer = max(Answer, V[1]);
    if (W[2] <= 500) Answer = max(Answer, V[2]);
    if (W[1] + W[2] <= 500) Answer = max(Answer, V[1] + V[2]);
    if (W[3] <= 500) Answer = max(Answer, V[3]);
    if (W[1] + W[3] <= 500) Answer = max(Answer, V[1] + V[3]);
    if (W[2] + W[3] <= 500) Answer = max(Answer, V[2] + V[3]);
    if (W[1] + W[2] + W[3] <= 500) Answer = max(Answer, V[1] + V[2] + V[3]);
    if (W[1] + W[4] <= 500) Answer = max(Answer, V[1] + V[4]);
    if (W[2] + W[4] <= 500) Answer = max(Answer, V[2] + V[4]);
    if (W[1] + W[2] + W[4] <= 500) Answer = max(Answer, V[1] + V[2] + V[4]);
    if (W[3] + W[4] <= 500) Answer = max(Answer, V[3] + V[4]);
    if (W[1] + W[3] + W[4] <= 500) Answer = max(Answer, V[1] + V[3] + V[4]);
    if (W[2] + W[3] + W[4] <= 500) Answer = max(Answer, V[2] + V[3] + V[4]);
    if (W[1] + W[2] + W[3] + W[4] <= 500) Answer = max(Answer, V[1] + V[2] + V[3] + V[4]);
    if (W[1] + W[5] <= 500) Answer = max(Answer, V[1] + V[5]);
    if (W[2] + W[5] <= 500) Answer = max(Answer, V[2] + V[5]);
    if (W[1] + W[2] + W[5] <= 500) Answer = max(Answer, V[1] + V[2] + V[5]);
    if (W[3] + W[5] <= 500) Answer = max(Answer, V[3] + V[5]);
    if (W[1] + W[3] + W[5] <= 500) Answer = max(Answer, V[1] + V[3] + V[5]);
    if (W[2] + W[3] + W[5] <= 500) Answer = max(Answer, V[2] + V[3] + V[5]);
    if (W[1] + W[2] + W[3] + W[5] <= 500) Answer = max(Answer, V[1] + V[2] + V[3] + V[5]);
    if (W[1] + W[4] + W[5] <= 500) Answer = max(Answer, V[1] + V[4] + V[5]);
    if (W[2] + W[4] + W[5] <= 500) Answer = max(Answer, V[2] + V[4] + V[5]);
    if (W[1] + W[2] + W[4] + W[5] <= 500) Answer = max(Answer, V[1] + V[2] + V[4] + V[5]);
    if (W[3] + W[4] + W[5] <= 500) Answer = max(Answer, V[3] + V[4] + V[5]);
    if (W[1] + W[3] + W[4] + W[5] <= 500) Answer = max(Answer, V[1] + V[3] + V[4] + V[5]);
    if (W[2] + W[3] + W[4] + W[5] <= 500) Answer = max(Answer, V[2] + V[3] + V[4] + V[5]);
    if (W[1] + W[2] + W[3] + W[4] + W[5] <= 500) Answer = max(Answer, V[1] + V[2] + V[3] + V[4] + V[5]);
    cout << Answer << endl;
    return 0;
}

3-3. N = 20 の場合

そこで、さらに $N$ の数が増えてしまった場合は、どう実装すれば良いのでしょうか。3-1. 節や 3-2. 節のサンプルコードのように全パターンそれぞれ条件分岐を書くのではなく、for 文などのループを使って効率的に処理する方法はないのでしょうか。1 つのアイデアとして、

2 進数を使って、各状態を 1 つの整数で表す

という方法が考えられます。まずはこのアイデアを説明した GIF 画像をご覧ください。

もう少し詳しく説明しましょう。$X = 0, 1, 2, \cdots, 2^N-1$ とループを回して、

整数 $X$ の下から $i \ (1 \leq i \leq N)$ 桁目が 1 のとき商品 $i$ を選び、0 のとき選ばない

とすると、なんと $2^N$ 通り全部の選び方を調べ上げることができているのです。例えば $N = 3$ の場合、次のようになります。

$X = 0$：$2$ 進数は $000$ で、1 である桁は存在しない。よってどれも選ばない。
$X = 1$：$2$ 進数は $001$ で、下から 1 桁目が 1 である。よって商品 1 を選ぶ。
$X = 2$：$2$ 進数は $010$ で、下から 2 桁目が 1 である。よって商品 2 を選ぶ。
$X = 3$：$2$ 進数は $011$ で、下から 1, 2 桁目が 1 である。よって商品 1, 2 を選ぶ。
$X = 4$：$2$ 進数は $100$ で、下から 3 桁目が 1 である。よって商品 3 を選ぶ。
$X = 5$：$2$ 進数は $101$ で、下から 1, 3 桁目が 1 である。よって商品 1, 3 を選ぶ。
$X = 6$：$2$ 進数は $110$ で、下から 2, 3 桁目が 1 である。よって商品 2, 3 を選ぶ。
$X = 7$：$2$ 進数は $111$ で、下から 1, 2, 3 桁目が 1 である。よって商品 1, 2, 3 を選ぶ。

このように、for 文ループを回すだけで、全通り調べ上げることができます。このようなアルゴリズムを bit 全探索といいます。実装例は次の通りです。（なお、& などのビット演算についてはこちらの記事をご覧ください）

#include <iostream>
#include <algorithm>
using namespace std;

int main() {
    // Step #1. 入力
    int N, V[53], W[53], Answer = 0;
    cin >> N;
    for (int i = 1; i <= N; i++) cin >> V[i] >> W[i];

    // Step #2. 全探索 [(1LL << N) は 2^N という意味です]
    for (long long X = 0; X < (1LL << N); X++) {
        // 整数 X を 2 進数に変換
        int bit[53];
        for (int j = 0; j < N; j++) {
            if ((X & (1LL << j)) == 0) bit[j] = 0;
            if ((X & (1LL << j)) != 0) bit[j] = 1;
        }

        // 合計値段と合計カロリーを求める
        int total_calories = 0;
        int total_money = 0;
        for (int j = 0; j < N; j++) {
            if (bit[j] == 1) {
                total_calories += V[j + 1];
                total_money += W[j + 1];
            }
        }
        if (total_money <= 500) {
            Answer = max(Answer, total_calories);
        }
    }

    // Step #3. 出力
    cout << Answer << endl;
    return 0;
}

最後に、計算回数はどの程度なのでしょうか。

1 重目（$X$）のループは $0 \sim (2^N-1)$ の範囲を、つまり $2^N$ 個の値をとる
2 重目（$j$）のループは $0 \sim (N-1)$ の範囲を、つまり $N$ 個の値をとる

ことから、ざっくり見積もって $2^N \times N$ 回程度の計算をしていることになり、計算量 $O(2^N \times N)$ と表すことができます²。なお、計算量オーダーについて詳しく知りたい方は、

Qiita｜計算量オーダーの求め方を総整理！〜どこから log が出て来るか〜

をご覧ください。

ここまで、全通り調べ上げる解法とその実装について紹介しました。全探索アルゴリズムでも、$N=20$ の場合は計算回数が $2^{20} \times 20 \fallingdotseq 2.1 \times 10^7$ 程度となり、家庭用コンピューターの計算速度が 1 秒当たり $10^8 \sim 10^9$ 回程度であることを考慮すると、「一瞬で答えが出る」ことが分かります。

では、この解法は現実のコンビニ買い物でも通用するのでしょうか。是非、引き続きお読みください。

4. レベル B｜現実のコンビニの場合

次に、本記事のメインテーマである問い「現実のコンビニではどのような買い方が最適であるか？」について考えていきたいと思います。一体どんな買い方をすると、$500$ 円以内で最も多くのカロリーを得ることができるのでしょうか。本章では、

の順に解説していきたいと思います。

4-1. 本章で扱うデータ

まず、コンビニには「Family Mart」「LAWSON」「Mini Stop」など色々ありますが、今回は日本で最も店舗数が多いセブンイレブンを考えます。つまり次の問題を解くということです。

セブンイレブンで $500$ 円以内の買い物をするとき、最大で何 kcal を得ることができるか？

そこで、セブンイレブンの商品データは、こちらのリンクによると、以下の通りです。³

商品 01｜151 円、188 kcal、おにぎり（紅しゃけ）
商品 02｜124 円、238 kcal、おにぎり（ツナマヨネーズ）
商品 03｜151 円、173 kcal、おにぎり（辛子明太子）
商品 04｜118 円、179 kcal、おにぎり（日高昆布）
商品 05｜124 円、164 kcal、おにぎり（紀州南高梅）
商品 06｜127 円、179 kcal、北海道男爵いものポテトサラダ105g
商品 07｜127 円、112 kcal、シャキシャキ食感のごぼうサラダ70g
商品 08｜205 円、 97 kcal、セブンイレブン ツナと玉子のサラダ
商品 09｜199 円、 59 kcal、10種具材のミックスサラダ
商品 10｜399 円、237 kcal、海老とブロッコリータルタルサラダ
商品 11｜138 円、293 kcal、コクと旨味のカレーパン
商品 12｜162 円、450 kcal、がっつり食べる！ソーセージドッグ
商品 13｜151 円、252 kcal、もちもちお好み焼きパン
商品 14｜127 円、339 kcal、サックサク食感！バター香るメロンパン
商品 15｜138 円、472 kcal、しっとり濃厚チョコブレッド
商品 16｜237 円、363 kcal、こだわりたまごのサンド
商品 17｜259 円、214 kcal、シャキシャキレタスサンド
商品 18｜270 円、227 kcal、ジューシーハムサンド
商品 19｜257 円、316 kcal、ミックスサンド
商品 20｜399 円、196 kcal、ローストビーフサンド
商品 21｜108 円、319 kcal、ビッグアメリカンドッグ
商品 22｜154 円、323 kcal、BIGポークフランク
商品 23｜108 円、190 kcal、燻製あらびきフランク
商品 24｜198 円、201 kcal、ななチキ
商品 25｜123 円、205 kcal、からあげ棒
商品 26｜464 円、668 kcal、お好み幕ノ内
商品 27｜453 円、634 kcal、たっぷりネギの豚塩カルビ弁当（麦飯）
商品 28｜464 円、601 kcal、焦がし醤油のチャーハン
商品 29｜298 円、413 kcal、鶏の旨味！国産鶏のたっぷり鶏そぼろごはん
商品 30｜321 円、326 kcal、青高菜と明太子の御飯
商品 31｜356 円、338 kcal、コシとのど越しが自慢 ざる蕎麦
商品 32｜486 円、491 kcal、ツルッとさっぱり！夏の冷し中華
商品 33｜399 円、454 kcal、ツルッともっちり！冷したぬきうどん
商品 34｜550 円、500 kcal、香ばし麺の五目あんかけ焼そば
商品 35｜516 円、502 kcal、豚玉＆焼きそば
商品 36｜213 円、 98 kcal、「サラダチキン」プレーン
商品 37｜213 円、114 kcal、「サラダチキン」ハーブ
商品 38｜213 円、115 kcal、「サラダチキン」スモーク
商品 39｜ 90 円、  5 kcal、「おでん」昆布巻
商品 40｜ 85 円、  9 kcal、「おでん」味しみ大根
商品 41｜ 84 円、 85 kcal、「おでん」こだわりたまご
商品 42｜ 75 円、  7 kcal、「おでん」つゆだく白滝
商品 43｜ 75 円、  9 kcal、「おでん」味しみこんにゃく
商品 44｜105 円、  0 kcal、寒天ゼリーカロリー0 ぶどう味
商品 45｜213 円、103 kcal、たまごの風味豊かな直火焼プリン 4個入
商品 46｜151 円、140 kcal、くちどけなめらか杏仁豆腐

なんと商品数が $N = 46$ と多いですね！！！

果たして 3-3. 節で紹介した bit 全探索による解法（計算量 $O(2^N \times N)$）では、現実的な時間で実行が終わるのでしょうか。検証してみましょう。

4-2. 全探索で解こうとすると？　～指数関数の恐ろしさ～

まず、計算回数 $2^N \times N$ の値とサンプルコードの実行時間は、次表の通りになります。⁴

N の値	2^N × N の値	実行時間
20	20 971 520	0.121 秒
22	92 274 688	0.518 秒
24	402 653 184	2.118 秒
26	1 744 830 464	8.907 秒
28	7 516 192 768	37.103 秒
30	32 212 254 720	153.604 秒
34	584 115 552 256	300 秒以上（理論上は約 50 分）
38	10 445 360 463 872	300 秒以上（理論上は約 14 時間）
42	184 717 953 466 368	300 秒以上（理論上は約 10 日間）
46	3 236 962 232 172 544	300 秒以上（理論上は約 160 日間）

このように、現実のセブンイレブンの場合、全探索で最適解を出すためには半年もの歳月が必要であり、全く現実的ではありません⁵。$2^x, 3^x$ など指数関数の恐ろしさがよく分かりますね。

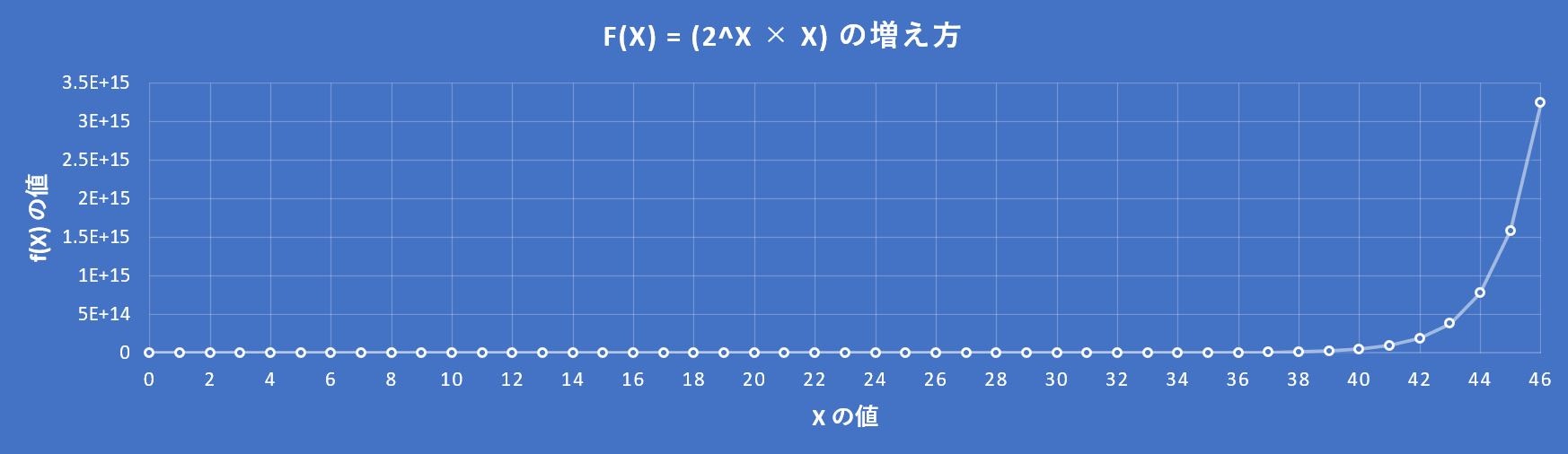
では、一体どうすればいいのでしょうか。
そこで登場するのが、動的計画法（DP）です。

4-3. 動的計画法とは何か？　～導入編～

「いきなりセブンイレブンの問題に…」と言いたいところなのですが、まずは動的計画法に慣れるために、最初はもっと簡単な問題を考えてみましょう。

$N$ 段の階段があります。あなたは一歩で $1$ 段か $2$ 段昇ることができます。
昇るのにかかる時間は次の通りです。下から上まで昇るには最小何秒必要ですか？
一度に 1 段　$i-1$ 段目から $i$ 段目に行くには $a_i$ 秒必要。$(1 \leq i \leq N)$
一度に 2 段　$i-2$ 段目から $i$ 段目に行くには $b_i$ 秒必要。$(2 \leq i \leq N)$

これは次のような動的計画法（DP）で解くことができます。

ステップ 1. 配列の使い方

以下のような配列 $\rm{dp[0], dp[1], \cdots, dp[N]}$ を用意することを考えます。
そこで、求める値は $\rm{dp[N]}$ です。

$\rm{dp[0]}$：$0$ 段目（一番下）にたどり着くために必要な最小秒数（明らかに $\rm{dp[0] = 0}$）
$\rm{dp[1]}$：$1$ 段目にたどり着くために必要な最小秒数
$\rm{dp[2]}$：$2$ 段目にたどり着くために必要な最小秒数
$:$
$\rm{dp[N]}$：$N$ 段目にたどり着くために必要な最小秒数

ステップ 2. 状態遷移

既に $\rm{dp[0], dp[1], dp[2], \cdots, dp[i-1]}$ が求まっていることを前提に $\rm{dp[i]}$ を求めることを考えましょう。$i$ 段目に一歩で昇る方法は、以下の $2$ 通りしかありません。

$i-1$ 段目から $i$ 段目まで一歩で昇る：$\rm{dp[i - 1] + a[i]}$ 秒
$i-2$ 段目から $i$ 段目まで一歩で昇る：$\rm{dp[i - 2] + b[i]}$ 秒

そこで、$\rm{dp[i - 1], dp[i - 2]}$ の値（最小値）は既に求まっているはずなので、$\rm{dp[i]}$ の値は $2$ つの状態遷移のうち小さい方、つまり以下の通りになるのです。

$$
\rm{dp[i] = min(dp[i - 1] + a[i], dp[i - 2] + b[i])} \ [i \geq 2]
$$

ただし、$i = 1$ の場合は 1 段昇る移動しかできないため、$\rm{dp[i] = dp[i - 1] + a[i]}$ となることに注意してください。

ステップ 3. 具体例・サンプルコード

より分かりやすく説明するため、$1$ 個具体例を紹介します。次表の場合を考えてみましょう。

i の値	1	2	3	4	5
a[i] の値	2 秒	4 秒	3 秒	7 秒	5 秒
b[i] の値	-	5 秒	12 秒	9 秒	20 秒

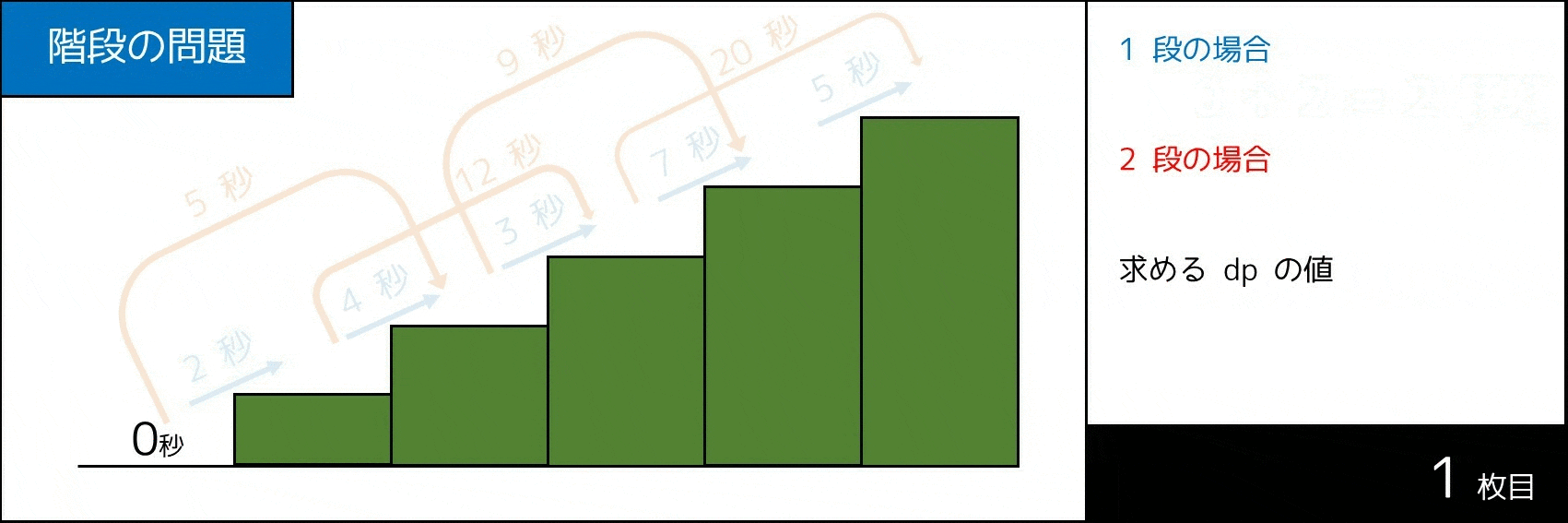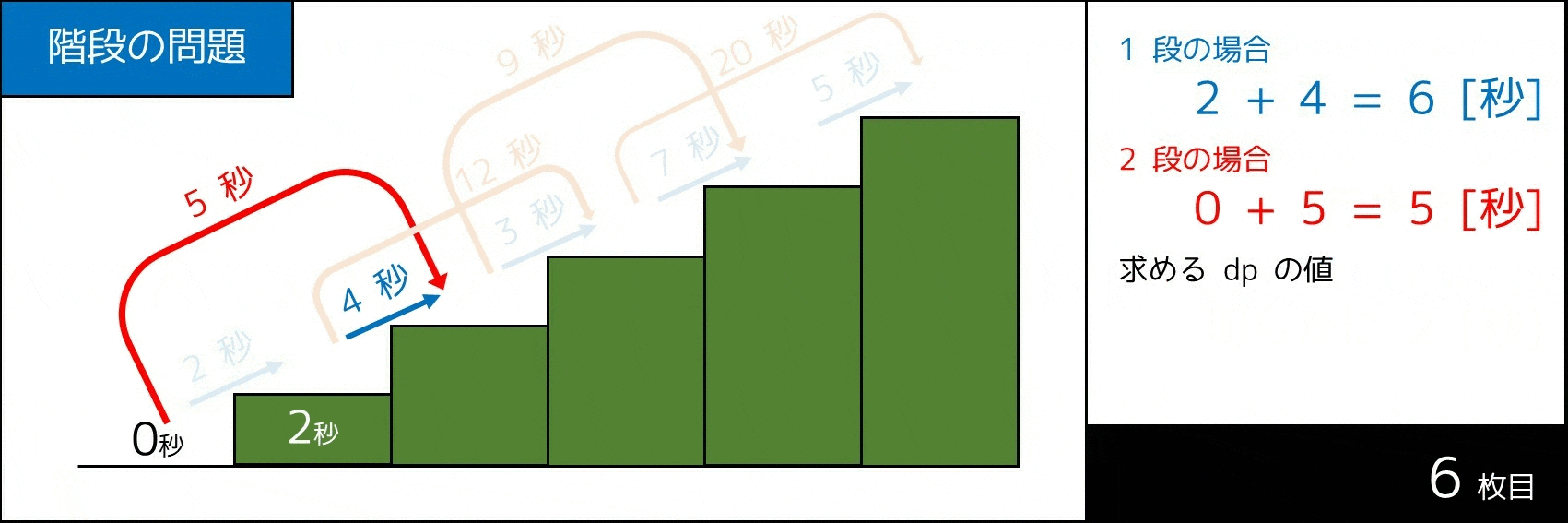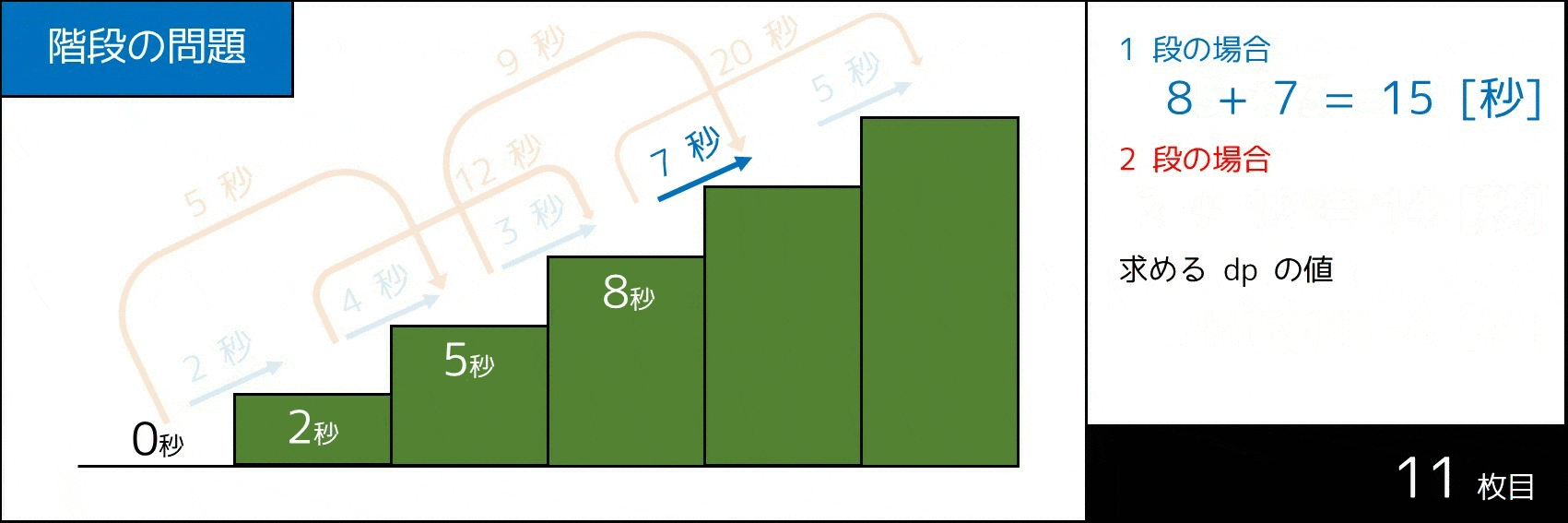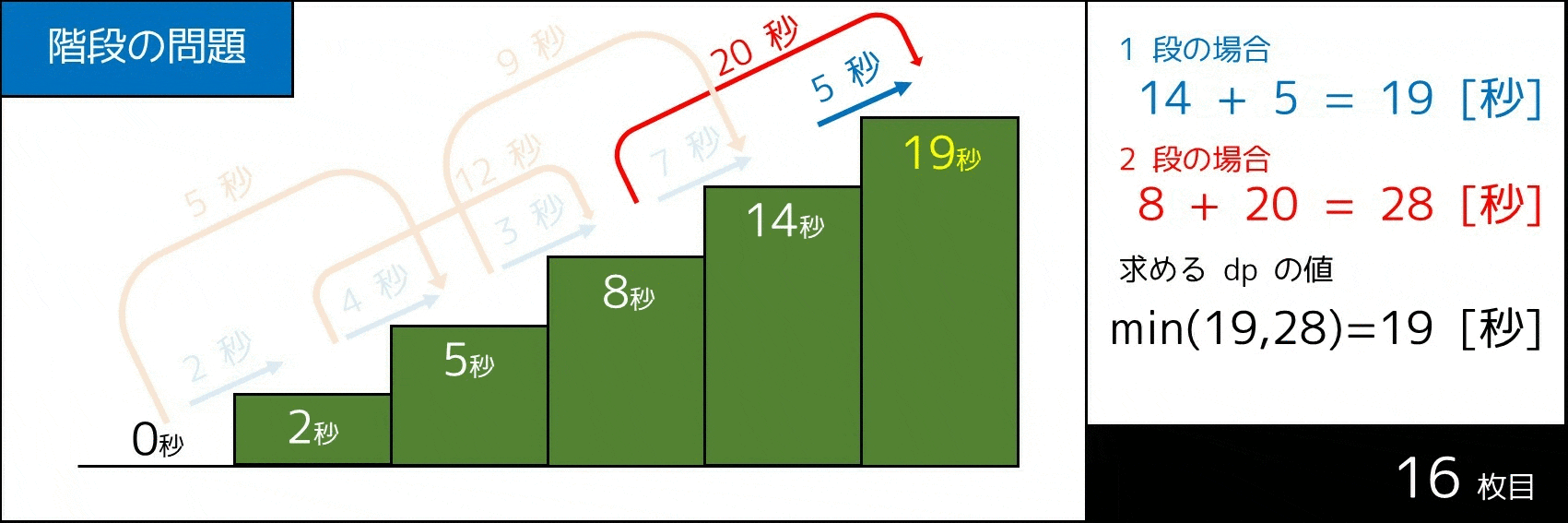
下図のような計算によって、答えが 19 秒であることが分かります。

また、プログラムは以下のように、簡単に実装することができます。

#include <iostream>
#include <algorithm>
using namespace std;

int N, A[100009], B[100009];
int dp[100009];

int main() {
    // Step #1. 入力
    cin >> N;
    for (int i = 1; i <= N; i++) cin >> A[i];
    for (int i = 2; i <= N; i++) cin >> B[i];

    // Step #2. 動的計画法・出力
    dp[0] = 0;
    for (int i = 1; i <= N; i++) {
        if (i == 1) dp[i] = dp[i - 1] + A[i];
        if (i >= 2) dp[i] = min(dp[i - 1] + A[i], dp[i - 2] + B[i]);
    }
    cout << dp[N] << endl;
    return 0;
}

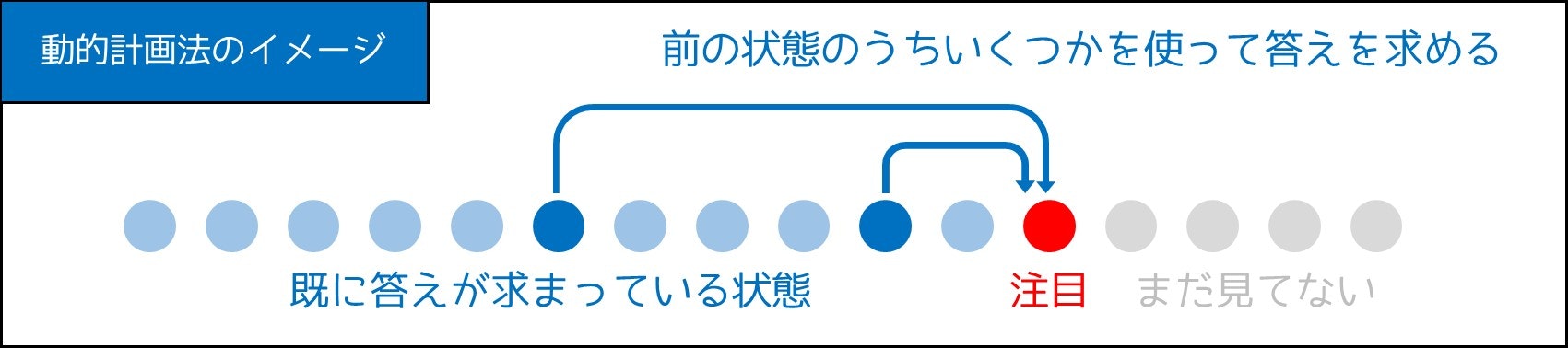
結局動的計画法とは何なのか？

ここまで「階段の問題」について解説していきましたが、動的計画法とは結局何なのでしょうか。次のようなイメージを持つと、分かりやすいと思います。

前の計算結果を利用して、（漸化式または状態遷移の式を立てて）答えを求める。

図で表すと、こんな感じです。動的計画法のイメージは付きましたでしょうか。次節では今度こそ、セブンイレブンの場合の解法を紹介したいと思います。⁶

4-4. 動的計画法でセブンイレブンのカロリー最大値を求める

ここでは便宜上、$N, L, V_i, W_i$ を次のように定義します。

$N$：商品の数（$N = 46$）
$L$：値段合計の上限（$L = 500$）
$V_i$：商品 $i$ のカロリー $(1 \leq i \leq N)$
$W_i$：商品 $i$ の値段 $(1 \leq i \leq N)$

そこで、セブンイレブンで $500$ 円以下の買い物をするときに摂取できるカロリーの最大値を求める問題は、次のようにして解くことができます。

ステップ 1. 配列の使い方

以下のような二次元配列 $\rm{dp[0][0], dp[0][1], \cdots, dp[N][L]}$ を用意することを考えます。
そこで、求める値は $\rm{dp[N][L]}$ です。

$\rm{dp[0][0]}$：商品 $0$ までを考えたときに、$0$ 円以下での買い物におけるカロリー最大値
$\rm{dp[0][1]}$：商品 $0$ までを考えたときに、$1$ 円以下での買い物におけるカロリー最大値
$:$
$\rm{dp[0][L]}$：商品 $0$ までを考えたときに、$L$ 円以下での買い物におけるカロリー最大値
$\rm{dp[1][0]}$：商品 $1$ までを考えたときに、$0$ 円以下での買い物におけるカロリー最大値
$:$
$\rm{dp[i][j]}$：商品 $i$ までを考えたときに、$j$ 円以下での買い物におけるカロリー最大値
$:$
$\rm{dp[N][L]}$：商品 $N$ までを考えたときに、$L$ 円以下での買い物におけるカロリー最大値

そこで、$\rm{dp[0][0], dp[0][1], \cdots, dp[0][L]}$ の値は $0$ となることに注意してください。（商品を全く考えていない状態なので、明らかに $0$ kcal です）

ステップ 2. 状態遷移

既に $\rm{dp[0][0], dp[0][1], \cdots, dp[i-1][L]}$ が求まっていることを前提に $\rm{dp[i][j]}$ を計算することを考えましょう。この状態に到達するための方法は、以下の $2$ 通りしかありません。

商品 $i$ を選ばない：商品 $i-1$ までの合計値段は $j$ 以下でなければならないので、ここまでの合計カロリーは $\rm{dp[i-1][j]}$
商品 $i$ を選ぶ：商品 $i-1$ までの合計値段は $j-W_i$ 以下でなければならないので、ここまでの合計カロリーは $\rm{dp[i-1][j-W_i]} + V_i$ kcal

ここで、$\rm{dp[i-1][j-W_i], dp[i-1][j]}$ の値は既に求まっているはずなので、$\rm{dp[i][j]}$ の値は $2$ つの状態遷移のうち大きい方、つまり以下の通りになるのです。

$$
\rm{dp[i][j] = max(dp[i-1][j-W_i] + V_i, dp[i-1][j])}
$$

ただし、$j < W_i$ の場合に商品 $i$ を選ぶ遷移を行うと、$i-1$ 個目までの値段合計が負になってしまうため、商品 $i$ を選ぶことはできず、$\rm{dp[i][j] = dp[i-1][j]}$ となることに注意してください。

ステップ 3. 具体例とサンプルコード

より分かりやすく説明するため、1 個具体例を紹介します。次の場合を考えてみましょう。（ただし、$500$ 円だとあまりにも大きいので、$L=10$ 円とします）

商品番号	商品 1	商品 2	商品 3	商品 4
カロリー $V_i$	100 kcal	210 kcal	130 kcal	57 kcal
値段 $W_i$	3 円	6 円	4 円	2 円

下図のような計算によって、答えが 340 kcal であることが分かります。

また、プログラムは以下のように、簡単に実装することができます。

#include <iostream>
#include <algorithm>
using namespace std;

int N, L;
int V[1009], W[1009];
int dp[1009][10009];

int main() {
    // Step #1. 入力
    cin >> N >> L;
    for (int i = 1; i <= N; i++) cin >> V[i] >> W[i];

    // Step #2. 動的計画法・出力
    for (int i = 1; i <= N; i++) {
        for (int j = 0; j <= L; j++) {
            if (j < W[i]) {
                dp[i][j] = dp[i - 1][j];
            }
            else {
                dp[i][j] = max(dp[i - 1][j - W[i]] + V[i], dp[i - 1][j]);
            }
        }
    }
    cout << dp[N][L] << endl;
    return 0;
}

ステップ 4. 結果

最後に、セブンイレブンで 500 円以内の買い物をするとき、最大何 kcal 得られるかを実際に求めてみましょう。サンプルコードに、

入力データ 1（セブンイレブンに対応したデータ）

を入力すると、1368 という出力が得られます。つまり、摂取できるカロリーの最大値は 1368 kcal であることが分かりました。成人の 1 食分を大幅に超えていますね！！！

また、$L$ の値を変えると、色々な値段で試すことができます。例えば、100～800 円以内の買い物におけるカロリー最大値は次表の通りです。800 円払えば 2111kcal も食べられるのはすごいですね。

値段	100 円	200 円	300 円	400 円	500 円	600 円	700 円	800 円
カロリー	85kcal	472kcal	922kcal	1130kcal	1368kcal	1584kcal	1903kcal	2111kcal

このように動的計画法（DP）のアルゴリズムを使うことで、摂取できるカロリーの最大値を求めることができました。計算回数はどの程度なのでしょうか。

1 重目（$i$）のループは $1 \sim N$ の範囲を、つまり $N$ 個の値をとる
2 重目（$j$）のループは $0 \sim L$ の範囲を、つまり $L+1$ 個の値をとる

ことから、ざっくり見積もって $N(L+1)$ 回程度の計算をしていることになり、計算量 $O(NL)$ と表すことができます。$N = 46, L = 500$ であるため、本当に一瞬で答えが出ます。

4-5. DP の復元　～どのような買い方が最適か？～

4-4. 節で紹介した動的計画法（DP）のアルゴリズムを使うと、「500 円以内で何 kcal 得られるか？」という疑問を解消できました。しかしそこまで来ると、

どのような買い方が最適なんだろう…

と、新たな疑問が生まれます。
そこで本節では「DP の復元」を用いて解決する方法を紹介します。

ステップ 1. DP の復元アルゴリズム

次のような手順で計算をすると、DP の配列から、最適な買い方を得ることができます。

最初 $x = L = 500$ とする。$i = N, N-1, \cdots, 1$ の順にループを回す。
- 現在見ている状態は $\rm{dp[i][x]}$ である。
- もし商品 $i$ を選ばない場合 $\rm{dp[i][x] = dp[i-1][x]}$ である。
- もし商品 $i$ を選ぶ場合 $\rm{dp[i][x] = dp[i-1][x-W_i] + V_i}$ である。
- 必ずどちらか一方が起こっているので、青・赤いずれかの式は成り立っている。
- そこで、成り立っている方の遷移を選ぶ。つまり、以下のことを行う。
  - $\rm{dp[i][x] = dp[i-1][x]}$ の場合：商品 $i$ を選ばない
  - そうでない場合：商品 $i$ を選び、$x$ に $W_i$ を減算する。

ステップ 2. 具体例

上の説明だけでは分かりにくいと思うので、具体例を 1 つ挙げます。4-4. 節でも述べた以下の例を考えてみましょう。（$L=10$ であることに注意してください）

商品番号	商品 1	商品 2	商品 3	商品 4
カロリー $V_i$	100 kcal	210 kcal	130 kcal	57 kcal
値段 $W_i$	3 円	6 円	4 円	2 円

この場合、最終的な DP の配列は下図の通りになります。

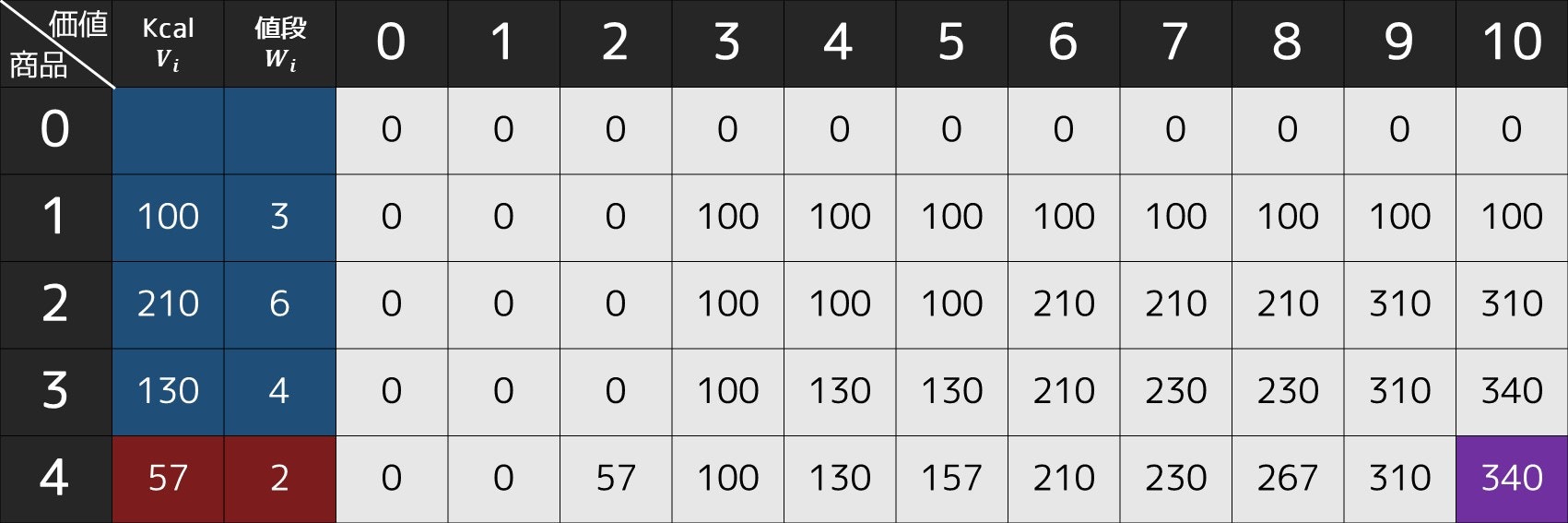
そこで、次のような手順をたどることで、商品 2, 3 を選ぶのが最適だと分かります。

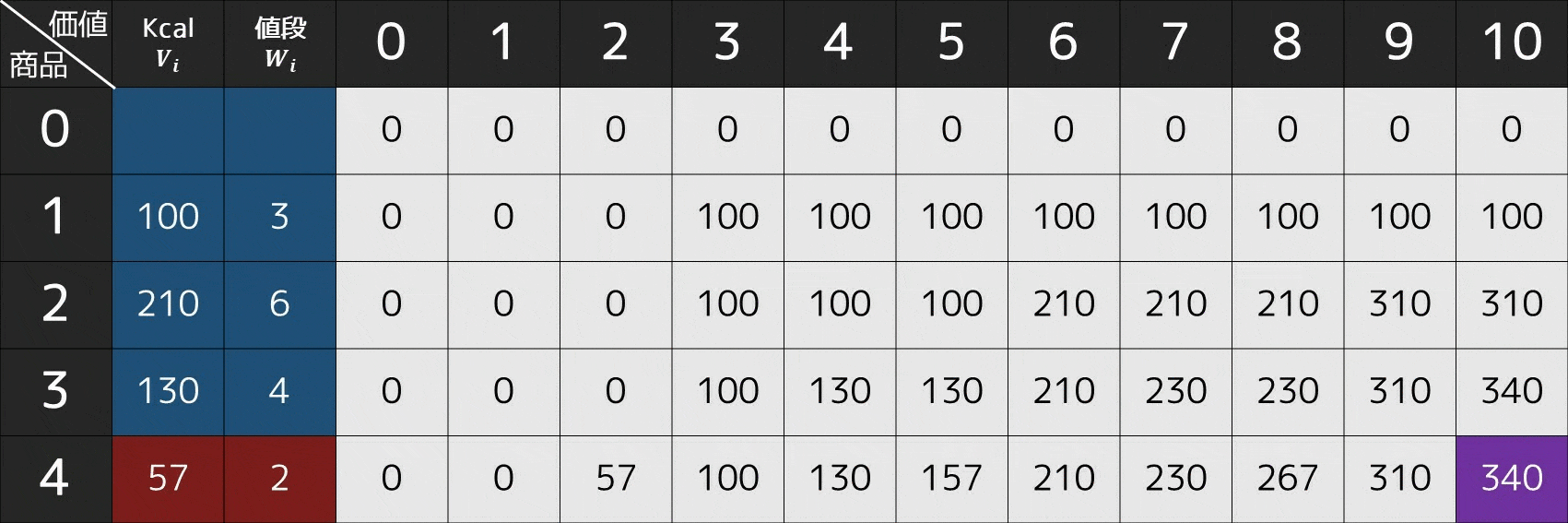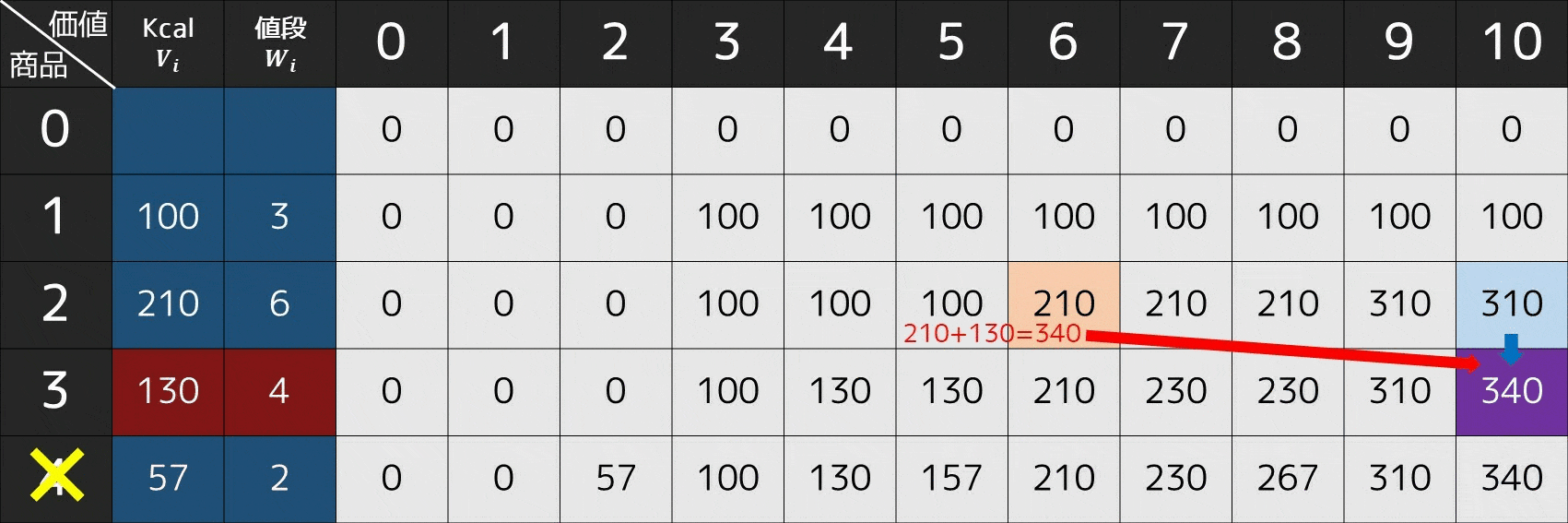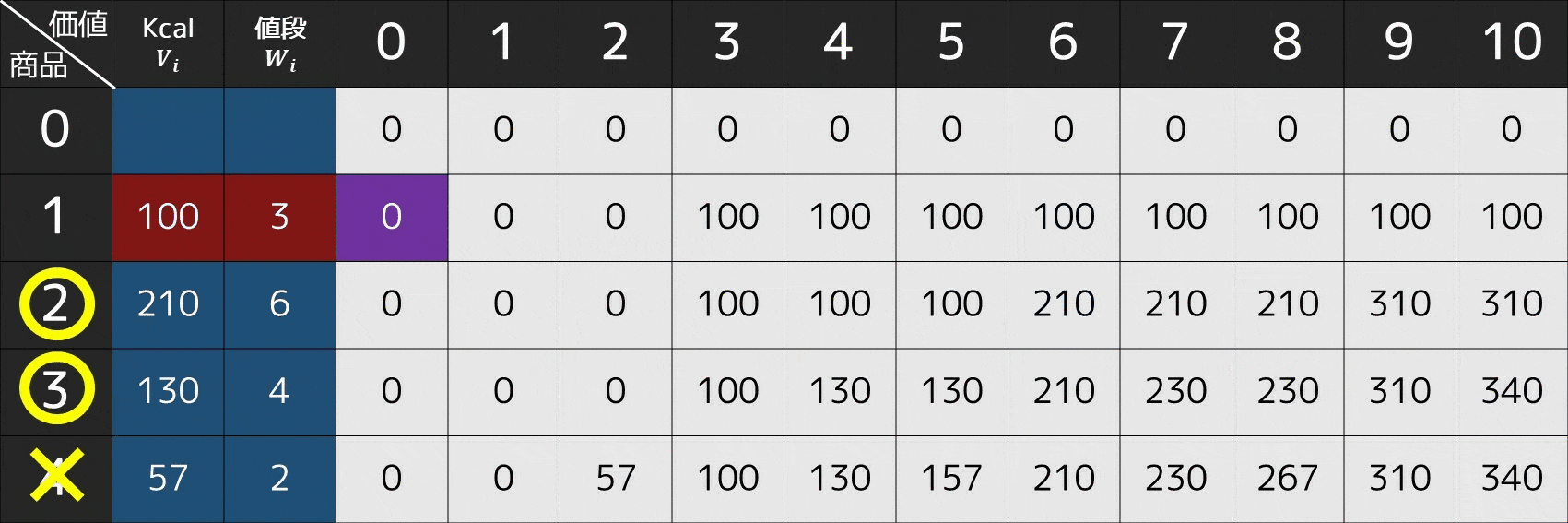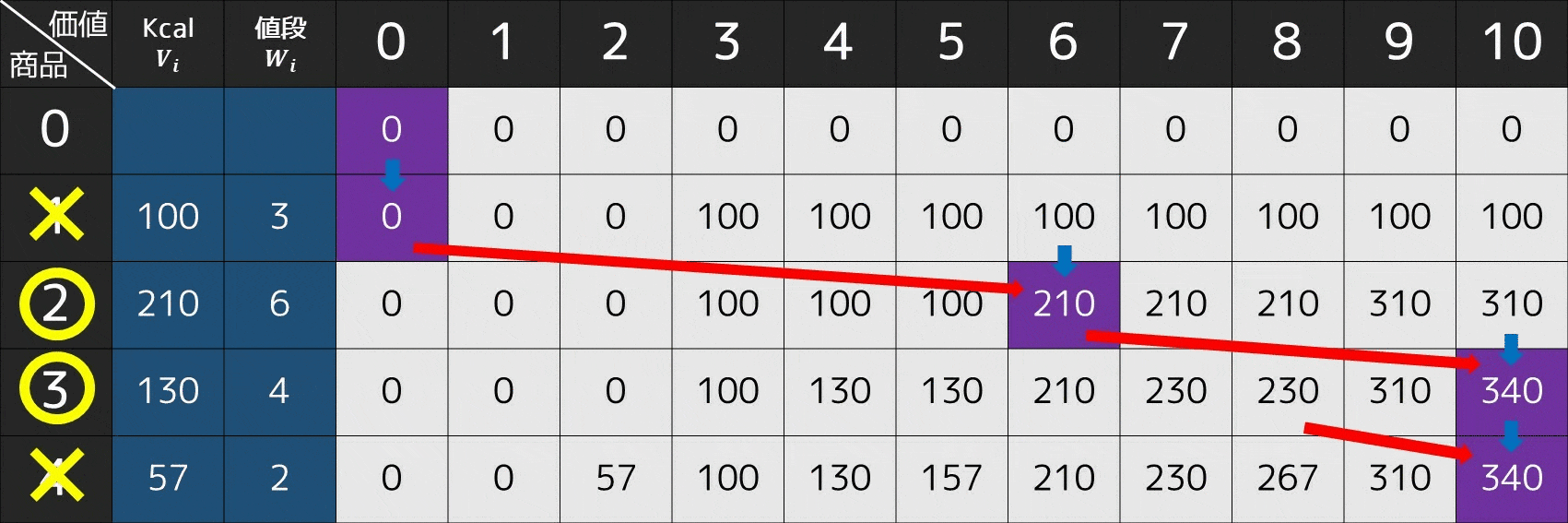
商品 $4$ を選ぶか？（現在 $\rm{x=10}$）
- $\rm{dp[3][x] = dp[3][10] = 340}$
- $\rm{dp[3][x - W_4] + V_4 = dp[3][8] + V_4 = 230 + 57 = 287}$
- 青色が今見ている場所 $\rm{dp[4][10]}=340$ と一致するため、商品 $4$ は選ばない
商品 $3$ を選ぶか？（現在 $\rm{x=10}$）
- $\rm{dp[2][x] = dp[2][10] = 310}$
- $\rm{dp[2][x - W_3] + V_3 = dp[2][6] + V_3 = 210 + 130 = 340}$
- 赤色が今見ている場所 $\rm{dp[3][10]}=340$ と一致するため、商品 $3$ は選ぶ
商品 $2$ を選ぶか？（現在 $\rm{x=6}$）
- $\rm{dp[1][x] = dp[1][6] = 100}$
- $\rm{dp[1][x - W_2] + V_2 = dp[1][0] + V_2 = 0 + 210 = 210}$
- 赤色が今見ている場所 $\rm{dp[2][6]}=210$ と一致するため、商品 $2$ は選ぶ
商品 $1$ を選ぶか？（現在 $\rm{x=0}$）
- $x < W_1$ であるため、商品 $1$ は選べない

手順全体を GIF 画像で表すと、次のような感じになります。

ステップ 3. サンプルコード

このようなアイデアを使うと、以下のように簡単に実装することができます。なお、DP の復元を行う関数 get_answer() のみのプログラムとなっていますので、手元で実行したい方は 4-4. 節のサンプルコードと組み合わせて使ってください。

vector<int> get_answer() {
    int x = L;
    vector<int> ret;
    for (int i = N; i >= 1; i--) {
        if (dp[i][x] == dp[i - 1][x]) {
            // 商品 x を選ばない
        }
        else {
            // 商品 x を選ぶ
            ret.push_back(i);
            x -= W[i];
        }
    }
    reverse(ret.begin(), ret.end());
    return ret;
}

4-6. 最終結果

本章では、この問題を解くにあたって、以下の 2 つのアルゴリズムを扱いました。

そうすると、どのような買い方が最適であるかを出力することができます。本章の最後に、プログラムを動かした結果を発表したいと思います。

500 円ショッピングの場合

出力結果は次のようになります。
おにぎりも $1$ 個含まれていますが、パンが多めな気がします。

Calories = 1368
Answer = {2, 14, 15, 21}
// つまり、買った商品は次の通り：
// 商品 02｜124 円、238 kcal、おにぎり（ツナマヨネーズ）
// 商品 14｜127 円、339 kcal、サックサク食感！バター香るメロンパン
// 商品 15｜138 円、472 kcal、しっとり濃厚チョコブレッド
// 商品 21｜108 円、319 kcal、ビッグアメリカンドッグ

せっかくですので、500 円以外の場合の結果も見てみましょう。

100 円ショッピングの場合

出力結果は次のようになります。

Calories = 85
Answer = {41}
// 商品 41｜ 84 円、 85 kcal、「おでん」こだわりたまご

200 円ショッピングの場合

出力結果は次のようになります。
200 円中 138 円しか使わなくて良いのは、かなり意外です。

Calories = 472
Answer = {15}
// 商品 15｜138 円、472 kcal、しっとり濃厚チョコブレッド

400 円ショッピングの場合

出力結果は次のようになります。

Calories = 1130
Answer = {14, 15, 21}
// 商品 14｜127 円、339 kcal、サックサク食感！バター香るメロンパン
// 商品 15｜138 円、472 kcal、しっとり濃厚チョコブレッド
// 商品 21｜108 円、319 kcal、ビッグアメリカンドッグ

600 円ショッピングの場合

出力結果は次のようになります。
本当にパンとホットドッグばっかりですね。

Calories = 1584
Answer = {12, 14, 15, 22}
// 商品 14｜127 円、339 kcal、サックサク食感！バター香るメロンパン
// 商品 15｜138 円、472 kcal、しっとり濃厚チョコブレッド
// 商品 21｜108 円、319 kcal、ビッグアメリカンドッグ
// 商品 22｜154 円、323 kcal、BIGポークフランク

800 円ショッピングの場合

出力結果は次のようになります。
6 個中 4 個がパンです。本当にそれで良いのでしょうか。

Calories = 2111
Answer = {2, 11, 12, 14, 15, 21}
// 商品 02｜124 円、238 kcal、おにぎり（ツナマヨネーズ）
// 商品 11｜138 円、293 kcal、コクと旨味のカレーパン
// 商品 12｜162 円、450 kcal、がっつり食べる！ソーセージドッグ
// 商品 14｜127 円、339 kcal、サックサク食感！バター香るメロンパン
// 商品 15｜138 円、472 kcal、しっとり濃厚チョコブレッド
// 商品 21｜108 円、319 kcal、ビッグアメリカンドッグ

このように、単純にカロリーを最大化しようとすると、パンばかりの食事になってしまいました。このままでは健康に悪く、継続させると最悪の場合病気にかかってしまいます。そこで 5 章では、別の解決策を紹介したいと思います。

5. レベル C｜食べ物の種類を偏らせない

4 章では、動的計画法（DP）のアルゴリズムを使うことで、現実のセブンイレブンの場合にも最適解を出すことができました。だが、その答えには次のような欠点がありました。

パンがとにかく多すぎる。
食べ物の種類が 1 つに偏り過ぎている。

そこで、同種の食べ物を多くしないという条件下で、摂取カロリーを最大化することはできないのでしょうか。実はできます。本章では、この問題を解決するアルゴリズムについて、

の順に解説していきたいと思います。

5-1. 商品を分類する

まず、「どの商品がパンであるか」「どの商品がおにぎりであるか」といった情報が分からないと何も始まりません。そこで、食べ物を以下の 8 種類に分類することを考えます。

タイプ 0（おにぎり）：商品 01・02・03
タイプ 1（パン）：商品 11・12・13・14・15・16・17・18・19・20
タイプ 2（揚げ物）：商品 21・22・23・24・25
タイプ 3（弁当）：商品 26・27・28・29・30
タイプ 4（麺類）：商品 31・32・33・34・35
タイプ 5（サラダ）：商品 06・07・08・09・10・36・37・38
タイプ 6（おでん）：商品 39・40・41・42・43
タイプ 7（デザート）：商品 44・45・46

なお、具体的な商品名については、

4-1. 節｜本章で扱うデータ

に書かれていますので、こちらを参照してください。

5-2. パンを 1 個以内にできないか？　～DP の拡張～

「いきなり全種類 1 個以内…」と言いたいところですが、少し難易度が高いので、まずは次の制限のみを加えることを考えます。

パン（タイプ 1）の商品は 1 個までしか買えない。

これは 3 次元配列を用いた動的計画法（DP）で解くことができます。

ステップ 1. 配列の使い方

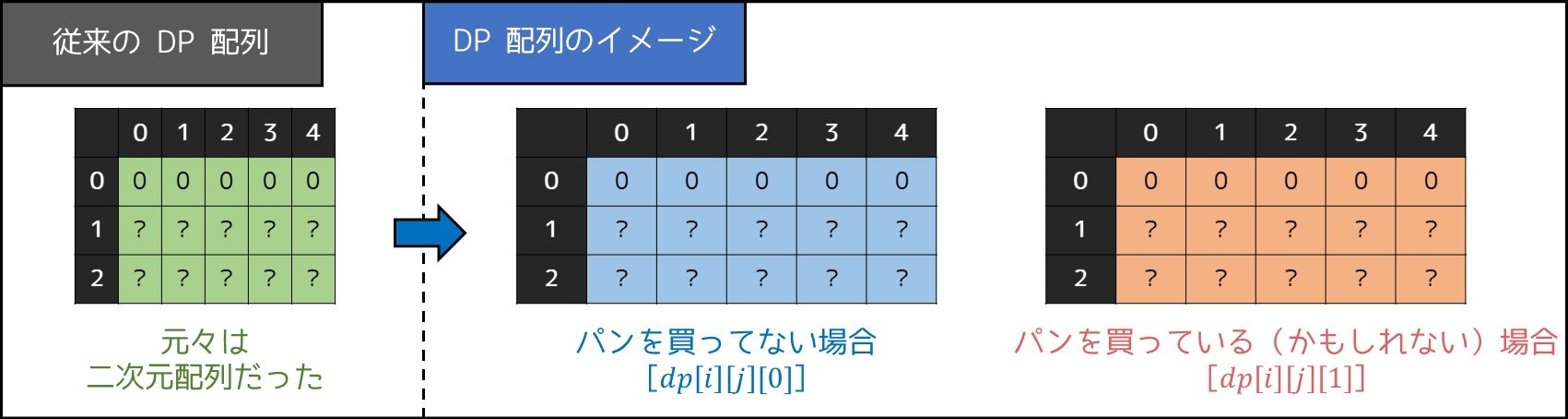
以下のような三次元配列 $\rm{dp[0][0][0], dp[0][0][1], dp[0][1][0], dp[0][1][1], \cdots, dp[N][L][1]}$ を用意することを考えます。そこで、求める値は $\rm{dp[N][L][1]}$ です。

$dp[i][j][k]$ の状態について
- $i$：商品 $i$ まで考えていること
- $j$：買い物の値段合計は $j$ 円以下であること（ここまでは 4 章の DP と同じ）
- $k$：パンを既に $k$ 個以下買っていること（$0 \leq k \leq 1$）
- このような状態におけるカロリー最大値を、配列 $\rm{dp[i][j][k]}$ にメモする

そこで、$\rm{dp[0][0][0], \cdots, dp[0][L][1]} = 0$ となっていることに注意してください。（商品を全く考えていない状態なので、明らかに $0$ kcal です）

ステップ 2. 状態遷移

既に $\rm{dp[0][?][?], dp[1][?][?], \cdots, dp[i-1][?][?]}$ が求まっていることを前提に $\rm{dp[i][j][k]}$ を計算することを考えましょう。まず、$\rm{dp[i][j][k]}$ が示す状態に到達する方法は、以下の $2$ 通りずつしかありません。

商品 $i$ がパンではない場合：
- 商品 $i$ を選ばない：$\rm{dp[i-1][j][k]}$ kcal
- 商品 $i$ を選ぶ：$\rm{dp[i-1][j-W_i][k] + V_i}$ kcal
商品 $i$ がパンである場合：
- 商品 $i$ を選ばない：$\rm{dp[i-1][j][k]}$ kcal
- 商品 $i$ を選ぶ：$\rm{dp[i-1][j-W_i][0] + V_i}$ kcal（$k = 1$ でなければ選べない）

これをまとめると、状態遷移は以下のようになります。

商品 $i$ がパン以外の場合

\rm{dp[i][j][k] = dp[i - 1][j][k] \ (k = 0 \ or \ j < W_i)} \\
\rm{dp[i][j][k] = max(dp[i - 1][j][k], dp[i - 1][j - W_i][k] + V_i) \ (otherwise)}

商品 $i$ がパンである場合

\rm{dp[i][j][k] = dp[i - 1][j][k] \ (j < W_i)} \\
\rm{dp[i][j][k] = max(dp[i - 1][j][k], dp[i - 1][j - W_i][0] + V_i) \ (otherwise)}

ステップ 3. サンプルコード

したがって、次のような実装が考えられます。4 章で扱った動的計画法を、少し複雑にしただけです。（やや長いので、直接書き込まずにリンクを貼っておきます）

5-2. 節のサンプルコード（C++）

5-3. 同種の食べ物を 1 個以下にできないか？

次に、以下の制約を加えた場合の問題を解くことを考えます。

食べ物のタイプは 8 種類あるが、各種類につき 1 個までしか買うことができない。

この問題は DP に限らず色々な解法が考えられますが⁷、今回は便宜上、

ビット DP（ビット演算を用いた DP）

を使った解法を紹介します。（注：さらに高速に解く方法もあり、本節の最後に読者への課題として載せています）

ステップ 1. まず思いつく解法

5-2. 節の方法を拡張して、以下のような DP 配列にメモすることを考えます。なお、$i$ は「何個目の商品まで考えたか」、$j$ は「現在何円使ったか」、$k_t$ はタイプ $t$ の商品を買ったかどうか（$0 \leq k_t \leq 1$）を意味します。

$$
\rm{dp[i][j][k_0][k_1][k_2][k_3][k_4][k_5][k_6][k_7]} = (この状態でのカロリー最大値)
$$

このような解法でも、頑張ってプログラムを書くことで解けますが、実装が相当面倒です。どうすれば良いのでしょうか。

ステップ 2. ビット DP の導入

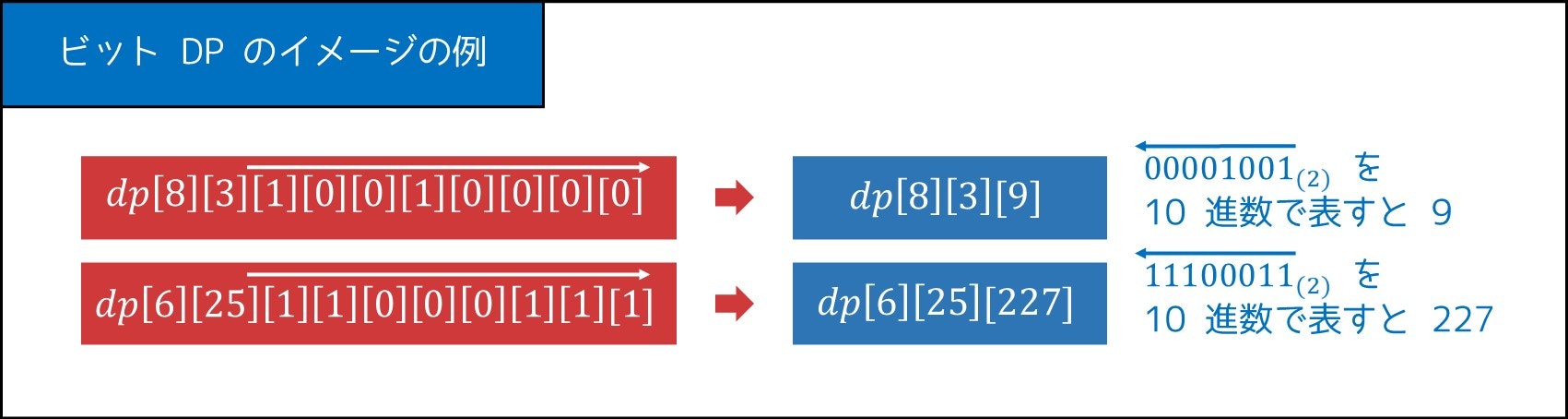
そこで、次のような DP 配列にメモすることを考えます。

$$
\rm{dp[i][j][mask]} = (この状態でのカロリー最大値)
$$

ここでは、$\rm{mask}$ は $k_0 \sim k_7$ の状態を $2$ 進数で表した値を指します。つまり、

$$
\rm{mask = k_0 + 2k_1 + 4k_2 + 8k_3 + 16k_4 + 32k_5 + 64k_6 + 128k_7}
$$

となります。3-3. 節で紹介した「bit 全探索」とアイデアがよく似ていますね。

ステップ 3. 状態遷移

次に、状態 $\rm{dp[i][j][mask]}$ になるときに、商品 $i$ を買えるための条件は次の通りです。なお、商品 $i$ のタイプを $c_i$ $(0 \leq c_i \leq 7)$ とします。

$j < W_i$ の場合、明らかに買えない。

そうでない場合、商品 $i$ まで考えた時点でタイプ $c_i$ の商品がまだ買われていない場合、つまり mask & (1 << c[i]) == 0 のとき買えない。

それ以外の場合は買える。

そこで、商品 $i$ が買えない場合の DP の遷移は、明らかに

$$
\rm{dp[i][j][mask] = dp[i-1][j][mask]}
$$

となります。また、商品 $i$ が買える場合は、

$$
\rm{dp[i][j][mask] = max(dp[i-1][j][mask], dp[i-1][j - W_i][mask - 2^{c_i}] + V_i)}
$$

となります。

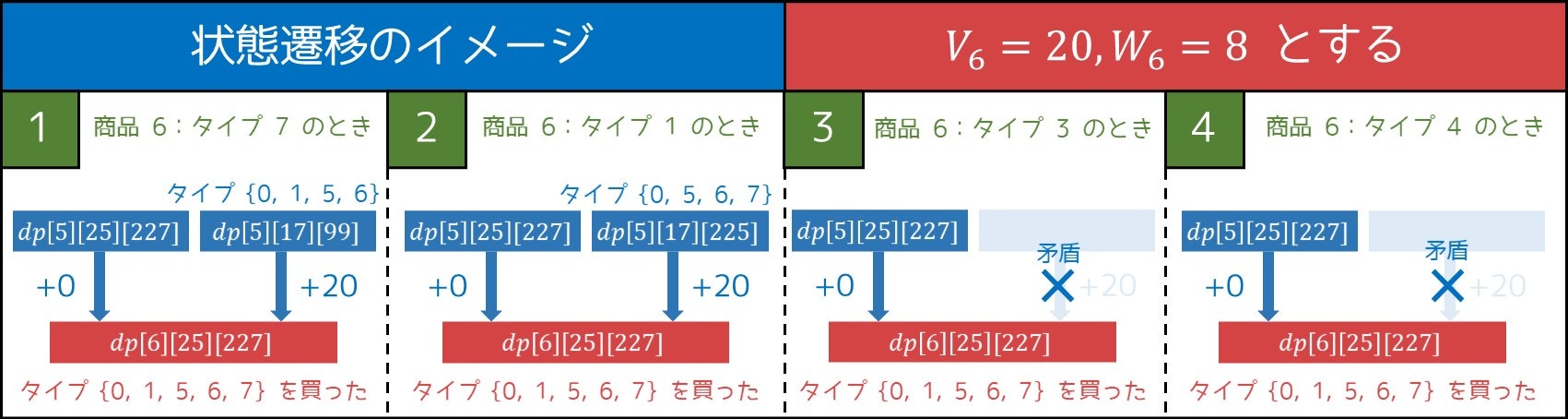
もう少し分かりやすく説明しましょう。例えば状態 $\rm{dp[6][25][227]}$ では、

商品 $6$ までを考えた時点で、タイプ $\{0, 1, 5, 6, 7\}$ は既に買われている
タイプ $\{2, 3, 4\}$ はまだ買われていない

ということになります。そこで $c_6=3$ の場合、タイプ $3$ を買ったのに「タイプ $3$ がまだ買われていない」ことになっており、矛盾するため買うことができません。一方 $c_6=7$ の場合、矛盾が起きないため買えます。

ステップ 4. サンプルコード

以上のことを踏まえて実装すると、次のようになります。
なお、DP の復元については、

4-5. 節｜DP の復元　～どのような買い方が最適か？～

と同じような要領で実装することができます。

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int N, L;
int V[109], W[109], C[109];
int dp[109][1009][256];

vector<int> get_answer() {
    int x = L, y = 255;
    vector<int> ret;
    for (int i = N; i >= 1; i--) {
        if (dp[i][x][y] == dp[i - 1][x][y]) {
            // 商品 x を選ばない
        }
        else {
            // 商品 x を選ぶ
            ret.push_back(i);
            x -= W[i];
            y -= (1 << C[i]);
        }
    }
    reverse(ret.begin(), ret.end());
    return ret;
}

int main() {
    // Step #1. 入力
    cin >> N >> L;
    for (int i = 1; i <= N; i++) cin >> V[i] >> W[i];

    // Step #2. 種類ごとに分ける
    for (int i = 1; i <= 5; i++) C[i] = 0;
    for (int i = 11; i <= 20; i++) C[i] = 1;
    for (int i = 21; i <= 25; i++) C[i] = 2;
    for (int i = 26; i <= 30; i++) C[i] = 3;
    for (int i = 31; i <= 35; i++) C[i] = 4;
    for (int i = 6; i <= 10; i++) C[i] = 5;
    for (int i = 36; i <= 38; i++) C[i] = 5;
    for (int i = 39; i <= 43; i++) C[i] = 6;
    for (int i = 44; i <= 46; i++) C[i] = 7;

    // Step #3. 動的計画法・出力
    for (int i = 1; i <= N; i++) {
        for (int j = 0; j <= L; j++) {
            for (int k = 0; k < 256; k++) {
                if (j < W[i]) dp[i][j][k] = dp[i - 1][j][k];
                else if ((k & (1 << C[i])) == 0) dp[i][j][k] = dp[i - 1][j][k];
                else dp[i][j][k] = max(dp[i - 1][j][k], dp[i - 1][j - W[i]][k - (1 << C[i])] + V[i]);
            }
        }
    }

    cout << "Calories = " << dp[N][L][255] << endl;
    vector<int> vec = get_answer();
    cout << "Answer = {";
    for (int i = 0; i < vec.size(); i++) { if (i) cout << ", "; cout << vec[i]; }
    cout << "}" << endl;
    return 0;
}

ステップ 5. 計算量と読者への課題

では、上のプログラムの計算回数は一体どの程度なのでしょうか。
商品のタイプの数を $K$（セブンイレブンでは $K=8$）とすると、

1 重目（$i$）のループは $1 \sim N$ の範囲を、つまり $N$ 個の値をとる
2 重目（$j$）のループは $0 \sim L$ の範囲を、つまり $L+1$ 個の値をとる
3 重目（$k$）のループは $0 \sim 2^K-1$ の範囲を、つまり $2^K$ 個の値をとる

ことから、ざっくり見積もって $N(L+1)2^K$ 回の計算をしていることになり、計算量 $O(2^KNL)$ と表すことができます。今回解くべきセブンイレブンの問題は $(N, L, K) = (46, 500, 8)$ であるため、数秒以内で答えが出ます。

なお、この問題はさらにアルゴリズムを改善することで、計算量を $O(NL)$ まで劇的に減らすことができます。読者への課題としておきますが、皆さん是非考えてみてください。（解法はこちら、サンプルコードはこちら）

5-4. 最終結果

最後に、ビット DP を用いたサンプルコードを実行してみた結果を発表します。

カロリー数

全体的にカロリー数が減っているように見えます。
200 円までは変わっていないですが、300 円以降徐々に「減少率」が伸びています。

値段	100 円	200 円	300 円	400 円	500 円	600 円	700 円	800 円
改善前	85kcal	472kcal	922kcal	1130kcal	1368kcal	1584kcal	1903kcal	2111kcal
改善後	85kcal	472kcal	795kcal	1029kcal	1208kcal	1293kcal	1442kcal	1621kcal
減少率	0.0%	0.0%	13.8%	8.9%	11.7%	18.4%	24.2%	23.2%

300 円ショッピングの場合

出力結果は次のようになります。
なんと肉が出ました。4 章には出現しなかった、新しいパターンです。

Calories = 795
Answer = {15, 22}
// 商品 15｜138 円、472 kcal、しっとり濃厚チョコブレッド
// 商品 22｜154 円、323 kcal、BIGポークフランク

400 円ショッピングの場合

出力結果は次のようになります。

Calories = 1029
Answer = {2, 15, 21}
// 商品 02｜124 円、238 kcal、おにぎり（ツナマヨネーズ）
// 商品 15｜138 円、472 kcal、しっとり濃厚チョコブレッド
// 商品 21｜108 円、319 kcal、ビッグアメリカンドッグ

500 円ショッピングの場合

出力結果は次のようになります。
ついにサラダメニューが入ってきました。

Calories = 1208
Answer = {2, 6, 15, 21}
// 商品 02｜124 円、238 kcal、おにぎり（ツナマヨネーズ）
// 商品 06｜127 円、179 kcal、北海道男爵いものポテトサラダ105g
// 商品 15｜138 円、472 kcal、しっとり濃厚チョコブレッド
// 商品 21｜108 円、319 kcal、ビッグアメリカンドッグ

600 円ショッピングの場合

出力結果は次のようになります。
おでんが出ました。かなり多様性が増えてきました！！！

Calories = 1293
Answer = {2, 6, 15, 21, 41}
// 商品 02｜124 円、238 kcal、おにぎり（ツナマヨネーズ）
// 商品 06｜127 円、179 kcal、北海道男爵いものポテトサラダ105g
// 商品 15｜138 円、472 kcal、しっとり濃厚チョコブレッド
// 商品 21｜108 円、319 kcal、ビッグアメリカンドッグ
// 商品 41｜ 84 円、 85 kcal、「おでん」こだわりたまご

700 円ショッピングの場合

出力結果は次のようになります。
弁当が出ました。弁当の中では鶏そぼろご飯のコスパが良いので、使われていますね。

Calories = 1442
Answer = {2, 15, 21, 29}
// 商品 02｜124 円、238 kcal、おにぎり（ツナマヨネーズ）
// 商品 15｜138 円、472 kcal、しっとり濃厚チョコブレッド
// 商品 21｜108 円、319 kcal、ビッグアメリカンドッグ
// 商品 29｜298 円、413 kcal、鶏の旨味！国産鶏のたっぷり鶏そぼろごはん

800 円ショッピングの場合

出力結果は次のようになります。

Calories = 1621
Answer = {2, 6, 15, 21, 29}
// 商品 02｜124 円、238 kcal、おにぎり（ツナマヨネーズ）
// 商品 06｜127 円、179 kcal、北海道男爵いものポテトサラダ105g
// 商品 15｜138 円、472 kcal、しっとり濃厚チョコブレッド
// 商品 21｜108 円、319 kcal、ビッグアメリカンドッグ
// 商品 29｜298 円、413 kcal、鶏の旨味！国産鶏のたっぷり鶏そぼろごはん

結果的に、以下の点で 4 章のアルゴリズムに比べ優れているといえます。

8 種類の食べ物の中で「デザート」「麺類」以外の 6 種類を出すことに成功した
4 章とは違い、パンばかりではない食事ができるようになった

このように、単純な「ナップザック DP」に「ビット DP」を組み合わせることで、食材のバランスをとりながら、カロリーを最大化することができるのです。

6. まとめ

今回の記事では、セブンイレブンでの 500 円以内の買い物で、最大何カロリー摂取できるかという問題を扱いました。3 章で紹介した最も単純な「全探索アルゴリズム」では N = 20 程度までにしか対応できず、現実のコンビニで通用しませんでした。しかし、

4 章で紹介した動的計画法を使うことで、現実のセブンイレブンにも対応できる
5 章で紹介したビット DP を使うことで、食材の偏りをなくす

ことができました。また、5 章のアルゴリズムを少し変えると、「一番最適」だけではなく、第 2 位・第 3 位などの買い方を求めることもできます。

このように、社会にあふれている問題や、実生活でふと考えたことのあるような問題も、アルゴリズムの改善によって解決できることがあるのです。このような理由で、アルゴリズムを学んでいくことは大切だと私は考えています。

本記事によって、「アルゴリズムって面白い！」と感じる人が増え、一人でも多くの方の役に立つことができれば、とても嬉しい気持ちです。

最後に、これは大学 1 年生が書いた記事なので、文章の分かりにくい部分があったかと思いますが、最後までお読みいただきありがとうございました。

7. 次回予告・参考資料

「実生活に学ぶアルゴリズム」第 2 回は、コロナ禍である今まさに重要となっているソーシャルディスタンスの話題について触れたいと思います。2021 年 5 月 12 日公開予定です。楽しみにお待ちください！！！

また、今回扱った「ナップザック問題」について、サイゼリヤで似たようなことを調べた方もいるので、以下の記事も是非お読みください。

追記（2021/5/15）

第 2 回記事を公開しました！！！

実生活に学ぶアルゴリズム【第 2 回：3 つのアルゴリズムで最適なソーシャルディスタンスを求める】

追記（2021/5/19）

最終回記事を公開しました！！！

実生活に学ぶアルゴリズム【最終回：1000 個の六角形ピースをたった 45 回の切断で作る方法、そしてアルゴリズムを学ぶ意義】

前半は大半の読者が理解できるような構成になっているつもりです。扱う問題のレベル感は、AtCoder のレーティングに例えると、第 1 回が 0 ～ 1400、第 2 回が 50 ～ 2100、第 3 回が 200 ～ 2800 程度となる予定です。 ↩
厳密に書くと $N$ 個の値をとるループが $2$ 個あるので、計算回数は $2^N \times 2N$ といった方が正しいかもしれませんが、ここでは定数倍（$N$ などに依存しないもの、$2$ 倍や $3$ 倍など）は無視します。 ↩
すべての商品が含まれているとは限らないことに注意してください。例えばドリンクや菓子などは $N = 46$ 個の中に含まれていません。 ↩
実行時間は Microsoft Visual Studio 2019 を用いた時の結果です。 ↩
6 カ月も経ったら、セブンイレブンの商品までが変わってしまいます。 ↩
これは「貰う DP」と呼ばれているタイプの動的計画法です。他にも「配る DP」というものがあります。詳しくはこちらの記事をご覧ください。 ↩
この問題は $N=46$ と小さいので、たとえば全探索でも解くことができます。各タイプについて「どれか $1$ 個選ぶ」「何も選ばない」のうちいずれかの選択ができるので、考えるべき通り数は $4 \times 11 \times 6 \times 6 \times 6 \times 9 \times 6 \times 4 = 2 \ 052 \ 864$ 通りです。しかし、あと少し $N$ が大きくなっただけで通用しなくなるため、あまり良いアルゴリズムではありません。 ↩

実生活に学ぶアルゴリズム【第 1 回：セブンイレブンでは 500 円で何カロリー得られるか？】

1. はじめに

2. 第 1 回で扱う問題

目次

3. レベル A｜小型のコンビニの場合

3-1. N = 3 の場合

3-2. N = 5 の場合

3-3. N = 20 の場合

4. レベル B｜現実のコンビニの場合

4-1. 本章で扱うデータ

4-2. 全探索で解こうとすると？ ～指数関数の恐ろしさ～

4-3. 動的計画法とは何か？ ～導入編～

ステップ 1. 配列の使い方

ステップ 2. 状態遷移

ステップ 3. 具体例・サンプルコード

結局動的計画法とは何なのか？

4-4. 動的計画法でセブンイレブンのカロリー最大値を求める

ステップ 1. 配列の使い方

ステップ 2. 状態遷移

ステップ 3. 具体例とサンプルコード

ステップ 4. 結果

4-5. DP の復元 ～どのような買い方が最適か？～

ステップ 1. DP の復元アルゴリズム

ステップ 2. 具体例

ステップ 3. サンプルコード

4-6. 最終結果

500 円ショッピングの場合

100 円ショッピングの場合

200 円ショッピングの場合

400 円ショッピングの場合

600 円ショッピングの場合

800 円ショッピングの場合

5. レベル C｜食べ物の種類を偏らせない

5-1. 商品を分類する

5-2. パンを 1 個以内にできないか？ ～DP の拡張～

ステップ 1. 配列の使い方

ステップ 2. 状態遷移

ステップ 3. サンプルコード

5-3. 同種の食べ物を 1 個以下にできないか？

ステップ 1. まず思いつく解法

ステップ 2. ビット DP の導入

ステップ 3. 状態遷移

ステップ 4. サンプルコード

ステップ 5. 計算量と読者への課題

5-4. 最終結果

カロリー数

300 円ショッピングの場合

400 円ショッピングの場合

500 円ショッピングの場合

600 円ショッピングの場合

700 円ショッピングの場合

800 円ショッピングの場合

6. まとめ

7. 次回予告・参考資料

追記（2021/5/15）

追記（2021/5/19）

4-2. 全探索で解こうとすると？　～指数関数の恐ろしさ～

4-3. 動的計画法とは何か？　～導入編～

4-5. DP の復元　～どのような買い方が最適か？～

5-2. パンを 1 個以内にできないか？　～DP の拡張～