初心者のためのダイクストラアルゴリズム

ダイクストラのアルゴリズムってあるじゃないですか？名前も覚えにくいしそもそも重み付きグラフの最短経路問題とか実務で実装することそうそうないのですぐ忘れちゃうんですよね。。。

ダイクストラアルゴリズムとは

ダイクストラアルゴリズムとはグラフの最短経路を求めるアルゴリズムです。名前だけは聞いたことのある方も多いかと思います。やってることはイージーでシンプルなんですが少しとっつきにくいですが一つ一つ理解していけば割とわかりやすいアルゴリズムです。
重み付き出ない、迷路の探索などは幅優先探索で解けるのですが、各辺に重みがついてる場合は結局全通りを計算しないといけないことになります。全ての頂点を一回だけ通るとして、辺E個あるとすればO(E!)となり計算量は爆発してしまします。
これだと計算するにも少し厳しいです。

そんな問題を効率的にといてくれるアルゴリズムそれがダイクストラアルゴリズムです。

ちなみに各辺のコストは非負の値(0以上)でなければなりません。負の数が含まれてる場合はベルマン-フォード法などを使用することになります。

手順

ダイクストラ法の手順はかなり単純です。

1. 始点に最短距離0を設定する
2. まだ辿ってない点の中から最短距離が分かっていて最も距離が短い頂点に移動する
3. その頂点から繋がっている頂点の最短距離を設定する。この時にその頂点の最短距離を更新できるなら更新する。
4. これを全ての頂点の最短距離をわかるまで行う

さてと言われても少し難しいと思いますので、実例をみていきましょう。

例

なんともアナログな手法ですが一番表現できたので。。。
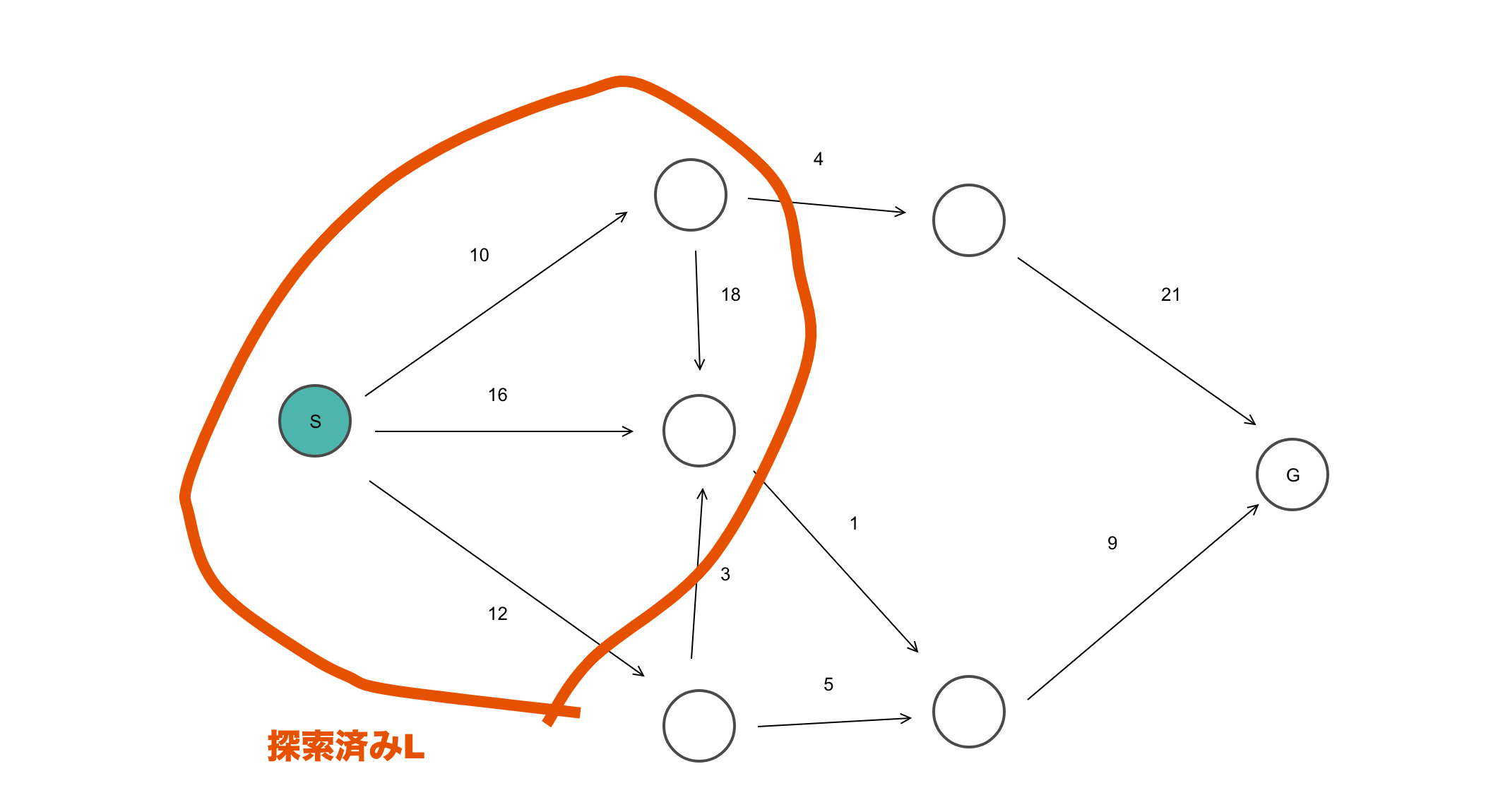
以下のような図の最短経路を考えていきます。

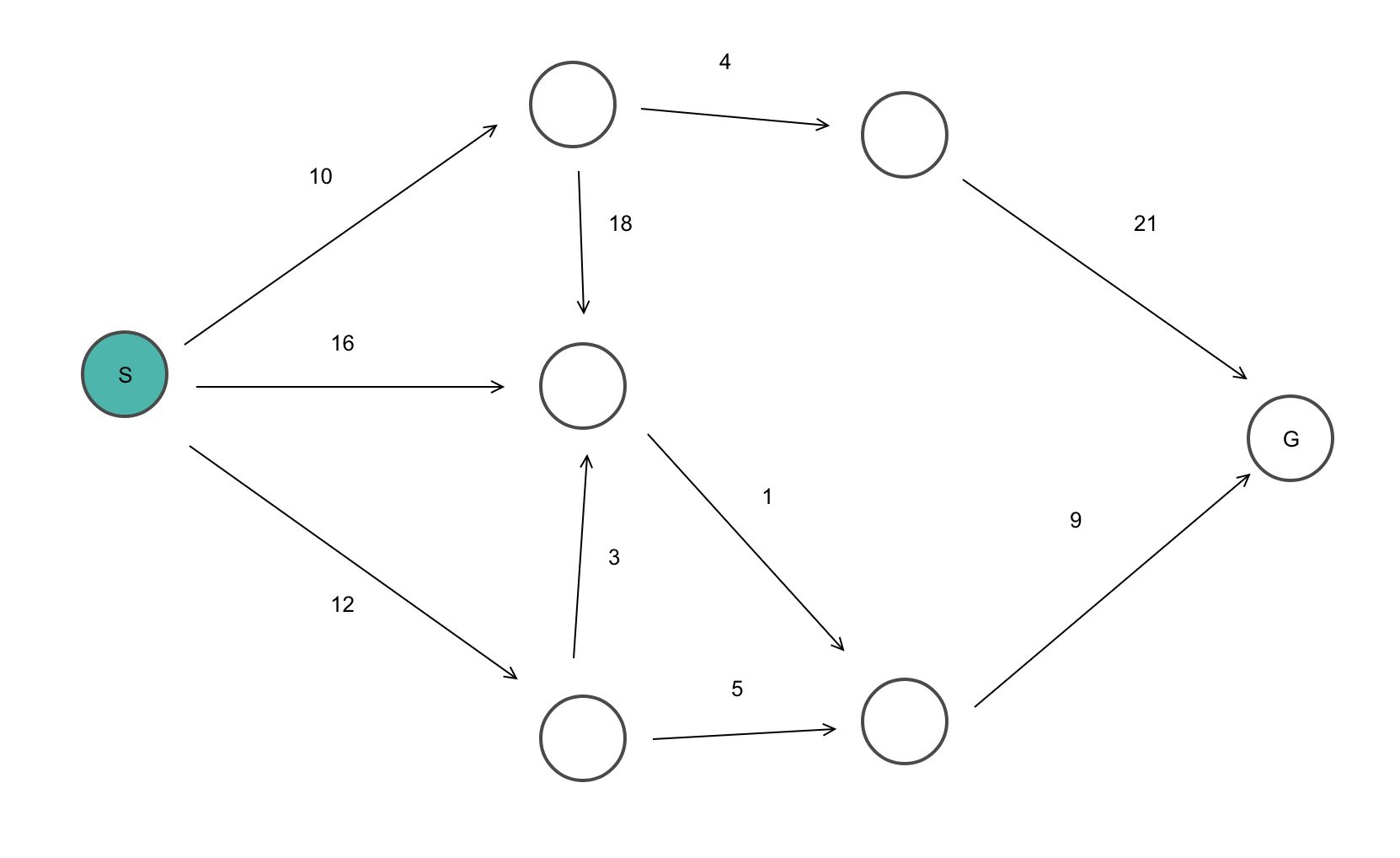
緑が最短経路が確定して移動ずみの頂点となります。赤が起点となる頂点です。各頂点の数字はその時の最短経路となります

さてみていただくと分かるようにスタート地点から順番にその時点での最短の頂点に移動してそこからまた隣り合う頂点の最短経路を計算しているのが分かるかと思います。

実装

さて実装に入っていきましょう。
上の手順を愚直に実装してみます。

function main(nodes) {
    const start = nodes[0]
    // 訪問済みの頂点を記録
    const visited = new Set()
    const routesFromStart = new Map()
     // 始点からの距離の記録

    routesFromStart.set(start, {distance: 0})
    for(const n of nodes) {
        if(n != start) {
            // スタート以外の全ての頂点に無限大を代入
            routesFromStart.set(n, {distance: Number.MAX_VALUE})
        }
    }
    let current = start
    let routes = new Map()
    while(current != null) {
        visited.add(current)
        for(const edge of current.edges) {
             // その頂点から隣り合う頂点の最短距離を計算して、計算済みの値より低ければ更新
            if(edge.cost + routesFromStart.get(current).distance < routesFromStart.get(edge.to).distance) {
                routesFromStart.set(edge.to, {distance: edge.cost + routesFromStart.get(current).distance})
                routes.set(current, edge.to)
            }
        }
        let cheapestNodeDistance = Number.MAX_VALUE
        current = null
        // 訪問してない最短距離を計算済みの頂点の中から最小の頂点を選ぶ

        for(const city of routesFromStart.keys()) {
            if(!visited.has(city) && cheapestNodeDistance > routesFromStart.get(city).distance){
                cheapestNodeDistance = routesFromStart.get(city).distance
                current = city
            }
        }
    }
    return routesFromStart.get(nodes[nodes.length - 1]).distance
}

このコードは各頂点をVとすると最大で各辺の個数を回るループの中で中で最小の頂点を選ぶためのループを回してるので計算量はO(V^2 + E)メモリについては各頂点分の記録を行わないといけないのでO(V)となります。

Priority Queueを用いた実装について

さて感のいい人ならお気づきになったかもしれませんが、このコード実は最小の頂点を決めるロジックを最適化することができます。それが優先度付きキューです。
優先度付きキューは挿入、取り出しにO(logN)の計算量が必要となりますが、最小の頂点を決める際の計算量が線形の探索より早くなります。

Priority QueueはJavaScriptには標準で実装はされてないので、Pythonでの実装です。

def dijkstra(nodes):
    start_node = nodes[0]
    routes_from_start = {n: math.inf for n in nodes}

    # 最初の頂点にゼロを設定
    routes_from_start[start_node] = 0

    minHeap = []

    # 最初の頂点を追加
    heappush(minHeap, (0, start_node))

    # ヒープがなくなるまで探索
    while minHeap:
        (cost, current_node) = heappop(minHeap)

        # priority keyは重複するのでここでチェックする
        if cost > routes_from_start[current_node]:
            continue

        for node in current_node.routes:
            price_info = current_node.routes[node]
            if routes_from_start[node] > price_info + routes_from_start[current_node]:
                routes_from_start[node] = price_info + routes_from_start[current_node]
                # 更新されたらpriorityに値を追加
                heappush(minHeap, (price_info + routes_from_start[current_node], node))

    return routes_from_start[nodes[-1]]

Priority Queueの説明はまたの機会にしましょう。
より計算効率がよく各頂点V, 各辺をVとするとVをmapに設定するO(V)とEの回数分heapを操作するのでO(ElogE)。の合計O(V + ElogE)で求まることがわかります。これは最初のアルゴリズムより効率的です。

経路を記憶する

さて最短のコストはわかりました。しかしこの問題は"最短経路"問題です。最短のコストが求まったらその経路も知りたくなるのが普通です。
上のコードを改善してみましょう。

def dijkstra(nodes):
    start_node = nodes[0]
    routes_from_start = {n: math.inf for n in nodes}

    # 最初の頂点にゼロを設定
    routes_from_start[start_node] = 0

    minHeap = []


    # 最初の頂点を追加
    heappush(minHeap, (0, start_node))
    path = collections.defaultdict(Node)

    # ヒープがなくなるまで探索
    while minHeap:
        (cost, current_node) = heappop(minHeap)

        # priority keyは重複するのでここでチェックする
        if cost > routes_from_start[current_node]:
            continue

        for node in current_node.routes:
            price_info = current_node.routes[node]
            if routes_from_start[node] > price_info + routes_from_start[current_node]:
                routes_from_start[node] = price_info + routes_from_start[current_node]
                # 最短距離を更新するノードを記録する
                path[node.id] = current_node.id
                # 更新されたらpriorityに値を追加
                heappush(minHeap, (price_info + routes_from_start[current_node], node))

    current_node = nodes[-1].id
    path_array = []

    #最短距離を記録したノードをゴールからたどる
    while current_node:
        path_array.append(current_node)
        if current_node not in path:
            break
        current_node = path[current_node]

    return routes_from_start[nodes[-1]], path_array[::-1]

ダイクストラアルゴリズムでは最短距離を更新するノードが分かるのでそれを記録して最後に辿ればよいことになります。
計算量は最短距離のノードの数分増えてしまうことになります。

ところでなんでこれで最短経路が求まるのか

さてここまでみてきて多くの人はこう思ったのではないでしょうか？確かにアルゴリズムは簡単だしそれを実装するのもそんなに難しくはない。でもなんで最短距離が求まるの？軽く確認していきましょう

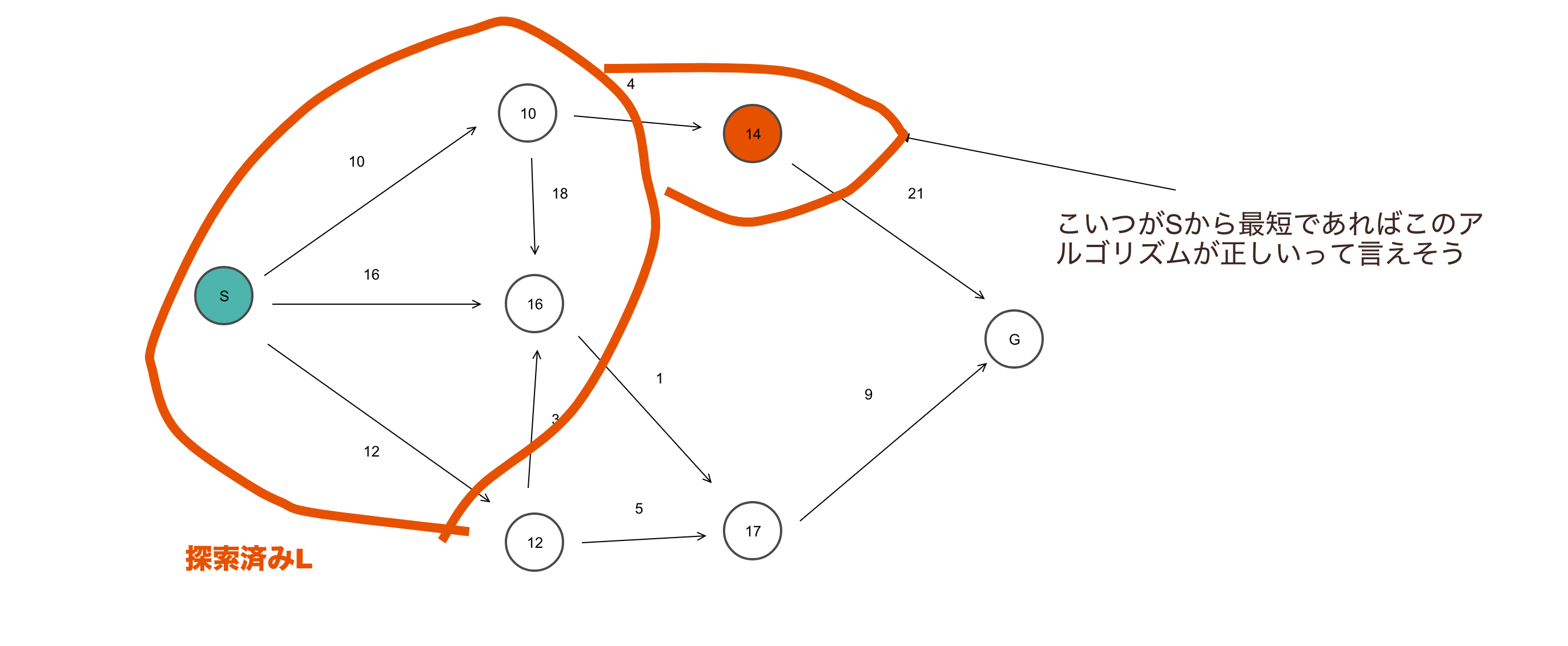
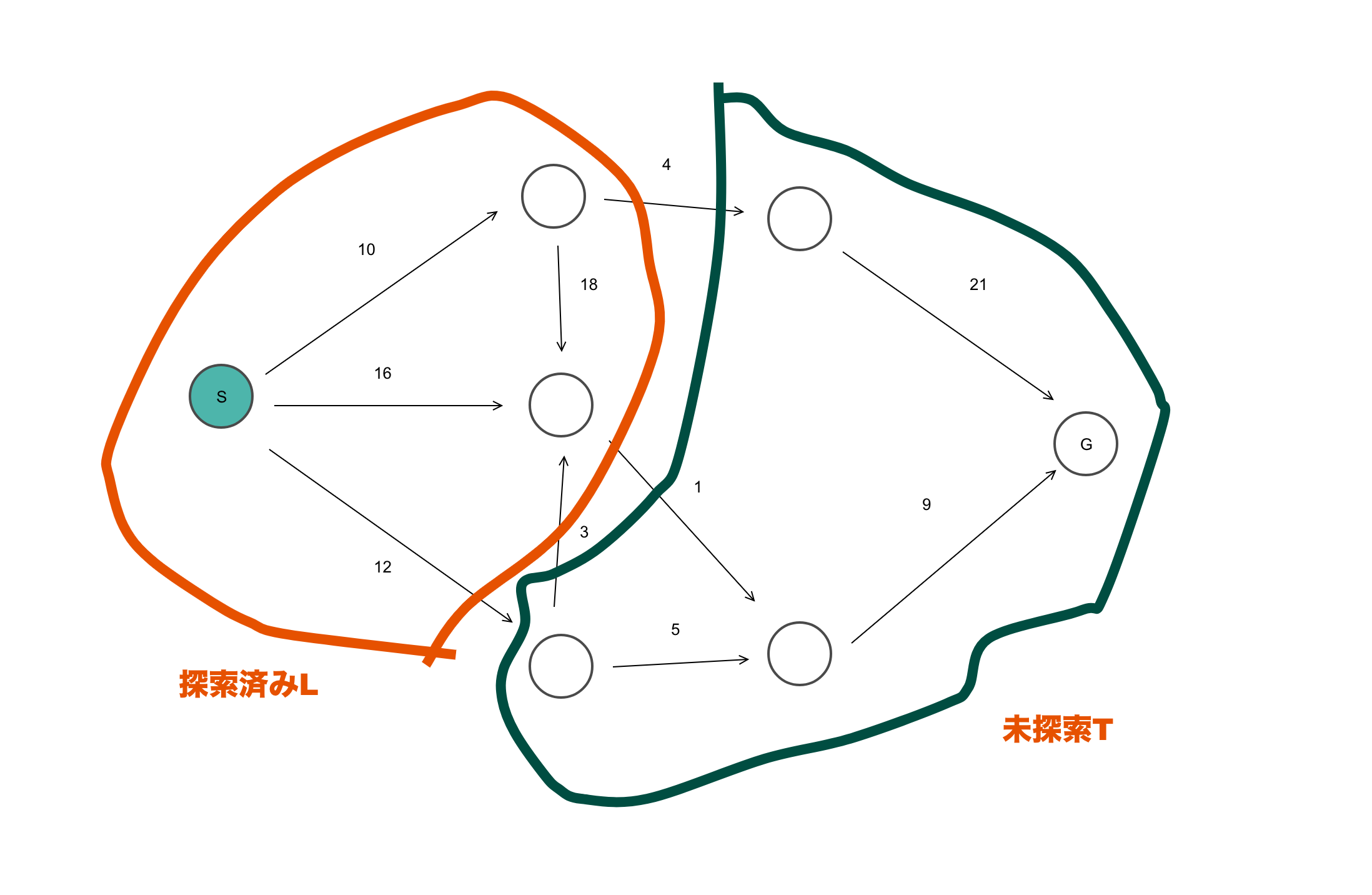
Lに入っている頂点はスタートSからの最短距離であると仮定して、そこから繋がる最短の頂点がまたSから最短距離であることを言えたら良さそうですね。

さてTに含まれるうちの最短の頂点に移動するので、最小の点をiとするとd[i] = min(T)ですよね。
さてここで各頂点をkとすると最短距離d[k] は d[k] >= d[i]であることは確定しますよね。d[i] は最小の点であり、各頂点は非負なので。
と次々やっていくと帰納法的に証明できます。

さてこれってよく考えたら漸化式ですよね。

d[i] = min(k ⊂ T) + iに隣接するLの頂点の最短距離

漸化式の時には動的計画法が

漸化式ときたらDPですよね。DPについてはこの記事がすごく参考になります(https://qiita.com/drken/items/a5e6fe22863b7992efdb)

ではDPならどういう風に値が更新されていくかというと

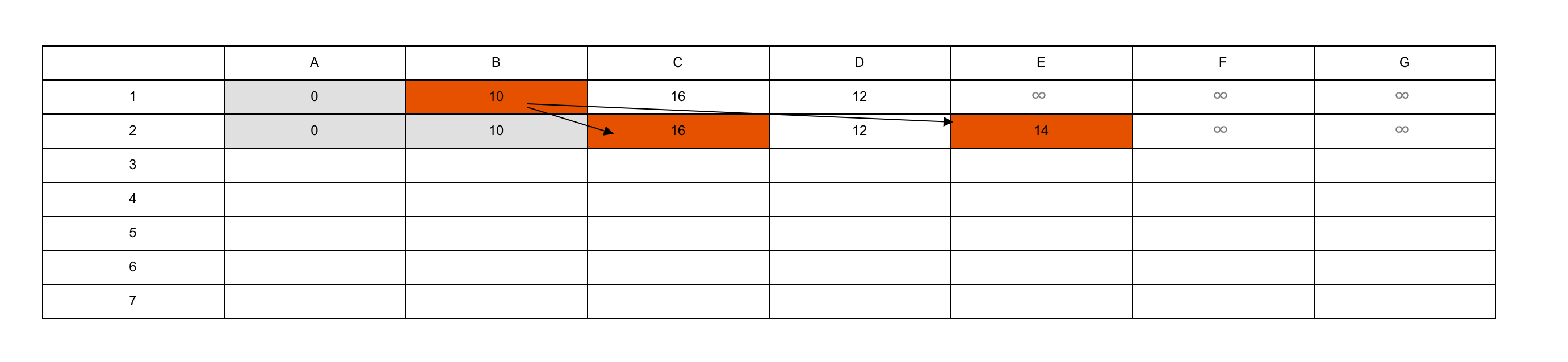
このような感じで値が更新されていきます。縦軸は試行の回数。横軸は頂点です。

なんだダイクストラアルゴリズムはDPの一種だったんだ。

まとめ

さてみてきましたダイクストラのアルゴリズムですが、一回理解してしまうと結構簡単に理解できます。あとは実装してみてアルゴリズムの問題で類似の問題に当たった時にあこれはあの時の！！という感じで解いていきたいものです。
*余談ですが僕もDPの記事書きたい

解説したyoutubeチャンネルはこちら
https://youtu.be/jz8b0q5R1Ss

参考

http://www.lab2.kuis.kyoto-u.ac.jp/~shuichi/algintro/alg-6s.pdf
https://www.youtube.com/watch?v=X1AsMlJdiok