こんにちは、高校 3 年生の E869120 です。
私は競技プログラミング(競プロ)が趣味で、AtCoder・情報オリンピックなどの各種コンテストに出場しています。ちなみに、2020 年 7 月 30 日現在、AtCoder では赤色(レッドコーダー)です。
今回は、競技プログラミングにおいて「実装を速くする」「効率よく実装する」テクニックをいくつか紹介していきたいと思います。是非お読みください。
1. はじめに
さて、競プロをやっている人の中では、
解法は分かるけど、実装が速くないせいで順位が上がらない。
といった考えや、
デバッグに時間がかかりすぎて、コンテスト中に D 問題を AC できなかった。
といった経験を持つ方も多いでしょう。そのような「実装で苦しむ人」を減らすことを目標にして、私は本記事を書くことにしました。今回は、
- 競技プログラミングでの実装を楽にするテクニック
- 競技プログラミングでより可読性の高い(デバッグしやすい)コードを書くテクニック
などを、実際にプログラムを改善してみる「実践編」も含めて解説します。
対象とする読者層
本記事の主なターゲットは、競技プログラミング初心者や、実装に苦手意識を感じている中級者です。「実装への苦手意識」を少しでも克服してもらうことが、本記事の最大の目標です。しかし黄色コーダー以上の上級者であっても、日本情報オリンピックや ICPC などのコンテストには数百行のコードを短時間で書くことが要求される問題もあるため、本記事から学ぶことはあると思います。
また、競技プログラミングをやっていない方にも是非読んでいただきたいです。理由は、
- 初心者プログラマを見ていると、そもそも長いコードの実装に慣れていない人が多い1
- 競プロで役立つ実装テクニックは、実務に共通するものもあるかもしれない
と考えるからです。
重要な注意
(2020/7/31 01:08 追記)
5 章で後述する通り、競技プログラミングと開発では「適切なコードの書き方」に相違点がいくつかあります。本記事では競技プログラミングに適切な実装方針について記すので、ご了承ください。
また、実装方針やコードの書き方には「正解」がない部分もあり、同じ競技プログラマーでも意見が分かれる話です。今回紹介するのは、あくまでも私が意識している点(一つの例)ですので、その点ご理解お願いします。
目次
| 章 | 内容 | 備考 |
|---|---|---|
| 1. | はじめに | |
| 2. | 競プロにおける「実装力」の大切さ | ここからサポートしていきます |
| 3. | 理論編 ~実装力向上の 14 のテクニック~ | 本記事のメインです |
| 4. | 実践編 ~実際にプログラムを改善してみる~ | |
| 5. | 注意 | テクニックを扱う注意点を記します |
| 6. | おわりに |
2. 競プロにおける「実装力」の大切さ
競技プログラミングは、パズル的な問題を制限時間内にできるだけ多く解くスポーツです。したがって、解法を思いつく力が高いほど、高順位を目指しやすいのは事実です。
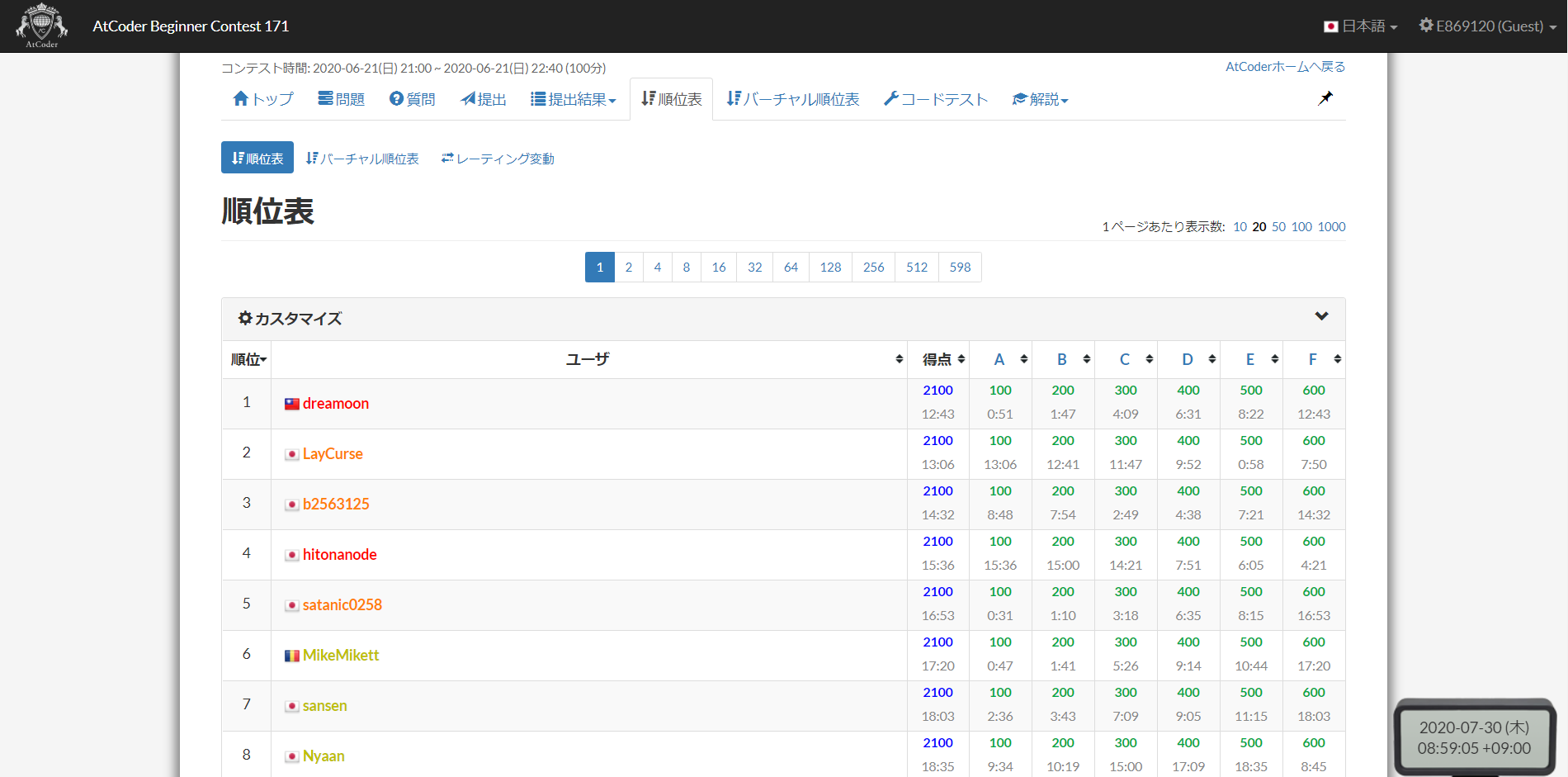
しかしながら、求められる能力はそれだけではありません。短時間で正確に実装する能力も求められているのです。例えば、AtCoder Beginner Contest 171 では 6 問合計で 200 行ほどの実装量がありますが、成績上位者は 20 分以内で 1 回の誤答もせずに全問正解しているのです。
実装力が必要な場面は成績上位者に限りません。競技プログラミングでは、たった 1 分間の実装速度差が相当なパフォーマンス2の差を生む場合だってあるのです。例えば、AtCoder Beginner Contest 172 において A, B 問題のみ正解した場合のパフォーマンスは以下のようになります。
| かかった時間 | 2 分 | 3 分 | 4 分 | 5 分 | 6 分 |
|---|---|---|---|---|---|
| パフォーマンス | 767 | 657 | 532 | 421 | 337 |
**このように、実装速度が大きな順位の差を生むこともあります。**もしかしたら、この数分の差が「タイピング速度の差」だと思う人もいるかもしれません。しかし、実際はそうではありません。例えば皆さんの多くは 1 分間に英文字 200 個以上タイピングできると思います。ただ、3000 バイトのコードを 15 分で実装できるような人は殆どいません。AtCoder Beginner Contest に参加している 10000 人の中でも、できる人は 50 人くらいだと思います。したがって、実装力の差は意外と重要な側面を持つのです。
3 章以降では、実装速度を上げ、バグを減らせるようなテクニックについて紹介していきます。続きも是非お読みください。
3. 理論編 ~実装力向上の 14 のテクニック~
実装力がいかに重要であるかは 2 章で紹介しました。ではどのようにして実装速度を上げ、デバッグを楽にすることができるのでしょうか。
3-0. 前提
大前提として、実装が苦手な人の中で、
- 確立したコーディングスタイルを持っていない
- 自分のコーディングスタイルが、莫大な実装量や時間を要求するものになっている
- 「実装のロジック」が洗練されていない
というパターンを持つ人は多いと思います。しかしこれは、自分の中で統一した適切なコーディングスタイルを持つことで解決できる場合があります。特に、1. と 2. のパターンを持つ人にとってはその可能性が高いです。
そこで本章では、競技プログラミングのコーディングスタイルとしての「一つの例」を紹介します。コードの書き方には何通りも「正解」がある側面もあり、この話題は競技プログラマーの間でも意見が分かれます。したがって、今回紹介するいくつかのテクニックの中で、自分に合ったものを選ぶことで、実装力向上を目指すことをお勧めします。
3-1. 節以降で、競プロでのコーディングにおいて、私が意識していることを 14 個のポイントに絞って紹介していきます。ただし、重要度を![]() の数で表します。
の数で表します。
3-1. ソースコードのインデントを整える( 5)
5)
以下の 2 つのソースコードを見比べてみましょう。どちらも C++ のソースコードで、$A_1, A_2, ..., A_N$ の中の偶数の和を出力しています。
コード 1
int sum=0;
for(int i=1;i <= N;i++) {
if(A[i]%2==0){
sum+=A[i];
}
}
cout<<sum<<endl;
コード 2
int sum = 0;
for (int i = 1; i <= N; i++) {
if (A[i] % 2 == 0) sum += A[i];
}
cout << sum << endl;
皆さんの多くは、「コード 2 の方が読みやすい!」と感じたはずです。これは、正しく規則的にインデントをしているからです。そこで、自動でインデントをしてくれるエディタがあります。これは**「Visual Studio」**です。
- for 文・if 文の中は 4 文字など適切な文字数分インデントをしてくれる
- 変数と演算子の間などには、スペースを 1 文字入れる(
a+bではなく、a + bになる)
などの機能があります。Visual Studio 以外でそのような機能が存在するものもありますが、Visual Studio 2019 ではコードを打っている最中に自動でこれをやってくれる機能がデフォルトで付いているので、とても便利です。
もし自動で行われない場合は「Ctrl + K」→「Ctrl + D」を押すことでコードが整理されます。詳しくはこちらの記事をお読みください。3
3-2. ステップごとに処理を行う場合、コメントを付ける( 5)
5)
例えば以下の 2 つのソースコードを見比べてみましょう。
コード 1
int A1, A2, A3, B1, B2, B3;
cin >> A1 >> A2 >> A3 >> B1 >> B2 >> B3;
int s1 = 0, s2 = 0;
s1 += A1;
s1 += A1 * A2;
s1 += A1 * A2 * A3;
s2 += B1;
s2 += B1 * B2;
s2 += B1 * B2 * B3;
cout << s1 * s2 << endl;
コード 2
// ステップ 1. 入力
int A1, A2, A3, B1, B2, B3;
cin >> A1 >> A2 >> A3 >> B1 >> B2 >> B3;
// ステップ 2. 計算
int s1 = 0, s2 = 0;
s1 += A1;
s1 += A1 * A2;
s1 += A1 * A2 * A3;
s2 += B1;
s2 += B1 * B2;
s2 += B1 * B2 * B3;
// ステップ 3. 出力
cout << s1 * s2 << endl;
皆さんの多くは、「コード 2 の方が読みやすい!」と感じたはずです。「実際同じくらいではないか…」「コード 2 のコメントの数が多すぎる…」と感じた人も少なくないと思いますが、コードがもっと長くなった場合は全然違います。なぜなら、コードが長くなってしまうと、デバッグをするときに「どこでどういう処理を行っているのか」分からなくなってしまうからです。
しかし、あまりにもコメントの数が多すぎると、逆に複雑になってしまうので、
- 「入力」「出力」部分はコメントを付ける
- そのほかの部分は、10-30 行に 1 個くらいの比率で、重要なところにコメントを付ける
という感じで良いと思います。コメントの比率については「10-30 行に 1 個」と書いてありますが、その人の実力やコードの書き方によって適切な比率は違うので、自分が良いと思った比率で良いです。
(2020/7/31 01:27 追記)
ただし、一部のエディタやサイト(HackerRank など)では ASCII コードではない日本語文字を受け付けない場合があるので、そのような場合は英語でコメントを書くなり、ステップ番号だけ書くなり、様々な対策が必要です。
3-3. 変数名を問題文に合わせる( 5)
5)
たとえば、以下の問題があったとします。
数列 $A_1, A_2, ..., A_N$ があります。
そのとき、$A_i + A_j = K$ となるような $(i, j)$ の組の個数を求めてください。
ただし、$N \leq 1000$、$0 \leq K, A_i \leq 10^9$ とします。
これは $(i, j)$ の組を全探索することによって解けるのですが、以下の 2 つのコードを見比べてみましょう。
コード 1
int M, L;
int P[1009], cnt = 0;
int main() {
cin >> M >> L;
for (int k = 1; k <= M; k++) cin >> P[k];
for (int l = 1; l <= M; k++) {
for (int m = 1; m <= M; l++) {
if (P[l] + P[m] == L) cnt++;
}
}
cout << cnt << endl;
return 0;
}
コード 2
int N, K;
int A[1009], cnt = 0;
int main() {
cin >> N >> K;
for (int i = 1; i <= N; i++) cin >> A[i];
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= N; j++) {
if (A[i] + A[j] == K) cnt++;
}
}
cout << cnt << endl;
return 0;
}
皆さんの多くは「コード 2 の方が読みやすい!」と感じたはずです。なぜなら、コード 1 のように適当に変数名を割り当てた場合、コードを書いている途中に「あれ、$m$ って何? $P$ って何?」「$L$ ってどういう機能を果たしているのか?」という感じで、各変数がどのような役割を果たしているのかを見失いやすいからです。
しかし、コード 2 のように問題文に変数名を合わせた場合、変数の役割が分からなくなった時に問題文を見返すと「ああ、$K$ は 2 つの数の和の合計値か」とすぐ分かって、とても便利なのです。
したがって、基本的に変数名は問題文に合わせることを推奨します。
3-4. Goto 文は使わない( 4)
4)
皆さん、「goto 文」をご存知でしょうか。例えば C++ の場合、以下のコードで $A = 3$ を入力すると 3 is prime と出力し、$A = 4$ を入力すると 4 is not prime と出力します。
int A; cin >> A;
for (int i = 2; i <= A - 1; i++) {
if (A % i == 0) { goto Pattern1: }
}
cout << A << " is prime" << endl;
return 0;
Pattern1:
cout << A << " is not prime" << endl;
return 0;
しかし、Goto 文は**競プロでは使わないことをお勧めします。**その代わりとして if 文、break 文、return 文 などを使うことをお勧めします。理由としては、以下が挙げられます。
- If / for 文に比べて Goto 文はコードの構造をつかみにくく、スパゲッティコードになりやすい
- Goto 文を使うと、ある入力に対してプログラムがどのように動くのかが見えにくいため、コードを書き間違えることで無限ループに陥ってしまうことが多い
- Goto 文は If / For 文と違ってインデントのしようがないので、コードが読みにくい
- したがって、長いプログラムではデバッグがしにくくなる
などが挙げられます。
例えば上のコードを Goto 文の代わりに return 文を使って書き換えると、以下のようになります。
int A; cin >> A;
for (int i = 2; i <= A - 1; i++) {
if (A % i == 0) {
cout << A << " is not prime" << endl;
return 0;
}
}
cout << A << " is prime" << endl;
return 0;
3-5. 関数を多用する( 4)
4)
以下の 2 つのコードを見比べてみましょう。入力で与えられた $A$ と $B$ それぞれについて、素数判定をするプログラムです。
コード 1
int main() {
int A, B; cin >> A >> B;
bool flagA = true;
for (int i = 2; i <= A - 1; i++) {
if (A % i == 0) flagA = false;
}
if (flagA == false) cout << "A is not prime" << endl;
else cout << "A is prime" << endl;
bool flagB = true;
for (int i = 2; i <= B - 1; i++) {
if (B % i == 0) flagB = false;
}
if (flagB == false) cout << "B is not prime" << endl;
else cout << "B is prime" << endl;
return 0;
}
コード 2
int prime(int x) {
for (int i = 2; i <= x - 1; i++) {
if (x % i == 0) return false;
}
return true;
}
int main() {
int A, B; cin >> A >> B;
bool flagA = prime(A);
if (flagA == false) cout << "A is not prime" << endl;
else cout << "A is prime" << endl;
bool flagB = prime(B);
if (flagB == false) cout << "B is not prime" << endl;
else cout << "B is prime" << endl;
return 0;
}
皆さんの多くは、「コード 2 の方が読みやすい!」と感じたはずです。コード 1 の方が長くなってしまっている他、同じ階層にたくさんの処理が書いてあるなどの理由が挙げられます。
このように、**関数を使うことによってコードが見やすくなり、デバッグがやりやすくなる場合があります。**特に、以下の場面では有効です。
- 同じような処理を何回か繰り返す場合(上の例など)
- ループが $5$ 重とか $6$ 重とかになる場合($3$ 重と $3$ 重など、適切な部分で関数に分けると良いこともあるが、これはケースバイケース)
3-6. For 文や If 文の書き方を整理する( 3)
3)
For 文や If 文は、競技プログラミングで書くソースコードでも頻出です。したがって、書き方を統一することが重要になります。本節では私のお勧めする書き方について紹介しますが、まずは以下の 2 つのコードを見比べてみましょう。
コード 1
for (int i = 1; i <= N; i++)
{
// 処理を書く
}
if (条件式)
{
// 処理を書く
}
コード 2
for (int i = 1; i <= N; i++) {
// 処理を書く
}
if (条件式) {
// 処理を書く
}
私はコード 1 のことを「3 行 for/3 行 if」、コード 2 のことを「2 行 for/2 行 if」と呼ぶことがあるのですが、2 行で書くことをお勧めしています。
- プログラムの長さが長くなった分だけコードが読みにくくなり、デバッグがしにくくなる
- 3 行で書くと
{のみの無駄な行が発生する - 2 行で書いても 3 行で書いても、読みやすさはほとんど変わらない
などの理由が挙げられます。また、読みやすさを考えて、for 文に出てくる $i, j$ などの変数は for 文の中で定義することをお勧めします。他にも、
- 1 重ループ目は $i$ で書く
- 2 重ループ目は $j$ で書く
- 3 重ループ目は $k$ で書く
- 4 重ループ目は $l$ で書く …(以下省略)
といったテクニックがあります。それを使うと、あるループがどの階層に属するのかが一目でわかるので、少しコードが見やすくなります。また、問題文に書かれている変数もそれに合わせている場合が多い($A_i, B_i, C_{i, j}$ など)ことも理由として挙げられます。
(2020/07/31 01:35 追記)
ただし、このテクニックについては、14 個の中でも特に人によって意見が分かれるところです。例えば、ループ変数を $i, j, k, l$ ではなく用途に応じて $i, j, x, y$ などに適切に変更したり、3 行 for を使った方が良いと主張する人もいます。これは全く問題のないことだと思いますが、自分の中で書き方を統一することが重要なので、どのように For/If 文を書くかは予め決めておいた方が良いと思います。
3-7. 基本問題は空で書けるようにする( 4)
4)
競技プログラミングの世界では、AtCoder Beginner Contest の E, F 問題レベルの難易度であっても、基本的な問題(最短経路問題、最大フロー問題など)に帰着させることで解けることも多いです。したがって、基本問題をしっかり理解し、何も見ずに正確なコードを書けるようにすることはとても重要です。もしそれができたならば、
- 基本問題の部分は絶対にバグらせない
といった点で有利になります。「何が基本問題であるか」が分からない人も多いと思いますが、基本的には
に載っている 23 個のアルゴリズムをすべて習得すれば、AtCoder Beginner Contest に出題される典型知識のほとんどはカバーできます。
3-8. 実装方針を紙に書く( 4)
4)
プログラミングコンテストに出題される問題の中には、
- 複雑な処理を要求する問題
- 多くの実装ステップを必要とする問題
も多く出題されます。そのような問題では、実装方針(どのようなステップでコードを書くのかの概略)を紙に書くことが重要です。例えば、
1. 入力
2. A[i] を昇順にソート
3. 答えを求める関数部分を実装
4. 全探索を実装
5. 出力
といった簡潔な実装方針を紙にメモするだけでも、長いコードが短い $5$ 個のコードに分解できるため、実装が楽になります。
3-9. 一行にまとめられるものはまとめる( 3)
3)
以下の 2 つのコードを見比べてみましょう。
コード 1
for (int i = 1; i <= N; i++) {
cin >> A[i];
}
for (int i = 1; i <= N; i++) {
cin >> B[i];
}
for (int i = 1; i <= N; i++) {
cin >> C[i];
}
// その後に 30 行くらいのコードが続く
コード 2
for (int i = 1; i <= N; i++) cin >> A[i];
for (int i = 1; i <= N; i++) cin >> B[i];
for (int i = 1; i <= N; i++) cin >> C[i];
// その後に 30 行くらいのコードが続く
皆さんの多くは、「コード 2 の方が読みやすい!」と感じたはずです。なぜなら、同じような処理を 1 行ずつに並べているからです。
一般に、連続する行に似たようなプログラムを書いているときに 1 行ごとにまとめることで、ビジュアル的に読みやすくなるだけでなく、実際にデバッグもしやすくなると考えています。
ただし、長いコードを無理に 1 行にまとめると、その行が 100 文字以上となり、ある特定の行だけ圧倒的に長いプログラムになってしまう場合があるので注意が必要です。そのようなときは、
- 関数を使うことで読みやすくする
- コード 1 のように、普通に 2 行以上を使って書く
などの対処法が挙げられます。
(2020/07/31 01:45 追記)
ただし、このテクニックは 14 個の中でも特に「人によって意見が分かれるもの」の 1 つです。例えば、「ソースコードの右のほうに重要なものが来てしまうから、コード 1 の方が良い」と主張する人もいます。これは一つの考え方なので全く問題ないと思いますが、3-0. 節で書いたように自分に合った実装方針を適切に選んで実装力を上げるのが重要です。
3-10. 変数名・関数名を用途に応じて統一する( 3)
3)
3-3. 節で「変数名は問題文に合わせた方が良い」と記しました。しかし、問題文にない変数の場合はどうすればよいのでしょうか。そこでお勧めするのが変数の統一です。以下に例を挙げます。
| 用途 | 使う変数名の例 |
|---|---|
| 合計値を表す変数 |
sum、sumA、sumB など |
| 答えを表す変数 |
Answer、FinalAns など |
| 関数内の答え(戻り値)を表す変数 |
ret など |
| グラフの情報を表す変数 |
G、Graph など |
| グラフ上の位置、配列上の位置を指し示す変数 |
pos など |
| 最短距離を表す変数 |
dist など |
| 二次元座標を表す変数 |
(px, py)、(sx, sy) など |
| 方向を表す変数 |
(dx, dy) など |
| 累積和を表す変数 |
SA、SB、wa など |
また、変数だけでなく、関数の統一も重要です。以下に例を挙げます。
| 用途 | 使う関数名の例 |
|---|---|
| 答えを求める関数 |
solve など |
| 深さ優先探索をする関数 |
dfs、dfs1、dfs2 など |
| $a^b \ (mod \ m)$ をを求める関数 |
modpow など |
| $a \div b$ の $mod \ m$ での逆元を求める関数 |
Div など |
このように、変数の統一・関数の統一を行うと、「ある変数がどんな役割を果たしているのか」が見えやすくなり、コードも読みやすくなります。
3-11. グローバル変数は用途に応じてコメントを付ける( 3)
3)
もし変数が 20 個、30 個と多くなってしまった場合、
を利用しても、「どの変数がどんな役割をしているのか」が見えにくくなってしまいます。
そこで使うのが、**「グローバル変数にコメントを付ける」**というテクニックです。例えば以下の 2 つのコードを見比べてみてください。コメントを付けた「コード 2」の方が、それぞれの変数がどんな用途で使われるのかが見えやすいと思います。
(2020/07/31 02:04 追記)
ただし、3-2. 節でも述べた通り、一部のエディタやサイト(HackerRank など)では ASCII コードではない日本語文字が使えない場合もあります。そのような場合は英語でコメントを書くなり、ステップ番号だけ書くなり、様々な対策が必要です。
コード 1
int N, M, K;
int A[100009], B[100009], C[100009], D[100009];
int LX[100009], LY[100009], RX[100009], RY[100009];
int SA[100009], SB[100009];
int dp[100009], dp2[100009];
int Answer[100009];
int main() {
// 50-100 行程度のプログラムが入る
}
コード 2
// 入力
int N, M, K;
int A[100009], B[100009], C[100009], D[100009];
// 計算パート
int LX[100009], LY[100009], RX[100009], RY[100009];
int SA[100009], SB[100009];
int dp[100009], dp2[100009];
// 出力
int Answer[100009];
int main() {
// 50-100 行程度のプログラムが入る
}
3-12. ライブラリ整備をする( 2)
2)
3-7. 節では、最短経路問題や最大フロー問題などといった基本問題を解くプログラムを、何も見ずに書けるようにすることが重要だと書きました。しかし、それができるようになっても、人間は完璧ではないので間違えることがあります。
そこで、**「ライブラリ整備」**というテクニックを紹介します。これは、
基本問題を解くプログラムを予め用意しておくこと
を指します。予め用意したプログラムをコピーするだけであれば、そのプログラムが間違っていない限り、基本問題を解く部分をバグらせることはありません。そこで、特に使う機会が多く、用意しておくべきライブラリを以下に記します。
※どのような問題かは、リンクをクリックすると閲覧できます。
3-13. <発展>L 以上 R 以下について求める場合の実装テク( 2)
2)
※このテクニックは難しいので、読み飛ばしていただいても構いません。
以下の問題を考えましょう。
$L$ 以上 $R$ 以下の正の整数で、$3$ の倍数の個数はいくつか。
制約:$1 \leq L \leq R \leq 2 \times 10^9$
この場合は、以下のように実装することもできます。
int L, R;
cin >> L >> R;
// 最初の 3 の倍数を求める
int cl = L;
if (cl % 3 != 0) { cl += 1; }
if (cl % 3 != 0) { cl += 1; }
// 最後の 3 の倍数を求める
int cr = R;
if (cr % 3 != 0) { cr -= 1; }
if (cr % 3 != 0) { cr -= 1; }
// 答えを求める
cout << (cr - cl + 3) / 3 << endl;
しかし、これだとソースコードが長くなってしまいます。そこで、**答え = 「R 以下での個数」 - 「L-1 以下での個数」**であるという性質を使うことができます。つまり func(x) を「x 以下の個数」とするとき、func(R) - func(L-1) が答えだということです。
そうすると、以下のように実装できます。とても楽な実装です。
int func(int x) {
return x / 3;
}
int main() {
int L, R;
cin >> L >> R;
cout << func(R) - func(L - 1) << endl;
return 0;
}
一般に、「$L$ 以上 $R$ 以下の中で、条件を満たす個数は何個か」という問題の多くではこのようなテクニックを使うことができます。以下の問題のように、桁 DP アルゴリズム と一緒にこのテクニックが使える場合も多いです。(この問題は難しいですが、是非挑戦してみてください。読者への課題とします)
$L$ 以上 $R$ 以下の数の中で、「増加的な数」はいくつあるか。ただし、増加的な数とは $1123$ や $1355679$ のような数の事を指す。
制約:$1 \leq L \leq R \leq 10^{17}$
3-14. <発展>二次元座標を扱う場合の実装テク( 2)
2)
※このテクニックは難しいので、読み飛ばしていただいても構いません。
二次元座標を扱う場合、回転させることで実装量が減る場合もあります。例えば以下の問題を考えましょう。
$N$ 個の飛行機が飛んでいます。番号 $i$ の飛行機は座標 $(X_i, Y_i)$ におり、方向 $U_i$(上下左右のいずれかの向き)に移動しています。このままだと最短で何秒後に 2 つの飛行機が同じ座標に来るか、求めてください。
制約:$1 \leq N \leq 200000, 0 \leq x_i, y_i \leq 200000$
出典:M-SOLUTIONS プロコンオープン 2020 F - Air Safety
紙面の関係上、詳しい解法は省略しますが、普通に実装すると、以下の 6 通りのパターンすべてを考える必要があります。
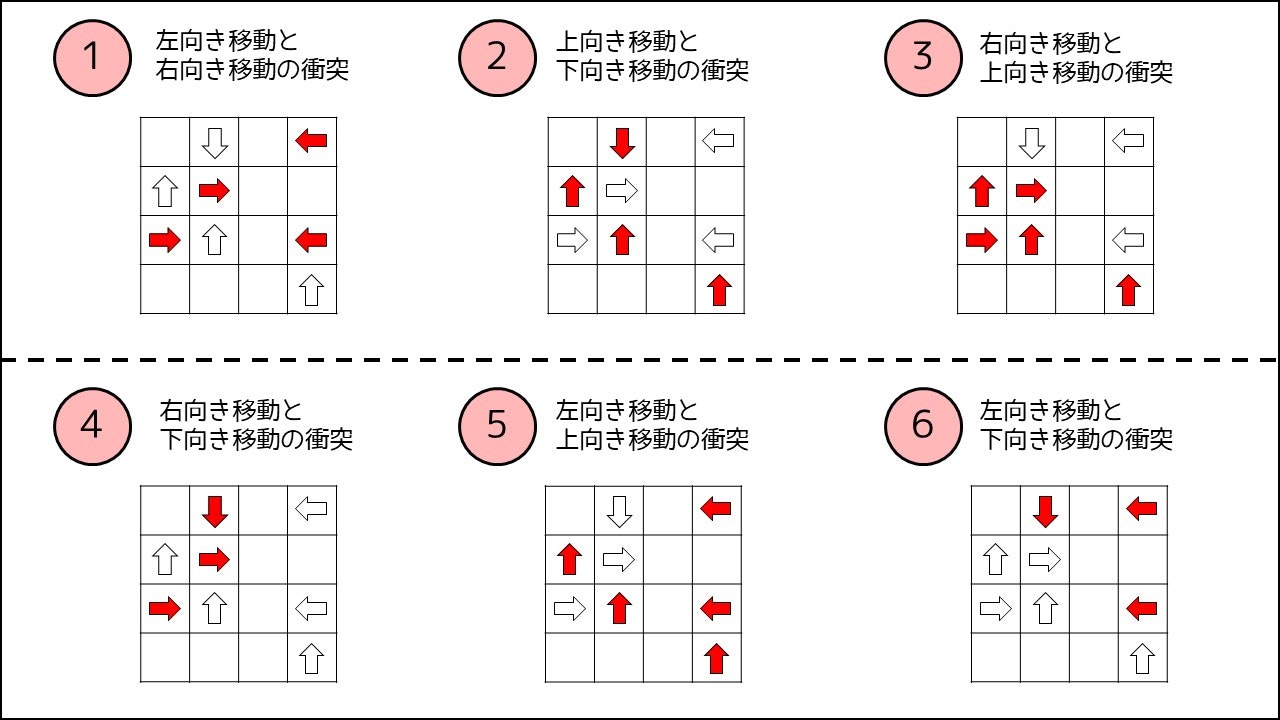
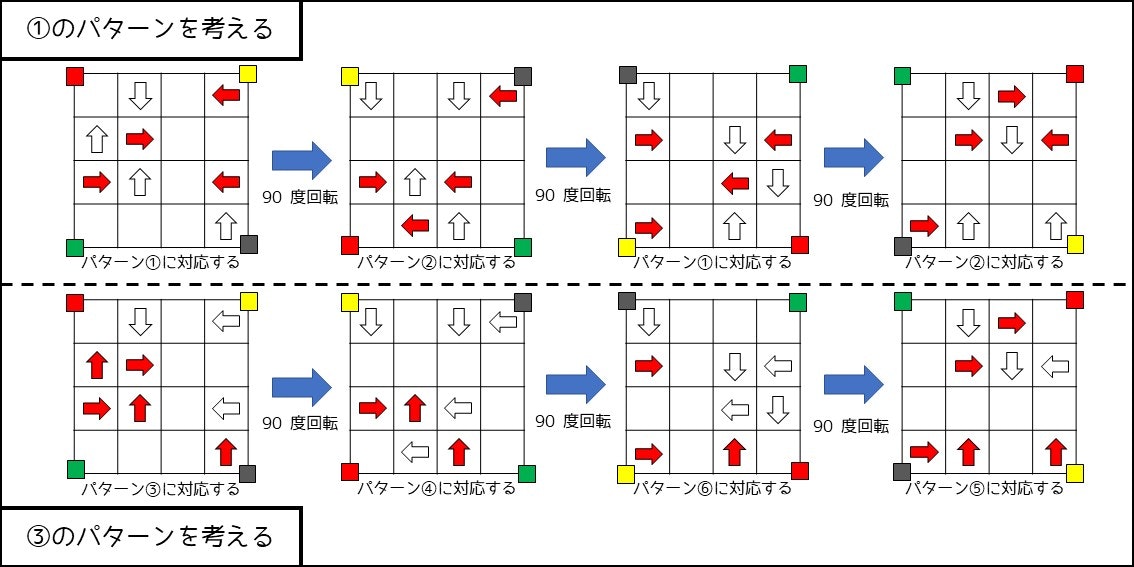
しかし、「座標を 90 度回転させること」を 4 回することによって、①と③のパターンしか考える必要がなくなり、実装量が大幅に減ります。詳しくは公式解説 p. 13-15をお読みください。
【番外】その他の実装テクニック
(2020/7/30 23:21 追記)
本章で紹介した 14 個のテクニック以外にも様々なテクニックがあります。これには私が意識していなかったが、他の人からの指摘などで気づいたものもあります。
- デバッグする時に assertion する
- $i, j, k, l$ だけではないループ変数($x, y, lx, ly, rx, ry$ など)を検討する
- ブロック文で積極的にスコープを切る
- バグらせた時に print デバッグ(適当なケースで試す時、出力をすることでデバッグする手法)を使う
- 4 個以上の引数をもつ配列を使いたいとき、構造体(struct 型)などを多用する
- 区間を扱うとき、半開区間で統一する
- バグらせた時にチェッカーを書く(実行速度が遅いが小さい入力で動くプログラムを書き、ランダムケースで試すことで、どのケースで間違っているかを確認する)
- バグらせた時にブレークポイントを打つ
- バグらせた時に部分部分(実装ステップごと)に分けてデバッグする
4. 実践編 ~実際にプログラムを改善してみる~
最後に、3 章で紹介した 14 個のテクニックを利用して、実際に人のコードを改善してみたいと思います。分かりやすいように、ステップを追って解説します。例として以下の問題を考えましょう。
4-1. 今回考える問題
$H$ 行 $W$ 列のマス目があります。上から $i$ 行目、左から $j$ 列目のマスを $(i, j)$ するとき、マス $(i, j)$ の地価は $A_{i, j}$ 円です。また、家を建設するのに、1 マス当たり $K$ 円かかります。
Qiita 君は $V$ 円を持っています。彼は予算の範囲内で、できるだけ大きい長方形領域を買い、購入した土地全体に家を建設することを考えます。最大で面積いくつの家を建設することができるでしょうか。
【出典】
【制約】
- $1 \leq H, W \leq 125$
- $1 \leq A_{i, j}, K, V \leq 10^{9}$
【入力例】
たとえば $(H, W) = (3, 3)$ で、下図の通りの地価の場合は、左上マス $(2, 2)$、右下マス $(3, 3)$ の長方形領域を買うのが最適です。その場合、面積 $4$ の家を建設できます。
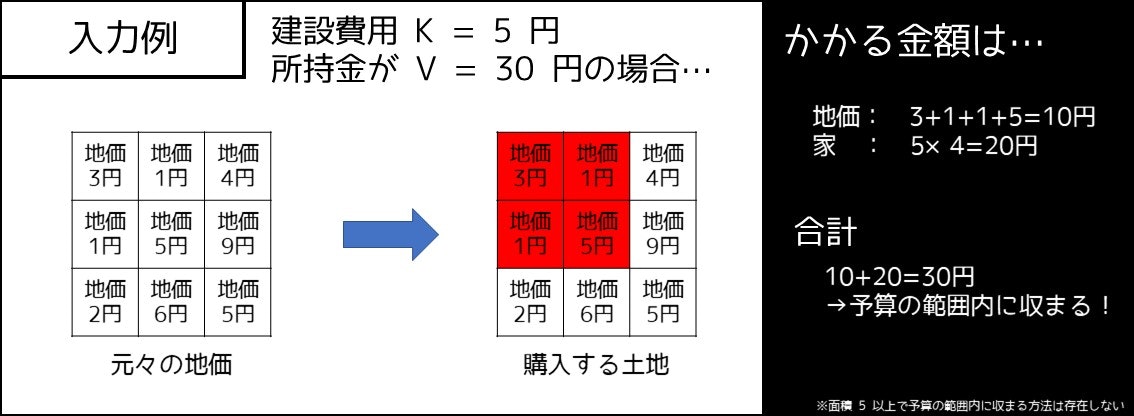
【解法】
長方形領域は $H, W = 125$ の最大ケースでも高々 $6200$ 万通り程度しか存在しないため、長方形領域を全探索することを考えます。
選ぶ長方形領域が決まったとき、家の建設費用は $K \times (マス目の数)$ なので $O(1)$ で計算できます。一方、合計地価は単純に計算すると $HW$ 回の計算が必要なので、二次元累積和というテクニックを使います。詳しくは以下の記事をお読みください。
この問題では、$1 \leq i \leq p, 1 \leq j \leq q$ についての $A_{i, j}$ の和を $B_{p, q}$ とするとき、左上座標 $(sx, sy)$、右下座標 $(gx, gy)$ の二次元領域に関する地価の和 $C$ は以下の式で表されます。
$$C = B_{sx-1, sy-1} + B_{gx, gy} - B_{sx-1, gy} - B_{gx, sy-1}$$
そうすると、合計地価の値も $O(1)$4 で計算できます。コンピューターの計算速度は $1$ 秒あたりおよそ $10^8$ ~ $10^9$ 回程度なので、実行時間制限である $2$ 秒に間に合います。5
【さらに速い解法(今回扱うコードの解法)】
左上のマス $(sx, sy)$ を固定することを考えます。
そこで、右下の x 座標 $gx$ を $W, W-1, W-2, ..., sx$ といった感じで範囲を狭めていくと、$gy$ の最大値は必ず増えていきます。例えば入力例で、左上マスを $(sx, sy) = (1, 1)$ とするとき、
- $gx=3$ のとき、$gy \leq 1$ まで建設できる
- $gx=2$ のとき、$gy \leq 2$ まで建設できる
- $gx=1$ のとき、$gy \leq 3$ まで建設できる
という感じになります。この性質を利用して、最初の解法の通りに累積和を用いて $gy$ の最大値を計算すると、各 $(sx, sy)$ について $O(H+W)$ で面積の最大値が判定できます。したがって、合計すると計算量が $O(HW(H+W))$ となり、とても高速に動きます。解法のイメージは下図の通りです。
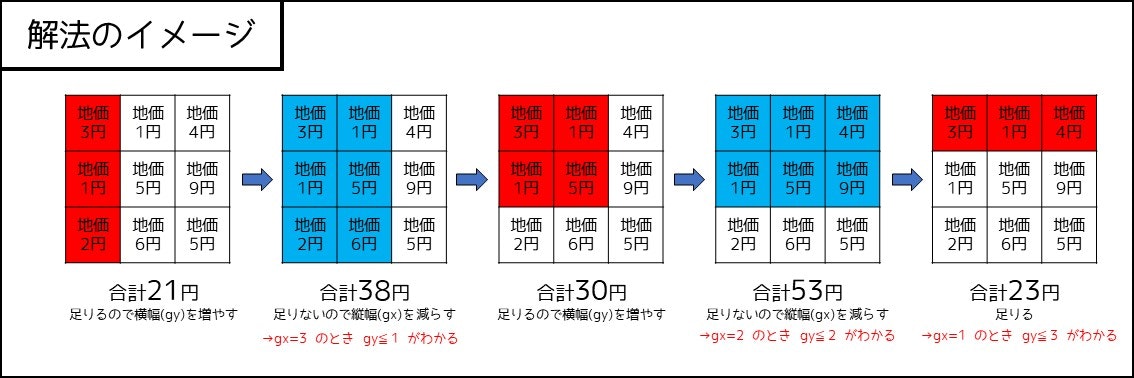
この解法は比較的難しいですが、理解できなくても 4-2. 節以降を読み進められる構成にしているので、ご安心ください。
解法はわかりましたでしょうか。この問題は、AtCoder Beginner Contest だと D 問題相当のレベルですが、実装が少し難しいです。そこで、4-2. 節以降では人のコードを「実装しやすくデバッグしやすいコード」に変えていきたいと思います。
4-2. 他の人の実装コード例
今回は、良い例として
を改善することを考えます。彼のソースコードは以下のようになります。(本人の許可を取っており、テンプレートを外すなどの多少の編集をしています)
# include <bits/stdc++.h>
using namespace std;
int main(void){
long long i,j,H,W,x,y,K,V,ans=0;cin>>H>>W>>K>>V;
static long long wa[126][126]={};
for(i=1;i<=H;i++){
for(j=1;j<=W;j++){
cin>>wa[i][j];
wa[i][j]+=K;
wa[i][j]+=wa[i-1][j]+wa[i][j-1]-wa[i-1][j-1];
}
}
for(i=0;i<H;i++){
for(j=0;j<W;j++){
int y=i,x=W;
while(true){
if(x<=j||y>H){break;}
long long cost=wa[y][x]+wa[i][j]-wa[y][j]-wa[i][x];
if(cost<=V){
ans=max(ans,1LL*(y-i)*(x-j));
y++;
}else{x--;}
}
}
}
cout<<ans<<endl;
return 0;
}
このコードは AC(正解)を出すのですが、少しだけプログラムが読みにくい気がします。
エンジニアを 10 年以上やっている方や、競技プログラミングで青コーダー以上の実力を持つような方の多くは、多少読みにくいコードでも一瞬でプログラムの構造をつかみ、バグ取りなどを行うことができるのですが、初級者プログラマなどそうでない人にとっては読むのに数分以上かかってしまいます。
4-3. 実装コードを改善してみる
そこで、3 章で紹介した 14 個の実装テクニックのうちいくつかを利用することで、ソースコードを改善してみることを考えます。
ステップ 1. 「コードのインデント整理」と「コメント」を付ける
まず最初の段階として、重要度 ![]() 5 が付いている
5 が付いている
に関して、修正することを考えます。
ステップ 1-A. インデント整理
Visual Studio 2019 で「Ctrl+K」→「Ctrl+D」を押すことで修正しました。簡単です。
ステップ 1-B. コメントを付ける
およそ 30-40 行のコードなので 3 ステップに分割します。このプログラムは「入力部分」「全探索部分」「出力部分」の 3 つに分けられているので、適切にコメントを付けました。
ステップ 1-C. 問題との変数合わせ
$H, W, K, V$ については問題文の通りですが、$A_{i, j}$ が定義されておらず、そのまま変数 wa に入力しています。通常の場合では問題文の変数と合わせるのですが、今回の場合は合わせるとソースコードが長くなってしまうため、修正しないことにします。(ただし、変更しても良いです。これは読者の感覚に任せます)
そのような改善を行うと、ソースコードは以下のようになります。以前に比べてかなりプログラムの構造が見やすくなったのではないかと思います。
# include <bits/stdc++.h>
using namespace std;
int main(void) {
long long i, j, H, W, x, y, K, V, ans = 0;
static long long wa[126][126] = {};
// ステップ 1. 入力
cin >> H >> W >> K >> V;
for (i = 1; i <= H; i++) {
for (j = 1; j <= W; j++) {
cin >> wa[i][j];
wa[i][j] += K;
wa[i][j] += wa[i - 1][j] + wa[i][j - 1] - wa[i - 1][j - 1];
}
}
// ステップ 2. 全探索による計算
for (i = 0; i < H; i++) {
for (j = 0; j < W; j++) {
int y = i, x = W;
while (true) {
if (x <= j || y > H) { break; }
long long cost = wa[y][x] + wa[i][j] - wa[y][j] - wa[i][x];
if (cost <= V) {
ans = max(ans, 1LL * (y - i) * (x - j));
y++;
}
else { x--; }
}
}
}
// ステップ 3. 出力
cout << ans << endl;
return 0;
}
ステップ 2. 変数を合わせ、for / if の書き方を統一する
次に、重要度 ![]() 4、
4、![]() 3が付いている、
3が付いている、
- 3-4. 節で紹介した、「Goto 文の消去」
- 3-6. 節で紹介した、「for / if 文の書き方の統一」
- 3-10. 節で紹介した、「変数名の統一」
- 3-11. 節で紹介した、「グローバル変数にコメントを付けるテクニック」
に関して、修正することを考えます。
ステップ 2-A. Goto 文の消去
元々のソースコードの時点で Goto 文は存在しないため、修正はしませんでした。この点では、最初の時点で読みやすいといえます。
ステップ 2-B. for / if の書き方を統一する
まず、for 文で使用する変数 $i, j$ は main 関数内に定義されていますが、それだと他の変数と混ざってしまい、実装が少しやりにくくなります。そこで、for 文の中に $i, j$ などの変数を定義するように修正しました。
ステップ 2-C. 変数名の統一
ここでは、累積和は wa、答えは ans という変数に記録されていますが、各役割に対してどのように変数名を定義するかは人それぞれの自由なので、特に修正しません。しかし、「自分がどんな変数名を使うのか」ということは、予め決めておいた方が良いです。
ステップ 2-D. グローバル変数にコメントを付ける
ここでは、便宜上すべての変数をグローバル変数に置き換えることにします。理由としては、
- 大きい配列(3000×3000など)を main 関数内に定義すると、スタックオーバーフローを起こす場合がある
- 競プロでは、グローバル変数でまとめた方が読みやすく、デバッグがしやすい場合の方が多い
からです。そこで、x, y, i, j 以外の全ての変数をグローバル変数に移したうえで、「入力で使われる変数」「出力に使われる変数」に分け、適切にコメントを付けておきました。
そのような改善を行うと、ソースコードは以下のようになります。4-2. 節で紹介した最初のプログラムに比べて、かなりプログラムの構造が見やすくなったのではないかと思います。
# include <bits/stdc++.h>
using namespace std;
// 入力
long long H, W, K, V;
long long wa[126][126];
// 出力
long long ans = 0;
int main(void) {
// ステップ 1. 入力
cin >> H >> W >> K >> V;
for (int i = 1; i <= H; i++) {
for (int j = 1; j <= W; j++) {
cin >> wa[i][j];
wa[i][j] += K;
wa[i][j] += wa[i - 1][j] + wa[i][j - 1] - wa[i - 1][j - 1];
}
}
// ステップ 2. 全探索による計算
for (int i = 0; i < H; i++) {
for (int j = 0; j < W; j++) {
int y = i, x = W;
while (true) {
if (x <= j || y > H) { break; }
long long cost = wa[y][x] + wa[i][j] - wa[y][j] - wa[i][x];
if (cost <= V) {
ans = max(ans, 1LL * (y - i) * (x - j));
y++;
}
else { x--; }
}
}
}
// ステップ 3. 出力
cout << ans << endl;
return 0;
}
5. 注意
最後に、今回私が紹介した「良い実装のやり方」に、いくつか注意点があるので、これについて解説します。
5-1. 慣れる実装のやり方は人それぞれ違う
3 章では 14 個の実装テクニックを紹介しました。しかし、それは私が今まで競技プログラミングをやってきた経験に基づいたものであり、一般論ではありません。
また、慣れている実装のやり方も、人それぞれ違うと思います。例えば、一部の人は初めにマクロを作るという戦略に出ています。多少読みやすさは落ちますが、コード長が削減できるので、慣れている人なら実装やデバッグもしやすいと思っています。
有名なマクロの例として、以下が挙げられます。やっていることは、for 文で $i = 0, 1, ..., n-1$ でループを回すのと同じです。
# define rep(i,n) for(int i=0;i<(int)(n);i++)
// for 文を書く時
rep(i, n) {
// ここに処理を書く
}
そのように、慣れる実装の仕方は人それぞれなので、競プロでは 14 個のテクニックの中で自分に合うものを選んで利用するのも良いと思います。
5-2. 実務でのコードの書き方とは異なる点がいくつかある
もう一つの注意として、「競プロでの良い実装の仕方」と「実務での良い実装の仕方」に一部相違点があるといえます。理由としては、求められる目標が異なるからです。
競プロでは、
- 制限時間内に素早く実装でき、かつバグが出さないプログラムの実装
が求められているのに対し、開発などの実務では、
- チームで活動することが多いので、誤解を生みにくいプログラムの実装が求められる
- そもそも Web 開発などの場合コードが数千行単位と非常に長く、複数のファイルにまたがる場合も多いため、エラーやバグが起こる主な原因が競プロと全然違う
などが挙げられます。例えば、本記事ではグローバル変数を推奨していますが、開発ではあまり推奨されません。開発での良い実装方針について知りたい方は、以下の記事をご覧ください。
したがって、競プロと開発を両方するような人は、実装方針を使い分けるのが重要です。
6. おわりに
競技プログラミングでは、解法を思いつく力だけでなく、実装力も大切です。したがって、正しい実装テクニックを身に付けることは大切です。
しかし、今回私が紹介した 14 個のテクニックは経験に基づいたものであり、自分に合った実装テクニックを選ぶのはとても重要なので、もし他に良い実装テクニック等があればコメントお願いします。
最後に、本記事が少しでも「実装が苦手な方」に役立ち、実装力の向上に繋ぐことができたならば、とても嬉しい気持ちです。高校生が書いた記事ですので分かりにくい部分も多かったかと思われますが、最後までお読みいただきありがとうございました。