グラフ理論の基礎 - Basics of Graph Theory -
ねらい
グラフ理論の基礎を学ぶ
- グラフ (graph)、頂点 (vertex, node) 、辺 (edge)
- 連結リスト (linked list)、次数 (degree)
- 深さ優先探索 (depth-first search) 、幅優先探索 (width-first search)
- 連結成分 (connected components, connected subgraph, cluster) 、シングルトン (singleton)
- 切断点 (cut vertices) 、切断辺 (cut edges)
- 経路 (path) 、閉路 (cycle)
- 最小木 (minimum spanning tree)、最短経路 (shortest path)
- 巡回セールスマン問題 (traveling salesman problem, TSP) 、中国人郵便配達問題 (Chinese postman problem)
- ハミルトングラフ (Hamilton graph)、オイラーグラフ (Eulerian graph)
- ハミルトンパス問題 (Hamilton path problem)、オイラーパス問題 (Eulerian path problem)
- de Bruijn Graph を使ったNGSデータの de novo アセンブリ
- グラフ同型問題 (graph isomorphism problem) 、化学情報学 (cheminformatics)
- 最大流問題 （maximum flow problem）、代謝流束解析 (metabolic flux balance analysis, FBA)
グラフ (graph)、頂点 (vertex, node) 、辺 (edge)
グラフ （Graph） とは、 頂点 (vertex, node) 群とその間の連結関係を表す 辺 (edge） 群で構成される抽象データ型である。グラフは G=(V,E) で表され、V は頂点 （vertices） の集合、E は頂点と頂点をつなぐ辺 （edges） の集合である。
(図の出典：http://www.slideshare.net/KMC_JP/graph-and-tree)
例として、日本の都道府県の県庁所在地の緯度・経度のデータを使います。
まずはデータ (Longitude and latitude of the prefectural capitals of Japan) のダウンロードから
# ウェブ上のリソースを指定する
url = 'https://raw.githubusercontent.com/maskot1977/ipython_notebook/master/toydata/location.txt'
# URL によるリソースへのアクセスを提供するライブラリをインポートする。
import urllib # Python 2 の場合
# import urllib.request # Python 3 の場合
# 指定したURLからリソースをダウンロードし、名前をつける。
urllib.urlretrieve(url, 'location.txt') # Python 2 の場合
# urllib.request.urlretrieve(url, 'location.txt') # Python 3 の場合
('location.txt', <httplib.HTTPMessage instance at 0x106118e60>)
# 先頭数行の確認
!head location.txt
Town,Longitude,Latitude
Sapporo,43.06417,141.34694
Aomori,40.82444,140.74
Morioka,39.70361,141.1525
Sendai,38.26889,140.87194
Akita,39.71861,140.1025
Yamagata,38.24056,140.36333
Fukushima,37.75,140.46778
Mito,36.34139,140.44667
Utsunomiya,36.56583,139.88361
# ダウンロードしたデータから、列ごとに数字を読み込んでリストに格納する。
col1 = [] # ０列目の数字を格納する予定のリスト
col2 = [] # １列目の数字を格納する予定のリスト
col3 = [] # ２列目の数字を格納する予定のリスト
for i, line in enumerate(open('location.txt')): # ファイルを開いて一行一行読み込む
if i == 0: # ０番目の行の場合
continue # 次の行に行く
c = line.split(",") # 行をコンマで分割したものをcというリストに入れる
col1.append(c[0]) # ０列目の単語col1に入れる
col2.append(float(c[1])) # １列目の単語を実数に変換してcol2に入れる
col3.append(float(c[2])) # ２列目の単語を実数に変換してcol3に入れる
# 都市名のリストの中身を確認する。
print (col1)
['Sapporo', 'Aomori', 'Morioka', 'Sendai', 'Akita', 'Yamagata', 'Fukushima', 'Mito', 'Utsunomiya', 'Maebashi', 'Saitama', 'Chiba', 'Tokyo', 'Yokohama', 'Niigata', 'Toyama', 'Kanazawa', 'Fukui', 'Kofu', 'Nagano', 'Gifu', 'Shizuoka', 'Nagoya', 'Tsu', 'Otsu', 'Kyoto', 'Osaka', 'Kobe', 'Nara', 'Wakayama', 'Tottori', 'Matsue', 'Okayama', 'Hiroshima', 'Yamaguchi', 'Tokushima', 'Takamatsu', 'Matsuyama', 'Kochi', 'Fukuoka', 'Saga', 'Nagasaki', 'Kumamoto', 'Oita', 'Miyazaki', 'Kagoshima', 'Naha']
問題1: 緯度のリスト、経度のリストの中身を確認してみましょう。
データの図示
Visualization
# 図やグラフを図示するためのライブラリをインポートする。
import matplotlib.pyplot as plt
%matplotlib inline
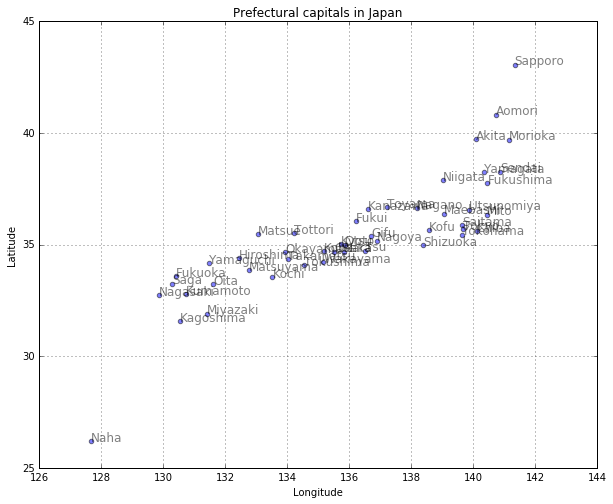
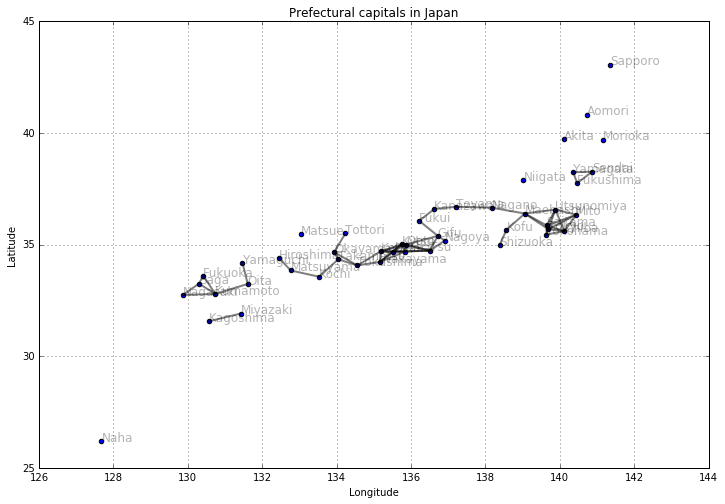
#都市をプロットする
plt.figure(figsize=(10, 8))
plt.scatter(col3, col2, alpha=0.5)
plt.title("Prefectural capitals in Japan")
plt.xlabel("Longitude")
plt.ylabel("Latitude")
plt.grid(True)
for city, x, y in zip(col1, col3, col2):
plt.text(x, y, city, alpha=0.5, size=12)
plt.show()
問題2: 都市名を書かずに、点だけプロットした図を作成してみましょう。
都市間の距離を求める
Distances between cities
# 都市間の距離を求める関数を作る。
import math
def distance(x1, y1, x2, y2):
return math.sqrt((x1 - x2)**2 + (y1 - y2)**2)
# すべての都市間で都市間の距離を計算する。
dist = []
for i, city1 in enumerate(zip(col1, col3, col2)):
for j, city2 in enumerate(zip(col1, col3, col2)):
if i >= j:
continue
dist.append(distance(city1[1], city1[2], city2[1], city2[2]))
# 図やグラフを図示するためのライブラリをインポートする。
import matplotlib.pyplot as plt
%matplotlib inline
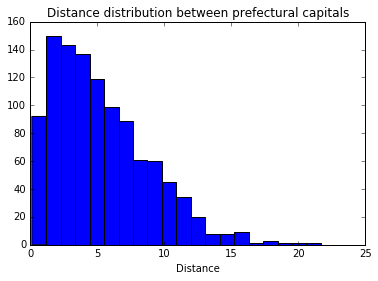
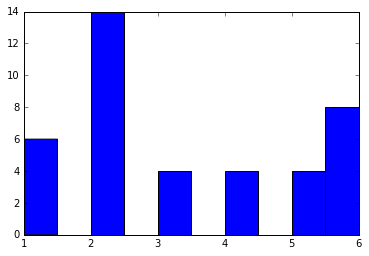
# 都市間距離の分布を見る
plt.hist(dist, bins=20)
plt.title("Distance distribution between prefectural capitals")
plt.xlabel("Distance")
plt.show()
都市間に辺を引く
Draw edges between cities
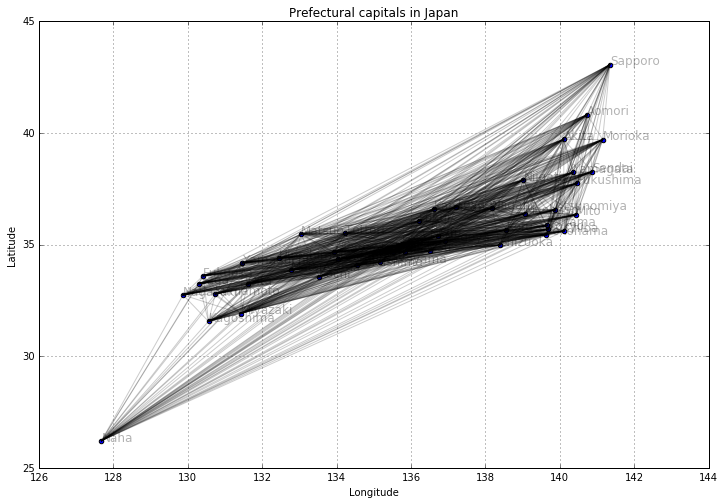
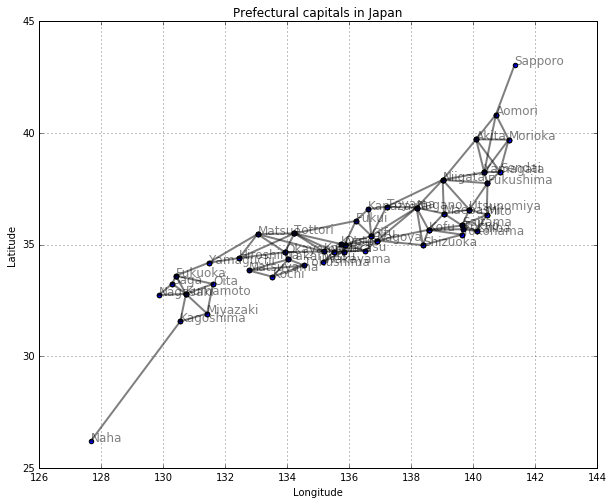
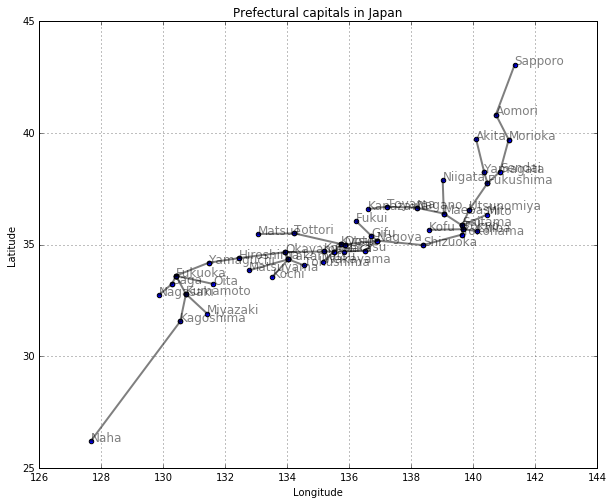
すべての都市間に辺を引く
# 図やグラフを図示するためのライブラリをインポートする。
import matplotlib.pyplot as plt
%matplotlib inline
#すべての都市間に辺を引く
plt.figure(figsize=(12, 8))
plt.title("Prefectural capitals in Japan")
plt.xlabel("Longitude")
plt.ylabel("Latitude")
plt.grid(True)
for city1, x1, y1 in zip(col1, col3, col2):
for city2, x2, y2 in zip(col1, col3, col2):
if city1 >= city2:
continue
plt.plot([x1, x2], [y1, y2], 'k-', alpha=0.2)
plt.scatter(col3, col2)
for city, x, y in zip(col1, col3, col2):
plt.text(x, y, city, alpha=0.3, size=12)
plt.show()
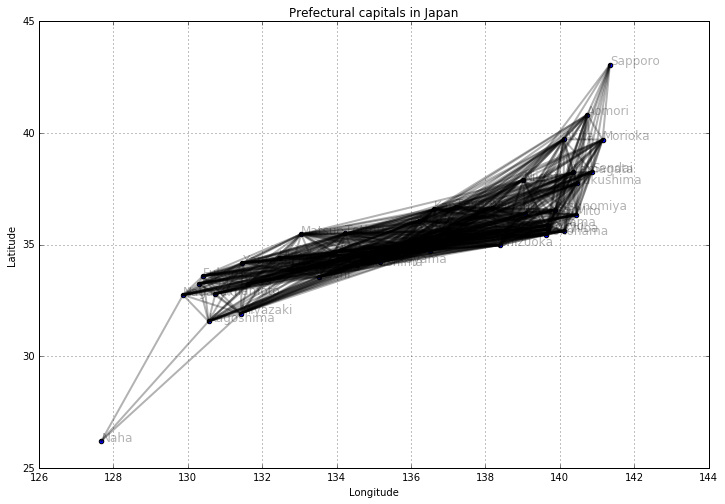
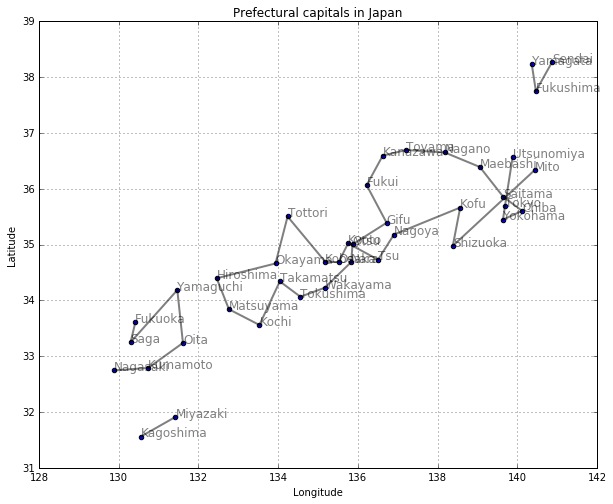
水平移動距離7以下の都市間だけ線を引く
# 図やグラフを図示するためのライブラリをインポートする。
import matplotlib.pyplot as plt
%matplotlib inline
#水平移動距離7以下の都市間だけ線を引く
plt.figure(figsize=(12, 8))
plt.title("Prefectural capitals in Japan")
plt.xlabel("Longitude")
plt.ylabel("Latitude")
plt.grid(True)
for city1, x1, y1 in zip(col1, col3, col2):
for city2, x2, y2 in zip(col1, col3, col2):
if city1 >= city2:
continue
if distance(x1, y1, x2, y2) > 7:
continue
plt.plot([x1, x2], [y1, y2], 'k-', alpha=0.3, lw=2)
plt.scatter(col3, col2)
for city, x, y in zip(col1, col3, col2):
plt.text(x, y, city, alpha=0.3, size=12)
plt.show()
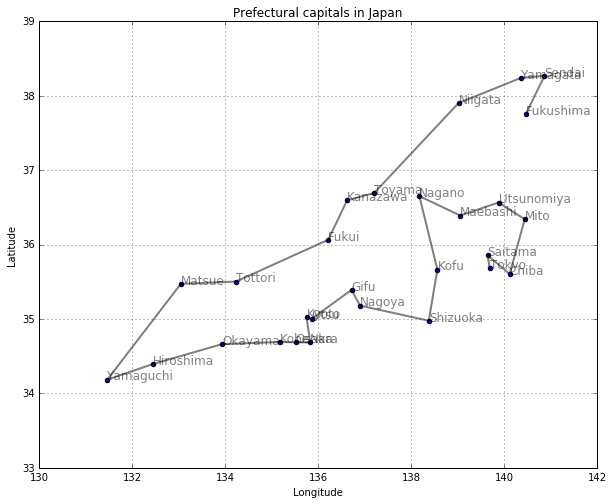
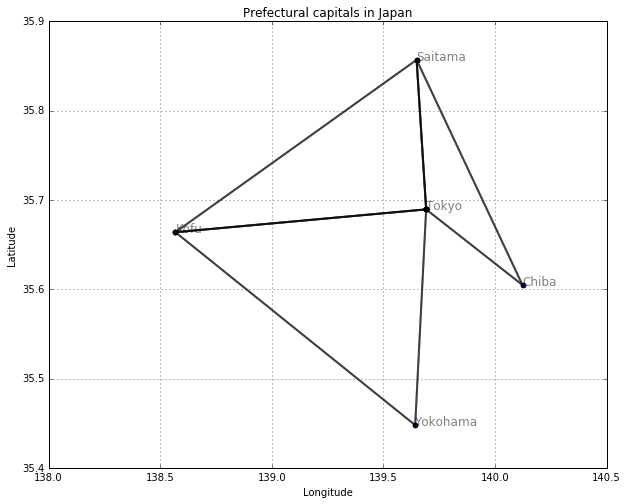
水平移動距離１以下の都市間だけ線を引く
# 図やグラフを図示するためのライブラリをインポートする。
import matplotlib.pyplot as plt
%matplotlib inline
#水平移動距離１以下の都市間だけ線を引く
plt.figure(figsize=(12, 8))
plt.title("Prefectural capitals in Japan")
plt.xlabel("Longitude")
plt.ylabel("Latitude")
plt.grid(True)
for city1, x1, y1 in zip(col1, col3, col2):
for city2, x2, y2 in zip(col1, col3, col2):
if city1 >= city2:
continue
if distance(x1, y1, x2, y2) > 1:
continue
plt.plot([x1, x2], [y1, y2], 'k-', alpha=0.5, lw=2)
plt.scatter(col3, col2)
for city, x, y in zip(col1, col3, col2):
plt.text(x, y, city, alpha=0.3, size=12)
plt.show()
問題3: 水平移動距離2以下の都市間だけ線を引いた場合に、どのようなネットワークが描けるか確認してみましょう。
上の図で、いくつかの「連結成分(connected components, connected subgraphs)」が見えています。連結成分のことをクラスター(clusters)と呼ぶこともあります。要素が１つしか存在しないクラスターのことをシングルトン（singleton）と呼びます。連結成分の取り出し方について、以下で説明します。
辺のリストを得る
List of edges
連結している都市の組をすべて取り出します。ここで、「連結している都市の組」とは、「水平移動距離１以下の都市の組」を指すものとします。
edges = []
for i, city1 in enumerate(zip(col1, col3, col2)):
for j, city2 in enumerate(zip(col1, col3, col2)):
if i >= j:
continue
if distance(city1[1], city1[2], city2[1], city2[2]) > 1:
continue
edges.append((city1[0], city2[0]))
print (edges)
[('Sendai', 'Yamagata'), ('Sendai', 'Fukushima'), ('Yamagata', 'Fukushima'), ('Mito', 'Utsunomiya'), ('Mito', 'Saitama'), ('Mito', 'Chiba'), ('Mito', 'Tokyo'), ('Utsunomiya', 'Maebashi'), ('Utsunomiya', 'Saitama'), ('Utsunomiya', 'Chiba'), ('Utsunomiya', 'Tokyo'), ('Maebashi', 'Saitama'), ('Maebashi', 'Tokyo'), ('Maebashi', 'Kofu'), ('Maebashi', 'Nagano'), ('Saitama', 'Chiba'), ('Saitama', 'Tokyo'), ('Saitama', 'Yokohama'), ('Chiba', 'Tokyo'), ('Chiba', 'Yokohama'), ('Tokyo', 'Yokohama'), ('Toyama', 'Kanazawa'), ('Toyama', 'Nagano'), ('Kanazawa', 'Fukui'), ('Fukui', 'Gifu'), ('Kofu', 'Shizuoka'), ('Gifu', 'Nagoya'), ('Gifu', 'Tsu'), ('Gifu', 'Otsu'), ('Nagoya', 'Tsu'), ('Tsu', 'Otsu'), ('Tsu', 'Kyoto'), ('Tsu', 'Osaka'), ('Tsu', 'Nara'), ('Otsu', 'Kyoto'), ('Otsu', 'Osaka'), ('Otsu', 'Kobe'), ('Otsu', 'Nara'), ('Kyoto', 'Osaka'), ('Kyoto', 'Kobe'), ('Kyoto', 'Nara'), ('Kyoto', 'Wakayama'), ('Osaka', 'Kobe'), ('Osaka', 'Nara'), ('Osaka', 'Wakayama'), ('Kobe', 'Nara'), ('Kobe', 'Wakayama'), ('Kobe', 'Tokushima'), ('Nara', 'Wakayama'), ('Wakayama', 'Tokushima'), ('Tottori', 'Okayama'), ('Okayama', 'Tokushima'), ('Okayama', 'Takamatsu'), ('Hiroshima', 'Matsuyama'), ('Yamaguchi', 'Oita'), ('Tokushima', 'Takamatsu'), ('Takamatsu', 'Kochi'), ('Matsuyama', 'Kochi'), ('Fukuoka', 'Saga'), ('Fukuoka', 'Kumamoto'), ('Saga', 'Nagasaki'), ('Saga', 'Kumamoto'), ('Nagasaki', 'Kumamoto'), ('Kumamoto', 'Oita'), ('Miyazaki', 'Kagoshima')]
連結リストを作成する
Linked list
どの頂点がどの頂点と連結しているかを表すデータ構造を「連結リスト」と言います。たとえば、水平移動距離が1以下の都市を「連結している」とみなした場合の連結リスト neighbor1 を作ってみましょう。
neighbor1 = {}
for i, city1 in enumerate(zip(col1, col3, col2)):
for j, city2 in enumerate(zip(col1, col3, col2)):
if i >= j:
continue
if distance(city1[1], city1[2], city2[1], city2[2]) > 1:
continue
if city1[0] not in neighbor1.keys():
neighbor1.update({city1[0]:[]})
if city2[0] not in neighbor1[city1[0]]:
neighbor1[city1[0]].append(city2[0])
if city2[0] not in neighbor1.keys():
neighbor1.update({city2[0]:[]})
if city1[0] not in neighbor1[city2[0]]:
neighbor1[city2[0]].append(city1[0])
print (neighbor1)
{'Utsunomiya': ['Mito', 'Maebashi', 'Saitama', 'Chiba', 'Tokyo'], 'Wakayama': ['Kyoto', 'Osaka', 'Kobe', 'Nara', 'Tokushima'], 'Nagasaki': ['Saga', 'Kumamoto'], 'Tokyo': ['Mito', 'Utsunomiya', 'Maebashi', 'Saitama', 'Chiba', 'Yokohama'], 'Okayama': ['Tottori', 'Tokushima', 'Takamatsu'], 'Miyazaki': ['Kagoshima'], 'Nagano': ['Maebashi', 'Toyama'], 'Toyama': ['Kanazawa', 'Nagano'], 'Maebashi': ['Utsunomiya', 'Saitama', 'Tokyo', 'Kofu', 'Nagano'], 'Nagoya': ['Gifu', 'Tsu'], 'Chiba': ['Mito', 'Utsunomiya', 'Saitama', 'Tokyo', 'Yokohama'], 'Sendai': ['Yamagata', 'Fukushima'], 'Tokushima': ['Kobe', 'Wakayama', 'Okayama', 'Takamatsu'], 'Kofu': ['Maebashi', 'Shizuoka'], 'Oita': ['Yamaguchi', 'Kumamoto'], 'Kobe': ['Otsu', 'Kyoto', 'Osaka', 'Nara', 'Wakayama', 'Tokushima'], 'Otsu': ['Gifu', 'Tsu', 'Kyoto', 'Osaka', 'Kobe', 'Nara'], 'Tsu': ['Gifu', 'Nagoya', 'Otsu', 'Kyoto', 'Osaka', 'Nara'], 'Nara': ['Tsu', 'Otsu', 'Kyoto', 'Osaka', 'Kobe', 'Wakayama'], 'Hiroshima': ['Matsuyama'], 'Matsuyama': ['Hiroshima', 'Kochi'], 'Fukui': ['Kanazawa', 'Gifu'], 'Kagoshima': ['Miyazaki'], 'Saitama': ['Mito', 'Utsunomiya', 'Maebashi', 'Chiba', 'Tokyo', 'Yokohama'], 'Fukuoka': ['Saga', 'Kumamoto'], 'Takamatsu': ['Okayama', 'Tokushima', 'Kochi'], 'Saga': ['Fukuoka', 'Nagasaki', 'Kumamoto'], 'Kyoto': ['Tsu', 'Otsu', 'Osaka', 'Kobe', 'Nara', 'Wakayama'], 'Osaka': ['Tsu', 'Otsu', 'Kyoto', 'Kobe', 'Nara', 'Wakayama'], 'Gifu': ['Fukui', 'Nagoya', 'Tsu', 'Otsu'], 'Shizuoka': ['Kofu'], 'Kumamoto': ['Fukuoka', 'Saga', 'Nagasaki', 'Oita'], 'Mito': ['Utsunomiya', 'Saitama', 'Chiba', 'Tokyo'], 'Yokohama': ['Saitama', 'Chiba', 'Tokyo'], 'Fukushima': ['Sendai', 'Yamagata'], 'Yamagata': ['Sendai', 'Fukushima'], 'Yamaguchi': ['Oita'], 'Kanazawa': ['Toyama', 'Fukui'], 'Tottori': ['Okayama'], 'Kochi': ['Takamatsu', 'Matsuyama']}
次数 (degree)
Degree - the number of edges for a vertex
次数 (degree)とは、グラフの頂点ごとの辺の数です。得られた連結リスト neighbor1 を用いて、次数の分布を見てみましょう。
# 図やグラフを図示するためのライブラリをインポートする。
import matplotlib.pyplot as plt
%matplotlib inline
plt.hist([len(x) for x in neighbor1.values()])
plt.show()
問題4: 水平移動距離が2以下の都市を「連結している」とみなした場合の連結リスト neighbor2 を作り、その次数分布を見てください。
深さ優先探索 (depth-first search, DFS)
深さ優先探索は、木やグラフを探索するためのアルゴリズムです。アルゴリズムは根から(グラフの場合はどのノードを根にするか決定する)始まり、バックトラックするまで可能な限り探索を行ないます。「縦型探索」とも呼ばれます。
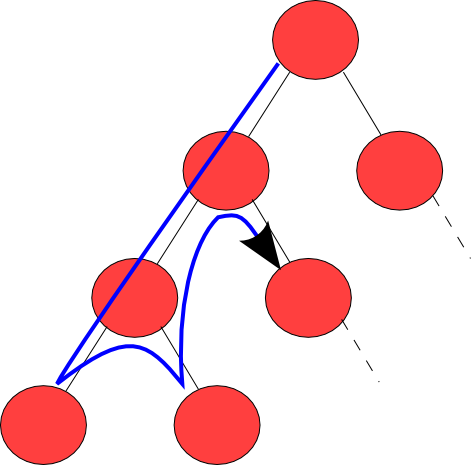
（図の出典：https://upload.wikimedia.org/wikipedia/commons/2/2c/Depthfirst.png）
まず関数の作成から。
def depth_first(neighbor, start):
visited = []
stack = []
stack.append(start)
result = []
while len(stack) > 0:
next_city = stack.pop()
if next_city in visited:
continue
result.append(next_city)
visited.append(next_city)
for nei in neighbor[next_city]:
stack.append(nei)
return [result]
東京を始点として深さ優先探索をしてみましょう。
print (depth_first(neighbor1, 'Tokyo'))
[['Tokyo', 'Yokohama', 'Chiba', 'Saitama', 'Maebashi', 'Nagano', 'Toyama', 'Kanazawa', 'Fukui', 'Gifu', 'Otsu', 'Nara', 'Wakayama', 'Tokushima', 'Takamatsu', 'Kochi', 'Matsuyama', 'Hiroshima', 'Okayama', 'Tottori', 'Kobe', 'Osaka', 'Kyoto', 'Tsu', 'Nagoya', 'Kofu', 'Shizuoka', 'Utsunomiya', 'Mito']]
得られた 経路 (path） を図にしてみましょう。まずは、それを実行する関数を作成します。
import matplotlib.pyplot as plt
%matplotlib inline
def draw_path(all_cities, all_xs, all_ys, paths):
city2xy = {}
path_xs = []
path_ys = []
for city, x, y in zip(all_cities, all_xs, all_ys):
city2xy.update({city:[x, y]})
for path in paths:
for city in path:
path_xs.append(city2xy[city][0])
path_ys.append(city2xy[city][1])
plt.figure(figsize=(10, 8))
plt.title("Prefectural capitals in Japan")
plt.xlabel("Longitude")
plt.ylabel("Latitude")
plt.grid(True)
shown_cities = []
for path in paths:
for i in range(len(path) - 1):
city1 = path[i]
city2 = path[i + 1]
x1 = city2xy[city1][0]
y1 = city2xy[city1][1]
x2 = city2xy[city2][0]
y2 = city2xy[city2][1]
plt.plot([x1, x2], [y1, y2], 'k-', alpha=0.5, lw=2)
if city1 not in shown_cities:
shown_cities.append(city1)
if city2 not in shown_cities:
shown_cities.append(city2)
plt.scatter(path_xs, path_ys)
for city in shown_cities:
plt.text(city2xy[city][0], city2xy[city][1], city, alpha=0.5, size=12)
plt.show()
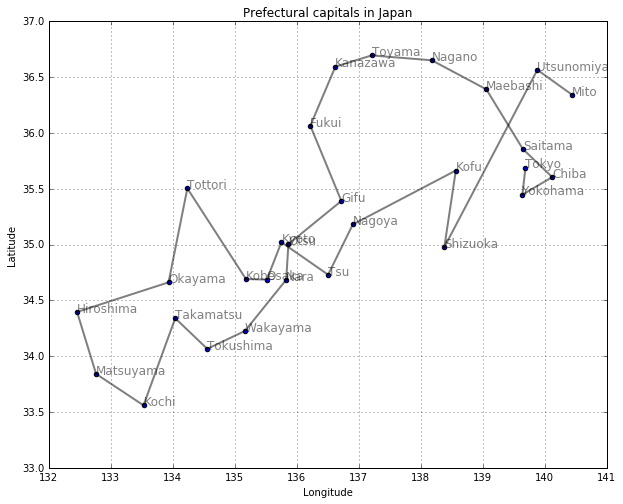
図示してみます。深さ優先探索では、まず行けるところまで遠くに行ってから、引き返すような探索になることがわかります。
draw_path(col1, col3, col2, depth_first(neighbor1, 'Tokyo'))
問題5： 京都からスタートしたらどのような経路になるか確認してみましょう。また、neighbor2を用いたらどうなるか確認してみましょう。
幅優先探索 (breadth first search)
幅優先探索アルゴリズムは根ノードで始まり隣接した全てのノードを探索します。それからこれらの最も近いノードのそれぞれに対して同様のことを繰り返して探索対象ノードをみつけます。「横型探索」とも言われます。深さ優先探索と、幅優先探索の探索順序の違いは下図の通り。
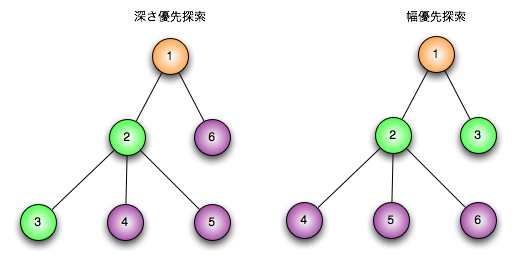
（図の出典：http://www.unfindable.net/images/search/dfs-bfs.png）
まずは関数の作成から。
def width_first(neighbor, start):
visited = []
queue = []
queue.append(start)
result = []
while len(queue) > 0:
next_city = queue.pop(0)
if next_city in visited:
continue
result.append (next_city)
visited.append(next_city)
for nei in neighbor[next_city]:
queue.append(nei)
return [result]
東京を始点として幅優先探索をしてみます。
print (width_first(neighbor1, 'Tokyo'))
[['Tokyo', 'Mito', 'Utsunomiya', 'Maebashi', 'Saitama', 'Chiba', 'Yokohama', 'Kofu', 'Nagano', 'Shizuoka', 'Toyama', 'Kanazawa', 'Fukui', 'Gifu', 'Nagoya', 'Tsu', 'Otsu', 'Kyoto', 'Osaka', 'Nara', 'Kobe', 'Wakayama', 'Tokushima', 'Okayama', 'Takamatsu', 'Tottori', 'Kochi', 'Matsuyama', 'Hiroshima']]
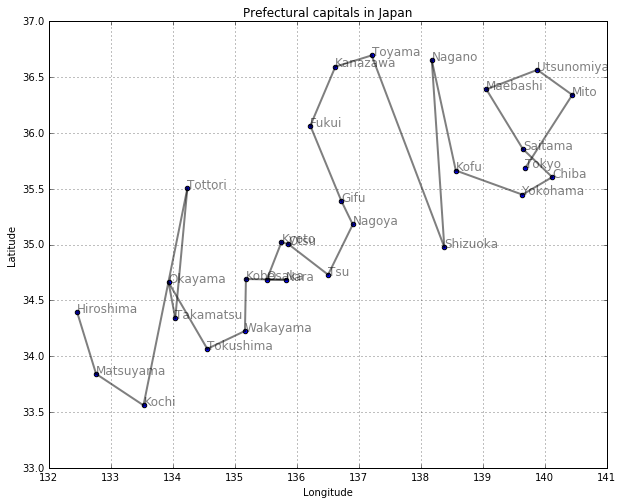
得られたパス（経路）を図にしてみましょう。幅優先探索では、始点からの距離の短い（ステップ数の小さい）場所から行くような探索になることがわかります。
draw_path(col1, col3, col2, width_first(neighbor1, 'Tokyo'))
問題6： 京都からスタートしたらどのような経路になるか確認してみましょう。また、neighbor2を用いたらどんな経路が得られるか確認してください。
連結成分 (connected components, connected subgraphs)
連結成分は、深さ優先探索、幅優先探索のどちらを使っても求められます。
def connected_components(neighbor):
visited = []
result = []
for city in neighbor.keys():
if city in visited:
continue
component = depth_first(neighbor, city)[0]
# component = width_first(neighbor, city)[0] でも良い
result.append(component)
for city2 in component:
visited.append(city2)
return result
for component in connected_components(neighbor1):
print (component)
['Utsunomiya', 'Tokyo', 'Yokohama', 'Chiba', 'Saitama', 'Maebashi', 'Nagano', 'Toyama', 'Kanazawa', 'Fukui', 'Gifu', 'Otsu', 'Nara', 'Wakayama', 'Tokushima', 'Takamatsu', 'Kochi', 'Matsuyama', 'Hiroshima', 'Okayama', 'Tottori', 'Kobe', 'Osaka', 'Kyoto', 'Tsu', 'Nagoya', 'Kofu', 'Shizuoka', 'Mito']
['Nagasaki', 'Kumamoto', 'Oita', 'Yamaguchi', 'Saga', 'Fukuoka']
['Miyazaki', 'Kagoshima']
['Sendai', 'Fukushima', 'Yamagata']
draw_path(col1, col3, col2, connected_components(neighbor1))
徒歩で日本を旅する
Wandering japan on foot
今までは緯度と経度を利用して都市間の距離を計算し、都市間の関係を考えてきました。ここからは、都市間を歩いて回ります。都市間を歩くと何時間かかるのか、Google Mapで予想した結果を用います（海を挟むため歩けない場合はフェリーに乗ります）。まずはデータのダウンロードから。
# ウェブ上のリソースを指定する
url = 'https://raw.githubusercontent.com/maskot1977/ipython_notebook/master/toydata/walk.txt'
# 指定したURLからリソースをダウンロードし、名前をつける。
urllib.urlretrieve(url, 'walk.txt') # Python 2 の場合
# urllib.request.urlretrieve(url, 'walk.txt') # Python 3 の場合
('walk.txt', <httplib.HTTPMessage instance at 0x110c33758>)
# 先頭数行の確認
!head walk.txt
Town1 Town2 Hour Ferry
Sapporo Aomori 55 True
Akita Aomori 36
Akita Sendai 45
Akita Niigata 52
Yamagata Aomori 75
Morioka Aomori 37
Morioka Akita 24
Yamagata Akita 41
Yamagata Morioka 46
# ダウンロードしたデータから、列ごとに数字を読み込んでリストに格納する。
col4 = [] # ０列目の数字を格納する予定のリスト
col5 = [] # １列目の数字を格納する予定のリスト
col6 = [] # ２列目の数字を格納する予定のリスト
for i, line in enumerate(open('walk.txt')): # ファイルを開いて一行一行読み込む
if i == 0: # ０番目の行の場合
continue # 次の行に行く
c = line.split() # 行を空白文字で分割したものをcというリストに入れる
col4.append(c[0]) # ０列目の単語をcol4に入れる
col5.append(c[1]) # １列目の単語をcol5に入れる
col6.append(float(c[2])) # ２列目の単語を実数に変換してcol6に入れる
まずは、徒歩ネットワークを図示してみます。
draw_path(col1, col3, col2, [[city1, city2] for city1, city2 in zip(col4, col5)])
このデータから 連結リスト を作りましょう。
walk_neighbor = {}
for city1, city2, walk in zip(col4, col5, col6):
if city1 not in walk_neighbor.keys():
walk_neighbor.update({city1:[]})
walk_neighbor[city1].append([walk, city2])
if city2 not in walk_neighbor.keys():
walk_neighbor.update({city2:[]})
walk_neighbor[city2].append([walk, city1])
# 東京に隣接している都市を、近い順に並べる
print (sorted(walk_neighbor["Tokyo"]))
[[5.0, 'Saitama'], [7.0, 'Yokohama'], [8.0, 'Chiba'], [28.0, 'Kofu']]
切断点 (cut vertices) 、切断辺 (cut edges)
- 切断点 とは、それを削除すると連結グラフが二分割されてしまう頂点のこと。
- 切断辺 とは、それを削除すると連結グラフが二分割されてしまう辺のこと。
切断点、切断辺は、交通の要所など、ネットワークが機能する上で重要な場所を同定するのに使えます。
切断点の見つけ方 How to find cut vertices
深さ優先探索の考え方を応用して同定します。
* 根（始点）に隣接している頂点が２つ未満の場合、その根は切断点ではない。
* 根（始点）に隣接している頂点が２つ以上のとき、深さ優先探索を行ない、「根から未訪問の頂点に行く」という動作が２回以上生じた場合、その根は切断点である。１回しか生じない場合、その根は切断点ではない。
切断点を見つける関数を作成しましょう。
def cut_vertices(neighbor):
result = []
for start, neigh in neighbor.items():
if len(neigh) == 1:
continue
stack = []
visited = []
for dist, nei in neigh:
stack.append([start, nei])
visited.append(start)
root_started = 0
while len(stack) > 0:
prev, curr = stack.pop()
if (prev == start) and (curr not in visited):
root_started += 1
if root_started > 1:
result.append(start)
break
visited.append(curr)
for dist, nei in neighbor[curr]:
if nei in visited:
continue
else:
stack.append([curr, nei])
return result
このグラフの切断点を求めましょう。
cut_vertices(walk_neighbor)
['Fukuoka', 'Takamatsu', 'Aomori', 'Kagoshima', 'Okayama', 'Yamaguchi']
切断辺の見つけ方 How to find cut edges
切断辺を求める関数は、切断点を求める関数を用いて作成します。
* どちらの頂点も切断点である辺は、切断辺である。
* 一方の頂点が切断点であり、もう一方の頂点の次数が１であるような辺は、切断辺である。
* 切断点を含まない辺は、切断辺ではない。
切断辺を求める関数を作成しましょう。
def cut_edges(neighbor):
result = []
seen = []
articulation = cut_vertices(neighbor)
for city in articulation:
for dist, nei in neighbor[city]:
if (nei not in articulation) and (len(neighbor[nei]) > 1):
continue
key = "_".join(sorted([city, nei]))
if key in seen:
continue
seen.append(key)
result.append([city, nei])
return result
このグラフの切断辺を求めましょう。
cut_edges(walk_neighbor)
[['Fukuoka', 'Yamaguchi'],
['Takamatsu', 'Okayama'],
['Aomori', 'Sapporo'],
['Kagoshima', 'Naha']]
同じ都市は二度と訪問しない
Never visit the same city again
上の地図をもとに、「同じ都市は二度と訪問しない」「ある都市に着いたら、その次は、未訪問の都市の中で最も近い都市に向かって歩く」という条件で彷徨い歩いてみましょう。東京から出発して彷徨い歩いたら、どこにたどり着けるでしょうか？
彷徨い歩くときは、深さ優先探索的な考え方を使います。まずは関数を作成しましょう。
def nearest_wander(neighbor, start):
visited = []
curr = start
result = []
while True:
result.append(curr)
visited.append(curr)
count = 0
for dist, next_city in sorted(neighbor[curr]):
if next_city in visited:
count += 1
else:
curr = next_city
break
if count == len(neighbor[curr]):
break
return [result]
東京から出発して彷徨い歩いてみます。
print (nearest_wander(walk_neighbor, "Tokyo"))
[['Tokyo', 'Saitama', 'Chiba', 'Mito', 'Utsunomiya', 'Maebashi', 'Nagano', 'Kofu', 'Shizuoka', 'Yokohama']]
経路を図示してみます。
draw_path(col1, col3, col2, nearest_wander(walk_neighbor, "Tokyo"))
問題7： 横浜からスタートすると、どこまで行けるか試してみてください。
続いて、「同じ都市は二度と訪問しない」という条件で、できるだけ長い経路を探してみましょう。これを無制限に実行すると時間がかかるので、「最大ステップ数（訪問する最大の都市の数）」を決めてから実行します。まずは関数の作成から。
import copy
def longest_wander(neighbor, start, max_cities):
queue = []
queue.append([start])
result = []
while True:
curr_path = queue.pop()
#print curr_path
last = curr_path[-1]
count = 0
for nei in reversed(sorted(neighbor[last])):
if nei[1] not in curr_path:
new_path = copy.copy(curr_path)
new_path.append(nei[1])
queue.append(new_path)
count += 1
if count == 0:
if len(result) == 0:
result = [curr_path]
elif len(result[0]) < len(curr_path):
result = [curr_path]
if len(curr_path) == len(neighbor.keys()):
break
if len(curr_path) == max_cities:
break
return result
東京からスタートして、最大ステップ数３０でどこまで行けるか見てみましょう。
draw_path(col1, col3, col2, longest_wander(walk_neighbor, "Tokyo", 30))
問題8: 同様に、東京からスタートして最大ステップ数35だとどこに行けるか確認してください。
閉路 (cycle)
指定した都市スタートで、「同じ都市は二度と訪問しない」という条件で、指定したステップ数で一周する回路（閉路）を探します。
import copy
def cycle(neighbor, start, ring_size):
stack = []
stack.append([start])
result = []
count = 0
while len(stack) > 0:
curr_path = stack.pop()
if len(curr_path) > ring_size:
continue
#print curr_path
count += 1
last = curr_path[-1]
for nei in neighbor[last]:
if nei[1] in curr_path:
if (len(curr_path) == ring_size) and (curr_path[0] == nei[1]):
new_path = copy.copy(curr_path)
new_path.append(nei[1])
result.append(new_path)
continue
new_path = copy.copy(curr_path)
new_path.append(nei[1])
stack.append(new_path)
continue
if count > 50:
break
return result
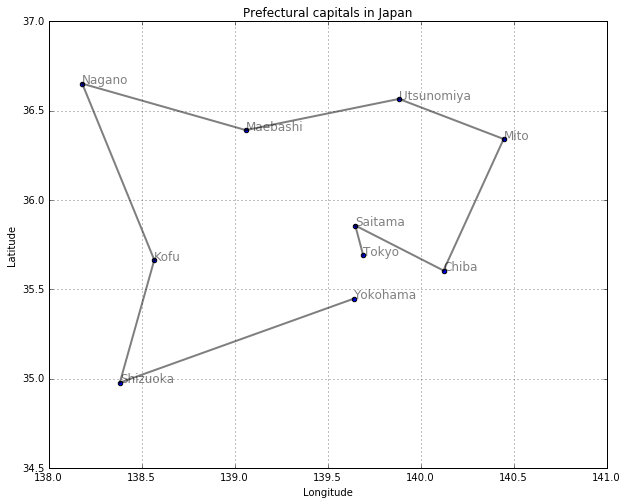
東京スタート、ステップ数３の場合
print (cycle(walk_neighbor, "Tokyo", 3))
[['Tokyo', 'Kofu', 'Yokohama', 'Tokyo'], ['Tokyo', 'Kofu', 'Saitama', 'Tokyo'], ['Tokyo', 'Yokohama', 'Kofu', 'Tokyo'], ['Tokyo', 'Chiba', 'Saitama', 'Tokyo'], ['Tokyo', 'Saitama', 'Kofu', 'Tokyo'], ['Tokyo', 'Saitama', 'Chiba', 'Tokyo']]
これらの閉路を全て図示すると
draw_path(col1, col3, col2, cycle(walk_neighbor, "Tokyo", 3))
問題9： 東京スタートで、ステップ数４の閉路を全て描いてください。
最小木 (minimum spanning tree)
- 木 (tree) とは、閉路を含まないグラフのこと。
- 全域木(Spanning tree) とは、連結グラフの全ての頂点とそのグラフを構成する辺の一部分のみで構成される木のこと。
- 最小木 (minimum spanning tree) とは、全域木のうち、辺の重み（距離など）の和が最小のもの。
最小木を得るときには、始点を決める必要があります。まずは関数の作成から。
def minimum_tree(neighbor, start):
visited = []
queue = []
result = []
queue.append([start, start, 0])
while len(queue) > 0:
queue = sorted(queue, key=lambda e: e[2])
curr_i, curr_j, accum_dist = queue.pop(0)
if (curr_i in visited) and (curr_j in visited):
continue
visited.append(curr_i)
visited.append(curr_j)
if curr_i != curr_j:
result.append([curr_i, curr_j])
for curr in [curr_i, curr_j]:
for nei in neighbor[curr]:
if nei[1] in visited:
continue
queue.append([curr, nei[1], nei[0] + accum_dist])
return result
日本各地から江戸（東京）に徒歩で参覲交代する大名の気持ちになってみましょう。東京を始点とした最小木を求めてみます。
print (minimum_tree(walk_neighbor, "Tokyo"))
[['Tokyo', 'Saitama'], ['Tokyo', 'Yokohama'], ['Tokyo', 'Chiba'], ['Saitama', 'Maebashi'], ['Saitama', 'Utsunomiya'], ['Saitama', 'Mito'], ['Tokyo', 'Kofu'], ['Yokohama', 'Shizuoka'], ['Maebashi', 'Nagano'], ['Utsunomiya', 'Fukushima'], ['Maebashi', 'Niigata'], ['Fukushima', 'Sendai'], ['Fukushima', 'Yamagata'], ['Shizuoka', 'Nagoya'], ['Nagoya', 'Gifu'], ['Nagano', 'Toyama'], ['Nagoya', 'Tsu'], ['Toyama', 'Kanazawa'], ['Nagoya', 'Otsu'], ['Otsu', 'Kyoto'], ['Tsu', 'Nara'], ['Sendai', 'Morioka'], ['Gifu', 'Fukui'], ['Kyoto', 'Osaka'], ['Yamagata', 'Akita'], ['Osaka', 'Kobe'], ['Osaka', 'Wakayama'], ['Kyoto', 'Tottori'], ['Kobe', 'Okayama'], ['Morioka', 'Aomori'], ['Okayama', 'Takamatsu'], ['Takamatsu', 'Tokushima'], ['Tottori', 'Matsue'], ['Okayama', 'Hiroshima'], ['Takamatsu', 'Kochi'], ['Takamatsu', 'Matsuyama'], ['Aomori', 'Sapporo'], ['Hiroshima', 'Yamaguchi'], ['Yamaguchi', 'Fukuoka'], ['Fukuoka', 'Saga'], ['Fukuoka', 'Kumamoto'], ['Fukuoka', 'Oita'], ['Saga', 'Nagasaki'], ['Kumamoto', 'Kagoshima'], ['Kumamoto', 'Miyazaki'], ['Kagoshima', 'Naha']]
draw_path(col1, col3, col2, minimum_tree(walk_neighbor, "Tokyo"))
問題10: 日本各地から京に上洛する大名の気持ちになってみましょう。京都を始点とした最小木を描いてください。
最短経路 (shortest path)
- 最短経路 (shortest path) とは、ある始点から終点までを結ぶ経路 (path) のうち、辺の重み（距離など）の和が最小のもの。
最短経路 (shortest path) は、最小木 (minimum spanning tree) から求めることができます。まずは関数の作成から。
import copy
def shortest_path(original_neighbor, start, goal):
neighbor = {}
for edge in minimum_tree(original_neighbor, start):
if edge[0] not in neighbor.keys():
neighbor.update({edge[0]:[]})
neighbor[edge[0]].append(edge[1])
if edge[1] not in neighbor.keys():
neighbor.update({edge[1]:[]})
neighbor[edge[1]].append(edge[0])
queue = []
queue.append([start])
result = []
while len(queue) > 0:
curr_path = queue.pop()
if curr_path[-1] == goal:
result.append(curr_path)
break
for nei in neighbor[curr_path[-1]]:
if nei in curr_path:
continue
new_path = copy.copy(curr_path)
new_path.append(nei)
queue.append(new_path)
return result
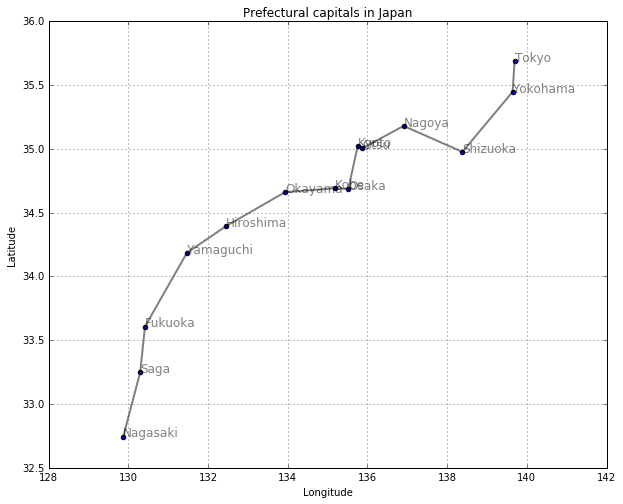
平戸（長崎）に来港して江戸（東京）の将軍に謁見するオランダ商人の気持ちになってみましょう。長崎から東京までの最短経路を求めてください。
print (shortest_path(walk_neighbor, "Tokyo", "Nagasaki"))
[['Tokyo', 'Yokohama', 'Shizuoka', 'Nagoya', 'Otsu', 'Kyoto', 'Osaka', 'Kobe', 'Okayama', 'Hiroshima', 'Yamaguchi', 'Fukuoka', 'Saga', 'Nagasaki']]
draw_path(col1, col3, col2, shortest_path(walk_neighbor, "Nagasaki", "Tokyo"))
問題11: 札幌から那覇に行く最短経路を求めてください。
巡回セールスマン問題 (traveling salesman problem, TSP) 、中国人郵便配達問題 (Chinese postman problem)
巡回セールスマン問題（traveling salesman problem、TSP）は、都市の集合と各2都市間の移動コスト（たとえば距離）が与えられたとき、全ての都市をちょうど一度ずつ巡り出発地に戻る閉路の総移動コストが最小のものを求める（セールスマンが所定の複数の都市を1回だけ巡回する場合の最短経路を求める）組合せ最適化問題である。
中国人郵便配達問題（Chinese postman problem）とは、都市の集合と各2都市間の移動コスト（たとえば距離）が与えられたとき、都市間の辺の全てをちょうど一度ずつ通り出発地に戻る閉路の総移動コストが最小のものを求める最適化問題である。
ハミルトングラフ(Hamilton graph)、オイラーグラフ(Eulerian graph)
- 一筆書き (One-stroke sketch) とは、始点と終点が違う場所であっても構わない。
- オイラーグラフ(Eulerian graph)とは、中国人郵便配達問題の答えが存在するようなグラフ、つまり、始点からスタートして全ての辺を一度ずつだけ通って終点に戻ってくるような閉路が存在するようなグラフのことを指す。オイラーグラフの特徴として「すべての頂点の次数（頂点に接続する辺の数）は偶数である」ことが挙げられる。
- 準オイラーグラフとは、一筆書きできるグラフのうち、始点と終点が同じにならないものを指す。準オイラーグラフの特徴として「次数（頂点に接続する辺の数）が奇数である頂点の数は１個か２個のどちらかである」ことが挙げられる。
- グラフ上の全ての頂点を 1 度ずつ通る閉路をハミルトン閉路という。ハミルトン閉路を含むグラフのことをハミルトングラフ(Hamilton graph)といい、ハミルトン路は含むがハミルトン閉路は含まないようなグラフのことを準ハミルトングラフという
（図の出典：http://farm8.staticflickr.com/7136/7620073798_0dcc924714.jpg）
ハミルトンパス問題 (Hamilton path problem)、オイラーパス問題 (Eulerian path problem)
- ハミルトンパス問題とは、与えられたグラフについて、全ての頂点を一度だけ通るハミルトン経路が存在するかどうか調べる問題。ハミルトンパス問題は、1974年に「NP困難問題」に認定されました。NP困難問題というのは、簡単にいうと、コンピュータで効率的に解く方法が見つかっていないし、今後も見つけることは非常に困難であろうとされる問題です。
- オイラーパス問題とは、与えられたグラフについて、全ての辺を一度だけ通るオイラー経路が存在するかどうか調べる問題。オイラーパス問題には、非常に効率的なアルゴリズムが存在します。
de Bruijn Graph を使った NGS データの de novo assembly
次世代シークエンサー (NGS) のデータのアセンブリは、ふつうに考えるとハミルトンパス問題という難しい問題になるところですが、一見複雑な de Bruijn Graph を作ることによって、オイラーパス問題という簡単な問題に変えて解決しています。
de Bruijn Graph を使った de novo アセンブリの発想がすごい件
- de novo assembly をハミルトンパス問題として解く場合： 「全ての頂点を訪問する経路を探せ」
（図の出典：http://cdn-ak.f.st-hatena.com/images/fotolife/h/hoxo_m/20100930/20100930112720.png）
- de novo assembly をオイラーパス問題として解く場合： 「全ての辺を通る経路を探せ」
（図の出典：http://cdn-ak.f.st-hatena.com/images/fotolife/h/hoxo_m/20100930/20100930113838.png）
グラフ同型問題 (graph isomorphism)、化学情報学 (cheminformatics)
（図の出典：http://slideplayer.com/slide/6593223/）
（図の出典：http://www.ra.cs.uni-tuebingen.de/forschung/terminiert/molsim/welcome_e.html）