厳選！C++ アルゴリズム実装に使える 25 の STL 機能【後編】

目次

• 厳選！C++ アルゴリズム実装に使える 25 の STL 機能【前編】

からの続きです！

前編

• 0 章: あいさつ
• 1 章: はじめに
• 2 章: C++ の標準ライブラリとは？
• 3 章: 今回紹介する 25 個の標準ライブラリ
• 4 章: 皆さんの疑問　「標準ライブラリ、結局どんな場面で使うのか？」

後編

• 5 章: 皆さんの疑問　「標準ライブラリ、結局どんな場面で使うのか？」　に対する答え 11 例
• 6 章: おわりに
• 7 章: 参考文献

5. 皆さんの疑問　「標準ライブラリ、結局どんな場面で使うのか？」　に対する答え 11 例

前編では、以下の 25 個の標準ライブラリを紹介しました。

導入編	初級編	中級編第一部	中級編第二部
abs	min/max	vector	assert
sin/cos/tan	swap	stack	count
string	__gcd	queue	find
	rand	priority_queue	next_permutation
	clock	map	__builtin_popcount
	reverse	lower_bound	bitset
	sort	set
		pair
		tuple

ですが、以下のように思った人も多いと思います。

今回の 25 個の標準ライブラリはわかったけど、どういう問題やどういうアルゴリズムの実装で活用できるのか？？？

そこで本章では、どのような問題を解くときに C++ の標準ライブラリが使えるのか、11 個の例を紹介します。

5-1. バブルソートの実装 (swap)

バブルソートは、アルゴリズム解説本や、大学の授業などでも教えられることが多いようです。以下のような発想に基づいたアルゴリズムです。

• 「配列の中から、大きさが逆転している部分があれば swap する」という操作を繰り返す。
• 最終的に、大きさが逆転している部分が無くなれば操作を終了する。
  

この「バブルソート」は、swap 関数 を使うことで実装しやすくなります。実装例は以下のようになります。

ソースコード

#include <iostream>
using namespace std;

int N, A[10009];

int main() {
    cin >> N;
    for (int i = 1; i <= N; i++) cin >> A[i];
    
    // {A[1], A[2], ..., A[N]} を小さい順にバブルソートする
    for (int i = 1; i <= N; i++) {
        for (int j = 1; j <= N - i; j++) {
            if (A[j] > A[j + 1]) swap(A[j], A[j + 1]);
        }
    }

    // ソートされた配列を出力する
    for (int i = 1; i <= N; i++) cout << A[i] << endl;
    return 0;
}

5-2. 高速なソート (sort)

AtCoder や yukicoder など競技プログラミングの過去問では、ソートを使う問題が多いです。その中でも、$N \leq 100000$ などといった大きなデータが与えられる問題はたくさんあります。

先程紹介したバブルソートを使った場合、計算量 $O(N^2)$ かかってしまい、大きなデータが与えられる場合、数秒で実行が終わりません。しかし、C++ の sort 関数 はソートアルゴリズムの中で最も高速なものの一つが採用されているため、計算量 $O(N \ log \ N)$ しかかからないのです。しかもたった 1 行で書けてしまい、可読性も上がります。

例えば、以下の問題は sort 関数を使うことで容易に実装できます。（解法はソースコードのコメントアウト参照。）

問題概要

$N$ 本の棒があり、$i$ 番目の棒の長さは $l_i$ です。あなたは $N$ 本の中から $K$ 本の棒を選び、それをつなげることで、ヘビのおもちゃを作りたいです。
ヘビのおもちゃの長さは、選んだ棒の長さの総和で表されます。ヘビの長さとしてあり得る最大値を求めてください。
制約：$1 \leq K \leq N \leq 10^{6}, 1 \leq l_i \leq 10^{9}$、高々 $10^{8}$ 回程度の計算で実行を終わらせること

(ABC067 B - Snake Toy より改題)

ソースコード

#include <iostream>
#include <algorithm>
using namespace std;

long long N, K, L[1000009];

int main() {
    scanf("%lld%lld", &N, &K);
    for (int i = 1; i <= N; i++) scanf("%lld", &L[i]);
    
    // 解法: まず、棒を短い順に並び替える
    sort(L + 1, L + N + 1);
    
    // 解法: 答えは、[1 番長い棒, 2 番目に長い棒, ..., K 番目に長い棒] を取るだけ
    long long ans = 0;
    for (int i = N - K + 1; i <= N; i++) ans += L[i];
    printf("%lld\n", ans);
    return 0;
}

その他の問題例

• ABC088 B - Card Game for Two
• ABC132 C - Divide the Problems
• AGC012 A - AtCoder Group Contest

5-3. バグらない二分探索 (lower_bound)

皆さん、二分探索をご存知でしょうか。知らない人は、以下の記事をお読みください！

• アルゴリズムを勉強するなら二分探索から始めよう！『なっとく！アルゴリズム』より

ただ、この二分探索を実装すると、プログラムをバグらせることが往々にしてあります。例えば、

• $left = mid;$ と $right = mid;$ の処理を逆に書いてしまった。
• 求める境界値が 1 個ずれてしまった。

しかし、lower_bound 関数 を使うとたった 1 行で書けるので、バグりやすさが半減します！¹ 例えば、以下の問題は二分探索によって解くことができますが、lower_bound 関数を使うことで実装量が大幅に削減されます。（解法はソースコードのコメントアウト参照。）

問題概要

$N$ 個の整数 {$a_1, a_2, ..., a_N$} が与えられます。そのとき、$L \leq a_i + a_j \leq R$ となるような $(i, j)$ の組の個数を求めてください。
制約：$1 \leq N \leq 10^{6}, 1 \leq a_i, K \leq 10^{9}$、高々 $10^{8}$ 回程度の計算で実行を終わらせること

ソースコード

#include <iostream>
#include <algorithm>
using namespace std;

long long N, L, R, A[1000009];

int main() {
    scanf("%lld%lld%lld", &N, &L, &R);
    for (int i = 1; i <= N; i++) scanf("%lld", &A[i]);
    
    // 解法: まず A を小さい順にソートする
    sort(A + 1, A + N + 1);
    
    // 解法: i を全探索すると、j の値は一つの区間になり、これは二分探索によって決まる
    long long ans = 0;
    for (int i = 1; i <= N; i++) {
        int left_j = lower_bound(A + 1, A + N + 1, L - A[i]) - A;
        int right_j = lower_bound(A + 1, A + N + 1, (R + 1LL) - A[i]) - A;
        ans += 1LL * (right_j - left_j);
    }
    cout << ans << endl;
    return 0;
}

その他の問題例

• JOI 2007 本選 5 - ダーツ
• ABC077 C - Snuke Festival

5-4. グラフを隣接リストで持つ (vector)

皆さん、「グラフ理論」をご存知でしょうか。知らない人は、以下の記事をお読みください。

• DFS (深さ優先探索) 超入門！ 〜 グラフ・アルゴリズムの世界への入口 〜【前編】 の 1 章

さて、グラフというものはどのように表現すればよいのでしょうか。このやり方の一つとして「隣接リスト」というものがあります。

「隣接リスト」とは？

各頂点に対し、隣接頂点（直接辺で繋がっている頂点）を格納する、グラフの表現の方法です。

他にも「隣接行列」という表現の方法がありますが、メモリ使用量が $O(N^2)$ と大きく、$N \leq 100000$ などデータが大きい場合は隣接リストを使う必要があります。

「隣接リスト」の実装

ここでは、グラフの頂点数を $N$、辺数を $M$ とします。
隣接行列・隣接リスト両方のグラフ表現方法において、普通の配列を使った場合、メモリ使用量² $O(N^2)$ かかってしまうため、$N = 100000, M = 300000$ など大きいデータの場合にメモリ制限超過を引き起こします。

しかし、vector 型でそれぞれの頂点における隣接頂点を格納しておくと、合計メモリ使用量 $O(M)$ で済み、データがある程度大きくてもメモリ制限超過 (MLE) を引き起こしません。

ソースコード

#include <iostream>
#include <vector>
using namespace std;

int N, M, A[100009], B[100009];
vector<int> G[100009];

int main() {
    // グラフを入力する
    cin >> N >> M;
    for (int i = 1; i <= M; i++) cin >> A[i] >> B[i];

    // グラフを隣接リストで表現する
    for (int i = 1; i <= M; i++) {
        G[A[i]].push_back(B[i]);
        G[B[i]].push_back(A[i]);
    }

    // 隣接リストで表現されたグラフを出力する
    for (int i = 1; i <= N; i++) {
        cout << "Vertex #" << i << ": {";
        for (int j = 0; j < G[i].size(); j++) {
            if (j >= 1) cout << " ";
            cout << G[i][j];
        }
        cout << "}" << endl;
    }
    return 0;
}

5-5. 幅優先探索 (queue, pair)

皆さん、幅優先探索をご存知でしょうか。知らない人は、以下の記事をお読みください。

• BFS (幅優先探索) 超入門！ 〜 キューを鮮やかに使いこなす 〜

そのアルゴリズムはどんな場面で使われるのでしょうか。例えば、迷路の最小移動回数を求めることを考えましょう。

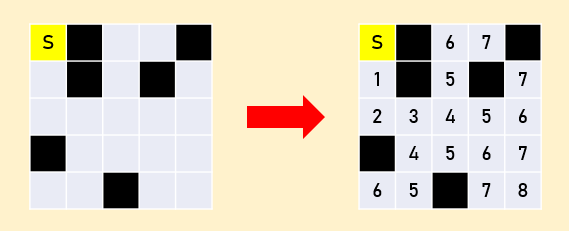
$H$ 行 $W$ 列の迷路における最小移動回数を求めるのに、幅優先探索を使うと計算量 $O(HW)$ で解くことができます。この幅優先探索の実装のために、queue と pair 型を使う必要があるのです。以下、実装コード例を示します。

ソースコード

#include <iostream>
#include <queue>
using namespace std;

int H, W; // 迷路の大きさ
char c[1009][1009]; // 迷路のマップ、'.' の場合白マス、'#' の場合黒マス
int dist[1009][1009];

int main() {
    // 迷路を入力する
    cin >> H >> W;
    for (int i = 1; i <= H; i++) {
        for (int j = 1; j <= W; j++) cin >> c[i][j];
    }

    // 距離を初期化する
    for (int i = 1; i <= H; i++) {
        for (int j = 1; j <= W; j++) dist[i][j] = 1000000007;
    }

    // 幅優先探索により、最短移動回数を求める
    queue<pair<int, int>> Q;
    Q.push(make_pair(1, 1));
    dist[1][1] = 0;

    while (!Q.empty()) {
        int cx = Q.front().first, cy = Q.front().second;
        Q.pop();

        int dx[4] = {1, 0, -1, 0};
        int dy[4] = {0, 1, 0, -1};
        for (int i = 0; i < 4; i++) {
            int ex = cx + dx[i], ey = cy + dy[i];
            if (c[ex][ey] != '.' || dist[ex][ey] != 1000000007) continue;
            Q.push(make_pair(ex, ey));
            dist[ex][ey] = dist[cx][cy] + 1;
        }
    }

    // 最短距離を出力する
    for (int i = 1; i <= H; i++) {
        for (int j = 1; j <= W; j++) {
            if (j >= 2) cout << " ";
            cout << dist[i][j];
        }
        cout << endl;
    }
    return 0;
}

問題例

• ABC007 C - 幅優先探索
• JOI 2011 予選 5 - チーズ
• ICPC2010 国内予選 2 - 迷図と命ず

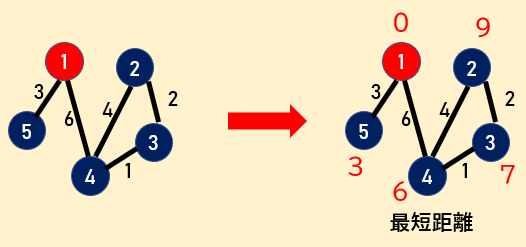
5-6. 最短経路問題・ダイクストラ法 (priority_queue)

皆さん、ダイクストラ法をご存知でしょうか。ダイクストラ法とは、以下の問題を計算量 $O(M \log N)$ で解くアルゴリズムです。

$1, 2, 3, ..., N$ と番号付けられている $N$ 個の都市と、$M$ 個の道路がある。道路 $i$ は都市 $a_i$ と $b_i$ の間を結び、移動に $c_i$ 分かかる。そのとき、都市 $S$ からその他の各都市への最短移動時間を求めよ。

つまり、グラフ理論でいう、$N$ 頂点 $M$ 辺のグラフにおいて、頂点 $S$ から各頂点への最短距離を求める問題を計算量 $O(M \log N)$ で解くアルゴリズムです。どういうアルゴリズムか知りたい方は、以下の記事をお読みください。

• 最短経路問題総特集！！！～BFSから拡張ダイクストラまで～

実は、ダイクストラ法の実装には priority_queue（優先度付きキュー）を使う必要があるのです。以下、実装例を載せておきます。

ソースコード

#include <iostream>
#include <queue>
#include <vector>
#include <functional>
using namespace std;

int N, M, S, A[500009], B[500009], C[500009];
int dist[100009];
vector<pair<int, int>> G[100009];
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> Q;

int main() {
    // グラフを入力する
    scanf("%d%d", &N, &M);
    for (int i = 1; i <= M; i++) {
        scanf("%d%d%d", &A[i], &B[i], &C[i]);
        G[A[i]].push_back(make_pair(B[i], C[i]));
        G[B[i]].push_back(make_pair(A[i], C[i]));
    }
    scanf("%d", &S);

    // 距離を初期化する
    for (int i = 1; i <= N; i++) dist[i] = 1000000007;

    // 優先度付きキューには (距離, 頂点番号) の組を入れる
    Q.push(make_pair(0, S));
    dist[S] = 0;
    while (!Q.empty()) {
        int pos = Q.top().second; Q.pop();
        for (int i = 0; i < G[pos].size(); i++) {
            int to = G[pos][i].first, cost = G[pos][i].second;
            if (dist[to] > dist[pos] + cost) {
                dist[to] = dist[pos] + cost;
                Q.push(make_pair(dist[to], to));
            }
        }
    }

    // 距離を出力する
    for (int i = 1; i <= N; i++) printf("%d\n", dist[i]);
    return 0;
}

問題例

• JOI 2008 予選 6 - 船旅
• SoundHound Inc. Programming Contest 2018 - Masters Tournament D - Saving Snuuk
• 技術室奥プログラミングコンテスト #4 Day1 H - don't be late

5-7. 乱択アルゴリズム・モンテカルロ法 (rand)

皆さん、モンテカルロ法をご存知でしょうか。以下のような手法です。

乱数を用いて、何回もシミュレーションを行うことで、近似解を求める手法。

例えば、円周率の近似値を求めるのに使われます。

解法

$0 \leq x < 1, 0 \leq y < 1$ の領域内のランダムな位置に100個の点を置き、$x^2 + y^2 \leq 1$ を満たす（円に含まれる）個数を $p$ とすると、円周率は $\frac{4p}{100}$ に近似できます。³

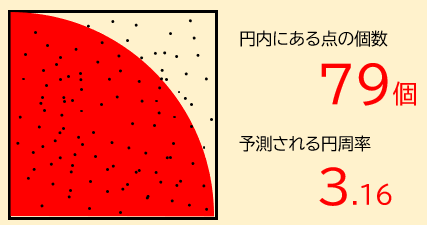
当然、置く点の数を増やせば増やすほど、正確な円周率の値が出ます。しかしどうやって乱数を使うのでしょうか。ここで使うのが rand 関数です。⁴　モンテカルロ法にも C++ 標準ライブラリの応用が利くのです。以下、実装例を載せておきます。

ソースコード

#include <iostream>
#include <ctime>
using namespace std;

const int NUMBER_OF_SAMPLES = 100;

int main() {
    srand((unsigned)time(NULL));

    // 円周率を計算する
    int cnt = 0;
    for (int i = 0; i < NUMBER_OF_SAMPLES; i++) {
        // gcc, Visual Studio 両方に対応させています (後者では 32767 までの乱数しか出ません)
        double px = 1.0 * (rand() % 32768 + 0.5) / 32768.0;
        double py = 1.0 * (rand() % 32768 + 0.5) / 32768.0;
        if (px * px + py * py <= 1.0) cnt++;
    }
    printf("PI = %.5lf\n", 4.0 * cnt / NUMBER_OF_SAMPLES);
    return 0;
}

その他の問題例

• ARC003 D - シャッフル席替え　※誤差が 0.002 以下の場合に正解となることに注意。

5-8. O(N×N!) の順列全探索 (next_permutation)

競技プログラミングでは、よく「順列全探索」というアルゴリズムが使われます。例えば、以下のような問題を考えてみましょう。

問題概要

$1, 2, ..., N$ と番号付けられている $N$ 個の都市がある。都市 $i$ から $j$ まで、他のどの都市も通らずに移動するのに $A_{i, j}$ 分かかる。qiita 君は、すべての都市をちょうど 1 回ずつ訪れたいが、どの都市からスタートしても良く、どの都市でゴールしても良い。そのとき、移動に最小で何分かかるか。
制約：$1 \leq N \leq 10, A_{i, i} = 0, A_{i, j} = A_{j, i}$

解法

これは、典型的な順列全探索の問題です。qiita 君が都市 {B[0], B[1], ..., B[N-1]} の順番に都市を訪れるものとします。最初 B = {1, 2, 3, ..., N} にして、next_permutation で全部の順列を回せば、計算量 $O(N \times N!)$ で解くことができます。

ソースコード

#include <iostream>
#include <algorithm>
using namespace std;

int N, A[12][12], B[12], perm[12], ans = 2000000000;

int main() {
    // 入力
    cin >> N;
    for (int i = 1; i <= N; i++) {
        for (int j = 1; j <= N; j++) cin >> A[i][j];
    }
    for (int i = 0; i < N; i++) B[i] = i + 1;

    // ここから順列全探索
    do {
        int sum = 0;
        for (int i = 0; i < N - 1; i++) {
            sum += A[B[i]][B[i + 1]];
        }
        ans = min(ans, sum);
    } while(next_permutation(B, B + N));

    // 答えを出力
    cout << ans << endl;
    return 0;
}

その他の問題例

• 巡回セールスマン問題
• ABC054 C - One-stroke Path

5-9. 部分和問題の高速化 (bitset)

皆さん、部分和問題をご存知でしょうか。以下のような問題です。

$N$ 個の整数 {$A_1, A_2, ..., A_N$} の中からいくつかを選び、合計を $K$ にすることができるかどうか判定する。

解法

この問題は、以下のように動的計画法で $O(NK)$ で解くことができます。

• 最初、$dp[0] = 1$、$dp[1], dp[2], ..., dp[K] = 0$ とする。
• $i = 1, 2, 3, ..., N$ の順に、以下の操作を繰り返す。
  • $j = K-A_i, K-A_i-1, ..., 0$ の順に、もし $dp[j] = 1$ の場合、$dp[j + A_i] = 1$ にする。

ソースコードで書くと、以下のようになります。

#include <iostream>
using namespace std;

int N, K, A[1009];
int dp[10009];

int main() {
    // 入力
    cin >> N >> K;
    for (int i = 1; i <= N; i++) cin >> A[i];
    
    // ここからが DP の遷移
    dp[0] = 1;
    for (int i = 1; i <= N; i++) {
        for (int j = K - A[i]; j >= 0; j--) {
            if (dp[j] == 1) dp[j + A[i]] = 1;
        }
    }

    // 答えを出力
    if (dp[K] == 1) cout << "Yes" << endl;
    else cout << "No" << endl;
    return 0;
}

もっと高速な解法

実は bitset を使うと、$NK$ 回よりも速い、$\frac{NK}{32}$ 回程度の計算で答えが求められてしまうのです。$K+1$ 桁の 2 進数ビット
$$E = dp[K]dp[K-1]dp[K-2]...dp[0]$$
を考えてみると、

• $j = K-A_i, K-A_i-1, ..., 0$ の順に、もし $dp[j] = 1$ の場合、$dp[j + A_i] = 1$ にする。

という操作は、ビット演算において、

• $E = (E \ or \ (E << A[i]))$

たったそれだけの操作なのです。ビット演算 1 回につき $\frac{K}{32}$ 回の計算しか必要ありません。$i = 1, 2, ..., N$ についてこの操作を行えばよいので、全体の計算量は $\frac{NK}{32}$ 回程度と非常に高速になります。以下、実装例を載せておきます。

ソースコード

#include <iostream>
#include <bitset>
using namespace std;

int N, K, A[100009];

int main() {
    // 入力
    cin >> N >> K;
    for (int i = 1; i <= N; i++) cin >> A[i];
    
    // DP の遷移を bitset に落とし込む
    bitset<100001> dp;
    dp.set(0);
    for (int i = 1; i <= N; i++) dp |= (dp << A[i]);
    
    // 答えを出力
    if (dp[K] == 1) cout << "Yes" << endl;
    else cout << "No" << endl;
    return 0;
}

その他の問題例

• AGC020 C - Median Sum
• M-SOLUTIONS プロコンオープン F - Random Tournament　※私が解けるかというレベルの難問です。

5-10. 実行時間を計測する (clock)

競技プログラミング、アルゴリズムの勉強、あるいは研究などにおいて、実行時間を測定したくなることは往々にしてあります。例えば競技プログラミングの場合、

このプログラムが、どれくらいの時間で動くか知りたい。

あるいは、

最適化課題（マラソン型課題⁵）において、実行時間制限が 3 秒である。時間ギリギリまで計算して、2.99 秒経過したら計算を打ち切りたい。

そのような場合に、clock 関数 を使えば、簡単に実行時間を計測することができるのです。以下、2 個目の例における実装例を載せておきます。

ソースコード

#include <iostream>
#include <ctime>
using namespace std;

int main() {
    // (前略)
    int ti = clock();
    while (clock() - ti < 299 * CLOCKS_PER_SEC / 100) {
        // 計算をここで行う
    }
    // (後略)
    return 0;
}

5-11. 問題の制約が本当に合っているか確認する (assert)

競技プログラミングのコンテストにおいて、

あれ、この問題の制約、間違ってませんか？

と思った経験はあるでしょうか。あるいは、競技プログラミングで作問をするときに、

テストデータ作成はやったけど、本当に制約を満たしているか不安だ。

と思った経験はあるでしょうか。これ、実は assert 関数を使えば簡単に解決できるのです。例えば、以下の問題を考えてみましょう。

$A + B$ を出力してください。
$1 \leq A, B \leq 5000$

「本当にテストケースが制約の条件を満たしているか」確認するプログラムは、以下のようになります。もし満たしていない場合は、一部のケースで**ランタイムエラー（RE）**が出ます。（※便宜上、入力される $A, B$ の値は必ず long long 整数型の範囲内に収まると仮定します。）

ソースコード

#include <iostream>
#include <cassert>
using namespace std;

int main() {
    long long A, B;
    cin >> A >> B;

    // この 2 行を追加するだけ！
    assert(1LL <= A && A <= 5000LL); // A の値が範囲外ならエラーを発生させる
    assert(1LL <= B && B <= 5000LL); // B の値が範囲外ならエラーを発生させる

    cout << A + B << endl;
    return 0;
}

6. おわりに

C++ の標準ライブラリは、アルゴリズムの学習・実装や競技プログラミングをやるにあたってはとても便利な機能なのです。いざプログラムを書いてみると、標準ライブラリを使うのと使わないのとでは実装量が大きく違います。どちらが短く簡潔かは、皆さんもうお分かりでしょう。

最後に、本記事を通して C++ の標準ライブラリに関する知見を深め、アルゴリズム学習や競プロの手助けに少しでもなれば、とても嬉しいです。

最後までお読みいただきありがとうございました！

7. 参考文献

本記事を書く上で参考にした資料たちを紹介します。

• C++ 標準ライブラリヘッダ | cppreference.com
• The C++ Standard Template Library (STL) | GeeksForGeeks
• 秋葉拓哉, 岩田陽一, 北川宜稔: プログラミングコンテストチャレンジブック, マイナビ出版 (2012)
• 渡部有隆: プログラミングコンテスト攻略のためのアルゴリズムとデータ構造, マイナビ出版 (2013)
• @drken: ソートを極める！　～なぜソートを学ぶのか～
• @drken: スタックとキューを極める！　～考え方と使いどころを特集～
• @drken: BFS (幅優先探索) 超入門！　～キューを鮮やかに使いこなす～
• @ageprocpp: 最短経路問題総特集！！！　～BFSから拡張ダイクストラまで～

1. 実装をバグらせない二分探索の手法について、詳しくは「二分探索アルゴリズムを一般化 〜 めぐる式二分探索法のススメ 〜」 by @drken をご覧ください。 ↩

2. プログラムの実行において使ったメモリのバイト数のことです。 ↩

3. 既にこの手法を実装している人がいます。詳しくは、【ハーレム】多すぎて選べない！Pythonで円周率πを計算する13の方法 by @POPPIN_FRIENDS の 9 個目の方法をご覧ください。 ↩

4. 前編 でも既に述べているのですが、rand は乱数の質が完璧ではないので、もう少し良い質の乱数を使いたい場合はメルセンヌツイスターなどをご利用ください。 ↩

5. 通常の競プロコンテストの形式「2 時間程度で 5～6 問を解く」とは異なり、「1 問の最適化課題を数時間～数週間かけて解く」形式をマラソンマッチといい、出される課題を「マラソン型課題」ということがあります。 ↩