Pythonでデータの挙動を見やすくする可視化ツールを作成してみた（ヒストグラム・確率分布編）

概要

近年、品質管理やマーケティングの分野で「ばらつき」分析の重要性が叫ばれていますが、
ばらつき分析と切っても切り離せないのが**「ヒストグラム」と「分布の種類の判断」**です。

今回はPythonのグラフ描画ライブラリ「seaborn」をベースにして、
分析の種類の判断を強力にサポートするツールを作成しました！

機能1. 正規分布かどうかの判断

機能2. 各種確率分布のフィッティングとあてはまり評価指標

2021/7 修正：pipでインストールできるよう改良しました

下記コマンドでインストール可能となりました

$ pip install seaborn-analyzer

こちらの記事で紹介しているseaborn_analyzerライブラリの一部として、githubにもアップロードしております。
histクラスが、本記事の内容に該当します。

バグや改善要望等ありましたら、コメント頂けますとありがたいです

また、もしこのツールを良いと思われたら、GitHubにStar頂けるとありがたいです！

ユースケース

業務での分析でありがちな場面に基づき、ユースケースを作成しました

ユースケース1：それ正規分布？

上司「この前のばらつきの分析はどうなった？」

私「平均が3.1、標準偏差が0.4でした？」

上司「数字で言われてもわからんなあ！グラフで見やすくしてくれ！」

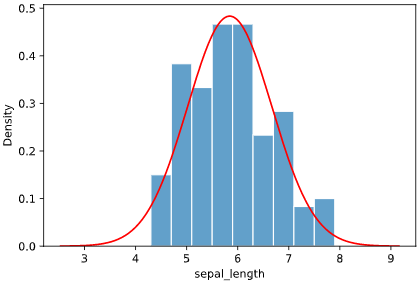
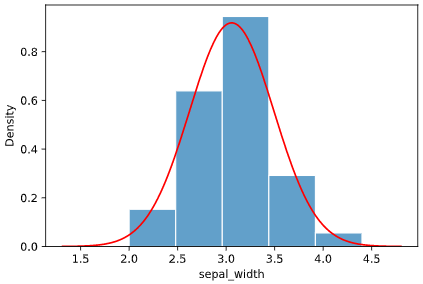
こういうとき、出すと喜ばれるグラフがヒストグラムです。

import seaborn as sns
iris = sns.load_dataset("iris")
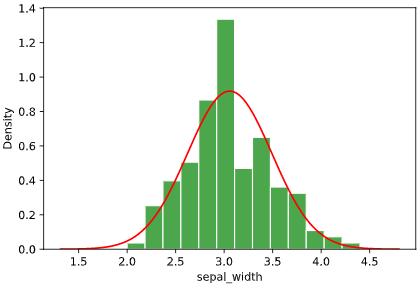
sns.distplot(iris['sepal_width'], kde=False)

しかし、統計に興味のある上司はこう言うかもしれません

上司「このヒストグラムで平均と標準偏差ってどこに当たるの？」

私「ヒストグラムに正規分布を当てはめた時、中心に来るのが平均、中心から68%のデータが収まるのが標準偏差です」

上司「正規分布を当てはめたときの値なのねー。で、これ本当に正規分布なの？」

私「多分、形を見る限り正規分布だと思います」

上司「多分でいいの？責任ある社会人なら正規分布と判断できる根拠を示さないとダメじゃない？」

私「ぴえん🥺」

このように、普段我々がよく使う標準偏差等、メジャーな統計指標の性質は、正規分布であることを前提としたものが多いです。
そして、その前提に対して「本当に正規分布なのか？」と問われると、答えに窮してしまう場面も多々あるかと思います。

ユースケース1の解決策：正規性検定とQQプロット

このようなケースで、強力なソリューションとなるのが、正規性検定です。
これは正規分布かどうかを判定する（厳密にいうと「正規分布であること」を帰無仮説とする）統計検定手法であり、

・シャピロ-ウィルク検定
・コルモゴロフ-スミルノフ検定

が代表的なアルゴリズムとなります。

一般的には、検定のP値が0.05あるいは0.01を下回ったら、正規分布ではないとみなします。

注意すべきが、P値が0.05あるいは0.01を上回った場合で、
厳密には、「有意水準を上回ったので正規分布である」とは言い切れません（帰無仮説が肯定されるわけではない）
ただし、正規性を裏付けるひとつの根拠にはなるので、
慣例的には「正規分布である可能性が高い」と言うために使われることが多いです。


また、正規性検定と共によく使われるのが、QQプロットです。

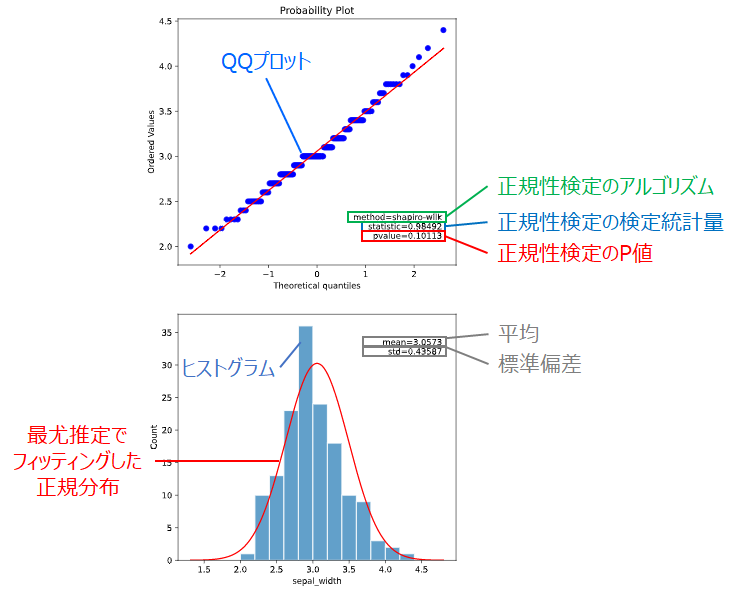
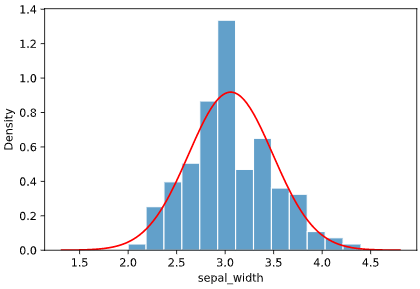
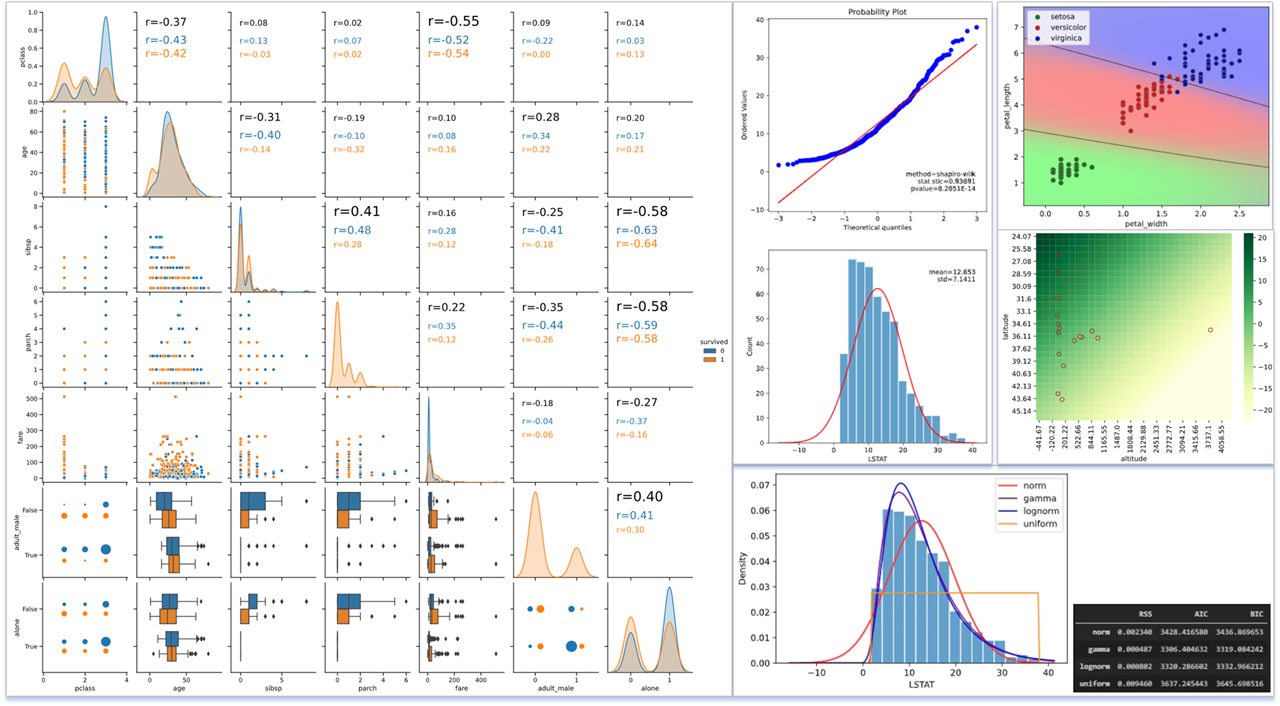
QQプロットは、サンプルデータが正規分布に従う場合の期待値を横軸にとり、観測値そのものを縦軸にとったグラフであり、プロットが直線状に乗れば、正規分布に従っているというような定性的な判断に使用されます

本ツールによる判断方法

本ツールでは、データに適した正規性検定アルゴリズムを選択して結果をプロットする、

hist.plot_normality()

というメソッドを用意しました。

具体的には、こちらを参考に、サンプル数が2000以下ならシャピロ-ウィルク検定、2000より大きいならコルモゴロフ-スミルノフ検定を使用します。

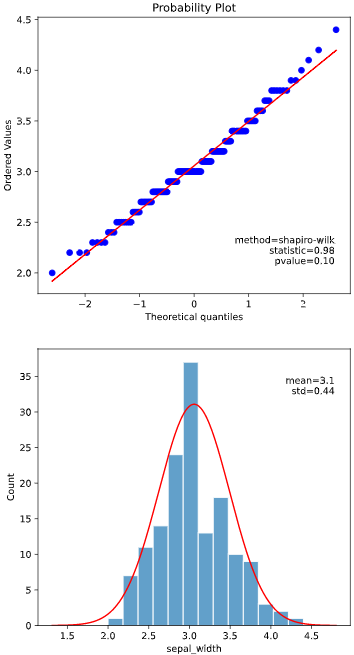
この選択したアルゴリズムに対し、下図のように検定結果、QQプロット、ヒストグラムを表示します

import seaborn as sns
from seaborn_analyzer import hist
iris = sns.load_dataset("iris")
hist.plot_normality(iris, x='sepal_width', norm_hist=False, rounddigit=5)

これにより、
・正規性検定のP値 > 有意水準(0.01 or 0.05)となるか
・QQプロットが直線上に乗るか
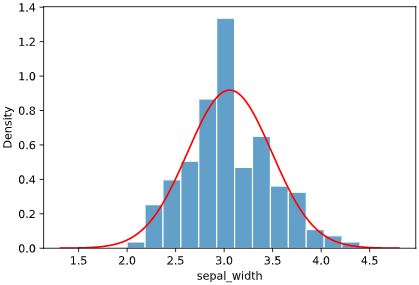
で、データが正規分布に従うかを判断することができます。

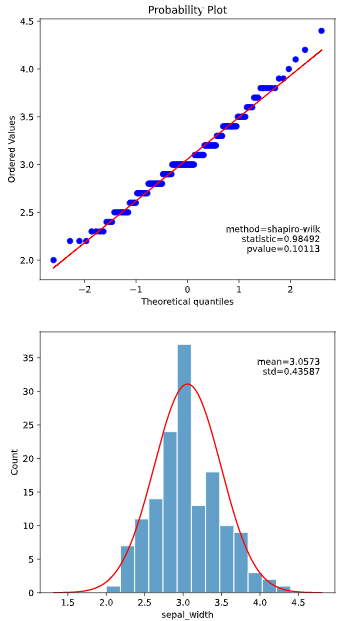
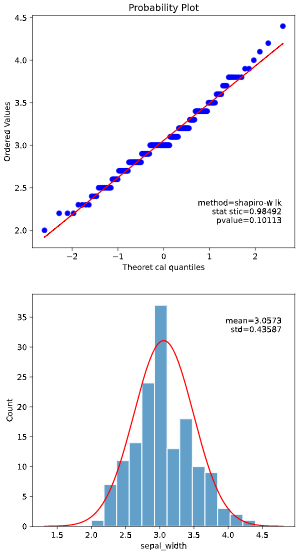
上図の例では、P値>0.05かつQQプロットが直線上に乗っているので、正規分布である可能性が高いとみなせます。

ユースケース2：正規分布でないなら何分布？

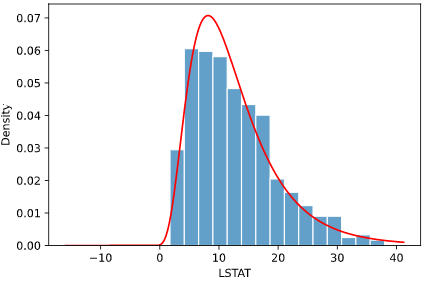
以下のような、ボストン住宅価格データセットの"LSTAT"変数（低所得者の割合）の分析を、前述のhist.plot_normalityメソッドで実施したとします。

from seaborn_analyzer import hist
from sklearn.datasets import load_boston
import pandas as pd
df = pd.DataFrame(load_boston().data, columns= load_boston().feature_names)
hist.plot_normality(df, x='LSTAT', norm_hist=False, rounddigit=5)

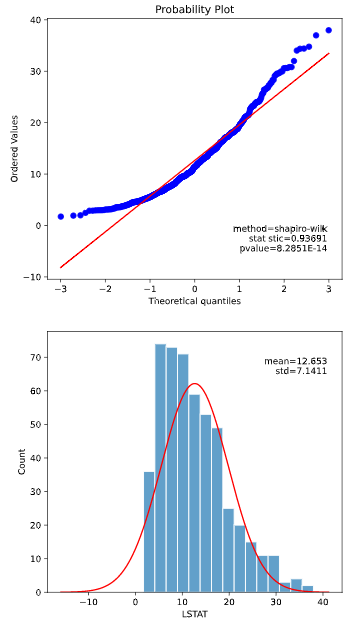
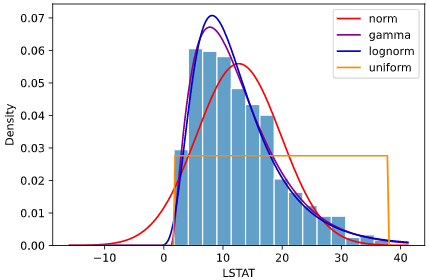
私「QQプロットが直線に乗らず、P値も0.01以下なので、正規分布でないと判断されます」

上司「わかった。それで、正規分布でないならなに分布なの？」

私「それは‥分かりません」

上司「分からないことに解決策を見つけるのがキミの仕事じゃないのかな？」

私「ぴえん🥺」

ばらつきを含めた予測や異常検知をしたい場合、正規分布でないと分かったとしても、**他の整合性の高い確率分布モデル**を当てはめる必要があります。

正規分布以外でフィッティング用途でよく使われるものには、用途別に

用途	代表的な確率分布
連続量の分析	一様分布、ガンマ分布、対数正規分布、コーシー分布、t分布、パレート分布
時間間隔の分析	指数分布、ガンマ分布、ワイブル分布
単位量あたり発生数の分析	二項分布、ポアソン分布

などがあります。
（それぞれの特徴は後述します）

しかし、統計の専門家でもない限り、正規分布以外はなじみが薄く、どう当てはめたらいいのか分からない、という場面が多いかと思います。

ユースケース2の解決策：最尤推定とフィッティング評価指標

このような正規分布以外の確率分布を当てはめる際に活用できるのが、最尤推定です。

最尤推定とは、確率分布のパラメータ(正規分布では平均,標準偏差、ガンマ分布では(k,θ)を、
そのパラメータにおいて分析対象のデータが観測される確率「尤度」を最大化するように、
パラメータを最適化する手法です。
（尤度に関しては、こちらの記事が大変参考になります）

例えば確率密度関数をk, θの2パラメータで表されるガンマ分布
$$f(x, \theta, k)=\frac{1}{\Gamma(k)\theta^k} x^{k-1} e^{-\frac{x}{\theta}}$$
としたとき、尤度は
$$\prod_{i=1}^{n} f(x_i, \theta, k)$$
で表されます。
この尤度を最小化するようにk、θを最適化するのが最尤推定です。
Pythonにおいては、scipy.stats.gamma等の確率分布クラスに含まれるfitというメソッドで、
最尤推定によってデータにフィットした確率分布パラメータを選択できます。

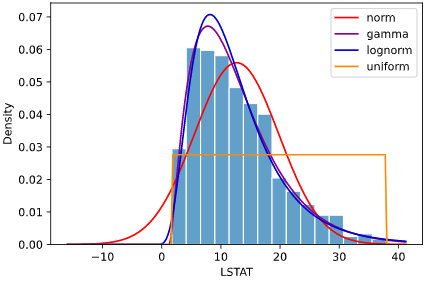
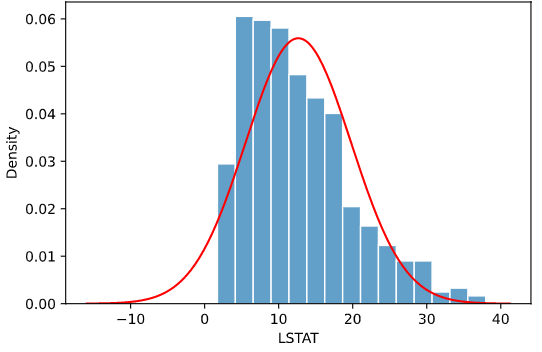
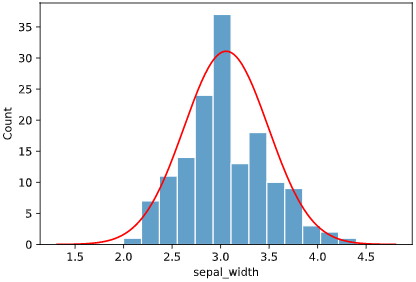
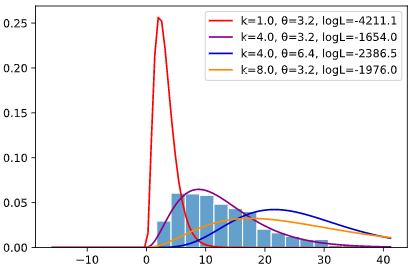
先ほどのボストン住宅価格データでは、最尤推定によりk=4.0、θ=3.2というパラメータが選択されますが、
下図紫線のように他のパラメータと比べて対数尤度(logL)が高く、
見た目でもヒストグラムと最もフィットしていることが分かります

なお、尤度を扱う際は尤度そのものよりも、その対数を取った「対数尤度」

ln\Bigl( \prod_{i=1}^{n} f(x_i)\Bigl)
=\sum_{i=1}^{n} ln\bigl(f(x_i)\bigl)

を使用することが多いです。主な理由は下記となります。
・尤度そのものは非常に小さな値なので、対数を取った方が現実的なスケールとなり表示しやすい
・対数を取れば積が和となるため、計算がしやすい（個々の対数尤度の総和が全体の対数尤度となる）

本ツールによる判断方法

本ツールでは、データに適した確率分布を最尤推定でフィッティングする

hist.hist_dist()

というメソッドを用意しました。

また、最尤推定した複数種類の確率分布のうち、どれが当てはまりの最も良いモデルか判断するため、

1. 残差平方和(RSS)
2. 赤池情報量規準(AIC)
3. ベイズ情報量規準(BIC)
   という3種類の指標を出力できます
   

どの指標も小さい方が当てはまりが良いと判断できますが、それぞれ以下のような特徴があります。

・RSS

RSSはヒストグラムと分布の座標上での距離の平方和を単純にとったもので、シンプルですがデータがビン上で丸められたり、パラメータ数を考慮できなかったりと厳密さに欠ける指標です。

・AIC

AICは対数尤度を用いているのでRSSのような丸め誤差は発生せず、かつ確率分布のパラメータ数も考慮した指標となっています。
パラメータが多いと「無理やり」フィッティングされ、機械学習での過学習に近い状態となってしまうため、
パラメータ数に応じて指標にペナルティを与え、パラメータが少ないシンプルな確率分布が選ばれやすいよう調整がなされています。

・BIC

BICはAICと同様、対数尤度をベースにパラメータ数に応じてペナルティを与える指標ですが、
こちらで詳説されております通り、AICよりもさらにパラメータ数の少ない確率分布が選ばれやすい傾向にあります
なお英語版Wikipediaによると、BICの差とフィッティング性能の関係は以下のように判断されるそうです

BICの差	フィッティング性能の差
<2	有意差なし
2-6	差あり
6-10	大きな差あり
10<	膨大な差あり

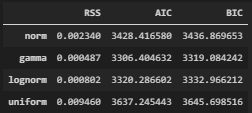
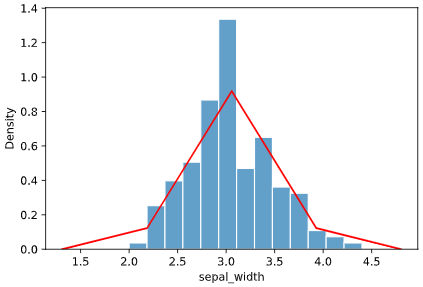
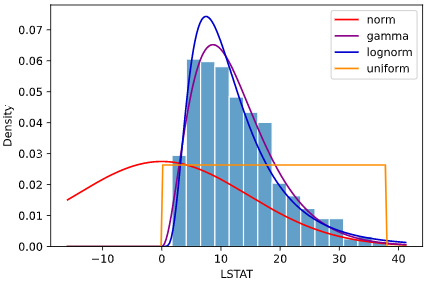
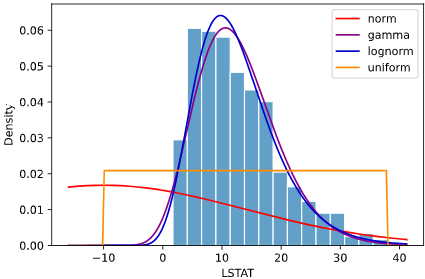
上の図の例では、正規分布(norm)、ガンマ分布(gamma)、対数正規分布(lognorm)、一様分布(uniform)の4種類の分布をフィッティングしていますが、
どの指標でもガンマ分布での値が最も小さく、ガンマ分布が最も当てはまりが良いと定量的に言えます
上司にも自信を持って「ガンマ分布が適切です」と言えるかと思います

使用に必要なもの

・Python本体 (動作確認時は3.9.1を使用)
・Matplotlibで表示可能な環境 (Jupyter等)
・下記ライブラリ (参考として動作確認時のライブラリバージョンも記載)
　seaborn (0.11.1)
　numpy (1.20.1)
　pandas (1.2.2)
　matplotlib (3.3.4)
　scipy (1.6.0)
　scikit-learn (0.24.1)

インストール方法

下記コマンドでインストール可能です

$ pip install seaborn-analyzer

※アンダースコアのpip install seaborn_analyzerでもインストール可能です。
インポート時はアンダースコアのimport seaborn_analyzerやfrom seaborn_analyzer
となるのでご注意ください

コード

モジュールcustom_hist_plot.py内のクラスhistに、必要な処理をまとめました。
GitHubにもアップロードしています

モジュール本体

seabornのdistplotぽいAPIで使用できるようにするため、クラスメソッドを利用しています

custom_hist_plot.py

from typing import Dict
import seaborn as sns
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
from scipy.stats import distributions
import decimal

class hist():
    DEFAULT_LINECOLORS = ['red', 'darkmagenta', 'mediumblue', 'darkorange',  'pink', 'brown', 'green', 'cyan', 'gold']
    DISCRETE_DISTRIBUTIONS = ['poisson', 'binom']
    
    def _fit_distribution(x: np.ndarray, distribution: distributions, sigmarange: float, linesplit: int, fit_params: Dict):
        """
        分布のフィッティング

        Parameters
        ----------
        x : ndarray
            フィッティング対象のデータ
        distribution : scipy.stats.distributions
            分布の種類
        sigmarange : float
            フィッティング線の表示範囲（標準偏差の何倍まで表示するか指定）
        linesplit : int
            フィッティング線の分割数（カクカクしたら増やす）
        fit_params : Dict
            フィッティング時に固定するパラメータ
        """
        # 表示範囲指定用に平均と不偏標準偏差計算(正規分布のときを基準に)
        mean = np.mean(x)
        std = np.std(x, ddof=1)

        # フィッティング実行
        params = distribution.fit(x, **fit_params)
        # フィッティング結果のパラメータを分割
        best_params = {'arg': params[:-2],
                      'loc': params[-2],
                      'scale': params[-1]
                      }
        # フィッティング曲線の生成
        Xline = np.linspace(min(mean - std * sigmarange, np.amin(x)), max(mean + std * sigmarange, np.amax(x)), linesplit)
        Yline = distribution.pdf(Xline, loc=best_params['loc'], scale=best_params['scale'], *best_params['arg'])

        # フィッティングの残差平方和を計算 (参考https://rmizutaa.hatenablog.com/entry/2020/02/24/191312)
        hist_y, hist_x = np.histogram(x, bins=20, density=True)  # ヒストグラム化して標準化
        hist_x = (hist_x + np.roll(hist_x, -1))[:-1] / 2.0  # ヒストグラムのxの値をビンの左端→中央に移動
        pred = distribution.pdf(hist_x, loc=best_params['loc'], scale=best_params['scale'], *best_params['arg'])
        rss = np.sum(np.power(pred - hist_y, 2.0))
        # AIC、BICを計算
        k = len(params) - len(fit_params)  # パラメータ数
        n = len(x)  # サンプル数
        logL = np.sum(distribution.logpdf(x, loc=best_params['loc'], scale=best_params['scale'], *best_params['arg']))  # 対数尤度
        aic = -2 * logL + 2 * k  # AIC
        bic = -2 * logL + k * np.log(n)  # BIC
        # 評価指標()
        fit_scores = {'RSS': rss,
                      'AIC': aic,
                      'BIC': bic
                      }

        return Xline, Yline, best_params, fit_scores

    def _round_digits(src: float, rounddigit: int = None, method='decimal'):
        """
        指定桁数で小数を丸める

        Parameters
        ----------
        src : float
            丸め対象の数値
        rounddigit : int
            フィッティング線の表示範囲（標準偏差の何倍まで表示するか指定）
        method : int
            桁数決定手法（'decimal':小数点以下, 'sig':有効数字(Decimal指定), 'format':formatで有効桁数指定）
        """
        if method == 'decimal':
            return round(src, rounddigit)
        elif method == 'sig':
            with decimal.localcontext() as ctx:
                ctx.prec = rounddigit
                return ctx.create_decimal(src)
        elif method == 'format':
            return '{:.{width}g}'.format(src, width=rounddigit)

    @classmethod
    def _round_dict_digits(cls, srcdict: Dict[str, float], rounddigit: int = None, method='decimal'):
        """
        指定桁数でDictの値を丸める

        Parameters
        ----------
        srcdict : Dict[str, float]
            丸め対象のDict
        rounddigit : int
            フィッティング線の表示範囲（標準偏差の何倍まで表示するか指定）
        method : int
            桁数決定手法（'decimal':小数点以下, 'sig':有効数字(Decimal指定), 'format':formatで有効桁数指定）
        """
        dstdict = {}
        for k, v in srcdict.items():
            if rounddigit is not None and isinstance(v, float):
                dstdict[k] = cls._round_digits(v, rounddigit=rounddigit, method=method)
            else:
                dstdict[k] = v
        return dstdict

    @classmethod
    def fit_dist(cls, data: pd.DataFrame, x: str=None, hue=None, dist='norm', ax=None, binwidth=None, bins='auto', norm_hist=True,
                  floc=None, sigmarange=4, linecolor='red', linesplit=200, hist_kws={}):
        """
        分布フィッティングと各指標の表示

        Parameters
        ----------
        data : pd.DataFrame or pd.Series or pd.ndarray
            フィッティング対象のデータ
        x : str
            ヒストグラム作成対象の変数カラム (列名指定、dataがDataFrameのときのみ指定可)
        hue : str
            色分け指定カラム (列名指定、dataがDataFrameのときのみ指定可)
        dist : str or List[str]
            分布の種類 ("norm", "lognorm", "gamma", "t", "expon", "uniform", "chi2", "weibull")
        ax : matplotlib.axes.Axes
            表示対象のax (Noneならmatplotlib.pyplot.gca()で1枚ごとにプロット)
        binwidth : float
            ビンの幅 (binsと共存不可)
        bins : int
            ビンの数 (bin_widthと共存不可、'auto'とするとスタージェスの公式で自動決定)
        norm_hist : bool
            ヒストグラムを面積1となるよう正規化するか？
        floc : float
            フィッティング時のX方向オフセット (Noneなら指定なし(weibullとexponは0))
        sigmarange : float
            フィッティング線の表示範囲 (標準偏差の何倍まで表示するか指定)
        linecolor : str or List[str]
            フィッティング線の色指定 (複数分布フィッティング時は、List指定)
        linesplit : int
            フィッティング線の分割数 (カクカクしたら増やす)
        hist_kws : Dict
            ヒストグラム表示(seaborn.histplot)の引数
        """

        # 描画用axがNoneのとき、matplotlib.pyplot.gca()を使用
        if ax == None:
            ax=plt.gca()
        
        # スタイルを変更 (デフォルト設定は見づらいため)
        if 'alpha' not in hist_kws.keys():
            hist_kws['alpha'] = 0.7
        if 'edgecolor' not in hist_kws.keys():
            hist_kws['edgecolor'] = 'white'

        # フィッティング対象データをndarrayで抽出
        if isinstance(data, pd.DataFrame):
            X = data[x].values
        elif isinstance(data, pd.Series):
            X = data.values
        elif isinstance(data, np.ndarray):
            X = data
        # フィッティング対象データの最小値よりflocが大きい場合、エラーを出す
        if floc is not None and floc >= np.amin(X):
            raise Exception('floc must be larger than minimum of data')

        # ビンサイズを設定
        if binwidth is not None:
            if bins == 'auto':
                bins = np.arange(np.floor(X.min()), np.ceil(X.max()), binwidth)
            else: # binsとbin_widthは同時指定できない
                raise Exception('arguments "bins" and "binwidth" cannot coexist')

        # norm_hist=Trueのとき、statをdensityに指定 (histplotの引数)
        stat = 'density' if norm_hist else 'count'
        # 色分けあるとき、ヒストグラム種類を積み上げに指定 (histplotの引数)
        multiple = 'layer' if hue is None else 'stack'

        # ヒストグラム描画
        ax = sns.histplot(data, x=x, hue=hue, ax=ax, bins=bins, stat=stat, multiple=multiple, **hist_kws)

        # 色分けあるとき、凡例を左上に表示
        if hue is not None:
            lg = ax.legend_
            handles = lg.legendHandles
            labels = [t.get_text() for t in lg.texts]
            leg_hist = ax.legend(handles, labels, loc='upper left')
            ax.add_artist(leg_hist)

        # distをList化
        dists = [dist] if not isinstance(dist, list) else dist
        # フィッティング線の色指定をリスト化
        linecolor = [linecolor] if isinstance(linecolor, str) else linecolor
        # 2種類以上をプロットしており、かつ色指定がListでないとき、他の色を追加
        if len(dists) >= 2:
            if len(linecolor) == 1:
                linecolor = cls.DEFAULT_LINECOLORS
            elif len(dists) != len(linecolor):
                raise Exception('length of "linecolor" must be equal to length of "dist"')

        # 分布をフィッティング
        all_params = {}
        all_scores = {}
        line_legends = []
        for i, distribution in enumerate(dists):
            fit_params = {}
            # 分布が文字列型のとき、scipy.stats.distributionsに変更
            if isinstance(distribution, str):
                if distribution == 'norm':
                    distribution = stats.norm
                elif distribution == 'lognorm':
                    distribution = stats.lognorm
                elif distribution == 'gamma':
                    distribution = stats.gamma
                elif distribution == 'cauchy':
                    distribution = stats.cauchy
                elif distribution == 't':
                    distribution = stats.t
                elif distribution == 'pareto':
                    distribution = stats.pareto
                elif distribution == 'uniform':
                    distribution = stats.uniform
                elif distribution == 'expon':
                    distribution = stats.expon
                    fit_params = {'floc': 0} # 指数分布のとき、locパラメータを0で固定
                elif distribution == 'weibull':
                    distribution = stats.weibull_min
                    fit_params = {'floc': 0} # ワイブル分布のとき、locパラメータを0で固定
                elif distribution == 'chi2':
                    distribution = stats.chi2
                    fit_params = {'floc': 0,  # カイ二乗分布のとき、locパラメータを0で固定
                                  'fscale': 1,  # カイ二乗分布のとき、scaleパラメータを1で固定
                                  }

            # flocしているとき、X方向オフセットを指定値で固定
            if floc is not None:
                fit_params['floc'] = floc
            # 分布フィット
            xline, yline, best_params, fit_scores = cls._fit_distribution(X, distribution, sigmarange, linesplit, fit_params)

            # 標準化していないとき、ヒストグラムと最大値の8割を合わせるようフィッティング線の倍率調整
            if norm_hist is False:
                line_max = np.amax(yline)
                hist_max = ax.get_ylim()[1]
                yline = yline * hist_max / line_max * 0.8
            # フィッティング線の描画
            leg, = ax.plot(xline, yline, color=linecolor[i])
            line_legends.append(leg)

            # フィッティング結果パラメータをdict化
            params = {}
            # 正規分布
            if distribution == stats.norm:
                params['mean'] = best_params['loc']
                params['std'] = best_params['scale']
                all_params['norm'] = params
                all_scores['norm'] = fit_scores  # フィッティングの評価指標
            # 対数正規分布 (通常の対数正規分布＋オフセット、参考https://analytics-note.xyz/statistics/scipy-lognorm/)
            elif distribution == stats.lognorm:
                params['mu'] = np.log(best_params['scale'])
                params['sigma'] = best_params['arg'][0]
                params['loc'] = best_params['loc']
                all_params['lognorm'] = params
                all_scores['lognorm'] = fit_scores  # フィッティングの評価指標
            # ガンマ分布 (通常のガンマ分布＋オフセット、参考https://qiita.com/kidaufo/items/2a5ba5a4bf100dc0f106)
            elif distribution == stats.gamma:
                params['theta'] = best_params['scale']
                params['k'] = best_params['arg'][0]
                params['loc'] = best_params['loc']
                all_params['gamma'] = params
                all_scores['gamma'] = fit_scores  # フィッティングの評価指標
            # コーシー分布 (通常のコーシー分布＋オフセット＋スケール、参考https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.cauchy.html)
            elif distribution == stats.cauchy:
                params['scale'] = best_params['scale']
                params['loc'] = best_params['loc']
                all_params['cauchy'] = params
                all_scores['cauchy'] = fit_scores  # フィッティングの評価指標
            # t分布 (通常のt分布＋オフセット＋スケール、参考https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.t.html)
            elif distribution == stats.t:
                params['scale'] = best_params['scale']
                params['df'] = best_params['arg'][0]
                params['loc'] = best_params['loc']
                all_params['t'] = params
                all_scores['t'] = fit_scores  # フィッティングの評価指標
            # パレート分布 (通常のパレート分布＋オフセット、参考https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.pareto.html)
            elif distribution == stats.pareto:
                params['scale'] = best_params['scale']
                params['b'] = best_params['arg'][0]
                params['loc'] = best_params['loc']
                all_params['pareto'] = params
                all_scores['pareto'] = fit_scores  # フィッティングの評価指標
            # 一様分布 (オフセット＋スケール、参考https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.uniform.html)
            elif distribution == stats.uniform:
                params['scale'] = best_params['scale']
                params['loc'] = best_params['loc']
                all_params['uniform'] = params
                all_scores['uniform'] = fit_scores  # フィッティングの評価指標
            # 指数分布 (オフセットなし、参考https://stackoverflow.com/questions/25085200/scipy-stats-expon-fit-with-no-location-parameter)
            elif distribution == stats.expon:
                params['lambda'] = 1 / best_params['scale']
                params['loc'] = best_params['loc']
                all_params['expon'] = params
                all_scores['expon'] = fit_scores  # フィッティングの評価指標
            # ワイブル分布 (オフセットなし、参考https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.weibull_min.html)
            elif distribution == stats.weibull_min:
                params['c'] = best_params['scale']
                params['k'] = best_params['arg'][0]
                params['loc'] = best_params['loc']
                all_params['weibull'] = params
                all_scores['weibull'] = fit_scores  # フィッティングの評価指標
            # カイ二乗分布 (オフセット・スケールなし、参考https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.chi2.html)
            elif distribution == stats.chi2:
                params['df'] = best_params['arg'][0]
                all_params['chi2'] = params
                all_scores['chi2'] = fit_scores  # フィッティングの評価指標
            # その他の分布
            else:
                all_params[distribution.name] = params
                all_scores[distribution.name] = fit_scores
            
        # フィッティング線の凡例をプロット (2色以上のときのみ)
        if len(dists) >= 2:
            line_labels = [d if isinstance(d, str) else d.name for d in dists]
            ax.legend(line_legends, line_labels, loc='upper right')

        return all_params, all_scores



    @classmethod
    def plot_normality(cls, data: pd.DataFrame, x: str=None, hue=None, binwidth=None, bins='auto', norm_hist=False,
                        sigmarange=4, linesplit=200, rounddigit=5,
                        hist_kws={}, subplot_kws={}):
        """
        正規性検定プロット

        Parameters
        ----------
        data : pd.DataFrame or pd.Series or pd.ndarray
            フィッティング対象のデータ
        x : str
            ヒストグラム作成対象の変数カラム (列名指定、dataがDataFrameのときのみ指定可)
        hue : str
            色分け指定カラム (列名指定、dataがDataFrameのときのみ指定可)
        binwidth : float
            ビンの幅 (binsと共存不可)
        bins : int
            ビンの数 (bin_widthと共存不可、'auto'とするとスタージェスの公式で自動決定)
        norm_hist : bool
            ヒストグラムを面積1となるよう正規化するか？
        sigmarange : float
            フィッティング線の表示範囲 (標準偏差の何倍まで表示するか指定)
        linesplit : int
            フィッティング線の分割数 (カクカクしたら増やす)
        rounddigit: int
            表示指標の小数丸め桁数
        hist_kws : Dict
            ヒストグラム表示(matplotlib.axes.Axes.hist())の引数
        subplot_kws : Dict
            プロット用のplt.subplots()に渡す引数 (例：figsize)
        """

        # 描画用のsubplots作成
        if 'figsize' not in subplot_kws.keys():
            subplot_kws['figsize'] = (6, 12)
        fig, axes = plt.subplots(2, 1, **subplot_kws)

        # QQプロット描画
        if isinstance(data, pd.DataFrame):
            X = data[x].values
        elif isinstance(data, pd.Series):
            X = data.values
        elif isinstance(data, np.ndarray):
            X = data
        stats.probplot(X, dist='norm', plot=axes[0])

        # ヒストグラムとフィッティング線を描画
        cls.fit_dist(data, x=x, hue=hue, dist='norm', ax=axes[1], binwidth=binwidth, bins=bins, norm_hist=norm_hist,
                      sigmarange=sigmarange, linecolor='red', linesplit=linesplit, hist_kws=hist_kws)
        # 平均と不偏標準偏差を計算し、ヒストグラム図中に記載
        mean = np.mean(X)
        std = np.std(X, ddof=1)
        if rounddigit > 0:  # rounddigitが0のときは文字表示しない
            params = {'mean':mean,
                    'std':std
                    }
            param_list = [f'{k}={v}' for k, v in cls._round_dict_digits(params, rounddigit, 'sig').items()]
            param_text = "\n".join(param_list)
            axes[1].text(axes[1].get_xlim()[0] + (axes[1].get_xlim()[1] - axes[1].get_xlim()[0]) * 0.95,
                        axes[1].get_ylim()[1] * 0.9,
                        param_text, verticalalignment='top', horizontalalignment='right')

        # 正規性検定
        if len(X) <= 2000: # シャピロウィルク検定 (N<=2000のとき)
            method = 'shapiro-wilk'
            normality=stats.shapiro(X)
        else: # コルモゴロフ-スミルノフ検定 (N>2000のとき)
            method = 'kolmogorov-smirnov'
            normality = stats.kstest(X, stats.norm(loc=mean, scale=std).cdf)
        # 検定結果を図中に記載
        if rounddigit > 0:  # rounddigitが0のときは文字表示しない
            params = {'statistic':normality.statistic,
                    'pvalue':normality.pvalue,
                    }
            param_list = [f'{k}={v}' for k, v in cls._round_dict_digits(params, rounddigit, 'sig').items()]
            param_list.insert(0, f'method={method}')
            param_text = "\n".join(param_list)
            axes[0].text(axes[0].get_xlim()[0] + (axes[0].get_xlim()[1] - axes[0].get_xlim()[0]) * 0.95,
                        axes[0].get_ylim()[0] + (axes[0].get_ylim()[1] - axes[0].get_ylim()[0]) * 0.1,
                        param_text, verticalalignment='bottom', horizontalalignment='right')

各メソッドの解説

・plot_normality()：外部から呼び出すメソッド1。ユースケース1で紹介した、正規性検定とQQプロットを結果表示
・fit_dist()：外部から呼び出すメソッド2。ユースケース2で紹介した、各種分布のフィッテイングおよび評価指標を表示
・_fit_distribution()：データに対し、1種類の分布をフィッティングし、評価指標(RSS,AIC,BIC)を算出
・_round_digits()：小数点以下N桁を丸めるメソッド
・_round_dict_digits()：dictのvalueすべての小数点以下N桁を丸めるメソッド（内部で_round_digitsメソッドを呼び出し）

使用方法

ユースケースで紹介した2メソッドの使用法を詳説します

plot_normalityメソッド実行方法

ユースケース1で紹介した、正規性検定とQQプロットを結果表示するplot_nomalityメソッドの実行方法です。
実行元スクリプトと同フォルダにcustom_hist_plot.pyを置き、下記のように実行します

# 参考としてirisデータを読み込んでいます
import seaborn as sns
iris = sns.load_dataset("iris")

# ここから実行部分
from seaborn_analyzer import hist
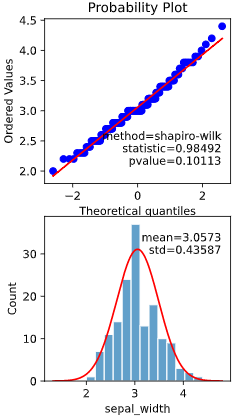
hist.plot_normality(iris, x='sepal_width')

実行すると下図のようなグラフ(QQプロット、正規性検定結果、ヒストグラム)が表示されます

fit_distメソッド実行方法

ユースケース2で紹介した、各種分布のフィッテイングおよび評価指標を表示するfit_distメソッドの実行方法です
実行元スクリプトと同フォルダにcustom_hist_plot.pyを置き、下記のように実行します

# 参考としてbostonデータを読み込んでいます
from sklearn.datasets import load_boston
df = pd.DataFrame(load_boston().data, columns= load_boston().feature_names)

# ここから実行部分
all_params, all_scores = hist.fit_dist(df, x='LSTAT', dist=['norm', 'gamma', 'lognorm', 'uniform'])

実行すると下図のようなグラフ(各種分布のフィッティング図)が表示されます

また、戻り値のうちall_paramsには各種分布の最尤推定結果パラメータが、all_scoresには評価指標(RSS, AIC, BIC)がdict形式で格納されます。

例えば、下記のようにDataFrame化すると、扱いやすいかと思います

df_scores = pd.DataFrame(all_scores).T  # 転置した方が扱いやすい
df_scores

引数の解説

引数"data"のみ指定必須で、残りは任意指定です。
・plot_normality・fit_dist共通引数
data
x
hue
binwidth
bins
norm_hist
sigmarange
linesplit
hist_kws

・plot_normalityのみ存在する引数
rounddigit
subplot_kws

・fit_distのみ存在する引数
dist
ax
linecolor
floc

引数を指定しないとき(plot_normality)

下記の引数が自動入力されます
(data, x=None, hue=None, binwidth=None, bins='auto', norm_hist=False,
sigmarange=4, linecolor='red', linesplit=200, rounddigit=5,
hist_kws={}, subplot_kws={})

・表示例
irisデータセットでの実行例

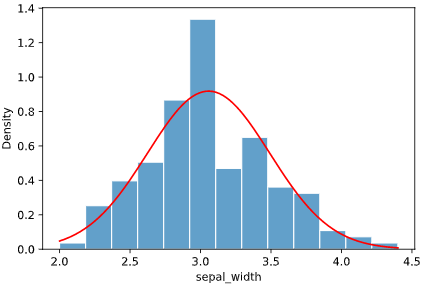
hist.plot_normality(iris['sepal_width'])

引数を指定しないとき(fit_dist)

下記の引数が自動入力されます
(data, x=None, hue=None, dist='norm', ax=None, binwidth=None, bins='auto', norm_hist=True,
floc=None, sigmarange=4, linecolor='red', linesplit=200, hist_kws={})

・表示例
bostonデータセットでの実行例

all_params, all_scores = hist.fit_dist(df['LSTAT'])

##plot_normality・fit_dist共通引数
plot_normalityとfit_dist共通の引数を、
irisデータセット＋fit_distでの表示例を交えて解説します。

data

分析対象となるデータを入力します。
pd.DataFrame、pd.Series、np.ndarray形式が指定可能です。
pd.DataFrameのときは、引数xの指定も必須となります

iris = sns.load_dataset("iris")
# 以下3つの実行例は全て同じ表示となる
all_params, all_scores = hist.fit_dist(iris, x='sepal_width')  # pd.DataFrameで指定
all_params, all_scores = hist.fit_dist(iris['sepal_width'])  # pd.Seriesで指定
all_params, all_scores = hist.fit_dist(iris['sepal_width'].values)  # np.ndarrayで指定

x

分析対象となるデータのカラム名(列名)を指定します。
dataがpd.DataFrame型のときのみ指定可能です

all_params, all_scores = hist.fit_dist(iris, x='sepal_length')

hue

ヒストグラムの色分け用カラム名(列名)を指定します。
dataがpd.DataFrame型のときのみ指定可能です

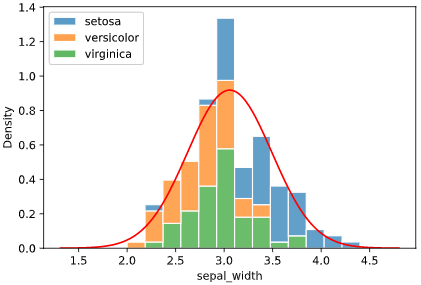
all_params, all_scores = hist.fit_dist(iris, x='sepal_width', hue='species')

binwidth

ヒストグラムのビン幅を指定します。引数'bins'との同時指定はできません

all_params, all_scores = hist.fit_dist(iris, x='sepal_width', binwidth=0.1)

bins

ヒストグラムのビン数を指定します。引数'binwidth'との同時指定はできません
binwidth、bins共に未指定のとき、スタージェスの公式でビン数が自動決定されます

all_params, all_scores = hist.fit_dist(iris, x='sepal_width', bins=5)

norm_hist

ヒストグラムの縦軸を面積が1となるよう標準化するか指定します

・標準化あり

all_params, all_scores = hist.fit_dist(iris, x='sepal_width', norm_hist=True)

・標準化なし

all_params, all_scores = hist.fit_dist(iris, x='sepal_width', norm_hist=False)

sigmarange

ヒストグラムの横軸表示範囲を指定します。標準偏差のsigmarange倍まで表示します

all_params, all_scores = hist.fit_dist(iris, x='sepal_width', sigmarange=8)

小さな値を指定しても、ヒストグラムの端までは表示されます

all_params, all_scores = hist.fit_dist(iris, x='sepal_width', sigmarange=1)

linesplit

フィッティング線の解像度を指定します。基本はデフォルトの200のままでよいかと思います

all_params, all_scores = hist.fit_dist(iris, x='sepal_width', linesplit=5)

hist_kws

ヒストグラム表示用seabornメソッドseaborn.histplotに渡す引数をdict指定できます。
渡せる引数の種類はこちらをご参照ください

all_params, all_scores = hist.fit_dist(iris, x='sepal_width', hist_kws={'color':'green'})

##plot_normality固有の引数
plot_normalityメソッドにのみ存在する引数を、
irisデータセットでの表示例を交えて解説します。

rounddigit

シャピロウィルク検定のp値や平均値など、数値表示の丸め桁数を指定します

hist.plot_normality(iris['sepal_width'], rounddigit=2)

文字を表示したくないとき

rounddigit=0を指定すると、文字が表示されなくなります。
こちらの記事でも触れられていますが、見栄え重視のエラい人から「文字を消してくれ」と指摘されるのは典型的な「ぴえん🥺」パターンなので、文字を消す機能を追加しました

hist.plot_normality(iris['sepal_width'], rounddigit=0)

subplot_kws

画像作成用メソッドmatplotlib.pyplot.subplotsに渡す引数をdict指定できます。
下の例のように、画像のサイズ（'figsize'、デフォルトは6×12）を変えたいときなどに便利です

hist.plot_normality(iris['sepal_width'], subplot_kws={'figsize': (3, 6)})

fit_dist固有の引数

fit_distメソッドにのみ存在する引数を、
bostonデータセットでの表示例を交えて解説します。

dist

フィッティング対象の分布をリスト指定します。
対応している分布の詳細はこちらご参照ください

all_params, all_scores = hist.fit_dist(df, x='LSTAT', dist=dist=['norm', 'gamma', 'lognorm', 'uniform'])

1個だけ指定したい場合は、リストでなく単体で指定可能です

all_params, all_scores = hist.fit_dist(df, x='LSTAT', dist='lognorm')

ax

表示対象のAxes（参考）を指定します

fig, axes = plt.subplots(2, 1, figsize=(6, 12))
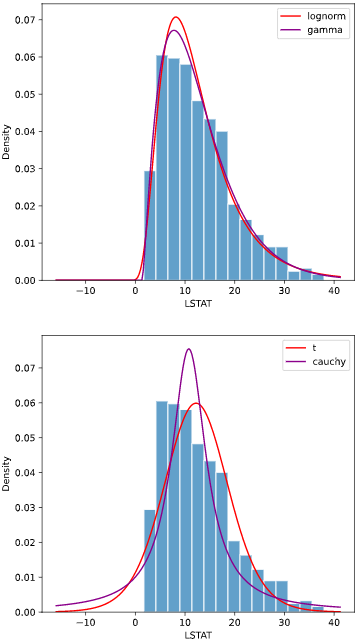
all_params0, all_scores0 = hist.fit_dist(df, x='LSTAT', dist=['lognorm', 'gamma'], ax=axes[0])
all_params1, all_scores1 = hist.fit_dist(df, x='LSTAT', dist=['t', 'cauchy'], ax=axes[1])

linecolor

線の色を指定します。
引数'dist'で複数の分布を指定した時は、こちらもリスト指定する必要があります

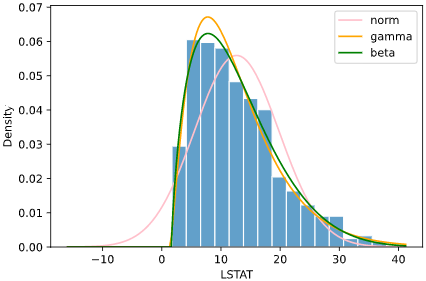
all_params, all_scores = hist.fit_dist(df, x='LSTAT', dist=['norm', 'gamma', scipy.stats.beta], linecolor=['pink', 'orange', 'green'])

floc

最尤推定対象のパラメータのうち、'loc'（オフセット量）を固定します
※データの最小値よりも小さな値を指定する必要があります

all_params, all_scores = hist.fit_dist(df, x='LSTAT', floc=0, dist=['norm', 'gamma', 'lognorm', 'uniform'])

all_params, all_scores = hist.fit_dist(df, x='LSTAT', floc=-10, dist=['norm', 'gamma', 'lognorm', 'uniform'])

※flocに関する注意点

・ここで固定したパラメータはAICやBICのパラメータ数にはカウントされません。

・指数分布'expon'、ワイブル分布'weibull'は、時間間隔を表現するために使用されるため、
　開始時刻をflocに固定する必要があります（例：開始時刻が15なら、floc=15を指定）
　デフォルトではfloc=0に固定されます

・ガンマ分布'gamma'を時間間隔の分析に使用する場合も、開始時刻をflocに固定する必要があります

・カイ二乗分布'chi2'は、基本的に標準化してから使用されるため、
　floc=0、fscale=1に固定されます（scaleも1に固定）

fit_distメソッドが対応する分布の種類

下記の分布に標準対応しています。

分類	対応する確率分布
連続量の分析	正規分布、一様分布、ガンマ分布、対数正規分布、コーシー分布、t分布、パレート分布
時間間隔の分析	指数分布、ガンマ分布、ワイブル分布
その他	カイ二乗分布
※二項分布やポアソン分布は母数が一定でなければ適用できず、
かつ最尤推定結果が自明（=発生数/母数）であるため、標準対応外としました

各分布の特徴を簡単にまとめると、下記となります（参考図書「共立出版　StanとRでベイズ統計モデリング」「東京大学出版会　統計学入門」）

確率分布名	本ツールdist引数指定	本ツールで推定するパラメータ	パラメータ数	従うデータ例
正規分布	'norm'	mean, std	2	基本
対数正規分布	'lognorm'	mu, sigma, loc	3	人間の体重、年収など
ガンマ分布	'gamma'	theta, k, loc	3	n個発生するまでの待ち時間、人間の体重など
コーシー分布	'cauchy'	scale, loc	2	外れ値の多いデータ
t分布	't'	df, scale, loc	3	外れ値の多いデータ
パレート分布	'pareto'	b, scale, loc	3	高額所得者の年収
一様分布	'uniform'	scale, loc	2	宝くじの当たり番号
指数分布	'expon'	lambda	1	1個発生するまでの待ち時間
ワイブル分布	'weibull'	c, scale	2	故障までの時間
カイ二乗分布	'chi2'	df	1	マハラノビス距離、ピアソンのカイ二乗検定

各分布の形状と概要に関して個別に解説します

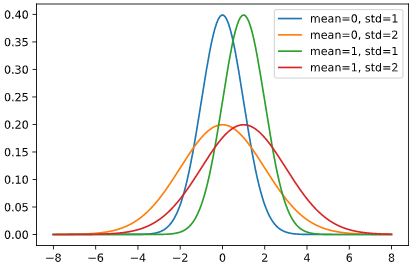
正規分布

基本中の基本です。まずはこの分布に従うかどうか確認しましょう
mean, stdの2個のパラメータを推定します

対数正規分布

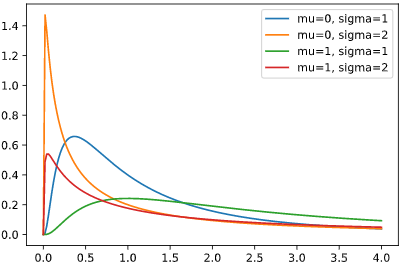
正規分布に従う変数Xに対し、exp(X)が従う分布です。
左右非対称、かつ裾が重い特徴があり、年収等が従う分布と言われています。
通常の対数正規分布のパラメータmu, sigmaに加え、本ツールではオフセット量（単純平行移動量）locを使って変形させ、3個のパラメータを推定します

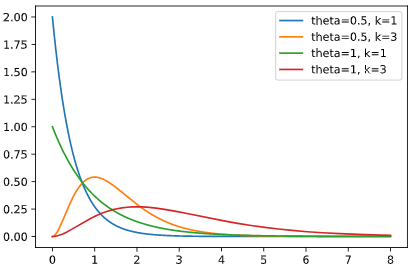
ガンマ分布

一定確率で起こる現象が、n回起こるまでの時間が従う分布です。
主に待ち時間等の分析に利用されますが、時間だけでなく連続量の分析にも使われる汎用性の広い分布です。
連続量においては、左右非対称な特徴をもつ、人間の体重等が従う分布と言われています。
通常のガンマ分布のパラメータtheta, kに加え、本ツールではオフセット量locを使って変形させ、3個のパラメータを推定します

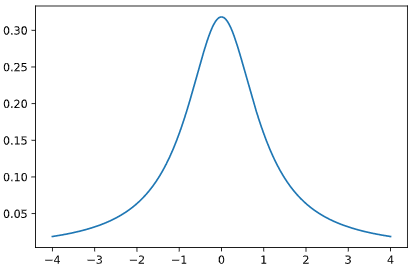
コーシー分布

裾が重い分布（外れ値が多い）の代表例で、外れ値が多いデータのモデル化によく利用されます。
通常のコーシー分布はパラメータを持ちませんが、本ツールではオフセット量loc、スケール倍率scaleを使って変形させ、2個のパラメータを推定します

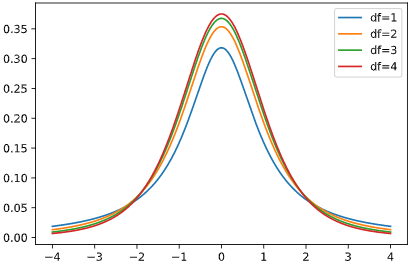
t分布

裾が重い分布で、パラメータdf(自由度)=1のとき、コーシー分布と一致します。
コーシー分布同様、外れ値が多いデータのモデル化によく利用され、コーシー分布よりも分布形状を柔軟に変えられます。
通常のt分布の自由度dfに加え、本ツールではオフセット量loc、スケール倍率scaleを使って変形させ、3個のパラメータを推定します

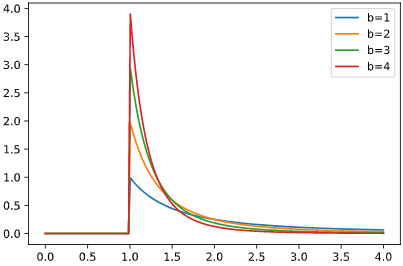
パレート分布

単調減少かつ裾が重い分布で、「パレート図」の語源となっていることからわかる通り、少数の上位層が総量（累積確率）の多くを占めるデータが従う分布です。高所得層の年収等が典型的です。
通常のパレート分布のパラメータbに加え、本ツールではオフセット量loc、スケール倍率scaleもを使って変形させ、3個のパラメータを推定します

一様分布

全ての値が一定確率で起こるときの分布です。宝くじやルーレットはこの分布に従います（従わなければイカサマ）
本ツールではオフセット量loc、スケール倍率scaleを使って変形させ、2個のパラメータを推定します

指数分布

一定確率で起こる現象が、1回起こるまでの時間が従う分布です。
時間間隔の分析において、最も基本的な分布となります。
通常の指数分布のパラメータlambdaの1個のパラメータを推定します（オフセットによる変形はしません）

ワイブル分布

発生確率が時間によって変化する現象が、1回起こるまでの時間が従う分布です。
パラメータc<1のときは時間と共に発生率が減少、c>1のときは発生率が増加、c=1のときは発生率一定となり指数分布と一致します。
建造物や工場設備など、時間と共に劣化する（安定する）特徴を持つデータが従います。
通常のワイブル分布のパラメータcおよびscale(指数分布のlambdaに相当)の2個のパラメータを推定します（オフセットによる変形はしません）

※上記以外の分布を使用したいとき

上記以外の分布も、scipy.stats内の各分布クラスを渡せばフィッティング自体はできるかと思います。
全ての分布を試したわけではないので、動作は保証できませんが‥

（例）ベータ分布をフィッティング

all_params, all_scores = hist.fit_dist(df, x='LSTAT', dist=scipy.stats.beta)
df_scores = pd.DataFrame(all_scores).T
df_scores

余談 (というより質問)　AICおよびBICの計算式

本ライブラリにおけるAIC、BICの計算式は、

確率分布のパラメータ数 k

サンプル数 n

最尤推定した確率分布の確率密度関数を
$$f(x)$$

対数尤度 (xiは各サンプルの値)
$$ ln(L) = \sum_{i=1}^{n} ln\bigl(f(x_i)\bigl)$$

としたとき、

AIC = -2\ln (L) + 2k\\
BIC = -2\ln (L) + k\ln (n)

のように求めています。
この式に絶対の自信があるわけではないので、ベイズ統計に詳しい方がいればご助言頂けるとありがたいです。