本記事の内容
- K-S検定(コルモゴロフ-スミルノフ検定)のpythonでの実装方法を紹介
- K-S検定の誤用について説明
K-S検定とは
多数の記事で紹介されているので詳細は割愛する。
要は、得られたデータの分布が「ある分布」と差があるかどうかを調べる検定である。
例えば、「30人の身長のデータが正規分布と差があるかどうか」といったことが知りたいときに使うことができる。
ここで、「ある分布」は連続分布であればどのような分布を仮定してもよい。
pythonでの実装
例えばデータの分布が正規分布と差があるかどうかを検定したい場合、pythonでは以下の通り非常に簡単に実装することができる。
得られたp値が有意水準(例:5%)以下であれば、データの分布は仮定した分布と差があると結論付けられる。
from scipy import stats
import numpy as np
from matplotlib import pyplot as plt
# 正規乱数から得たデータの分布が正規分布と差があるか検定
data = stats.norm.rvs(size=500)
pv = stats.kstest(data, "norm")[1]
print('p-value:' + str(pv))
# 正規分布の平均と分散を指定したい場合
mu = 5
sigma2 = 3
data = stats.norm.rvs(size=500) * sigma2 + mu
pv = stats.kstest(data, stats.norm(loc=mu, scale=sigma2).cdf)[1]
print('p-value:' + str(pv))
# 仮定する分布を変えてみる(平均値を1増やす)
pv = stats.kstest(data, stats.norm(loc=mu + 1, scale=sigma2).cdf)[1]
print('p-value:' + str(pv))
# 可視化
x = np.linspace(-5, 15, 100)
pdf_norm1 = stats.norm.pdf(x, loc=mu, scale=sigma2)
pdf_norm2 = stats.norm.pdf(x, loc=mu + 1, scale=sigma2)
plt.hist(data, normed=True)
plt.plot(x, pdf_norm1, 'r')
plt.plot(x, pdf_norm2, 'k')
plt.show()
結果
p-value:0.744667043116 # p > 0.05
p-value:0.664134130033 # p > 0.05
p-value:7.51353201878e-10 # p < 0.05
仮定する正規分布の平均値を1増やすと帰無仮説を棄却する、つまり分布に差があるという結果となった。
可視化結果は以下。赤線がp>0.05、黒線がp<0.05と判定された分布の密度関数である。
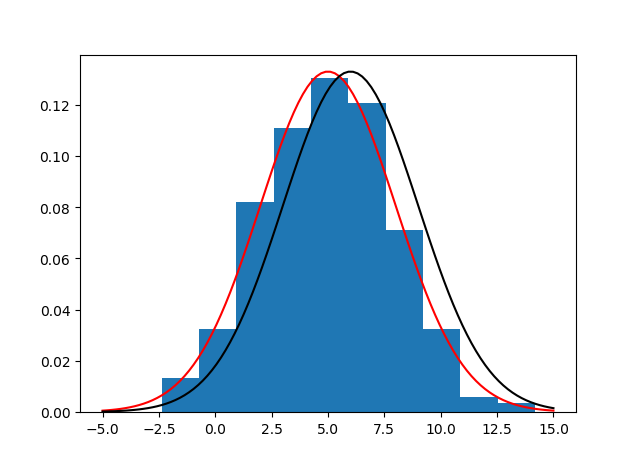
K-S検定の誤用について
ここまでは調べればすぐに出てくる内容である。
本記事の主旨は「K-S検定の誤用が乱用されている」ことに対する指摘である。
多くの記事で紹介されているK-S検定が**「データの分布が仮定した分布と一致するかを調べる」ことを目的として使用されている。
しかし、K-S検定で得られる結論は、帰無仮説「データの分布が仮定した分布に一致している」を棄却できるかどうかだけである。
そのため、帰無仮説を棄却した結果は「データの分布が仮定した分布と一致しているとは言えない」であり、帰無仮説を棄却できない場合は「データの分布が仮定した分布と一致しているかどうかは何とも言えない**」であり、決して「仮定した分布と一致している」ではない。
「帰無仮説の採用」という検定の定番の誤用については様々な記事で解説されているのだが、K-S検定ではこれが(他の検定と比較して)まかり通っている、かつ指摘がされていないのが現状である。他の検定と同様に、p値が0.05より大きいからと言って帰無仮説を採用する理由にはならない。
なぜK-S検定でこの誤用が多用されているかというと(想像ではあるが)、「2つの分布に差があること」を示すことよりも「分布が一致していること」を示すことのニーズが大きいからであろう。例えば、データが正規分布していると仮定できれば様々な都合の良い分析を行うことができる。
記事を書いている途中、以下にもK-S検定の誤用に関する記載を見つけた。
外部リンク:差がないと検定していますか?
コルモゴロフ・スミルノフ検定は使い方がちがいますね。よく見るのは、Aというデータセットが正規分布からずれているかどうかの検定に使います。ここでp>0.05であればAというデータセットは正規分布から大きく外れてはいない。よって正規分布とみなす。と考えて、パラメトリック検定(T-test,ANOVAであったりあと直線回帰もそう)を行えるとします。ただし実際は、「差が検出されない」からといって群間に違いがない、という結論は、厳密には導けないと思ってます。信頼区間を示して、まあ重なってます、というのがいいかなあとおもう。
[追記]以下にも指摘が見つかった。
外部リンク:任意の累積分布関数を仮定した一標本コルモゴロフ・スミルノフ検定
帰無仮説を棄却できないとき,「標本がその累積分布関数に適合していないとはいえない」だけであって,積極的に任意の累積分布関数から発生した標本だとか,母集団の分布はまさにこれだとか,ちょっと厳しくいえば正規分布に従っている,とか,そういうように語気強くいうべきではないかも。もちろん,正規性を示すひとつの証拠であることは間違いないけど。
[追記]
ではp値が0.05より大きい場合で、分布が一致していない、というのはどのような状況なのか。
例えばサンプルサイズが小さいときである。
試しにサンプルサイズを0~500まで変えたときのp値をプロットしてみた。
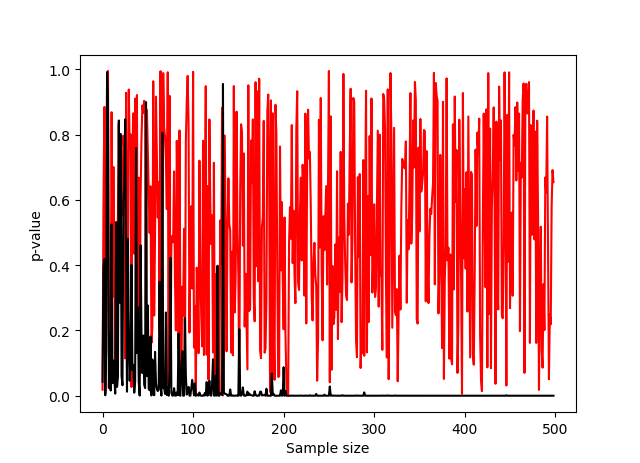
黒が仮定する正規分布の平均値を1ずらした場合、赤が正しい正規分布の場合である。
確率の問題なので当然だが、分布が異なっていてもp>0.05となることはあるし、その逆も起こりうる。
サンプルサイズが小さくなればp<0.05の割合が減少するのは他の検定と同様である。
終わりに
K-S検定の誤用について述べてきたが、私は統計学の専門家ではない(単なる検定ユーザである)ので本記事の主張は間違っているかもしれない。これが誤用ではないと判明した場合は本記事を削除する・補足するなどの対応を取るつもりである。