概要
Pythonのグラフ描画ライブラリ「seaborn」をベースにして、
相関係数や散布図などを一括で確認できる可視化ツールを作ってみました。

試行錯誤の結果、様々なデータパターンに対応した、汎用性の高いツールが出来た!
と感じています
2021/7 修正:pipでインストールできるよう改良しました
下記コマンドでインストール可能となりました
$ pip install seaborn-analyzer
※関連ツールを1つの記事にまとめました!よければこちらもご覧ください
もしこのツールを良いと思われたら、GitHubにStar頂けるとありがたいです!
2021/8 注意点
~最新のseaborn 0.11.1では以下のように正しく表示されません~
→最新版の0.11.2でも正しく表示されるよう修正しました(2021/10/31)
背景と機能
本ツールの機能と、作成した背景を解説します
seabornとは?
Pythonのグラフ描画ライブラリで、ベースとなっているライブラリmatplotlibよりも、簡単なコードで綺麗なグラフを描くことができます
中でも、散布図とヒストグラムを組み合わせた「pairplot」は、
多変数の関係性を一度に可視化することができるため、
データ分析の初期段階で非常によく使われています。
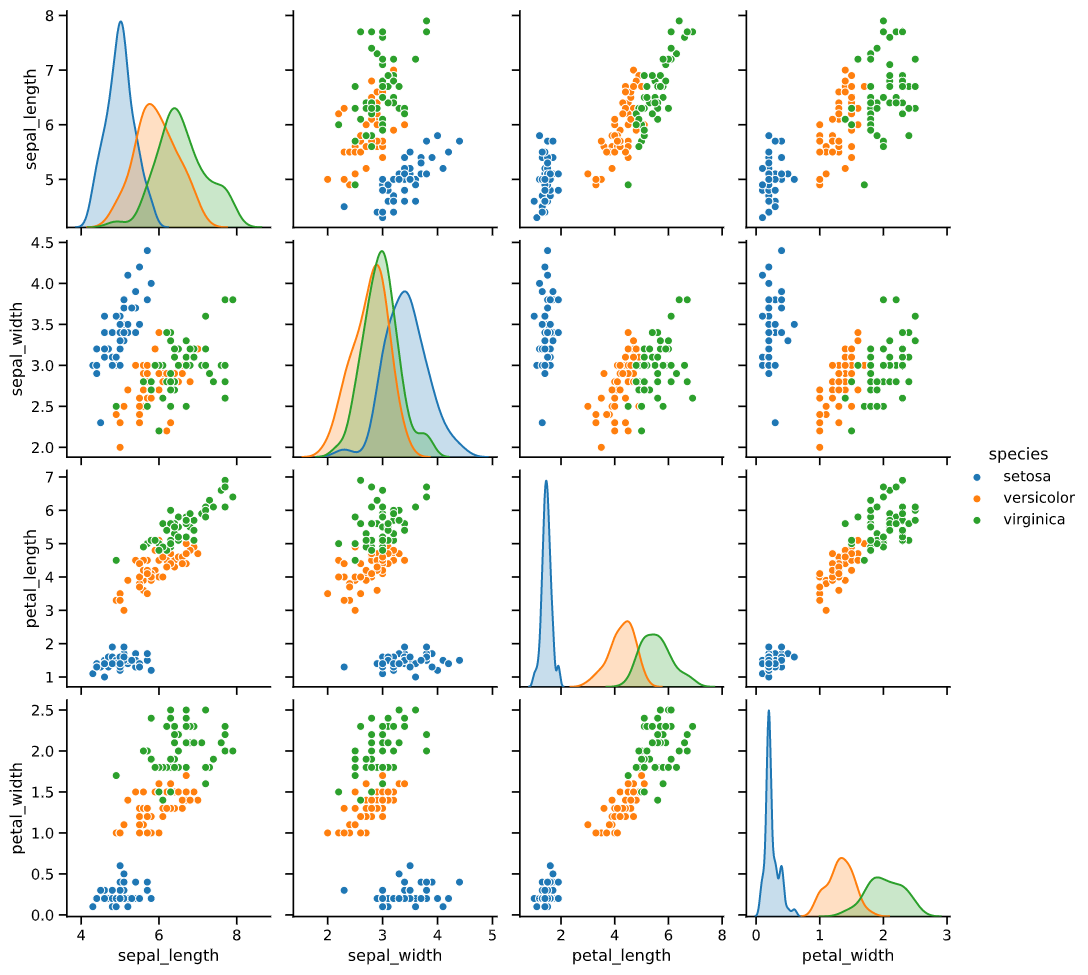
pairplotの課題
とても便利なpairplotですが、下記のようにいくつか課題があります。
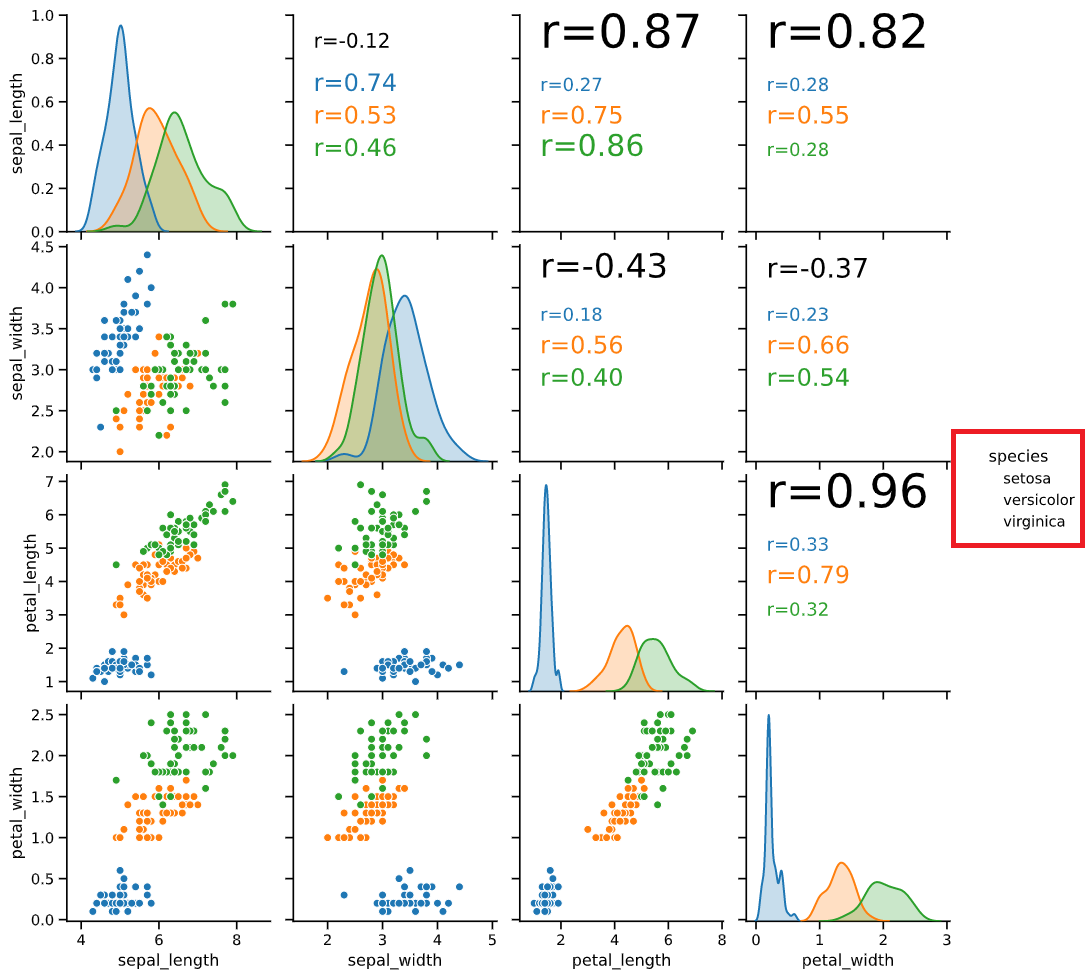
課題1:右上の散布図が情報量ゼロ
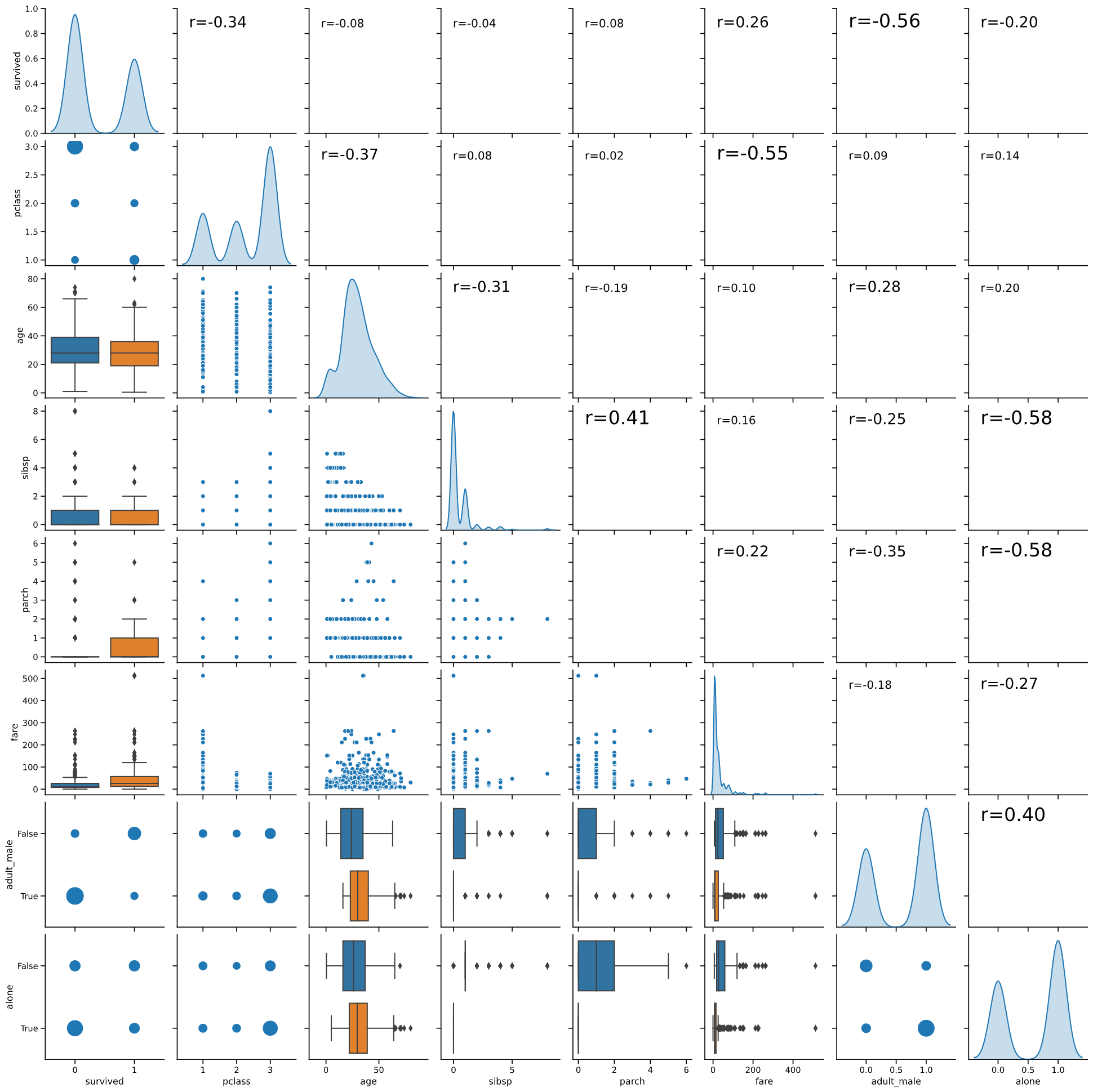
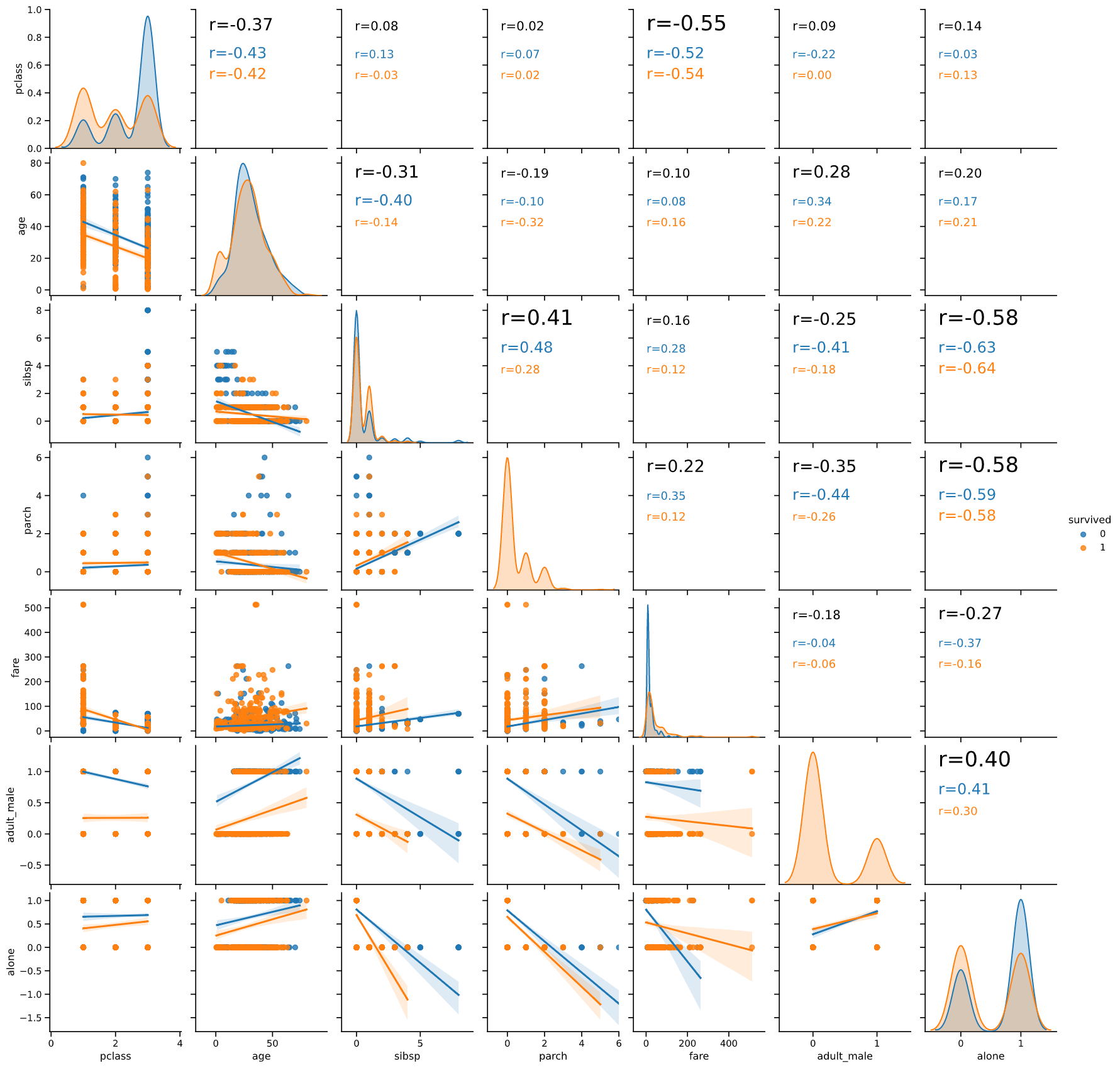
pairplotの左下(下の図の赤枠)と右上(青枠)の散布図を見比べてください
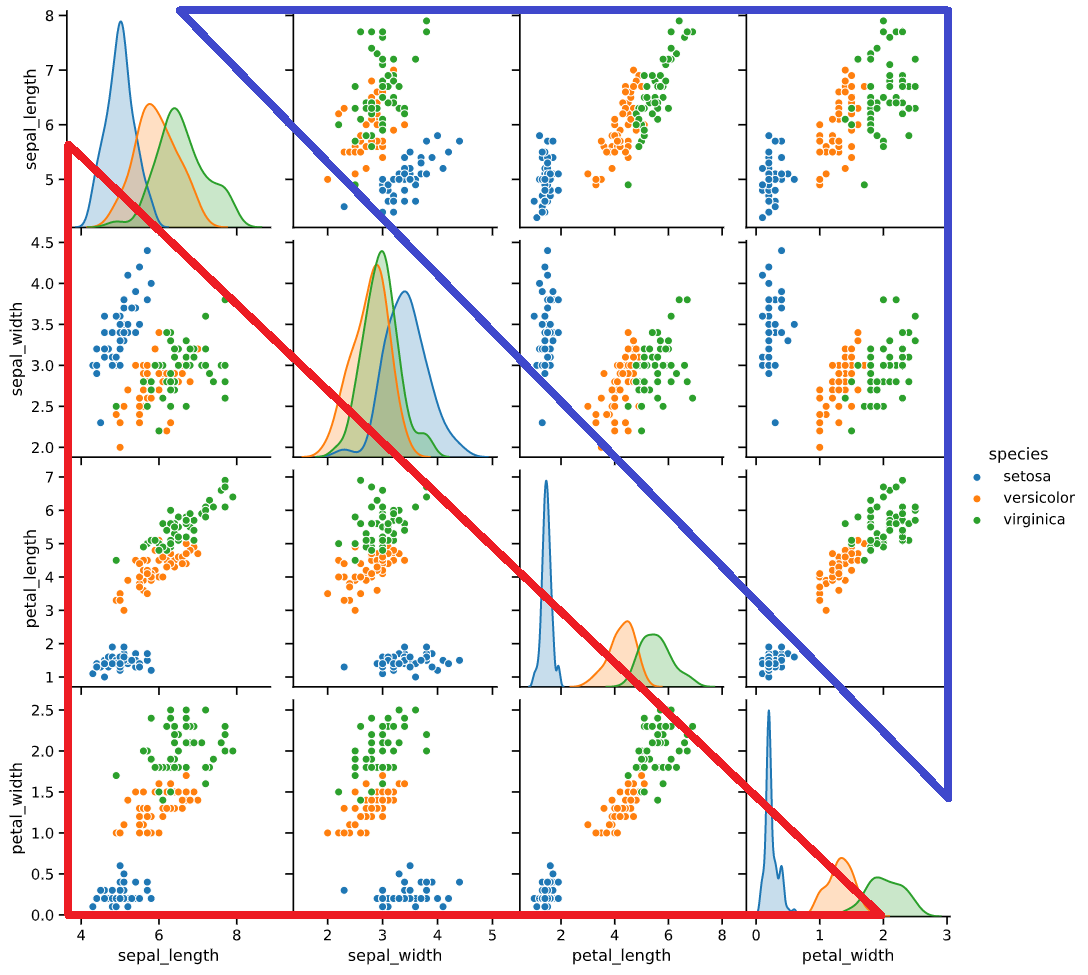
よく見ると右上の散布図は左下の散布図の軸を反転させただけで、表示している情報は全く同じです。
右上の散布図は情報量ゼロ‥むしろ分析者に意味のない情報を見せている分、マイナスの効果すら生み出していると言えます。
(一応、縦軸横軸どちらの要素からスタートしても目的の2変数に辿り着けるというメリットはありますが‥)
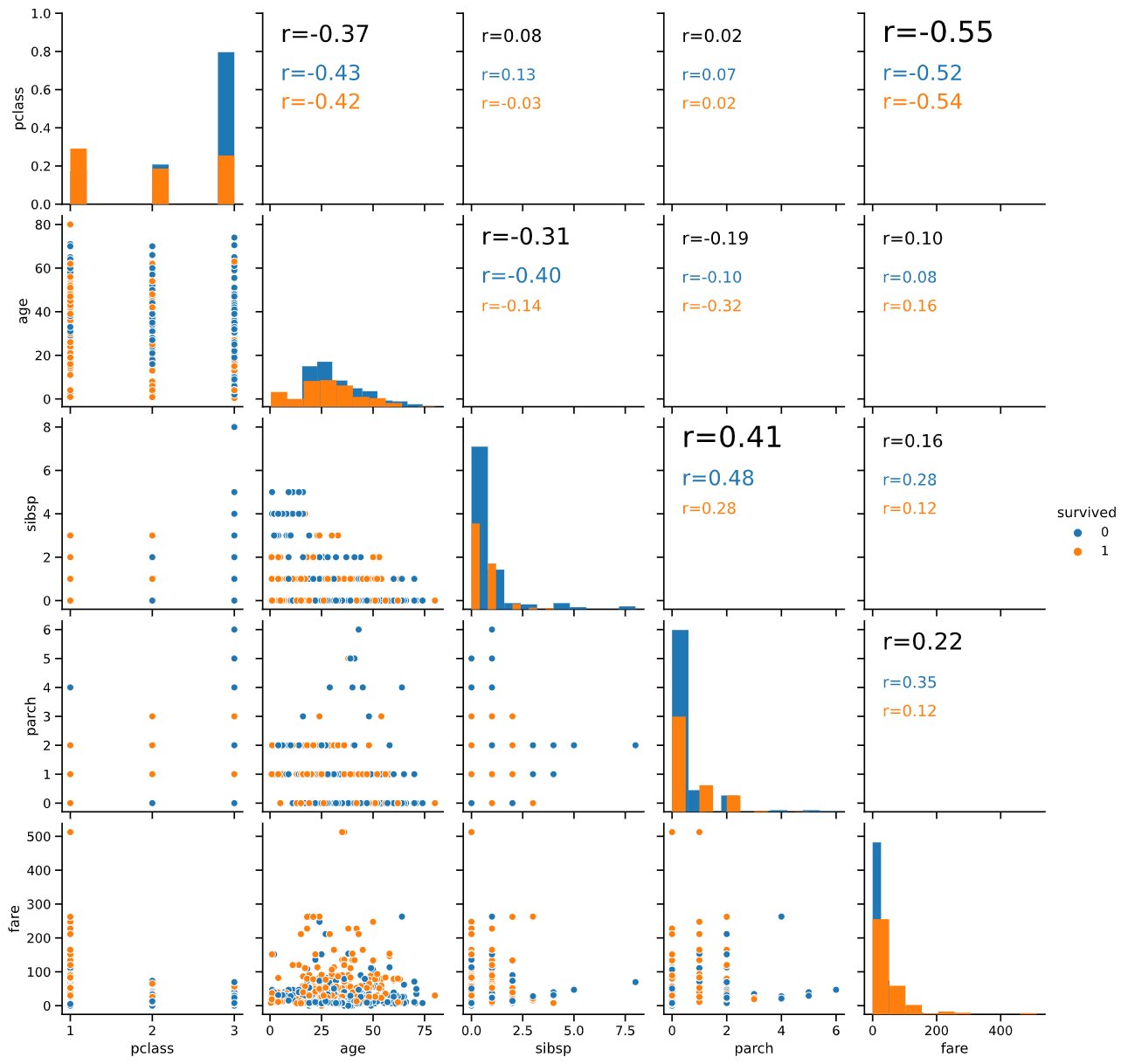
課題2:離散的な変数は、散布図だと挙動が分かりずらい
今まで扱ってきた「iris」データセットは全て連続的な変数なので散布図がフィットしますが、
「titanic」データセットではどうでしょう?
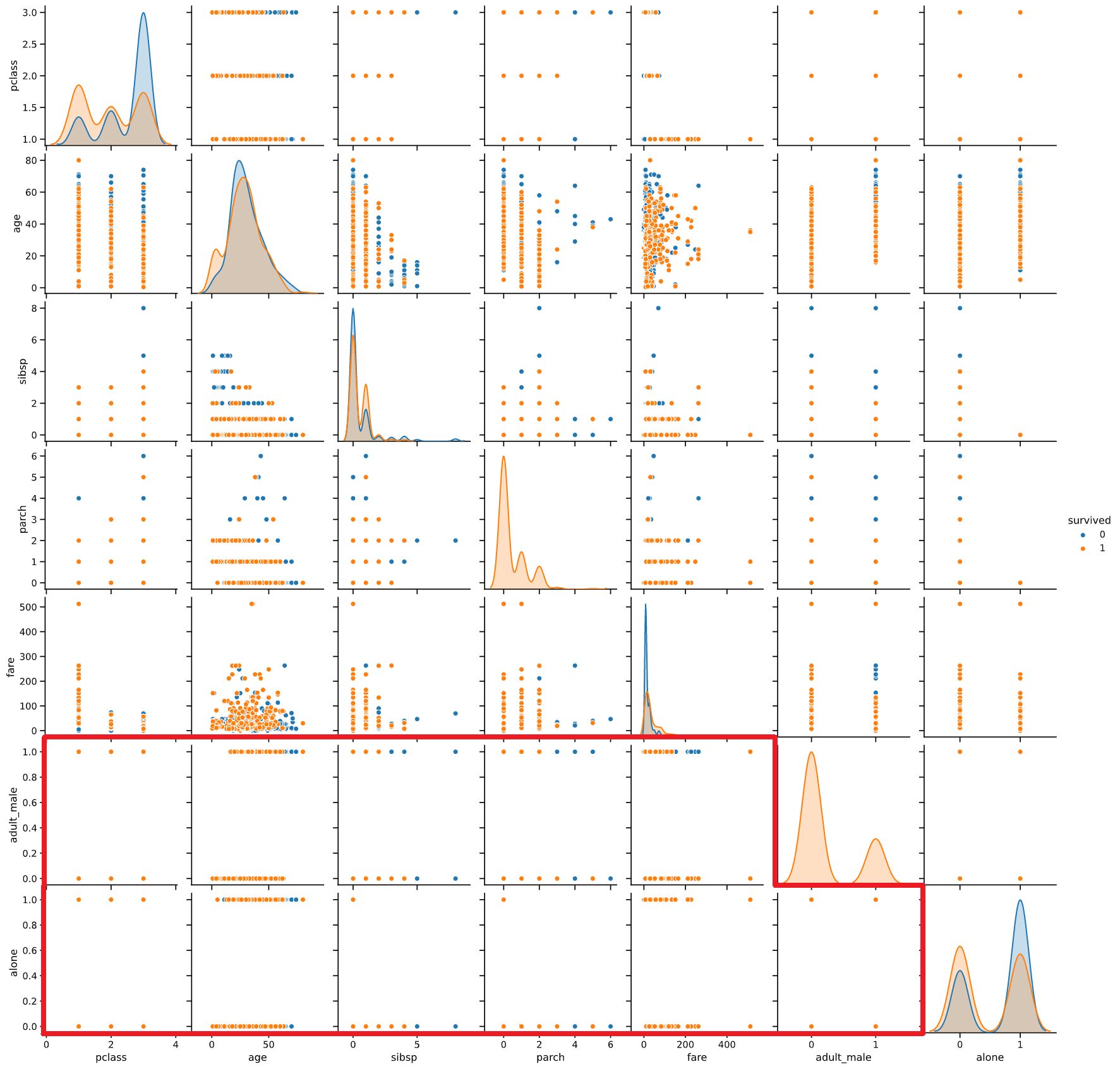
"adult_male"、"alone"などの、離散的でとる値の少ない変数(赤枠で囲った部分)では、
点が重なってしまって挙動がよく分からないですね。
しかも、このような離散的な変数こそ実際のデータ分析では重要な場面も多い(下の「余談」を参照ください)ので、無視できる課題ではありません。
追加した機能
上記課題1、2をクリアするため、
R言語の可視化ライブラリ「GGally」等を参考にしつつ、
下記の2つの機能を加えてデータの傾向を見やすくしたメソッド
pairanalyzer
を作成しました
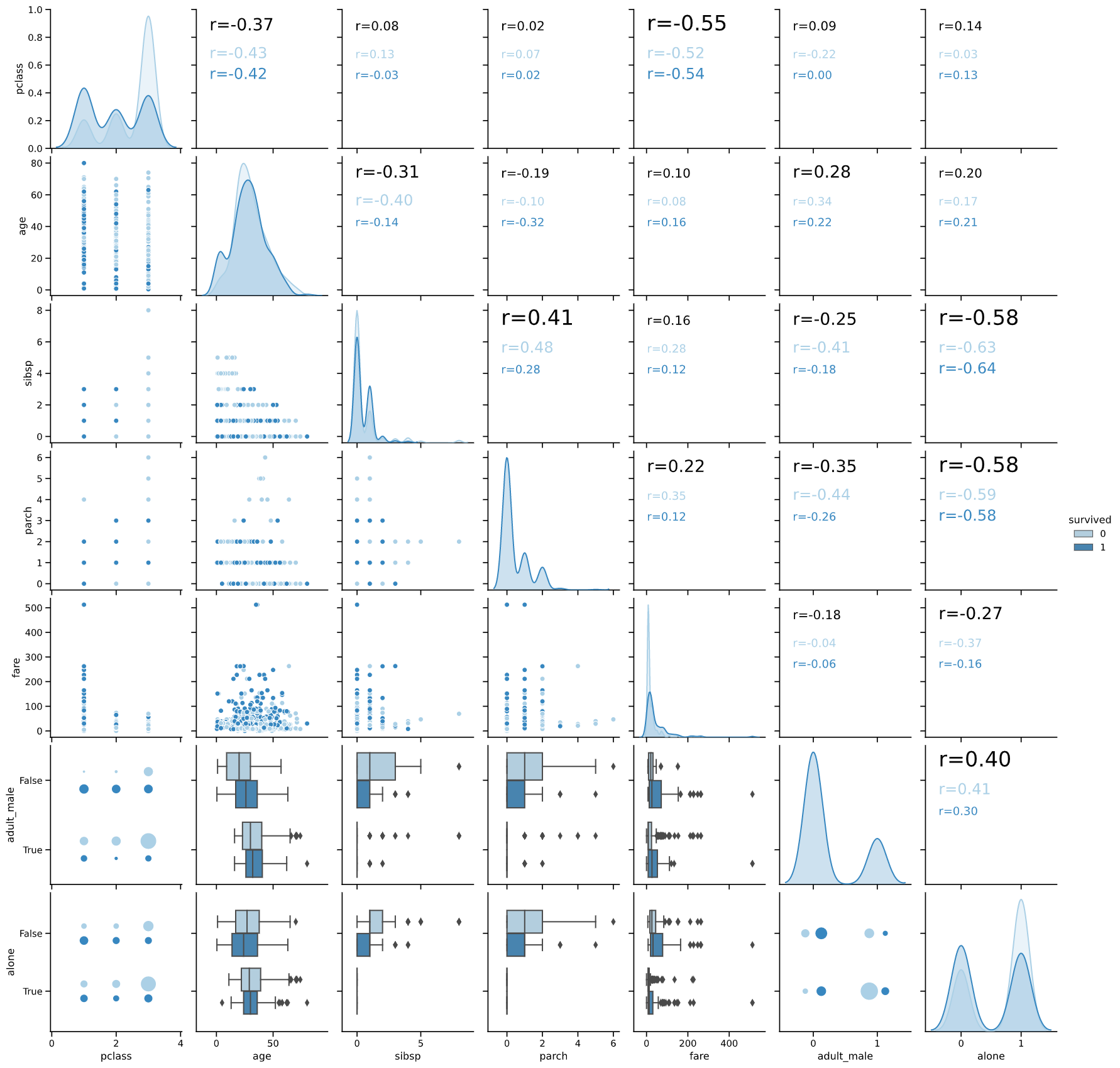
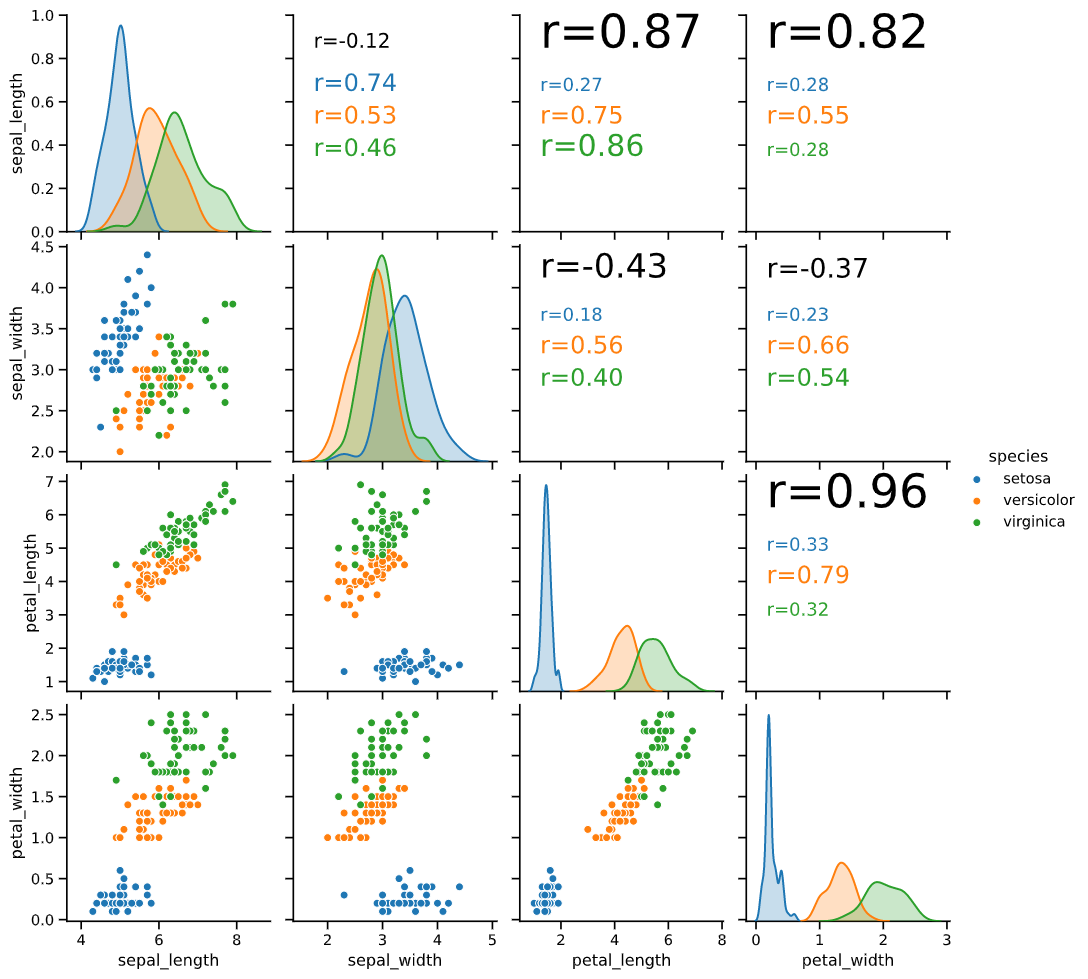
機能1:相関係数の表示
「課題1:右上の散布図の情報量がゼロ」をクリアするため、意味のある情報を載せたいと思い、
右上には相関係数を表示することとしました
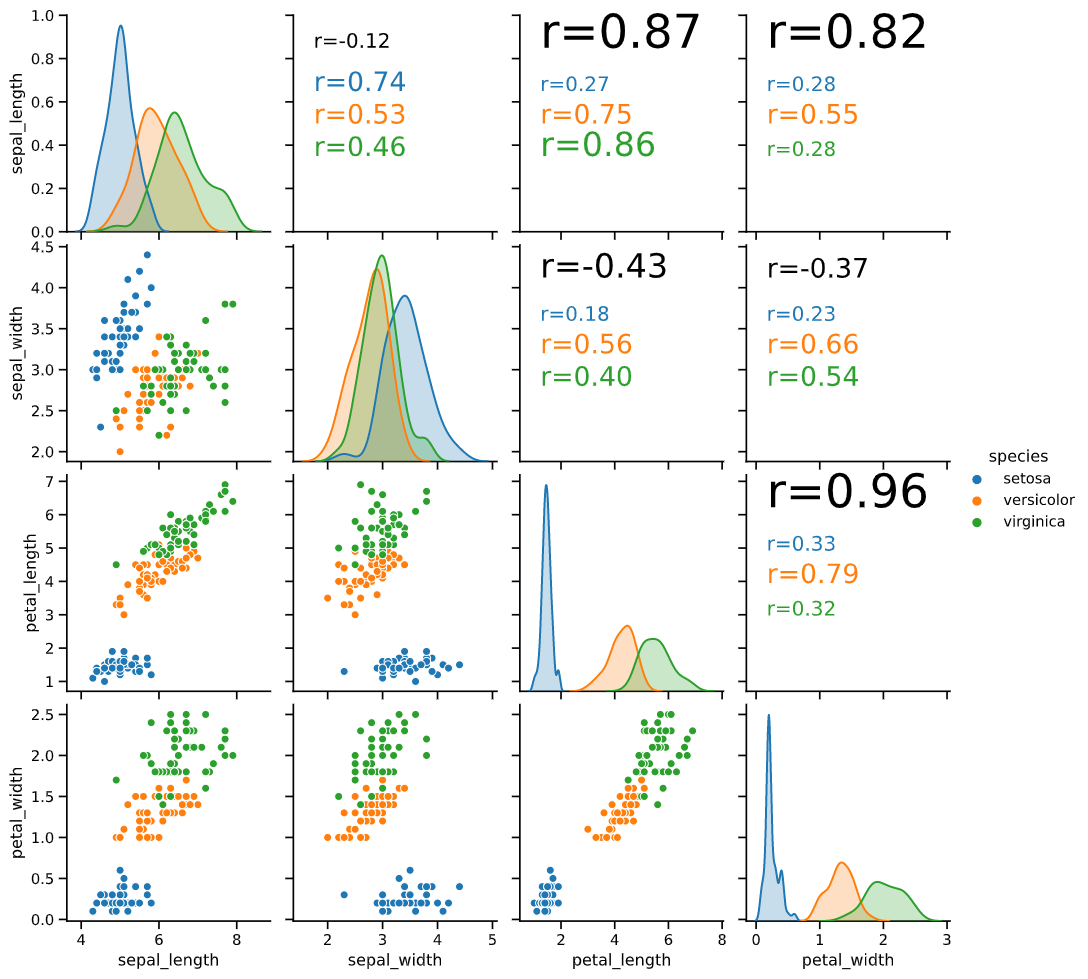
相関係数の大小を直感的に分かりやすくするため、下記の機能も付け加えました
・相関係数の大小に応じて文字サイズを変更
・全体の相関係数を黒で、hue(後で解説します)ごとの相関係数を色分けして表示
機能2:箱ひげ図、バブルチャートへの自動表示変更
課題2で問題となっていた離散的な変数の傾向を把握しやすいよう、
・X,Yいずれかの変数の取る値が2種類以下のとき、箱ひげ図で表示
・もう1つの変数が4種類以下のとき箱ひげ図が作れないので、バブルチャートの大きさでデータの重複数を表示
に自動で表示変更する機能を追加し、データの挙動を見やすくしました

hueによる色分け機能もあるので、元のpairplotとそう変わらない感覚で使えると思います
使用に必要なもの
・Python本体 (動作確認時は3.7.7を使用)
・Matplotlibで表示可能な環境 (Jupyter等)
・下記ライブラリ (参考として動作確認時のライブラリバージョンも記載)
seaborn (0.10.1)
numpy (1.18.5)
pandas (1.0.5)
matplotlib (3.2.2)
scipy (1.5.0)
インストール方法
下記コマンドでインストール可能です
$ pip install seaborn-analyzer
※アンダースコアのpip install seaborn_analyzerでもインストール可能です。
インポート時はアンダースコアのimport seaborn_analyzerやfrom seaborn_analyzer
となるのでご注意ください
コード
モジュールcustom_pair_plot.py内のクラスCustomPairPlotに、必要な処理をまとめました。
GitHubにもアップロードしています
モジュール本体
import seaborn as sns
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
class CustomPairPlot():
#初期化
def __init__(self):
self.df = None
self.hue = None
self.hue_names = None
self.corr_mat = None
#hueごとに相関係数計算
def _corrfunc(self, x, y, **kws):
if self.hue_names is None:
labelnum=0
hue_num = 0
else:
labelnum=self.hue_names.index(kws["label"])
hue_num = len(self.hue_names)
#xまたはyがNaNの行を除外
mask = ~np.logical_or(np.isnan(x), np.isnan(y))
x, y = x[mask], y[mask]
#相関係数算出&0.4ごとにフォントサイズ拡大
r, _ = stats.pearsonr(x, y)
fsize = min(9, 45/hue_num) + min(4.5, 22.5/hue_num) * np.ceil(abs(r)/0.4)
fsize = min(9, 45/hue_num) if np.isnan(fsize) else fsize
#該当マスのaxを取得
ax = plt.gca()
#既に表示したhueの分だけ下にさげて相関係数表示
ax.annotate("r={:.2f}".format(r), xy=(.1, .65-min(.15,.75/hue_num)*labelnum), xycoords=ax.transAxes, size=fsize, color=kws["color"])
#hueを分けない相関係数計算して上半分に表示
def _corrall_upper(self, g):
#右上を1マスずつ走査
for i, j in zip(*np.triu_indices_from(g.axes, 1)):
#該当マスのaxesを取得
ax = g.axes[i, j]
plt.sca(ax)
#フィールド名を取得
x_var = g.x_vars[j]
y_var = g.y_vars[i]
#相関係数
r = self.corr_mat[x_var][y_var]
#相関係数0.2ごとにフォントサイズ拡大
fsize = 10 + 5 * np.ceil(abs(r)/0.2)
fsize = 10 if np.isnan(fsize) else fsize
#一番上に表示
ax.annotate("r={:.2f}".format(r), xy=(.1, .85), xycoords=ax.transAxes, size=fsize, color="black")
#重複数に応じたバブルチャート
def _duplicate_bubblescatter(self, data, x, y, hue=None, hue_names=None, hue_slide="horizontal", palette=None):
#hueの要素数および値を取得
if hue is not None:
#hue_nameを入力していないとき、hueの要素から自動生成
if hue_names is None:
hue_names = data[hue].dropna().unique()
hue_num = len(hue_names)
hue_vals = data[hue]
#hueを入力していないときも、groupby用にhue関係変数生成
else:
hue_names = ["_nolegend_"]
hue_num = 0
hue_vals = pd.Series(["_nolegend_"] * len(data),
index=data.index)
#hueで区切らない全データ数(NaNは除外)をカウント
ndata = len(data[[x,y]].dropna(how="any"))
######hueごとにGroupByして表示処理######
hue_grouped = data.groupby(hue_vals)
for k, label_k in enumerate(hue_names):
try:
data_k = hue_grouped.get_group(label_k)
except KeyError:
data_k = pd.DataFrame(columns=data.columns,
dtype=np.float)
#X,Yごとに要素数をカウント
df_xy = data_k[[x,y]].copy()
df_xy["xyrec"] = 1
df_xycount = df_xy.dropna(how="any").groupby([x,y], as_index=False).count()
#hueが2個以上存在するとき、表示位置ずらし量(対象軸のユニーク値差分最小値÷4に収まるよう設定)を計算
if hue_num >=2:
if hue_slide == "horizontal":
x_distinct_sort = sorted(data[x].dropna().unique())
x_diff_min = min(np.diff(x_distinct_sort))
x_offset = k * (x_diff_min/4)/(hue_num - 1) - x_diff_min/8
y_offset = 0
else:
y_distinct_sort = sorted(data[y].dropna().unique())
y_diff_min = min(np.diff(y_distinct_sort))
x_offset = 0
y_offset = k * (y_diff_min/4)/(hue_num - 1) - y_diff_min/8
else:
x_offset = 0
y_offset = 0
#散布図表示(要素数をプロットサイズで表現)
ax = plt.gca()
ax.scatter(df_xycount[x] + x_offset, df_xycount[y] + y_offset, s=df_xycount["xyrec"]*1000/ndata, color=palette[k])
#plotter=scatterかつ要素数が2以下なら箱ひげ図、それ以外ならscatterplotを使用
def _boxscatter_lower(self, g, **kwargs):
#kw_color = kwargs.pop("color", None)
kw_color = g.palette
#左下を走査
for i, j in zip(*np.tril_indices_from(g.axes, -1)):
ax = g.axes[i, j]
plt.sca(ax)
#軸表示対象のフィールド名を取得
x_var = g.x_vars[j]
y_var = g.y_vars[i]
#XY軸データ抽出
x_data = self.df[x_var]
y_data = self.df[y_var]
#XY軸のユニーク値
x_distinct = x_data.dropna().unique()
y_distinct = y_data.dropna().unique()
#箱ひげ図(x方向)
if len(x_distinct) ==2 and len(y_distinct) >= 5:
sns.boxplot(data=self.df, x=x_var, y=y_var, orient="v",
hue=self.hue, palette=g.palette, **kwargs)
#重複数に応じたバブルチャート(x方向)
elif len(x_distinct) ==2 and len(y_distinct) < 5:
self._duplicate_bubblescatter(data=self.df, x=x_var, y=y_var, hue=self.hue, hue_names=g.hue_names, hue_slide="horizontal", palette=g.palette)
#箱ひげ図(y方向)
elif len(y_distinct) ==2 and len(x_distinct) >= 5:
sns.boxplot(data=self.df, x=x_var, y=y_var, orient="h",
hue=self.hue, palette=g.palette, **kwargs)
#重複数に応じたバブルチャート(y方向)
elif len(y_distinct) ==2 and len(x_distinct) < 5:
self._duplicate_bubblescatter(data=self.df, x=x_var, y=y_var, hue=self.hue, hue_names=g.hue_names, hue_slide="vertical", palette=g.palette)
#散布図
else:
if len(g.hue_kws) > 0 and "marker" in g.hue_kws.keys():#マーカー指定あるとき
markers = dict(zip(g.hue_names, g.hue_kws["marker"]))
else:#マーカー指定ないとき
markers = True
sns.scatterplot(data=self.df, x=x_var, y=y_var, hue=self.hue,
palette=g.palette, style=self.hue, markers=markers)
#凡例を追加
g._clean_axis(ax)
g._update_legend_data(ax)
if kw_color is not None:
kwargs["color"] = kw_color
#軸ラベルを追加
g._add_axis_labels()
#メイン関数
def pairanalyzer(self, df, hue=None, palette=None, vars=None,
lowerkind="boxscatter", diag_kind="kde", markers=None,
height=2.5, aspect=1, dropna=True,
lower_kws={}, diag_kws={}, grid_kws={}):
#メンバ変数入力
if diag_kind=="hist":#ヒストグラム表示のとき、bool型の列を除外してデータ読込
self.df = df.select_dtypes(exclude=bool)
else:#kde表示のとき、bool型を含めデータ読込
self.df = df
self.hue = hue
self.corr_mat = df.corr(method="pearson")
#文字サイズ調整
sns.set_context("notebook")
#PairGridインスタンス作成
plt.figure()
diag_sharey = diag_kind == "hist"
g = sns.PairGrid(self.df, hue=self.hue,
palette=palette, vars=vars, diag_sharey=diag_sharey,
height=height, aspect=aspect, dropna=dropna, **grid_kws)
#マーカーを設定
if markers is not None:
if g.hue_names is None:
n_markers = 1
else:
n_markers = len(g.hue_names)
if not isinstance(markers, list):
markers = [markers] * n_markers
if len(markers) != n_markers:
raise ValueError(("markers must be a singleton or a list of "
"markers for each level of the hue variable"))
g.hue_kws = {"marker": markers}
#対角にヒストグラム or KDEをプロット
if diag_kind == "hist":
g.map_diag(plt.hist, **diag_kws)
elif diag_kind == "kde":
diag_kws.setdefault("shade", True)
diag_kws["legend"] = False
g.map_diag(sns.kdeplot, **diag_kws)
#各変数のユニーク数を計算
nuniques = []
for col_name in g.x_vars:
col_data = self.df[col_name]
nuniques.append(len(col_data.dropna().unique()))
#左下に散布図etc.をプロット
if lowerkind == "boxscatter":
if min(nuniques) <= 2: #ユニーク数が2の変数が存在するときのみ、箱ひげ表示
self._boxscatter_lower(g, **lower_kws)
else: #ユニーク数が2の変数が存在しないとき、散布図(_boxscatter_lowerを実行すると凡例マーカーが消えてしまう)
g.map_lower(sns.scatterplot, **lower_kws)
elif lowerkind == "scatter":
g.map_lower(sns.scatterplot, **lower_kws)
else:
g.map_lower(sns.regplot, **lower_kws)
#色分け(hue)有無で場合分けしてプロット&相関係数表示実行
#hueなし
if self.hue is None:
#右上に相関係数表示
self.hue_names = None
self._corrall_upper(g)
#hueあり
else:
#右上に相関係数表示(hueごとに色分け&全体の相関係数を黒表示)
self.hue_names = g.hue_names
g.map_upper(self._corrfunc)
self._corrall_upper(g)
g.add_legend()
各メソッドの解説
・pairanalyzer():メインの処理。外部から呼び出すのはこのメソッド
・_boxscatter_lower():変数の取る値に応じ、散布図・箱ひげ図・バブルチャートを切り替えるメソッド(上記「機能2」)
・_duplicate_bubblescatter():バブルチャート表示メソッド
・_corrall_upper():hueを分けない相関係数計算して上半分に表示
・_corrfunc():hueごとに相関係数計算して表示
使用方法
実行方法と引数の解説をします
実行方法
実行元スクリプトと同フォルダにcustom_pair_plot.pyを置き、下記のように実行します
#参考としてtitanicデータを読み込んでいます
import seaborn as sns
titanic = sns.load_dataset("titanic")
#ここから実行部分
from seaborn_analyzer import CustomPairPlot
gp = CustomPairPlot()
gp.pairanalyzer(titanic, hue='survived')
引数の解説
hue、lowerkind以外の引数は、
ベースとしたseabornのクラス「PairGrid」の引数と同仕様なので、
こちらもご参照ください
引数を指定しないとき
下記の引数が自動入力されます
(df, hue=None, palette=None, vars=None, lowerkind="boxscatter", diag_kind="kde", markers=None, height=2.5, aspect=1, dropna=True, lower_kws={}, diag_kws={}, grid_kws={})
・表示例
gp.pairanalyzer(titanic)
hue
ここで指定した列名で色分け表示します。相関係数もhueごとに計算されます。
離散変数以外を指定するととんでもない事になるので、注意してください‥(笑)
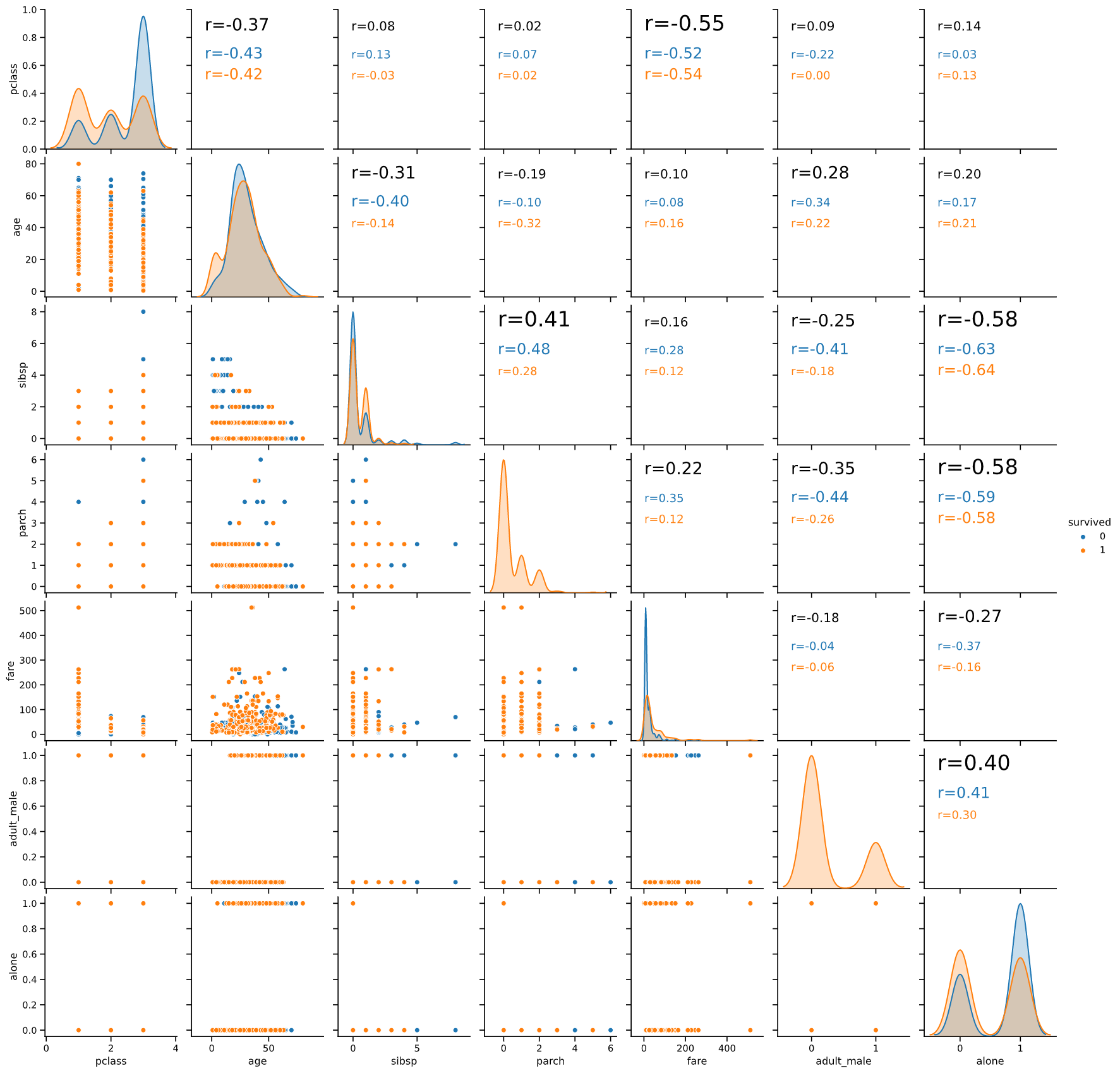
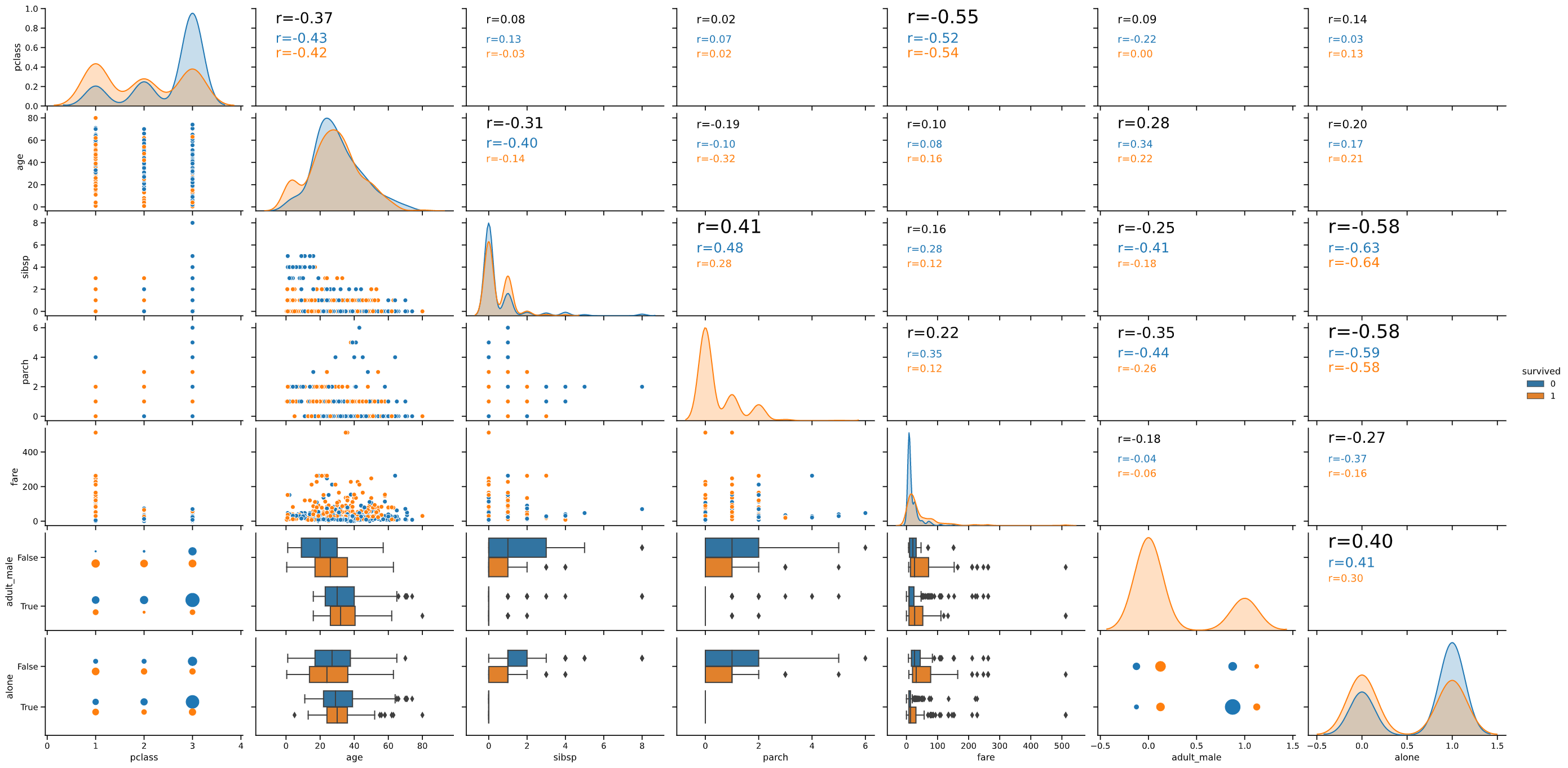
gp.pairanalyzer(titanic, hue='survived')
palette
hueによる色分け用のカラーパレットを指定します
gp.pairanalyzer(titanic, hue='survived', palette='Blues')
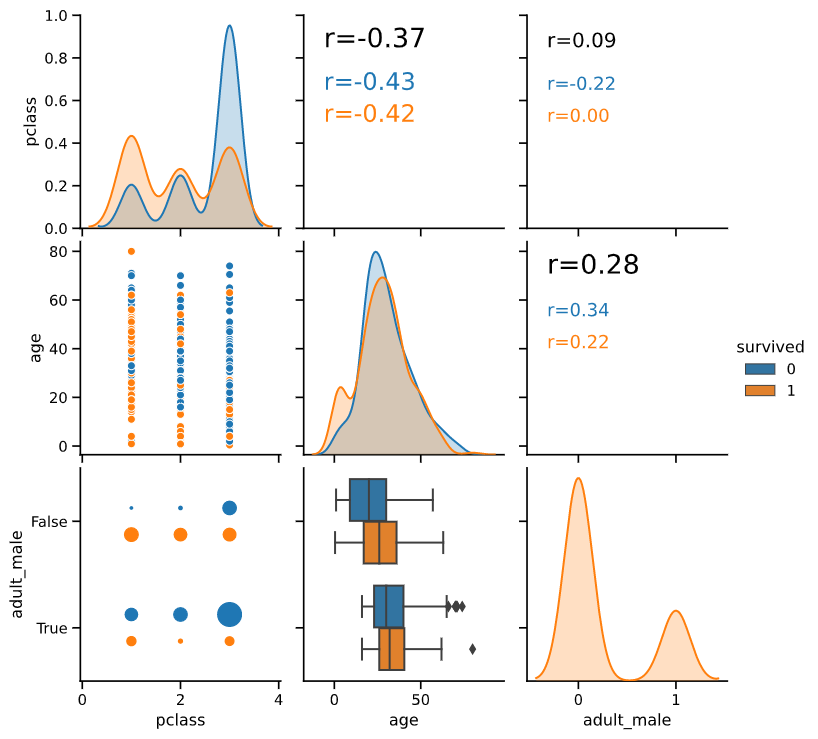
vars
グラフ化する列を選択する(指定しなければ全ての数値型&Boolean型の列を使用)
gp.pairanalyzer(titanic, hue='survived', vars=['pclass', 'age', 'adult_male'])
lowerkind
左下に表示するグラフを下記3種類から選択します(指定しなければ、'boxscatter'を選択)
'boxscatter':前記「機能2」に従い、散布図・箱ひげ図・バブルチャートを自動切替
'scatter':散布図(通常のpairplotと同じ)
'reg':回帰直線
boxscatter
gp.pairanalyzer(titanic, hue='survived', lowerkind='boxscatter')
scatter
gp.pairanalyzer(titanic, hue='survived', lowerkind='scatter')
reg
gp.pairanalyzer(titanic, hue='survived', lowerkind='reg')
diag_kind
対角に表示するグラフを下記2種類から選択します(指定しなければ、'kde'を選択)
'hist':ヒストグラム
'kde':ヒストグラムをカーネル密度推定で円滑化
hist
gp.pairanalyzer(titanic, hue='survived', diag_kind='hist')
※pairplotおよびベースとなるseabornのクラスPairGridには、bool型をヒストグラム表示するとエラーを吐くバグがあるので、pairanalyzerではbool型の列(titanicでは'adult_male','alone')を事前に削除する処理を加えています
kde
gp.pairanalyzer(titanic, hue='survived', lowerkind='kde')
markers
hueにより色分けしたデータの、散布図プロット形状を指定します
指定方法はこちらを参照ください
gp.pairanalyzer(titanic, hue='survived', markers='+')
List指定することで、hueごとに形状を変えることもできます。
gp.pairanalyzer(titanic, hue='survived', markers=['s','X'])
height, aspect
グラフの高さと縦横比を指定します
gp.pairanalyzer(titanic, hue='survived', height=2, aspect=2)
その他の引数(dropna, lower_kws, diag_kws, grid_kws)
ベースとしたPairGridの仕様をそのまま使用していますが、
使いどころが分からなかったので本ページでは割愛します。
仕様はこちら参照ください
※その他の引数は動作テストも実施していないので、もしバグ等見つけた場合はコメント頂けるとありがたいです。
余談
本題とは直接関係ありませんが、タイタニック号のデータを本ツールで分析して面白い事実が可視化できたので、記載します
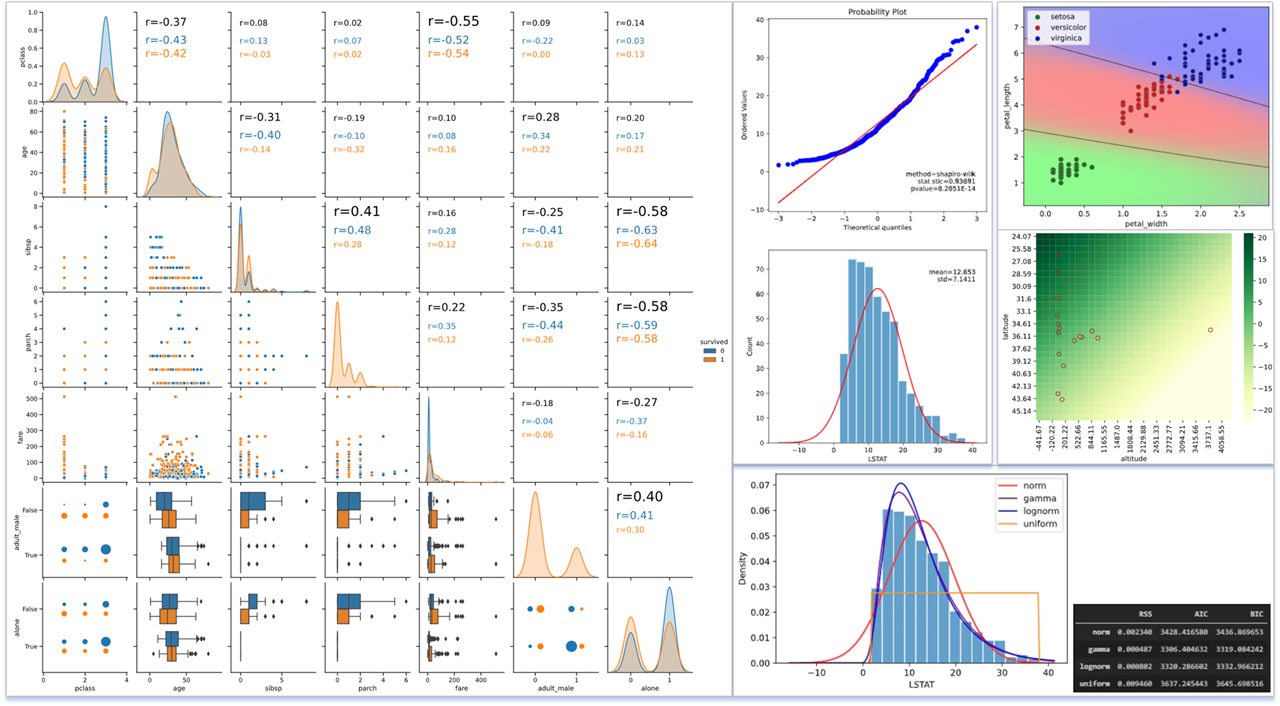
タイタニック号生還率と相関係数
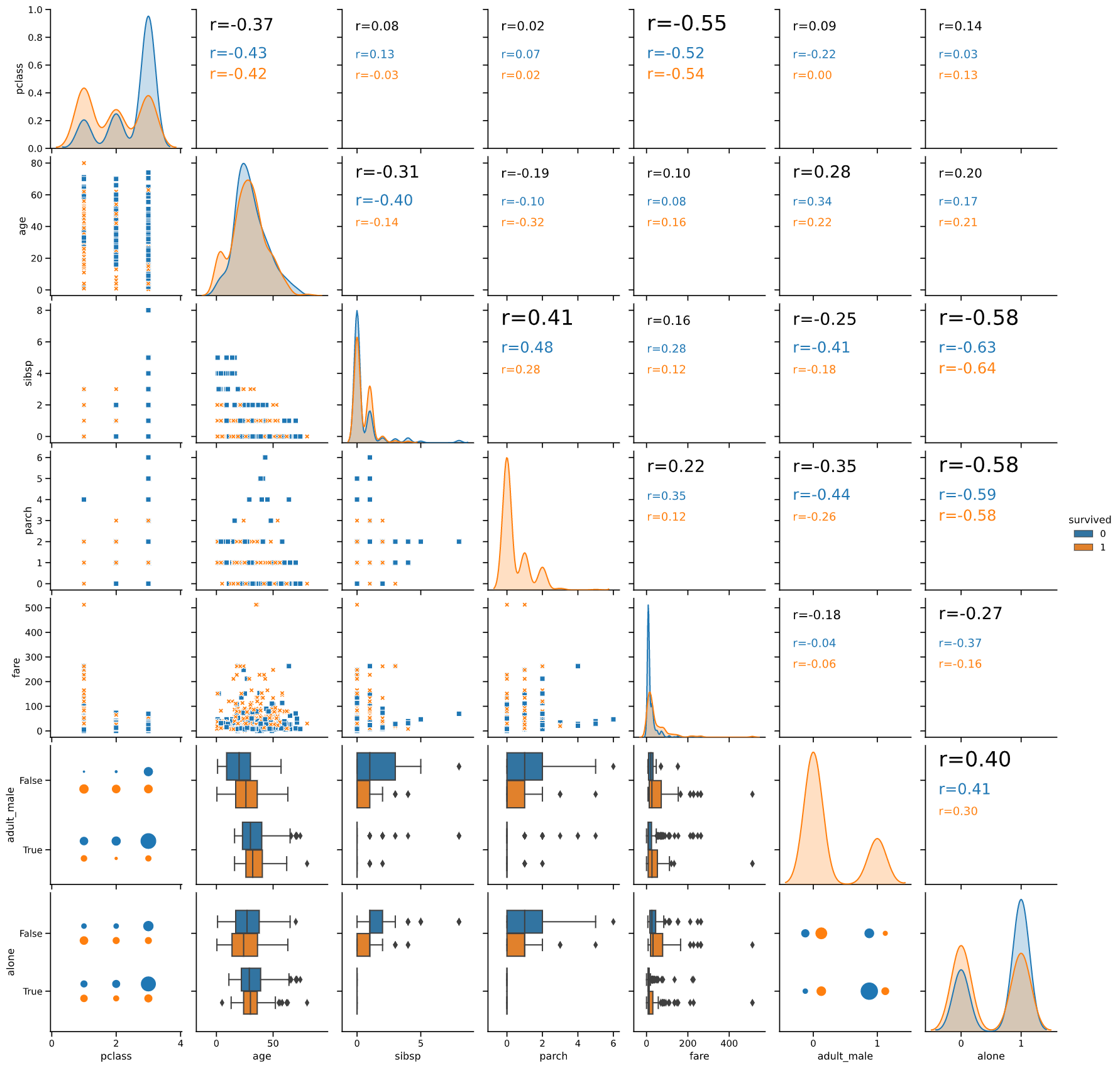
titanicのデータで、生還を表す"survived"との相関係数を見てみます(下の図の赤枠)
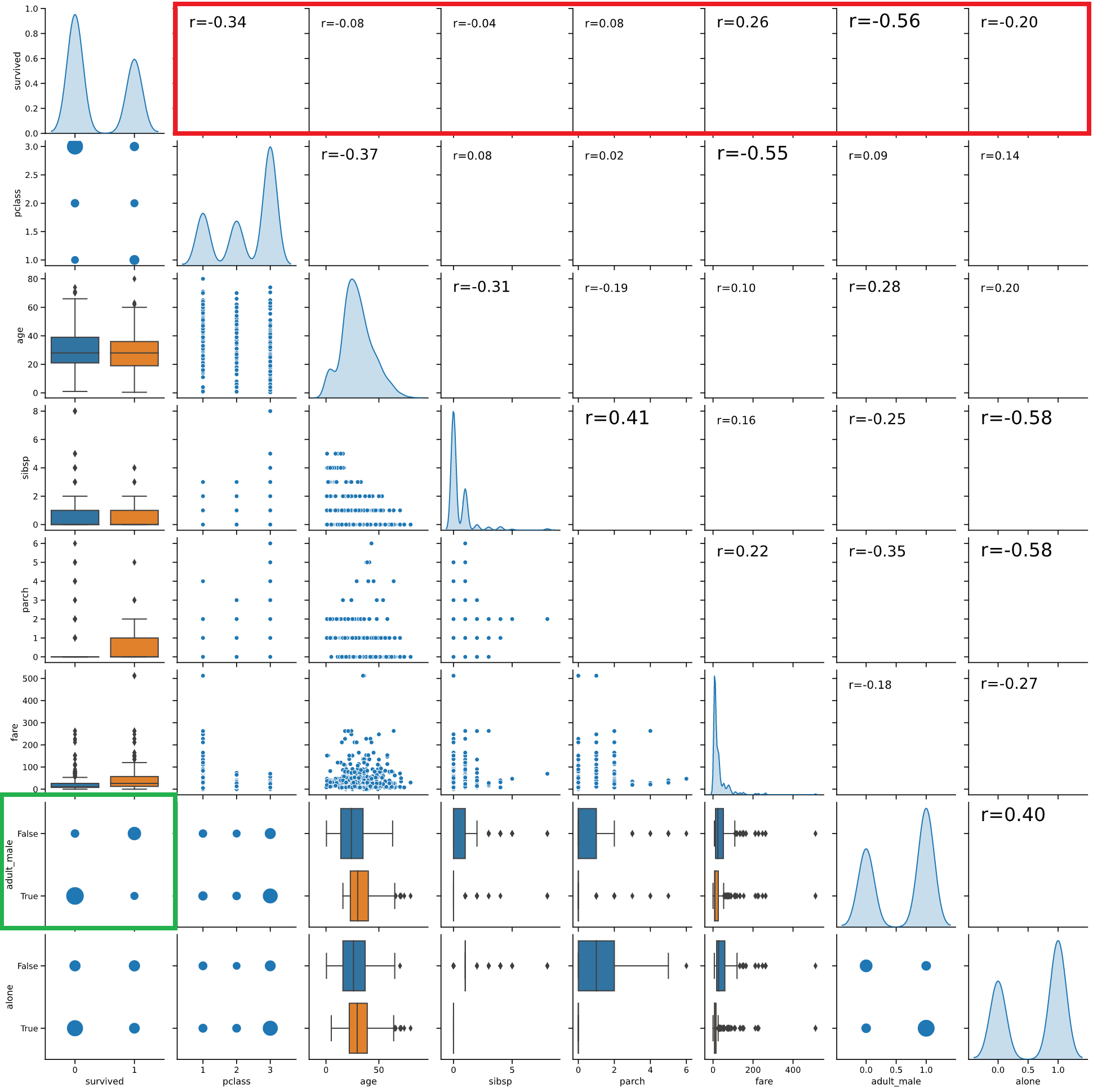
相関係数の絶対値順位は下記のようになります
| 順位 | 変数名 | 相関係数 |
|---|---|---|
| 1 | adult_male | -0.56 |
| 2 | pclass | -0.34 |
| 3 | fare | 0.26 |
・2位のpclass(等級)、3位のfare(運賃)
どちらも乗船に支払った金額と関係するもので、
「金持ちの生還率が高い」
という結果が読み取れます(1等室はデッキが近く、避難距離が短く済んだそうです)
やはり世の中カネなのか‥というやるせない気分になります‥
・1位のadult_male(成人男性かどうか)
R = -0.56と生還率と強い相関がありそうです。
これは一見「成人男性は体力があるので生存率が高い」という、これまた当たり前の結論に見えます
しかしよく見ると、相関係数にマイナスがついています。
すなわち「体力のある成人男性の生存率が有意に低い」という、
感覚と矛盾した結果が導き出されます。
このことは上図緑枠で囲ったバブルチャートでもはっきりと確認できます
英国紳士はダテではなかった
気になって調べてみたところ、下のような記事が見付かりました。
https://www.afpbb.com/articles/fp/2564918
どうやら多くの乗客が、
女性や子供を優先して助ける
という行動をとった結果が、上記の相関として現れたようです。
驚くべきは、極限状況で数百人もの成人男性が、このような理性的な行動を取った事です。
下の記事のように、船長を始めとしたクルーの指揮が的確だったことも、秩序だった行動の理由として挙げられていますが、
いずれにせよ、英国紳士の自己犠牲の精神には頭が下がりますね
http://blog.livedoor.jp/science_q/archives/1652343.html
おわりに
以上のように分析からドラマが生まれる事もあるのだと、データの価値を再認識することができました。
私も100年後の分析者から後ろ指を差されないよう、清く正しく生きたいと思います…(笑)
追記:2020/11/8 凡例マーカが表示されないバグ修正
lowerkinde="boxscatter"を指定して箱ひげが存在しない時、凡例マーカが表示されないバグがあったので、修正いたしました(トップのGitHubにPush済みです)
見ての通り、割と重大なバグです‥‥
今まで放置していてスミマせんでした‥
ひとまずこれで、使い勝手は向上したかと思います!
修正:2021/3/20 seaborn.scatterplotクラスの仕様変更対応
"markers"引数未指定時、seaborn.scatterplotクラスの引数"markers"にNoneを入れておりましたが、これでは動作しなくなる仕様変更があったようなので、Trueを入れるよう修正しました。
(本ライブラリの使用法自体は変化ありません)
seabornは開発が活発で仕様変更も多いライブラリなので、適宜対応していこうと思います。
他にも動作しない引数等ございましたら、コメント頂けると有難いです