はじめに
数値流体力学(CFD)の勉強も兼ねて、液体の数値流体解析コードの構築に必要な知識などをまとめていきたいと思います。数値流体力学は結構とっつきづらい学問な気がするで、できるだけ初学者にもわかりやすいように書いていきたいと思います。間違い等多々含まれていると思われますので、発見された際にはご連絡していただいけると幸いでございます。また、どこがわかりにくいとかをコメントして頂けたらありがたいです。随時更新していきます。
対象読者
- Pythonを使える人
- 数値計算に興味がある人
- 流体力学に興味がある人
- 基本的な大学物理や数学を理解している人(簡単な微分方程式と線形代数くらい?)
シリーズ
- 1章:【Python】流体シミュレーション:移流方程式を実装する
- 2章:【Python】流体シミュレーション : 拡散方程式を実装する
- 2章の補足的な立ち位置:【Python】疎行列計算が高速にできるようになる記事
- 3章:この記事
- 4章:【Python】流体シミュレーション : 非圧縮性 Navier-Stokes 方程式
本記事の大まかな内容
水のシミュレーションで必要な流体の基礎方程式を構築する前段階として、非線形の方程式の扱い方を説明します。最終的に、非線形方程式であるバーガース方程式の数値シミュレーションを行います。
使用ライブラリ:Numpy・Scipy・Matplotlib
こういうやつとこの二次元版を作ります。
目次
| 章 | タイトル | 備考 |
|---|---|---|
| 1. | 線形と非線形 | |
| 1-2. | 線形と非線形方程式の特徴 | |
| 1-3. | 線形と非線形の見分け方 | 豆知識的な |
| 2. | 線形移流拡散方程式の実装 | |
| 2-1. | 線形移流拡散方程式 | |
| 2-2. | 実装 | |
| 3. | バーガース方程式の実装 | |
| 3-1. | バーガース方程式とは? | 非線形の移流拡散方程式に相当するもの |
| 3-2. | 実装 | |
| 3-3. | 離散化式の補足 | |
| 4. | 2次元へ拡張 | |
| 4-1. | 2次元移流方程式 | |
| 4-2. | 2次元拡散方程式 | |
| 4-3. | 2次元バーガース方程式 |
1. 線形と非線形
1-1. 線形と非線形方程式の特徴
線形と非線形の方程式について簡単にまとめると以下のような感じになるかと思います。
| 方程式 | 特徴 |
|---|---|
| 線形 | 1. 比例っぽい関係が成り立つ 2. 解を求めることができる |
| 非線形 | 1. 比例っぽい関係が成り立たない 2. 基本的に解を求められない(kdV方程式等ごく一部の方程式は解ける) |
今後扱う流体の方程式などは非線形方程式に分類され、基本的に解が求めることができません。そのため、非線形方程式の解を求める際には、これまでの記事で紹介したような離散化した式を用いた数値計算を行いて、近似的に解を求めていくことが基本的な方針となります。
1-2. 線形と非線形の見分け方
主題とは離れますが、線形と非線形の方程式を見分ける手段について述べておきます。線形と非線形の方程式を見分けるには、解の重ね合わせが成立かするかどうかで判断します。
以前の記事で紹介した移流方程式を例に説明していきたいと思います。
移流方程式(Advection equation)は
$$
\frac{\partial u}{\partial t} + c \frac{\partial u}{\partial x} = 0
$$
で表されていました。ただし、移流速度cは定数とします(物質がcという一定の速度で移動していくことを意味する)。
この方程式に2つの解$u_1$と$u_2$があった時、それぞれ
$$
\frac{\partial u_1}{\partial t} + c \frac{\partial u_1}{\partial x} = 0
$$
$$
\frac{\partial u_2}{\partial t} + c \frac{\partial u_2}{\partial x} = 0
$$
が成り立ちます。そのため、2つの解を足し合わせた$u_1+u_2$に関しても、
$$
\frac{\partial (u_1+u_2)}{\partial t} + c \frac{\partial (u_1+u_2)}{\partial x} = 0
$$
が成立し、この方程式が線形であることがわかります。
さて、定数とした移流速度cを変数のuに変更してみます。
$$
\frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} = 0
$$
$$
\frac{\partial (u_1+u_2)}{\partial t} + (u_1+u_2) \frac{\partial (u_1+u_2)}{\partial x} \neq \frac{\partial (u_1+u_2)}{\partial t} + u_1 \frac{\partial u_1}{\partial x}+ u_2 \frac{\partial u_2}{\partial x} = 0
$$
すると、この方程式では、2つの解を足し合わせた$u_1+u_2$が解にならないので、非線形方程式であることがわかります。
本記事ではこうした非線形方程式を扱っていきたいと思います。
2. 線形移流拡散方程式の実装
2-1. 線形移流拡散方程式
まず初めに、これまでのシリーズの発展的な意味も兼ねて、線形移流拡散方程式を扱っていきたいと思います。この方程式は、下の式に表されるように移流方程式(物質の移動を意味する式)と拡散方程式(物理量の一様化を意味する式)が組み合わさったものみたいなやつです(cと$\nu$は定数です)。ちなみに、これを非線形にしたものが次の章で出てくるバーガース方程式というやつです。
-
移流拡散方程式(=(移流方程式+拡散方程式)的なイメージ)
$$
\frac{\partial u}{\partial t} + c \frac{\partial u}{\partial x} = \nu \frac{\partial^2 u}{\partial x^2}
$$ -
移流方程式(物質が移動する効果)
$$
\frac{\partial u}{\partial t} + c \frac{\partial u}{\partial x} = 0
$$ -
拡散方程式(一様化する効果)
$$
\frac{\partial u}{\partial t} = \nu \frac{\partial^2 u}{\partial x^2}
$$
2-2. 実装
とりあえずCIP法と非定常反復法を用いて実装していきます。CIP法を簡単に言えば、現在の値とその微分値から未来の値を予測する手法です。詳しくは、これまでに書いた記事やこのpdfを見てください。非定常反復法は、係数を変更しながら一次元連立方程式の解を求める手法のことで、詳しく知りたい場合はこれまでに書いた拡散方程式に関する記事やPythonの非定常反復法ライブラリについて述べた記事をご覧ください。
やることはそんなに難しくはないです。CIP法では、移流フェーズと非移流フェーズに分けて考えます。要するに、移流方程式からuを計算して、その計算結果uを用いて拡散方程式を解くってだけです。イメージ的には、移流で進む速度と拡散で一様化される速度?(周波数?)が異なるので、別々に考えましょうみたいな感じかと思います。移流フェーズと非移流フェーズに分割して、移流拡散方程式を表すと以下のようになります。CIP法を用いる際には、微分値$\frac{\partial u}{\partial x}$の情報も必要なので、uの計算と同時に行います。
* 移流フェーズ
\left\{
\begin{array}{l}
\frac{\partial u}{\partial t} + c \frac{\partial u}{\partial x} = 0 \\
\frac{\partial (\partial u / \partial x)}{\partial t} + c \frac{\partial (\partial u / \partial x)}{\partial x} = 0
\end{array}
\right.
- 非移流フェーズ(拡散フェーズ)
\left\{
\begin{array}{l}
\frac{\partial u}{\partial t} = \nu \frac{\partial^2 u}{\partial x^2} \\
\frac{\partial (\partial u / \partial x)}{\partial t} = \frac{\partial \left(\nu \frac{\partial^2 u}{\partial x^2}\right)}{\partial x}
\end{array}
\right.
import sys
import os
import numpy as np
import matplotlib.pyplot as plt
import scipy
import scipy.sparse
import scipy.sparse.linalg as spla
from scipy.sparse import csr_matrix
from matplotlib.animation import ArtistAnimation
from mpl_toolkits.mplot3d import Axes3D
# Make stencils
# Creat square wave
Num_stencil_x = 101
x_array = np.arange(Num_stencil_x)
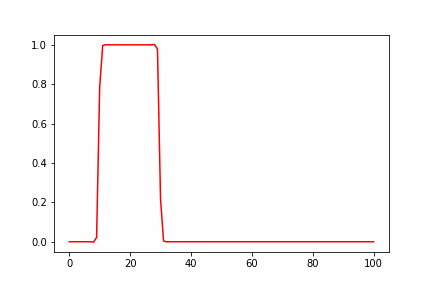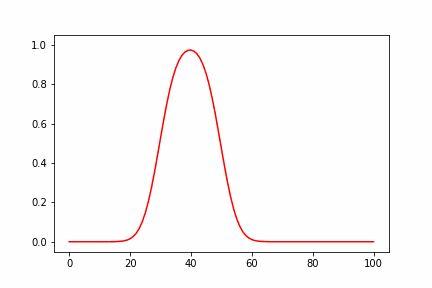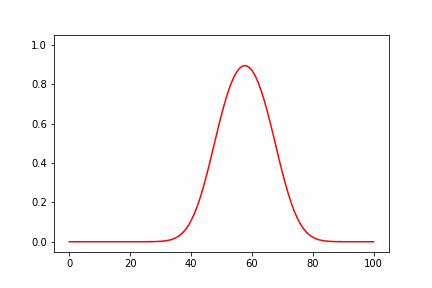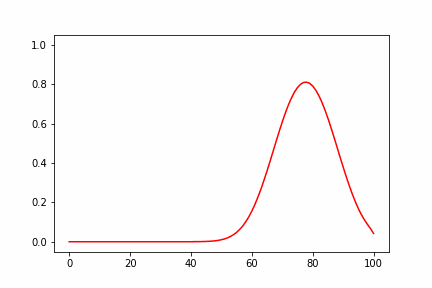
u_array = np.where(((x_array >= 30) |(x_array < 10)), 0.0, 1.0)
u_lower_boundary = 0.0
u_upper_boundary = 0.0
Time_step = 300
Delta_x = max(x_array) / (Num_stencil_x-1)
C = 1
Nu = 0.5
Delta_t = 0.2
CFL = C * Delta_t / Delta_x
diffusion_number = Nu * Delta_t / Delta_x**2
total_movement = C * Delta_t * (Time_step+1)
exact_u_array = np.where(((x_array >= 30 + total_movement) |(x_array < 10 + total_movement)), 0.0, 1.0)
plt.plot(x_array, u_array, label="Initial condition")
plt.legend(loc="upper right")
plt.xlabel("x")
plt.ylabel("u")
plt.xlim(0, max(x_array))
plt.ylim(-0.5,1.5)
print("Δx:", Delta_x, "Δt:", Delta_t, "CFL:", CFL, "ν:", Nu, "d:", diffusion_number)
def solve_advection_cip(u_cip, partial_u_cip, lower_boundary, velocity=C):
u_old = u_cip.copy()
partial_u_old = partial_u_cip.copy()
u_cip[0] = lower_boundary
partial_u_cip[0] = 0 # 境界値を0とした
a = (partial_u_old[1:] + partial_u_old[:-1]) / Delta_x**2 - 2.0 * np.diff(u_old, n=1) / Delta_x**3
b = 3 * (u_old[:-1] - u_cip[1:]) / Delta_x**2 + (2.0*partial_u_old[1:] + partial_u_old[:-1]) / Delta_x
c = partial_u_old[1:]
d = u_old[1:]
xi = - velocity * Delta_t # C > 0
u_cip[1:] = a * xi**3 + b * xi**2 + c * xi + d
partial_u_cip[1:] = 3 * a * xi**2 + 2 * b * xi + c
return u_cip, partial_u_cip
def solve_diffusion(u_array, upper_boundary, lower_boundary, diffusion_number):
a_matrix = np.identity(len(u_array)) * 2 *(1/diffusion_number+1) \
- np.eye(len(u_array), k=1) \
- np.eye(len(u_array), k=-1)
temp_u_array = np.append(np.append(
lower_boundary,
u_array), upper_boundary)
b_array = 2 * (1/diffusion_number - 1) * u_array + temp_u_array[2:] + temp_u_array[:-2]
b_array[0] += lower_boundary
b_array[-1] += upper_boundary
a_csr = scipy.sparse.csr_matrix(a_matrix)
u_array = spla.isolve.bicgstab(a_csr, b_array)[0]
return u_array
fig = plt.figure()
images = []
u_cip= u_array.copy()
partial_u_cip = ((np.append(u_cip[1:], u_upper_boundary) + u_cip)/2 - (np.append(u_lower_boundary, u_cip[:-1]) + u_cip)/2)/ Delta_x
# 時間発展させる
for n in range(Time_step):
u_cip_star, partial_u_cip_star = solve_advection_cip(u_cip, partial_u_cip, u_lower_boundary)
u_cip = solve_diffusion(u_cip_star, u_upper_boundary, u_lower_boundary, diffusion_number)
partial_u_cip = solve_diffusion(partial_u_cip_star, 0, 0, diffusion_number) # 境界値を0とした
if n % 10 == 0:
line, = plt.plot(x_array, u_cip, "r")
images.append([line])
# plt.plot(x_array, u_array, label="Initial condition")
# plt.plot(x_array, u_cip, label="CIP method")
animatoin_gif = ArtistAnimation(fig, images)
animatoin_gif.save('linear_adv_diff.gif', writer="pillow")
plt.show()
3. バーガース方程式の実装
3-1. バーガース方程式とは?
非線形の偏微分方程式の一つで、前章で説明した移流拡散方程式を非線形化したものです。流体の方程式に仮定とかおいて、かなり簡略化したらバーガース方程式になります。この式は非線形方程式ですが、コールホップ変換というものを用いれば厳密解を求めることが可能であることが知られています。そのため、数値計算手法の妥当性の検討で用いられることが多いです。
-
バーガース方程式
$$
\frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} = \nu \frac{\partial^2 u}{\partial x^2}
$$ -
移流拡散方程式
$$
\frac{\partial u}{\partial t} + c \frac{\partial u}{\partial x} = \nu \frac{\partial^2 u}{\partial x^2}
$$
3-2. 実装
バーガース方程式を実装します。これもまたCIP法で実装します。移流フェーズと非移流フェーズに分割すると以下のようになります。
* 移流フェーズ
\left\{
\begin{array}{l}
\frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} = 0 \\
\frac{\partial (\partial u / \partial x)}{\partial t} + u \frac{\partial (\partial u / \partial x)}{\partial x} = 0
\end{array}
\right.
- 非移流フェーズ(拡散フェーズ)
\left\{
\begin{array}{l}
\frac{\partial u}{\partial t} = \nu \frac{\partial^2 u}{\partial x^2} \\
\frac{\partial (\partial u / \partial x)}{\partial t} = \frac{\partial \left(\nu \frac{\partial^2 u}{\partial x^2}\right)}{\partial x} - \left(\frac{\partial u}{\partial x} \right)^2
\end{array}
\right.
線形移流拡散方程式からの変更点は多くありません。変更するところは、
- CIP法での1タイムステップでの移動量$\xi = - c \Delta t$を$\xi = - u \Delta t$へ変更する
- CFL条件(移流方程式の安定条件)と拡散条件を満たしているかどうかをチェックする
- $\frac{\partial u}{\partial x}$の更新の式を変更する
くらいかと思います。離散化に関して少し修正を加えたので、詳細については次の項をご覧ください。
簡単に計算結果について考察すると、高さが高いほど速度が速くなるので、途中で波の上側が下側に追いつき、衝撃波に似た急峻な不連続面を形成することが見てとれます。その後、拡散の効果で徐々に解が鈍っていくのがわかります。
def solve_advection_cip(u_cip, partial_u_cip, lower_boundary, dt=Delta_t, velocity=C):
"""
CIP法によって移流方程式を解く
"""
u_old = u_cip.copy()
partial_u_old = partial_u_cip.copy()
u_cip[0] = lower_boundary
partial_u_cip[0] = (u_cip[0] - lower_boundary) / Delta_x
a = (partial_u_old[1:] + partial_u_old[:-1]) / Delta_x**2 - 2.0 * np.diff(u_old, n=1) / Delta_x**3
b = 3 * (u_old[:-1] - u_cip[1:]) / Delta_x**2 + (2.0*partial_u_old[1:] + partial_u_old[:-1]) / Delta_x
c = partial_u_old[1:]
d = u_old[1:]
xi = - velocity * dt # C > 0
u_cip[1:] = a * xi**3 + b * xi**2 + c * xi + d
partial_u_cip[1:] = 3 * a * xi**2 + 2 * b * xi + c
return u_cip, partial_u_cip
def solve_diffusion(u_array, lower_boundary, upper_boundary, diffusion_number,
update_partial=False, u_array_integral=None, prop_lambda=1/2):
"""
拡散方程式を解く。
Parameters
----------
u_array : array-like
nのベクトル
upper_boundary : numpy.float64
u_array[n]の隣
lower_boundary : numpy.float64
u_array[0]の隣
diffusion_number : numpy.float64
拡散数。正の数。
update_partial : Bool, default False
微分式の更新の時Trueにする。
u_array_integral : array-like, default None
微分式の更新の時に使用。[lower_boundary, u_array, upper_boudary]の形のn+2のベクトル。
prop_lambda : numpy.float64, default 1/2
0: Explicit method. Centered sapce difference.
1/2: 半陰解法。Crank-Nicolson scheme
1: Fully implicit method. 時間後退差分。
Returns
-------
u_array : array-like
n行の行列
"""
a_matrix = np.identity(len(u_array)) * (1/diffusion_number+2 * prop_lambda) \
- prop_lambda * np.eye(len(u_array), k=1) \
- prop_lambda * np.eye(len(u_array), k=-1)
temp_u_array = np.append(np.append(
lower_boundary,
u_array), upper_boundary)
b_array = (1/diffusion_number - 2 * (1-prop_lambda)) * u_array + (1-prop_lambda)*temp_u_array[2:] + (1-prop_lambda)*temp_u_array[:-2]
b_array[0] += prop_lambda * lower_boundary
b_array[-1] += prop_lambda * upper_boundary
if update_partial:
# 微分式の更新の時にこれを実行
b_array -= ((u_array_integral[2:] - u_array_integral[:-2]) / 2 / Delta_x)**2
a_csr = scipy.sparse.csr_matrix(a_matrix)
u_array = spla.isolve.bicgstab(a_csr, b_array)[0]
return u_array
fig = plt.figure(1)
images = []
u_cip= u_array.copy()
partial_u_cip = ((np.append(u_cip[1:], u_upper_boundary) + u_cip)/2
- (np.append(u_lower_boundary, u_cip[:-1]) + u_cip)/2)/ Delta_x
# 安定条件の設定
cfl_condition = 1
diffusion_number_restriction = 1/2
# 時間発展させる
for n in range(Time_step):
delta_t = Delta_t
cfl_max = np.max(np.abs(u_cip)) * delta_t / Delta_x
diffusion_max = Nu * delta_t / Delta_x**2
if cfl_max > cfl_condition:
# CFL条件の判定
# cfl_conditionより大きかったら、時間刻み幅dtを小さくしてCFL条件を満たすようにする
delta_t = cfl_condition * Delta_x / np.max(np.abs(u_cip))
if diffusion_number > diffusion_number_restriction:
# 拡散数の判定
# diffusion_number_restrictionより大きかったら、時間刻み幅dtを小さくして拡散数の条件を満たすようにする
delta_t = diffusion_max * Delta_x ** 2 / Nu
# 移流方程式を解く
u_cip_star, partial_u_cip_star = solve_advection_cip(u_cip, partial_u_cip, u_lower_boundary, delta_t, u_cip[1:])
# 拡散方程式を解く
u_cip = solve_diffusion(u_cip_star, u_lower_boundary, u_upper_boundary, diffusion_number)
u_cip_with_boundary = np.append(np.append(
u_lower_boundary,
u_cip_star),
u_upper_boundary)
partial_u_cip = solve_diffusion(partial_u_cip_star, 0, 0, diffusion_number,
update_partial=True,
u_array_integral=u_cip_with_boundary) # 境界値を0とした
if n % 10 == 0:
line, = plt.plot(x_array, u_cip, "r")
images.append([line])
# plt.plot(x_array, u_array, label="Initial condition")
# plt.plot(x_array, u_cip, label="Burgers")
animatoin_gif = ArtistAnimation(fig, images)
animatoin_gif.save('burgers.gif', writer="pillow")
3-3. 拡散フェーズの離散化式
拡散方程式
\frac{\partial u}{\partial t} = \nu \frac{\partial^2 u}{\partial x^2}
を離散化した式で表すと
$$
\frac{u_j^{n+1} - u_j^n}{\Delta t} = \nu \left((1 - \lambda) \frac{u_{j+1}^n - 2 u_j^n + u_{j-1}^n }{\Delta x^2} + \lambda \frac{u_{j+1}^{n+1} - 2 u_j^{n+1} + u_{j-1}^{n+1} }{\Delta x^2}\right)
$$
となります。今後のことを考えて、拡散方程式に関する記事とは異なり、$\lambda$を用いて離散化式を表しております。この$\lambda$の値についてまとめると、
| $\lambda$ | 離散化手法 | 特徴 |
|---|---|---|
| 0 | 中心差分 | 陽解法。現在時刻の値のみを用いて時間に関する差分を計算する。 |
| 1/2 | クランク・ニコルソンの陰解法 | 半陰解法。現在の値と次の時刻の値を半分ずつ用いて時間に関する差分を計算する。 |
| 1 | 時間後退差分 | 完全陰解法。次の時刻の値のみを用いて時間に関する差分を計算する。 |
となります。要するに、$\lambda$を用いて3種類の離散化手法を実装できますということです。
これを変形して、時刻n+1の値を左辺に持ってくると
$$
-\lambda u_{j+1}^{n+1} +\left(\frac{1}{d} + 2 \lambda \right) u_j^{n+1} - \lambda u_{j-1}^{n+1} = (1-\lambda) u_{j+1}^{n} + \left(\frac{1}{d} - 2 (1 - \lambda) \right) u_j^{n} + (1 - \lambda) u_{j-1}^{n} \
d = \nu \frac{\Delta t}{\Delta x^2}
$$
格子点が1~Mまでの範囲で存在するとして、境界値を$u_0, u_{M+1}$で表し、行列表示に直すと
\left(
\begin{array}{cccc}
\frac{1}{d} + 2 \lambda & -\lambda & 0 & \ldots & \ldots & 0 \\
-\lambda & \frac{1}{d} + 2 \lambda & -\lambda & 0 & \ldots & 0 \\
0 &-\lambda & \frac{1}{d} + 2 \lambda & -\lambda & 0 & \ldots \\
\vdots & \ddots & \ddots & \ddots & \ddots & \ddots\\
0 & 0 & \ddots & -\lambda & \frac{1}{d} + 2 \lambda & -\lambda \\
0 & 0 & \ldots & 0 & -\lambda & \frac{1}{d} + 2 \lambda
\end{array}
\right)
\left(
\begin{array}{c}
u_1^{n+1} \\
u_2^{n+1} \\
u_3^{n+1} \\
\vdots \\
u_{M-1}^{n+1} \\
u_M^{n+1}
\end{array}
\right)
=
\left(
\begin{array}{c}
(1 - \lambda) u_2^{n} + \left(\frac{1}{d} - 2 (1 - \lambda) \right) u_1^{n} + \left((1-\lambda) u_0^n + \lambda u_0^{n+1}\right) \\
(1-\lambda) u_3^{n} + \left(\frac{1}{d} - 2 (1 - \lambda) \right) u_2^{n} + (1-\lambda) u_1^n \\
(1-\lambda) u_4^{n} + \left(\frac{1}{d} - 2 (1 - \lambda) \right) u_3^{n} + (1-\lambda)u_2^n \\
\vdots \\
(1-\lambda)u_M^{n} + \left(\frac{1}{d} - 2 (1 - \lambda) \right) u_{M-1}^{n} + (1-\lambda)u_{M-2}^n \\
\left((1-\lambda)u_{M+1}^n + \lambda u_{M+1}^{n+1}\right) + \left(\frac{1}{d} - 2 (1 - \lambda) \right) u_{M}^{n} + (1-\lambda)u_{M-1}^n
\end{array}
\right)
$\frac{\partial u}{\partial x}$を更新する場合は、この行列のuを$\frac{\partial u}{\partial x}$に変え、右辺に
\left(
\begin{array}{c}
- \left(\frac{u_2^{n} - u_0^{n}}{2 \Delta x} \right)^2 \\
- \left(\frac{u_3^{n} - u_1^{n}}{2 \Delta x} \right)^2 \\
- \left(\frac{u_4^{n} - u_2^{n}}{2 \Delta x} \right)^2 \\
\vdots \\
- \left(\frac{u_M^{n} - u_{M-1}^{n}}{2 \Delta x} \right)^2 \\
- \left(\frac{u_{M+1}^{n} - u_M^{n}}{2 \Delta x} \right)^2
\end{array}
\right)
を加えます。
これを前項では実装してます。反復解法はBiCGSTAB法を使いました。理由は名前がかっこいいからです。
4. 2次元へ拡張
かっこいい絵を書きたいので、この章で二次元にしていきます。ひたすら数式展開だけです。
4-1. 2次元移流方程式
例のごとくCIP法で実装していきます。詳しい式展開は、参考文献の2次元CIP法を参照してください。未知数が10個あるので方程式を10個作るだけです。微分の時の(i+1, j+1)座標のことは考えなくて大丈夫です。参考文献ではうまくやって計算量を減らしてますが、わかりにくいのでここでは愚直にやります。
一次元の時と同様に、
$$
F(X,Y) = a_3 X^3 + a_2 X^2 + a_1 X + b_3 Y^3 + b_2 Y^2 + b_1 Y + c_3 X^2 Y + c_2 X Y^2 + c_1 XY + d \quad ,where \quad X = x - x_j
$$
のように$F(X, Y)$を3次補完で定義します。関数の値と微分値が格子点上で連続という条件から、
$$
F(0, 0) = f_{i,j}, \quad F(\Delta x, 0) = f_{i+1, j}, \quad F(0, \Delta y) = f_{i, j+1}, \quad F(\Delta x, \Delta y) = f_{i+1, j+1}\
\frac{\partial F(0,0)}{\partial x} = \frac{\partial f_{i,j}}{\partial x}, \quad \frac{\partial F(\Delta x, 0)}{\partial x} = \frac{\partial f_{i+1, j}}{\partial x},\quad \frac{\partial F(0, \Delta y)}{\partial x} = \frac{\partial f_{i, j+1}}{\partial x} \
\frac{\partial F(0,0)}{\partial y} = \frac{\partial f_{i,j}}{\partial y}, \quad \frac{\partial F(\Delta x, 0)}{\partial y} = \frac{\partial f_{i+1, j}}{\partial y},\quad \frac{\partial F(0, \Delta y)}{\partial y} = \frac{\partial f_{i, j+1}}{\partial y} \
, where \quad \Delta x = x_{i+1} - x_i, \quad \Delta y = y_{j+1} - y_{j}
$$
の10個の式が成立します。ただし、関数fの格子点(i,j)での値と微分値をそれぞれ$f_{i,j}, \frac{\partial f_{i,j}}{\partial x} $と表すことにします。これを$F(X, Y)$の式に代入して、係数を求めると、
$$
a_3 = \frac{\partial f_{i+1,j} / \partial x + \partial f_{i, j} / \partial x }{\Delta x^2} + \frac{2 (f_{i,j} - f_{i+1, j})}{\Delta x^3} \
a_2 = \frac{3 (f_{i+1, j} - f_{i,j})}{\Delta x^2} - \frac{(2 \partial f_{i,j} / \partial x + \partial f_{i+1, j} / \partial x )}{\Delta x} \
a_1 = \frac{\partial f_{i,j}}{\partial x}\
b_3 = \frac{\partial f_{i,j+1} / \partial y + \partial f_{i, j} / \partial y }{\Delta y^2} + \frac{2 (f_{i,j} - f_{i, j+1})}{\Delta y^3} \
b_2 = \frac{3 (f_{i, j+1} - f_{i,j})}{\Delta y^2} - \frac{(2 \partial f_{i,j} / \partial y + \partial f_{i, j+1} / \partial y )}{\Delta y} \
b_1 = \frac{\partial f_{i,j}}{\partial y}\
c_3 = \frac{\partial f_{i+1,j}/\partial y - \partial f_{i,j}/\partial y }{(\Delta x)^2} - \frac{c_1}{\Delta x}\
c_2 = \frac{\partial f_{i,j+1}/\partial x - \partial f_{i,j}/\partial x }{(\Delta y)^2} - \frac{c_1}{\Delta y}\
c_1 = - \frac{f_{i+1,j+1} - f_{i, j+1} - f_{i+1,j} + f_{i, j}}{\Delta x \Delta y} + \frac{\partial f_{i+1,j}/\partial y - \partial f_{i,j}/\partial y }{\Delta x} + \frac{\partial f_{i,j+1}/\partial x - \partial f_{i,j}/\partial x }{\Delta y}\
d = f_{i,j}
$$
以上より、速度が一定の場合、$\frac{\partial u}{\partial t} + c_1 \frac{\partial u}{\partial x} + c_2 \frac{\partial u}{\partial y}= 0$は微分値も満たすので、時間刻み幅$\Delta t(n+1ステップ目)$秒後における値と微分値は、
u_{i,j}^{n+1} = F(x_i - c_1 \Delta t, y_j -c_2 \Delta t)= a_3 \xi^3 + a_2 \xi^2 + a_1 \xi + b_3 \zeta^3 + b_2 \zeta^2 + b_1 \zeta + c_3 \xi^2 \zeta + c_2 \xi \zeta^2 + c_1 \xi \zeta + d \\
\frac{\partial u_{i,j}^{n+1}}{\partial x} = \frac{\partial F(x_i - c_1 \Delta t, y_j - c_2 \Delta t)}{\partial x} = 3 a_3 \xi^2 + 2 a_2 \xi + a_1 + 2 c_3 \xi \zeta c_2 \zeta^2 + c_1 \zeta \\
\frac{\partial u_{i,j}^{n+1}}{\partial y} = \frac{\partial F(x_i - c_1 \Delta t, y_j - c_2 \Delta t)}{\partial y} = 3 b_3 \zeta^2 + 2 b_2 \zeta + b_1 + 2 c_2 \xi \zeta c_3 \xi^2 + c_1 \xi \\
, where \quad \xi = - c_1 \Delta t, \quad \zeta = - c_2 \Delta t \quad (c_1, c_2 < 0)
速度一定でない$\frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x}+ v \frac{\partial u}{\partial y} = 0$の場合、空間微分して出てくる余分な項は非移流項で計算することになります。
4-2. 2次元拡散方程式
二次元の拡散方程式
\frac{\partial u}{\partial t} = \nu \left\{ \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2}\right\}
を離散化した式で表すと
\frac{u_{i,j}^{n+1} - u_{i,j}^n}{\Delta t} = \nu \left\{(1 - \lambda) \left( \frac{u_{i+1,j}^n - 2 u_{i,j}^n + u_{i-1,j}^n }{\Delta x^2} + \frac{u_{i,j+1}^n - 2 u_{i,j}^n + u_{i,j-1}^n }{\Delta y^2} \right) + \lambda \left( \frac{u_{i+1,j}^{n+1} - 2 u_{i,j}^{n+1} + u_{i-1,j}^{n+1} }{\Delta x^2} + \frac{u_{i,j+1}^{n+1} - 2 u_{i,j}^{n+1} + u_{i,j-1}^{n+1} }{\Delta y^2} \right) \right\}
これをコードで実装しやすいように、格子を並び替えて一列にします。系全体の格子点が$M=NX \times NY$とし、格子点(i,j)の位置を格子点(0,0)から数えてm番目(Pythonの表記に合わせて0番目スタート)とします。すると、格子点(i+1, j)はm+1番目、格子点(i, j+1)はm+NX番目になります。これを上の式に適用して、時刻n+1の値を左辺に持ってくると
- d_2 \lambda u_{m+NX}^{n+1} - d_1 \lambda u_{m+1}^{n+1} +s u_{m}^{n+1} - d_1 \lambda u_{m-1}^{n+1} - d_2 \lambda u_{m-NX}^{n+1} = d_2 (1-\lambda) u_{m+NX}^{n} + d_1 (1-\lambda) u_{m+1}^{n} + t u_m^{n} + d_1 (1 - \lambda) u_{m-1}^{n} + d_2 (1 - \lambda) u_{m-NX}^{n} \\
,where \quad s = 1 + 2 \lambda (d_1 + d_2), \quad t = 1 - 2 (1-\lambda) (d_1 + d_2)\\
d_1 = \nu \frac{\Delta t}{\Delta x^2}, \quad d_2 = \nu \frac{\Delta t}{\Delta y^2}
なので、これに境界値も含めて実装すれば完了です。行列表示は長いのでここでは飛ばします。
4-3. 2次元バーガース方程式
とりあえず二次元にしてみます。表記を変更して、速度との区別を明確にするためにuをfに変更します。
* 移流フェーズ
\left\{
\begin{array}{l}
\frac{\partial f}{\partial t} + u \frac{\partial f}{\partial x} + v \frac{\partial f}{\partial y} = 0 \\
\frac{\partial (\partial f / \partial x)}{\partial t} + u \frac{\partial (\partial f / \partial x)}{\partial x} + v \frac{\partial (\partial f / \partial x)}{\partial x}= 0 \\
\frac{\partial (\partial f / \partial y)}{\partial t} + u \frac{\partial (\partial f / \partial y)}{\partial x} + v \frac{\partial (\partial f / \partial y)}{\partial x}= 0
\end{array}
\right.
- 非移流フェーズ(拡散フェーズ)
\left\{
\begin{array}{l}
\frac{\partial f}{\partial t} = \nu \left( \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2}\right) \\
\frac{\partial (\partial f / \partial x)}{\partial t} = \frac{\partial \left\{ \nu \left( \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2}\right)\right\}}{\partial x} - \left(\frac{\partial u}{\partial x} \right)\left(\frac{\partial f}{\partial x} \right) - \left(\frac{\partial v}{\partial x} \right) \left(\frac{\partial f}{\partial y} \right) \\
\frac{\partial (\partial f / \partial y)}{\partial t} = \frac{\partial \left\{ \nu \left( \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2}\right)\right\}}{\partial y} - \left(\frac{\partial u}{\partial y} \right)\left(\frac{\partial f}{\partial x} \right) - \left(\frac{\partial v}{\partial y} \right) \left(\frac{\partial f}{\partial y} \right)
\end{array}
\right.
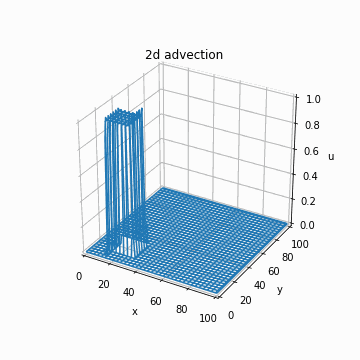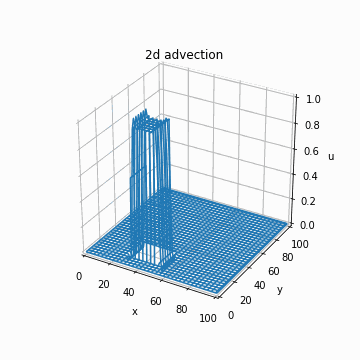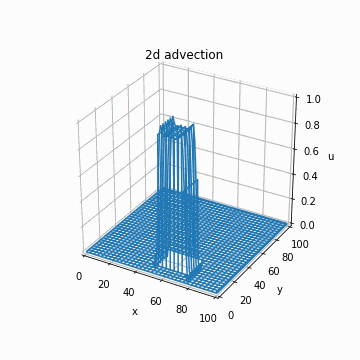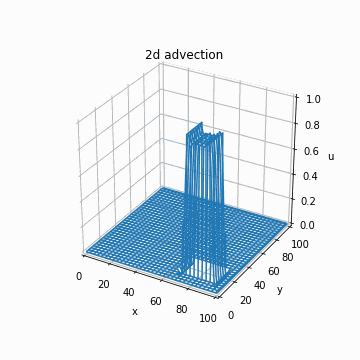
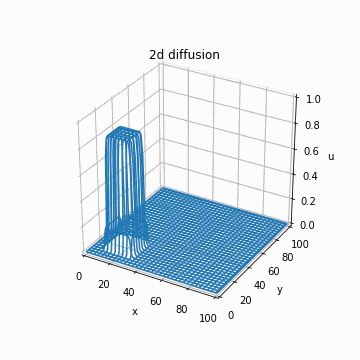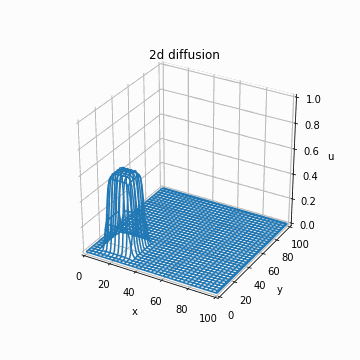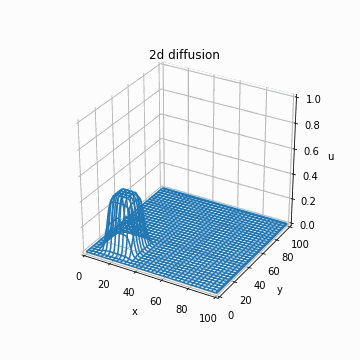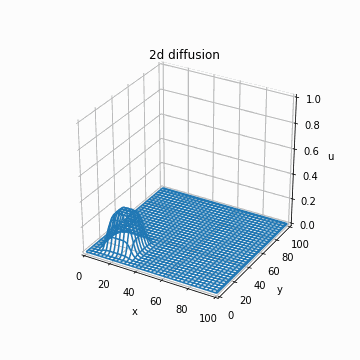
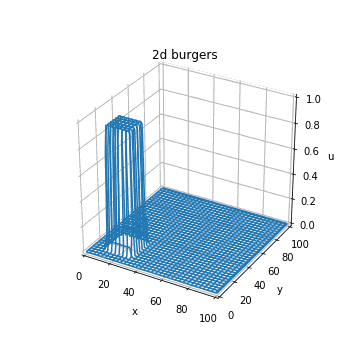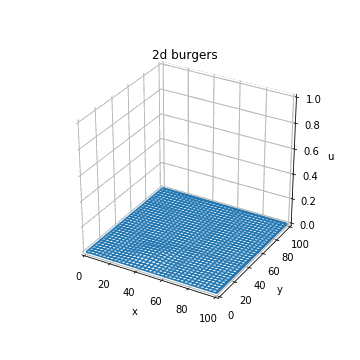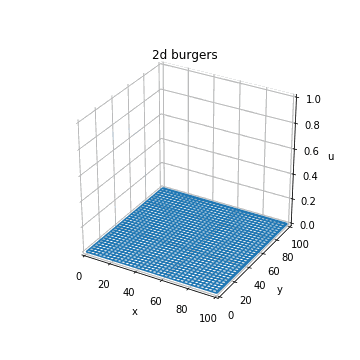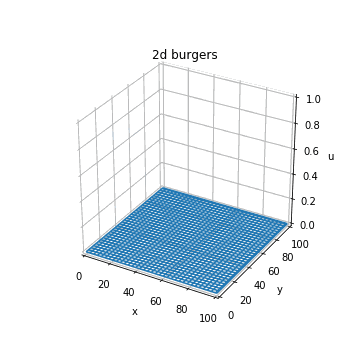
これを実装するだけです。以下のように、あっているかどうかわかりませんがそれっぽい計算結果が得られます。
# Make stencils
# Creat square wave
Num_stencil_x = 101
Num_stencil_y = 101
x_stencil = np.arange(Num_stencil_x)
y_stencil = np.arange(Num_stencil_y)
x_array, y_array = np.meshgrid(x_stencil, y_stencil)
u_array = np.where(((30 >x_array) & (x_array >= 10) & (30 > y_array) & (y_array >= 10)), 1.0, 0.0)
u_x_lower_boundary = np.zeros(Num_stencil_x)
u_y_lower_boundary = np.zeros(Num_stencil_y)
u_x_upper_boundary = np.zeros(Num_stencil_x)
u_y_upper_boundary = np.zeros(Num_stencil_y)
ux_x_lower_boundary = np.zeros(Num_stencil_x)
ux_y_lower_boundary = np.zeros(Num_stencil_y)
ux_x_upper_boundary = np.zeros(Num_stencil_x)
ux_y_upper_boundary = np.zeros(Num_stencil_y)
uy_x_lower_boundary = np.zeros(Num_stencil_x)
uy_y_lower_boundary = np.zeros(Num_stencil_y)
uy_x_upper_boundary = np.zeros(Num_stencil_x)
uy_y_upper_boundary = np.zeros(Num_stencil_y)
coner_xlow_ylow = np.zeros(1)
coner_xup_ylow = np.zeros(1)
coner_xlow_yup = np.zeros(1)
coner_xup_yup = np.zeros(1)
Time_step = 300
Delta_x = max(x_stencil) / (Num_stencil_x-1)
Delta_y = max(y_stencil) / (Num_stencil_y-1)
C = 1
Nu = 0.5
Delta_t = 0.2
CFL_x = C * Delta_t / Delta_x
CFL_y = C * Delta_t / Delta_y
CFL = min(CFL_x, CFL_y)
diffusion_number_x = Nu * Delta_t / Delta_x**2
diffusion_number_y = Nu * Delta_t / Delta_y**2
total_movement = C * Delta_t * (Time_step+1)
print("Δx:", Delta_x, "Δt:", Delta_t, "CFL:", CFL_x, "ν:", Nu, "d:", diffusion_number_x)
fig = plt.figure(2)
axe = fig.add_subplot(111, projection='3d')
surface = axe.plot_surface(x_array, y_array, u_array, cmap="bwr", label="Initail condition")
fig.colorbar(surface)
axe.set_xlabel("x")
axe.set_ylabel("y")
axe.set_zlabel("u")
axe.set_xlim(0, 100)
axe.set_ylim(0, 100)
axe.set_zlim(0, 1)
axe.set_title("2d initial condition")
plt.show()
def solve_advection_cip_2d(u_cip, ux_cip, uy_cip,
x_lower_boundary, x_upper_boundary,
y_lower_boundary, y_upper_boundary,
ux_x_lower_boundary, ux_x_upper_boundary,
ux_y_lower_boundary, ux_y_upper_boundary,
uy_x_lower_boundary, uy_x_upper_boundary,
uy_y_lower_boundary, uy_y_upper_boundary,
coner_ll, coner_lu, coner_ul, coner_uu,
dt=Delta_t,
velocity_x=C, velocity_y=0.0):
"""
Solve the advection equation by using CIP method.
- x +
- 5333337
1*****2
y 1*****2
1*****2
1*****2
+ 6444448
*: u_cip or ux_cip or uy_cip
1: x_lower_boundary or ux_x_lower_boundary or uy_x_lower_boundary
2: x_upper_boundary or ux_x_upper_boundary or uy_x_upper_boundary
3: y_lower_boundary or ux_y_lower_boundary or uy_y_lowerboundary
4: y_upper_boundary or ux_y_upper_boundary or uy_y_upper_boundary
5: coner_ll
6: coner_lu
7: coner_ul
8: coner_uu
"""
if type(velocity_x) is not np.ndarray:
velocity_x = np.ones(u_cip.shape) * velocity_x
if type(velocity_y) is not np.ndarray:
velocity_y = np.ones(u_cip.shape) * velocity_y
# Memory the present values
u_old = u_cip.copy()
ux_old = ux_cip.copy()
uy_old = uy_cip.copy()
# Prepare for calculation
xi = - np.sign(velocity_x) * velocity_x * dt
zeta = - np.sign(velocity_y) * velocity_y * dt
dx = - np.sign(velocity_x) * Delta_x
dy = - np.sign(velocity_y) * Delta_y
# Set the neighbourhood values for reducing the for loop
u_with_xlower_bc = np.concatenate([x_lower_boundary[:, np.newaxis], u_old[:, :-1]], axis=1)
u_with_xupper_bc = np.concatenate([u_old[:, 1:], x_upper_boundary[:, np.newaxis]], axis=1)
u_with_ylower_bc = np.concatenate([y_lower_boundary[np.newaxis, :], u_old[:-1, :]], axis=0)
u_with_yupper_bc = np.concatenate([u_old[1:, :], y_upper_boundary[np.newaxis, :]], axis=0)
temp_u_with_all_bc = np.concatenate([x_lower_boundary[:, np.newaxis], u_old,
x_upper_boundary[:, np.newaxis]], axis=1)
u_with_all_bc = np.concatenate([np.concatenate([coner_ll, y_lower_boundary,coner_ul])[np.newaxis, :],
temp_u_with_all_bc,
np.concatenate([coner_lu, y_upper_boundary, coner_uu])[np.newaxis, :]], axis=0)
u_next_x = np.where(velocity_x > 0.0, u_with_xlower_bc, u_with_xupper_bc)
u_next_y = np.where(velocity_y > 0.0, u_with_ylower_bc, u_with_yupper_bc)
u_next_xy = np.where(((velocity_x > 0.0) & (velocity_y > 0.0)), u_with_all_bc[:-2, :-2],
np.where(((velocity_x < 0.0) & (velocity_y > 0.0)), u_with_all_bc[:-2, 2:],
np.where(((velocity_x > 0.0) & (velocity_y < 0.0)), u_with_all_bc[2:, :-2], u_with_all_bc[2:, 2:])))
ux_next_x = np.where(velocity_x > 0,
np.concatenate([ux_x_lower_boundary[:, np.newaxis], ux_old[:, :-1]], axis=1),
np.concatenate([ux_old[:, 1:], ux_x_upper_boundary[:, np.newaxis]], axis=1))
ux_next_y = np.where(velocity_y > 0,
np.concatenate([ux_y_lower_boundary[np.newaxis, :], ux_old[:-1, :]], axis=0),
np.concatenate([ux_old[1:, :], ux_y_upper_boundary[np.newaxis, :]], axis=0))
uy_next_x = np.where(velocity_x > 0,
np.concatenate([uy_x_lower_boundary[:, np.newaxis], uy_old[:, :-1]], axis=1),
np.concatenate([uy_old[:, 1:], uy_x_upper_boundary[:, np.newaxis]], axis=1))
uy_next_y = np.where(velocity_y > 0,
np.concatenate([uy_y_lower_boundary[np.newaxis, :], uy_old[:-1, :]], axis=0),
np.concatenate([uy_old[1:, :], uy_y_upper_boundary[np.newaxis, :]], axis=0))
u_next_x = np.where(velocity_x == 0.0, u_old, u_next_x)
u_next_y = np.where(velocity_y == 0.0, u_old, u_next_y)
u_next_xy = np.where(((velocity_x == 0.0) & (velocity_y != 0.0)), u_next_y,
np.where(((velocity_x != 0.0) & (velocity_y == 0.0)), u_next_x,
np.where(((velocity_x == 0.0) & (velocity_y == 0.0)), u_old, u_next_xy)))
ux_next_x = np.where(velocity_x == 0, ux_old, ux_next_x)
ux_next_y = np.where(velocity_y == 0, ux_old, ux_next_y)
uy_next_x = np.where(velocity_x == 0, uy_old, uy_next_x)
uy_next_y = np.where(velocity_y == 0, uy_old, uy_next_y)
dx = np.where(velocity_x == 0, 1.0, dx)
dy = np.where(velocity_y == 0, 1.0, dy)
# Calculate the cip coefficient
c_1 = - (u_next_xy - u_next_x - u_next_y + u_old) / dx / dy \
+ (ux_next_y - ux_old) / dy + (uy_next_x - uy_old) / dx
c_3 = (uy_next_x - uy_old) / dx ** 2 - c_1 / dx
c_2 = (ux_next_y - ux_old) / dy ** 2 - c_1 / dy
a_1 = ux_old
a_2 = 3 * (u_next_x - u_old) / dx**2 - (ux_next_x + 2 * ux_old) / dx
a_3 = (ux_next_x - ux_old) / 3 / dx**2 - 2 * a_2 / 3 / dx
b_1 = uy_old
b_2 = 3 * (u_next_y - u_old) / dy**2 - (uy_next_y + 2 * uy_old) / dy
b_3 = (uy_next_y - uy_old) / 3 / dy**2 - 2 * b_2 / 3 / dy
d = u_old
# Calculate the values
u_cip = a_3 * xi**3 + a_2 * xi**2 + a_1 * xi + \
b_3 * zeta**3 + b_2 * zeta**2 + b_1 * zeta + \
c_3 * xi**2 * zeta + c_2 * xi * zeta**2 + c_1 * xi * zeta + d
ux_cip = 3 * a_3 * xi**2 + 2 * a_2 * xi + a_1 + 2 * c_3 * xi * zeta + c_2 * zeta**2 + c_1 * zeta
uy_cip = 3 * b_3 * zeta**2 + 2 * b_2 * zeta + b_1 + 2 * c_2 * xi * zeta + c_2 * xi**2 + c_1 * xi
return u_cip, ux_cip, uy_cip
def update_boundary_condition(u_cip, x_lower_boundary, x_upper_boundary,
y_lower_boundary, y_upper_boundary):
x_lower_boundary = min(0.0, np.min(u_cip[:, 0]))
x_upper_boundary = max(0.0, np.max(u_cip[:, -1]))
y_lower_boundary = min(0.0, np.min(u_cip[0, :]))
y_upper_boundary = max(0.0, np.max(u_cip[-1, :]))
def solve_diffusion_2d(u_2d,
x_lower_boundary, x_upper_boundary,
y_lower_boundary, y_upper_boundary,
d_number_x, d_number_y,
v_x=None, v_y=None,
v_x_lower_bc=None, v_x_upper_bc=None,
v_y_lower_bc=None, v_y_upper_bc=None,
update_partial=0, u_array_integral=None,
prop_lambda=1/2):
"""
拡散方程式を解く。非移流項の要素も含んでいる。
Parameters
----------
u_2d : array-like
nx×ny行の行列
upper_boundary : numpy.float64
u_array[n]の隣
lower_boundary : numpy.float64
u_array[0]の隣
d_number_* : numpy.float64
拡散数。正の数。
update_partial : Bool, default False
微分式の更新の時Trueにする。
u_array_integral : array-like, default None
微分式の更新の時に使用。[lower_boundary, u_array, upper_boudary]の形のn+2のベクトル。
prop_lambda : numpy.float64, default 1/2
0: Explicit method. Centered sapce difference.
1/2: 半陰解法。Crank-Nicolson scheme
1: Fully implicit method. 時間後退差分。
Returns
-------
u_2d : array-like
nx×ny行の行列
"""
# 行列サイズ取得
nx, ny = u_2d.shape
matrix_size = nx * ny
# Ax=bのAとbを作成
s_param = 1 + 2 * prop_lambda * (d_number_x + d_number_y)
t_param = 1 - 2 * (1 - prop_lambda) * (d_number_x + d_number_y)
east_matrix = np.eye(matrix_size, k=1)
east_matrix[np.arange(nx-1, matrix_size-nx, nx), np.arange(nx, matrix_size-nx+1, nx)] *= 0
west_matrix = np.eye(matrix_size, k=-1)
west_matrix[np.arange(nx, matrix_size-nx+1, nx), np.arange(nx-1, matrix_size-nx, nx)] *= 0
a_matrix = np.identity(matrix_size) * s_param \
- prop_lambda * d_number_x * east_matrix \
- prop_lambda * d_number_x * west_matrix \
- prop_lambda * d_number_y * np.eye(matrix_size, k=nx) \
- prop_lambda * d_number_y * np.eye(matrix_size, k=-nx)
b_array = t_param * u_2d.flatten()
temp_csr = d_number_x * (1 - prop_lambda) * (csr_matrix(east_matrix) + csr_matrix(west_matrix)) \
+ d_number_y * (1 - prop_lambda) * (csr_matrix(np.eye(matrix_size, k=nx)) + csr_matrix(np.eye(matrix_size, k=-nx)))
b_array += temp_csr.dot(b_array)
# 境界条件を設定 / Setting of boundary condition
b_array[:nx] += ((1 - prop_lambda) * y_lower_boundary + prop_lambda * y_lower_boundary) * d_number_y
b_array[matrix_size-nx:] += ((1 - prop_lambda) * y_upper_boundary + prop_lambda * y_upper_boundary) * d_number_y
b_array[np.arange(nx-1, matrix_size, nx)] += ((1 - prop_lambda) * x_upper_boundary + prop_lambda * x_upper_boundary) * d_number_x
b_array[np.arange(0, matrix_size-nx+1, nx)] += ((1 - prop_lambda) * x_lower_boundary + prop_lambda * x_lower_boundary) * d_number_x
if update_partial == 1:
# x方向の微分式の更新の時に実行される。普通の拡散方程式を解く時は使わない。
if type(v_x) is not np.ndarray:
v_x = np.ones(u_2d.shape) * v_x
if type(v_y) is not np.ndarray:
v_y = np.ones(u_2d.shape) * v_y
v_x_with_bc = np.concatenate([v_x_lower_bc[:, np.newaxis], v_x, v_x_upper_bc[:, np.newaxis]], axis=1)
v_y_with_bc = np.concatenate([v_y_lower_bc[:, np.newaxis], v_y, v_y_upper_bc[:, np.newaxis]], axis=1)
u_with_xbc = np.concatenate([x_lower_boundary[:, np.newaxis], u_array_integral, x_upper_boundary[:, np.newaxis]], axis=1)
u_with_ybc = np.concatenate([y_lower_boundary[np.newaxis, :], u_array_integral, y_upper_boundary[np.newaxis, :]], axis=0)
temp_b_array = - ((v_x_with_bc[:, 2:] - v_x_with_bc[:, :-2]) / 2 / Delta_x) * \
((u_with_xbc[:, 2:] - u_with_xbc[:, :-2]) / 2 / Delta_x)
temp_b_array -= ((v_y_with_bc[:, 2:] - v_y_with_bc[:, :-2]) / 2 / Delta_x) * \
((u_with_ybc[2:, :] - u_with_ybc[:-2, :]) / 2 / Delta_y)
b_array += temp_b_array.flatten()
elif update_partial == 2:
# y方向の微分式の更新の時に実行される。普通の拡散方程式を解く時は使わない。
if type(v_x) is not np.ndarray:
v_x = np.ones(u_2d.shape) * v_x
if type(v_y) is not np.ndarray:
v_y = np.ones(u_2d.shape) * v_y
v_x_with_bc = np.concatenate([v_x_lower_bc[np.newaxis, :], v_x, v_x_upper_bc[np.newaxis, :]], axis=0)
v_y_with_bc = np.concatenate([v_y_lower_bc[np.newaxis, :], v_y, v_y_upper_bc[np.newaxis, :]], axis=0)
u_with_xbc = np.concatenate([x_lower_boundary[:, np.newaxis], u_array_integral, x_upper_boundary[:, np.newaxis]], axis=1)
u_with_ybc = np.concatenate([y_lower_boundary[np.newaxis, :], u_array_integral, y_upper_boundary[np.newaxis, :]], axis=0)
temp_b_array = - ((v_x_with_bc[2:, :] - v_x_with_bc[:-2, :]) / 2 / Delta_y) * \
((u_with_xbc[:, 2:] - u_with_xbc[:, :-2]) / 2 / Delta_x) \
- ((v_y_with_bc[2:, :] - v_y_with_bc[:-2, :]) / 2 / Delta_y) * \
((u_with_ybc[2:, :] - u_with_ybc[:-2, :]) / 2 / Delta_y)
b_array += temp_b_array.flatten()
a_csr = csr_matrix(a_matrix)
u_2d = spla.isolve.bicgstab(a_csr, b_array)[0]
return u_2d.reshape(nx, ny)
# 2d Bugers 方程式
images = []
fig_5 = plt.figure(5, figsize=(5,5))
axe = fig_5.add_subplot(111, projection='3d')
# surface = axe.plot_surface(x_array, y_array, u_array, cmap="bwr")
# fig.colorbar(surface)
axe.set_xlabel("x")
axe.set_ylabel("y")
axe.set_zlabel("u")
axe.set_xlim(0, 100)
axe.set_ylim(0, 100)
axe.set_zlim(0, 1)
axe.set_title("2d burgers")
u_cip = u_array.copy()
partial_u_cip_x \
= (np.concatenate([u_cip[:, 1:], u_x_upper_boundary[:, np.newaxis]], axis=1) \
- np.concatenate([u_x_lower_boundary[:, np.newaxis], u_cip[:, :-1]], axis=1)) / 2 / Delta_x
partial_u_cip_y \
= (np.concatenate([u_cip[1:, :], u_y_upper_boundary[np.newaxis, :]], axis=0) \
- np.concatenate([u_y_lower_boundary[np.newaxis, :], u_cip[:-1, :]], axis=0)) / 2 / Delta_y
u_boundary = (u_x_lower_boundary, u_x_upper_boundary, u_y_lower_boundary, u_y_upper_boundary)
# 安定条件の設定
cfl_condition = 1
diffusion_number_restriction = 1/2
# 時間発展させる
for n in range(21):
update_boundary_condition(u_cip, *u_boundary)
delta_t = Delta_t
cfl_max = np.max(np.abs(u_cip)) * delta_t / min(Delta_x, Delta_y)
if cfl_max > cfl_condition:
# CFL条件の判定
# cfl_conditionより大きかったら、時間刻み幅dtを小さくしてCFL条件を満たすようにする
delta_t = CFL * min(Delta_x, Delta_y) / np.max(np.abs(u_cip))
diffusion_max = Nu * delta_t / (Delta_x**2 + Delta_y**2)
if diffusion_max > diffusion_number_restriction:
# 拡散数の判定
# diffusion_number_restrictionより大きかったら、時間刻み幅dtを小さくして拡散数の条件を満たすようにする
delta_t = diffusion_max * (Delta_x ** 2 + Delta_y**2) / Nu
diffusion_number_x *= delta_t / Delta_t
diffusion_number_y *= delta_t / Delta_t
u_props = (u_cip, partial_u_cip_x, partial_u_cip_y)
u_boundary = (u_x_lower_boundary, u_x_upper_boundary, u_y_lower_boundary, u_y_upper_boundary)
ux_boundary = (ux_x_lower_boundary, ux_x_upper_boundary, ux_y_lower_boundary, ux_y_upper_boundary)
uy_boundary = (uy_x_lower_boundary, uy_x_upper_boundary, uy_y_lower_boundary, uy_y_upper_boundary)
u_coner = (coner_xlow_ylow, coner_xlow_yup, coner_xup_ylow, coner_xup_yup)
diffusion_numbers = (diffusion_number_x, diffusion_number_y)
u_cip_star, partial_u_cip_x_star, partial_u_cip_y_star \
= solve_advection_cip_2d(*u_props, *u_boundary, *ux_boundary, *uy_boundary, *u_coner, dt=delta_t)
velocities = (u_cip_star, 0.0)
velocity_x_boundaries = (u_x_lower_boundary, u_x_upper_boundary, u_y_lower_boundary, u_y_upper_boundary)
velocity_y_boundaries = (u_x_lower_boundary, u_x_upper_boundary, u_y_lower_boundary, u_y_upper_boundary) # とりあえず
u_cip = solve_diffusion_2d(u_cip_star, *u_boundary, *diffusion_numbers)
partial_u_cip_x = solve_diffusion_2d(partial_u_cip_x_star, *ux_boundary, *diffusion_numbers,
*velocities, *velocity_x_boundaries,
update_partial=1, u_array_integral=u_cip_star)
partial_u_cip_y = solve_diffusion_2d(partial_u_cip_y_star, *uy_boundary, *diffusion_numbers,
*velocities, *velocity_y_boundaries,
update_partial=2, u_array_integral=u_cip_star)
if n % 1 == 0 and n > 0:
img = axe.plot_wireframe(x_array, y_array, u_cip, cmap="bwr")
images.append([img])
ani = animation.ArtistAnimation(fig_5, images, interval=100)
# ani.save('wf_anim_art.mp4',writer='ffmpeg',dpi=100)
ani.save('2d-burgers.gif', writer="pillow")
HTML(ani.to_html5_video())
まとめ
- 線形移流拡散方程式を実装し、それを非線形にしたバーガース方程式も実装しました。
- CIP法で移流拡散方程式等を解く時は、フェーズ分割により移流方程式と拡散方程式(+移流方程式の一部)に分けて計算する。
次回は、流体の基礎方程式などを扱っていきたいと思います。また、計算がなかなかに重くなってきたので、気が向いたら高速化も行っていきたいと思います。
参考文献
- 2次元CIP法
- CIP法入門
- 石井秀征, 長嶋康雄, 相澤正満, CIP法によるBurgers方程式の解法とその評価, 平成23年度日本大学理工学部学術講演会論文集
- 高橋雄樹, 新部達大, 惠藤浩朗, 西條修, CIP 法を適用した 2 次元移流方程式の解析, 平成21年度日本大学理工学部学術講演会論文集
- 中島研吾, OpenMP によるプログラミング入門(II)