はじめに
数値流体力学(CFD)の勉強も兼ねて、液体の数値流体解析コードの構築に必要な知識などをまとめていきたいと思います。間違い等多々含まれていると思われますので、発見された際にはご連絡していただいけると幸いです。
対象読者
- Pythonを使える人
- 数値計算に興味がある人
- 流体力学に興味がある人
- 基本的な大学物理や数学を理解している人(簡単な微分方程式と線形代数くらい?)
シリーズ
- 1章:【Python】流体シミュレーション:移流方程式を実装する
- 2章:【Python】流体シミュレーション : 拡散方程式を実装する
- 2章の補足的な立ち位置:【Python】疎行列計算が高速にできるようになる記事
- 3章:【Python】流体シミュレーション : 線形から非線形へ
- この記事
本記事の大まかな内容
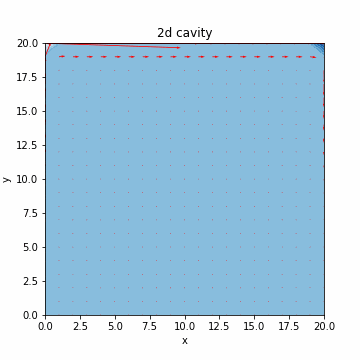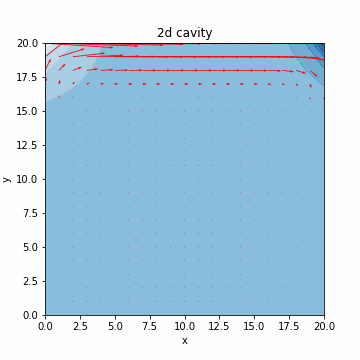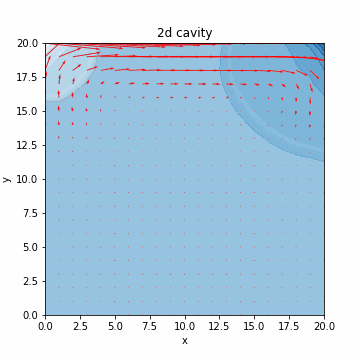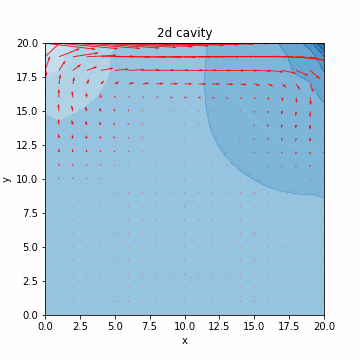
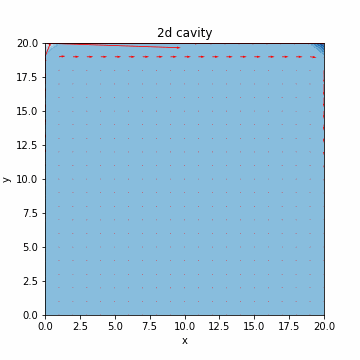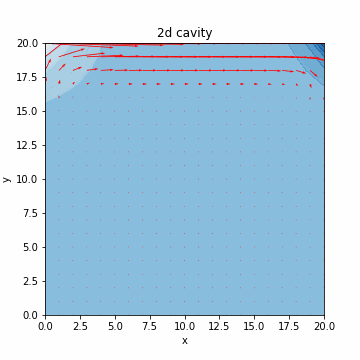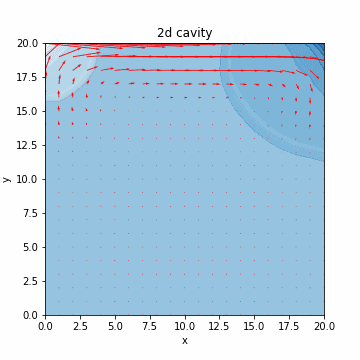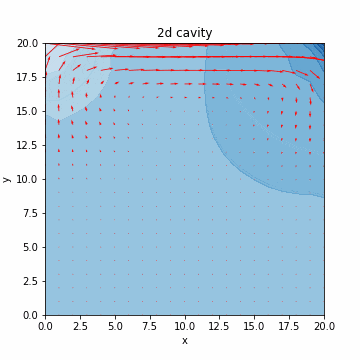
本記事では、気体のみや液体のみなど単相の数値シミュレーションを扱います。流体の支配方程式について簡単に説明した後、液体のシミュレーションで必要となる非圧縮性流体の数値計算アルゴリズムを実装する構成となっております。最終的には、キャビティ流れのシミュレーション(流体を領域内でグルグル回す感じ/下図)を行います。キャビティ流れに関しては、@eigsさんの非圧縮性 Navier-Stokes 方程式の数値解法1:導入編がわかりやすく、グラフもきれいです。
目次
| 章 | タイトル | 備考 |
|---|---|---|
| 1. | 流体解法 | |
| 1.1. | 流体の支配方程式 | |
| 1.2. | 圧縮性と非圧縮性 | |
| 2. | 非圧縮性流体の計算アルゴリズム | |
| 2.1. | MAC法 | Marker And Cell method |
| 2.2. | Fractional Step法 | 部分段階法とも言う |
| 2.3. | SIMPLE法 | Semi-Implicit Method for Pressure-Linked Equation method |
| 2.4. | CCUP法 | CIP-Combined Unified Procedure method |
| 2.5. | 空間差分 | 変数配置に関して |
| 3. | 実装 | CCUP法 |
1. 流体解法
1-1. 流体の支配方程式
流体は、連続の式・Navier Stokes方程式・エネルギー方程式の3つの方程式から成り立ちます。それぞれの方程式は、質量保存・運動量保存・エネルギー保存から導出されるものです。余計わかりにくくする可能性もありますが、それぞれの式のイメージもつけておきます。
a. 連続の式
\frac{\partial \rho}{\partial t} + (\vec{u} \cdot \nabla) \rho = - \rho \nabla \cdot \vec{u} \\
\quad or \\
\frac{\partial \rho}{\partial t} + \nabla \rho \vec{u} = 0
ある検査体積内の質量変化が、表面から流出入する質量流量$\rho \vec{u}$を面積分したものに等しいことから導けます。わかりやすい例で説明すると、財布の中のお金の変化量は、財布の出入り口を通過した金額を差し引きしたものと等しいことを上式は表しております。

b. Navier Stokes 方程式(流体の運動方程式)
\rho \frac{\partial \vec{u}}{\partial t} + \rho (\vec{u} \cdot \nabla)\vec{u} = - \nabla p + \mu \nabla^2 \vec{u} + (\mu + \lambda) \nabla (\nabla \cdot \vec{u}) + \vec{F_B} \\
\quad or \\
\rho \frac{\partial \vec{u}}{\partial t} + \rho (\vec{u} \cdot \nabla)\vec{u} = - \nabla p + \nabla \cdot {\bf T}_{\nu} + \vec{F_B} \\
, where \quad {\bf T}_{\nu} = \lambda (\nabla \cdot \vec{u}) {\bf I} + 2 \mu {\bf D} \quad : 粘性応力テンソル \\
{\bf D} = \frac{1}{2} \left\{(\nabla \vec{u}) + (\nabla \vec{u})^T \right\} : ひずみ速度テンソル \\
\quad \vec{F_B} \quad : 体積力(主に重力) \\
\quad \mu : 粘性係数
流体の運動量が、$圧力勾配:\nabla p$、$粘性による拡散:\nabla \cdot {\bf T}_{\nu}$、$体積力(重力等):\vec{F_B}$の影響を受けることを表しています。イメージ的な例を示すと、ある少年がボールを蹴った時に、そのボールは圧力差、粘性、重力の影響で速度が変わっていくことをイメージするとわかりやすいかもしれません。

c. エネルギー方程式
\rho \frac{\partial e}{\partial t} + \rho (\vec{u} \cdot \nabla) e = -p \nabla \cdot \vec{u} - \nabla \cdot (\kappa \nabla T) + {\bf T}_{\nu} : {\bf D} + \dot{L} \\
, where \quad \dot{L} : 化学反応などによる熱の発生量 \\
\quad \kappa : 熱伝導率
ただし、
{\bf T}_{\nu} : {\bf D} = tr({\bf T}_{\nu} \cdot {\bf D})
流体の内部エネルギー変化量は、圧力による仕事$\nabla \cdot \vec{u}$、熱伝導によるエネルギー収支$\nabla \cdot (\kappa \nabla T)$、粘性による散逸エネルギー${\bf T}_{\nu} \cdot \nabla \vec{u}$、化学反応など$\dot{L}$の影響を受けることを意味します。この式により、流体の温度変化が計算できるようになります。要するに、流体の温度変化は、加えた熱量に等しいということです。

まとめ
上で示した図をまとめると以下のようになるかと思います。

上で示したのは非保存系での流体の支配方程式で、右辺を0にすれば密度・速度・内部エネルギーの移流方程式(物質の移動を意味する式)を意味します。非保存系とは微分の外に変数が存在する形のことで、計算結果が保存則を満たしている保証がないため、数値計算の際には保存性の確認を行う必要があります。非保存系の逆は保存系と呼び、微分の中に全ての変数が入っている式のことです。
1-2. 圧縮性と非圧縮性
1-1節で示した式は圧縮性流体の支配方程式です。圧縮性流体とは流れの速度が音速の0.3倍程度(マッハ数が0.3)の流体のことで、これよりも遅い流れの流体のことを非圧縮性流体と一般的に認識されています。要するに、流体の動きが速すぎると、流体自体が伸び縮み(密度が変化)してしまうため圧縮性となり、遅かったり密度が大きいと流体は伸び縮みしないため非圧縮性として扱われます。そのため、液体は基本的に非圧縮として扱われます。
- 圧縮性
- $\frac{\partial \rho}{\partial t} \ne 0$
- 非圧縮性
- $\frac{\partial \rho}{\partial t} = 0$

1-1節で示した式を非圧縮の式に変形します。やることとしては、密度を変数ではなく定数で扱うようにして式を簡略化します。Navier Stokes方程式とエネルギー方程式は連続の式を用いることで簡単になります。また、ここでは化学反応などによる影響は無視することにします。
a. 連続の式
$$
\nabla \cdot \vec{u} = 0
$$
b. Navier Stokes方程式
$$
\rho \frac{\partial \vec{u}}{\partial t} + \rho (\vec{u} \cdot \nabla)\vec{u} = - \nabla p + \mu \nabla^2 \vec{u} + \vec{F_B}
$$
c. エネルギー方程式
$$
\rho \frac{\partial e}{\partial t} + \rho (\vec{u} \cdot \nabla) e = - \nabla \cdot (\kappa \nabla T) + 2 \mu {\bf D}:{\bf D}
$$
圧縮性と非圧縮性の流体方程式をまとめると以下のようになります。
| 基礎方程式 | 圧縮性 | 非圧縮性 |
|---|---|---|
| a. 連続の式 | $\frac{\partial \rho}{\partial t} + (\vec{u} \cdot \nabla) \rho = - \rho \nabla \cdot \vec{u}$ | $ \nabla \cdot \vec{u} = 0$ |
| b. Navier Stokes方程式 | $\rho \frac{\partial \vec{u}}{\partial t} + \rho (\vec{u} \cdot \nabla)\vec{u} = - \nabla p + \mu \nabla^2 \vec{u} + (\mu + \lambda) \nabla (\nabla \cdot \vec{u}) + \vec{F_B} $ | $\rho \frac{\partial \vec{u}}{\partial t} + \rho (\vec{u} \cdot \nabla)\vec{u} = - \nabla p + \mu \nabla^2 \vec{u} + \vec{F_B} $ |
| c. エネルギー方程式 | $$ \rho \frac{\partial e}{\partial t} + \rho (\vec{u} \cdot \nabla) e = -p \nabla \cdot \vec{u} - \nabla \cdot (\kappa \nabla T) + {\bf T}_{\nu} : {\bf D} + \dot{L}$$ | $$ \rho \frac{\partial e}{\partial t} + \rho (\vec{u} \cdot \nabla) e = - \nabla \cdot (\kappa \nabla T) + 2 \mu {\bf D}:{\bf D}$$ |
2. 非圧縮性流体の計算アルゴリズム
液体のシミュレーションを目指しているので、本章で非圧縮性流体の解き方について述べていきます。基本的に非圧縮性の方程式を用いて、離散化式を構築していきます。煩雑さを避けるために、ここではエネルギー方程式に関しては無視し、「陽的に解く」を陽解法で「陰的に解く」を陰解法で解くことを意味することにします。基本的に、圧縮性流体力学 Compressible Fluid Dynamicsなどを参考にしてます。
代表的な計算アルゴリズムを以下の表にまとめております。MAC(Maker And Cell)法、Fractional Step法、SIMPLE法は非圧縮性流体の基礎的な計算アルゴリズムとなります。様々なサイトや本で実装されているので、ここでは原理について述べるだけにします。本章の最後に、CCUP(CIP-Combined Unified Procedure)法に関して言及し、次の章で実装も行います。CCUP法は、これまでの記事で用いたCIP法による流体方程式を解く手法となります。
| アルゴリズム | 移流項 | 拡散項 | 圧力項 |
|---|---|---|---|
| MAC法系統 | 陽解法 | 陽解法 | 陰解法 |
| Fractioanl Step法 | 陽解法 | 陰解法 | 陰解法 |
| ---- | 陰解法 | 陽解法 | 陰解法 |
| SIMPLE法系統 | 陰解法 | 陰解法 | 陰解法 |
| CCUP法 | 陽解法 | 陽解法or陰解法 | 陰解法 |
2-1. MAC法
MAC(Maker And Cell)法は、種々の流れを安定的に解くことができるため、流体計算における基本的な解法となります。計算手順は以下のとおりです。
- 圧力の方程式を陰解法で解き、圧力$p^{n+1}$を求める。
- 速度に関する式を時間進行させて、速度$\vec{u^{n+1}}$を求める。
圧力の方程式と速度に関する式は次のように求めます。Navier Stokes方程式に$\nabla$をかけて発散をとり離散化すると、
- 圧力方程式
\nabla^2 p^{n+1} = - \nabla \cdot \left\{(\vec{u^n} \cdot \nabla )\vec{u^n} \right\} + \frac{\nabla \cdot \vec{u^n}}{\Delta t} + \nabla \cdot \left\{ \nu \nabla^2 \vec{u^n} + \frac{1}{\rho}\vec{F}_B\right\}
が得られます。また、Navier Stokes方程式の移流項と粘性項を陽的に時間離散すると、
- 速度に関する式
\frac{\vec{u^{n+1}} - \vec{u^n}}{\Delta t} = - (\vec{u} \cdot \nabla)\vec{u^n} - \frac{1}{\rho} \nabla p^n + \nu \nabla^2 \vec{u^n} \\
\nabla \cdot \vec{u^{n+1}} = 0
が得られます。あえて$\nabla \cdot \vec{u^n}$を0とせずに解くことで、離散化時の誤差を抑える工夫をしてます。
MAC法系統の計算アルゴリズムとしては、SMAC(Simplified MAC)法・HSMAC(Highly Simplified MAC)法などがあります。これらは高速にMAC法を解くために提案されたものです。
2-2. Fractional Step法
MAC法では粘性項を陽解法で解いており、時間刻み幅の制限(CFL条件)の影響を大きく受けます。粘性項を陰的に評価することでCFL条件の問題を解決する手法が、本項で述べるFractional Step法です。部分段階法とも呼ばれています。特徴としては、MAC法で用いた速度に関する式では右辺に速度と圧力が混在した形でしたが、Fractional Step法では以下のように右辺の速度と圧力を完全に分離して考えます。
- 速度に関する式
\frac{\bar{u} - \vec{u^n}}{\Delta t} = - (\vec{u} \cdot \nabla)\vec{u^n} + \nu \nabla^2 \vec{u^n} \\
\frac{\vec{u^{n+1}} - \bar{u}}{\Delta t} = - \frac{1}{\rho} \nabla p^{n+1} \\
\nabla \cdot \vec{u^{n+1}} = 0
- 圧力方程式
$$
\nabla^2 p^{n+1} = \frac{\nabla \cdot \bar{u}}{\Delta t}
$$
計算手順としては、
- 仮の速度$\bar{u}$を速度に関する式の一番上の式から求めます。
- 圧力の方程式を用いて、圧力$p^{n+1}$を求めます。
- 速度に関する式の上から二番目の式を用いて速度$\vec{u^{n+1}}$を求めます。
2-3. SIMPLE法
Semi-Implicit Method for Pressure-Linked Equation法の略で、陰解法を基に公式化されています。もっと知りたい! 熱流体解析の基礎64 第6章 熱流体解析の手法:6.5.4 SIMPLE法で詳しく解説されています。
- 陰的に仮の速度$\bar{u}$を求めます。
\bar{u} = \vec{u^n} - \Delta t \left\{(\bar{u} \cdot \nabla)\bar{u} + \nabla p - \nu \nabla^2 \bar{u}\right\}
- 圧力方程式を用いて圧力を更新します。
$$
\nabla^2 \delta p = \frac{\nabla \cdot \bar{u}}{\Delta t}\
p^{n+1} = p + \delta p
$$
- 求めた圧力で速度$\vec{u}$を更新します。
$$
\vec{u^{n+1}} - \bar{u} = - \Delta t \nabla(p^{n+1} - p)
$$
2-4. CCUP法
CCUP法はCIP法を考案した矢部らによって構築された手法で、前回記事でのバーガース方程式をCIP法で解いた時のように、流体の支配方程式を移流フェイズと非移流フェイズに分けて計算します。清水らや姫野らの論文がわかりやすいです。移流項と非移流項の解く順番等が人によって違うため、以下では後者の論文で紹介されている順番で解いていきます。アルゴリズムとしては、
- 移流フェイズで$密度: \rho$、$速度:\vec{u}$、$内部エネルギー:e$、$圧力: p$を移流させる。
- 非移流フェイズに移る。
- 拡散段階で速度・内部エネルギー・圧力を更新する。(密度は一定)
- 圧力方程式を陰的に解き圧力を更新する。
- 新しい圧力を用いて密度・速度・内部エネルギーを求める。
という順番で解いていきます。要するに、物質の移流と拡散を行った後に、移動速度が圧倒的に速い圧力(音速と同じ速度)で辻褄を合わせていくっていう感じかと思います。

2-5. 空間差分
実装に入る前に空間差分の方法に関して、知らなくても実装できますが簡単に述べておきます。空間上のどこに変数を配置するかによって、チェッカーボード不安定と呼ばれる圧力振動が生じる場合があるからです。
レギュラー格子
- コーディングが楽
- 圧力振動が生じやすいという欠点があります。

スタッガード格子
- 食い違い格子と呼ばれ、圧力などのスカラー量と速度を別々の点で代表させる方法です。
- この手法を用いることでチェッカーボード不安定を防ぐことができます。
- コーディングが少し大変。

コロケート格子
- レギュラー格子とは基本的には同じですが、変数をセル中心に配置する手法です。
- セル間に流束(単位時間当たり、単位面積当たりの物理量の流量)の情報が付加されますが下図では省略してます。詳しく知りたい方は、梶島先生の乱流の数値シミュレーションという本をご覧ください。(@youiidaさん、コメントありがとうございます!)

前述した手法では、スタガード格子を用いて計算するのが基本的な方針となりますが、本記事の実装ではレギュラー格子で数値計算を行います(スタッガード格子などを使うとモチベがわかなかったので)。
3. 実装
CCUP法での実装を行います。解く問題はキャビティ流れで、上部の壁に横向きに速度を与えて、領域内に時計回りの風を引き起こす感じのものです。コードは、Githubに上げておきます。エネルギー方程式は無視してます。移流項と拡散項に関しては前回記事で述べたので、コード内での新しい内容は圧力方程式の部分ですが、拡散項の計算と構造はほぼ同じです。圧力に関する計算では、移流項などいくつか省略してます。また、境界条件はかなり雑です

速度を赤線で、圧力を青のコンターで表すと、それっぽいグラフが出力されるのがわかります。
scipy.sparse.dia_matrix
${\bf A}\vec{x}=\vec{b}$という一次元連立方程式の行列${\bf A}$を作成する際に、scipy.sparse.dia_matrixを使ってます。この行列${\bf A}$は疎行列と呼ばれる、行列の要素のほとんどが0で構成されているものなので、scipy.sparse.dia_matrixで規定される対角圧縮格納方式 (DIA)で作成するとメモリなどの点で効率的です。この他の疎行列の格納形式に関しては、【Python】疎行列計算が高速にできるようになる記事に載せています。
一例を以下に示します。
# 同じ長さの配列を一つもしくは複数用意。同じ長さのものが必要な点に注意。
data = np.array([np.arange(10), np.arange(20,30)], np.arange(30,40))
# dataのindexに従い対角行列のoffsetを決める。0: 対角行列, 正の数: 上側, 負の数: 下側
# offsetを正にすると先頭から順に、負にすると後ろから順に配列が削られる点に注意。
offsets = np.array([0, 2, -3])
a_matrix = scipy.sparse.dia_matrix((data, offsets), shape=(len(data[0]), len(data[0]))) # shapeで行列の形を設定。
print(a_matrix)
# <10x10 sparse matrix of type '<class 'numpy.int64'>'
# with 25 stored elements (3 diagonals) in DIAgonal format>
print(a_matrix.todense())
# matrix([[ 0, 0, 22, 0, 0, 0, 0, 0, 0, 0],
# [ 0, 1, 0, 23, 0, 0, 0, 0, 0, 0],
# [ 0, 0, 2, 0, 24, 0, 0, 0, 0, 0],
# [30, 0, 0, 3, 0, 25, 0, 0, 0, 0],
# [ 0, 31, 0, 0, 4, 0, 26, 0, 0, 0],
# [ 0, 0, 32, 0, 0, 5, 0, 27, 0, 0],
# [ 0, 0, 0, 33, 0, 0, 6, 0, 28, 0],
# [ 0, 0, 0, 0, 34, 0, 0, 7, 0, 29],
# [ 0, 0, 0, 0, 0, 35, 0, 0, 8, 0],
# [ 0, 0, 0, 0, 0, 0, 36, 0, 0, 9]])
4. まとめ
- 圧縮性と非圧縮性の流体の支配方程式に関して簡単に説明しました。
- 非圧縮性の流体方程式の計算アルゴリズムには、MAC法、Fractional Step法、SIMPLE法、CCUP法などがあることを確認しました。
- CCUP法を用いてキャビティ流れのシミュレーションを行いました。
次は、気液二相(気体と液体)シミュレーションについて述べたいと思います。
参考文献
- 圧縮性流体力学 Compressible Fluid Dynamics
- ナビエ・ストークス方程式を導出する
- もっと知りたい! 熱流体解析の基礎64 第6章 熱流体解析の手法:6.5.4 SIMPLE法
- 清水文雄, 田中和博, 畠中清史, 重藤博司, 清水 剛, CCUP 法を用いた水槽内における気液界面の数値解析, 第 15回数値流体力学シンポジウム.
- 姫野武洋, 渡辺紀徳, 低重力環境における熱流体管理に関する研究 : 第1報,熱流動解析に適したCCUP法-TCUP法-の提案, 日本機械学会B編 69 巻 678 号 p. 266-273, 2003.
- 姫野武洋, 根岸秀世, 野中聡, 井上智博, 渡辺紀徳, 鵜沢聖治, 様々な加速度環境における自由表面流の数値解析 : CIP法,MARS法,Level Set法を協調した解法の改良, 日本機械学会B編 76 巻 765 号 p. 778-788, 2010.
- Yabe, T., Wang, P. Y., Unified Numerical Procedure for Compressible and Incompressible Fluid, J. Phys. Soc. Japan, 60-7 (1991), pp. 2105-2108.
- 2.5.2.2.1. 対角圧縮格納方式 (DIA)
- Hessam Babaee and Sumanta Acharya, A Hybrid Staggered/SemistaggeredFinite-Difference Algorithm for Solving Time-Dependent Incompressible Navier-Stokes Equationson Curvilinear Grids, Numerical Heat Transfer, Part B: Fundamentals : An International Journal ofComputation and Methodology, 65:1, 1-26, DOI: 10.1080/10407790.2013.827012
- 峯村 吉泰, Javaによる流体・熱流動の数値シミュレーション, 森北出版, 2005年, p.89