Go to Qiita Advent Calendar 2024 Top
LoginSignup
97
107

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 3 years have passed since last update.

@KQTS

【Python】流体シミュレーション：移流方程式を実装する

Last updated at Posted at 2020-02-19

はじめに

空気や水といった流体のシミュレーションに関する学問である数値流体力学(CFD)の勉強も兼ねて、水の数値流体解析コードの構築に必要な知識などを(複数の記事で)まとめていきたいと思います。

初心者にもわかりやすいように書いていきたいと思います。間違い等多々含まれていると思われますので、発見された際にはご連絡していただいけると幸いでございます。また、どこがわかりにくいとかをコメントして頂けたらありがたいです。随時更新していきます。

対象読者

  • Pythonを使える人
  • 数値計算に興味がある人
  • 流体力学に興味がある人
  • 基本的な大学物理や数学を理解している人(微分方程式くらい？)

シリーズ

本記事の大まかな内容

水のシミュレーションで必要な流体の基礎方程式を扱う前段階として、移流方程式について簡単にまとめて、実装も行います。

更新履歴

  • 2020/02/19 文章中に誤りがあったため、修正しました。コメントして頂いた@picric_acid 様ありがとうございます！
  • 2020/02/21 コードにバグあったため、修正しました。コメントして頂いた@fluxCapacitor 様ありがとうございます！

移流方程式(物質の移動を表す式)

一次元の移流方程式を有限差分法で解いていきます。

移流方程式(Advection equation)
$$
\frac{\partial u}{\partial t} + c \frac{\partial u}{\partial x} = 0
$$

この式が意味することは、ある関数uが速度cで移動していくということである。要するに、速度cという流れに沿って物理量が移動していくことを表す方程式である。

advection_example.png

これを離散化して、方程式を解いていく。今回は陽解法と呼ばれる方法で解いていく。陽解法は簡単に言えば、現在の時間の値のみを用いて、未来の値を求める方法です。陽解法の他に陰解法と呼ばれる手法もあり、現在の値と未来の値を元に計算していく方法です。

今回実装する陽解法は以下の通り。以下の４つは気の赴くままに選びました。

  • FTCS(Forward in Time and Central Difference in Space)
  • 一次風上差分(Upwind differencing)
  • Lax-Wendroff scheme
  • CIP(Constrained Interpolation Profile scheme) method

それぞれについて、離散化した式を書き下していきます。式では、添え字jは場所を意味し、nは時刻を意味することとします。そのため、$f_j^n$は時刻$n$に場所$x_j$に位置する関数fの値を意味します。

  1. FTCS(Forward in Time and Central Difference in Space)
    2. $$
    u_j^{n+1} = u_j^{n} - \frac{c}{2} \left( \frac{\Delta t}{\Delta x} \right) \left(u_{j+1}^n - u_{j-1}^n \right)
    $$

  2. Upwind differencing
    3. $$
    u_j^{n+1} = u_j^{n} - c \left( \frac{\Delta t}{\Delta x} \right) \left(u_{j}^n - u_{j-1}^n \right)
    $$

  3. Lax-Wendroff scheme
    4. $$
    u_j^{n+1} = u_j^{n} - \frac{c}{2} \left( \frac{\Delta t}{\Delta x} \right) \left(u_{j+1}^n - u_{j-1}^n \right) + \frac{c^2}{2} \left( \frac{\Delta t}{\Delta x} \right)^2 \left(u_{j+1}^n - 2 u_j^n+ u_{j-1}^n \right)
    $$

  4. CIP(Constrained Interpolation Profile scheme) method

詳細は後述。または、CIP法入門を参照してください。

陽解法の安定条件

陽解法を用いる際に重要な安定条件について簡単に述べておきます。数値的に情報伝播速度$\frac{\Delta t}{\Delta x}$(格子幅を時間で割ることにより求まる速度)は、物理的な信号速度$c$以上でなければならない。そうでなければ、物理現象の方が数値計算より速い速度で移動することになり、物理現象を数値的に表せれなくなるからです。その考えをもとに
$$
c \leq \frac{\Delta x}{\Delta t}
$$
という条件が導き出されます。これを変形した
$$
\nu = c \frac{\Delta t}{\Delta x} \leq 1
$$
がCFL条件と呼ばれ、数値的に安定する条件として使用されます。また、左辺はクーラン数とも呼ばれます。要は、時間刻み幅$ \Delta t$が$\frac{\Delta x}{c}$以下であれば良い。なお、こうしたCFL条件は陰解法を用いる際には関係がなくなるため、陰解法は陽解法より時間刻み大きくできるメリットがあります。ただ、その分計算が複雑になります。

実装

使用言語はPython。計算式がわかりやすいよう、Numpyの関数を多用せずに書いていきます。

計算対象

矩形波の移流を計算する。格子幅$\Delta x$、物理的な信号速度$c$、時間刻み幅$\Delta t$は全て定数として計算する。今回は参考文献に合わせて、$\Delta x=1$、$c=1$、$\Delta t=0.2$として計算する。なので、$CFL=0.2$で固定されCFL条件は満たしている状態。

advection_answer.png 
# Creat square wave
Num_stencil_x = 101
x_array = np.arange(Num_stencil_x)
u_array = np.where(((x_array >= 30) |(x_array < 10)), 0.0, 1.0)
u_lower_boundary = 0.0
u_upper_boundary = 0.0
Time_step = 200
Delta_x = max(x_array) / (Num_stencil_x-1)
C = 1
Delta_t = 0.2
CFL = C * Delta_t / Delta_x
total_movement = C * Delta_t * (Time_step+1)
exact_u_array = np.where(((x_array >= 30 + total_movement) |(x_array < 10 + total_movement)), 0.0, 1.0)
plt.plot(x_array, u_array, label="Initial condition")
plt.plot(x_array, exact_u_array, label="Answer")
plt.legend(loc="upper right")
plt.xlabel("x")
plt.ylabel("u")
plt.xlim(0, max(x_array))
plt.ylim(-0.5,1.5)

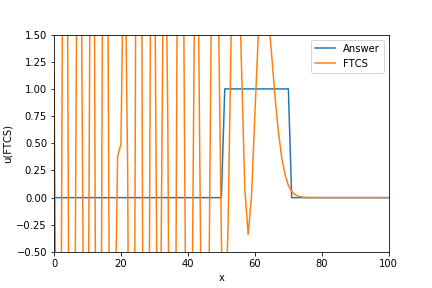
1. FTCS(Forward in Time and Central Difference in Space)

$$
u_j^{n+1} = u_j^{n} - \frac{c}{2} \left( \frac{\Delta t}{\Delta x} \right) \left(u_{j+1}^n - u_{j-1}^n \right)
$$

answer_ftcs.png

解が振動します。全く答えが合いません

u_ftcs = u_array.copy()
# タイムステップを設定
for n in range(Time_step):
    u_old = u_ftcs.copy()
    u_ftcs[0] = u_old[0] - CFL / 2 * (u_old[1] - u_lower_boundary)
    u_ftcs[-1] = u_old[-1] - CFL / 2 * (u_upper_boundary - u_old[-1])
    for j in range(1,Num_stencil_x-1, 1):
        u_ftcs[j] = u_old[j] - CFL / 2 * (u_old[j+1] - u_old[j-1])
plt.plot(x_array, exact_u_array, label="Answer")
plt.plot(x_array, u_ftcs, label="FTCS")
plt.legend(loc="upper right")
plt.xlabel("x")
plt.ylabel("u(FTCS)")
plt.xlim(0, max(x_array))
plt.ylim(-0.5,1.5)

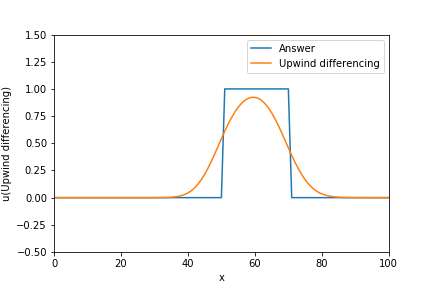
2. 一次精度風上差分(Upwind differencing)

$$
u_j^{n+1} = u_j^{n} - c \left( \frac{\Delta t}{\Delta x} \right) \left(u_{j}^n - u_{j-1}^n \right)
$$

answer_upwing.png

数値拡散が大きく解が滑らかになる。

u_upwind = u_array.copy()
# タイムステップを設定
for n in range(Time_step):
    u_old = u_upwind.copy()
    u_upwind[0:1] = u_old[0] - CFL * (u_old[1] - u_lower_boundary)
    for j in range(1,Num_stencil_x):
        u_upwind[j:j+1] = u_old[j] - CFL * (u_old[j] - u_old[j-1])
plt.plot(x_array, exact_u_array, label="Answer")
plt.plot(x_array, u_upwind, label="Upwind differencing")
plt.legend(loc="upper right")
plt.xlabel("x")
plt.ylabel("u(Upwind differencing)")
plt.xlim(0, max(x_array))
plt.ylim(-0.5,1.5)

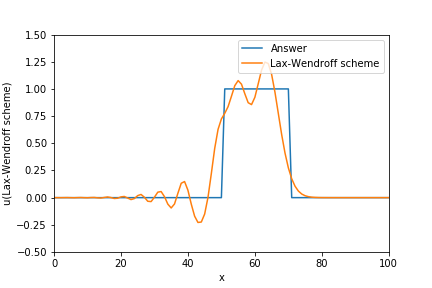
3. Lax-Wendroff scheme

$$
u_j^{n+1} = u_j^{n} - \frac{c}{2} \left( \frac{\Delta t}{\Delta x} \right) \left(u_{j+1}^n - u_{j-1}^n \right) + \frac{c^2}{2} \left( \frac{\Delta t}{\Delta x} \right)^2 \left(u_{j+1}^n - 2 u_j^n+ u_{j-1}^n \right)
$$

answer_laxw.png

数値振動と解の鈍りがある。

u_lw= u_array.copy()
# タイムステップを設定
for n in range(Time_step):
    u_old = u_lw.copy()
    u_lw[0:1] = u_old[0] - CFL / 2 * (u_old[1] - u_lower_boundary) \
                    + CFL**2 / 2 * (u_old[1] - 2 * u_old[0] + u_lower_boundary)
    u_lw[-1] = u_old[-1] - CFL / 2 * (u_upper_boundary - u_old[-1]) \
                    + CFL**2 / 2 * (u_upper_boundary - 2 * u_old[-1] + u_old[-2])
    for j in range(1,Num_stencil_x-1, 1):
        u_lw[j] = u_old[j] - CFL / 2 * (u_old[j+1] - u_old[j-1]) \
                    + CFL**2 / 2 * (u_old[j+1] - 2 * u_old[j] + u_old[j-1])
plt.plot(x_array, exact_u_array, label="Answer")
plt.plot(x_array, u_lw, label="Lax-Wendroff scheme")
plt.legend(loc="upper right")
plt.xlabel("x")
plt.ylabel("u(Lax-Wendroff scheme)")
plt.xlim(0, max(x_array))
plt.ylim(-0.5,1.5)

4. CIP(Constrained Interpolation Profile scheme) method

CIP法の基本的な考え方としては、まずある関数fについて離散化した際、ある点$x_j$とその隣の点$x_{j-1}$の物理量は滑らかに繋がっていると考えます。こうすることにより、それぞれの物理量$f_j$と$f_{j-1}$の微分値を用いて、格子間の傾きを発散させずに時間発展させることができるようになります。

つまり、関数の値と微分値が格子点上で連続という条件のもと、3次補完関数$F(x)$により格子2点間の関係を表すことができるようになる。

$x_{j-1}<= x < x_j$の領域において、
$$
F(x) = a X^3 + b X^2 +c X + d \quad ,where \quad X = x - x_j
$$
のように$F(x)$を3次補完で定義すると、関数の値と微分値が格子点上で連続という条件から、

$$
F(0) = f_j^n, \quad F(\Delta x) = f_{j+1}^n, \quad \frac{\partial F(0)}{\partial x} = \frac{\partial f_j^n}{\partial x}, \quad \frac{\partial F(\Delta x)}{\partial x} = \frac{\partial f_{j+1}^n}{\partial x} \ , where \quad \Delta x = x_{j+1} - x_j
$$
が成立するので、これを$F(x)$の式に代入して、$a, b, c, d$を求めると、

a = \frac{\partial f_j^n / \partial x + \partial f_{j+1}^n / \partial x }{\Delta x^2} + \frac{2 (f_j^n - f_{j+1}^n)}{\Delta x^3} \\
b =  \frac{3 (f_{j+1}^n - f_j^n)}{\Delta x^2} - \frac{2( \partial f_j^n / \partial x + \partial f_{j+1}^n / \partial x )}{\Delta x} \\
c = \frac{\partial f_j^n}{\partial x}\\
d = f_j^n

以上より、速度cが一定の場合、$\frac{\partial u}{\partial t} + c \frac{\partial u}{\partial x} = 0$は微分値も満たすので、時間刻み幅$\Delta t(n+1ステップ目)$秒後における値と微分値は、

u_j^{n+1} = F(x_j - c \Delta t)= a \xi^3 + b \xi^2 + c\xi + d \\
\frac{\partial u_j^{n+1}}{\partial x} = \frac{d F(x_j - c \Delta t)}{d x} = 3 a \xi^2 + 2 b \xi + c \\
, where \quad \xi = - c \Delta t

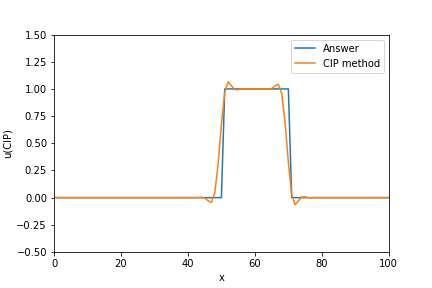
answer_cip.png

他の三つの手法より数値拡散や振動が圧倒的に小さい。しかし、参考文献ほどうまく移流できなかった。(2020/02/20 コメントで頂いた修正をかけたところかなり良くなりました。)

u_cip= u_array.copy()
partial_u_cip = ((np.append(u_cip[1:], u_upper_boundary) + u_cip)/2 - (np.append(u_lower_boundary, u_cip[:-1]) + u_cip)/2)/ Delta_x
# 時間発展させる
for n in range(Time_step):
    u_old = u_cip.copy()
    partial_u_old = partial_u_cip.copy()
    u_cip[0] = 0
    partial_u_cip[0] = 0
    for j in range(1, Num_stencil_x):
        a = (partial_u_old[j] + partial_u_old[j-1]) / Delta_x**2 - 2.0 * (u_old[j] - u_old[j-1]) / Delta_x**3
        b = 3 * (u_old[j-1] - u_cip[j]) / Delta_x**2 + (2.0*partial_u_old[j] + partial_u_old[j-1]) / Delta_x
        c = partial_u_old[j]
        d = u_old[j]
        xi = - C * Delta_t  # C > 0
        u_cip[j:j+1] = a * xi**3 + b * xi**2 + c * xi + d
        partial_u_cip[j:j+1] = 3 * a * xi**2 + 2 * b * xi + c
plt.plot(x_array, exact_u_array, label="Answer")
plt.plot(x_array, u_cip, label="CIP method")
plt.legend(loc="upper right")
plt.xlabel("x")
plt.ylabel("u(CIP)")
plt.xlim(0, max(x_array))
plt.ylim(-0.5,1.5)

まとめ

流体方程式を構成する移流方程式の基礎について簡単に実装とともにまとめました。
実装したのは以下の4つです。

  • FTCS(Forward in Time and Central Difference in Space)
  • 一次風上差分(Upwind differencing)
  • Lax-Wendroff scheme
  • CIP(Constrained Interpolation Profile scheme) method

次回は、拡散方程式についてです。

参考文献

  1. http://zellij.hatenablog.com/entry/20140805/p1
  2. https://www.cradle.co.jp/media/column/a233
  3. http://www.slis.tsukuba.ac.jp/~fujisawa.makoto.fu/cgi-bin/wiki/index.php?%B0%DC%CE%AE%CB%A1
  4. http://www.astro.phys.s.chiba-u.ac.jp/netlab/mhd_summer2001/cip-intro.pdf
  5. http://www.astro.phys.s.chiba-u.ac.jp/netlab/summer-school_2004/TEXTBOOK/text3-1.pdf
97
107
6

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
97
107

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?