深層学習におけるモデル構造違いによる影響を中間層可視化から考えてみる

0.はじめに

深層学習において、モデル構造設計において正解なモデルを一発で構築することは難しい。そもそも正解なモデルなんてあるのか？
特にレビュー時になんでこのモデルでいいの？？とか聞かれて「なんとなく...」としか言いようがない時もある。
今回は、一般的によく用いられるSeqtuentialなモデルと、Inceptionモデルと、Residualモデルを比較してみる。

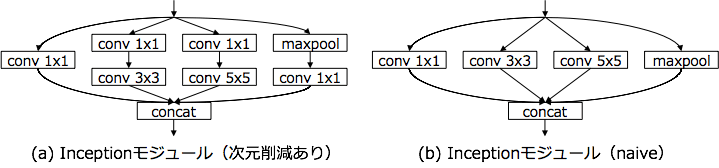
1.Inceptionモデルとは

2014年のILSVRCの優勝モデルであるGoogLeNetで採用されたInceptionモジュールを搭載したモデルを指す。複数の畳み込み層やpooling層から構成されるInceptionモジュールと呼ばれる小さなネットワークを定義し、これを通常の畳み込み層のように重ねていくことで1つの大きなCNNを作り上げている点が特徴と言える。Inceptionモジュールでは，ネットワークを分岐させ，サイズの異なる畳み込みを行った後、それらの出力をつなぎ合わせるという処理を行っている。

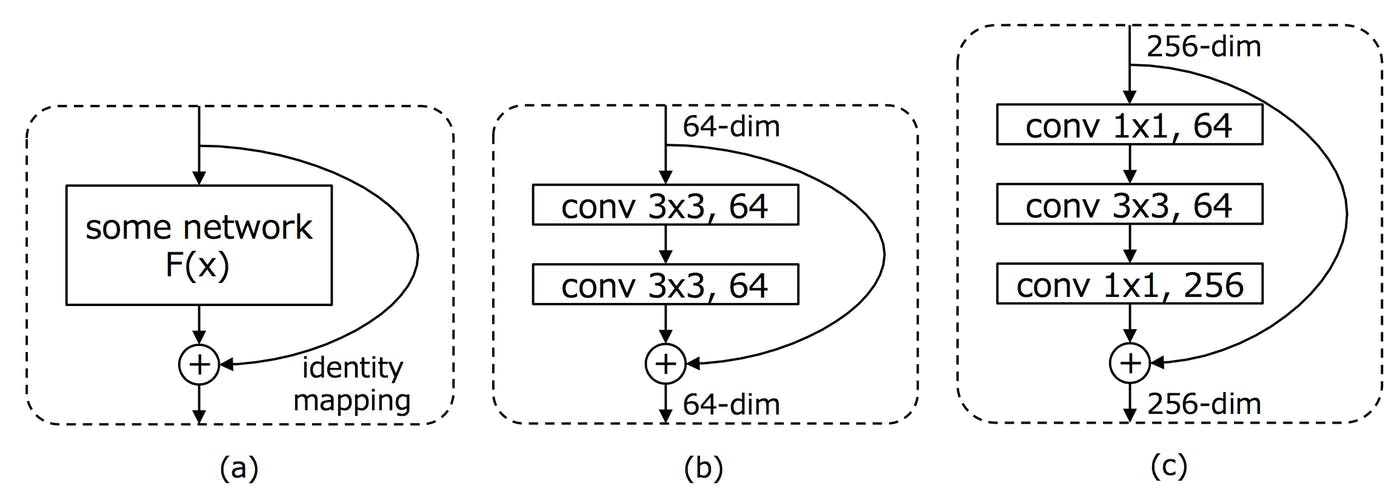
2.Residualモデルとは

Residual Networks (ResNet)は、2015年のILSVRCの優勝モデルである。ResNetは、通常のネットワークのように、何かしらの処理ブロックによる変換$F(x)$を単純に次の層に渡していくのではなく、その処理ブロックへの入力$x$をショートカットし、$H(x) = F(x)+x$を次の層に渡すことが行われる。このショートカットを含めた処理単位をresidualモジュールと呼ぶ。ResNetでは，ショートカットを通して，backpropagation時に勾配が直接下層に伝わっていくことになり、非常に深いネットワークにおいても効率的に学習ができるようになった。

3.学習用データ準備

今回はMNISTデータセットでは違いがあまり見られそうにないため、Fashion MNSITを使う。

### ライブラリ　インポート ###
import matplotlib.pyplot as plt
import numpy as np
from keras.datasets import fashion_mnist
from keras.models import *
from keras.layers import *
from keras.utils import *
from sklearn.svm import SVC
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV
import umap
from scipy.sparse.csgraph import connected_components
from sklearn.metrics import confusion_matrix, classification_report, accuracy_score
import seaborn as sns
from keras.utils import plot_model

### Fashion MNISTをロード ###
(X_train,y_train),(X_test, y_test) = fashion_mnist.load_data()

### Trainデータをシャッフル ###
l = list(zip(X_train, y_train))
np.random.shuffle(l)
X_train, y_train = zip(*l)

### データを確認 ###
plt.figure(figsize=(20,20))
for i in range(100):
    plt.subplot(10,10,i+1)
    plt.imshow(X_train[i])
    plt.axis('off')
    plt.title(str(y_train[i]),fontsize=14)
    plt.savefig('./cifar10.png', bbox_inches='tight')
plt.show()

### 学習用に変換
## 正規化
X_train = np.array(X_train, dtype='float32')/255.
X_test = X_test/255.

# Reshape
X_train = np.reshape(X_train, (-1,28,28,1))
X_test = np.reshape(X_test, (-1,28,28,1))

## One-hot化
y_train = np_utils.to_categorical(y_train,10)
y_test = np_utils.to_categorical(y_test,10)

4.モデル構築

今回は、Sequential、Inception、Residual、InceptionとResidualの組み合わせの4つのモデルを構築し、それぞれの中間層出力と精度を比較する。

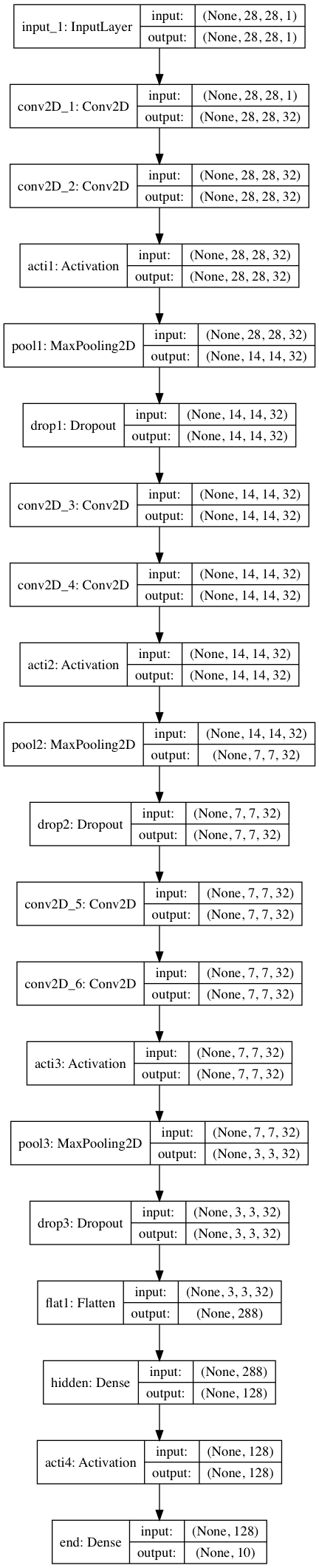
4.1.Sequentialモデル

通常の畳み込み層を重ねたモデル。

input1 = Input((28,28,1,))

conv1 = Conv2D(32, (2,2), padding='same', name='conv2D_1', kernel_initializer='he_normal')(input1)
conv1 = Conv2D(32, (2,2), padding='same', name='conv2D_2', kernel_initializer='he_normal')(conv1)
acti1 = Activation('relu', name='acti1')(conv1)
pool1 = MaxPool2D(pool_size=(2,2), name='pool1')(acti1)
drop1 = Dropout(0.2, name='drop1')(pool1)

conv2 = Conv2D(32, (2,2), padding='same', name='conv2D_3', kernel_initializer='he_normal')(drop1)
conv2 = Conv2D(32, (2,2), padding='same', name='conv2D_4', kernel_initializer='he_normal')(conv2)
acti2 = Activation('relu', name='acti2')(conv2)
pool2 = MaxPool2D(pool_size=(2,2), name='pool2')(acti2)
drop2 = Dropout(0.2, name='drop2')(pool2)

conv3 = Conv2D(32, (2,2), padding='same', name='conv2D_5', kernel_initializer='he_normal')(drop2)
conv3 = Conv2D(32, (2,2), padding='same', name='conv2D_6', kernel_initializer='he_normal')(conv3)
acti3 = Activation('relu', name='acti3')(conv3)
pool3 = MaxPool2D(pool_size=(2,2), name='pool3')(acti3)
drop3 = Dropout(0.2, name='drop3')(pool3)


flat1 = Flatten(name='flat1')(drop3)
dens1 = Dense(128, name='hidden')(flat1)
acti4 = Activation('relu', name='acti4')(dens1)
dens2 = Dense(10,activation='softmax', name='end')(acti4)

model = Model(inputs=input1, outputs=dens2)
model.summary()
model.compile(loss='categorical_crossentropy',
              optimizer='Adam',
              metrics=['accuracy'])

# モデル出力
plot_model(model, to_file='./model/sequential.png',show_shapes=True)

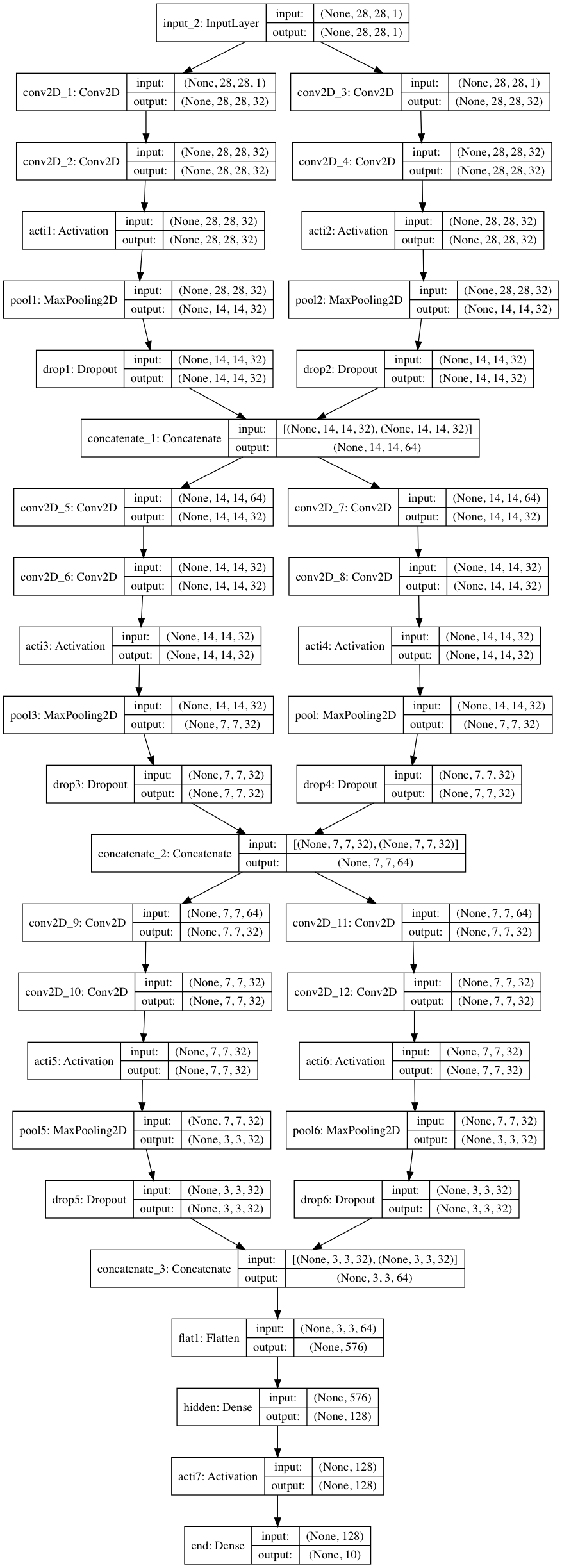
4.2.Inceptionモデル

Inceptionモジュールを搭載したモデル。今回は簡単に横に1層増やしたが、もっと増やしてもよかったかもしれない。

input1 = Input((28,28,1,))

conv1 = Conv2D(32, (2,2), padding='same', name='conv2D_1', kernel_initializer='he_normal')(input1)
conv1 = Conv2D(32, (2,2), padding='same', name='conv2D_2', kernel_initializer='he_normal')(conv1)
acti1 = Activation('relu', name='acti1')(conv1)
pool1 = MaxPool2D(pool_size=(2,2), name='pool1')(acti1)
drop1 = Dropout(0.2, name='drop1')(pool1)

conv2 = Conv2D(32, (3,3), padding='same', name='conv2D_3', kernel_initializer='he_normal')(input1)
conv2 = Conv2D(32, (3,3), padding='same', name='conv2D_4', kernel_initializer='he_normal')(conv2)
acti2 = Activation('relu', name='acti2')(conv2)
pool2 = MaxPool2D(pool_size=(2,2), name='pool2')(acti2)
drop2 = Dropout(0.2, name='drop2')(pool2)

conc1 = concatenate([drop1, drop2], axis=3)

conv3 = Conv2D(32, (2,2), padding='same', name='conv2D_5', kernel_initializer='he_normal')(conc1)
conv3 = Conv2D(32, (2,2), padding='same', name='conv2D_6', kernel_initializer='he_normal')(conv3)
acti3 = Activation('relu', name='acti3')(conv3)
pool3 = MaxPool2D(pool_size=(2,2), name='pool3')(acti3)
drop3 = Dropout(0.2, name='drop3')(pool3)

conv4 = Conv2D(32, (3,3), padding='same', name='conv2D_7', kernel_initializer='he_normal')(conc1)
conv4 = Conv2D(32, (3,3), padding='same', name='conv2D_8', kernel_initializer='he_normal')(conv4)
acti4 = Activation('relu', name='acti4')(conv4)
pool4 = MaxPool2D(pool_size=(2,2), name='pool')(acti4)
drop4 = Dropout(0.2, name='drop4')(pool4)

conc2 = concatenate([drop3, drop4], axis=3)

conv5 = Conv2D(32, (2,2), padding='same', name='conv2D_9', kernel_initializer='he_normal')(conc2)
conv5 = Conv2D(32, (2,2), padding='same', name='conv2D_10', kernel_initializer='he_normal')(conv5)
acti5 = Activation('relu', name='acti5')(conv5)
pool5 = MaxPool2D(pool_size=(2,2), name='pool5')(acti5)
drop5 = Dropout(0.2, name='drop5')(pool5)

conv6 = Conv2D(32, (3,3), padding='same', name='conv2D_11', kernel_initializer='he_normal')(conc2)
conv6 = Conv2D(32, (3,3), padding='same', name='conv2D_12', kernel_initializer='he_normal')(conv6)
acti6 = Activation('relu', name='acti6')(conv6)
pool6 = MaxPool2D(pool_size=(2,2), name='pool6')(acti6)
drop6 = Dropout(0.2, name='drop6')(pool6)

conc3 = concatenate([drop5, drop6], axis=3)

flat1 = Flatten(name='flat1')(conc3)
dens1 = Dense(128, name='hidden')(flat1)
acti7 = Activation('relu', name='acti7')(dens1)
dens2 = Dense(10,activation='softmax', name='end')(acti7)

incep_model = Model(inputs=input1, outputs=dens2)

incep_model.summary()
incep_model.compile(loss='categorical_crossentropy',
                    optimizer='Adam',
                    metrics=['accuracy'])

plot_model(incep_model, to_file='./model/incep_model.png',show_shapes=True)

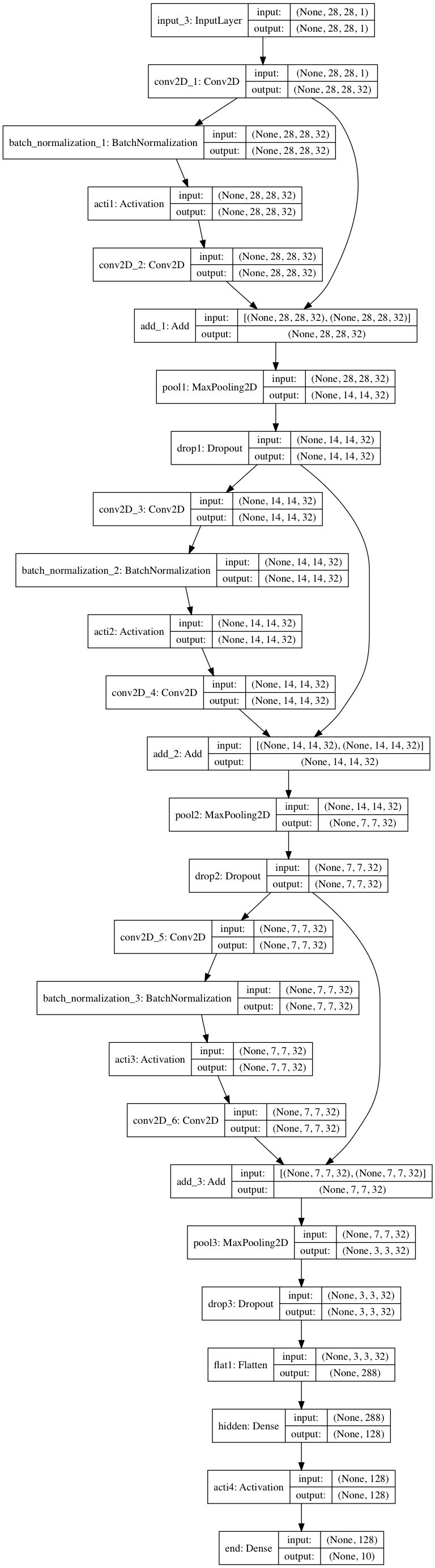
4.3.Residualモデル

スキップ構造をもつResidualモジュールを搭載したモデル。

input1 = Input((28,28,1,))

conv1_ = Conv2D(32, (2,2), padding='same', name='conv2D_1', kernel_initializer='he_normal')(input1)
batc1 = BatchNormalization()(conv1_)
acti1 = Activation('relu', name='acti1')(batc1)
conv1 = Conv2D(32, (2,2), padding='same', name='conv2D_2', kernel_initializer='he_normal')(acti1)

add1  = add([conv1_, conv1])
pool1 = MaxPool2D(pool_size=(2,2), name='pool1')(add1)
drop1 = Dropout(0.2, name='drop1')(pool1)

conv2 = Conv2D(32, (2,2), padding='same', name='conv2D_3', kernel_initializer='he_normal')(drop1)
batc2 = BatchNormalization()(conv2)
acti2 = Activation('relu', name='acti2')(batc2)
conv2 = Conv2D(32, (2,2), padding='same', name='conv2D_4', kernel_initializer='he_normal')(acti2)

add2  = add([drop1, conv2])
pool2 = MaxPool2D(pool_size=(2,2), name='pool2')(add2)
drop2 = Dropout(0.2, name='drop2')(pool2)


conv3 = Conv2D(32, (2,2), padding='same', name='conv2D_5', kernel_initializer='he_normal')(drop2)
batc3 = BatchNormalization()(conv3)
acti3 = Activation('relu', name='acti3')(batc3)
conv3 = Conv2D(32, (2,2), padding='same', name='conv2D_6', kernel_initializer='he_normal')(acti3)

add3  = add([drop2, conv3])
pool3 = MaxPool2D(pool_size=(2,2), name='pool3')(add3)
drop3 = Dropout(0.2, name='drop3')(pool3)


flat1 = Flatten(name='flat1')(drop3)
dens1 = Dense(128, name='hidden')(flat1)
acti6 = Activation('relu', name='acti4')(dens1)
dens2 = Dense(10,activation='softmax', name='end')(acti6)

resi_model = Model(inputs=input1, outputs=dens2)

resi_model.summary()
resi_model.compile(loss='categorical_crossentropy',
                   optimizer='Adam',
                   metrics=['accuracy'])

plot_model(resi_model, to_file='./model/resi_model.png',show_shapes=True)

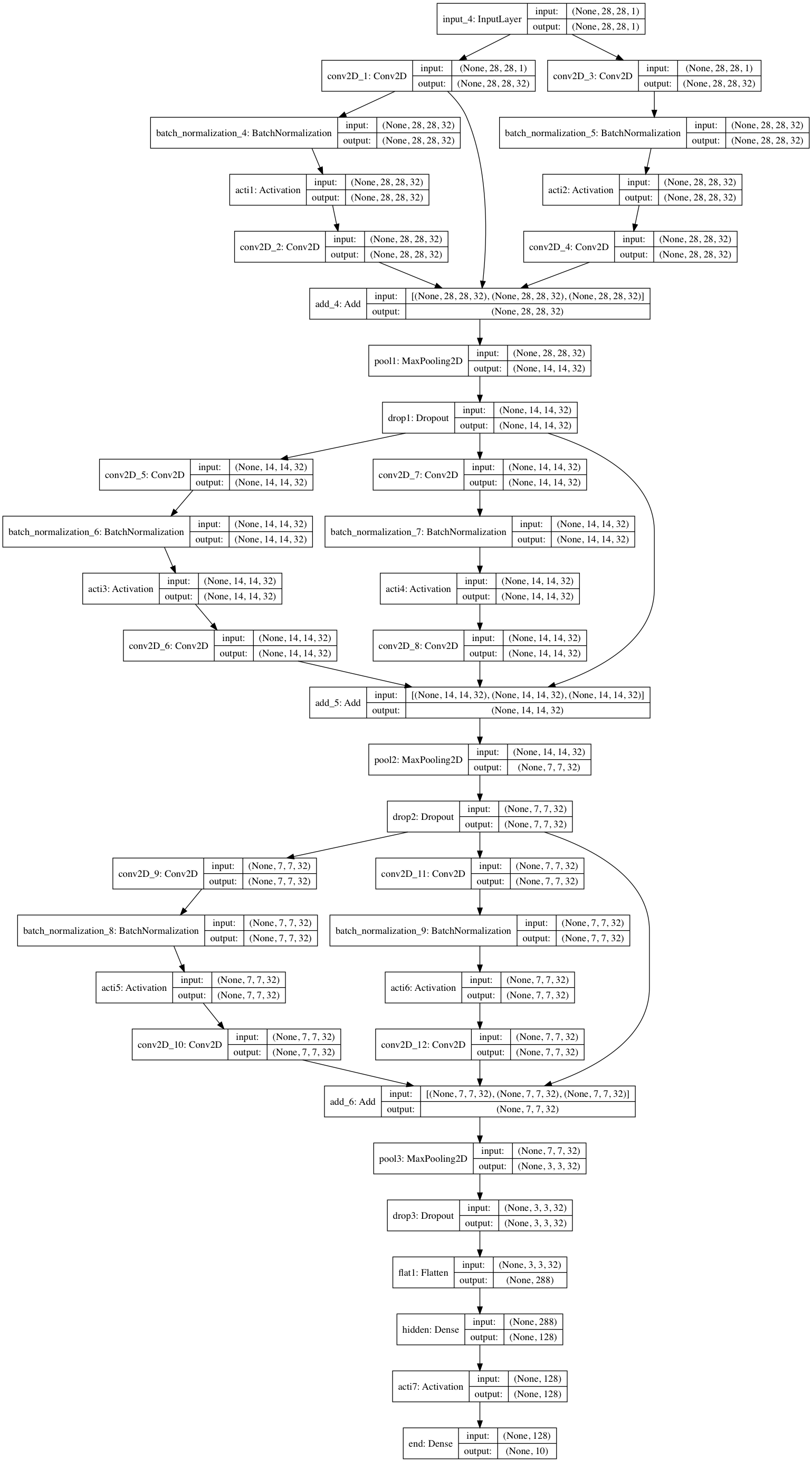
4.4.Inception + Residualモデル

InceptionとResidualを結合したモデル。

input1 = Input((28,28,1,))


#### 1st Layer #####
conv1_ = Conv2D(32, (2,2), padding='same', name='conv2D_1', kernel_initializer='he_normal')(input1)
batc1 = BatchNormalization()(conv1_)
acti1 = Activation('relu', name='acti1')(batc1)
conv1 = Conv2D(32, (2,2), padding='same', name='conv2D_2', kernel_initializer='he_normal')(acti1)

conv2_ = Conv2D(32, (3,3), padding='same', name='conv2D_3', kernel_initializer='he_normal')(input1)
batc2 = BatchNormalization()(conv2_)
acti2 = Activation('relu', name='acti2')(batc2)
conv2 = Conv2D(32, (3,3), padding='same', name='conv2D_4', kernel_initializer='he_normal')(acti2)

add1  = add([conv1_, conv1, conv2])
pool1 = MaxPool2D(pool_size=(2,2), name='pool1')(add1)
drop1 = Dropout(0.2, name='drop1')(pool1)

conv3 = Conv2D(32, (2,2), padding='same', name='conv2D_5', kernel_initializer='he_normal')(drop1)
batc3 = BatchNormalization()(conv3)
acti3 = Activation('relu', name='acti3')(batc3)
conv3 = Conv2D(32, (2,2), padding='same', name='conv2D_6', kernel_initializer='he_normal')(acti3)

conv4 = Conv2D(32, (3,3), padding='same', name='conv2D_7', kernel_initializer='he_normal')(drop1)
batc4 = BatchNormalization()(conv4)
acti4 = Activation('relu', name='acti4')(batc4)
conv4 = Conv2D(32, (3,3), padding='same', name='conv2D_8', kernel_initializer='he_normal')(acti4)


add2  = add([drop1, conv3, conv4])
pool2 = MaxPool2D(pool_size=(2,2), name='pool2')(add2)
drop2 = Dropout(0.2, name='drop2')(pool2)


conv5 = Conv2D(32, (2,2), padding='same', name='conv2D_9', kernel_initializer='he_normal')(drop2)
batc5 = BatchNormalization()(conv5)
acti5 = Activation('relu', name='acti5')(batc5)
conv5 = Conv2D(32, (2,2), padding='same', name='conv2D_10', kernel_initializer='he_normal')(acti5)

conv6 = Conv2D(32, (3,3), padding='same', name='conv2D_11', kernel_initializer='he_normal')(drop2)
batc6 = BatchNormalization()(conv6)
acti6 = Activation('relu', name='acti6')(batc6)
conv6 = Conv2D(32, (3,3), padding='same', name='conv2D_12', kernel_initializer='he_normal')(acti6)


add3  = add([drop2, conv5, conv6])
pool3 = MaxPool2D(pool_size=(2,2), name='pool3')(add3)
drop3 = Dropout(0.2, name='drop3')(pool3)


flat1 = Flatten(name='flat1')(drop3)
dens1 = Dense(128, name='hidden')(flat1)
acti7 = Activation('relu', name='acti7')(dens1)
dens2 = Dense(10,activation='softmax', name='end')(acti7)

inre_model = Model(inputs=input1, outputs=dens2)

inre_model.summary()
inre_model.compile(loss='categorical_crossentropy',
                   optimizer='Adam',
                   metrics=['accuracy'])

plot_model(inre_model, to_file='./model/inre_model.png',show_shapes=True)

5.中間層出力

それぞれのモデルで中間層出力をするモデルを定義。

layer_name = 'hidden'

### Sequential
hidden_model = Model(inputs=model.input, outputs=model.get_layer(layer_name).output)

### Inception
hidden_incep_model = Model(inputs=incep_model.input, outputs=incep_model.get_layer(layer_name).output)

### Residual
hidden_resi_model = Model(inputs=resi_model.input, outputs=resi_model.get_layer(layer_name).output)

### Inception + Residual
hidden_inre_model = Model(inputs=inre_model.input, outputs=inre_model.get_layer(layer_name).output)

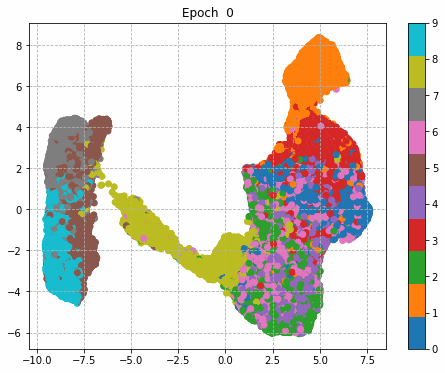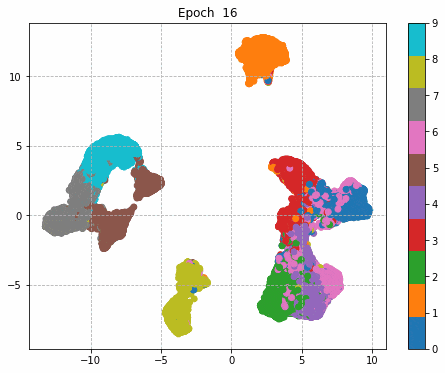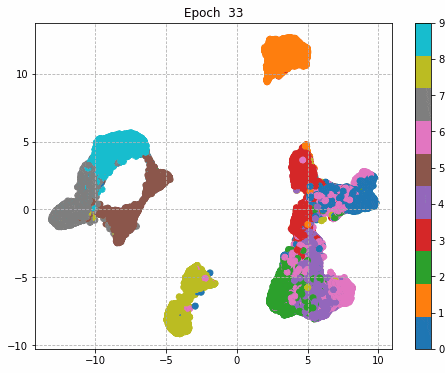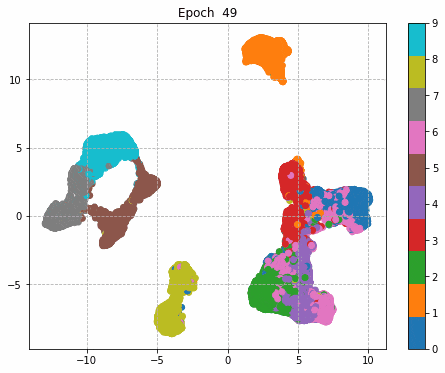
6.Epochごとに中間層を可視化

前回同様に、1epochごとに中間層を次元圧縮により低次元MAP化し、中間層における特徴量空間の可視化をしてみる。

def train(X_train, y_train, epoch, batch):

    acc1 = []
    val_acc1 = []
    loss1 = []
    val_loss1 = []

    acc2 = []
    val_acc2 = []
    loss2 = []
    val_loss2 = []    

    acc3 = []
    val_acc3 = []
    loss3 = []
    val_loss3 = []

    acc4 = []
    val_acc4 = []
    loss4 = []
    val_loss4 = []

    for i in range(0,epoch, 1):
        ############# Sequntial ################
        # パラメータ更新前の分布
        print(' ###############  Epoch ' + str(i) + ' ################')


        hidden = hidden_model.predict(X_train)
        hid_co = umap.UMAP(n_components=2, n_neighbors=40, verbose=0).fit(hidden)
        plt.figure(figsize=(8,6))
        plt.scatter(hid_co.embedding_[:,0],
                    hid_co.embedding_[:,1],
                    c = np.argmax(y_train, axis=1),
                    cmap='tab10')
        plt.colorbar()
        plt.title('Epoch  ' + str(i))
        plt.grid(linestyle='dashed')
        plt.savefig('./fmnist/fig/umap/sequential/epoch_' + '{0:03d}'.format(i) + '.png', bbox_inches='tight')
        plt.close()
        # 1epochだけ学習
        history1 = model.fit(X_train,
                             y_train,
                             epochs=1,
                             batch_size=batch,
                             validation_split=0.2,
                             verbose=1)

        # Lossなど保存
        acc1.append(history1.history['acc'])
        val_acc1.append(history1.history['val_acc'])
        loss1.append(history1.history['loss'])
        val_loss1.append(history1.history['val_loss'])

        ############# Inception ################
        # パラメータ更新前の分布
        hidden_i = hidden_incep_model.predict(X_train)
        hid_co_i = umap.UMAP(n_components=2, n_neighbors=40, verbose=0).fit(hidden_i)
        plt.figure(figsize=(8,6))
        plt.scatter(hid_co_i.embedding_[:,0],
                    hid_co_i.embedding_[:,1],
                    c = np.argmax(y_train, axis=1),
                    cmap='tab10')
        plt.colorbar()
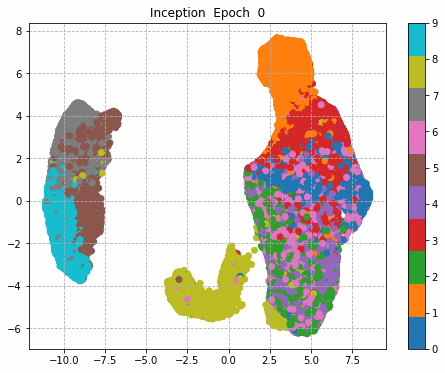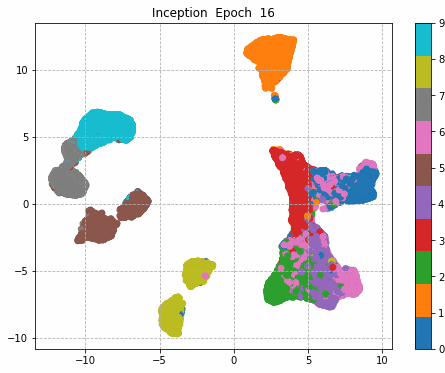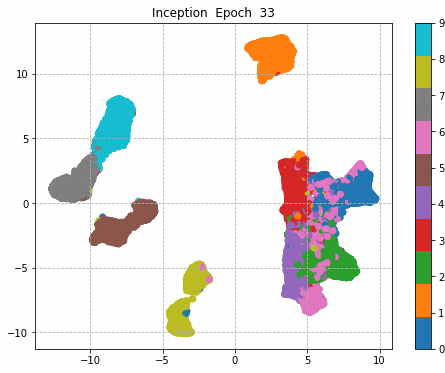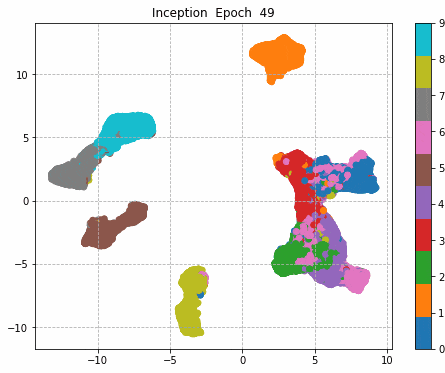
        plt.title('Inception  Epoch  ' + str(i))
        plt.grid(linestyle='dashed')
        plt.savefig('./fmnist/fig/umap/inception/epoch_' + '{0:03d}'.format(i) + '.png', bbox_inches='tight')
        plt.close()
        # 1epochだけ学習
        history2 = incep_model.fit(X_train,
                                   y_train,
                                   epochs=1,
                                   batch_size=batch,
                                   validation_split=0.2,
                                   verbose=1)

        # Lossなど保存
        acc2.append(history2.history['acc'])
        val_acc2.append(history2.history['val_acc'])
        loss2.append(history2.history['loss'])
        val_loss2.append(history2.history['val_loss'])


        ############# Residual ################
        # パラメータ更新前の分布
        hidden_r = hidden_resi_model.predict(X_train)
        hid_co_r = umap.UMAP(n_components=2, n_neighbors=40, verbose=0).fit(hidden_r)
        plt.figure(figsize=(8,6))
        plt.scatter(hid_co_r.embedding_[:,0],
                    hid_co_r.embedding_[:,1],
                    c = np.argmax(y_train, axis=1),
                    cmap='tab10')
        plt.colorbar()
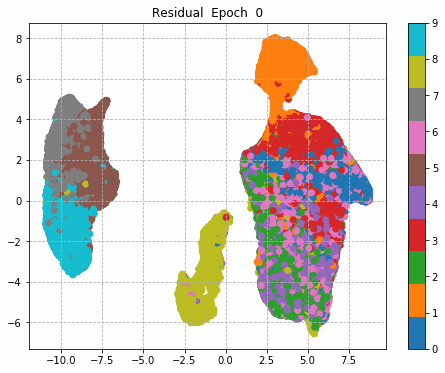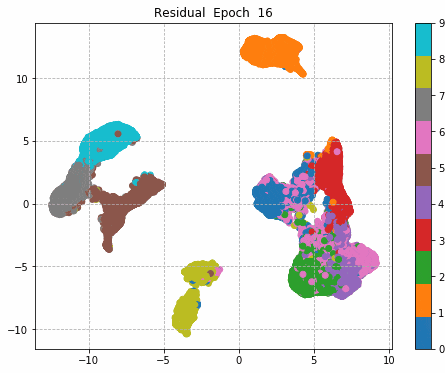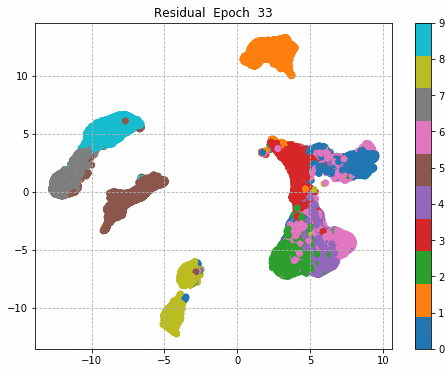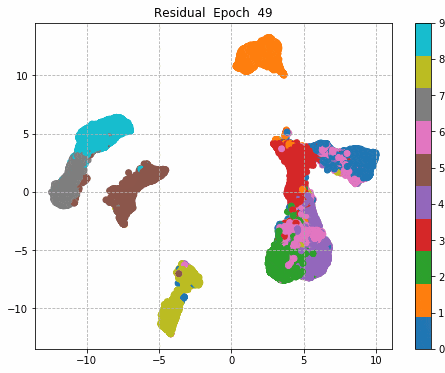
        plt.title('Residual  Epoch  ' + str(i))
        plt.grid(linestyle='dashed')
        plt.savefig('./fmnist/fig/umap/residual/epoch_' + '{0:03d}'.format(i) + '.png', bbox_inches='tight')
        plt.close()
        # 1epochだけ学習
        history3 = resi_model.fit(X_train,
                                  y_train,
                                  epochs=1,
                                  batch_size=batch,
                                  validation_split=0.2,
                                  verbose=1)

        # Lossなど保存
        acc3.append(history3.history['acc'])
        val_acc3.append(history3.history['val_acc'])
        loss3.append(history3.history['loss'])
        val_loss3.append(history3.history['val_loss'])

        ############# Inception + Residual ################
        # パラメータ更新前の分布
        hidden_ir = hidden_inre_model.predict(X_train)
        hid_co_ir = umap.UMAP(n_components=2, n_neighbors=40, verbose=0).fit(hidden_ir)
        plt.figure(figsize=(8,6))
        plt.scatter(hid_co_ir.embedding_[:,0],
                    hid_co_ir.embedding_[:,1],
                    c = np.argmax(y_train, axis=1),
                    cmap='tab10')
        plt.colorbar()
        plt.title('Inception Residual  Epoch  ' + str(i))
        plt.grid(linestyle='dashed')
        plt.savefig('./fmnist/fig/umap/incepresi/epoch_' + '{0:03d}'.format(i) + '.png', bbox_inches='tight')
        plt.close()
        # 1epochだけ学習
        history4 = inre_model.fit(X_train,
                                  y_train,
                                  epochs=1,
                                  batch_size=batch,
                                  validation_split=0.2,
                                  verbose=1)

        # Lossなど保存
        acc4.append(history4.history['acc'])
        val_acc4.append(history4.history['val_acc'])
        loss4.append(history4.history['loss'])
        val_loss4.append(history4.history['val_loss'])


        acc = np.array([acc1, acc2, acc3, acc4], dtype=float)
        val_acc = np.array([val_acc1, val_acc2, val_acc3, val_acc4], dtype=float)
        loss = np.array([loss1, loss2, loss3, loss4], dtype=float)
        val_loss = np.array([val_loss1, val_loss2, val_loss3, val_loss4], dtype=float)

        print(acc.shape)

        plt.figure(figsize=(8,3))
        plt.subplot(1,2,1)
        plt.title('Accuracy')
        plt.plot(range(i+1), acc1, c='red', marker='o', label='Seqential')
        plt.plot(range(i+1), acc2, c='forestgreen', marker='o', label='Inception')
        plt.plot(range(i+1), acc3, c='royalblue', marker='o', label='Residual')
        plt.plot(range(i+1), acc4, c='orchid', marker='o', label='Incep + Resi')
        plt.grid(linestyle='dashed')
        plt.legend(frameon=False, bbox_to_anchor=(0, -0.1), loc='upper left')

        plt.subplot(1,2,2)
        plt.title('Loss')
        plt.plot(range(i+1), loss1, c='red', marker='o', label='Seqential')
        plt.plot(range(i+1), loss2, c='forestgreen', marker='o', label='Inception')
        plt.plot(range(i+1), loss3, c='royalblue', marker='o', label='Residual')
        plt.plot(range(i+1), loss4, c='orchid', marker='o', label='Incep + Resi')
        plt.grid(linestyle='dashed')
        plt.legend(frameon=False, bbox_to_anchor=(0, -0.1), loc='upper left' )
        plt.savefig('./fmnist/fig/train/train_' + '{0:03d}'.format(i) + '.png', bbox_inches='tight')
        plt.show()

        plt.figure(figsize=(8,3))
        plt.subplot(1,2,1)
        plt.title('Valid Accuracy')
        plt.plot(range(i+1), val_acc1, c='red', marker='o', label='Seqential')
        plt.plot(range(i+1), val_acc2, c='forestgreen', marker='o', label='Inception')
        plt.plot(range(i+1), val_acc3, c='royalblue', marker='o', label='Residual')
        plt.plot(range(i+1), val_acc4, c='orchid', marker='o', label='Incep + Resi')
        plt.grid(linestyle='dashed')
        plt.legend(frameon=False, bbox_to_anchor=(0, -0.1), loc='upper left', )

        plt.subplot(1,2,2)
        plt.title('Valid Loss')
        plt.plot(range(i+1), val_loss1, c='red', marker='o', label='Seqential')
        plt.plot(range(i+1), val_loss2, c='forestgreen', marker='o', label='Inception')
        plt.plot(range(i+1), val_loss3, c='royalblue', marker='o', label='Residual')
        plt.plot(range(i+1), val_loss4, c='orchid', marker='o', label='Incep + Resi')
        plt.grid(linestyle='dashed')
        plt.legend(frameon=False, bbox_to_anchor=(0, -0.1), loc='upper left')
        plt.savefig('./fmnist/fig/valid/valid_' + '{0:03d}'.format(i) + '.png', bbox_inches='tight')
        plt.show()

    return history1, history2, history3, history4

7.学習

学習させてみる。

history1, history2, history3, history4 = train(X_train, y_train, epoch=100, batch=500)

8.学習結果

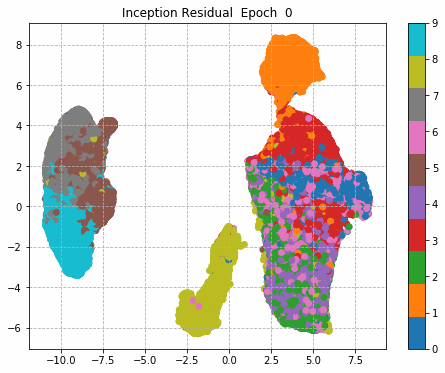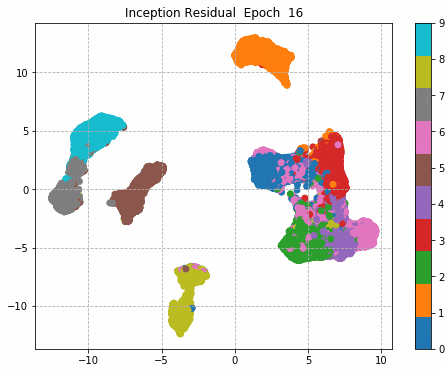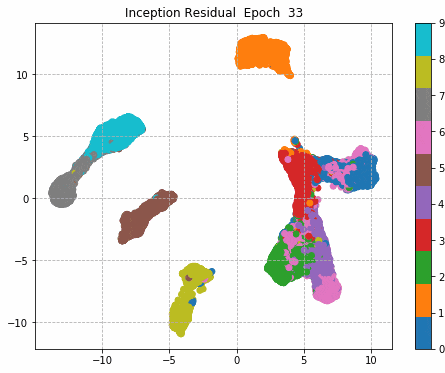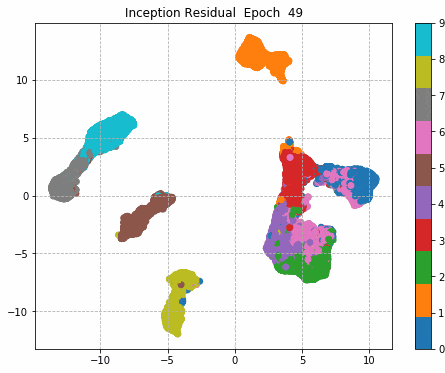
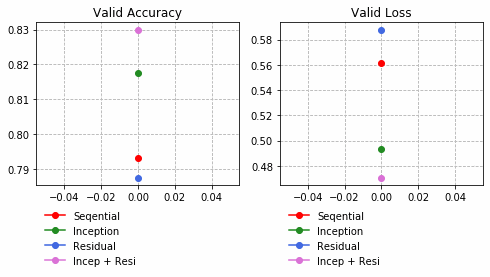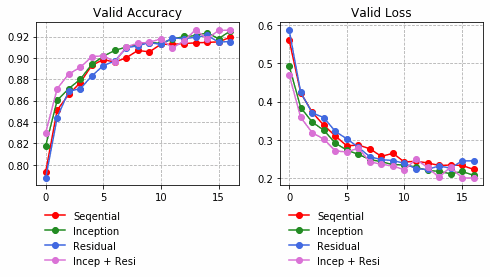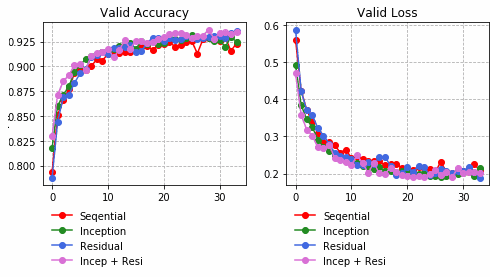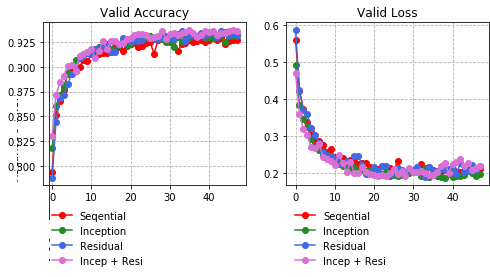
それぞれの中間層出力と学習時のLoss、Accuracy曲線を並べる。

Sequential	Inception	Residual	Inception + Residual

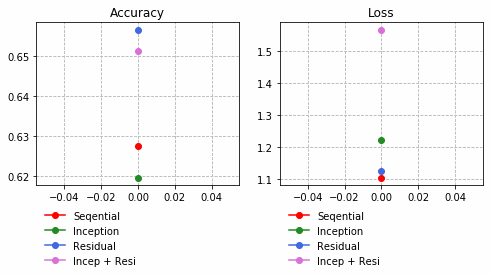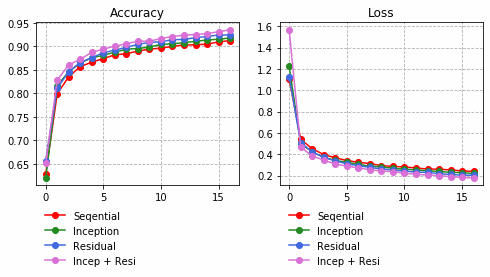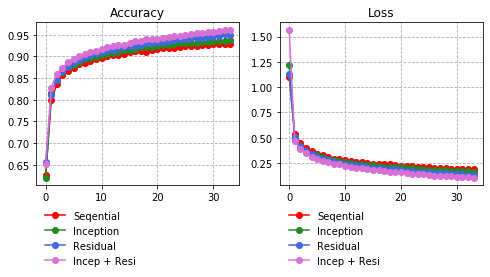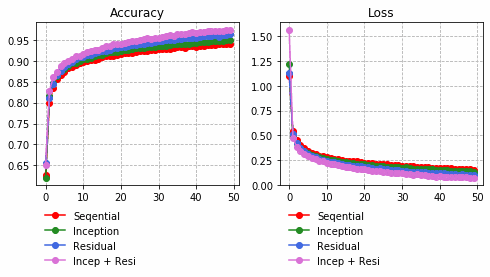
Train	Validation

9.おわりに

Inception + Residualの学習モデルが一番精度も高く、中間層の出力を見ても各クラスタがはっきりしている。
今回はそれぞれの学習モデルは3層で固定しているが、本来であればResidualはさらに深くすることも可能である上に
Inceptionもさらに横に広げることも可能である。
モデル設計に正解の形を見つけるのは難しいが、歴史的に見れば「広く、深く」することは一つのアプローチになるかもしれない。

参考

・畳み込みニューラルネットワークの最新研究動向 (〜2017)
・深層学習における学習過程の可視化を中間層出力からやってみる
・最新の次元圧縮法"UMAP"について