0.はじめに
深層学習をやっている人にとって、「AIってブラックボックスなんでしょ?」と一度は言われたことがあるのではないだろうか。今回は、AIがどのように学習しているのかを中間層を可視化することによって、少し覗いてみたい。
対象データには画像の分類を行い、簡単に分類できるMNISTで試してみる。
1.ライブラリインポート
from keras.datasets import mnist
import numpy as np
import matplotlib.pyplot as plt
from keras.models import *
from keras.layers import *
from keras.utils import *
import umap
from scipy.sparse.csgraph import connected_components
import seaborn as sns
from sklearn.metrics import *
2.データの確認
(X_train,y_train),(X_test, y_test) = mnist.load_data()
print('X_train:', X_train.shape, 'y_train:', y_train.shape)
print('X_test:', X_test.shape, 'y_test:', y_test.shape)
X_train: (60000, 28, 28) y_train: (60000,)
X_test: (10000, 28, 28) y_test: (10000,)
MNISTは、0~9までの手書き文字の28x28ピクセルのデータセットとなっている。
l = list(zip(X_train, y_train))
np.random.shuffle(l)
X_train, y_train = zip(*l)
plt.figure(figsize=(20,20))
for i in range(100):
plt.subplot(10,10,i+1)
plt.imshow(X_train[i],cmap='gray')
plt.axis('off')
plt.title(str(y_train[i]),fontsize=14)
plt.savefig('./MNIST.png', bbox_inches='tight')
plt.show()
3.学習データ化
今回のCNNモデルに入力できるようにちょっと変形させる必要がある。
# 正規化
X_train = np.array(X_train, dtype='float32')/255.
X_test = X_test/255.
# Reshape
X_train = np.reshape(X_train, (-1,28,28,1))
X_test = np.reshape(X_test, (-1,28,28,1))
# One-hot化
y_train = np_utils.to_categorical(y_train,10)
y_test = np_utils.to_categorical(y_test,10)
4.CNNモデル構築
今回は簡単にSequentialなモデルを用意。
中間層出力をあとで取り出しやすいように、各層に名前をつける。
input1 = Input((28,28,1,))
conv1 = Conv2D(32, (2,2), padding='same', name='conv2D_1', kernel_initializer='he_normal')(input1)
conv1 = Conv2D(32, (2,2), padding='same', name='conv2D_2', kernel_initializer='he_normal')(conv1)
acti1 = Activation('relu', name='acti1')(conv1)
pool1 = MaxPool2D(pool_size=(2,2), name='pool1')(acti1)
drop1 = Dropout(0.2, name='drop1')(pool1)
conv2 = Conv2D(32, (2,2), padding='same', name='conv2D_3', kernel_initializer='he_normal')(drop1)
conv2 = Conv2D(32, (2,2), padding='same', name='conv2D_4', kernel_initializer='he_normal')(conv2)
acti2 = Activation('relu', name='acti2')(conv2)
pool2 = MaxPool2D(pool_size=(2,2), name='pool2')(acti2)
drop2 = Dropout(0.2, name='drop2')(pool2)
flat1 = Flatten(name='flat1')(drop2)
dens1 = Dense(512, name='hidden')(flat1)
acti3 = Activation('relu', name='acti3')(dens1)
dens2 = Dense(10,activation='softmax', name='end')(acti3)
model = Model(inputs=input1, outputs=dens2)
4.1.中間層出力モデル
全結合層の1つ前の層から出力を取り出し、学習が進むにつれてその層の分布がどのように変化しているかを可視化する。まずは、全結合層の1つ前の層から出力を取り出す。
layer_name = 'hidden'
hidden_model = Model(inputs=model.input, outputs=model.get_layer(layer_name).output)
5. 1epochごとに学習
1epochごとに中間層出力がどのように変わるかを見るために、1epochのパラメータ更新が終わるたびに出力させてやれば良い。
def train(model, X_train, y_train, epoch, batch):
acc = []
val_acc = []
loss = []
val_loss = []
for i in range(0,epoch, 1):
# パラメータ更新前の分布
hidden = hidden_model.predict(X_train)
hid_co = umap.UMAP(n_components=2, n_neighbors=40, verbose=1).fit(hidden)
plt.figure(figsize=(8,6))
plt.scatter(hid_co.embedding_[:,0],
hid_co.embedding_[:,1],
c = np.argmax(y_train, axis=1),
cmap='tab10')
plt.colorbar()
plt.title('Epoch ' + str(i))
plt.savefig('./fig/epoch_' + '{0:03d}'.format(i) + '.png', bbox_inches='tight')
plt.close()
# 1epochだけ学習
history = model.fit(X_train, y_train, epochs=1, batch_size=batch, validation_split=0.2, verbose=1)
# Lossなど保存
acc.append(history.history['acc'])
val_acc.append(history.history['val_acc'])
loss.append(history.history['loss'])
val_loss.append(history.history['val_loss'])
return acc, val_acc, loss, val_loss
実際に学習させてみる。
acc, val_acc, loss, val_loss = train(model, X_train, y_train, epoch=100, batch=100)
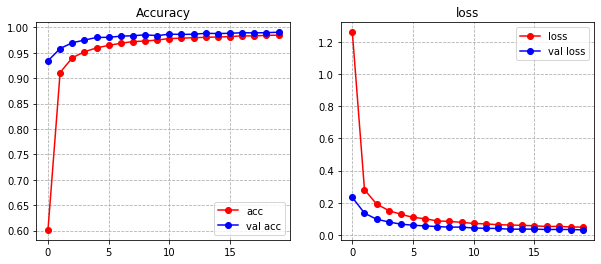
学習した結果のAccuracy曲線と、Loss曲線を並べてみる。
plt.figure(figsize=(10,4))
plt.subplot(1,2,1)
plt.plot(range(len(acc)),acc, 'ro-', label='acc')
plt.plot(range(len(val_acc)),val_acc, 'bo-', label='val acc')
plt.grid(linestyle='dashed')
plt.legend()
plt.title('Accuracy')
plt.subplot(1,2,2)
plt.plot(range(len(acc)),loss, 'ro-', label='loss')
plt.plot(range(len(val_acc)),val_loss, 'bo-', label='val loss')
plt.grid(linestyle='dashed')
plt.legend()
plt.title('loss')
plt.savefig('./acc_loss.png', bbox_inches='tight')
plt.show()
6.中間層の出力
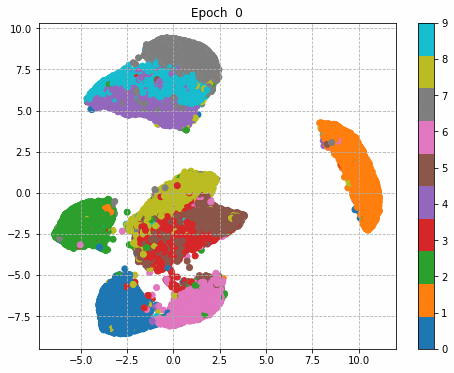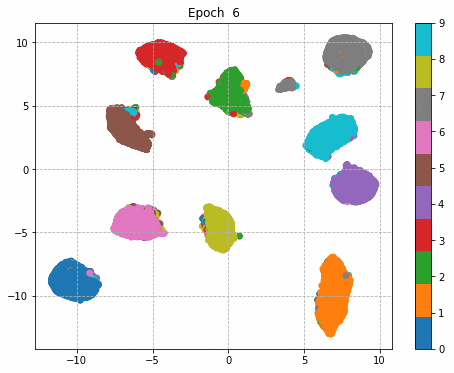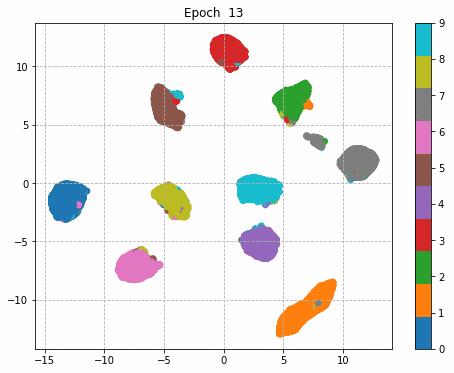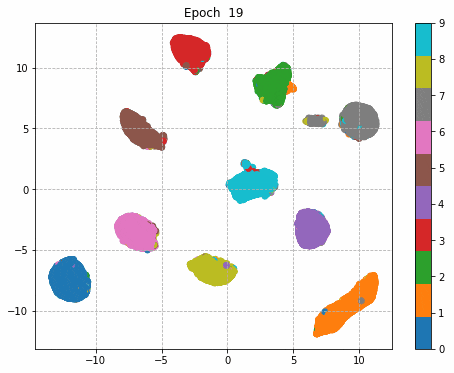
中間層で出力した結果をgifのアニメーションに変形。
from PIL import Image
import glob
files = sorted(glob.glob('./fig/*.png'))
images = list(map(lambda file: Image.open(file), files))
images[0].save('mnist.gif', save_all=True, append_images=images[1:], duration=500, loop=0)
学習初期は、大きな3つくらいの塊に分かれているが、学習が進むにつれてそれぞれの数字ごとに塊を持つような分布へと変貌している。
すごく大げさに極端に言えばDeep Learningでは学習が進むにつれこのような分布表現を獲得していると言えるのかもしれない。
これを基に予測をしてみる。
7.予測
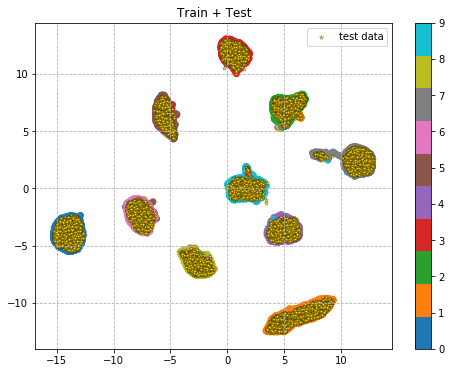
まずは、学習によって得られた分布上にテストデータを並べてみる。
# Trainデータで分布作成
hidden = hidden_model.predict(X_train, verbose=1)
hid_co = umap.UMAP(n_components=2, n_neighbors=40, verbose=0).fit(hidden)
# Testデータ
pred_hid = hidden_model.predict(X_test, verbose=1)
pred_hid = hid_co.transform(pred_hid)
plt.figure(figsize=(8,6))
plt.scatter(hid_co.embedding_[:,0],
hid_co.embedding_[:,1],
c = np.argmax(y_train, axis=1),
cmap='tab10')
plt.colorbar()
plt.scatter(pred_hid[:,0],
pred_hid[:,1],
c = 'gold',
marker='*',
s=20,
edgecolors='black',
linewidths=0.2,
label='test data')
plt.title('Train + Test')
plt.legend()
plt.grid(linestyle='dashed')
plt.savefig('./train_test_dist' + '.png', bbox_inches='tight')
plt.show()
だいたいそれぞれの分布にデータが置かれており、予測結果も精度高く分類ができそう。
実際に予測してみる。
pred = model.predict(X_test)
pred_class = np.argmax(pred, axis=1)
true_class = np.argmax(y_test, axis=1)
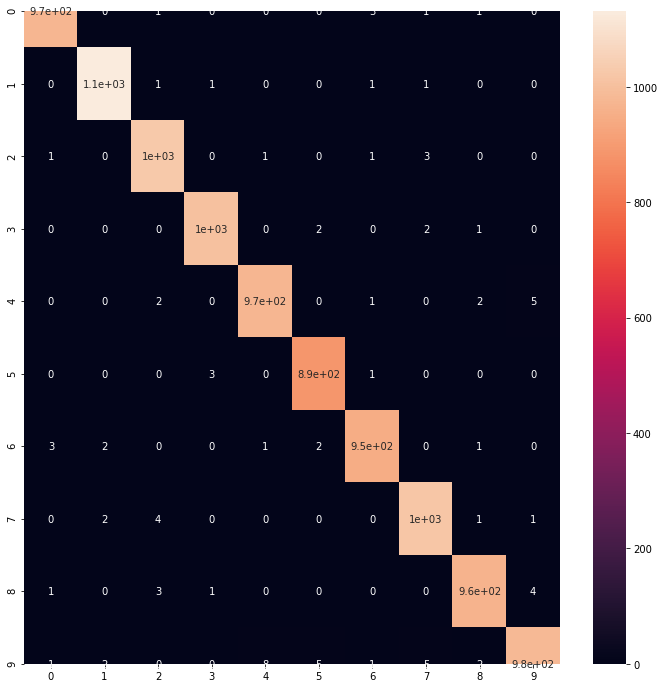
cmx = confusion_matrix(true_class, pred_class)
plt.figure(figsize=(12,12))
sns.heatmap(cmx, annot=True)
plt.savefig('./cnn_predict.png', bbox_inches='tight')
plt.show()
print("Accuracy: {0}".format(accuracy_score(true_class, pred_class)))
Accuracy: 0.9915
事前に分布で確認した通り、分類精度はかなり高く**精度 99.1%**であった。
8.おわりに
今回、中間層出力を1epochごとに出力して、学習過程でどのような分布表現を獲得しているかを可視化した。
これを「AIってブラックボックスなんでしょ?」と言ってくる思考停止おじさんに向かって、見せることで判断根拠の一つになるかもしれない。
実際は、どのようなデータを分類する上で苦手としているんだろうとかを可視化する上で使われると精度向上に役立てると思います。