最新の次元圧縮法"UMAP"について

はじめに

こんにちは！
皆さん次元圧縮手法といえばどのようなものを思いつきますか？
PCA,Isomap,t-SNEなどでしょう。
こちらの記事が大変よくまとめられています。
高次元データの次元削減および2次元プロット手法

今日ご紹介したいのはUMAPという次元削減手法です。
論文がarXivに2018年2月9日に上がったばかりの手法です。
なんと、t-SNEと同程度の次元削減を数倍の速さでできてしまいます。
論文については、リーマン幾何学と代数トポロジーを背景にされているようなのでじっくり読み込んで後日まとめたいと思います。
興味のある方はこちらからどうぞ
UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction

使ってみよう

なんと早くもライブラリが公開されています。
ひとまず使ってみましょう。

インストール

pip3 install umap-learn

使い方は基本的にscikit-learnと同じです。
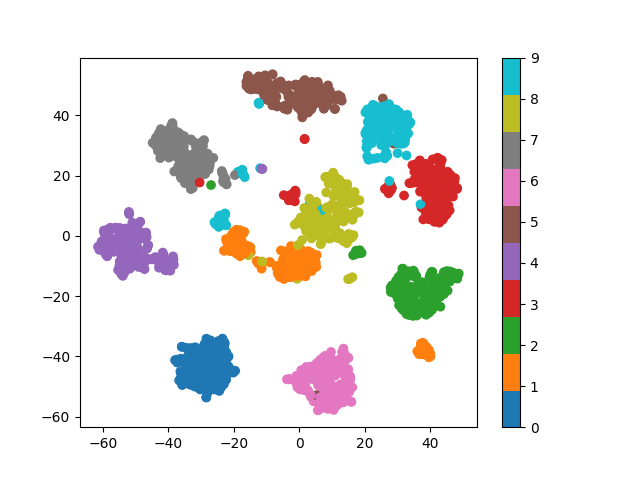
MNISTを使ってt-SNEと比較してみました。
t-SNEによるイケてる次元圧縮&可視化

公式GitHubには書いてあるのですが、

from scipy.sparse.csgraph import connected_components

を書かないとエラーが出てしまいます。

reduction.py

import umap
from sklearn.datasets import load_digits
from scipy.sparse.csgraph import connected_components
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from sklearn.manifold import TSNE
import time

def main():
    digits = load_digits()
    digits.target = [float(digits.target[i]) for i in range(len(digits.target))]

    # UMAP
    start_time = time.time()
    embedding = umap.UMAP().fit_transform(digits.data)
    interval = time.time() - start_time
    plt.scatter(embedding[:,0],embedding[:,1],c=digits.target,cmap=cm.tab10)
    plt.colorbar()
    plt.savefig('umap.png')

    # t-SNE
    plt.clf()
    start_time2 = time.time()
    tsne_model = TSNE(n_components=2)
    tsne = tsne_model.fit_transform(digits.data)
    interval2 = time.time() - start_time2
    plt.scatter(tsne[:,0],tsne[:,1],c=digits.target,cmap=cm.tab10)
    plt.colorbar()
    plt.savefig('tsne.png')

    print('umap : {}s'.format(interval))
    print('tsne : {}s'.format(interval2))

if __name__ == "__main__":
    main()

出力結果がこちらです。
t-SNE

UMAP

UMAPの方がよりはっきり分かれている印象ですね。

驚くべきは実行時間の差です。

umap : 5.383596897125244s
tsne : 34.21198582649231s

なんと僕の出力結果では６倍以上の速度を計測しました。

大変興味深いですね。
数学の復習をしながら論文を読んで、解説記事を更新したいと思います。