こんにちは,クラスタリング&可視化おじさんです.
本記事は「機械学習と数学」Advent Calendar14日目です.
(ちなみにAdvent Calendar初投稿です.よろしくお願いします)
はじめに
データ分析とか機械学習やられてる方は高次元データの次元削減と可視化よくやりますよね.
この分野の代表選手といえばPCA(主成分分析)とかMDS(多次元尺度構成法)ですが,
これらの線形変換系手法には以下の問題があります.
- 高次元空間上で非線形構造を持っているデータに対しては適切な低次元表現が得られない
- 「類似するものを近くに配置する」ことよりも「類似しないものを遠くに配置する」ことを優先するようアルゴリズムが働く
1.に関して,よく例に出されるのがSwiss roll dataset(下図)のようなヤツですね.
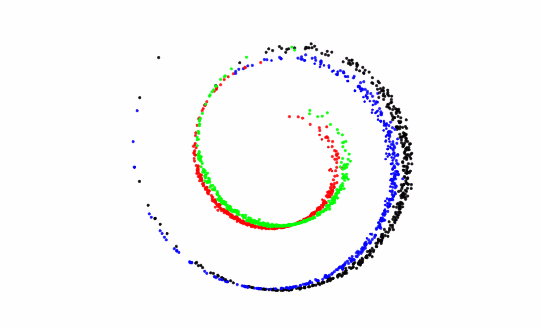
PCAはデータが多次元正規分布に従うことを仮定しているので,
その仮定から外れる非線形データに対してはうまく働かないという問題があります.
2.に関しては,「大域的なクラスタ構造は信頼できるが,局所的なデータ間の関係はあまり信頼できない」というマップが得られることになります.
可視化などで類似度の近いデータを探す,といった用途に使おうとした時にこれは問題ですね.
これらの問題に対処すべく,非線形な変換を行う次元圧縮の手法がいろいろ提案されていますが,
今回はその中で(比較的)新しい手法であるt-SNEの紹介をしてみようと思います.
理論の説明をした後にライブラリ使用例の紹介をします.
t-SNE(t-distributed Stochastic Neighbor Embedding)とは?
概要
可視化を主な目的とした次元削減の問題は,「高次元空間上の類似度をよく表現する低次元空間の類似度を推定する」問題だと考えられるわけですが,
t-SNEはこれを確率分布に基づくアプローチで解くものです.
具体的には,(1)高次元空間上の類似度 と (2)低次元空間上の類似度 をそれぞれ確率分布$p_{ij}$と$q_{ij}$で表現して,$p_{ij}$と$q_{ij}$を最小化するように確率分布のパラメータを最適化します.
t-SNEの以前にSNEという手法が提案されており,SNEでは$p$,$q$ともに正規分布でモデル化していました.
対してt-SNEでは以下の変更が加えられています.
- $p_{ij}$,$q_{ij}$を条件付き確率 -> 同時確率に変更
- $q_{ij}$をStudentのt-分布でモデル化
上記2点の変更により最適化を容易にした,という位置づけです.
t-SNEのモデル
まず,高次元空間上の類似度を以下の正規分布$p_{ij}$で表現します.
p_{ij} = \frac{ p_{j|i} + p_{i|j} }{2n}
p_{j|i} = \frac{ \exp(-||x_{i}-x_{j}||^{2}/2\sigma_{i}^{2}) }{ \sum_{k \neq i}\exp(-||x_{i}-x_{k}||^{2}/2\sigma_{i}^{2})}
ここで,$p_{j|i}$は$x_{i}$から見た$x_{j}$の類似度の条件付き確率を表します.
$n$は観測データ点数を表します.
$p_{j|i}$と$p_{i|j}$を平均することで対称化して同時確率$p_{ij}$に変換しているわけですね.
さらに,低次元空間上の類似度を以下のStudentのt-分布(自由度1)で表現します.
q_{ij} = \frac{1 + ||y_{i}-y_{j}||^2)^{-1}}{\sum_{k \neq l}(1 + ||y_{k}-y_{l}||^{2})^{-1}}
このt-分布は下図のように正規分布と比べて裾野の重みが高いことが特徴です.

推定すべきパラメータは$q_{ij}$の${y_{i},y_{j}}$ですね.
$p_{ij}$の$\sigma_{i}$も未知パラメータですが,こちらはユーザが指定するperplexityという値により決定されます.
Perp(P_{i}) = 2^{H(P_{i})}
$H$は以下で定義されるエントロピーです.
H(P_{i}) = \sum_{j}p_{j|i}\log_{2}p_{j|i}
$Perp(P_{i})$が指定した値になるように$\sigma_{i}$を決定します.
この値で近傍のクラスタ構造が定まるので,$Perp(P_{i})$に適切な値を設定することは非常に重要です.
実用上は$5~50$の間に設定されることが多いようです.
で,$p_{ij}$と$q_{ij}$が近くなるようパラメータを最適化するわけですが,
t-SNEではみんな大好きKullback-Leibler divergence(KLD)をコスト関数として,勾配法で最適化します.
全てのデータ点に対する$p$の集合$P$と$q$の集合$Q$に対するKLDは以下で定義されます.
C = KL(P, Q) = \sum_{i}\sum_{j}p_{ij}\log \frac{ p_{ij} }{ q_{ij} }
$C$の勾配は以下で計算できます.
\frac{\delta C}{\delta y_{i}} = 4\sum_{j}(p_{ij}-q_{ij})(y_{i}-y_{j})(1+||y_{i}-y_{j}||^{2})^{-1}
以下の更新式を用いて$Y=(y_{1},y_{2},...,y_{n})$を更新していきます.
Y^{(t)} = Y^{(t-1)} + \eta \frac{\delta C}{\delta Y}+\alpha(t)(Y^{(t-1)}-Y^{(t-2)})
t-SNEの欠点
- うまくいくことが保証されているのは2or3次元への圧縮のみ
- 局所構造が次元の呪いの影響を受けやすい
- 最適化アルゴリズムの収束性が保証されていない
1については,低次元側の類似度に裾野の広い(=端の確率値が高い)t-分布を用いたことの副作用で,次元数が大きくなるとデータの局所的な構造を維持できなくなるようです.
必ず失敗するというわけではないですが,次元数4以上の場合は結果は保証されませんということですね.
基本的には可視化のための手法ということで,通常は2or3次元への圧縮へ用いるべきかと思います.
2については,t-SNEの次元圧縮は局所的なデータ間の特性に基づいて行われるので,高次元でかつ分散の大きいデータに対しては
類似度を正規分布でモデル化している(=ユークリッド距離で距離を測っている)ことが厳密には正しくなくなる,ということのようです.
この問題を緩和する手段としては,データをいったんいくつかの非線形層をもつモデル(AutoEncoderなど)でのデータ表現に変換して
その空間上でt-SNEを実行する手法が提案されています.
3については,勾配法の宿命ではありますが,凸最適化などの収束が保証されているアルゴリズムに比べると
最適化パラメータの調整が必要になったりと少々ダーティなアルゴリズムですし,ちゃんと収束しているのかの検証は必要になります.
初期値を変えながら複数回実行して最もコスト関数が小さくなった試行を選ぶ,などすれば
「実は収束してませんでした」エンドを回避できる可能性が高くなるかもしれません.
使ってみるには
ライブラリがいくつか公開されています(他にもあるかも).
Pythonで動かすならscikit-learnがお手軽ではありますが,速度が遅い,デフォルトの学習率が高い,などいくつか問題があるようです.
(使ったことないので間違っていたらすみません)
僕はpython-bhtsneを使っています.
こちらはこちらでmax_iterationが指定できないという(結構痛い)欠点がありますが…
(max_iterationデフォルト値の100はいくらなんでも少なすぎると思う…)
なのでちょっと改造してmax_iterationをAPIで指定できるようにしたバージョンを使っています.ご参考までに.
動かしてみる
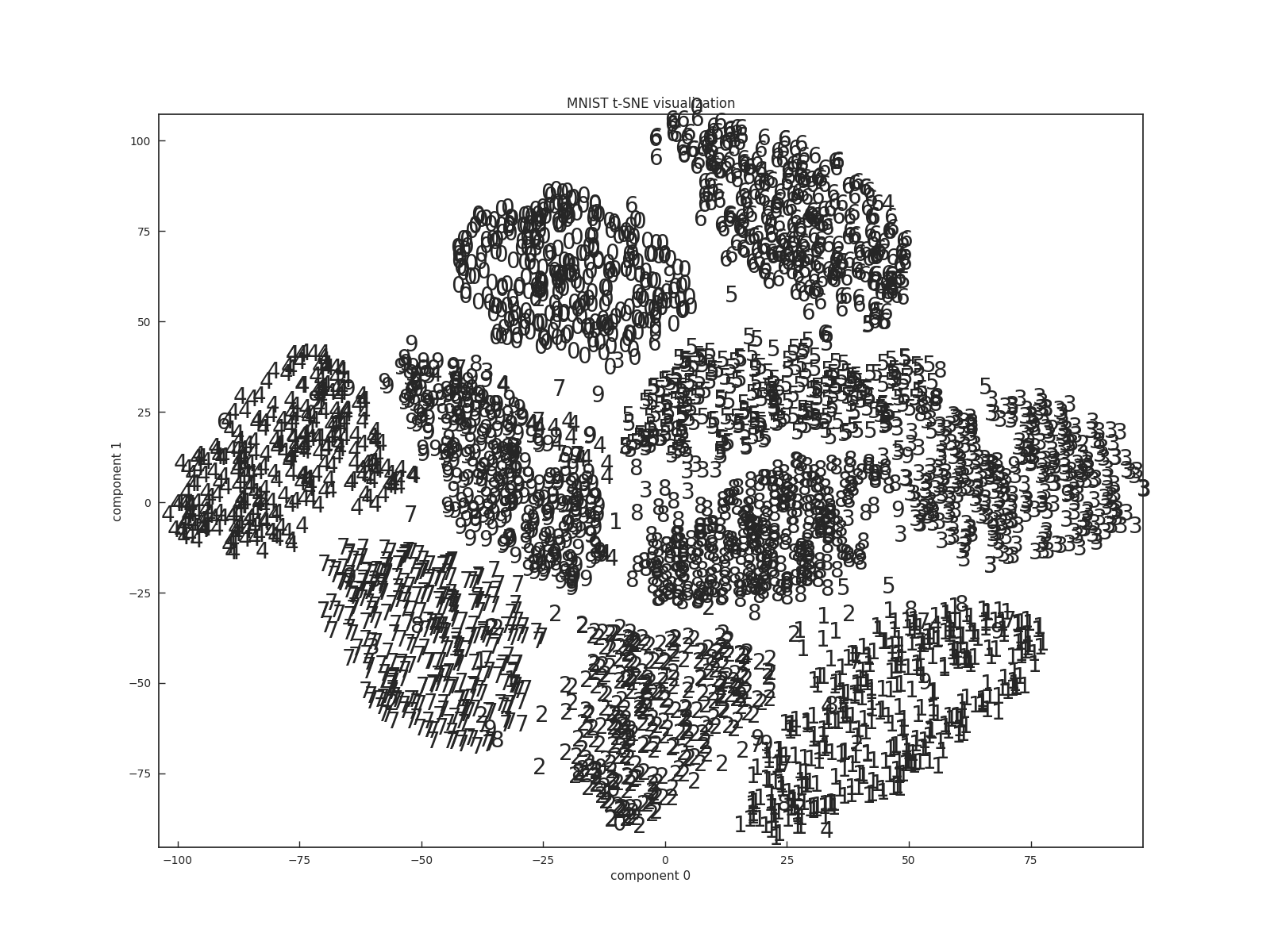
MNISTをt-SNEで可視化してみました.
# !/usr/bin/env python
# -*- coding: utf-8 -*-
"""
@package
@brief
@author stfate
"""
import scipy as sp
from sklearn.datasets import fetch_mldata
import sklearn.base
import bhtsne
import matplotlib.pyplot as plot
class BHTSNE(sklearn.base.BaseEstimator, sklearn.base.TransformerMixin):
def __init__(self, dimensions=2, perplexity=30.0, theta=0.5, rand_seed=-1, max_iter=100):
self.dimensions = dimensions
self.perplexity = perplexity
self.theta = theta
self.rand_seed = rand_seed
self.max_iter = max_iter
def fit_transform(self, X):
return bhtsne.tsne(
X.astype(sp.float64),
dimensions=self.dimensions,
perplexity=self.perplexity,
theta=self.theta,
rand_seed=self.rand_seed,
max_iter=self.max_iter
)
if __name__ == "__main__":
mnist = fetch_mldata("MNIST original", data_home="./")
mnist_data = mnist["data"]
mnist_labels = mnist["target"]
bhtsne = BHTSNE(dimensions=2, perplexity=30.0, theta=0.5, rand_seed=-1, max_iter=10000)
mnist_tsne = bhtsne.fit_transform(mnist_data)
xmin = mnist_tsne[:,0].min()
xmax = mnist_tsne[:,0].max()
ymin = mnist_tsne[:,1].min()
ymax = mnist_tsne[:,1].max()
plot.figure( figsize=(16,12) )
for _y,_label in zip(mnist_tsne[::20],mnist_labels[::20]):
plot.text(_y[0], _y[1], _label)
plot.axis([xmin,xmax,ymin,ymax])
plot.xlabel("component 0")
plot.ylabel("component 1")
plot.title("MNIST t-SNE visualization")
plot.savefig("mnist_tsne.png")
実行結果が下図になります.
少しゴミが混じっていたりはしますが,概ね数字ごとにクラスタが形成されていますね.
仕事でも使っていたりしますが,PCAやMDSではよくわからないマップしか得られていなかったのが
t-SNEだと人間の直感に合うクラスタ構造が得られたりするので,線形変換系の手法だとうまくいかない!という時に使ってみるといいかもしれません.
まとめ
PCAやMDSが不得手な非線形構造をもつデータの可視化にt-SNEは強力な手法です.(ただし2or3次元に限る)
高次元データの可視化に悩んでいる方はぜひお試しあれ.
参考文献
2019.03.16追記
t-SNEをCUDAで高速化するt-SNE-CUDAの記事も書きましたので,そちらもご参考に.