Pythonで〇×ゲームのAIを一から作成する　その104　木構造のデータに対する幅優先と深さ優先アルゴリズムによる繰り返し処理

Last updated at 2024-08-08Posted at 2024-08-04

目次と前回の記事

これまでに作成したモジュール

以下のリンクから、これまでに作成したモジュールを見ることができます。

リンク	説明
marubatsu.py	Marubatsu、Marubatsu_GUI クラスの定義
ai.py	AI に関する関数
util.py	ユーティリティ関数の定義。現在は `gui_play` のみ定義されている
tree.py	ゲーム木に関する Node、Mbtree クラスの定義
gui.py	GUI に関する処理を行う基底クラスとなる GUI クラスの定義

ルールベースの AI の一覧については、下記の記事を参照して下さい。

木構造のデータに対する繰り返し処理

前回の記事では分岐する繰り返し処理の例として、複数の項で表される漸化式をトップダウンな再帰呼び出しで記述する場合を説明しました。

今回の記事では、分岐が必須 となる繰り返し処理の例として、木構造のデータに対する繰り返し処理について説明します。

その前に、木構造についていくつかの補足説明をします。

木構造の例

これまでの記事では木構造の具体例として〇×ゲームのゲーム木を取り上げてきましたが、木構造 で表されるデータは 世の中で広く使われています。

例えば、学校の生徒は下記のような木構造で表現することができます。

ルートノードは学校そのものを表し、その子ノードは学年を表す
学年を表すノードの子ノードはその学年のクラスを表す
クラスを表すノードの子ノードは、そのクラスの生徒を表す

この木構造を図で表すと以下のようになります。なお、図が大きくなりすぎるので、2 年の子ノードや、2 組の兄弟ノードなどは省略しています。

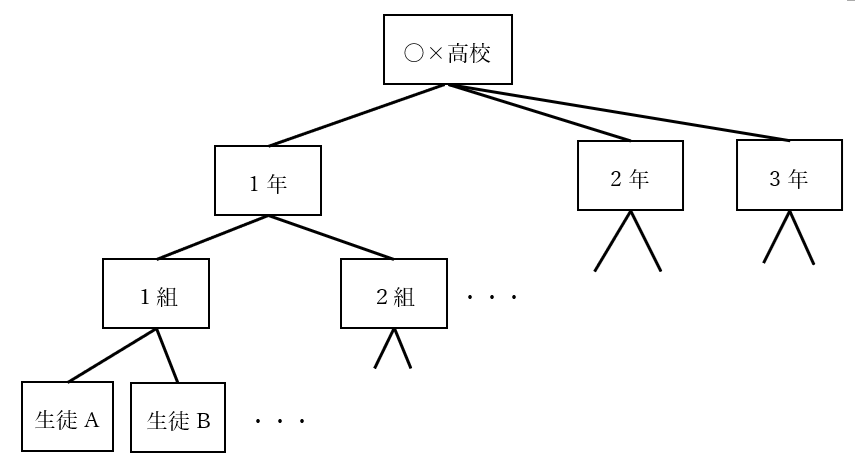
他にも、家の住所、本の章や節など、様々なデータが木構造で表現できます。

木構造では、データを学年、クラス、クラスの生徒のように、大きな分類から少しずつ細かい分類にわけてデータを 階層的に表現 します。そのため、木構造は 階層構造 を表します。

実は、〇×ゲームのゲーム木よりはるか前に、この記事では木構造で表現されるデータを扱ってきました。その一つが、〇×ゲームのゲーム盤のデータです。

下図のように〇×ゲームのゲーム盤を表すと、木構造には見えないかもしれません。どのようにすれば木構造で表現できるかについて少し考えてみて下さい。

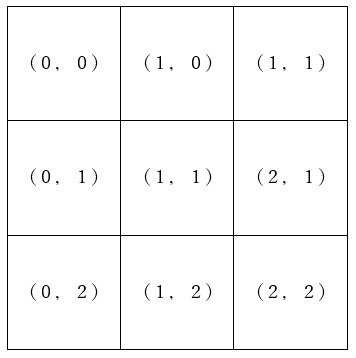
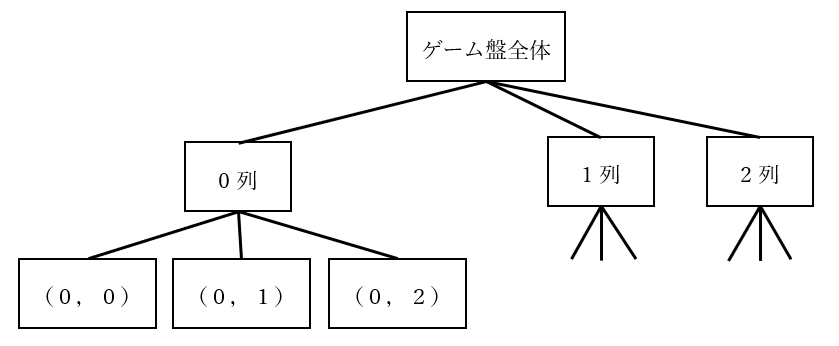
〇×ゲームのゲーム盤は、下記のような木構造で表現することができます。

ルートノードはゲーム盤そのものを表し、その子ノードは列のデータを表す
列のノードの子ノードは、その列のマスを表す

この木構造を図で表すと以下のようになります。

木構造の表現方法

〇×ゲームのゲーム盤は、Marubatsu クラスのインスタンスの board 属性に代入されています。mb に Marubatsu クラスのインスタンスが代入されている場合は、それぞれの深さのノードは下記の表のように表現されます。

	対応するノード
`mb.board`	深さ 0 のルートノード
`mb.board[x]`	深さ 1 のノード
`mb.board[x][y]`	深さ 2 のノード

上記の表から、先頭から i 番目の添え字 が、木構造の ノードの深さに対応 します。

board には 2 次元配列を表す list が代入されていますが、複数のデータを扱うことができる dict も同様の性質を持つので、list や dict で表されるデータは、インデックスやキー をノードが表す データ とし、その 要素を子ノード とする 木構造のノード と考えることができます。従って、list と dict を組み合わせる ことで 木構造を表現 することができます。

インデックスやキー以外 のデータを、ノードのデータ とした木構造を表現する場合は、Mbtree クラスのように、ノードをオブジェクトで表し、その属性に ノードのデータ と、子ノードの一覧を代入 する必要があります。

ネットワーク構造との違い

木構造は、以下のような性質を持つデータ構造です。

ノードとノードの間に、親ノードと子ノードという、方向の関係 がある
ルートノードが 1 つだけ存在 する。別の言い方で言うと、ルートノード以外のノードの親ノードを辿っていくと、必ず一つのルートノードにたどり着く
ノードの 子ノードを辿って行く と、必ず子ノードが存在しない リーフノード にたどり着く。別の言い方で言うと、ノードの子ノードを辿った際に、元のノードにたどり着くような、ループが存在しない

上記の性質を満たさないような場合は、木構造ではなく、ネットワーク構造やグラフ構造と呼びます¹。ネットワーク構造に対する繰り返し処理では、ループがある場合 は 無限ループが発生しないように注意 してプログラムを記述する必要がありますが、木構造にはループは存在しない のでそのことを注意しなくても良いという利点があります。なお、ネットワーク構造に対する繰り返し処理は複雑になるので、今回の記事では取り上げません。

分岐する繰り返し処理を行うアルゴリズム

分岐する繰り返し処理 を行うアルゴリズムには、幅優先アルゴリズム と 深さ優先アルゴリズム があります。またそれぞれのアルゴリズムは ボトムアップ な繰り返し処理と、トップダウン な繰り返し処理に分類することができます。

これまでの記事では〇×ゲームのゲーム木の作成などで、既に木構造に対する繰り返し処理を記述しましたが、その性質までは説明していませんでした。そこで、今回の記事では、これまで記述してきたプログラムを踏まえながら、それぞれの性質について説明します。

なお、今回の記事の説明はすべて木構造のデータに対する繰り返し処理です。

幅優先アルゴリズムによる繰り返し処理

ボトムアップな繰り返し処理による実装

木構造に対する 幅優先アルゴリズム による ボトムアップ な繰り返し処理は、以下のようなアルゴリズムで行います。ただし、次に処理を行う木の深さを d で表すことにします。

d を 0 とする
深さ d の全てのノードに対する処理を行う。ノードが存在しない場合は処理を終了する
d に 1 を足して手順 2 へ戻る

while 文による実装

これまでの記事では、〇×ゲームのゲーム木を幅優先アルゴリズムで作成する Mbtree クラスの下記の create_tree_by_bf で while 文を使ってその処理を記述しました。

 1  def create_tree_by_bf(self):
 2      # 深さ 0 のノードを、子ノードを作成するノードのリストに登録する
 3      nodelist = [self.root]
 4      depth = 0
 5      # 各深さのノードのリストを記録する変数を初期化する
 6      self.nodelist_by_depth = [ nodelist ]
 7    
 8      # 深さ depth のノードのリストが空になるまで繰り返し処理を行う
 9      while len(nodelist) > 0:
10           childnodelist = [] 
11           for node in nodelist:
12               if node.mb.status == Marubatsu.PLAYING:
13                   node.calc_children()
14                   childnodelist += node.children
15           self.nodelist_by_depth.append(childnodelist)
16           nodelist = childnodelist
17           depth += 1
略

上記のアルゴリズムで処理を行うためには、以下のデータを記録する必要があります。

深さ d の値
深さ d のノードの一覧
次の深さのノードの一覧

また、上記のデータに対して、下記の処理を記述する必要があります。（）の中に記述した内容は、上記のプログラムで対応する値を記録する変数と、処理が記述されている行数です

深さ d の値（depth）
- 初期化処理：0 で初期化する（4 行目）
- 更新処理：深さ d のノードの一覧に対する処理の最後で、次に処理を行うノードの深さを表すように 1 を加算する（17 行目）
深さ d のノードの一覧（nodelist）
- 初期化処理：ルートノードを要素とする list で初期化する（3 行目）
- データの利用：while 文で要素を一つずつ取り出し、深さ d のノードの一覧に対する処理を行う（9 ~ 17 行目）
- 更新処理：深さ d のノードの一覧に対する処理の最後で、次に処理を行う、次の深さのノードの一覧を代入する（16 行目）
次の深さのノードの一覧（childnodelist）
- 初期化処理：深さ d のノードの一覧に対する処理を開始する際に空の list で初期化する（10 行目）
- 更新処理：深さ d のノードの処理を行った後で、そのノードの子ノードの一覧を追加する（14 行目）

なお、上記のプログラムの 6 行目と 15 行目で nodelist_by_depth に 深さ d のノードの一覧を記録 する処理は、ゲーム木を作成する際に 必要のない処理 で、そのデータがあると、ゲーム木を作成した後で便利だという理由で用意したものです。また、上記のプログラムの「略」以降では、各深さのノードの数を数える処理など を行っていますが、それらの処理も、ゲーム木を作成する際に 必要となる処理ではありません。

実は、幅優先アルゴリズムによるボトムアップな繰り返し処理の最中に、ノードの深さを表す情報が必要ない場合 は、深さ d を記録する必要はありません。上記のプログラムでも、depth は 4 行目と 11 行目以外では使われていないので、4 行目と 11 行目を削除してもプログラムは正しく動作します。

再帰呼び出しによる実装

以前の記事で説明したように、ボトムアップな再帰呼び出しでは、処理に必要なデータを仮引数で受け取り ます。create_tree_by_bf の場合は、処理を行う深さの ノードの一覧のデータが必要になる ので、そのデータを代入する仮引数 nodelist を追加することにします。また、そのデフォルト値を None し、None の場合はルートノードを要素とする list を代入する処理を記述することで、最初に create_tree_by_bf を呼び出した際に、nodelist に対応する実引数を記述しなくても良いように工夫します。

それ以降の処理の修正の基本的な考え方は以前の記事で説明した、for 文で定義した fib_by_f を fib_by_br に修正した方法と同じです。なお、このプログラムでは、depth や node_list_by_depth などの、ゲーム木の作成に必要のない処理は削除しました。

4 行目：仮引数 depth を削除し、デフォルト値を None とする仮引数 nodelist を追加
5、6 行目：nodelist が None の場合に、nodelist をルートノードを要素とする list で初期化する
8 行目：繰り返し処理は再帰呼び出しで行うので、while 文を if 文に修正する
14 行目：次の深さのノードの一覧を表す childnode を実引数として再帰呼び出しを行うことで、繰り返し処理を行う

 1  from tree import Mbtree
 2  from marubatsu import Marubatsu
 3
 4  def create_tree_by_bf(self, nodelist=None):
 5      if nodelist is None:
 6          nodelist = [self.root]
 7 
 8      if len(nodelist) > 0:
 9          childnodelist = [] 
10          for node in nodelist:
11              if node.mb.status == Marubatsu.PLAYING:
12                  node.calc_children()
13                  childnodelist += node.children
14          self.create_tree_by_bf(childnodelist)
15               
16  Mbtree.create_tree_by_bf = create_tree_by_bf

行番号のないプログラム

from tree import Mbtree
from marubatsu import Marubatsu

def create_tree_by_bf(self, nodelist=None):
    if nodelist is None:
        nodelist = [self.root]
  
    if len(nodelist) > 0:
        childnodelist = [] 
        for node in nodelist:
            if node.mb.status == Marubatsu.PLAYING:
                node.calc_children()
                childnodelist += node.children
        self.create_tree_by_bf(childnodelist)
               
Mbtree.create_tree_by_bf = create_tree_by_bf

修正箇所

-def create_tree_by_bf(self):
+def create_tree_by_bf(self, nodelist=None):
-   nodelist = [self.root]
+   if nodelist is None:
+       nodelist = [self.root]
-   depth = 0
-   self.nodelist_by_depth = [ nodelist ]

+   while len(nodelist) > 0:
-   if len(nodelist) > 0:
        childnodelist = [] 
        for node in nodelist:
            if node.mb.status == Marubatsu.PLAYING:
                node.calc_children()
                childnodelist += node.children
-       self.nodelist_by_depth.append(childnodelist)    
-       nodelist = childnodelist
-       depth += 1                   
+       self.create_tree_by_bf(childnodelist)
               
Mbtree.create_tree_by_bf = create_tree_by_bf

ゲーム木を GUI で表示する Mbtree_GUI クラスでは、nodelist_by_depth などの、上記の修正で削除した情報は使用していないので、下記のプログラムで create_tree_by_bf でゲーム木を作成した Mbtree クラスのインスタンスを GUI で表示することができます。

from tree import Mbtree_GUI

mbtree_bf = Mbtree()
mbtree_gui = Mbtree_GUI(mbtree_bf)

実行結果

Mbtree_Anim クラスでは、上記で削除した nodenum や nodelist_by_depth 属性などの情報が必要になるので、Mbtree_Anim でアニメーションを行うことはできません。

return 文を記述しない理由

ボトムアップな再帰呼び出しを行う fib_by_br では、下記のプログラムのように return 文が記述されていますが、create_tree_by_bf には return 文が記述されていない 点が気になっている人がいるかもしれません。

def fib_by_br(n, i=2, fib_p1=1, fib_p2=0):
    if n == 0:
        return 0
    elif n == 1:
        return 1
        
    if i <= n:
        fib = fib_p1 + fib_p2
        fib_p2 = fib_p1
        fib_p1 = fib
        i += 1
        return fib_by_br(n, i, fib_p1, fib_p2)
    else:
        return fib_p1

return 文が必要ない理由は、以前の記事で説明した return 文を使わない再帰呼び出しの例と同様です。ただし、以前の記事の例では、仮引数に代入したミュータブルなデータに対して処理を行っていましたが、create_tree_by_bf の場合は、root 属性に代入したミュータブルなデータに対して処理を行っています。

トップダウンな繰り返し処理による実装

木構造に対する 幅優先アルゴリズム による トップダウン な繰り返し処理は、以下のようなアルゴリズムで行います。ただし、次に処理を行う木の深さを d で表すことにします。

ルートノードから順に各深さのノードの一覧を幅優先アルゴリズムで計算する
d を最も深いノードの深さとする
深さ d の全てのノードに対する処理を行う
d から 1 を引いて手順 3 へ戻る。ただし、d が負になった場合は処理を終了する

上記の 手順 1 は先ほど説明した ボトムアップな繰り返し処理と基本的には同じ ですが、各深さのノードの一覧を記録しておく必要がある 点が異なります。その後、記録しておいた各深さのノードの一覧の情報を使って、手順 2 ~ 4 の処理を行います。

これまでの記事では、Mbtree クラスで ゲーム木の部分木を描画 する際に必要となる、各ノードの高さを計算 する、下記の calc_node_height でその処理を記述しました。各ノードの高さを計算するためには、ルートノードから計算することはできず、最も深いノードから計算する必要がある ので、この処理は トップダウン な繰り返し処理に分類されます。

なお、calc_node_height では、centernode をルートノード とし、深さが maxdepth までの部分木 に対する処理を行いますが、部分木は木構造の一種 なので、上記と同じアルゴリズム で処理を行うことができます。

calc_node_height の処理を忘れた方は、以前の記事を復習して下さい。

 1  def calc_node_height(self, centernode, maxdepth):
 2      nodelist = [centernode]
 3      depth = centernode.depth
 4      # 各深さのノードのリストを記録する変数を初期化する
 5      nodelist_by_depth = [None] * centernode.depth
 6      nodelist_by_depth.append(nodelist)
 7   
 8      # 深さ depth のノードのリストが空になるまで繰り返し処理を行う
 9      while len(nodelist) > 0:
10          childnodelist = [] 
11          for node in nodelist:
12              childnodelist += node.children
13          nodelist_by_depth.append(childnodelist)
14          nodelist = childnodelist
15          depth += 1
16      
17      for depth in range(maxdepth, centernode.depth - 1, -1):
18          for node in nodelist_by_depth[depth]:
19              if depth == maxdepth:
20                  node.height = 4
21              else:
22                  node.calc_height()

上記のアルゴリズムで処理を行うためには、先程説明したボトムアップな処理で必要なデータに加え、以下のデータを記録し、処理を行う必要があります。（）の中に記述した内容は、上記のプログラムで対応する値を記録する変数と、処理が記述されている行数です。

各深さのノードの一覧（nodelist_by_depth）
- 初期化処理：空の list で初期化する。ただし、部分木の場合は、部分木のルートノードより浅い深さのノードは利用しないので、上記のプログラムではそれらの深さに対応する要素は None としている（5、6 行目）
- 更新処理：ルートノードを要素とする list を要素に追加する（6 行目）。各深さのノードの一覧の情報を追加する（13 行目）
- データの利用：最も深い深さから順にノードのリストを取り出し、取り出したノードのリストから要素を取り出して処理を行う（18 ~ 23 行目）

このプログラムを、再帰呼び出しで記述する場合は、手順 1 を行う再帰呼び出しの関数と、手順 2 ~ 4 を行う再帰呼び出しの関数を 別々に定義する必要があります。そのため、わざわざ再帰呼び出しで記述する必要はあまりないと思いますので、本記事では記述しませんが、プログラミングの練習にはなると思いますので、興味がある方は記述してみて下さい。

`calc_node_height` のバグ

今回の記事を執筆中に、calc_node_height にはバグがあることが判明しましたので、そのバグの修正方法を説明します。

〇×ゲームでは、どのような着手を行っても 8 手目以内で決着がつく ような局面が存在します。例えば、下記の局面では、7 手目でどのマスに〇が着手を行っても〇が勝利するので 7 手目で必ず決着がつきます。

このような局面のノードを centernode に代入し、maxdepth に 9 を代入 して calc_node_height を呼び出すと、nodelist_by_depth には、深さが 7 まで のノードの一覧しか 代入されません。その状態で、calc_node_height の下記のプログラムを実行すると、depth に maxdepth に代入された 9 が代入された状態で、18 行目のプログラムが実行されるので、18 行目では「IndexError: list index out of range」というエラーが発生します。実際に先程実行した GUI で上記の局面を選択するとエラーが発生することを確認して下さい。

17      for depth in range(maxdepth, centernode.depth - 1, -1):
18          for node in nodelist_by_depth[depth]:

このエラーを修正する方法の一つは、17 行目で depth に nodelist_by_depth の要素の数以上の値が 代入されないようにする といものです。具体的には下記のプログラムのように、最小値を計算する組み込み関数 min を利用して 2 行目の range を下記のように修正します。

1  def calc_node_height(self, centernode, maxdepth):
元と同じなので省略
2      for depth in range(min(maxdepth, len(nodelist_by_depth) - 1), centernode.depth - 1, -1):
3          for node in nodelist_by_depth[depth]:
元と同じなので省略
                
Mbtree.calc_node_height = calc_node_height

行番号のないプログラム

def calc_node_height(self, centernode, maxdepth):
    nodelist = [centernode]
    depth = centernode.depth
    # 各深さのノードのリストを記録する変数を初期化する
    nodelist_by_depth = [None] * centernode.depth
    nodelist_by_depth.append(nodelist)
    
    # 深さ depth のノードのリストが空になるまで繰り返し処理を行う
    while len(nodelist) > 0:
        childnodelist = [] 
        for node in nodelist:
            childnodelist += node.children
        nodelist_by_depth.append(childnodelist)
        nodelist = childnodelist
        depth += 1
    
    for depth in range(min(maxdepth, len(nodelist_by_depth) - 1), centernode.depth - 1, -1):
        for node in nodelist_by_depth[depth]:
            if depth == maxdepth:
                node.height = 4
            else:
                node.calc_height()    
                
Mbtree.calc_node_height = calc_node_height

修正箇所

def calc_node_height(self, centernode, maxdepth):
元と同じなので省略
    for depth in range(min(maxdepth, len(nodelist_by_depth) - 1), centernode.depth - 1, -1):
        for node in nodelist_by_depth[depth]:
元と同じなので省略
                
Mbtree.calc_node_height = calc_node_height

実行結果は省略しますが、上記の修正後に、下記のプログラムを実行し、上記の局面を選択してもエラーが発生しなくなることを確認して下さい。

mbtree_gui = Mbtree_GUI(mbtree_bf)

他にも以下のような修正方法などの、様々な修正方法が考えられます。

5 行目：nodelist_by_depth の初期化処理を、空の list を要素とする、要素の数が 11 の list で初期化するようする。この修正で、18 行目でエラーが発生しなくなる。なお、13 行目の処理で、深さが 9 のノードに対して nodelist_by_depth[10] に代入処理が行われる ので、要素の数は 11 にする必要がある点に注意すること
6 行目：centernode の深さのノードの一覧を nodelisst_by_depth に記録する
13 行目：深さが depth の子ノードの一覧を nodelist_by_depth に記録する。その際に、子ノードの深さは depth + 1 である点に注意すること
17 行目：range の実引数を元に戻す

 1  def calc_node_height(self, centernode, maxdepth):
 2      nodelist = [centernode]
 3      depth = centernode.depth
 4      # 各深さのノードのリストを記録する変数を初期化する
 5      nodelist_by_depth = [[] for i in range(11)]
 6      nodelist_by_depth[centernode.depth] = nodelist
 7   
 8      # 深さ depth のノードのリストが空になるまで繰り返し処理を行う
 9      while len(nodelist) > 0:
10          childnodelist = [] 
11          for node in nodelist:
12              childnodelist += node.children
13          nodelist_by_depth[depth + 1] = childnodelist
14          nodelist = childnodelist
15          depth += 1
16      
17      for depth in range(maxdepth, centernode.depth - 1, -1):
18          for node in nodelist_by_depth[depth]:
19              if depth == maxdepth:
20                  node.height = 4
21              else:
22                  node.calc_height()    
23                
24  Mbtree.calc_node_height = calc_node_height

行番号のないプログラム

def calc_node_height(self, centernode, maxdepth):
    nodelist = [centernode]
    depth = centernode.depth
    # 各深さのノードのリストを記録する変数を初期化する
    nodelist_by_depth = [[] for i in range(11)]
    nodelist_by_depth[centernode.depth] = nodelist
    
    # 深さ depth のノードのリストが空になるまで繰り返し処理を行う
    while len(nodelist) > 0:
        childnodelist = [] 
        for node in nodelist:
            childnodelist += node.children
        nodelist_by_depth[depth + 1] = childnodelist
        nodelist = childnodelist
        depth += 1
    
    for depth in range(maxdepth, centernode.depth - 1, -1):
        for node in nodelist_by_depth[depth]:
            if depth == maxdepth:
                node.height = 4
            else:
                node.calc_height()    
                
Mbtree.calc_node_height = calc_node_height

修正箇所

def calc_node_height(self, centernode, maxdepth):
    nodelist = [centernode]
    depth = centernode.depth
    # 各深さのノードのリストを記録する変数を初期化する
-   nodelist_by_depth = [None] * centernode.depth
+   nodelist_by_depth = [[] for i in range(11)]
-   nodelist_by_depth.append(nodelist)
+   nodelist_by_depth[centernode.depth] = nodelist
    
    # 深さ depth のノードのリストが空になるまで繰り返し処理を行う
    while len(nodelist) > 0:
        childnodelist = [] 
        for node in nodelist:
            childnodelist += node.children
-       nodelist_by_depth.append(childnodelist)
+       nodelist_by_depth[depth + 1] = childnodelist
        nodelist = childnodelist
        depth += 1
    
-   for depth in range(min(maxdepth, len(nodelist_by_depth) - 1), centernode.depth - 1, -1):
+   for depth in range(min(maxdepth, centernode.depth - 1, -1):
        for node in nodelist_by_depth[depth]:
            if depth == maxdepth:
                node.height = 4
            else:
                node.calc_height()    
                
Mbtree.calc_node_height = calc_node_height

実行結果は省略しますが、上記の修正後に、下記のプログラムを実行し、上記の局面を選択してもエラーが発生しなくなることを確認して下さい。

mbtree_gui = Mbtree_GUI(mbtree_bf)

幅優先アルゴリズムの性質

幅優先アルゴリズム は、深さの順で処理を行うという 処理の流れがわかりやすい という利点はありますが、処理を行う際に、次の深さのノードの一覧を記録する処理 を記述する必要があるため、プログラムが複雑 になります。また、トップダウン な繰り返し処理の場合は、すべての深さのノードの一覧を記録 する必要が生じます。

前回の記事で説明したように、木構造 のデータに対する繰り返し処理のような、繰り返しの回数が増えると 指数関数的 に処理の数が増えるという性質があります。そのため、木構造の深さが深くなるとに ノードの数が急激に増加する ので、深い木構造 のデータに対して 幅優先アルゴリズム で処理を行うと、ノードを記録するためのメモリが大量に必要になる という欠点があります。

なお、今回の記事では説明しませんが、幅優先アルゴリズム には 利点もあります。また、幅優先アルゴリズムで 行う必要がある 繰り返し処理もあるので、幅優先アルゴリズムが良くないアルゴリズムであるとは言えません。状況に応じて 幅優先アルゴリズムと深さ優先アルゴリズムを 使い分ける必要があります。

分岐しない再帰呼び出しと多重再帰

幅優先アルゴリズムを再帰呼び出しで記述した場合のプログラムの特徴として、再帰呼び出しの関数の中で、再帰呼び出しが 1 回しか行われない という点が挙げられます。これは、幅優先アルゴリズム が、0、1、2・・・のように表現される、深さの順 という 分岐しない 繰り返し処理を行うからです。木構造 は、ノードが 複数の子ノードを持つ ので 分岐します が、その 分岐の情報 は再帰呼び出しの 仮引数に代入 されるため、再帰呼び出し の処理は 分岐しません。create_tree_by_bf の場合は、再帰呼び出しを行うたびに、nodelist に代入された list の要素の数は急激に増えていきますが、再帰呼び出し そのものは、分岐しません。

一方、再帰呼び出しの関数の中で、複数の再帰呼び出し が行われて 分岐する ようなものを 多重再帰 と呼びます。この後で説明する、深さ優先アルゴリズムを再帰呼び出しで実装する場合は、再帰呼び出しは多重再帰になります。

深さ優先アルゴリズムによる繰り返し処理

ボトムアップな繰り返し処理による実装

木構造に対する 深さ優先アルゴリズム による ボトムアップ な繰り返し処理は、以下のようなアルゴリズムで行います。ただし、次に処理を行うノードを N とします。

N をルートノードとする
N に対する処理 を行う
N の子ノードのうち、まだ処理を行っていない子ノードが存在するか を判定する
1. 処理を行っていない子ノードが 存在する場合 は、その中から 1 つを選び、そのノードを N として 手順 2 に戻る
2. 処理を行っていない子ノードが 存在しない場合 は、親ノードが存在するか を判定する
  1. 親ノードが 存在する場合 は、親ノードを N として 手順 2 に戻る
  2. 親ノードが 存在しない場合 は、処理を終了する

while 文による実装

これまでの記事では、以前の記事で説明したように、〇×ゲームのゲーム木を以下のようなアルゴリズムで作成しました。下記のアルゴリズムは、上記のアルゴリズムに、N に対して行う具体的な処理として、子ノードを作成するという処理を記述したものです。

ゲーム開始時の局面を表すノードを、ルートノードとするゲーム木を作成する
子ノードを作成する 処理を行う ノードを N と表記 し、N をルートノードで初期化 する
N にまだ 作成していない子ノードが存在するか を判定する
1. 作成していない子ノードが 存在する場合 は、その子ノードを作成 し、作成した子ノードを N として手順 3 に戻る
2. 作成していない子ノードが 存在しない場合 は、親ノードが存在するか を判定する
  1. 親ノードが 存在する場合 は、親ノードを N として手順 3 に戻る
  2. 親ノードが 存在しない場合 は、ゲーム木が完成しているので 処理を終了する

また、上記の処理は Mbtree クラスの下記の create_tree_by_df で記述しました。このプログラムの意味については、以前の記事で詳しく説明したので忘れた方は復習して下さい。

def create_tree_by_df(self):
    self.nodelist = [self.root]
    self.nodelist_by_depth = [[] for _ in range(10)]
    self.nodelist_by_depth[0].append(self.root)
    self.nodenum = 0
  
    N = self.root
  
    while N is not None:
        legal_moves = N.mb.calc_legal_moves()
        childnum = len(N.children)
        if N.mb.status == Marubatsu.PLAYING and childnum < len(legal_moves):
            x, y = legal_moves[childnum]
            mb = deepcopy(N.mb)
            mb.move(x, y)
            node = Node(mb, parent=N, depth=N.depth + 1)
            N.insert(node)
            self.nodelist.append(node)
            self.nodelist_by_depth[N.depth + 1].append(node)
            self.nodenum += 1
            N = node
        else:
            N = N.parent

上記のプログラムの中で、ノードの数やノードの一覧を記録する nodenum、nodelist、nodelist_by_depth は、ゲーム木を作成する処理では 必要はありません。そこで、下記のプログラムのように、ゲーム木を作成するために必要のない処理を削除したプログラムで説明することにします。

 1  from tree import Node
 2  from copy import deepcopy
 3
 4  def create_tree_by_df(self):
 5      N = self.root
 6   
 7      while N is not None:
 8          legal_moves = N.mb.calc_legal_moves()
 9          childnum = len(N.children)
10          if N.mb.status == Marubatsu.PLAYING and childnum < len(legal_moves):
11              x, y = legal_moves[childnum]
12              mb = deepcopy(N.mb)
13              mb.move(x, y)
14              node = Node(mb, parent=N, depth=N.depth + 1)
15              N.insert(node)
16              N = node
17          else:
18              N = N.parent
19            
20  Mbtree.create_tree_by_df = create_tree_by_df

行番号のないプログラム

from tree import Node
from copy import deepcopy

def create_tree_by_df(self):
    N = self.root
    
    while N is not None:
        legal_moves = N.mb.calc_legal_moves()
        childnum = len(N.children)
        if N.mb.status == Marubatsu.PLAYING and childnum < len(legal_moves):
            x, y = legal_moves[childnum]
            mb = deepcopy(N.mb)
            mb.move(x, y)
            node = Node(mb, parent=N, depth=N.depth + 1)
            N.insert(node)
            N = node
        else:
            N = N.parent
            
Mbtree.create_tree_by_df = create_tree_by_df

修正箇所

from tree import Node
from copy import deepcopy

def create_tree_by_df(self):
-   self.nodelist = [self.root]
-   self.nodelist_by_depth = [[] for _ in range(10)]
-   self.nodelist_by_depth[0].append(self.root)
-   self.nodenum = 0

    N = self.root
    
    while N is not None:
        legal_moves = N.mb.calc_legal_moves()
        childnum = len(N.children)
        if N.mb.status == Marubatsu.PLAYING and childnum < len(legal_moves):
            x, y = legal_moves[childnum]
            mb = deepcopy(N.mb)
            mb.move(x, y)
            node = Node(mb, parent=N, depth=N.depth + 1)
            N.insert(node)
-           self.nodelist.append(node)
-           self.nodelist_by_depth[N.depth + 1].append(node)
-           self.nodenum += 1
            N = node
        else:
            N = N.parent
            
Mbtree.create_tree_by_df = create_tree_by_df

実行結果は先ほどと同じなので省略しますが、下記のプログラムで create_tree_by_df でゲーム木を作成した Mbtree クラスのインスタンスを GUI で表示することができます。

mbtree_df = Mbtree(algo="df")
mbtree_gui = Mbtree_GUI(mbtree_df)

while 文による実装が複雑になる理由

上記のプログラムでは、while 文 を使って 深さ優先アルゴリズム によるゲーム木を作成していますが、while 文を使ったプログラムでは、下記のアルゴリズムの中の 手順 3 の処理の 記述が複雑 になります。

N をルートノードとする
N に対する処理 を行う
N の子ノードのうち、まだ処理を行っていない子ノードが存在するか を判定する
1. 処理を行っていない子ノードが 存在する場合 は、その中から 1 つを選び、そのノードを N として 手順 2 に戻る
2. 処理を行っていない子ノードが 存在しない場合 は、親ノードが存在するか を判定する
  1. 親ノードが 存在する場合 は、親ノードを N として 手順 2 に戻る
  2. 親ノードが 存在しない場合 は、処理を終了する

1 つ目の複雑な処理の記述として、手順 3 では、N の子ノードのうち、まだ処理を行っていない子ノードを探す 処理があります。そのような処理を行うためには、処理を行った子ノードとそうでない子ノードを区別する必要 があります。〇×ゲームのゲーム木を作成する処理の場合は、作成済の子ノードの数と、合法手の数を比較することでその判定を行うことができましたが、calc_node_height のような、既に作成済のゲーム木 に対して処理を行う場合は、そのような判定を行うことは それほど簡単ではありません²。

2 つ目の複雑な処理の記述として、手順 3-2 では、親ノードを辿る処理が必要 となります。〇×ゲームのノードを表す Node クラスには、親ノードを表す parent 属性があるので親ノードを辿る処理は簡単に記述できますが、parent 属性がない場合 は、繰り返し処理の中 で、親ノードの情報を記録しておく必要が生じます。

再帰呼び出しによる実装

再帰呼び出し でボトムアップな深さ優先アルゴリズムを記述する場合は、上記で説明した while 文で記述する場合の 問題は生じません。その理由について説明します。

下図は、前回の記事で紹介した、再帰呼び出しで計算を行う fib_by_tr を使って $F_4$ を計算した際の処理の流れを表す図です。

下図は、以前の記事で紹介したゲーム木の一部を再帰呼び出しで作成した場合にノードが作成される順番を表す図です。

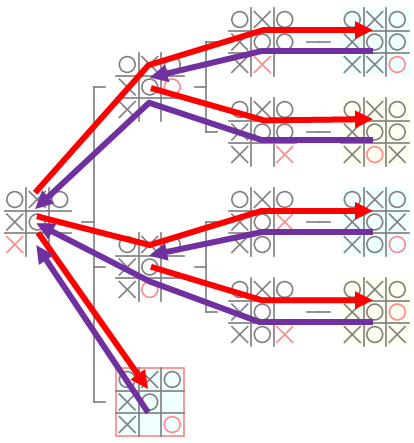
両者を見比べるとわかると思いますが、どちらも同じ順番で木のノードの処理を行っています。fib_by_tr は、その関数の中で 複数回 の fib_by_br を 再帰呼び出し しているので、先程説明した 多重再帰 です。このように、多重再帰 では、深さ優先アルゴリズム で処理が行われるので、ゲーム木の作成の処理も、多重再帰によって、深さ優先アルゴリズムで作成することができます。

そこで、多重再帰でゲーム木を作成するように create_tree_by_df を修正することにします。再帰呼び出しでは、ゲーム木を作成する処理の中の、特定のノードに対する処理のみを記述 するので、そのノード を代入する 仮引数を用意 する必要があります。そこで、その仮引数の名前を N とします。

多重再帰を使った create_tree_by_df は、下記のように定義することができます。

1 行目：処理を行うノードを代入する N を追加する
2 行目：ゲームの決着がついてない場合のみ、子ノードが存在するので、そのことを判定する。なお、ゲームの決着がついていない場合は何もする必要はないので、else を記述する必要はない
3、4 行目：合法手の一覧を計算し、合法手を順番に取り出す繰り返し処理を行う
5 ~ 7 行目：N のゲーム盤を表す N.mb をコピーし、取り出した合法手を着手し、その局面を表すノードを作成する
8 行目：作成したノードを N の子ノードに追加する
9 行目：作成したノードを実引数に記述して、create_tree_by_df を再帰呼び出しすることで、そのノードに対する処理を行う。この再帰呼び出しは、子ノードの数だけ行われる ので、create_tree_by_df は 多重再帰 である

 1  def create_tree_by_df(self, N):
 2      if N.mb.status == Marubatsu.PLAYING:
 3          legal_moves = N.mb.calc_legal_moves()
 4          for x, y in legal_moves:
 5              mb = deepcopy(N.mb)
 6              mb.move(x, y)
 7              node = Node(mb, parent=N, depth=N.depth + 1)
 8              N.insert(node)
 9              self.create_tree_by_df(node)
10            
11  Mbtree.create_tree_by_df = create_tree_by_df

行番号のないプログラム

def create_tree_by_df(self, N):
    if N.mb.status == Marubatsu.PLAYING:
        legal_moves = N.mb.calc_legal_moves()
        for x, y in legal_moves:
            mb = deepcopy(N.mb)
            mb.move(x, y)
            node = Node(mb, parent=N, depth=N.depth + 1)
            N.insert(node)
            self.create_tree_by_df(node)
            
Mbtree.create_tree_by_df = create_tree_by_df

create_tree_by_df を修正したので、それにあわせて、create_tree_by_df を呼び出す __init__ メソッドを下記のプログラムのように修正する必要があります。

8 行目：実引数にルートノードを記述するように修正する

 1  def __init__(self, algo="bf"):
 2      self.algo = algo
 3      Node.count = 0
 4      self.root = Node(Marubatsu())
 5      if self.algo == "bf":  
 6          self.create_tree_by_bf()
 7      else:
 8          self.create_tree_by_df(self.root)
 9        
10  Mbtree.__init__ = __init__

行番号のないプログラム

def __init__(self, algo="bf"):
    self.algo = algo
    Node.count = 0
    self.root = Node(Marubatsu())
    if self.algo == "bf":  
        self.create_tree_by_bf()
    else:
        self.create_tree_by_df(self.root)
        
Mbtree.__init__ = __init__

修正箇所

def __init__(self, algo="bf"):
    self.algo = algo
    Node.count = 0
    self.root = Node(Marubatsu())
    if self.algo == "bf":  
        self.create_tree_by_bf()
    else:
-       self.create_tree_by_df()
+       self.create_tree_by_df(self.root)
        
Mbtree.__init__ = __init__

mbtree_df = Mbtree(algo="df")
mbtree_gui = Mbtree_GUI(mbtree_df)

プログラムを簡潔に記述できる理由

下記は修正前と修正後の create_tree_by_df のプログラムです。再帰呼び出しによるプログラムのほうが、プログラムを簡潔に記述できていることを確認して下さい。

# while 文による実装
def create_tree_by_df(self):
    N = self.root
    
    while N is not None:
        legal_moves = N.mb.calc_legal_moves()
        childnum = len(N.children)
        if N.mb.status == Marubatsu.PLAYING and childnum < len(legal_moves):
            x, y = legal_moves[childnum]
            mb = deepcopy(N.mb)
            mb.move(x, y)
            node = Node(mb, parent=N, depth=N.depth + 1)
            N.insert(node)
            N = node
        else:
            N = N.parent

# 再帰呼び出しによる実装
def create_tree_by_df(self, N):
    if N.mb.status == Marubatsu.PLAYING:
        legal_moves = N.mb.calc_legal_moves()
        for x, y in legal_moves:
            mb = deepcopy(N.mb)
            mb.move(x, y)
            node = Node(mb, parent=N, depth=N.depth + 1)
            N.insert(node)
            self.create_tree_by_df(node)
            
Mbtree.create_tree_by_df = create_tree_by_df

再帰呼び出しによってプログラムを簡潔に記述できる理由は以下の通りです。

1 つ目の理由は、下記のように、まだ処理を行っていない子ノードを探す処理 が for 文で簡潔に記述できる というものです。なお、上記の while 文による実装では、比較的簡潔にまだ処理を行っていない子ノードを探す処理を記述できていますが、多くの場合はこのように簡潔にその処理を記述できるとは限らないので、この性質はかなり大きな利点です。

再帰呼び出しでは、for 文によって子ノードに対する処理を順番に行う
for 文のブロックの処理では、子ノードを実引数として再帰呼び出しを行う
再帰呼び出しの処理が終了すると、for 文によって次の子ノードに対する処理が行われる

2 つ目の理由は、下記のように、親ノードを辿る処理を記述する必要がない 点です。

create_tree_by_df の再帰呼び出しは、親ノードを処理する create_tree_by_df から呼び出される
従って、create_tree_by_df の処理が終了すると、親ノードを処理する create_tree_by_df に処理が戻る
そのため、親ノードを辿る処理をプログラムで記述する必要はない

下記の修正版の create_tree_by_df プログラムに、まだ処理が行われていない子ノードを探す処理や、親ノードを辿る処理が記述されていないことを確認して下さい。また、下記のプログラムでは、Node クラスの parent 属性は記述されていません。そのため、Node クラスに parent 属性が存在しなくても正しく動作 します。

def create_tree_by_df(self, N):
    if N.mb.status == Marubatsu.PLAYING:
        legal_moves = N.mb.calc_legal_moves()
        for x, y in legal_moves:
            mb = deepcopy(N.mb)
            mb.move(x, y)
            node = Node(mb, parent=N, depth=N.depth + 1)
            N.insert(node)
            self.create_tree_by_df(node)
            
Mbtree.create_tree_by_df = create_tree_by_df

深さ優先アルゴリズムでは、子ノードの処理が完了した後 で、親ノードの処理へ戻る 処理を行う必要があるが、その処理は、子ノードの処理を行う関数呼び出し によって 自動的に行われる
子ノードの処理が完了した後で、次の子ノードの処理を行う 処理は、親ノードを処理する関数の中 で、for 文や while 文 を使って行われる

`nodelist` などの計算

Mbtree_Anim クラスなどで必要になる、元の create_tree_by_df で計算していた nodelist などを計算するように修正します。元の create_tree_by_df では、その関数のブロックの中でそれらの変数の初期化を行っていましたが、再帰呼び出しの場合は、最初に create_tree_by_df を呼び出す前にその処理を行う必要があります。下記は、そのように __init__ メソッドを修正したプログラムです。

8 ~ 12 行目：それぞれの変数を初期化する処理を記述する。この部分は、修正前の create_tree_by_df の最初に記述されていた内容と同じである

 1  def __init__(self, algo="bf"):
 2      self.algo = algo
 3      Node.count = 0
 4      self.root = Node(Marubatsu())
 5      if self.algo == "bf":  
 6          self.create_tree_by_bf()
 7      else:
 8          self.nodelist = [self.root]
 9          self.nodelist_by_depth = [[] for _ in range(10)]
10          self.nodelist_by_depth[0].append(self.root)
11          self.nodenum = 0
12          self.create_tree_by_df(self.root)
13        
14  Mbtree.__init__ = __init__

行番号のないプログラム

def __init__(self, algo="bf"):
    self.algo = algo
    Node.count = 0
    self.root = Node(Marubatsu())
    if self.algo == "bf":  
        self.create_tree_by_bf()
    else:
        self.nodelist = [self.root]
        self.nodelist_by_depth = [[] for _ in range(10)]
        self.nodelist_by_depth[0].append(self.root)
        self.nodenum = 0
        self.create_tree_by_df(self.root)
        
Mbtree.__init__ = __init__

修正箇所

def __init__(self, algo="bf"):
    self.algo = algo
    Node.count = 0
    self.root = Node(Marubatsu())
    if self.algo == "bf":  
        self.create_tree_by_bf()
    else:
+       self.nodelist = [self.root]
+       self.nodelist_by_depth = [[] for _ in range(10)]
+       self.nodelist_by_depth[0].append(self.root)
+       self.nodenum = 0
        self.create_tree_by_df(self.root)
        
Mbtree.__init__ = __init__

次に、create_tree_by_df を以下のように修正します。

9 ~ 11 行目：それぞれの属性の値を更新する。この部分も、修正前の create_tree_by_df に記述されていた内容と同じである

 1  def create_tree_by_df(self, N):
 2      if N.mb.status == Marubatsu.PLAYING:
 3          legal_moves = N.mb.calc_legal_moves()
 4          for x, y in legal_moves:
 5              mb = deepcopy(N.mb)
 6              mb.move(x, y)
 7              node = Node(mb, parent=N, depth=N.depth + 1)
 8              N.insert(node)
 9              self.nodelist.append(node)
10              self.nodelist_by_depth[node.depth].append(node)
11              self.nodenum += 1
12              self.create_tree_by_df(node)
13            
14  Mbtree.create_tree_by_df = create_tree_by_df

行番号のないプログラム

def create_tree_by_df(self, N):
    if N.mb.status == Marubatsu.PLAYING:
        legal_moves = N.mb.calc_legal_moves()
        for x, y in legal_moves:
            mb = deepcopy(N.mb)
            mb.move(x, y)
            node = Node(mb, parent=N, depth=N.depth + 1)
            N.insert(node)
            self.nodelist.append(node)
            self.nodelist_by_depth[node.depth].append(node)
            self.nodenum += 1
            self.create_tree_by_df(node)
            
Mbtree.create_tree_by_df = create_tree_by_df

修正箇所

def create_tree_by_df(self, N):
    if N.mb.status == Marubatsu.PLAYING:
        legal_moves = N.mb.calc_legal_moves()
        for x, y in legal_moves:
            mb = deepcopy(N.mb)
            mb.move(x, y)
            node = Node(mb, parent=N, depth=N.depth + 1)
            N.insert(node)
+           self.nodelist.append(node)
+           self.nodelist_by_depth[node.depth].append(node)
+           self.nodenum += 1
            self.create_tree_by_df(node)
            
Mbtree.create_tree_by_df = create_tree_by_df

上記の修正後に、下記のプログラムで create_tree_by_df でゲーム木を作成した Mbtree クラスのインスタンスを使って、Mbtree_Anim でアニメーションを表示することができます。

from tree import Mbtree_Anim
mbtree_df = Mbtree(algo="df")
mbtree_anim = Mbtree_Anim(mbtree_df)

実行結果

トップダウンな繰り返し処理による実装

木構造に対する 深さ優先アルゴリズム による トップダウン な繰り返し処理は、以下のようなアルゴリズムで行います。ただし、次に処理を行うノードを N とします。

ボトムアップ な繰り返し処理との違いは、ノードに対する処理は、子ノードの処理を行った後で行う 点です。

N をルートノードとする
N の子ノードが存在しない場合は、そのノードの処理を行い、手順 4 へ移動する
N の子ノードが存在する場合は、子ノードのうち、まだ処理を行っていない子ノードが存在するかどうかを判定する
1. 処理を行っていない子ノードが存在する場合は、その中から 1 つを選び、そのノードを N として手順 2 に戻る
2. 処理を行っていない子ノードが存在しない場合は、子ノードが行なった処理の結果に対する処理を行う
親ノードが存在するかを判定する
1. 親ノードが存在する場合は、親ノードを N として手順 2 に戻る
2. 親ノードが存在しない場合は、処理を終了する

そこで、トップダウンな再帰呼び出しを使って計算を行うように calc_node_height を修正することにします。

先程の while 文を使ってボトムアップな手順で記述した calc_node_height では、部分木の ルートノード を centernode という仮引数に代入していました。一方、再帰呼び出しでは、特定のノードに対する処理のみを記述 するので、そのノードを代入する仮引数 を用意する必要があります。そこで、仮引数の名前を centernode から N に変更 することにします。

なお、部分木の深さを代入する仮引数 maxdepth は、再帰呼び出しの処理でも必要となるので、そのまま利用することにします。

次に、再帰呼び出しでの calc_node_height 行う処理について説明します。

N に 子ノードが存在しない 場合か、maxdepth と同じ深さ の場合は、子ノードを描画しない ので 高さは 4 になります。

N に 子ノードが存在する 場合の高さは、以下のような考え方で計算できます。

ノードの高さは 子ノードの高さの合計 で計算できる
トップダウンな繰り返し処理では、上記の手順 3-2 からわかるように、子ノードの処理の結果に対して 処理を行う
子ノードの処理は、再帰呼び出しによって行う
従って、calc_node_height が、処理を行った ノードの高さ を 返り値として返す ようにすれば、N の子ノードの処理を行うために再帰呼び出しを行った calc_node_height の返り値が 子ノードの高さを表す ようになる
その合計を計算 すれば、N の高さを計算できる

下記は、そのように calc_node_height を修正したプログラムです。

1 行目：仮引数 centernode の名前を N に修正する
2 ~ 4 行目：N の子ノードが存在しない場合か、N の深さが maxdepth の場合は子ノードを描画しないので、ノードの高さを表す height 属性に 4 を代入し、4 を返す
6 行目：子ノードの高さの合計を計算するための height を 0 で初期化する
7 行目：子ノードに対して for 文で繰り返し処理を行う
8 行目：子ノードを実引数として再帰呼び出しを行う。その返り値は、子ノードの高さを表すので、height に返り値の値を加算する
9 行目：子ノードに対する繰り返し処理が終了した時点で、height に子ノードの高さの合計が代入されているので、N の height 属性にその値を代入する
10 行目：height を返り値として返す

 1  def calc_node_height(self, N, maxdepth):
 2      if len(N.children) == 0 or N.depth == maxdepth:
 3          N.height = 4
 4          return 4
 5   
 6      height = 0
 7      for childnode in N.children:
 8          height += self.calc_node_height(childnode, maxdepth)
 9      N.height = height
10      return height
11
12  Mbtree.calc_node_height = calc_node_height

行番号のないプログラム

def calc_node_height(self, N, maxdepth):
    if len(N.children) == 0 or N.depth == maxdepth:
        N.height = 4
        return 4
    
    height = 0
    for childnode in N.children:
        height += self.calc_node_height(childnode, maxdepth)
    N.height = height
    return height

Mbtree.calc_node_height = calc_node_height

calc_node_height の仮引数の名前を変更したので、calc_node_height を呼び出す draw_subtree を下記のプログラムのように修正する必要があります。

6 行目：キーワード引数 centernode=centernode を N=centernode に修正する

1  def draw_subtree(self, centernode=None, selectednode=None, ax=None, size=0.25, lw=0.8, maxdepth=2):
2      self.nodes_by_rect = {}
3
4      if centernode is None:
5          centernode = self.root
6      self.calc_node_height(N=centernode, maxdepth=maxdepth)
元と同じなので省略
7
8  Mbtree.draw_subtree = draw_subtree

行番号のないプログラム

def draw_subtree(self, centernode=None, selectednode=None, ax=None, size=0.25, lw=0.8, maxdepth=2):
    self.nodes_by_rect = {}

    if centernode is None:
        centernode = self.root
    self.calc_node_height(N=centernode, maxdepth=maxdepth)
    width = 5 * (maxdepth + 1)
    height = centernode.height
    parent = centernode.parent
    if parent is not None:
        height += (len(parent.children) - 1) * 4
        parent.height = height
    if ax is None:
        fig, ax = plt.subplots(figsize=(width * size, height * size))
        ax.set_xlim(0, width)
        ax.set_ylim(0, height)   
        ax.invert_yaxis()
        ax.axis("off")        
    
    nodelist = [centernode]
    depth = centernode.depth
    while len(nodelist) > 0 and depth <= maxdepth:        
        dy = 0
        if parent is not None:
            dy = parent.children.index(centernode) * 4
        childnodelist = []
        for node in nodelist:
            if node is None:
                dy += 4
                childnodelist.append(None)
            else:
                dx = 5 * node.depth
                emphasize = node is selectednode
                rect = node.draw_node(ax=ax, maxdepth=maxdepth, emphasize=emphasize, size=size, lw=lw, dx=dx, dy=dy)
                self.nodes_by_rect[rect] = node
                dy += node.height
                if len(node.children) > 0:  
                    childnodelist += node.children
                else:
                    childnodelist.append(None)
        depth += 1
        nodelist = childnodelist
        
    if parent is not None:
        dy = 0
        for sibling in parent.children:
            if sibling is not centernode:
                sibling.height = 4
                dx = 5 * sibling.depth
                rect = sibling.draw_node(ax, maxdepth=sibling.depth, size=size, lw=lw, dx=dx, dy=dy)
                self.nodes_by_rect[rect] = sibling
            dy += sibling.height
        dx = 5 * parent.depth
        rect = parent.draw_node(ax, maxdepth=maxdepth, size=size, lw=lw, dx=dx, dy=0)
        self.nodes_by_rect[rect] = parent
    
        node = parent
        while node.parent is not None:
            node = node.parent
            node.height = height
            dx = 5 * node.depth
            rect = node.draw_node(ax, maxdepth=node.depth, size=size, lw=lw, dx=dx, dy=0)
            self.nodes_by_rect[rect] = node

Mbtree.draw_subtree = draw_subtree

修正箇所

def draw_subtree(self, centernode=None, selectednode=None, ax=None, size=0.25, lw=0.8, maxdepth=2):
    self.nodes_by_rect = {}

    if centernode is None:
        centernode = self.root
-   self.calc_node_height(centernode=centernode, maxdepth=maxdepth)
+   self.calc_node_height(N=centernode, maxdepth=maxdepth)
元と同じなので省略

Mbtree.draw_subtree = draw_subtree

実行結果は同じなので省略しますが、上記の修正後に、下記のプログラムでアニメーションを正しく表示できることが確認できます。

mbtree_anim = Mbtree_Anim(mbtree_df)

プログラムを簡潔に記述できる理由

下記は修正前と修正後の calc_node_height のプログラムを並べたものです。修正後のほうが、かなり簡潔に記述できている ことを確認して下さい。

# 修正前
def calc_node_height(self, centernode, maxdepth):
    nodelist = [centernode]
    depth = centernode.depth
    # 各深さのノードのリストを記録する変数を初期化する
    nodelist_by_depth = [None] * centernode.depth
    nodelist_by_depth.append(nodelist)
    
    # 深さ depth のノードのリストが空になるまで繰り返し処理を行う
    while len(nodelist) > 0:
        childnodelist = [] 
        for node in nodelist:
            childnodelist += node.children
        nodelist_by_depth.append(childnodelist)
        nodelist = childnodelist
        depth += 1
    
    for depth in range(maxdepth, centernode.depth - 1, -1):
        for node in nodelist_by_depth[depth]:
            if depth == maxdepth:
                node.height = 4
            else:
                node.calc_height()   
                
# 修正後
def calc_node_height(self, N, maxdepth):
    if len(N.children) == 0 or N.depth == maxdepth:
        N.height = 4
        return 4
    
    height = 0
    for childnode in N.children:
        height += self.calc_node_height(childnode, maxdepth)
    N.height = height
    return height

再帰呼び出しによってプログラムを簡潔に記述できる理由は、先程の create_tree_by_df で説明した理由に加えて、各深さのノードの一覧を計算しておく必要がない 点です。また、各深さのノードの一覧を計算しておく必要がないので、先程説明した node_list_by_depth が原因 となるような バグが発生することもありません。

ボトムアップとトップダウンな処理の記述場所

深さ優先アルゴリズムを再帰呼び出しで記述する場合は、ボトムアップ な処理は、再帰呼び出しが行われた順番 に処理を行う必要があるため、その処理は再帰呼び出しの関数の中で、再帰呼び出しを行う処理の前 に記述する必要があります。実際に create_tree_by_df では、再帰呼び出しを行う処理の前で、子ノードを作成する処理を記述しています。

一方、トップダウン な処理の場合は、末端の再帰呼び出しから逆の順番 で処理を行う必要があるため、その処理は再帰呼び出しの関数の中で、再帰呼び出しを行った後 で記述する必要があります。実際に calc_node_height では、子ノードの高さを計算する再帰呼び出しが 終了した際に得られる返り値を使って 高さの計算を行っています。

なお、トップダウンな再帰呼び出しを行う fib_by_tr では、下記のプログラムのように return の後 に fib_by_tr(n - 1) + fib_by_tr(n - 2) という 再帰呼び出しが記述されている ので再帰呼び出しの前に処理が行われているように見えるかもしれません。しかし、この式は実際には fib_by_tr(n - 1) と fib_by_tr(n - 2) の再帰呼び出しが行われた結果得られた 返り値を使って計算している ので、再帰呼び出しを行った後で行われた処理です。

return fib_by_tr(n - 1) + fib_by_tr(n - 2)

再帰呼び出しでは、ボトムアップな処理は再帰呼び出しの処理の前に記述し、トップダウンな処理は再帰呼び出しの処理の後で記述する。

深さ優先アルゴリズムの性質

深さ優先アルゴリズム は、処理の流れがわかりづらい という利点はありますが、プログラムの記述を幅優先アルゴリズムよりは 簡潔に記述できる という利点があります。

また、深さ優先アルゴリズムでは、幅優先アルゴリズムのように、大量のノードを記憶しておく必要がないので、メモリの消費が大幅に少なくて済む という利点もあります。

具体的には、深さ優先アルゴリズムでは、繰り返しのたびに一つ深い深さのノードの計算を行います。また、ノードの処理が終了した時点で、親ノードへ処理が戻る ので、記憶しておく必要があるデータ は、最大でも ルートノードから、最も深いノードまでのデータ だけで済むので、幅優先アルゴリズムよりは圧倒的に少ないメモリ消費で済みます。なお、データの記憶 は、関数が呼び出された際に作成される、ローカルな名前空間 によって行われます。以前の記事で説明したように、ローカルな名前空間は、関数が作られてからその関数の処理が終了するまでの間存在する ので、再帰呼び出しで呼び出された関数の処理が終了するまでの間は、呼び出し元の関数だけでなく、最初に呼び出された再帰呼び出しの関数までさかのぼった、すべての関数の名前空間が残り続けます。

なお、同じ木構造のデータに対して計算を行うノードの数は、幅優先アルゴリズムでも、深さ優先アルゴリズムでも変わらないので、計算時間はどちらもほぼ同じ です。

木構造のデータに対する繰り返し処理に関する補足

木構造のデータに対する繰り返し処理に関するいくつかの補足説明を行います。

幅優先と深さ優先アルゴリズムのどちらを使うべきか

今回の記事で説明したように、木構造のデータに対する繰り返し処理は、深さ優先アルゴリズムのほうが、プログラムの記述のしやすさや、消費メモリが少ないなど、多くの利点 があります。そのため、どちらのアルゴリズムを利用しても構わない ような場合は、深さ優先アルゴリズムを再帰呼び出しを使って記述する と良いでしょう。

ただし、幅優先アルゴリズムが必要な場合もあるので、常に深さ優先アルゴリズムを使えば良いというわけではない 点に注意が必要です。

再帰呼び出しの欠点に関する補足

上記で再帰呼び出しを使って記述すると良いと説明しましたが、以前の記事で説明した、再帰呼び出しには 繰り返しの回数に制限がある という欠点と、処理時間が for 文や while 文よりも若干長くなる という欠点がある点が気になっている人がいるかもしれません。

木構造のデータ に対する繰り返し処理に関して言えば、それらの欠点はあまり問題にはなりません。その理由について説明します。

前回の記事で説明したように、分岐する繰り返し処理 は、繰り返しの 回数が増える と 処理の数が爆発的に増える という性質があります。実際に木構造のデータは、深さが深くなると ノードの数が大きくなりすぎるため、時間がかかりすぎるという理由で 計算を行うことが実質的に不可能 になります。そのため、木構造に対して再帰呼び出しを使う際に、繰り返しの回数が 問題になることはほとんどありません。

処理時間が長くなる原因は、関数呼び出しの処理に時間がかかることですが、木構造のデータに対して for 文や while 文を使って繰り返し処理を記述する場合は、再帰呼び出しで記述する際には必要のない、ノードの一覧を記録する処理などが必要になります。それらの処理にかかる時間を考慮すると、多くの場合で両者の間で処理時間に大きな違いは生じません。なお、再帰呼び出しでは、それらの処理は関数のローカルな名前空間によって行われます。

ボトムアップとトップダウンの両方を行う繰り返し処理

これまでの例は、繰り返し処理をボトムアップとトップダウンのいずれかの方法で行うものばかりでしたが、ボトムアップとトップダウンの両方を行う 繰り返し処理も存在します。例えば、ゲーム木の作成と、ノードの高さの計算を 同時に行う場合 などです。

そのような処理を再帰呼び出しで行う場合は、ボトムアップな処理を再帰呼び出しの前に記述し、トップダウンな処理を再帰呼び出しの後に記述します。

深さによって異なる処理を行う場合

〇×ゲームのゲーム木は、どのノードも 〇×ゲームの局面という、同一の種類の情報 を表す木構造ですが、そうではない木構造のデータも多数存在 します。

その例が、今回の記事の最初で紹介した〇×ゲームのゲーム盤や、学校の生徒を表す木構造で、以下のように 深さによって ノードが表す データが異なります。

深さ	ゲーム盤	学校の生徒
0	ゲーム盤全体	学校
1	行のデータ	学年
2	セルのデータ	クラス
3		生徒

再帰呼び出し による繰り返し処理は、対象となるデータの種類がすべて同じ場合は向いていますが、上記のような 異なるデータ に対して行う場合は あまり向いていません。このような場合は、再帰呼び出しではなく、for 文や while 文 による繰り返し処理を 入れ子にして記述 するのが一般的です。例えば、〇×ゲームのゲーム盤の場合は、以下のような for 文を入れ子にしたプログラムを記述しました。

# ここにゲーム盤全体に対するボトムアップな処理を記述する
for x in range(3):
    # ここに x 列に対するボトムアップな処理を記述する
    for y in range(3):
        # ここに (x, y) のマスに対する処理を記述する
    # ここに x 列に対するトップダウンな処理を記述する
# ここにゲーム盤全体に対するトップダウンな処理を記述する

これまでの記事では説明していませんでしたが、上記の処理は下記の順番で繰り返し処理が行われるので、深さ優先アルゴリズム による繰り返し処理です。

x を 0 として、y を 0 から 2 まで計算する
x を 1 として、y を 0 から 2 まで計算する
x を 2 として、y を 0 から 2 まで計算する

また、上記のコメントに記述したように、for 文の 前後のどこにプログラムを記述するか によって、どのノードに対する処理 であるかと、ボトムアップとトップダウン の どちらの処理であるか が決まります。

今回の記事のまとめ

今回の記事では、木構造で表現できるデータに対する分岐する繰り返し処理について、以下の分類で記述する方法とその性質を説明しました。

幅優先アルゴリズムと深さ優先アルゴリズムで記述する場合
ボトムアップな手順で記述する場合と、トップダウンな手順で記述する場合
for 文や while 文で記述する場合と、再帰呼び出しで記述する場合

繰り返し処理は、木構造以外の様々なデータに対して行うことができますが、〇×ゲームの AI に必要な繰り返し処理は当面の間はゲーム木を表す木構造のデータなので、繰り返し処理に関する説明は今回の記事で一旦終了し、次回の記事からは、〇×ゲームのゲーム木を使った AI の作成に話を戻します。

本記事で入力したプログラム

今回の記事で作成した mbtree_bf と mbtree_df の中身は、以前にファイルに保存したデータと全く同じなので、改めてファイルに保存することはしません。

リンク	説明
marubatsu.ipynb	本記事で入力して実行した JupyterLab のファイル
tree_new.py	今回の記事で更新した tree.py

次回の記事

木構造は、グラフ構造の一種です ↩
例えば、それぞれのノードに、処理が行われたかどうかを表す属性を追加するという方法などが考えられるでしょう ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up

Pythonで〇×ゲームのAIを一から作成する その104 木構造のデータに対する幅優先と深さ優先アルゴリズムによる繰り返し処理

目次と前回の記事

これまでに作成したモジュール

木構造のデータに対する繰り返し処理

木構造の例

木構造の表現方法

ネットワーク構造との違い

分岐する繰り返し処理を行うアルゴリズム

幅優先アルゴリズムによる繰り返し処理

ボトムアップな繰り返し処理による実装

while 文による実装

再帰呼び出しによる実装

return 文を記述しない理由

トップダウンな繰り返し処理による実装

calc_node_height のバグ

幅優先アルゴリズムの性質

分岐しない再帰呼び出しと多重再帰

深さ優先アルゴリズムによる繰り返し処理

ボトムアップな繰り返し処理による実装

while 文による実装

while 文による実装が複雑になる理由

再帰呼び出しによる実装

プログラムを簡潔に記述できる理由

nodelist などの計算

トップダウンな繰り返し処理による実装

プログラムを簡潔に記述できる理由

ボトムアップとトップダウンな処理の記述場所

深さ優先アルゴリズムの性質

木構造のデータに対する繰り返し処理に関する補足

幅優先と深さ優先アルゴリズムのどちらを使うべきか

再帰呼び出しの欠点に関する補足

ボトムアップとトップダウンの両方を行う繰り返し処理

深さによって異なる処理を行う場合

今回の記事のまとめ

本記事で入力したプログラム

次回の記事

Pythonで〇×ゲームのAIを一から作成する　その104　木構造のデータに対する幅優先と深さ優先アルゴリズムによる繰り返し処理

`calc_node_height` のバグ

`nodelist` などの計算