目次と前回の記事
これまでに作成したモジュール
以下のリンクから、これまでに作成したモジュールを見ることができます。
| リンク | 説明 |
|---|---|
| marubatsu.py | Marubatsu、Marubatsu_GUI クラスの定義 |
| ai.py | AI に関する関数 |
| test.py | テストに関する関数 |
| util.py | ユーティリティ関数の定義 |
| tree.py | ゲーム木に関する Node、Mbtree クラスなどの定義 |
| gui.py | GUI に関する処理を行う基底クラスとなる GUI クラスの定義 |
AI の一覧とこれまでに作成したデータファイルについては、下記の記事を参照して下さい。
図を使った前回の記事の補足説明
前回の記事を読み直してみてわかりづらい点が多いと思いましたので、最初に図を使った補足説明を行ないます。
用語
本記事では前回の記事に引き続き下記の表の用語を用いることにします。記号については今回の記事でもう一度説明します。
| 用語と記号 | 意味 |
|---|---|
| 正確なミニマックス値 | 深さの制限がないゲーム木の探索によって計算される、局面の正確なミニマックス値のこと |
| 近似値 | 静的評価関数が計算する 正確なミニマックス値とは異なる 不正確な値が計算される場合がある 評価値のこと |
| 近似値のミニマックス値 | 深さ制限探索 によって計算される、静的評価関数が計算する 近似値に対するミニマックス値 のこと |
| $\boldsymbol{d}$ | 局面の形勢判断の難しさを表す数値 |
| $\boldsymbol{N(d)}$ | 局面の形勢判断の難しさが $d$ の 局面の集合 |
| $\boldsymbol{M(d)}$ | $N(d)$ の局面に対して静的評価関数が計算する 近似値の平均値 |
| $\boldsymbol{S(d)}$ | $N(d)$ の局面に対して静的評価関数が計算する 近似値の標準偏差(standard variation) |
| $\boldsymbol{N_{mean}(s)}$ | $M(d) = s$ となる局面の集合。静的評価関数の ばらつきをなくした場合 にその局面に対して 計算される近似値 が $s$ となる局面の集合 |
前提条件の説明
説明を簡単にするために以下のような前提条件を付けることにします。
- ゲームには 引き分けがない ものとする
- 最短の勝利や最遅の敗北を目指さないものとする
- 静的評価関数は決着がついた局面の正確なミニマックス値を正しく計算できるものとする
- それ以外の局面で静的評価関数が計算する 近似値の精度がある程度以上高い ものとする
- 大きな正の整数 $\boldsymbol{s}$ を決め、静的評価関数が近似値を 下記の表のように計算 するものとする。なお、$s$ の具体的な値は重要ではないので、本記事では具体的な値は設定しない
| 状況 | 近似値 |
|---|---|
| 決着がついた先手の勝利の局面 | $s + 1$ |
| 先手の必勝と正確に判定できる局面 | $s$ |
| 先手が有利と判定する局面 | $1$ 以上 $s$ 未満の整数 |
| 互角だと判定する局面 | $0$ |
| 後手が有利と判定する局面 | $s-1$ 以上 $-1$ 以下の整数 |
| 後手の必勝と正確に判定できる局面 | $-s$ |
| 決着がついた後手の勝利の局面 | $-s - 1$ |
以前の記事で説明したように、静的評価関数が でたらめな近似値 や、精度が低い近似値 を計算すると、深さの上限を上げても 近似値のミニマックス値の精度が高くなることはありません。「静的評価関数が計算する近似値の精度がある程度以上高いものとする」という前提条件を付けた理由はそのためです。ある程度以上という表現はあいまいですが、そのゲームの上級者以上のレベルの強さの AI を作成できるような精度だと考えて下さい。
静的評価関数が計算する近似値の意味
静的評価関数は決着がついている局面に対しては正確なミニマックス値を計算できるので、以後は 決着がついていない局面の説明を行う ことにします。
ゲームに引き分けがないことにしたので、すべての局面 は 先手の必勝の局面 と 後手の必勝の局面 の 2 種類 に分類されます。従って決着がついていない局面の 正確なミニマックス値 は $\boldsymbol{s}$ または $\boldsymbol{-s}$ となります。
静的評価関数 が 先手の必勝の局面 に対して 正の近似値を計算 した場合は、その局面が先手の必勝の局面であると 正しく判定している という意味になり、その数値が 小さいほど自信がなく、大きいほど 先手の必勝であることを 確信している という事を意味します。負の近似値を計算した場合はその逆の意味になります。
局面の形勢判断の難しさの概念の導入
静的評価関数が計算する 近似値 は、局面の 形勢判断の難しさ を表していると考えることができます。形勢判断が難しく、どちらの必勝であるかが はっきりしない局面 は近似値として 0 に近い値が計算 され、形勢判断が簡単で 先手の必勝 であることが 明確な局面 は近似値として $\boldsymbol{s}$ に近い値が計算 されます。
また、ある程度以上強い複数の将棋の AI が 同じ局面でほぼ同じ評価値を計算 することから、形勢判断の難しさ を 数値として計算できる と 仮定 して話を進めることにします。具体的には、局面の 形勢判断の難しさ を 0 以上 $\boldsymbol{m}$ 以下の整数 で計算する 仮想的な関数を仮定 することにします。ゲームの 決着がついた局面 は局面の状況を必ず正しく判定できるので 難しさは 0、どちらの必勝の局面かが 判断できない最も形勢判断が難しい局面 の 難しさは $\boldsymbol{m}$ となります。
以後は説明を簡潔にするために、その仮想的な関数によって計算される 局面の形勢判断の難しさ を単に $\boldsymbol{d}$ と表記 することにします。また、形勢判断の難しさが $d$ の 局面の集合 を $N(\boldsymbol{d})$ と表記することにします。
形勢判断の難しさに関する補足
実際には将棋や囲碁のような複雑なゲームの局面の形勢判断の難しさを 厳密に計算 する関数を定義することは 現実的には不可能 だと思います。その理由の一つは、形勢判断の難しさを 厳密に定義することがほぼ不可能 だからです。
難しさを定義することが困難な具体例として、小学校で学ぶ 整数の四則演算(+-×÷)が挙げられると思います。一般的に四則演算は +、-、×、÷ の順で難しい と言えるように 思えるかもしれません が、そうとは限りません。
例えば 2 桁の整数の四則演算 であれば、足し算の方が掛け算よりも難しいと思う かもしれませんが、$89 + 48$ と $20 × 30$ を比べるとおそらく ほとんどの方 が $\boldsymbol{20 × 30}$ の方が簡単 だというと思います。
また、多くの人 は $\boldsymbol{19 × 21}$ は難しいと思う のではないかと思いますが、$\boldsymbol{(x - 1)(x + 1) = x^2 -1}$ という 数学の公式を知っていれば、$19 × 21 = (20 - 1)(20 + 1) = 20 ^2 - 1 = 400 - 1 = 399$ のように、暗算で簡単に計算 することができます。
また、ほとんどの人が暗算はとても無理だと思う $\boldsymbol{255 × 257}$ は、コンピューター科学を専門とする人 であれば $(256 - 1) × (256 + 1) = 256 × 256 - 1 × 1 = 65536 - 1 = 65535$ のように 簡単に暗算できる人が多いでしょう。これは、コンピューター科学を専門とする人は 2 進数に関する計算に親しんでおり、$2^8 = 256$、$256 × 256 = 2 ^ {16} = 65536$ であることを 暗記している人が多い からです。
このように一見すると難しさを簡単に定義できそうな整数の四則演算でさえ、実際には 厳密な難しさを定義することは困難 で、その人の 知識によって 同じ問題でも 難しさは大きく変わります。これは将棋や囲碁のようなゲームの局面も同様で、プロであっても自分が 得意な局面とそうでない局面 があるため、同じ局面であっても形勢判断が簡単だと考える人と、そうでないと考える人が存在します。クイズの問題の難易度なども同様でしょう。
ただし、厳密な難しさを定義することはできなくても 大雑把で良いのであれば何らかの方法 で、多くの人が ある程度納得できるような 整数の四則演算の 難しさを定義することはできる のではないかと 思います。本記事で仮定する形勢判断の難しさ も厳密なものではなく、何らかの方法で定義した そのゲームの上級者が納得できるようなもの だと考えて下さい。
静的評価関数の誤差の精度を表すグラフ
静的評価関数の 近似値 の 誤差の精度が高い ということは、形勢判断が難しい局面に対して精度が低い静的評価関数よりも 自信をもって形勢判断を行うことができる ということを意味します。現実の世界に当てはめると、将棋の初心者にとってどちらが優勢であるかを判断できないよう 難解な局面でも、将棋が強くなればなるほど どちらが有利であるかを 正確に判断することができる ようになります。
前回の記事ではこのことを言葉だけで説明したのでわかりづらかったのではないかと思いましたので、そのことを 図で説明する ことにします。なお、下図はあくまでイメージです。実際の静的評価関数がこのような 単調増加 する 滑らかな形のグラフになるとは限らない 点に注意して下さい。静的評価関数によっては 特定の性質を持つ局面の形勢判断を行うことが得意 なものもあるので、グラフが 波打つような形になるものもある でしょう。
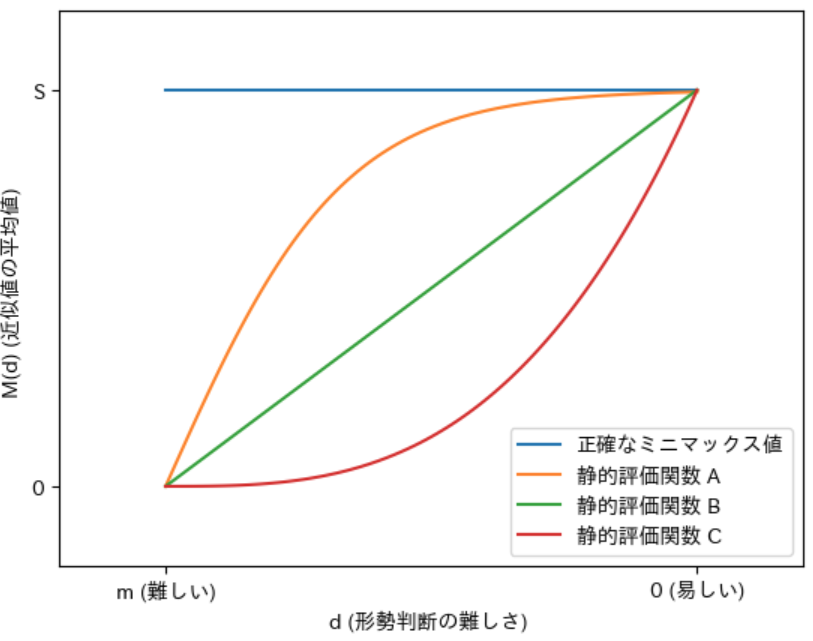
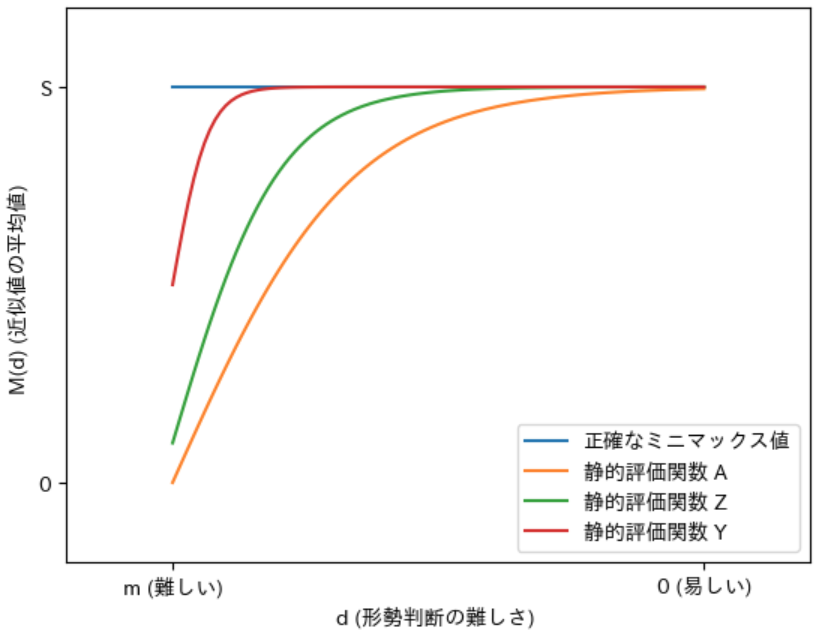
上図は 先手の必勝の局面 に対して 3 種類の静的評価関数 が計算する 近似値を表す グラフです。グラフの 横軸が局面の形勢判断の難しさ を、縦軸 がその難しさの局面に対して静的評価関数が計算する 近似値の平均値 を表します。前回の記事では局面の難しさが $d$ の局面に対して計算される近似値の平均値を $\boldsymbol{M(d)}$ と表記しましたので、本記事でもその記号で表記することにします。また、以後はグラフ内の「静的評価関数 A」のグラフを単に A のように表記することにします。
先手の必勝の局面 なので、正確なミニマックス値 は 常に青色の線 が表す $\boldsymbol{s}$ となります。従って、$\boldsymbol{s}$ と 静的評価関数が計算した $\boldsymbol{M(d)}$ との差 が 誤差 となります。
図から 3 種類の静的評価関数は すべての $\boldsymbol{d}$ で A、B、C の順 で $\boldsymbol{M(d)}$ と $\boldsymbol{s}$ との誤差が小さい ので、誤差の精度は A、B、C の順で精度が高い と言えます。
実際には静的評価関数によって 形勢判断が得意な局面が異なる ことがあるので、ある $d$ に対しては A のほうが誤差が少ないが、別の $d$ に対しては B の方が誤差が少ないこともあります。そのような場合は上記の グラフの線は交差 します。
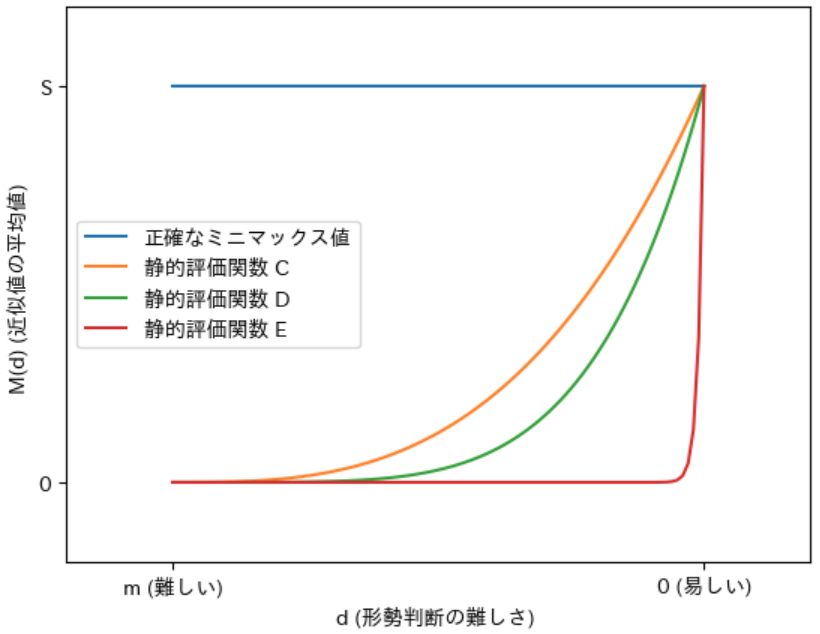
上図の A の静的評価関数の精度 を さらに高める と、下図の Z、Y のようにグラフが 正確なミニマックス値 を表す 青色のグラフに近づいていきます。このことから、静的評価関数の 誤差の精度を高める ということは 青色のグラフ の近似値を 計算することを目指す という事を意味し、精度が 100 % になると 青色のグラフと一致する ようになることがわかります。
逆に静的評価関数の 精度が低くなる と、下図の D、E のように計算される $\boldsymbol{M(d)}$ が 0 に近づいていきます。このことから、近似値として 常に 0 を計算 する ai2s は 最も精度が低い 静的評価関数であると 考えることができます。
静的評価関数のばらつき
上記のグラフは静的評価関数が、同じ難しさ の形勢判断の局面に対して計算する 近似値の平均値 を表しますが、実際に計算 される近似値には ばらつきが生じます。また、その ばらつき は前回の記事で説明した 標準偏差 で 数値として表す ことができます。
同じテストを受けた学生のテストの点数の分布のように、同じ種類のデータを複数計測 した際に得られるデータのヒストグラムは、下図のような 平均値付近を中心とした山形の分布 になるのが 一般的 です。

もちろん、実際の静的評価関数が $N(d)$ に対して計算する近似値の分布は平均値を中心とした山形になるとは限りませんが、ばらつきが少なくなる(精度が高くなる)と ほとんどの値が平均値に近くなる ので、平均値を中心 とした 左右対称の山形の分布 に 近づきます。先程「静的評価関数が計算する 近似値の精度がある程度以上高い ものとする」という前提条件をつけたので、本記事では $N(d)$ に対して静的評価関数が計算する 近似値の分布 が近似値の 平均値である $\boldsymbol{M(d)}$ を中心 とする 左右対称となる山形 であるものとします。
形勢判断の難しさとばらつきの精度の関係
形勢判断が簡単な局面 であればあるほど、正確な形勢判断を行なえる ことは明らかです。実際に、形勢判断が最も容易 なゲームの 決着がついた局面 は必ず正確なミニマックス値を計算できるので、近似値のばらつきを表す 標準偏差は 0 になります。従って、形勢判断が難しいほど 近似値のばらつきを表す 標準偏差は大きくなる と考えることができます。本記事では $M(d)$ の局面に対して計算された 近似値の標準偏差 を $\boldsymbol{S(d)}$ と表記することにします。
下図は 先手の必勝の局面 に対して 3 種類の静的評価関数が計算する $\boldsymbol{S(d)}$ を表すグラフ です。グラフの 横軸が局面の形勢判断の難しさ を、縦軸 がその難しさの局面に対して静的評価関数が計算する 近似値の標準偏差 を表します。図から 3 種類の静的評価関数はすべての場合で F、G、H の順で標準偏差が小さい ので、ばらつきの精度 は F、G、H の順で高い と言えます。

上記のグラフは単調減少する直線ですが、実際の静的評価関数に対するグラフの形状は単調減少するとは限らないので、波打つような曲線になるものもあるでしょう。
このように、局面の形勢判断の難しさ によって ばらつきは変化 しますが、一方で局面の形勢判断の難しさを表す $\boldsymbol{d}$ が近い、すなわち近似値の平均値を表す $\boldsymbol{M(d)}$ の値が近ければ、ばらつきはほぼ同じになる とみなすことができます。前回の記事で 形勢判断の難しさに関わらず、計算される 近似値の分布の形が同じ であるとした理由は、前回の記事 で 深さの上限が 1 の場合の近似値のミニマックス値の 標準偏差の計算 を行う際に、静的評価関数が計算する子ノードの $\boldsymbol{M(d)}$ が 0 と -1 のように 近い場合 に対する計算を行なったからです。
静的評価関数の誤差の精度と形勢判断の正確さの関係
次に、誤差の精度 が 形勢判断の正確さに及ぼす影響 について図で説明します。なお、具体的な数値を使って計算するとかえってわかりづらくなると思いますので、具体的な数値は最小限 にし、図の見た目から判断できる ような例で説明します。
B のほうが誤差の精度が高い 2 つの静的評価関数 A と B があり、近似値のばらつきの精度は同じ であるとします。B のほうが誤差の精度が高いので、先手の必勝で $d$ が同じである $N(d)$ の局面に対して計算する 近似値の平均値 $\boldsymbol{M(d)}$ は B のほうが大きく なります。
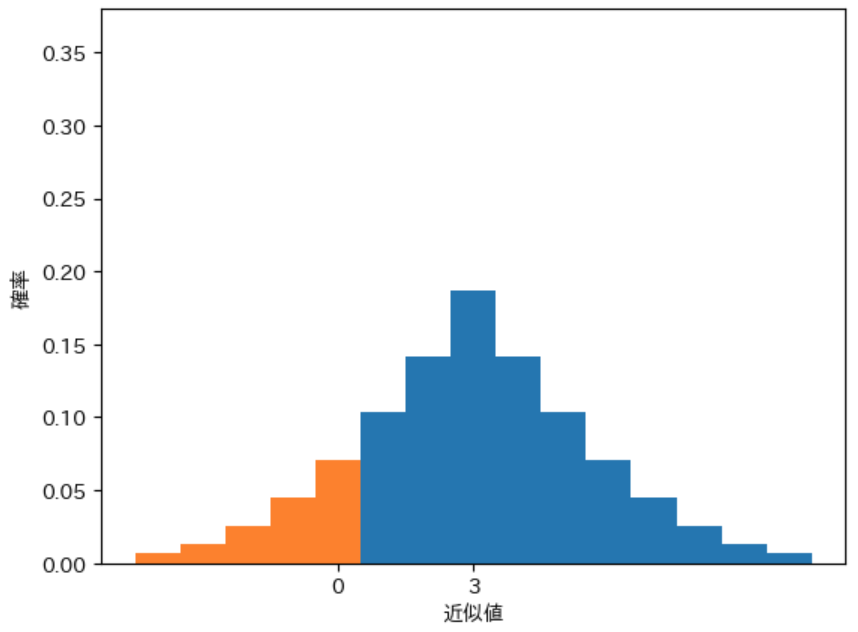
下図は、先手が必勝で形勢判断の難しさが $d$ の局面に対する 近似値の平均値 $\boldsymbol{M(d)}$ を A が 3、B が 5 と計算した場合に計算される近似値の 確率分布のヒストグラム です。
$M(d) = 3$ の場合
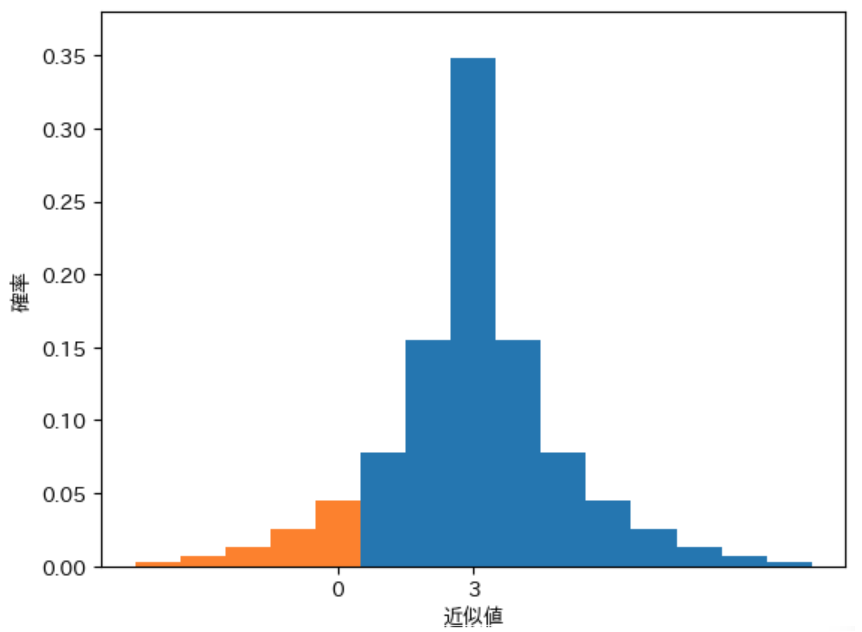
$M(d) = 5$ の場合

ばらつきの精度が同じ で $\boldsymbol{M(d)}$ の値が近い ことから、グラフの形状はどちらも同じ としました。先手の必勝の局面 なので、正の近似値を計算 した場合に 形勢を正しく評価 したことになります。従って 0 以下の近似値が計算 される、オレンジの部分 の 全体の面積に対する割合 が 間違った形勢判断 を行う 割合 を表します。図から明らかに 近似値の平均値が高い B のヒストグラムのほうが オレンジの部分の面積が狭い ので、B のほうが 形勢を正しく評価できる確率が高い ことがわかります。このことから、静的評価関数の 誤差の精度が高いほう が 形勢判断をより正確に行なえる確率が高い ことがわかります。
静的評価関数のばらつきの精度と形勢判断の正確さの関係
次に、ばらつきの精度 が 形勢判断の正確さに及ぼす影響 について図で説明します。
D のほうがばらつきの精度が高い 2 つの静的評価関数 C と D があり、近似値の誤差の精度は同じ であるとします。下記の 2 つのグラフは 先手の必勝の局面 で、C と D が $\boldsymbol{M(d)}$ が 3 の局面に対して計算した 近似値の確率分布のヒストグラム を表します。D のほうが ばらつきの精度が高い ので ヒストグラムの幅が狭 くなり、間違った形勢判断 を行う オレンジの部分の面積が狭く なります。
ばらつきの精度が低い C のヒストグラム
ばらつきの精度が高い D のヒストグラム
見た目ではその違いがわかりづらいのではないかと思いましたので、上記の 2 つのグラフを重ねた 下図のグラフを示します。
赤色の部分 が D が間違った形勢判断を行う 0 以下の近似値を計算した 部分です。図から 明らかに C が間違った形勢判断を行うオレンジ色の面積 よりも小さい ことがわかります。このように、ばらつきの精度が高いほう が 形勢判断をより正確に行える ことがわかります。
上記から、静的評価関数の 誤差の精度 と、ばらつきの精度 が、どちらも 形勢判断をより正確に行うために 重要であることが確認 できました。
高い近似値を選択したほうが良い理由
静的評価関数が計算する 近似値にばらつきが存在せず、静的評価関数が 先手の必勝の局面に対して正の近似値、後手の必勝の局面に対して負の近似値 を計算する場合は、その 値の大小に関わらず常に正しく形勢判断を行う ことができます。その場合は、静的評価関数が計算した 近似値が正の合法手を指し続ければ、それが どの子ノードの合法手であっても 先手が 必ず勝利する ことができます。
一方、現実の静的評価関数 が計算する 近似値 には ばらつきが存在 します。ばらつきが存在する場合 は、先程説明したように、近似値の平均値が高い 子ノードの 合法手を選択したほうが、形勢判断を間違う可能性が低く なります。前回の記事で説明したように、二人零和有限確定完全情報ゲーム では、一度のミスが勝率に大きな影響 を及ぼすので、形勢判断を正しく行う ことができる 確率が高い局面になるような合法手を選択 することが 非常に重要 です。これが、静的評価関数が 正確なミニマックス値を計算できなくても、ミニマックス法 に従って max ノードで 最も高い近似値 の子ノードを 選択するべきである理由 です。min ノードで最も低い近似値の子ノードを選択するべきである理由も同様です。
深さの上限が 1 の場合の計算を行う関数の定義
前回の記事では、深さの上限が 1 の場合に計算される 近似値のミニマックス値 の 確率分布 とその 期待値1と標準偏差 の計算を 手作業で行いました が、その際に かなりの手間 がかかりました。前回の記事とは異なる 様々な状況で同様の計算を行う のは 大変なの で、その確率分布の計算を行う 下記のような 関数を定義 することにします。なお、確率分布の期待値と標準偏差の計算を行う関数についてはその後で定義することにします。
名前:近似値のミニマックス値の 確率分布(probability distribution)の計算 を行うので calc_pdist とする
処理:2 つの子ノード に対して計算される 近似値の確率分布 を使って max ノード である局面の近似値のミニマックス値の 確率分布を計算 する
入力:仮引数 pdistA、pdistB に 2 つの子ノードの 近似値の確率分布 を代入する
出力:max ノード の近似値のミニマックス値の 確率分布を表すデータ
確率分布を表すデータ構造
上記の関数を定義するためには、近似値の確率分布 を表すデータの データ構造を考える 必要があります。どのようなデータ構造にすれば良いかについて少し考えてみて下さい。
本記事では下記のようなデータ構造で確率分布を表すことにします。なお、list で表現しなかった理由 は、list の インデックス に 負の値を設定できない からです。
- キーを近似値、キーの値を その近似値が計算される 確率 とした dict
例えば、前回の記事で用いた、任意の $d$ に対して下記のような 確率分布で近似値を計算 する 静的評価関数 を考えることにします。
| 近似値の平均値 $\boldsymbol{M(d)}$ との差 | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| 局面の割合 | 5% | 20% | 50% | 20% | 5% |
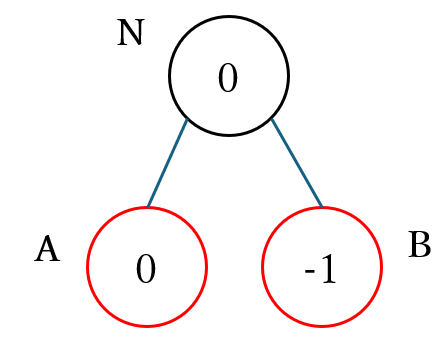
前回の記事と同様に、下図の max ノードである ノード N の近似値のミニマックス値を 深さの上限が 1 の深さ制限探索で計算した場合の 確率分布 とその 標準偏差を計算 することにします。黒枠のノードが max ノード、赤枠のノードが min ノードを表します。円の中の数値 は、その局面が $\boldsymbol{M(d) =}$ 円の中の数値 となる局面の集合に属することを表し、静的評価関数の ばらつきをなくした場合 にその局面に対して 計算される近似値 を表します。前回の記事ではこの $M(d) = s$ となる局面の集合を $\boldsymbol{N_{mean}(s)}$ と表記することにしました。
上図の $M_{mean}(0)$ と $M_{mean}(1)$ に属する ノード A と ノード B を静的評価関数で計算した際の 確率分布 pdistA と pdistB は下記のプログラムのように記述できます。
pdistA = {
-2: 0.05,
-1: 0.2,
0: 0.5,
1: 0.2,
2: 0.05
}
pdistB = {
-3: 0.05,
-2: 0.2,
-1: 0.5,
0: 0.2,
1: 0.05
}
product による直積の計算方法
前回の記事で行なったように、上図のノード N の近似値のミニマックス値の 確率分布を計算 するためには、ノード A と ノード B で計算される 近似値のすべての組み合わせ と その確率を計算 する必要があります。そのような 複数の集合の中 から 1 つずつ要素を取り出した 場合の すべての組み合わせの事 を 直積 と呼び、Python で効率的な イテレータ を作成する関数を集めた itertools という組み込みモジュールの product という関数を利用して 直積を計算 することができます。イテレータについてはこの後で説明します。
product は実引数に記述した 集合を表す list などの 反復可能オブジェクト の 直積を計算 し、計算した 直積を表すイテレーター を 返り値として返す 処理を行います。
product の詳細については下記のリンク先を参照して下さい。
product の具体的な 使用例 を示します。下記のプログラムは、["A", "B", "C"] と [1, 2] を実引数に記述して product を呼び出すプログラムで、直積の集合を表す イテレータ が返されます。
from itertools import product
prod = product(["A", "B", "C"], [1, 2])
print(prod)
実行結果
<itertools.product object at 0x0000019BF4620580>
イテレータの性質
以前の記事で list などの 反復可能オブジェクト と イテレータ は似ているが 異なるものである と説明しました。その 違いの一つ が print での内容の表示 で、イテレータの場合は上記の実行結果のようにその 具体的な内容は表示されません。
一方、イテレータ は反復可能オブジェクトと同様に、下記のプログラムのように for 文 を利用することでその 中身を順番に取り出す ことができ、実行結果から ["A", "B", "C"] と [1, 2] の すべての組み合わせ が tuple の形式 で 計算されている ことが確認できます。
for data in prod:
print(data)
実行結果
('A', 1)
('A', 2)
('B', 1)
('B', 2)
('C', 1)
('C', 2)
また、product で作成した イテレータ を list の実引数に記述 して呼び出すことで、下記のプログラムのように list の形式にデータを変換 することができます。
print(list(product(["A", "B", "C"], [1, 2])))
実行結果
[('A', 1), ('A', 2), ('B', 1), ('B', 2), ('C', 1), ('C', 2)]
先程 for 文で使用した prod を下記のプログラムで list に変換して表示すると中身が空の list が表示されます。このように、イテレータは list などの反復可能オブジェクトと異なり for 文での使用後は利用できなくなる ので、再利用できない 使い捨てのデータ であると言えます。
print(list(prod))
実行結果
[]
イテレータと反復可能オブジェクト(iterable)の具体的な違いについての知識は、product を利用する際に必要ではないので必要になった時点で説明することにします。興味がある方は下記の Python の公式のドキュメントを参照して下さい。
product による確率分布を表す集合の直積の計算方法
下記のプログラムで先程の pdistA と pdistB を product の実引数に記述 して list に変換 すると、実行結果のようにノード A と ノード B で計算される 5 × 5 = 25 通り の 近似値の組み合わせを表す tuple を要素として持つ list が表示されますが、それぞれの 組み合わせの確率を計算するために必要 な 確率のデータが含まれていない という問題があります。
from pprint import pprint
pprint(list(product(pdistA, pdistB)))
実行結果
[(-2, -3),
(-2, -2),
(-2, -1),
(-2, 0),
(-2, 1),
(-1, -3),
(-1, -2),
(-1, -1),
(-1, 0),
(-1, 1),
(0, -3),
(0, -2),
(0, -1),
(0, 0),
(0, 1),
(1, -3),
(1, -2),
(1, -1),
(1, 0),
(1, 1),
(2, -3),
(2, -2),
(2, -1),
(2, 0),
(2, 1)]
近似値が計算される確率 を 組み合わせのデータ内に入れる ためには、下記のプログラムのように dict の キーとキーの値の一覧 を表す items メソッドの返り値 を product の実引数に記述します。実行結果から、 ((ノード A の近似値, その確率), (ノード B の近似値, その確率)) という tuple で 25 通りの組み合わせが計算 されることが確認できます。
pprint(list(product(pdistA.items(), pdistB.items())))
実行結果
[((-2, 0.05), (-3, 0.05)),
((-2, 0.05), (-2, 0.2)),
((-2, 0.05), (-1, 0.5)),
((-2, 0.05), (0, 0.2)),
((-2, 0.05), (1, 0.05)),
((-1, 0.2), (-3, 0.05)),
((-1, 0.2), (-2, 0.2)),
((-1, 0.2), (-1, 0.5)),
((-1, 0.2), (0, 0.2)),
((-1, 0.2), (1, 0.05)),
((0, 0.5), (-3, 0.05)),
((0, 0.5), (-2, 0.2)),
((0, 0.5), (-1, 0.5)),
((0, 0.5), (0, 0.2)),
((0, 0.5), (1, 0.05)),
((1, 0.2), (-3, 0.05)),
((1, 0.2), (-2, 0.2)),
((1, 0.2), (-1, 0.5)),
((1, 0.2), (0, 0.2)),
((1, 0.2), (1, 0.05)),
((2, 0.05), (-3, 0.05)),
((2, 0.05), (-2, 0.2)),
((2, 0.05), (-1, 0.5)),
((2, 0.05), (0, 0.2)),
((2, 0.05), (1, 0.05))]
calc_pdict の定義
下記は calc_pdict を定義するプログラムです。近似値のミニマックス値の 確率分布 は、それぞれの組み合わせ で計算される 近似値の確率を加算 することで計算します。その際に、以前の記事で説明した defaultdict を利用した集計 を行なっています。
- 1 行目:確率分布を計算する際に必要となる defaultdict をインポートする
-
3 行目:仮引数
pdistA、pdistBを持つ関数として定義する -
4 行目:近似値のミニマックス値の確率分布を表す
resultをデフォルト値を 0 とする defaultdict で初期化する -
5 行目:
pdistAとpdistBの直積を表すデータを計算する - 6 行目:直積からそれぞれの子ノードの近似値と確率を取り出して繰り返し処理を行う
- 7 行目:max ノードなので 2 つの子ノードの近似値の最大値が近似値のミニマックス値となるのでその計算を行う
- 8 行目:その組み合わせの近似値が計算される確率を計算する
-
9 行目:
resultの 近似値のミニマックス値のキーの値に、8 行目で計算した確率を加算する - 10 行目:計算された近似値のミニマックス値の確率分布を返り値として返す
1 from collections import defaultdict
2
3 def calc_pdist(pdistA, pdistB):
4 result = defaultdict(int)
5 productdata = product(pdistA.items(), pdistB.items())
6 for ((scoreA, probA), (scoreB, probB)) in productdata:
7 score = max(scoreA, scoreB)
8 prob = probA * probB
9 result[score] += prob
10 return result
行番号のないプログラム
from collections import defaultdict
def calc_pdist(pdistA, pdistB):
result = defaultdict(int)
productdata = product(pdistA.items(), pdistB.items())
for ((scoreA, probA), (scoreB, probB)) in productdata:
score = max(scoreA, scoreB)
prob = probA * probB
result[score] += prob
return result
下記は、pdistA と pdistB を子ノード A、B が計算する近似値の確率分布とした場合の、近似値のミニマックス値の確率分布を計算するプログラムで、前回の記事で計算した確率分布とほぼ同じ 内容が計算されていることが確認できます。
pprint(calc_pdist(pdistA, pdistB))
実行結果
defaultdict(int,
{-2: 0.012500000000000002,
-1: 0.17500000000000002,
0: 0.525,
1: 0.23750000000000004,
2: 0.05000000000000001})
誤差についての補足
前回の記事では 近似値が -2 に対する 確率を 0.0125 と計算 しましたが、上記では 0.012500000000000002 というほんの少しだけ異なる確率が計算されています。
これは、Python に限らずコンピューターが内部では数値を 2 進数で計算しているため、小数点以下を含む 10 進数の数値を正確に計算することができない場合があるからです。
具体例として 10 進数の 0.1 は 2 進数では .00011001100110011・・・ のような 無限に 0011 が繰り返される 値になるので正確に表現することはできません。
このような誤差は、四捨五入などを行うことで 見た目は発生していないような工夫 がされていますが、誤差が無くなっているわけではないので下記の 0.1 * 3 の計算結果が 0.30000000000000004 になることから、誤差の存在が表面化 することが実際にあります。
print(0.1 * 3)
実行結果
0.30000000000000004
このような 誤差は非常に小さい ので 多くの計算では無視しても問題ありません が、場合によってはこのような 誤差によって意図しない計算結果が生じる という バグが発生することがある 点に注意が必要です。バグの具体例については今後の記事で紹介する予定です。
期待値と標準偏差の計算
次に、確率分布 から 期待値(expectation value)、分散(variance)、標準偏差(standard deviation) の 統計データ(statistic value)を計算する関数 calc_stval を下記のプログラムのように定義することにします。行っている処理は、前回の記事で説明した式で確率分布の期待値、分散、標準偏差を計算して返しているだけなので説明は省略します。
def calc_stval(pdist):
e = 0
for s, p in pdist.items():
e += s * p
var = 0
for s, p in pdist.items():
var += ((s - e) ** 2) * p
std = var ** 0.5
return e, var, std
下記のプログラムで、pdistA、pdistB、と先程計算した ノード N の確率分布 の統計データを計算すると、実行結果のように 前回の記事とほぼ同じ 結果が計算されるので 正しい値が計算された ことが確認できます。なお、下記の計算でも先程説明した極微小な誤差が発生しています。
print(calc_stval(pdistA))
print(calc_stval(pdistB))
print(calc_stval(calc_pdist(pdistA, pdistB)))
実行結果
(-2.7755575615628914e-17, 0.8, 0.8944271909999159)
(-1.0, 0.8, 0.8944271909999159)
(0.13750000000000007, 0.6435937500000002, 0.8022429494860022)
今回の記事のまとめ
今回の記事では最初に図を使った前回の記事の補足説明を行いました。
次に、深さの上限が 1 の深さ制限探索での近似値のミニマックス値の確率分布と統計データを計算する関数を定義しました。
本記事で入力したプログラム
今回の記事で定義した calc_pdist と calc_stval はゲーム木に関連する処理なので、tree.py に保存することにします。
| リンク | 説明 |
|---|---|
| marubatsu.ipynb | 本記事で入力して実行した JupyterLab のファイル |
| tree.py | 本記事で更新した tree_new.py |
次回の記事
-
期待値 はデータの集合から複数のデータを取り出した場合に 想定される平均値 のことを表す用語です。一方、平均値は 実際に取り出したデータ に対する平均値のことなのでその意味は異なります。確率分布 は個々の データが発生する確率を表す ので、確率分布から計算される平均値は 期待値 と表現されます ↩