Pythonで〇×ゲームのAIを一から作成する　その175　静的評価関数の近似値の誤差の精度とばらつきの精度

Last updated at 2025-06-14Posted at 2025-06-08

目次と前回の記事

これまでに作成したモジュール

以下のリンクから、これまでに作成したモジュールを見ることができます。

リンク	説明
marubatsu.py	Marubatsu、Marubatsu_GUI クラスの定義
ai.py	AI に関する関数
test.py	テストに関する関数
util.py	ユーティリティ関数の定義
tree.py	ゲーム木に関する Node、Mbtree クラスなどの定義
gui.py	GUI に関する処理を行う基底クラスとなる GUI クラスの定義

AI の一覧とこれまでに作成したデータファイルについては、下記の記事を参照して下さい。

深さの上限と評価値の近似値の精度の関係

前回の記事では、深さ制限探索で 深さの上限を上げる と 精度が高くなる理由 には以下のようなものがあることを示しました。ただし、静的評価関数が決着がついた局面の評価値を正確に計算できるものとします。

深さの上限を上げると、正確な評価値を計算できる 決着がついた局面 を静的評価関数が 計算する割合が増える ため
深さの上限を上げると、より多くの着手が行われた局面 に対して静的評価関数が評価値を計算することになる。一般的 に 着手が行われるほど形勢を判断しやすくなる ので 評価値の精度が上がる

ただし、これらは 決着がつくまでに長い手数がかかる オセロや将棋などの ゲームの序盤 では あてはまりません ので、今回の記事では他の理由について説明します。

今回の記事からしばらくは、〇×ゲームのような小規模なゲーム木ではなく、オセロや将棋のような ノードの数 が現実的な時間で 計算しきれないほど多いゲーム木 に対する深さ制限探索について説明します。

用語の整理

これまでは、ミニマックス値の近似値という用語を、静的評価関数が計算した評価値と、深さ制限探索で計算された評価値の両方の場合で使用してきましたが、記事を書いていて自分でも混乱しましたので、以後は以下の用語を使うことにします。

本記事では 静的評価関数が計算する評価値 のことを、深さの制限のないゲーム木の探索によって計算されるミニマックス値とは異なる 不正確な値が計算される場合がある ことから、近似値と表記 することにします。

深さ制限探索 によって計算されるミニマックス値は、静的評価関数が計算する近似値を元に計算されるので 近似値のミニマックス値 と表記することにし、深さの制限のないゲーム木の探索によって計算される値を 正確なミニマックス値 と表記することにします。なお、深さの上限を 0 とした場合は、近似値 と 近似値のミニマックス値 は 同じ意味 を表します。

なお、一般的 には上記のような用語の区別は行わず、AI が何らかのアルゴリズムで計算した 局面の状況を表す数値 の事を単に 評価値 と呼び、強解決な AI でない限り評価値は誤差を持ちます。

近似値のミニマックス値の精度の定義

深さ制限探索で深さの上限を上げると近似値のミニマックス値の精度が高くなる理由について説明するためには、精度の意味を明確にする 必要があります。そこで、本記事における近似値のミニマックス値の 精度を定義 することにします¹。

静的評価関数が計算する近似値の設定

最初に 静的評価関数 が どのような近似値を計算するか について決めることにします。

決着がついた局面の計算

決着がついた局面 は、ゲームのルールから局面の状況を正確に計算することができるので、静的評価関数は決着がついた局面の 正確なミニマックス値を計算する ものとします。

近似値のデータ型

深さ制限探索 では、スカウト法などの null window search を利用 する探索アルゴリズムをベースとすることがあります。null window search を行うためには、計算される 評価値が整数であることが望ましい ので、静的評価関数が 整数の近似値を計算する ことにします。

近似値の範囲と引き分けの除外

多くのゲームの AI では、静的評価関数が計算する 近似値の範囲 を以前の記事で説明したように 大きな正の整数 $\boldsymbol{s}$ を決め、近似値を 下記の表のように計算 します。なお、最短の勝利と最遅の敗北を目指す場合は下記の表と若干異なりますが、話を簡単にするために以後の説明では 最短の勝利と最遅の敗北を目指さない場合 を説明します。

状況	近似値
決着がついた先手の勝利の局面	$s + 1$
先手の必勝と正確に判定できる局面	$s$
先手が有利と判定する局面	$1$ 以上 $s$ 未満の整数
決着がついた引き分けの局面引き分けと正確に判定できる局面互角だと判定する局面	$0$
後手が有利と判定する局面	$s-1$ 以上 $-1$ 以下の整数
後手の必勝と正確に判定できる局面	$-s$
決着がついた後手の勝利の局面	$-s - 1$

上記の表からわかるように、近似値として 0 が計算 された場合は、決着がついた引き分けの局面、引き分けと正確に判定できる局面、互角だと判定する局面の 3 種類がある点が複雑 です。そこで、以後は説明を簡単にするために、引き分けがないゲームの場合の説明 を行うことにします。下記は上記の表の修正版です。なお、引き分けがあった場合でも深さの上限を上げると精度が高くなることに変わりはないと思います。

状況	近似値
決着がついた先手の勝利の局面	$s + 1$
先手の必勝と正確に判定できる局面	$s$
先手が有利と判定する局面	$1$ 以上 $s$ 未満の整数
互角だと判定する局面	$0$
後手が有利と判定する局面	$s-1$ 以上 $-1$ 以下の整数
後手の必勝と正確に判定できる局面	$-s$
決着がついた後手の勝利の局面	$-s - 1$

近似値は、正の値で大きいほど先手が有利、負の値で小さいほど後手が有利、0 に近いほ互角であると静的評価関数がみなしていることを表します。

将棋の AI の評価値 の多くは -32768 ~ 32767 の整数を表現できる 2 バイトの 整数で表現されている ようで、その場合は $\boldsymbol{s}$ に 約 30000 という大きな値が設定 されているようです。

本記事では具体的な $s$ は設定しませんが、上記の表のような近似値を静的評価関数が計算することにします。

将棋の AI が計算する評価値の範囲は約 -30000 ~ 約 30000 と幅広いようですが、その数値の意味の目安は以下のように考えられているので、ほぼ互角を意味する評価値の範囲は -300 ~ 300 のようにかなり狭いようです。また、強い AI どうしが対戦した場合に、評価値が先手の優勢になると、ほぼ確実に先手が勝利するようです。

評価値	目安
1000 以下	後手が勝勢
-700 ~ -600	後手が優勢
-300 前後	後手が有利
0 前後	互角
300 前後	先手が有利
600 ~ 700	先手が優勢
1000 以上	先手が勝勢

約 -30000 ~ 約 30000 という評価値はわかりづらいので、評価値に計算を行う²ことで 0 ~ 1 の範囲に置き換えて 59 % のようにパーセントで表記することがよくあります。0 % に近いほど後手が有利、50 % に近いほど互角、100 % に近い程先手が有利であることを意味します。なお、小数点以下の数値は四捨五入して表示しますが、どちらかが必勝の局面であることが判明していない場合に 0 % や 100 % と表記すると誤解が生じるため、その場合は 1 % や 99 % と表記するのが一般的なようです。

パーセントで評価値が表示された場合に、その値を 80 % の確率で先手が勝利するという、先手の勝率の意味だと誤解している人が多いのではないかと思いますが、この数字は勝率を表す値ではありません。80 % という数字は有利さの目安を表す数字だと考えて下さい。100 点満点の 80 点のように考えると良いかもしれません。

静的評価関数の近似値の誤差の精度

二人零和有限確定完全情報ゲーム は、すべての 局面の状態 が「先手の勝利の局面」、「引き分けの局面」、「後手の勝利の局面」の 3 種類のいずれかに分類 されます。先程 引き分けがない ことにしたので、その場合はそれぞれの局面の状態の 正確なミニマックス値 は、最短の勝利を目指さない場合は $-s-1$、$s+1$ のように 2 種類の整数で表現 できます。

ただし、ほとんどの局面 では、その 局面の情報だけから その局面が どの状況であるかを判断 することは 不可能 です。そのため、静的評価関数はゲームの決着がついていない局面では様々な計算を行うことで、その局面が 先手にとってどれだけ有利であるか を表す $-s$ ~ $s$ という 幅広い範囲の近似値を計算 します。別の言葉で説明すると、引き分けの無いゲーム の場合の 正の近似値 は、その局面が 先手の必勝の局面 であることを静的評価関数が どれだけ自信をもって判定しているかを表す と考えることができます。

静的評価関数の 近似値の精度 は、そうして計算された 近似値 とその局面の 正確なミニマックス値の間の誤差 で表されます。誤差が少ないほど精度が高く、誤差が 0 の場合に精度が 100 % になります。この後で説明するもう一つの精度と区別するため、以後はこの精度の事を 近似値の誤差の精度 と表記することにします。

ただし、この 近似値の誤差は一定ではなく、局面の 形勢判断が困難であるほど大きく なるため、近似値の誤差 は局面の 形勢判断の困難さによって決まる と考えることができます。具体的には、先手の必勝の局面の場合は 形勢判断が困難であるほど $s$ からの 誤差が大きくなる ので 0 に近い近似値 や、形勢判断を間違った場合は負の近似値が計算されます。

従って、近似値の誤差の精度が高い 静的評価関数は、精度が低い静的評価関数と比べて、形勢判断の難しさが同程度 の局面に対して計算される 近似値の誤差が少ない と言い換えることができます³。

一般的にゲームの序盤の局面は形勢判断が難しいため誤差が大きく、終盤の局面は形勢判断が簡単なので誤差は小さくなります。

例えば、現状で存在するどの将棋の AI も、ゲーム開始時の局面の評価値はわずかに先手が有利であることを表す小さな正の整数を近似値として計算するようです。将棋のゲーム開始時の局面がどの状況の局面であるかはまだ判明していませんが、一般的に将棋は先手のほうが有利なゲームだと考えられています。もし将棋が先手の必勝のゲームであれば、ゲーム開始時の局面の正確なミニマックス値は $s$ になるはずなので非常に大きな誤差が発生していることになります。

囲碁には引き分けはないので、ゲーム開始時の局面は先手の必勝または後手の必勝の局面のどちらかです。しかし、現状で存在するどの囲碁の AI もゲーム開始時の局面の評価値はほぼ 0 に近い近似値を計算するようなのでその誤差は $s$ という大きな値になります。

これらのことから、将棋や囲碁のゲームの開始時の局面は最も形勢判断が困難な局面の一つであると言えるのではないかと思います。

なお、将棋には引き分けがあるので、将棋が引き分けのゲームであればゲーム開始時の局面の誤差はほとんどないことになりますが、ゲーム開始時の局面の形勢判断が困難であることは間違いないでしょう。先程引き分けを除外した理由は、引き分けの局面の誤差の性質が、それ以外の状況の局面の誤差と大きく異なるからです。

形勢判断の難しさを判定する仮想的な関数

残念ながら 局面の形勢判断の難しさ を 正確に判定する方法はありません が、現状で存在する 強い将棋や囲碁の AI が、同じ局面 に対して 似たような評価値を計算する ことを考えると、局面の形勢判断の難しさ というものが 実際に存在する ことは間違いなさそうです⁴。また、将棋や囲碁などでプロ棋士が この局面は難解な局面 であり、どちらが優勢かを判断することができない という解説を行うことが実際に良くあります。そこで、本記事では 形勢判断の難しさを正確に判定 できる以下のような 関数が存在すると仮定 し、その 仮想的な関数 を使って説明を行うことにします。

局面の形勢判断の難しさを、ある程度以上大きな正の整数である m 段階⁵で判定し、0 ~ m の整数 を計算する 関数が存在する ものとする。一定範囲の整数とした理由 は、m を無限大にしたり、難しさを実数で表すと 同じ難しさの局面が 1 または数個しか存在しない ことになってしまい、この後で説明する ばらつきが生じなくなってしまう からである
形勢判断の難しさは 0 が最も簡単 で、大きくなるほど難しい ものとする。ゲームの決着がついた局面は必ず形勢判断を正確にできるので難しさは 0 である

近似値のばらつきの精度

先手の必勝 の局面と 後手の必勝 の局面で計算される 近似値が異なりますが、その 性質はほぼ同じ なので、以後は 先手の必勝の局面での説明 を行うことにします。

理想的 には、静的評価関数は 形勢判断が同じ難しさの局面 に対して 同じ誤差の近似値 を計算するべきですが、そのような静的評価関数を定義することは 現実的に不可能 です。具体的には、先手の必勝局面で 形勢判断の難しさ（difficulty）が $\boldsymbol{d}$ の局面を集めた 局面の集合を $\boldsymbol{N(d)}$ と表記すると、$N(d)$ の局面に対して計算される 近似値 には ばらつきが生じます。これは、プロの棋士 であっても 形勢判断を常に正しく行うことができない 点に似ています。実際にプロの棋士が 形勢判断が簡単な局面で形勢判断を大きく誤る ことがあるように、精度の高い静的評価関数であっても 形勢判断が簡単な局面 で 大きな誤差の近似値を計算 することがあります。

そこで、本記事では $N(d)$ の局面に対して計算される近似値の 平均値 と正確なミニマックス値との誤差を、形勢判断の難しさが $\boldsymbol{d}$ の局面に対して計算される 近似値の精度 とみなすことにします。また、その平均値を平均を表す英単語の mean の頭文字を取って $\boldsymbol{M(d)}$ と表記することにします。近似値の精度が高い と同じ $d$ に対して $M(d)$ の正確なミニマックス値に対する 誤差が小さくなる ということです。

静的評価関数の精度には、誤差の精度以外に $N(d)$ の局面に対して計算された 近似値のばらつき があり、ばらつきが少ない ほうが $M(d)$ に近い値が計算されやすいので ばらつきの精度が高い と表記します。毎回「$N(d)$ の局面に対して計算された近似値のばらつき」と表記するのは長いので、以後は 近似値のばらつき のように短く表記することにします。

近似値のばらつきの精度 は、誤差の精度と同様に AI の強さに大きな影響 を及ぼします。その理由について少し考えてみて下さい。

局面の状況の判定の正しさと誤差とばらつきの精度の関係

静的評価関数が、先手の必勝 の局面に対して 正の近似値 を、後手の必勝 の局面に対して 負の近似値 を計算した場合は その局面の状況を正しく判定 できています。従って、深さ制限探索で静的評価関数が近似値を計算する すべてのノードでそのような計算が行われた場合 は、正確なミニマックス値が $s$ である最善手を選択 することができます。

一方、先手の必勝 の局面に対して負の 近似値が計算 された場合や、後手の必勝 の局面に対して 負の近似値が計算 された場合は、その局面の状況を正しく判定できていない ので、深さ制限探索で 最善手以外の合法手が選択される可能性 が生じます。

静的評価関数が先手の必勝の局面の状況の 判定を間違える のは、$\boldsymbol{M(d)}$ よりも大きなばらつき で近似値が 小さく計算された場合 です。従って下記の理由から、近似値の 誤差の精度 と、近似値の ばらつきの精度が高い と静的評価関数が局面の状況を 正しく判定できる可能性が高くなり、結果として 最善手が計算される可能性が高く なります。

近似値の 誤差の精度が高い 場合は、$M(d)$ は $s$ に近くなるので 大きな値になる
$M(d)$ が 大きな値であればあるほど、大きなばらつきが生じない限り 局面の状況を 正しく判定できる
一般的に 大きなばらつきが起きる確率 は、小さなばらつきが起き確率よりも低いので、$M(d)$ が 大きな値であればあるほど 間違った判定となる 負の近似値が計算される確率が低くなる
近似値の ばらつきの精度が高い 場合は、大きなばらつき が起きる 確率が低くなる
そのため、ばらつきの精度が高い場合は、$M(d)$ が小さくても 間違った判定となる 負の近似値が計算される確率が低くなる

上記から、誤差の精度 と、ばらつきの精度 の両方が静的評価関数が 局面の状況を正しく判定できるかどうかに大きく関わる ことがわかります。

局面の状況を正しく判定できることの重要性

静的評価関数が局面の状況を判定できず、最善手以外の合法手を選択した場合は、二人零和有限確定完全情報ゲームの 勝率に大きな影響 を及ぼします。その理由は、以前の記事で説明したように、最善手以外の着手 を行うと 局面の状況が必ず悪化 し、相手が常に最善手を着手し続けた場合 は、局面の状況が好転することは決してない からです。このように、二人零和有限確定完全情報ゲームは 一度のミス を犯すことが 致命的な結果をもたらすゲーム であり、相手が弱ければ相手が最善手を着手しないことで状況が好転することはありますが、相手が強ければ強いほど一度のミスが敗北につながってしまいます。

この性質は、局面の状況を表す正確なミニマックス値だけでなく、近似値のミニマックス値でも同様 で、近似値のミニマックス値が 減るような合法手を選択 すると、相手がミスをしない限り 近似値のミニマックス値が 増えることは基本的にはありません。

この性質は、ミニマックス法の計算方法から明らか です。ミニマックス法では max ノードの評価値を子ノードの評価値の最大値で計算するので、どの合法手を選択してもその子ノードの評価値は 必ず親ノードの評価値以下の値 になります。将棋などで良く言われる 良い手 とは、それによって局面が直接有利になる手ではなく、相手がミスをしやすい局面にする ことで、相手のミスを誘うことで自分が有利になる ような着手の事を意味します。

静的評価関数 の 近似値の精度 には、誤差の精度 と ばらつきの精度 があり、その 両方が重要 である。

誤差の精度が高い ほど、局面の状況を 正しく判定できる可能性が高くなる。

ばらつきの精度が高い ほど、誤差の精度が低くても局面の状況を 正しく判定できる可能性が高くなる。

静的評価関数の誤差の精度を上げることは簡単ではありませんが、この後で説明するように ばらつきの精度 は 深さ制限探索の深さの上限を上げる ことで 高めることができます。

ばらつきが小さいことの重要性

ばらつきがあっても静的評価関数が局面の状況を正しく判定できる場合でも、ばらつきは小さいほうが望ましい と言えます。その理由は、ばらつきによって $M(d)$ から離れた近似値が計算された結果、ばらつきがなく $M(d)$ が近似値として計算された場合に選択される最善手よりも 形勢判断が難しい局面になる最善手が計算される場合がある からです。形勢判断が容易な局面ほど、次の手番 での局面の状況を 正しく判定できる可能性が高まります。

ばらつきの指標

複数の数値データ の ばらつきを表す指標 に 標準偏差 があります。本記事では 標準偏差を利用 して、深さの上限を大きくした場合に近似値の ばらつきの精度が上がることを説明 するので、標準偏差について説明します。

標準偏差とは何か

標準偏差（standard deviation）とは データの散らばり具合 を表す 統計学や確率論の用語 で、大きいほど データが 散らばっており、0 の場合 はデータが 散らばっていない、すなわち すべてのデータが同じ値 であることを表します。

標準偏差を計算 するためには、平均と分散を計算する必要があります。平均は良く使われる概念なので知っている人が多いと思いますが、$n$ 個のデータを $x_1$、$x_2$、・・・、$x_n$ と表記すると、それらの 合計を $\boldsymbol{n}$ で割った下記の式 で計算できます。なお、数学では平均を $\boldsymbol{\bar{x}}$ のように記述します。

$\bar{x} = \frac{1}{n}\sum_{i=1}^{n}x_i$

分散（variance）はそれぞれの データと平均の差の 2 乗 の 合計の平均 で、分散を $v$ と表記すると下記の式で計算できます。

$v = \frac{1}{n}\sum_{i=1}^{n}(x_i - \bar{x})^2$

分散には下記のような性質があり、すべての値が等しく、値が全く散らばっていない場合は 0 が計算 されます。

平均との差の 2 乗を計算することで、それぞれの値 に対して 0 以上の値が計算 される
すべての値が同じ場合 は、すべての値がが 平均と等しくなる ので、分散は 0 となる

標準偏差 は、分散の平方根 を計算します。標準偏差を $s$ と表記すると下記の式で計算できます。

$s = \sqrt{v}$

分散は 2 乗を計算 するので、平均との差が大きな値が存在 すると 非常に大きな値 になりますが、分散の 平方根を計算 することで平均との差が大きな値が存在しても 標準偏差は分散のような大きな値にはなりません。

分散と標準偏差には他にも様々な重要な性質がありますが、説明すると非常に長くなるのでそれらについては必要になった時点で説明することにします。参考までに分散と標準偏差の Wikipedia のリンクを下記に紹介しますので興味がある方は勉強してみて下さい。

データの分布による標準偏差の比較

標準偏差がどのような性質を持つかを示すために、いくつかのデータの集合 の 標準偏差を比較 します。

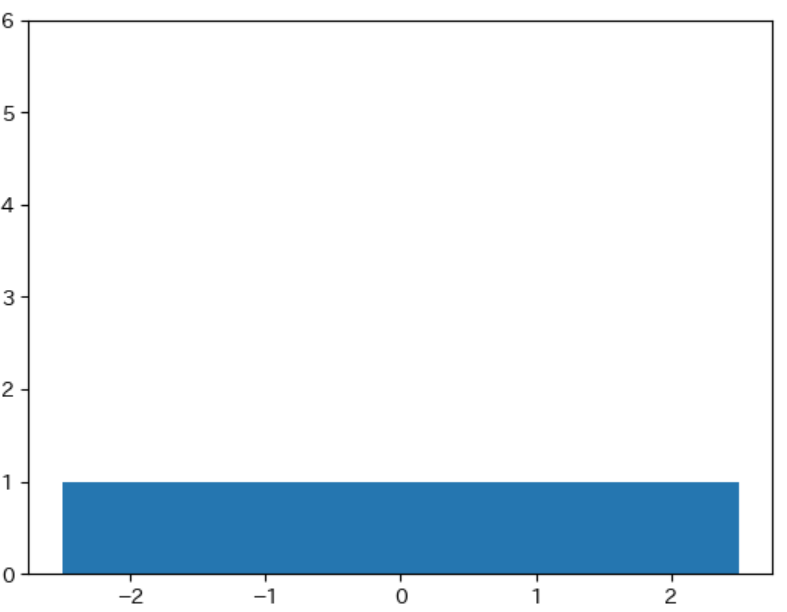
-2, 1, 0, 1, 2 という 5 つのデータの平均、分散、標準偏差は下記のようになります。また、このデータの値ごとの数を表すグラフは下記のようになります。このような値に応じたデータの数を表すグラフの事を ヒストグラム （度数分布図）と呼びます。

$\bar{x} = (-2 + -1 + 0 + 1 + 2) ÷ 5 = 0$

$v = ((-2)^2 + (-1)^2 + 1^2 + 2^2) ÷ 5 = 2$

$s = \sqrt{2} = 1.414$

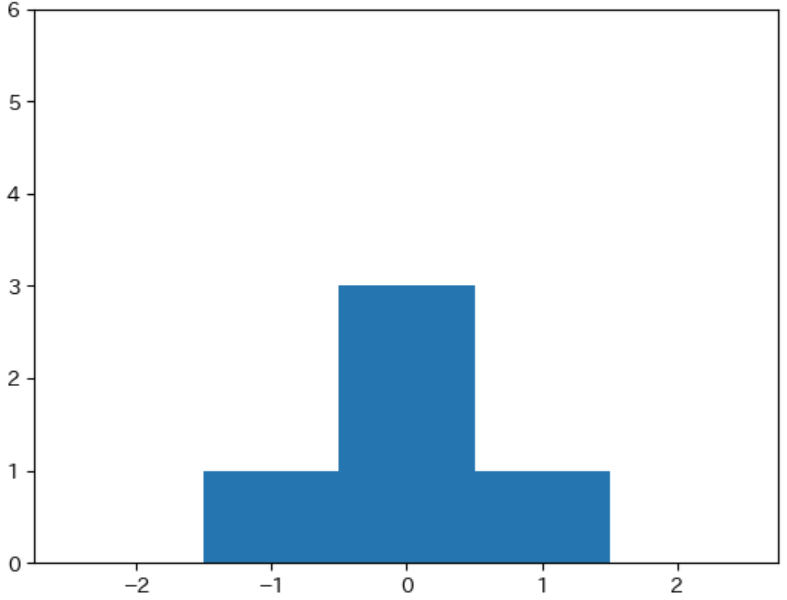
-1, 0, 0, 0, 1 のデータの平均、分散、標準偏差、ヒストグラムは下記のようになります。

$\bar{x} = (-1 + 0 + 0 + 0 + 1) ÷ 5 = 0$

$v = ((-1)^2 + 1^2) ÷ 5 = 0.4$

$s = \sqrt{0.4} = 0.632$

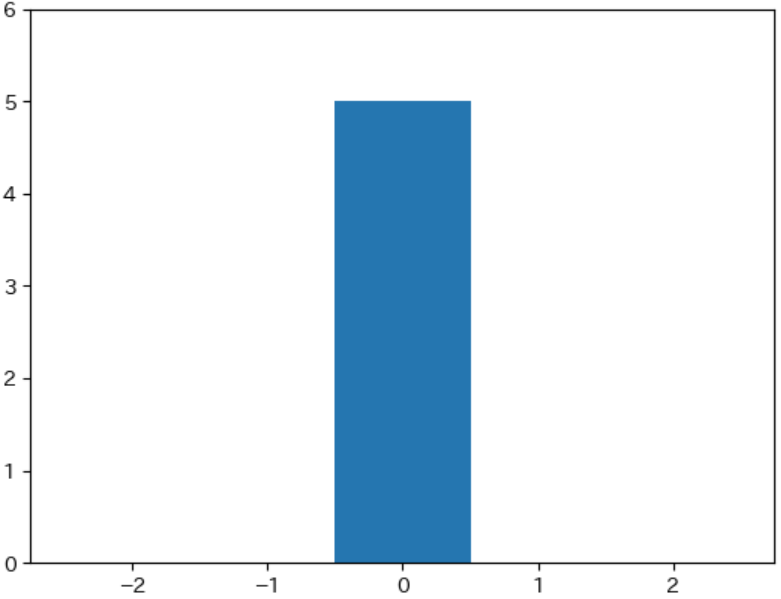
0, 0, 0, 0, 0 のデータの平均、分散、標準偏差、ヒストグラムは下記のようになります。

$\bar{x} = (0 + 0 + 0 + 0 + 0) ÷ 5 = 0$

$v = 0 ÷ 5 = 0$

$s = \sqrt{0} = 0$

下記は上記の結果を表にまとめたものです。3 種類のデータの集合の 平均値はいずれも 0 ですが、標準偏差 はヒストグラムからわかるように、データが平均値に近い値が多く、平均値からの ばらつきが少ない程小さく なり、すべての値が同じ場合は 0 になります。

データ	$v$	$s$
-2, 1,0, 1, 2	2.0	1.414
-1, 0, 0, 0, 1	0.4	0.632
0, 0,0, 0, 0	0.0	0.000

matplotlib では hist という関数でヒストグラムを描画することができます。下記は、上記の 3 つのヒストグラムを表示するプログラムです。

それぞれのヒストグラムで縦軸の範囲を統一するために、plt.ylim(0, 6) で y 軸の表示範囲を 0 ~ 6 に設定しています。

hist の最初の実引数にデータを表す list を、キーワード引数 range にヒストグラムで表示するデータの範囲を、bins にデータの範囲内を区切る数を記述します。ヒストグラムは区切られた範囲に含まれるデータの数を棒グラフのように表示します。

下記では、ヒストグラムで表示するデータの範囲を -2.5 から 2.5 とし、その区間を 5 つに分割したヒストグラムを表示しています。-2.5 ~ 2.5 の範囲を 5 つに分割すると、-2.5 ~ -1.5、-1.5 ~ -0.5、-0.5 ~ 0.5、0.5 ~ 1.5、1.5 ~ 2.5 の 5 つの範囲に分割され、それらの中に -2, -1, 0, 1, 2 の数値が含まれるので、分割された部分にそれぞれの数値の個数を表すヒストグラムのグラフが表示されます。

import matplotlib.pyplot as plt

plt.ylim(0, 6)
plt.hist([-2, -1, 0, 1, 2], range=(-2.5, 2.5), bins=5)
plt.show()
plt.ylim(0, 6)
plt.hist([-1, 0, 0, 0, 1], range=(-2.5, 2.5), bins=5)
plt.show()
plt.ylim(0, 6)
plt.hist([0, 0, 0, 0, 0], range=(-2.5, 2.5), bins=5)
plt.show()

ヒストグラムの Wikipedia の記事を参考までに下記に紹介します。また、matplotlib の hist の詳細については下記のリンク先を参照して下さい。

深さの上限と標準偏差の関係

深さの上限を増やす ことで、近似値のばらつき を表す 標準偏差が減る ことを具体例を挙げて説明します。

なお、ゲームの決着がついた局面に対して静的評価関数は必ず正確なミニマックス値を計算することができるので、ばらつきは生じません。ばらつきが減ることを示す際に その性質は邪魔になる ので、話を簡単にするために以後の説明では静的評価関数が ゲームの決着がついた局面の評価値を計算しない ものとします。

静的評価関数の設定

計算を簡単にするために、静的評価関数 が 下記のような近似値を計算 するものとします。

形勢判断の難しさが $d$ の局面の集合 $N(d)$ に対して計算される近似値の平均値を $M(d)$ とした場合に、任意の $\boldsymbol{N(d)}$ の局面に対して 下記の割合で近似値を計算する。

$M(d)$ を近似値として計算する割合が最も高い
$i$ を自然数とした場合に $M(d) + i$ が近似値として計算される割合は、$i$ が大きくなるほど小さくなる
$M(d) + i$ と $M(d) - i$ が近似値として計算される割合は同じである
$d$ が異なっていても、すべての整数 $i$ に対して $M(d) + i$ が近似値として計算される割合は同じである

上記のような説明は非常に分かりづらいと思いますので、別の言葉で説明すると以下のようになります。

$N(d)$ の中で近似値の 平均値 である $M(d)$ が計算される 局面が最も多い
平均値に近い値であるほど、近似値としてその値が計算される 局面が多い
平均値との差が同じ であれば、近似値としてその値が計算される 局面の数は同じである
形勢判断の難しさが異なっていても、$M(d) + i$ が計算される 割合は同じである

具体例としては下記のような設定が考えられます。

近似値	$M(d) -2$	$M(d) -1$	$M(d)$	$M(d) + 1$	$M(d)+2$
局面の割合	5%	20%	50%	20%	5%

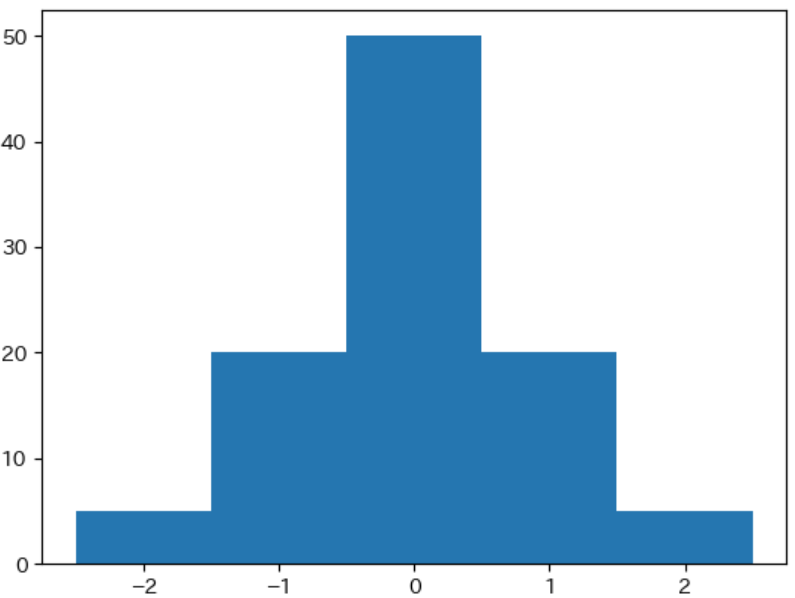
この設定で $M(d)$ が 0、$N(d)$ のノードの数が 100 の場合は、下記の表のようになります。

近似値	-2	-1	0	1	2
局面の数	5	20	50	20	5

上記をヒストグラムで表示すると下記のような性質を持つ、下図のような 左右対称 な 山形のグラフ になります。

平均値が最も多い
平均値から離れると少なくなる
平均値を軸に左右対称である

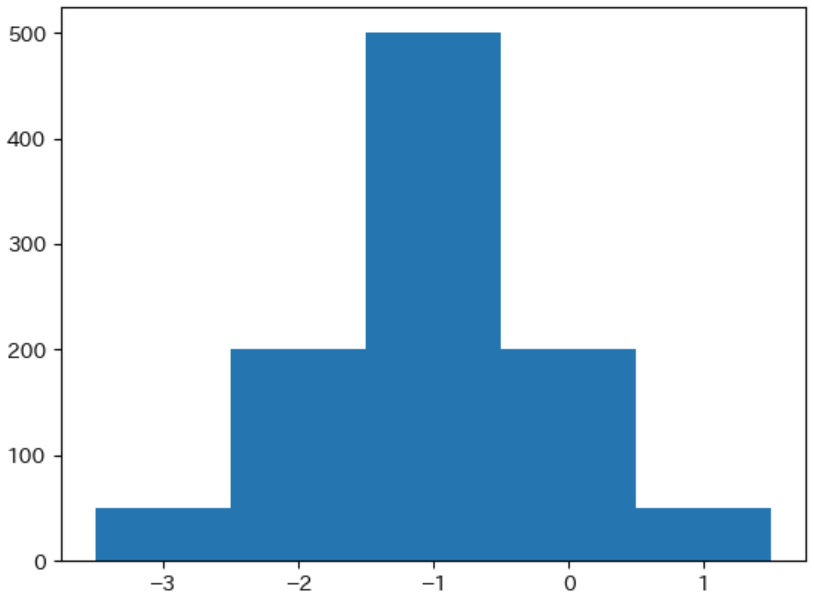
この設定で d とは別の局面の難しさ d' に対する $M(d')$ が -1、$N(d')$ に属するノードの数が 1000 の場合は下記の表のようになります。

近似値	-3	-2	-1	0	1
局面の数	50	200	500	200	50

下記はそのヒストグラムで、平均値からの差で割合が決まる ので、ヒストグラムの 形状は全く同じ になります。

ヒストグラムで、データごとの数（度数と呼びます）を指定したい場合は、下記のプログラムのようにキーワード引数 weight を使ってそれぞれのデータの数を記述します。下記のプログラムは上記の 2 つのヒストグラムを表示するプログラムです。

plt.hist([-2, -1, 0, 1, 2], weights=[5, 20, 50, 20, 5], 
         range=(-2.5, 2.5), bins=5)
plt.show()
plt.hist([-3, -2, -1, 0, 1], weights=[50, 200, 500, 200, 50],
         range=(-3.5, 1.5), bins=5)
plt.show()

設定の理由

当然ですが、現実の静的評価関数 は上記の設定とは 異なる性質 を持ちます。そのため、本記事の説明は すべての静的評価関数に当てはまるわけではありません が、下記で説明する理由から、精度が高い静的評価関数 は おおむね上記の設定を満たす と考えることができると思います。

静的評価関数 を上記のように設定した理由は、平均値の数が一番多く、平均値から離れるほど数が少なく、平均値を中心として 左右対象 な データの分布 は、同じテストを受けた学生のテストの点数の分布のように、同じ種類のデータを複数計測 した際に得られるデータで実際に よく見られるからです。

また、実際の静的評価関数が上記のような性質を正確に満たすことはありませんが、ばらつきの精度が小さくなるほど ほとんどのデータが 平均値に近い値になっていく ので 上記の性質に近く なります。

このようなデータの分布として正規分布と呼ばれる分布が有名です。正規分布については次回の記事で紹介する予定です。

実際には形勢判断が優しいほど計算される近似値のばらつきが減る傾向があるので、形勢判断の難しさが異なっていても $M(d) + i$ が計算される 割合は同じである という設定が 満たされることはありません。特にゲームの決着がついた局面は必ず正確なミニマックス値を計算できるのでばらつきは生じません。ただし、形勢判断の難しさがあまり変わらなければ、計算される近似値の ばらつきはほぼ同じである と考えることができます。その点と、計算のしやすさを考慮して設定を決めました。

確率分布の期待値と標準偏差

先程の表は、近似値の平均値との差 を使って下記の表のように書き直すことができます。

近似値の平均との差	-2	-1	0	1	2
局面の割合	5%	20%	50%	20%	5%

この表の近似値の平均との差のような、特定の値に応じた確率が存在する変数 のことを 確率変数 と呼び、数学では $\boldsymbol{X}$ のように 大文字で表記 します。$X$ を 大文字で表記 するのは、$X$ が 複数の数値の集合 であることを意味します。

確率変数 と 対応する確率 をまとめたものを 確率分布 と呼び、$\boldsymbol{X}$ の要素 である $\boldsymbol{x_i}$ に対応する確率（probability）の事を $\boldsymbol{P(x_i)}$ または、$\boldsymbol{p_i}$ と表記します。また、確率は必ず合計が 1 となるので、$X= x_1, x_2, ..., x_n$ の場合は $\boldsymbol{\sum_{i=1}^{n}p_i = 1}$ となります。

確率分布 に対しても平均、分散、標準偏差 を計算することができ、標準偏差 は先ほどと同様に データの分布のばらつき を表します。

確率分布 では 平均値 のことを 期待値（expectation value）と呼び、$\boldsymbol{E(X)}$ または $\boldsymbol{μ}$（ミュー）と表記します。

$X= x_1, x_2, ..., x_n$ の場合に 期待値 は下記の式で計算できます。

$E(X) = μ = \sum_{i=1}^{n}x_{i}p_i$

確率分布の分散（variation）は $\boldsymbol{V(X)}$ と表記し、下記の式で計算できます。

$V(X) = \sum_{i=1}^{n}(x_{i} - μ)^2p_i$

確率分布の 標準偏差 は $\boldsymbol{σ(X)}$⁶と表記し、先程と同様に 分散の平方根 で下記の式で計算できます。

$σ(X) = \sqrt{V(X)}$

下記は上記の表の確率分布の 期待値、分散、標準偏差 の計算です。

$μ = (m - 2) × 0.05 + (m - 1) × 0.2 + m × 0.5 + (m + 1) × 0.2 + (m + 2) ×0.5 = m$

$V(X)= (-2)^2 × 0.05 + (-1)^2 × 0.2 + 0^2 × 0.5+ 1^2 × 0.2+ 2^2 × 0.05 = 0.8$

$σ(X) = \sqrt{0.8} = 約 0.89$

上記から、先程の表の確率分布で近似値の計算を行う静的評価関数が計算する 近似値のばらつき を表す 標準偏差が約 0.89 になることがわかります。

深さの上限によるばらつきの違いの比較方法

上記で説明した標準偏差を利用して、形勢判断の難しさが同じ 局面に対して計算される 近似値のばらつき が、深さ制限探索で 深さの上限を上げると減る ことを 具体例を挙げて示す ことにします。

形勢判断の難しさが同じ 局面に対して計算される 近似値の平均値が $\boldsymbol{s}$ となる局面の集合を $\boldsymbol{N_{mean}(s)}$ と表記することにします。$\boldsymbol{N_{mean}(s)}$ は 近似値のばらつきがなくなる ように 改良した静的評価関数 が計算する評価値と考えることができます。

具体的には、$\boldsymbol{N_{mean}(0)}$ の局面の近似値を 深さの上限が 0 と 1 の深さ制限探索で計算した場合の 標準偏差を計算して比較 し、深さの上限を 1 としたほうが標準偏差が減って ばらつきが減る ことを示します。

また、静的評価関数は先程と同様に下記の表の設定で近似値を計算するものとします。

近似値の平均との差	-2	-1	0	1	2
局面の割合	5%	20%	50%	20%	5%

深さの上限が 0 の場合の標準偏差

$\boldsymbol{N_{mean}(0)}$ の局面の評価値を 深さの上限が 0 の深さ制限探索で計算するということは、その局面の近似値を 静的評価関数で直接計算 するということです。その場合の近似値の期待値（平均値）と標準偏差は、先程計算した値と同じになるので、下記の表のようになります。

	期待値	標準偏差
深さの上限が 0	0	0.89

深さの上限が 1 の場合の標準偏差

次に、max ノードの場合で、下図のような 深さが 1 で子ノード A、B があるゲーム木のルートノード N の 近似値のミニマックス値 を静的評価関数で計算した場合の 標準偏差を計算 することにします。黒丸が max ノード、赤丸が min ノードを表し、〇の中の数字はばらつきがない場合に静的評価関数が計算する近似値を表します。ばらつきない場合 の静的評価関数で 近似値を計算した際 に $\boldsymbol{N_{mean}(0)}$ である ノード N の近似値が 0 となる ように、2 つの子ノードは $\boldsymbol{N_{mean}(0)}$ と $\boldsymbol{N_{mean}(-1)}$ のノードとしました。

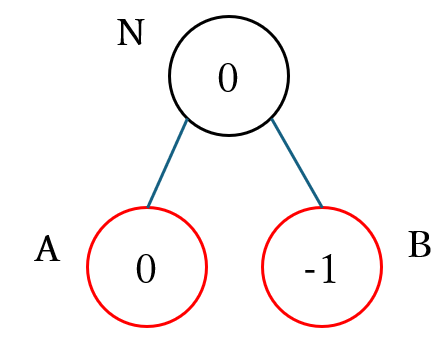
$\boldsymbol{N_{mean}(0)}$ である ノード A の近似値 は下記の表の確率分布で計算されます。

近似値	$-2$	$- 1$	$0$	$1$	$2$
確率	5%	20%	50%	20%	5%

$\boldsymbol{N_{mean}(1)}$ である ノード B の近似値 は下記の表の確率分布で計算されます。

近似値	$-3$	$-2$	$-1$	$0$	$1$
確率	5%	20%	50%	20%	5%

$N_{mean}(0)$ である ノード N の 近似値のミニマックス値 の 確率分布を計算 するためには、ノード A とノード B で計算される 近似値のすべての組み合わせ と その確率を計算 する必要があります。下記は すべての組み合わせ で計算される ルートノードの近似値とその確率 を計算した表です。

ノード A	ノード B	ノード N	確率の計算式	確率
-2	-3	-2	0.05*0.05	0.0025
-2	-2	-2	0.05*0.20	0.0100
-2	-1	-1	0.05*0.5	0.0250
-2	0	0	0.05*0.20	0.0100
-2	1	1	0.05*0.05	0.0025
-1	-3	-1	0.2*0.05	0.0100
-1	-2	-1	0.2*0.20	0.0400
-1	-1	-1	0.2*0.5	0.1000
-1	0	0	0.2*0.20	0.0400
-1	1	1	0.2*0.05	0.0100
0	-3	0	0.5*0.05	0.0250
0	-2	0	0.5*0.20	0.1000
0	-1	0	0.5*0.5	0.2500
0	0	0	0.5*0.20	0.1000
0	1	1	0.5*0.05	0.0250
1	-3	1	0.2*0.05	0.0100
1	-2	1	0.2*0.20	0.0400
1	-1	1	0.2*0.5	0.1000
1	0	1	0.2*0.20	0.0400
1	1	1	0.2*0.05	0.0100
2	-3	2	0.05*0.05	0.0025
2	-2	2	0.05*0.20	0.0100
2	-1	2	0.05*0.5	0.0250
2	0	2	0.05*0.20	0.0100
2	1	2	0.05*0.05	0.0025

上記のような、複数の集合の中 から 1 つずつ要素を取り出し た場合の すべての組み合わせの事 を直積またはデカルト積と呼びます。参考までに Wikipedia の直積に関する項目のリンクを下記に紹介します。

上記の表から、ノード N のそれぞれの近似値 が計算される 確率を計算 すると下記の表のようになります。また、式は省略しますが 期待値と標準偏差を計算 し、深さの上限が 0 の場合と 比較できる ようにしました。

評価値	-2	-1	0	1	2	期待値	標準偏差
深さの上限が 1	1.25%	17.5%	52.5%	23.75%	5%	0.1375	0.80
深さの上限が 0	5.00%	20.0%	50.0%	20.00%	5%	0	0.89

上記から、深さの上限を 1 とすることで、実際に 標準偏差が少し減る ことが確認できます。一方で、期待値が少し増える という問題があることもわかります。

下図は 2 つの確率分布のヒストグラムを重ねて表示するプログラムです。重ねて表示 すると 最初に表示したヒストグラムが見えなくってしまう ので、深さの上限が 1 のヒストグラムを表示する際に グラフの透明度 を表す キーワード引数 alpha を記述して後ろが 透けて見える半透明なグラフ を表示しました。

import japanize_matplotlib

plt.hist([-2, -1, 0, 1, 2], weights=[0.05, 0.2, 0.5, 0.2, 0.05], 
         range=(-2.5, 2.5), bins=5, label="深さの上限が 0")
plt.hist([-2, -1, 0, 1, 2], weights=[0.0125, 0.175, 0.525, 0.2375, 0.05],
         range=(-2.5, 2.5), bins=5, alpha=0.7, label="深さの上限が 1")
plt.legend()

実行結果

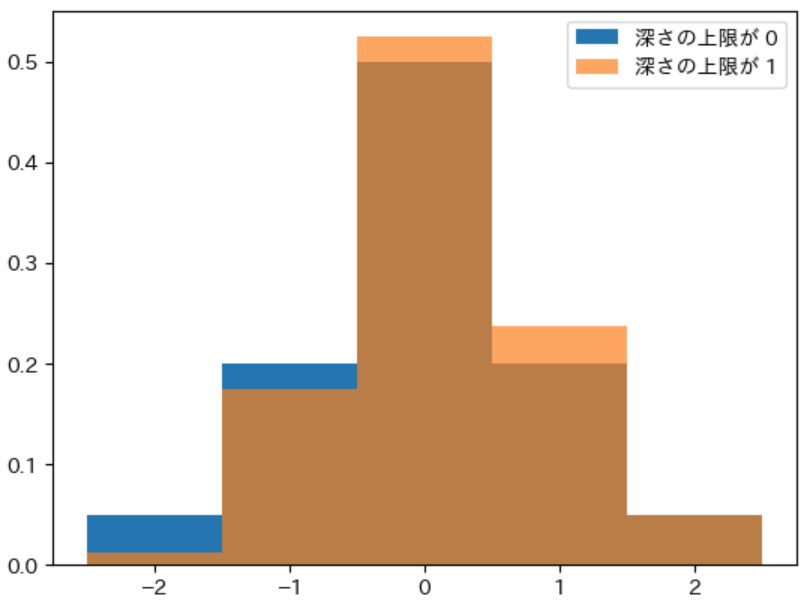
グラフからばらつきが減っていることが実感できないかもしれませんが、オレンジ色のグラフが少し右にずれているので、平均値が少し増えていることは目で確認できると思います。

今回の記事のまとめ

今回の記事では、静的評価関数が計算する近似値の精度には、誤差の精度 と ばらつきの精度 があることを説明しました。

また、ばらつきを表す指標 として 標準偏差 を紹介し、標準偏差を利用して深さ制限探索で 深さの上限を 0 から 1 とした場合に、ばらつきを表す 標準偏差が実際に少しだけ減る という具体例を示しました。

ただし、その際に平均値が少し上昇してしまうという問題があることもわかりました。次回の記事では深さの上限を増やした場合の性質についてより詳しく説明します。

本記事で入力したプログラム

リンク	説明
marubatsu.ipynb	本記事で入力して実行した JupyterLab のファイル

次回の記事

この定義は筆者が独自に考えたものなので一般的ではないと思います ↩
説明は省略しますが、評価値を $s$ とした場合に、$\frac{1}{1 + e^{-as}}$ という計算を行ないます。$a$ は正の定数で、この計算を行う関数のことをシグモイド関数と呼びます。詳細は Wikipedia のシグモイド関数を参照して下さい ↩
これは、難しい局面に対して正確に形勢を判断できる人が強いという、ごく当たり前のことです ↩
すべての局面で正確なミニマックス値を計算することができれば、すべての局面の形勢判断をそれを使って行うことができるので局面の形勢判断は常に容易になりますが、将棋のようなゲームでそのようなことを行うことは現状では不可能です ↩
例えば数千から数万程度の値が考えられます ↩
$σ$ はギリシャ文字のシグマの小文字です ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up

Pythonで〇×ゲームのAIを一から作成する その175 静的評価関数の近似値の誤差の精度とばらつきの精度