Go to Qiita Advent Calendar 2024 Top
LoginSignup
1185
393

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 5 years have passed since last update.

@youwhtin株式会社野村総合研究所

直近１年のQiita記事分析で分かった７つの「驚愕」

Last updated at Posted at 2018-07-03

背景

Qiita殿堂入り記事ランキングを作った物語のつづき。

前回の投稿は以下を参照：

今回は、その第二の目的、記事の分析結果についてお伝えする。

全部の分析が済んでから公開する予定だったが、
途中段階でもかなり興味深い結果もあったため、
データ取得時から日数がたって鮮度が落ちないうちに公開したいと思った。

本投稿の内容

  • 直近１年＝2017年6月～2018年5月の投稿とする。
    • 過去記事の方が、平均いいね値が数倍高くなる傾向を、前回述べた。
    • ご参考：　Qiita殿堂入り記事ランキングを作った物語
      • 2018年5月いいね平均＝ 6.9
      • 2017年6月いいね平均＝ 8.1　 （ここまでの期間を対象）
      • 2016年6月いいね平均=15.6　　(仕様変更も影響.。もっと前はより差が大きい）
    • そのため、あまり長期間にわたっての分析は望ましくない。
    • また、技術の流行り廃りも変わるため、直近１年とした。
  • 一般的な観点における「いいね数」分析を実施し、今後の考察の基礎値を得る
  • 特に興味深い７つのポイントについて、記載する。
  • コードの実行環境は全て、Windows10 + Python3 +JupyterNotebook を前提。

驚愕①「いいね」の平均値は8.02。半分以上は０～２

  • 2017年6月～2018年5月の全記事数 ＝ 79,072
  • 同記事に対する、「いいね」の合計 ＝ 634,493

⇒ 平均値＝8.02

なお、中央値は 2 だった。

つまり、半分以上が、０～２なのだ。
これは結構衝撃的な割合ではないだろうか？

続いて、いいね数の分布をグラフ化すると、この意味が分かってくる。

驚愕②「いいね」の分布はグラフ化出来ないほど偏る

まず普通にいいね数の分布グラフを作ってみる。

各記事の情報をAPIで取得する部分についてはコードは未掲載だが、
APIで月次ごとに取ってきたデータを、
１記事ごとに、パースして「item_info」に格納。
各月でそれぞれ作った「item_info」のlistを、繋げたものを事前に準備しておく。

いいね数のリストを作って、seabornで図示
import seaborn as sns
%matplotlib inline

iine_list=[]

for item_info in item_info_list:
    # item_infoの最初に「いいね」数が入れてある
    iine_list.append(item_info[0])
    
sns.distplot(iine_list)

iine_gl_01.PNG

はい。全く意味が分かりません。
「０」近辺（１桁台）が極端に多すぎるのだ。

いいねが十分に多い領域は１００刻みで見る、とかでもダメ。
対数を取って、log2で見てもダメ（対数化しても、下位が多すぎ）。

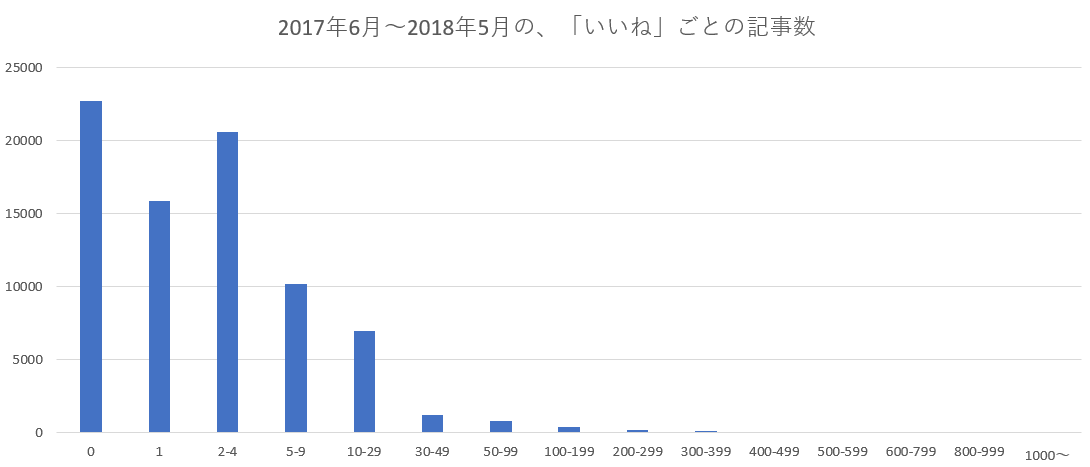
結局行きついたのは、図示ではなく、刻み幅を可変にした「表」
少しまとめた形の素データを見るのが一番分かりやすい。
「いいね数」の幅が変わっているので注意してご参照。

いいね数 記事数
0 22,733
1 15,854
2-4 20,572
5-9 10,209
10-29 6,932
30-49 1,173
50-99 757
100-199 385
200-299 148
300-399 88
400-499 53
500-599 48
600-799 45
800-999 32
1000～ 43

一応上の表をグラフにしてみると・・・後半が少なすぎて、これでも良くわからない。

iinegotokijisuu.PNG

なお、下記の殿堂入り記事については、

「月」によって、100台の後半から殿堂入りの可能性があり、
400以上はだいたい殿堂入りする、という感じになる。
（グラフ内の、ほぼ見えない右側の部分が殿堂入りですね）

範囲の指定の仕方はいろいろご意見があるだろう。
ただ、今回のこの「いいね」の全体分布表については、
後続の分析でも頻繁に参照していたので、
私個人としては、これくらいの幅ごとで確認出来ると、便利だった。

驚愕②の追記：「いいね数と記事数の公式」を発見！

7/4追記：　mokemokechickenさんからのコメントより、
**「べき分布」**になっているのでは、とご教示をいただいた。

いいね数に対数を取るところまではやっていたが、
記事数は離散的な値になるために、
（いいね値が一定以上では、０個か１個のどちらかで、数値を扱えないため）
対数化を試していなかったと、ご教示より気付く。
いいね数が、一定値以下であれば、それを気にしなくてよかったのだ！

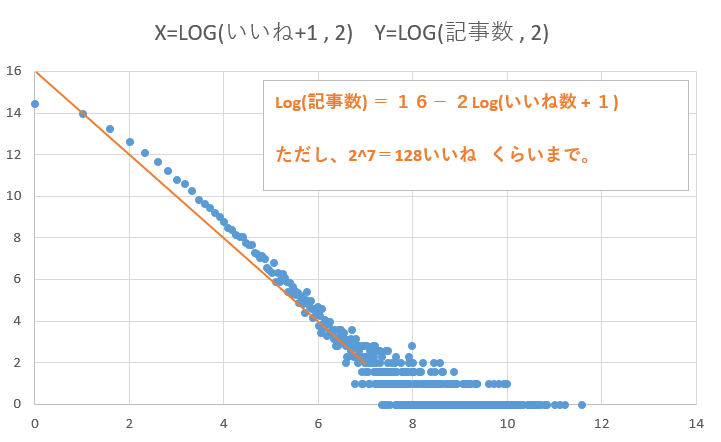
ということで、記事数にも対数を取ってグラフ化した。

loglogiine.PNG

結果、
１２８いいねくらいまでならば適用出来る「いいね数と記事数の公式」を発見した。

図内のオレンジの補助線がその公式を示したもの。
Log(記事数) ≒　１６－２Log(いいね数＋１)

ただし、対数の底は２。
また、ｙ切片と傾きを分かりやすい値にするため、ちょっとズレている。
「いいね数＋１」で＋１している理由は、いいね数が０のものが多く、
０に対しては対数を取れないために、＋１している。
いいね数がある程度大きいと、やはり０個or１個or２個の値が、
飛び飛びで現れる形になるため、適用出来ない。
（グラフの右下の尻尾的な部分は表現されていない）

公式の使い方としては、
例えば、いいね数＝３１である記事数を求めてみる。
LOG(32)＝5
16 - 2*5 = 6 (公式の右辺の計算)
2^6 = 64記事
ということで、この１年間に、64記事程度、31いいねの記事があるということ。
※実際は、線よりちょい上なので82記事ある。
　より正確にするには、マジメに赤線を引いて、傾きと切片を調整したり、
　対数の底を変えて調整したりすると良いかもしれない。

人気投票は、べき分布になることがあるそうだが、興味深い結果となった。
まさにmokemokechickenさんのご教示の通り。
勉強になりました、大変ありがとうございます！

驚愕③２年前の昔の記事のほうが「いいね」が３倍

すいません、これは直近１年ではなく、直近２年半以上分析した結果です。
詳細は、前回記事＝ Qiita殿堂入り記事ランキングを作った物語　をご参照。

「いいね」は基本的には減らないため、
投稿後に時間が経過した方が、総数としては貯まるのは当然だが、
その差分は、１年で「２以下」
（ 2018年5月いいね平均＝ 6.9、　 2017年6月いいね平均＝ 8.1）

２年前比較時の差は、時期を見ると「いいね」と「ストック」の分離による、
仕様変更の影響が大きいと考えられる。

「いいね」「ストック」は使い分けるべきとか、べき論は置いておき、
方法が２つになってしまっていることで、
「いいね」を使わずに「ストック」だけで済ましているという人も、
一定の割合で生じてしまっているのではないか？

好循環を回すための最も重要な貢献は「いいね」をつけること

  • 良い記事にいいねが集まれば、良い記事は人々の目にふれるようになる（トレンド等の仕組み）。
  • 良い記事を人々が得やすくなれば、人々はQiitaというコミュニティを利用する。
  • Qiitaの人気が高まれば、良い記事を書いて投稿しようという投稿モチベーションも上がる。

結果、もっと「いいね」すれば、もっと良い記事を読めるようになる。

好循環を回すための最も重要な貢献は「いいね」をつけること

「いいね」をつけないでいる人や、つける基準が厳しい人は、
大きな損をしているので、どんどん「いいね」しましょう！

まずはこの記事からいいねしてみましょう

驚愕④文字数は、少なすぎるとダメだが多ければ良いわけではない

つづいて、文字数と、いいねの関係性を確認した。
文字数＆いいね数で散布図を作るのだが、
分布が全く分からなくなるため、
「２を底として対数を取った値」で記載している。
（2の10乗 ≒ 1000というやつで、約1000を「10」と表現）

文字数といいね数の関係を見る
import pandas as pd
import seaborn as sns

%matplotlib inline

iine_list_log=[]
mojisuu_list_log=[]

#文字数といいねの関係を見る。[0]はいいね数、[9]はbody
for item_info in item_info_list:    
    iine=item_info[0]
    mojisuu=len(item_info[9])
    #対数を取るので、いいね=0は不可のため、除外する。
    if(iine>0):
        iine_list_log.append(math.log(iine,2))
        mojisuu_list_log.append(math.log(mojisuu,2))

# リスト→データフレーム
df = pd.DataFrame({'iine_log' : iine_list_log, 'mojisuu_log' : mojisuu_list_log})  
#df.head()

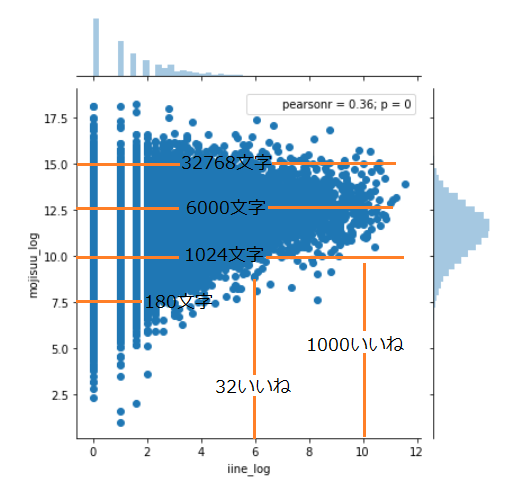
sns.jointplot(x="iine_log", y="mojisuu_log", data=df)

mojisuu_iinesuu_kakou.PNG

対数表記が分かりにくいため、橙色の補助線をつけた。

1000文字以下の、文字数が少ない記事については、
いいね数が少ない傾向にあるが、
1000文字以上、どんなにいっぱい書いて、数万文字になったとしても、
その文字数が直接いいね数に反映されるわけではない、ということが分かる。

「驚愕」としたが、まあこれは当たり前の話かもしれない。
短くまとまっていれば良いわけでも、長くいっぱいかけば良いわけでもない。
ただしあまりにも短いと、反応されませんよ、ってこと。

また、グラフの上側と、右側の分布にも着目してほしい。
文字数については、対数を取ると比較的綺麗な分布になるが、
いいね数については、前述の通り全くそうならない。

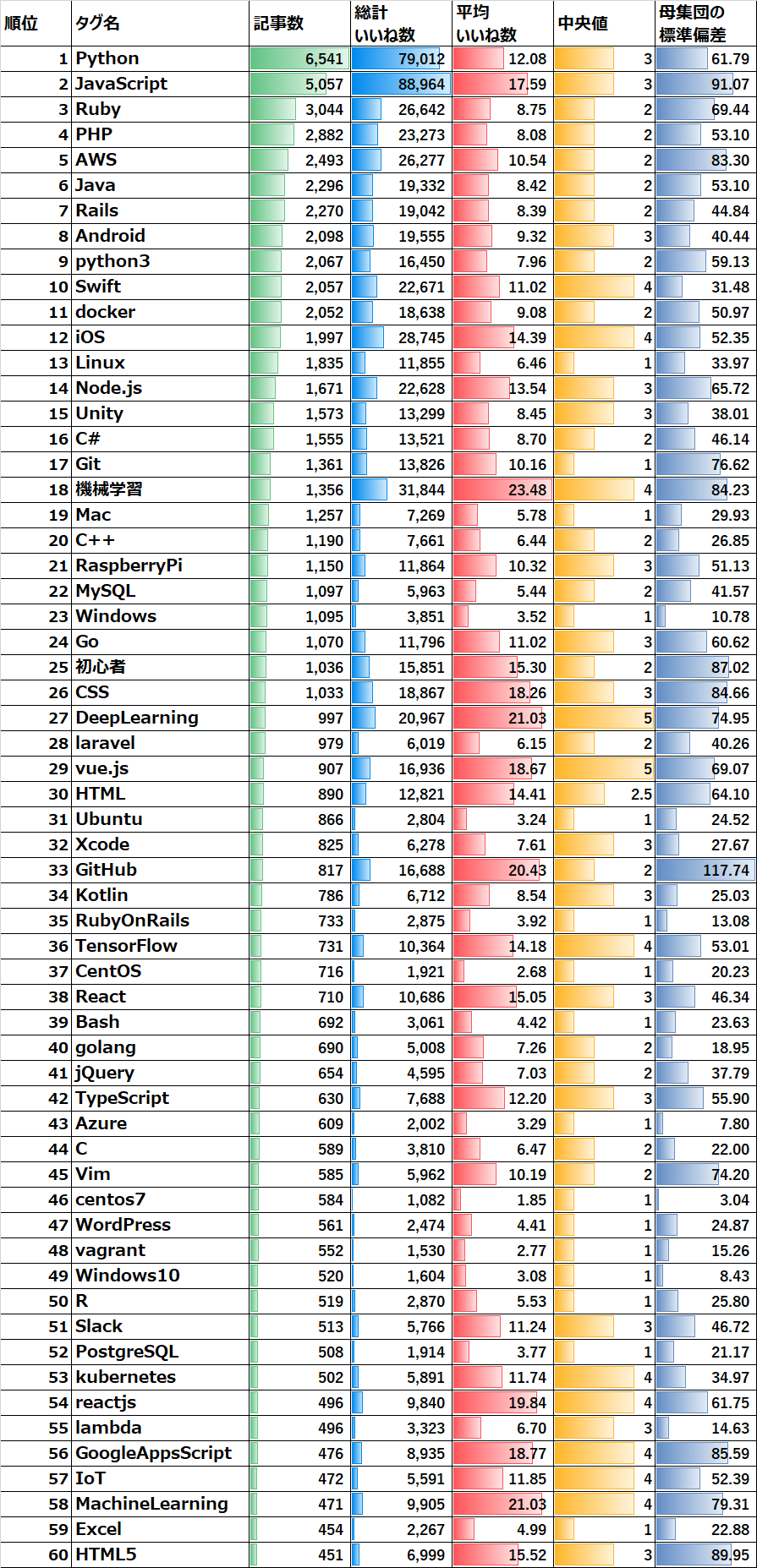
驚愕⑤人気のタグが「いいね」が多いわけではない

もしかしたらこれが今回一番の驚愕かもしれない。

各タグごとの、集計データを取ってみる。
一つの記事に対して、最大で５タグまで付与出来るため、
当然同じ記事が複数のタグでカウントされる場合もある点はご注意。

今回は、最も投稿数の多かった６０位までのタグについて、
様々な統計指標とって、その結果をグラフ化する。

ご参考まででに、結果を見ると６０位までの単純合計件数で、記事の約95%になる。
一つの記事が複数カウントされている場合もあるため、
実際のカバー率はもう少し低い。

文字数といいね数の関係を見る
##タグごとのいいね数の集計をやるよ。
##辞書形式で、タグ名：　いいねの値のリスト、という形式を作る。
tag_iine_list={}
for item_info in item_info_list:
    iine = item_info[0]
    tag_list=item_info[2]
    for tag_info in tag_list:
        tag_name=tag_info["name"]
        #初めて出た語なら空白のリストがデフォ。
        tag_iine_list.setdefault(tag_name, [])
        tag_iine_list[tag_name].append(iine)

print(len(tag_iine_list))
各タグごとに、様々な統計指標を算出し、データフレーム化
import statistics
import math
import pandas as pd

tag_iine_all_info=[]
for tag_name in tag_iine_list.keys():
    kosuu = len(tag_iine_list[tag_name])
    totalsum = sum(tag_iine_list[tag_name]) 
    mean = statistics.mean(tag_iine_list[tag_name])
    median = statistics.median(tag_iine_list[tag_name])
    pstdev = statistics.pstdev(tag_iine_list[tag_name])
    tag_iine_all_info.append([tag_name,kosuu,totalsum,mean,median,pstdev])

tag_iine_all_info_df = pd.DataFrame(tag_iine_all_info,
                  columns=['tag_name', 'kosuu', 'total_iine','mean_iine','median_iine','pstdev_iine'])

#個数でソートして表示する。
df_for_show=tag_iine_all_info_df.sort_values(by='kosuu', ascending=False)
df_for_show.head(60)

この分析は、実はやりなおしをしている。
一番最初に書いた時は、平均、記事数、だけ見ていたため、
「辞書形式で、タグ名：　いいねの値のリスト、という形式を作る。」
といったことをせずに、直接最初のforループだけで、
個数のカウント、平均値の算出も実施していた。

しかし、それでは「中央値」は出せなくなってしまう。
平均値を見たあとで、あれ、意外と差が出るな、と思って、
タグごとの分析は意義があると考えて、
中央値なども出せるようにして、最初からやりなおしている。
いろいろ試行錯誤しているんですね

上記のプログラムの結果をエクセルに張り付けて見栄えを良くしたものが以下：

tag_gl01.png

てっきり、「python」「JavaScript」「ruby」などの、
Qiitaのトップ画面でも良く見る人気のタグが、
平均いいね値も高く、それ以外のタグは、
記事数が少なくなればなるほど、（見るユーザも少なくなるために）
いいね数は下がっていくものだと考えていた。

また、タグが違っていても、１０００記事以上の集団だと、
平均値としては、そんなに大きなブレは無いのではないか？
（全体平均の「８」に近くなるのではないか？）
と考えていた。

結果は、予想と大きく異なるもので、
「タグ」の内容によって、かなりのバラツキがあり、
また、投稿数が多いからといって、平均も多いというわけではない。

眺めれば眺めるほど、味のある表な気がする。

驚愕⑥流行りは１位「機械学習系」２位「JavaScript系」３位「Python系」

グラフについては上の内容を参照。

「機械学習」「DeepLearning」「MachineLearning」「TensorFlow」
など、機械学習に関するタグが比較的いいねが高いように見える。

また、「JavaScript系」というまとめも方もイマイチだが、
「JavaScript」に関係の深いXXX.jsやXXXscript系,HTML系も、
比較的に高いように見える。

３位は何にするか微妙なところで、iOS系も高めではあるものの、
同じくらいであれば、投稿数が圧倒的な、pythonを選びたい。

ということで、流行りは
１位「機械学習系」
２位「JavaScript系」
３位「Python系」

他に気になった点としては、「OS」に関するものは、どれも全体的に低い。
「Ruby」「PHP」「Java」は普通くらい。

タグごとにこれくらいの差が出るならば、
技術の流行り廃りの傾向を見るのにも面白いかもしれない。

なお、タグの種類の総数としては、
19561 種類
もあったことを合わせて報告しておく。
※多すぎじゃない・・？タグの付け方や使い方を誤っている記事も多そう。。。

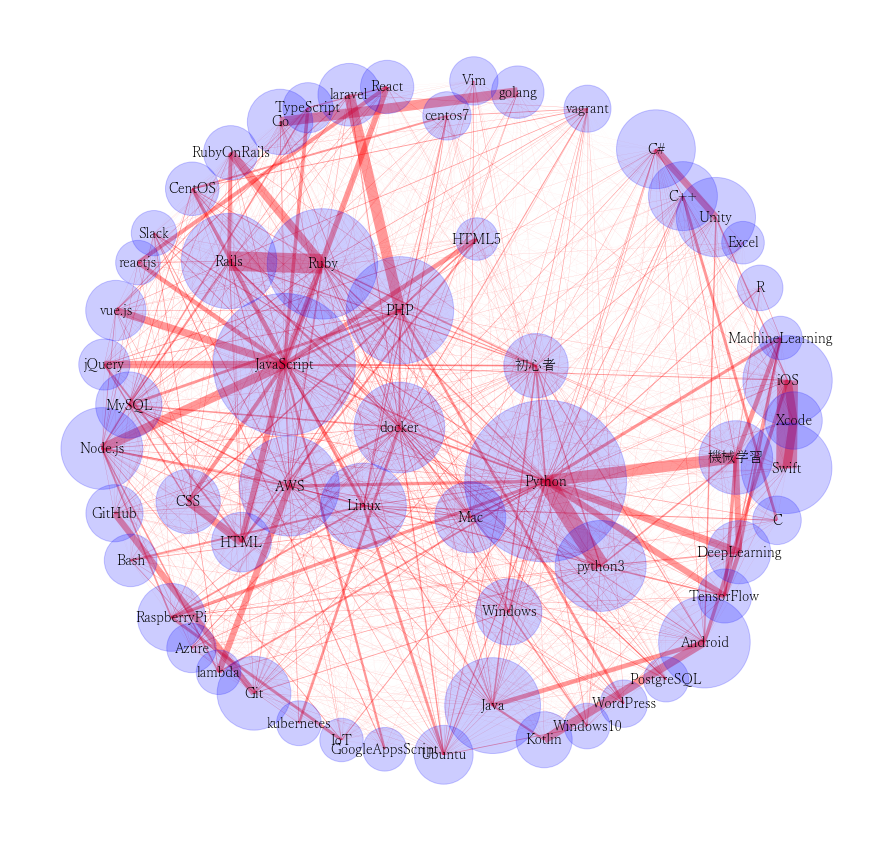
驚愕⑥の追記：タグのネットワーク図の可視化

7/6追記：
PythonでQiitaタグのネットワークを可視化する

の素晴らしい記事を拝見し、同様に今回のデータ間でのタグの
ネットワーク関係を可視化してみる。一言で言うと、
どのタグとどのタグが一緒に使われているのか、紐づきの強さを図示します。

いいね数とタグの関係の表と合わせて見るととても面白かった。

  • リンク先の記事よりだいぶデータ量が多いため、パラメータは調整。
  • こちらは上位60で実施していたため、設定は変更。
  • また、リンク先では省略していた、ネットワーク図の日本語化を実施。
  • matplotlibの設定だけでは、ネットワーク図は日本語にならず少々苦戦。
データ加工、下準備
import collections
import itertools

tags_list = []
for item_info in item_info_list:
    #パース時に["tags"]は[2]に入れていた。
    tags_data = item_info[2]
    tag_name_list = [tag["name"] for tag in tags_data]
    tags_list.append(tag_name_list)

print(len(tags_list))

tag_count = collections.Counter(itertools.chain.from_iterable(tags_list)).most_common(60)
可視化表示（＆グラフ日本語化）＝コードは引用元とほぼ同様です。
import networkx as nx
%matplotlib inline
import matplotlib.pyplot as plt

G = nx.Graph()
G.add_nodes_from([(tag, {"count":count}) for tag, count in tag_count])

for tags in tags_list:
    for tag0, tag1 in itertools.combinations(tags, 2):
        if not G.has_node(tag0) or not G.has_node(tag1):
            continue
        if G.has_edge(tag0, tag1):
            G[tag0][tag1]["weight"] += 1
        else:
            G.add_edge(tag0, tag1, weight=1)

plt.figure(figsize=(15,15)) # グラフのサイズを定義
pos = nx.spring_layout(G, k=1.5) # ノード間の反発力を定義。値が小さいほど密集する

# ★ノードの大きさを調整
node_size = [ d['count']*4 for (n,d) in G.nodes(data=True)] 
# ノードのスタイルを定義
nx.draw_networkx_nodes(G, pos, node_color='b', alpha=0.2, node_size=node_size, font_weight="bold", font_family='Yu Mincho')

#matplotlibのフォントは反映されないため、注意が必要。以下のコマンドなどで日本語らしきものを探すと良い。
####### matplotlibで日本語を豆腐にしないために、使えるフォントを探す。
##### import matplotlib.font_manager as fm
##### # フォント一覧
##### fonts = fm.findSystemFonts() 
##### # フォントのパスと名前を取得、とりあえず300個表示
##### print([[str(font), fm.FontProperties(fname=font).get_name()] for font in fonts[:300]])

nx.draw_networkx_labels(G,pos, font_size=14,font_family='Yu Mincho')

# ★エッジの太さを調整
edge_width = [ d['weight']*0.02 for (u,v,d) in G.edges(data=True)]
# エッジのスタイルを定義
nx.draw_networkx_edges(G, pos, alpha=0.4, edge_color='r', width=edge_width)

plt.axis('off')

networkZU.png

記事数がかなり多いため、ちょっとごちゃごちゃしています。

いろいろ示唆に富んだグラフな気がします。
どの技術分野が好きなのかによって考察はいろいろあると思いますので今は省略。

（３位pythonとしていましたが、機械学習系の強さに、
　引っ張られているところはあるかもしれないですね。）

驚愕⑦７つの驚愕なのに６つまでしかない。

ネタが尽きたので、別なネタに走る。

実は、最後に「自然言語解析」を実施した結果を書くつもりだった。

最近は、以下のように自然言語処理ネタばかりやっている。
メロンとメロンパンを、キカイが探す物語
平成の次の元号を、AIだけで決めさせる物語
「赤の他人」の対義語は「白い恋人」 これを自動生成したい物語

むしろ、①～⑥までの話は、
自然言語処理による分析を行うための、前提データ集めとしてやっていた。
①～⑥までで、既に少し興味深い結果であるため、先出ししてしまう。

分析の途中段階の状態としては、以下のような可能性を感じるものの、
「精度」が難しく、まだまだ考慮中、という感じ。

  • 機械による査読評価を行うことで、獲得予定いいねの傾向が予想出来るかもしれない。
    • 投稿前に、５段階くらいで予想を出してくれるなど。
    • 数値そのものを当てるのは、流行りもあるため不可能に近い。
  • 埋もれた良記事を、機械によって発掘出来るかもしれない。
  • 各位の好みの記事傾向から、オススメ記事を出せるかもしれない。
    • これは普通のリコメンドの話だ。。。

もしかしたらこっちはあまりうまくいかずに
発表出来ないかもしれない。

応援する気持ちがある方は「いいね」で送ろう

⇒7/12 追記：　かなり苦戦しながらも、自分なりには納得の結果を作れた。
AIが見つけた、埋もれたQiita良記事100選

あとがき

今回の記事は、以下の記事の継続でして、
実施に至った動機や、各種データの取得日時/詳細、
また、Qiitaへの考察に関するあとがき自体も、以下記事をご参照ください。

また、Qiitaに対する考察や情報としてだけではなく、
pythonで、実際のデータを分析する時の事例や
考え方としても、何かの一助になれば幸いです。

以上です。

1185
393
13

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
1185
393

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?