この記事は教科書に出てくる等高線を描いてみる(Fortan+gnuplot)及び教科書に出てくる等高線を描いてみる(Python)の続編です.
はじめに
筆者は大学の工学部で習う流体力学を勉強しているが,流体力学の最初のほう(完全流体の理論)では速度ポテンシャル $\phi$ や流れ関数 $\psi$ といった物理量が現れ,それらの量を用いた代表的な流れの例がいくつか出てくる(二重わき出しなど). これらの量の2次元での等高線が教科書の図として載っているが,自分でも作図できたら理解が深まるような気がする.しかしながら,関数 $y = f(x)$を手軽に描画できるグラフソフト・サービスでは,2次元面でのある物理量の等高線を描くのは難しいことが多い.前回までの記事ではFortranやPythonを用いてみたが,プログラムミングの知識が少し必要&環境準備が必要ということで若干敷居が高い.そこで今回は,有料だけれども必ずPCにインストールされていると思われるExcelを使って等高線を描画してみる(アンチExcelの方はこの記事を無視してください).
事前準備: Excelがインストールされたパソコン
まず,Excelが使える環境・PCを必要とします.互換ソフトであるLibreOfficeのCalcやGoogleのスプレッドシートでも途中のデータ生成まではできそうですが,等高線の描画については当方は知識を持っていないので何とも言えません.
対象とする流れ場
前回の記事と同じ吹き出し・吸い込みについて対象とする. 原点からの距離を $r$ とすると, 3次元での速度ポテンシャル $\phi$ は以下のように表せる.
$$
\phi = -\frac{m}{r},, r = \sqrt{x^2+y^2+z^2} \tag{1}
$$
ここで$m$は吹き出しの強さと呼ばれる係数である.2次元での等高線が描きたいので, $z=0$ として,
$$
\phi = -\frac{m}{r},, r = \sqrt{x^2+y^2} \tag{2}
$$
を描画してみる.
作業方針
作業はExcelのみで解決することを目指す.
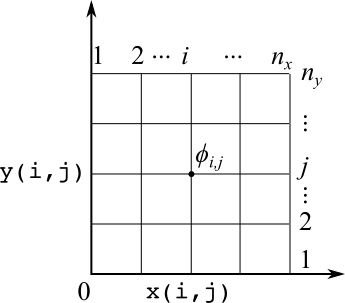
- 下の図のような2次元の格子点(等間隔のマス目)をエクセルシート内に作成し,各格子点(セル)での $\phi (= \phi_{i,j})$の値を計算する.
- グラフ機能で等高線を描画する.
という流れでExcelを活用する.見栄えはあまり気にしない.
Excel操作手順
パラメータの入力
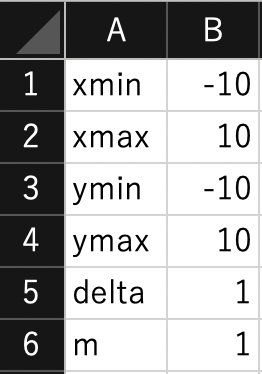
計算に用いる以下のパラメータを適当なセルに入力する.
- 領域の大きさ(
xmin,xmax,ymin,ymax) - 格子点刻み(
delta) - わき出しの強さ(
m)
x座標, y座標の設定
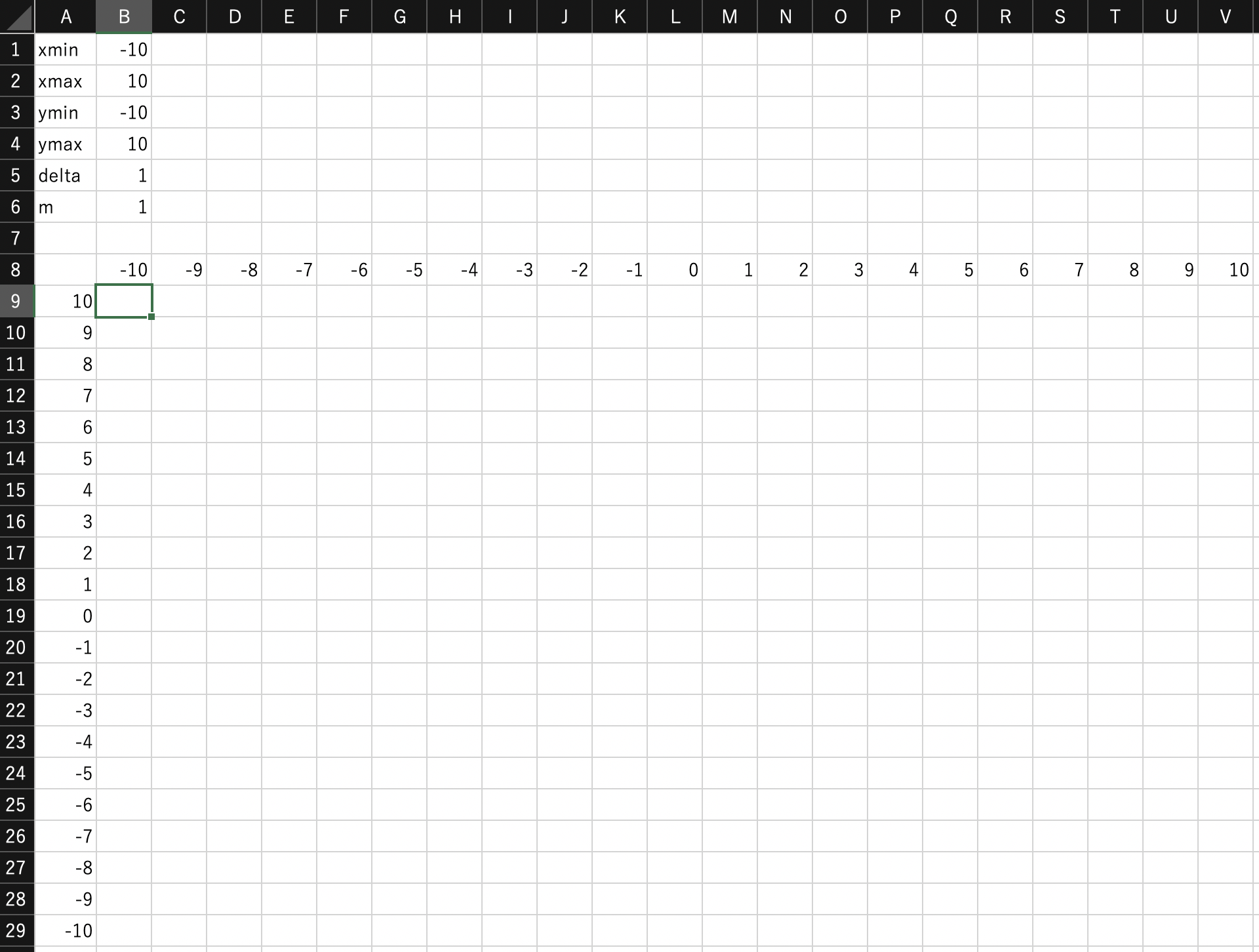
$x$座標,$y$座標を2次元データを計算する領域の外側2辺に設定する.
パラメータであるxmin,ymin,deltaのセルを絶対参照しても良いし,規則的なデータなので数セル分値を入力してオートフィルしても良い.
2次元データの計算
2次元データ$\phi_{i,j}$を座標値で囲まれた空白セルで計算する.このとき,エクセルの絶対参照・相対参照の機能を活用して式を設定する.絶対参照・相対参照の切り替えはF4キーを押すことで素早くできる.
先ほどの座標値を設定した図において,B9のセルには以下の式を代入する.
=-$B$6/SQRT(B$8^2+$A9^2)
$が付くと絶対参照になるので,SQRTの中では行の絶対参照,列の絶対参照を組みわせている.あとはオートフィルで全てのセルで式計算をさせて値を埋める.
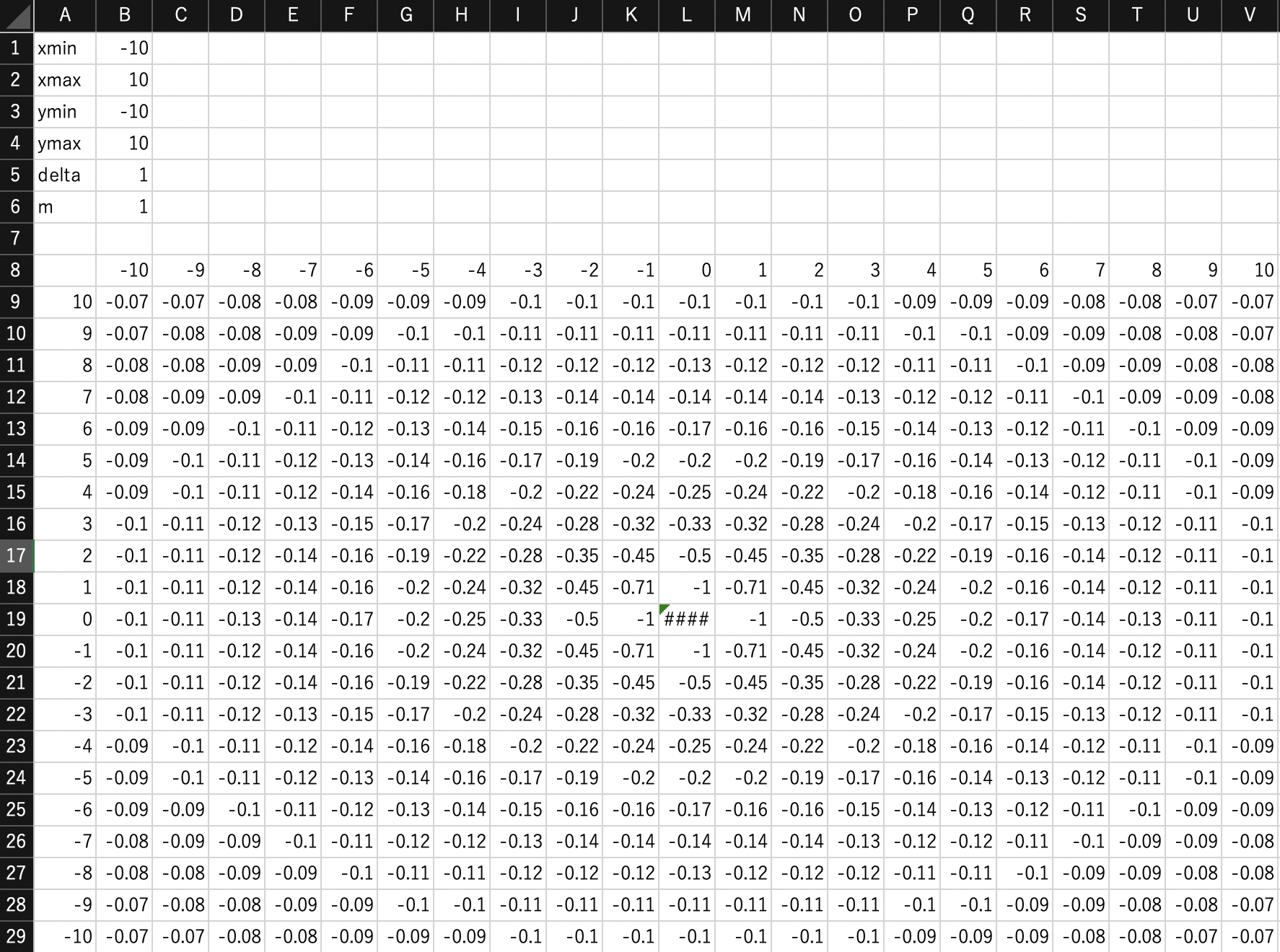
ここでそれぞれのセル数値を確認する必要はないが表示をうまく切り替えて正しそうなことを確認する.
等高線グラフの挿入
計算された数値が入っているセルを選択し,「挿入」メニューの「グラフ」から「等高線」を選択する。塗りつぶしありのカラーコンターまたはワイヤーフレームの等高線を描画できる。
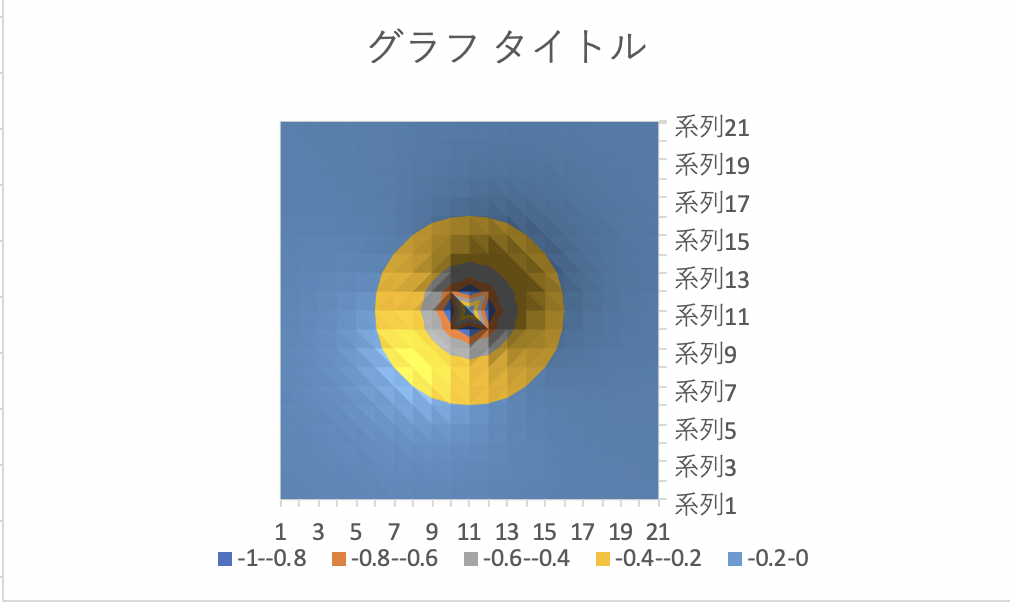
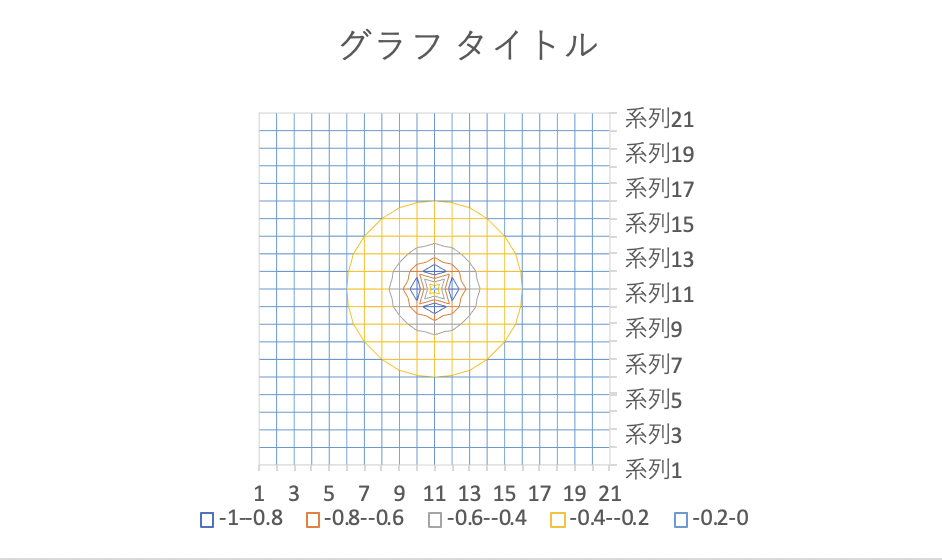
なお,この記事ではMicrosoft Excel for Mac Version 16.39を用いた.
まとめ
Excelの表計算で2次元関数の値を計算し,グラフ挿入機能を用いて等高線を描画する方法を紹介した.Excelを用いた描画ではあまり広い領域or大きな格子点数の処理には向いていないが,Excelが入ったPCがあれば気軽に等高線描画を試すことができる.筆者はExcelの使用にあまり慣れていないので細かな設定を説明できないが,工夫次第ではそれなりの見た目にすることもできるかもしれない.