はじめに
筆者は大学の工学部で習う流体力学を勉強しているが,流体力学の最初のほう(完全流体の理論)では速度ポテンシャル $\phi$ や流れ関数 $\psi$ といった物理量が現れ,それらの量を用いた代表的な流れの例がいくつか出てくる(二重わき出しなど). これらの量の2次元での等高線が教科書の図として載っているが,自分でも作図できたら理解が深まるような気がする.しかしながら,関数 $y = f(x)$を手軽に描画できるグラフソフト・サービスでは,2次元面でのある物理量の等高線を描くのは難しいことが多い.この記事では古き良き大学工学部で習得するであろうプログラミング言語であるFortranと,科学技術系のグラフ描画ソフトの古株であるgnuplotを使って速度ポテンシャル $\phi$ や流れ関数 $\psi$ の等高線を描いてみる.
事前準備: 各ソフトウェアのインストール
Fortranのインストール
Fortranはフリーの物としてはgfortranが有名である. マルチプラットフォームなので,自分の環境に合わせてインストールを行う.
gnuplotのインストール
gnuplotもマルチプラットフォームなので,自分の環境に合わせてインストールを行う.gnuplotはバージョンによって機能や使えるコマンドが異なるので,なるべく新しいものを用意することが好ましい. GUI機能がついたgnuplotもあるが,本記事ではコマンドorスクリプトを用いて利用する.
端末ソフトの確認
上記2つのソフトウェアはコマンドで実行するのが主流である. Fortranでのコンパイルやgnuplotの起動・操作をできる端末ソフトウェアを各環境で確認されたい. WindowsではコマンドプロンプトやPowershell, Macではターミナルがすぐに利用できる. Windowsでは Windows Subsystem for Linux (WSL) を利用しても良い(インストール,設定が必要).
対象とする流れ場
流体力学の教科書には具体的な流れ場の例として幾つかの流れ場が載っているが、一つ描画できればあとは同じなので,比較的簡単な吹き出し・吸い込みについて対象とする. 原点からの距離を $r$ とすると, 3次元での速度ポテンシャル $\phi$ は以下のように表せる.
$$
\phi = -\frac{m}{r},, r = \sqrt{x^2+y^2+z^2} \tag{1}
$$
ここで$m$は吹き出しの強さと呼ばれる係数である.2次元での等高線が描きたいので, $z=0$ として,
$$
\phi = -\frac{m}{r},, r = \sqrt{x^2+y^2} \tag{2}
$$
を描画してみる.
作業方針
式(2)は$x$,$y$を変数とする初等関数なのでグラフソフトに直接描画させることもできるが,それだと汎用性がないので,
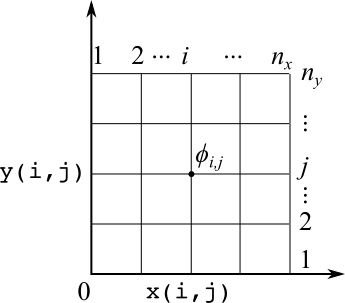
- Fortranで2次元の格子点(等間隔のマス目)を作成し,各格子点での $\phi (= \phi_{i,j})$の値をデータファイルとして出力する(下図参照).
- gnuplotで出力されたデータファイルを読み込み,等高線を描画する.
という手順で作業を行う.
Fortranプログラムによる2次元データの生成
プログラムに入力するパラメータとしては,
- 格子点数または格子セル数(
nx,ny) - 領域の大きさ(
xmin,xmax,ymin,ymax) - わき出しの強さ(
m)
である. gnuplot用にデータを出力するためには,2次元データであることを認識させるために,1行のデータ書き出しごとに空行を入れる必要がある. Fortran90の自由形式で書いたサンプルプログラムを以下に示す.
phi_source1.f90
!=============================================!
! Velocity potential for source and sink
!=============================================!
program phi_source
implicit none
!
integer :: nx,ny,i,j
real(8) :: xmin,xmax,ymin,ymax,dx,dy
real(8) :: r,m
!
real(8), allocatable :: phi(:,:)
real(8), allocatable :: x(:),y(:)
!
print *, ' nx, ny = ?'
read(5,*) nx, ny
print *, ' nx, ny = ', nx, ny
!
print *, ' xmin, xmax = ?'
read(5,*) xmin, xmax
print *, ' xmin, xmax = ', xmin, xmax
!
print *, ' ymin, ymax = ?'
read(5,*) ymin, ymax
print *, ' ymin, ymax = ', ymin, ymax
!
print *, ' m = ?'
read(5,*) m
print *, ' m = ', m
!
open(12, file = 'output.d', form = 'formatted')
!
allocate(x(1:nx))
allocate(y(1:ny))
allocate(phi(1:nx,1:ny))
!
dx = (xmax - xmin)/dble(nx)
dy = (ymax - ymin)/dble(ny)
!
do i = 1, nx
x(i) = xmin + dx*dble(i-1)
enddo
!
do j = 1, ny
y(j) = ymin + dy*dble(j-1)
enddo
!
do j = 1,ny
do i = 1,nx
r = sqrt(x(i)**2 + y(j)**2)
phi(i,j) = -m/r
write(12,'(3e12.4)') x(i),y(j),phi(i,j)
enddo
write(12,*)
enddo
!
close(12)
!
end program phi_source
簡単なプログラムなので内容の説明は省略する. このプログラムでは入力パラメータを対話的にキーボードから入力しているが繰り返しプログラムを実行するときは面倒なので,以下にnamelistを使った入力データを用いるプログラムを示す.
phi_source2.f90
!=============================================!
! Velocity potential for source and sink
!=============================================!
program phi_source
implicit none
!
integer :: nx,ny,i,j
real(8) :: xmin,xmax,ymin,ymax,dx,dy
real(8) :: r,m
!
real(8), allocatable :: phi(:,:)
real(8), allocatable :: x(:),y(:)
!
namelist /grid/nx,ny,xmin,xmax,ymin,ymax
namelist /coef/m
!
open(11, file = 'input.d', form = 'formatted')
read(11, nml=grid)
read(11, nml=coef)
close(11)
!
print *, ' nx, ny = ', nx, ny
print *, ' xmin, xmax = ', xmin, xmax
print *, ' ymin, ymax = ', ymin, ymax
print *, ' m = ', m
!
open(12, file = 'output.d', form = 'formatted')
!
allocate(x(1:nx))
allocate(y(1:ny))
allocate(phi(1:nx,1:ny))
!
dx = (xmax - xmin)/dble(nx)
dy = (ymax - ymin)/dble(ny)
!
do i = 1, nx
x(i) = xmin + dx*dble(i-1)
enddo
!
do j = 1, ny
y(j) = ymin + dy*dble(j-1)
enddo
!
do j = 1,ny
do i = 1,nx
r = sqrt(x(i)**2 + y(j)**2)
phi(i,j) = -m/r
write(12,'(3e12.4)') x(i),y(j),phi(i,j)
enddo
write(12,*)
enddo
!
close(12)
!
end program phi_source
インプットデータは以下のようにする.
input.d
&grid
nx=20
ny=20
xmin=-10.d0
xmax= 10.d0
ymin=-10.d0
ymax= 10.d0
/
&coef
m=1.d0
/
いずれかのプログラムをコンパイル,実行すると2次元データoutput.dが出力される. 出力ファイル名を入力パラメータごとに変更したい場合は自分でプログラムを改良されたい.
gnuplotによる等高線図(contour)の作成
gnuplotをoutput.dが存在するディレクトリ(フォルダ)で起動する.等高線(contour)を設定してから2次元データの3次元プロットコマンド(splot)を行ってみる.
gnuplot> set contour
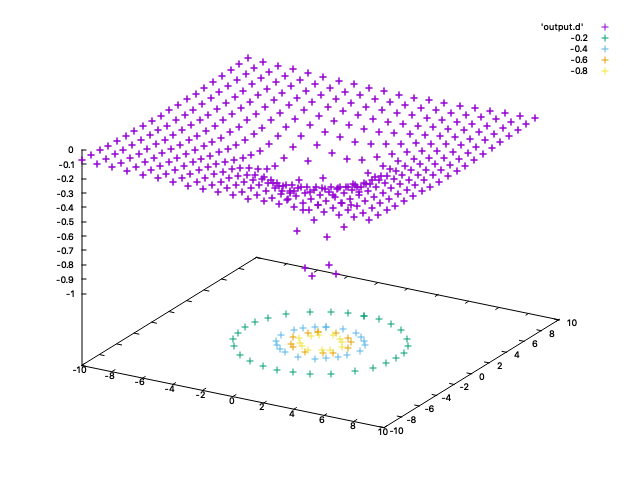
gnuplot> splot 'output.d'
筆者はMac用の GNUPLOT Version 5.2 patchlevel 8 を用いている. 必要なのは下面($x$-$y$平面)に描かれた等高線のみで3次元ビューも必要ないので,以下のように再度描画してみる.
gnuplot> set contour
gnuplot> unset surface
gnuplot> set view 0,0
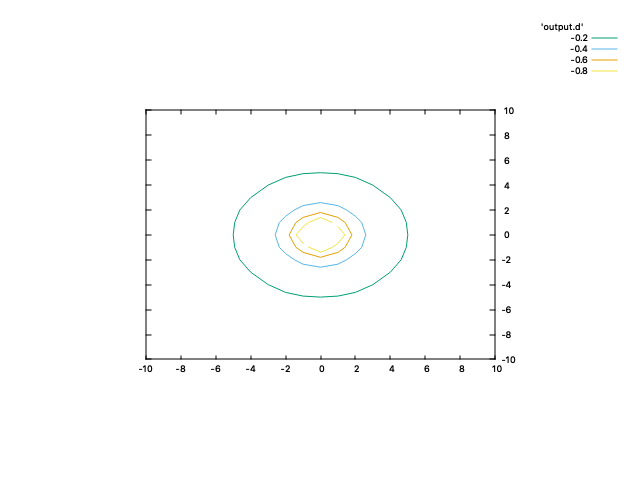
gnuplot> splot 'output.d' w l
splotのところで点ではなく線で描画するオプションw lを追加した.ちょっと見た目がしょぼい感じもするが,データさえあれば手軽に描画できる.たくさんのデータに対してgnuplotのコマンドを毎回入力するのは面倒なので,以下のようなコマンドスクリプトを用意して実行すると便利である.
等高線プロットスクリプト(contour.plt)
set contour
unset surface # or set nosurface
set view 0,0
set view equal xy
set key at screen 0.95, 0.7
set size 1.0,1.0
set cntrparam levels incremental -1.0,0.1,0.1
set terminal png
set output 'c1.png'
splot 'output.d' w l
描画を正方形にする(set view equal xy),凡例ラベルの場所(set key),描画サイズの調整(set size),等高線値の指定(set cntrparam),ファイル保存(set terminalとset ouput)を追加した. このスクリプトを動かすためには端末で以下のようにする.
gnuplot contour.plt
あるいは以下のようにgnuplotが起動した状態でスクリプトをloadしても実行できる.
gnuplot> load 'contour.plt'
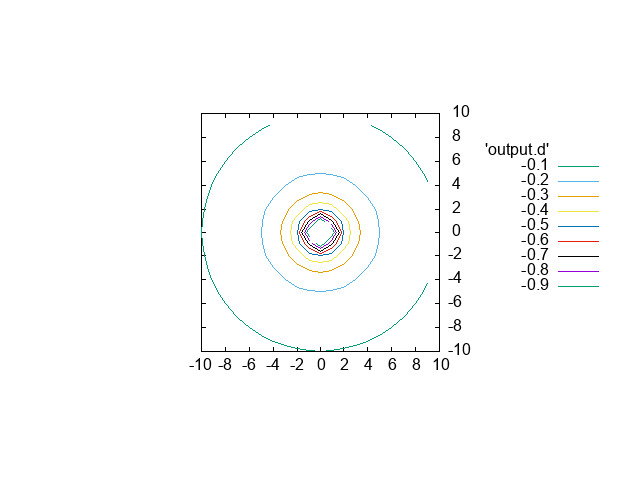
失敗しなければ以下に示すc1.pngという画像pngファイルが出力される.古いpngファイルがあると上書きされないこともあるので,等高線間隔を変更した場合などはpngファイルを消してからgnuplotを実行するのが無難である. 出力形式はpng以外も指定できるので必要に応じて変更されたい(svgで出力してラベルを微調整など).
まとめ
Fortran+gnuplotで等高線を簡単に描画する方法を紹介した. 必要に応じて出力する2次元データの解像度を変更したり,描画する関数を変更することができる.また,gnuplotには今回紹介したもの以外の機能・設定パラメータがあるので,自分で好きな様式にカスタマイズされたい.