この記事は教科書に出てくる等高線を描いてみる(Fortan+gnuplot)の続編です.
はじめに
筆者は大学の工学部で習う流体力学を勉強しているが,流体力学の最初のほう(完全流体の理論)では速度ポテンシャル $\phi$ や流れ関数 $\psi$ といった物理量が現れ,それらの量を用いた代表的な流れの例がいくつか出てくる(二重わき出しなど). これらの量の2次元での等高線が教科書の図として載っているが,自分でも作図できたら理解が深まるような気がする.しかしながら,関数 $y = f(x)$を手軽に描画できるグラフソフト・サービスでは,2次元面でのある物理量の等高線を描くのは難しいことが多い.前回の記事ではFortran+gnuplotで描画してみたが,やはり人気があるプログラミング言語でやってみたいので,今回はPythonを用いて等高線を描いてみる.
事前準備: Pythonと必要なモジュールのインストール
Pythonはマルチプラットフォームなので各環境に合わせてインストールを行う.Pythonのインストール方法は色々あるので自分で調べて良さそうなものを選んで欲しい.インストールが難しそう or PCに色々インストールしたくない,という人にはGoogle Colaboratoryの利用をおすすめする.
Python本体以外に,モジュールとしてnumpyとmatplotlibが必要である.OSに元々入っているPythonなどを利用する場合は追加インストールする.
対象とする流れ場
前回の記事と同じ吹き出し・吸い込みについて対象とする. 原点からの距離を $r$ とすると, 3次元での速度ポテンシャル $\phi$ は以下のように表せる.
$$
\phi = -\frac{m}{r},, r = \sqrt{x^2+y^2+z^2} \tag{1}
$$
ここで$m$は吹き出しの強さと呼ばれる係数である.2次元での等高線が描きたいので, $z=0$ として,
$$
\phi = -\frac{m}{r},, r = \sqrt{x^2+y^2} \tag{2}
$$
を描画してみる.
作業方針
Pythonのmatplotlibモジュールは各種の描画をできるので作業はPythonのみで解決する.
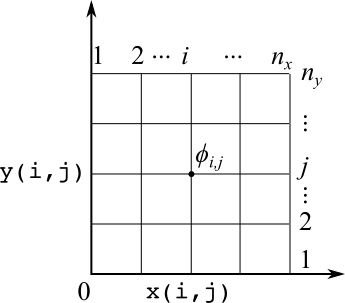
- numpyの機能で2次元の格子点(等間隔のマス目)を作成し,各格子点での $\phi (= \phi_{i,j})$の値を計算する.
- matplotlibの機能で等高線を描画する.
という流れでPythonスクリプトを作る.高度なことはしないので,オブジェクト指向などは考慮しない.
Pythonスクリプト
以下にスクリプト例を示す.
contour.py
import matplotlib
import numpy as np
import matplotlib.pyplot as plt
xmin = -10.0
xmax = 10.0
ymin = -10.0
ymax = 10.0
delta = 0.1
x = np.arange(xmin,xmax,delta)
y = np.arange(xmin,xmax,delta)
m = 1.0
X, Y = np.meshgrid(x,y)
r = np.sqrt(X**2 + Y**2)
Z = -m/r
fig, ax = plt.subplots(figsize=(6,6))
levels = np.arange(-1.0,0.0,0.2)
cont = ax.contour(X,Y,Z,levels)
cont.clabel(fmt='%1.1f', fontsize=12)
plt.show()
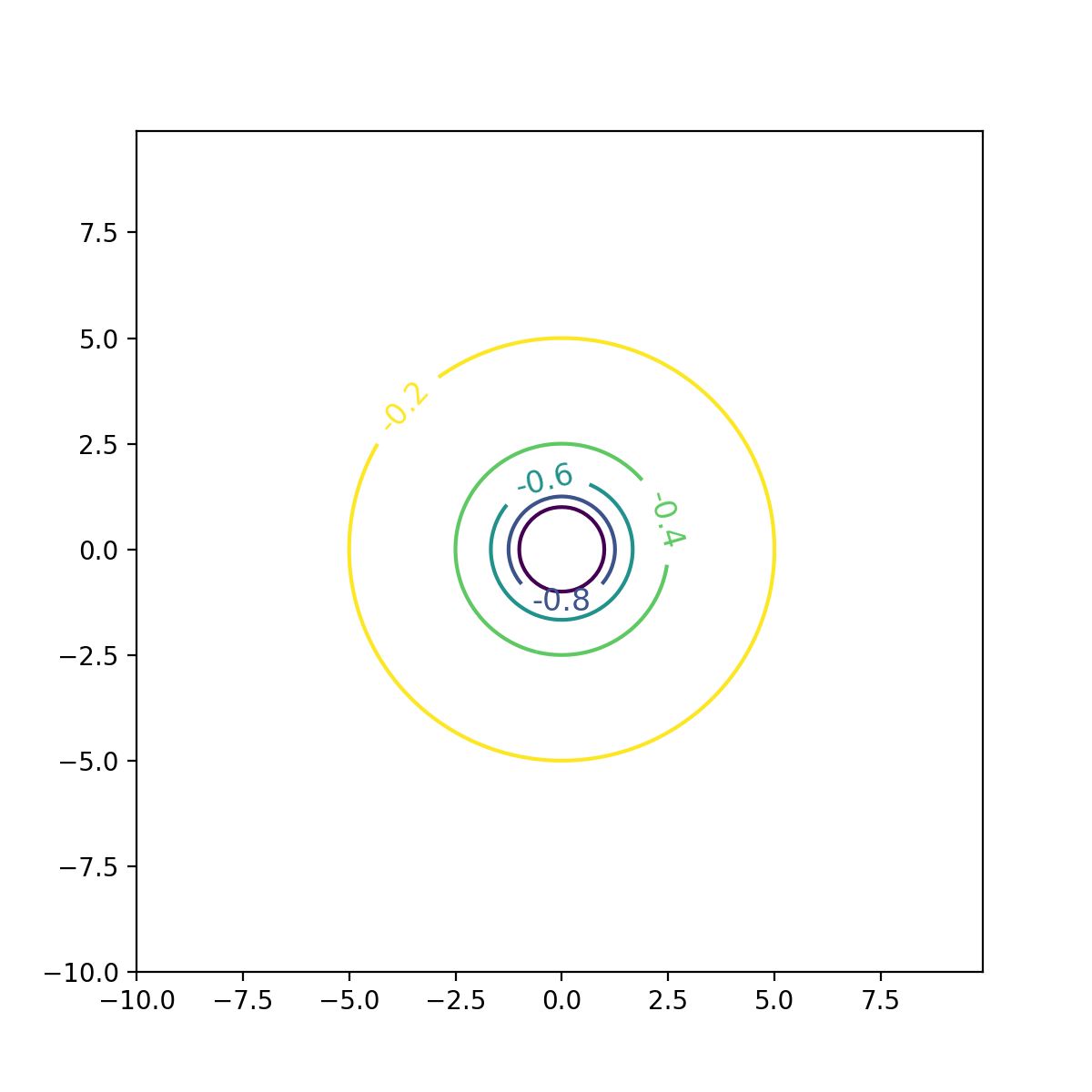
最初に$x$,$y$に座標値を入れ,$X$,$Y$が格子点に変換したものである.matplotlibのグラフ描画では2つの流儀があるが,Artistオブジェクトを使う方法を用いている.等高線に数値を入れられるのはmatplotlibの長所の一つなので入れておいた.
端末で上記スクリプトを実行するのは以下のとおりであり,等高線図が別ウィンドウで現れる.
python contour.py
画像を保存したい場合はこの描画ウィンドウで保存(Save)ボタンを押して保存するか,スクリプト最後のplt.show()を以下に変更する.
plt.savefig('c2.png')
まとめ
Pythonのmatplotlibの機能を用いて等高線を簡単に描画する方法を紹介した.今回はmatplotlibの設定に関して必要最低限のものしか設定していないが,matplotlibはグラフの隅々まで詳細に設定できるので,こだわれば教科書に載っている図を正しく綺麗に描画することも可能である.