今回の目標
前回の考察に従い、15で行った遺伝的アルゴリズムの改善案を試します。
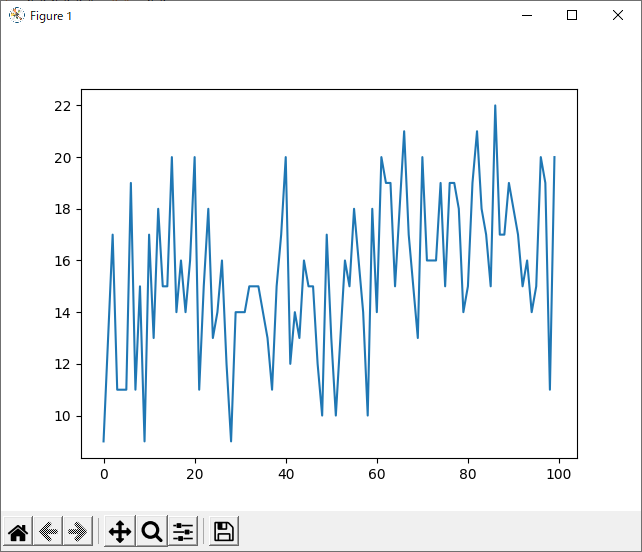
まずは乱数から。
ここから本編
本題ではありませんが、マクロで以下のように表記を変更しています。
static_cast<int>(num) => INT(num)
static_cast<double>(num) => DOUBLE(num)
「static_cast<BOARD>(num)」についてはいい別名が思いつかなかったのでそのままです。
また、「read_goal」を要素2個の一次元配列に変更し、それぞれ黒と白の「何手先まで読むか」の数字としました。今回はあまり関係ないです。
srandへの引数を変える
クラス内で新たに「srand_num」というpublic変数を用意し、クラス内でこれをsrand関数の引数に使うことで、外部からこの値を書き換えればsrand関数への引数を変えられるようにしました。
実行ファイルは以下の通り。
なお、15で使用した「run_1hand_rand」の改造です。
また、よく考えたらepoc変数が名前と全く関係のないことをしていたのでchildに改名しました。
# include "osero_genetic.h"
const int child = 30;
const int entire = 1000;
int main(void){
int win, win_sum;
int i, j, k;
double eva[child][64], new_eva[child][64];
osero_genetic * run;
FILE * fp = fopen("data_1hand_rand.csv", "w");
printf("progress ");
for (i = 0; i < child; i++) printf(".");
printf("\n");
fprintf(fp, "num,win_per\n");
srand(0);
for (i = 0; i < child; i++)
for (j = 0; j < 64; j++)
eva[i][j] = DOUBLE(rand()) / (RAND_MAX >> 1) - 1;
for (i = 0; i < entire; i++){
printf("%3d/%3d: ", i + 1, entire);
win_sum = 0;
for (j = 0; j < child; j++){
printf(".");
run = new osero_genetic(
INT(PLAY_WAY::nhand),
eva[j],
INT(PLAY_WAY::random)
);
run -> read_goal[INT(TURN::black)] = 1;
run -> srand_num = i + j;
win = INT(run -> play());
if (win) {
for (k = 0; k < 64; k++)
new_eva[win_sum][k] = eva[j][k];
win_sum++;
}
delete run;
}
if (win_sum){
for (j = 0; j < child; j++){
for (k = 0; k < 64; k++){
if (rand() % 100 > 5)
eva[j][k] = new_eva[rand() % win_sum][k];
else
eva[j][k] = DOUBLE(rand()) / (RAND_MAX >> 1) - 1;
}
}
}
printf("\n");
fprintf(fp, "%d,%d\n", i, win_sum);
}
fclose(fp);
fp = fopen("eva_1hand_rand.csv", "w");
for (i = 0; i < child; i++){
for (j = 0; j < 64; j++){
fprintf(fp, "%2.4f", eva[i][63 - j]);
if ((j + 1) % 8 == 0) fprintf(fp, "\n");
else fprintf(fp, ",");
}
fprintf(fp, "\n");
}
fclose(fp);
return 0;
}
ここには載せませんが、15で作成した「run_1hand_1hand」についても同様の変更をしました。
実行結果
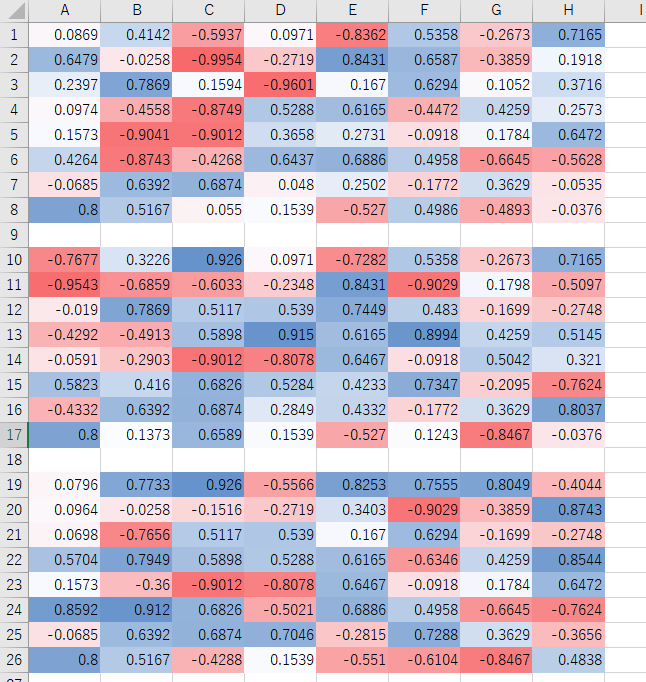
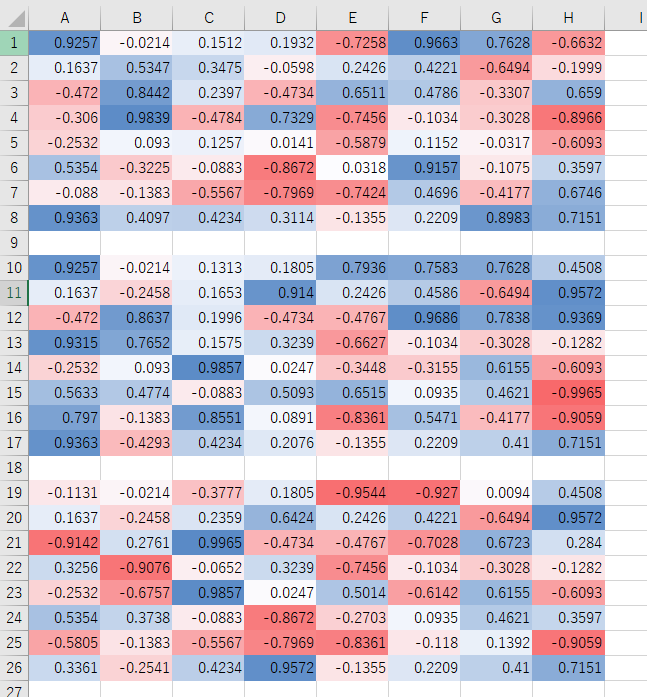
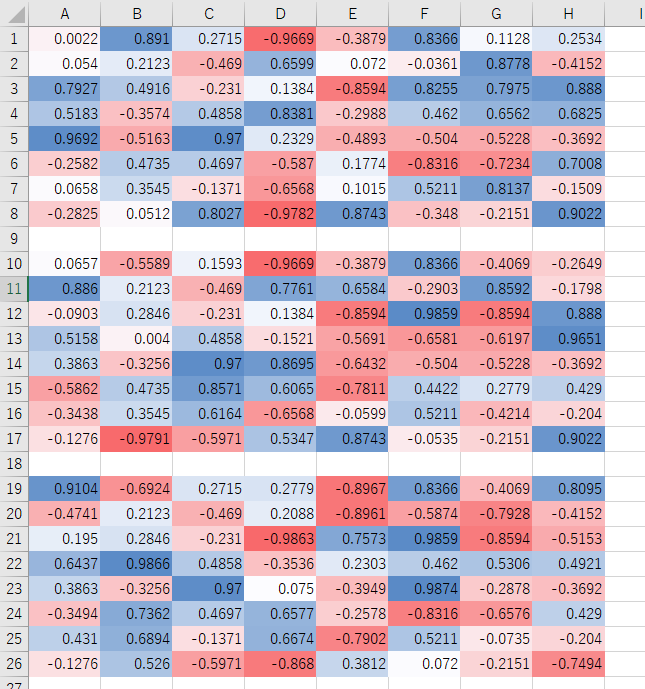
15と同様、Excelで評価値に色を付け、Pythonでグラフを書きました。
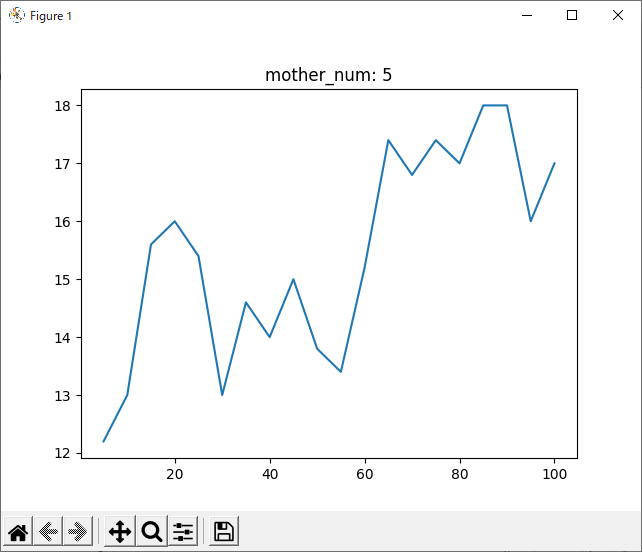
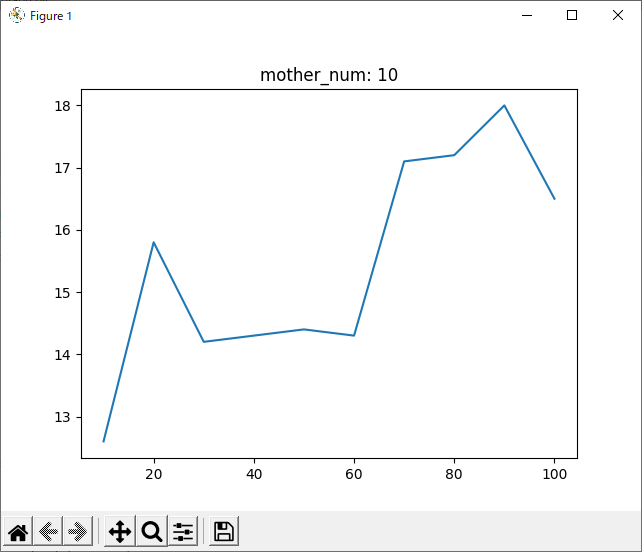
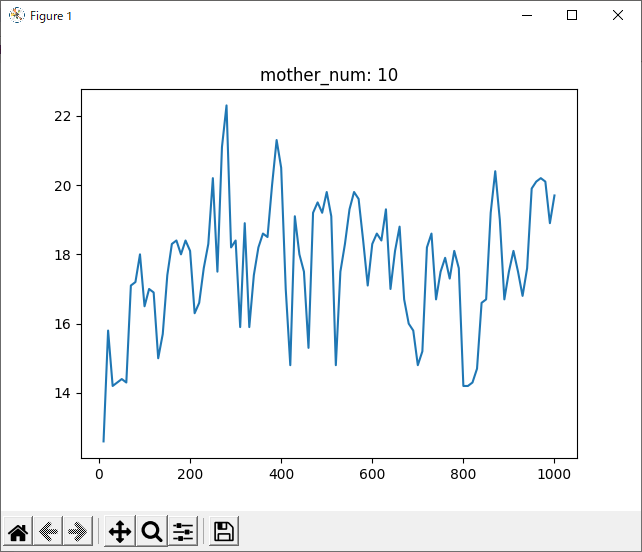
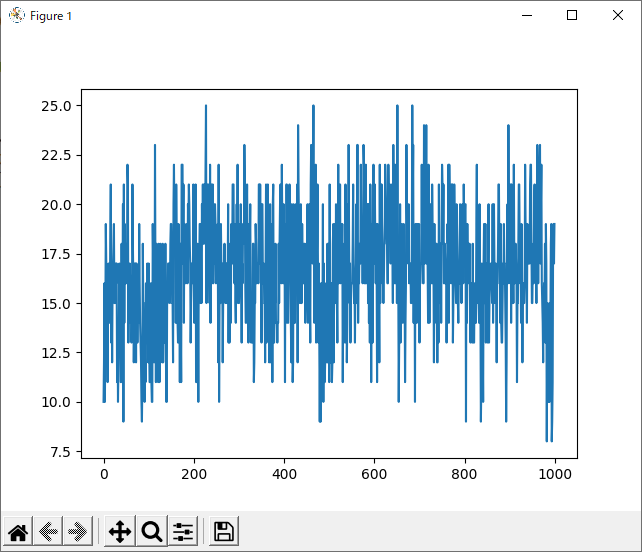
run_1hand_rand
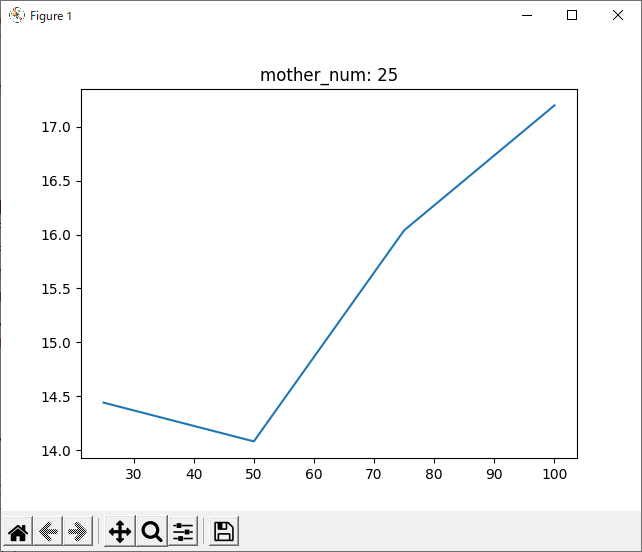
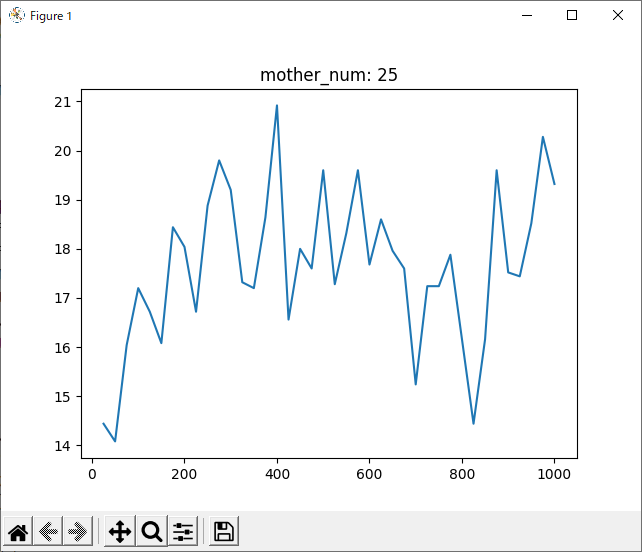
run_1hand_1hand
run_1hand_1hand 1000回
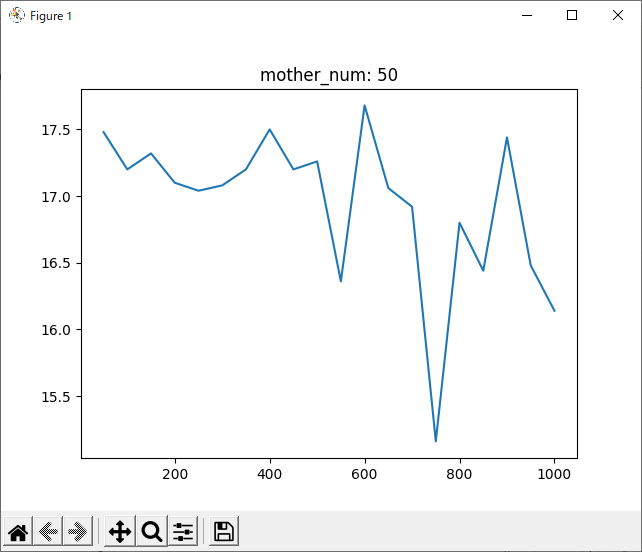
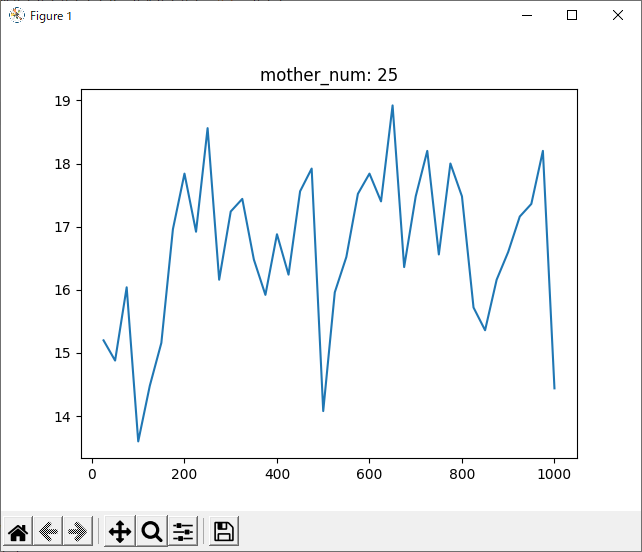
ここで、run_1hand_randと同様に、run_1hand_1handについても1000回進化させてみました。
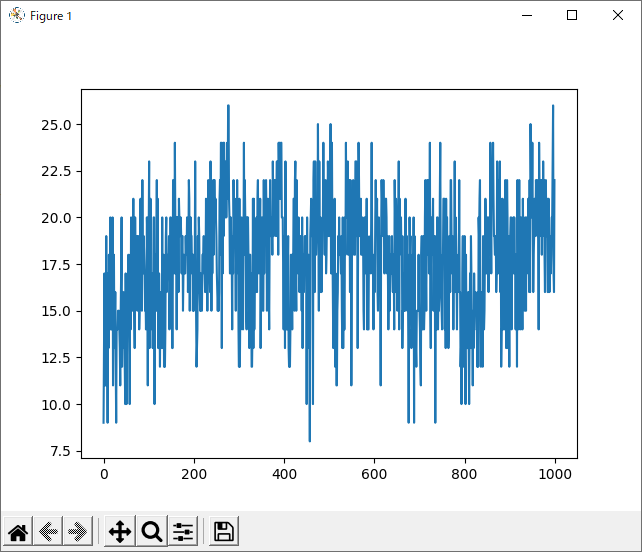
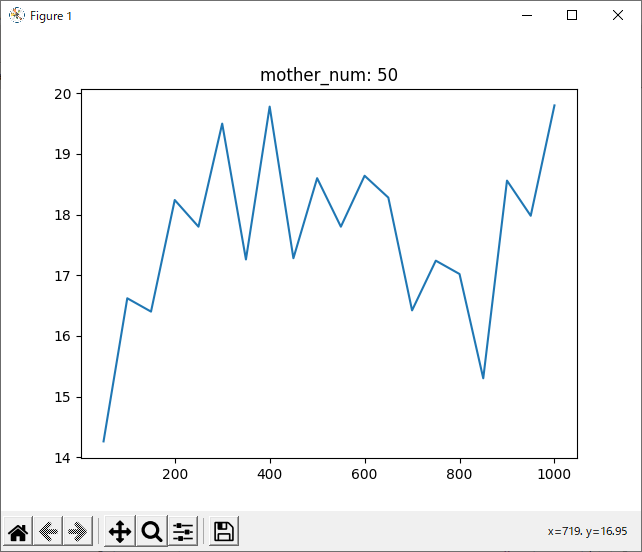
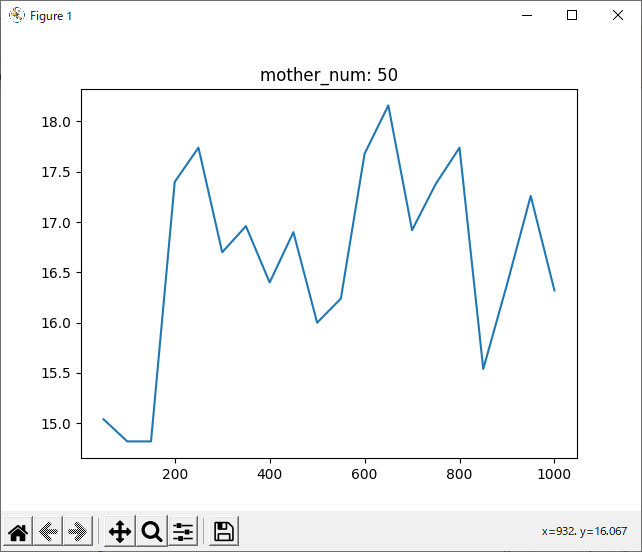
run_2hand_2hand
ついでに2hand VS 2hand、黒側が強化学習をやってみました。
進化回数は1000回です。
まあまあ時間かかりました。
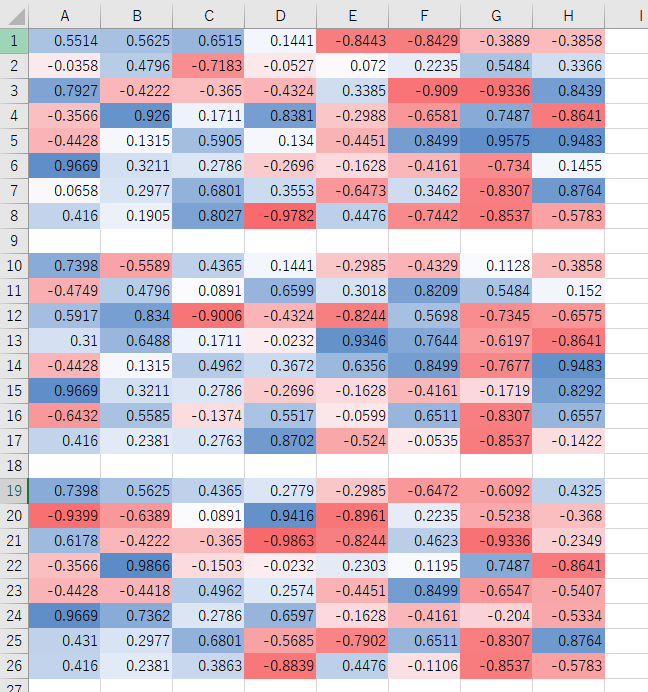
全体
ついでに、前回作成した、データの平均と分散を求めるプログラムを以下のように改造し実行してみました。
大した改造ではないですが、私自身がこれをできることを知らなかったので載せます。
import pandas as pd
import glob
for filename in glob.glob("data*.csv"):
df = pd.read_csv(filename)
per = df["win_per"]
print(filename, ": ")
print("mean:", per.mean())
print("var: ", per.var())
print()
実行結果は以下の通り。
data_1hand_1hand.csv :
mean: 17.639
var: 10.154833833833834
data_1hand_rand.csv :
mean: 16.943
var: 7.953704704704704
data_2hand_2hand.csv :
mean: 16.62
var: 9.575175175175175
考察
まず本題
まずは本題、「srand関数の引数を逐次変えることで学習結果はどうなるか」ですが、平均を見る限りやはり0は前回予想した通りプレイヤー側に有利となる数字であると考えられます。
理由は同じプログラムなのに今回のほうが勝率が下がったからです。
今後は今回のように、srand関数の引数は逐次更新していきたいと思います。
谷部分
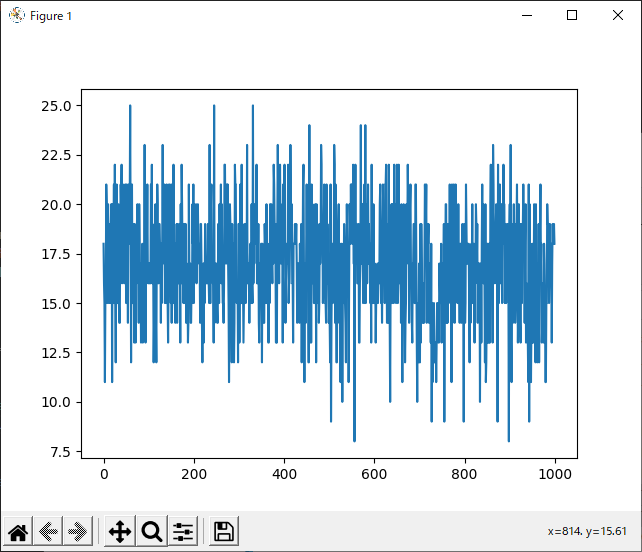
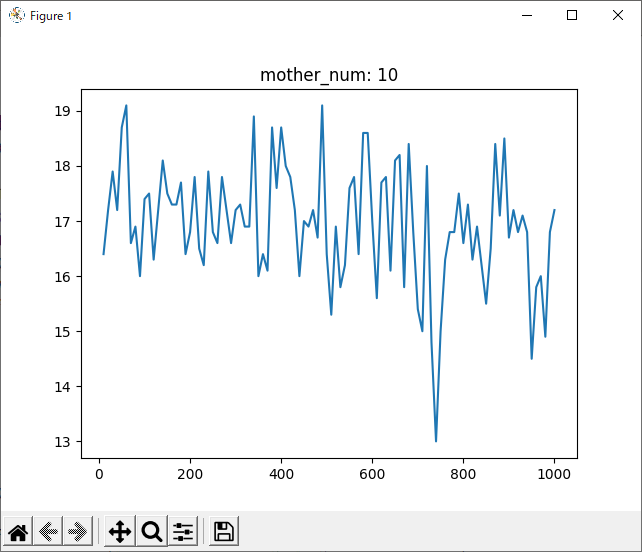
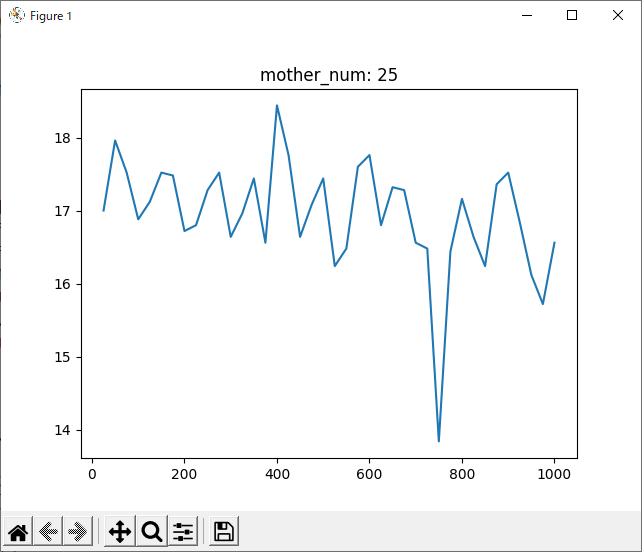
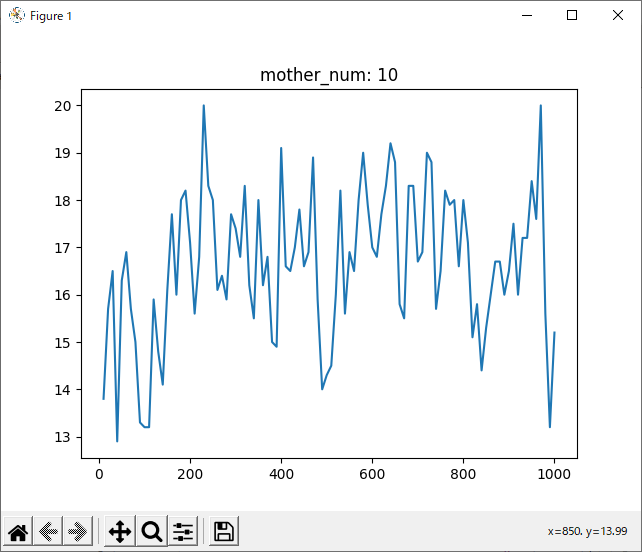
次に気になったのは、1000回学習させたデータについて、800回付近で一度勝率が下がっていることです。
全てのデータを記録したグラフでは分かりづらいですが、数回ごとの平均を記録したグラフでは分かりやすいと思います。
理由として考えられるのは二つあります。一つ目は、「800付近が極端にプレイヤー(役)に有利なsrand引数なのでは?」ということです。これは、実際0がコンピュータに有利な数字だったことからも可能性が高いと思います。
二つ目として考えられるのは過学習や局所解です。しかし、学習後の評価値が本当に正しいのか? がよく分からないため検証の必要があると思います。ですが可能性としてはあり得ると考えます。2hand_2handでその特徴が顕著ですが、青と赤の配置が、3つの最終評価値で似た形になっています。「端の評価値が高く、その隣は低くなるはず」という当初の予想とは違うものの一応一つのパターンを作っているのが分かります。
つまり、「これは局所最適解である」または「実はこれが最適解である」、このどちらかが考えられるのでは? といえます。
フルバージョン
randフォルダ内に入っています。
なお、data_1hand_1hand.csv及びeva_1hand_1hand.csvの中身は1000回進化時のものが入っています。
実際にやってみた
やってません。
次回は
今回得られた評価値がどの程度正しいものなのかについて検証していきたいと思います。
進化方法や突然変異の割合をいじるのはその後に行いたいと思います。