今回の目標
今までこのシリーズで「カスタムスコア」と呼んでいたものですが、調べたところこの概念は既にあり、一般に「評価値」と呼ぶようです。なので以降の記事では、これまで「カスタムスコア」と呼んでいたものを「評価値」と呼び改めます。
さて、この評価値ですが、ネットで調べたところ有用とされるパターンがすでにいくつかあるようです。しかし私の感覚とは少し違う気がするので、いくつかの記事を使って評価値の検証をしていきたいと思います。
今回は前回作成したプログラムを改造して遺伝的アルゴリズム(っぽいこと)を行い、最適な評価値を探し出します。
ここから本編
今回のアルゴリズムは以下に示すとおりです。
- 評価値をランダムで初期化したものを30通り作る。
- それぞれの評価値を用いて1handでランダムに打ち返すプログラムと対戦する。
- 勝利した際の評価値を次代につなぐ。
なお、5%の確率で突然変異を起こさせます。
遺伝的アルゴリズム(っぽいこと)に使用したプログラム
ヘッダファイル
publicにread_goal、mode、そしてplayerとcomputerを追加しました。
それぞれ「何手先まで読むか」「学習モードか、そうでないか」「プレイヤーとコンピュータがどちらのターン(黒ないし白)なのか」を指定します。
evaが評価値です。具体的な値はコンストラクタによって指定されます。
# ifndef osero_genetic_h
# define osero_genetic_h
# include <stdio.h>
# include <stdlib.h>
# include <time.h>
const bool BLACK = false;
const bool WHITE = true;
typedef unsigned long BOARD;
enum class TURN{
black,
white
};
enum class PLAY_WAY{
nhand,
random,
sentinel
};
class osero_genetic{
private:
// other
const int SIZE = 8;
bool turn = BLACK;
int bmethod, wmethod;
void (osero_genetic:: * play_method[static_cast<int>(PLAY_WAY::sentinel)]) (int *, int *) = {
&osero_genetic::nhand,
&osero_genetic::random
};
// board
BOARD bw[2];
double eva[2][64];
// function
bool check(BOARD * now, int line, int col);
bool check_all(void);
bool count_last(void);
void put(BOARD * now, int line, int col, bool turn);
void printb(void);
void nhand(int * line, int * col);
void random(int * line, int * col);
int popcount(BOARD now);
double count(BOARD * now);
double board_add(BOARD * now, int num, bool turn);
public:
osero_genetic(int player_b, int player_w);
osero_genetic(int player_b, double * eva, int player_w);
osero_genetic(int player_b, int player_w, double * eva);
osero_genetic(int player_b, double * eva1, int player_w, double * eva2);
~osero_genetic();
int read_goal = 1;
int mode = 0;
int player, computer;
bool print = false;
bool play(void);
};
# endif
ソースファイル
count関数以外は今までのプログラムのつぎはぎなので詳細は省きます。
また、play関数を呼ぶことで、実行ファイルで指定した条件での試合が一回実行されます。
double osero_genetic::count(BOARD * now){
int my = static_cast<int>(this -> turn);
int opp = static_cast<int>(!(this -> turn));
int i = 0;
double score = 0;
double * myeva = this -> eva[my];
BOARD place = 1;
while (place){
if (now[my] & place)
score += myeva[i];
else if (now[opp] & place)
score -= myeva[i];
i++;
place = place << 1;
}
return score;
}
実行ファイル
epocが一世代の数、entireが進化回数です。
30x1000で三万試合行います。
ここで、具体的なアルゴリズムについて説明します。用語や詳しい説明はその下に書きます。
- 評価値をランダムで初期化したものを30通り作る(なお、数字はすべて-1~1の実数です。その範囲にした理由はプログラムが作りやすかったというだけです)
- クラスからインスタンスを作る。今回は黒がコンピューターで白がプレイヤー(役)です。黒は評価値に従った1hand、白はランダムで打ち返します。
- read_goalを設定し、試合を行い、勝敗を記録する。
- 勝利した場合、その時の評価値をnew_evaに保存し、また勝利回数(win_sum)を更新します。
- 30試合終了後、5%の確率で評価値を初期化し、95%の確率で勝利した際に使っていた評価値を、ランダムで次の評価値に分配します。
- 1000回進化後、評価値をファイル出力し終了。
「評価値に従った1hand」について説明します。これまでの1handは「このターンで最もひっくりかえせる場所を選ぶ」という思考方法でしたが、これを「評価値が盤面全て1の状態で、次のターンで自分の評価値が最も高くなる場所を選ぶ」と解釈し、これを「評価値に従った1hand」と呼ぶことにします。
この評価値をいじることで思考方法自体は変えずとも強くなれるのではと考えました。
また、なぜこんな進化方法をとるのか説明します。
遺伝的アルゴリズムの例題としてよく挙げられるナップザック問題では0か1で表現された遺伝子を交叉によって進化させるのが一般的です。これは各箇所の遺伝子情報よりも、0と1の並び方が重要だからなのではないかと考えました。
オセロでは評価値の並び方よりも、各箇所の具体的な評価値のほうが重要です。そのため、勝利した際に使っていた評価値の、いくつか存在する「右上の数字」からランダムで、新しい評価値の右上にその値をコピーする、右上以外も同様、という手法をとりました。一世代で30試合もするので、何もしなくても平均15試合は勝ちます。
(追記)
上の進化方法の説明が分かりづらいと思うので、順序だてて説明しなおします。
- 30通りの評価値がある。それぞれの評価値は8x8の盤面に対応すべく64個の、範囲-1~1のdouble型実数を持つ。64個の実数一つ一つが盤面の中の64か所ある位置に対応する。
- それぞれの評価値に従って、30回ランダムとの試合を行う。
- 勝ったパターンの評価値のみ取り出す。例えば10回勝った場合、64x10で640個のdouble型実数が保存される。配列としては10個である。
- 新しい評価値は30個の配列である。この30個の配列の0番目には、保存しておいた10個の配列の、10通りある0番目の中からランダムで選ぶ。
- 1~63番目についても同様。また、5%の確率で初期化(乱数を入れること)をする。
以下は使用したプログラムです。
# include "osero_genetic.h"
const int epoc = 30;
const int entire = 1000;
int main(void){
int win, win_sum;
int i, j, k;
double eva[epoc][64], new_eva[epoc][64];
osero_genetic * run;
FILE * fp = fopen("data_1hand_rand.csv", "w");
printf("progress ");
for (i = 0; i < epoc; i++) printf(".");
printf("\n");
fprintf(fp, "num,win_per\n");
// srand(static_cast<unsigned int>(time(NULL)));
srand(0);
for (i = 0; i < epoc; i++)
for (j = 0; j < 64; j++)
eva[i][j] = static_cast<double>(rand()) / (RAND_MAX >> 1) - 1;
for (i = 0; i < entire; i++){
printf("%3d/%3d: ", i + 1, entire);
win_sum = 0;
for (j = 0; j < epoc; j++){
printf(".");
run = new osero_genetic(
static_cast<int>(PLAY_WAY::nhand),
eva[j],
static_cast<int>(PLAY_WAY::random)
);
run -> read_goal = 1;
win = static_cast<int>(run -> play());
if (win) {
for (k = 0; k < 64; k++)
new_eva[win_sum][k] = eva[j][k];
win_sum++;
}
delete run;
}
if (win_sum){
for (j = 0; j < epoc; j++){
for (k = 0; k < 64; k++){
if (rand() % 100 > 5)
eva[j][k] = new_eva[rand() % win_sum][k];
else
eva[j][k] = static_cast<double>(rand()) / (RAND_MAX >> 1) - 1;
}
}
}
printf("\n");
fprintf(fp, "%d,%d\n", i, win_sum);
}
fclose(fp);
fp = fopen("eva_1hand_rand.csv", "w");
for (i = 0; i < epoc; i++){
for (j = 0; j < 64; j++){
fprintf(fp, "%2.4f", eva[i][63 - j]);
if ((j + 1) % 8 == 0) fprintf(fp, "\n");
else fprintf(fp, ",");
}
fprintf(fp, "\n");
}
fclose(fp);
return 0;
}
実行結果
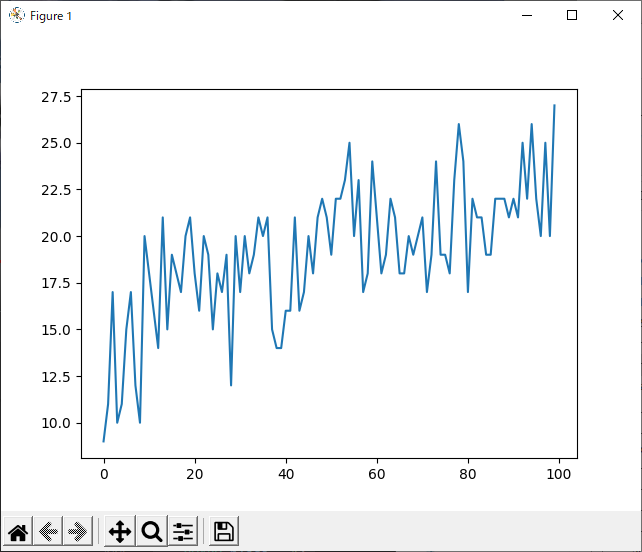
勝利した回数の世代ごとの記録をpythonで見てみました。
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv("data_1hand_rand.csv")
x = df["num"]
y = df["win_per"]
fig = plt.figure()
plt.plot(x, y)
plt.show()
plt.clf()
plt.close()
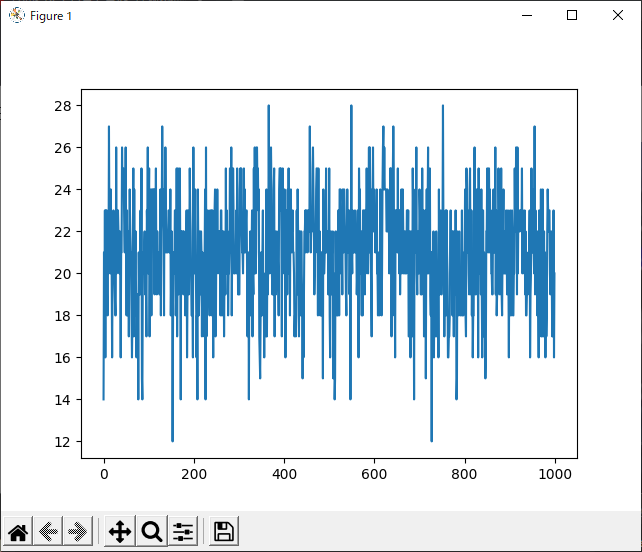
上のプログラムの実行結果が下の写真です。
一切勝率上がってませんでした。
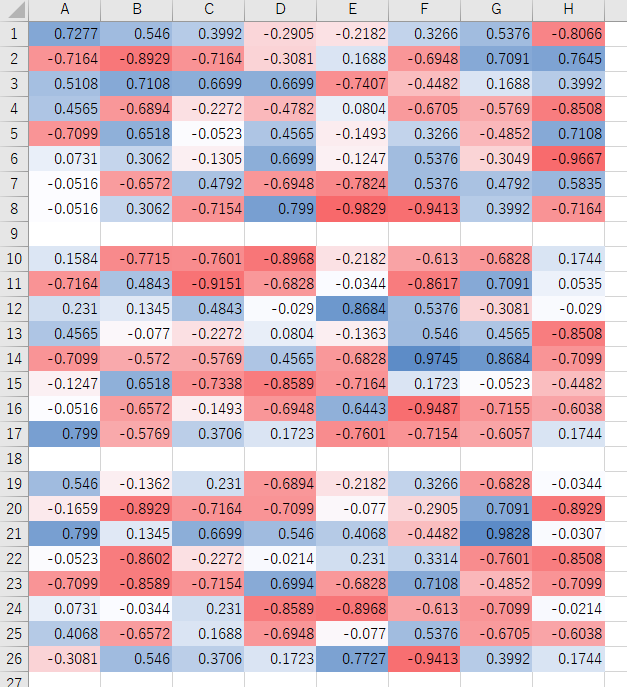
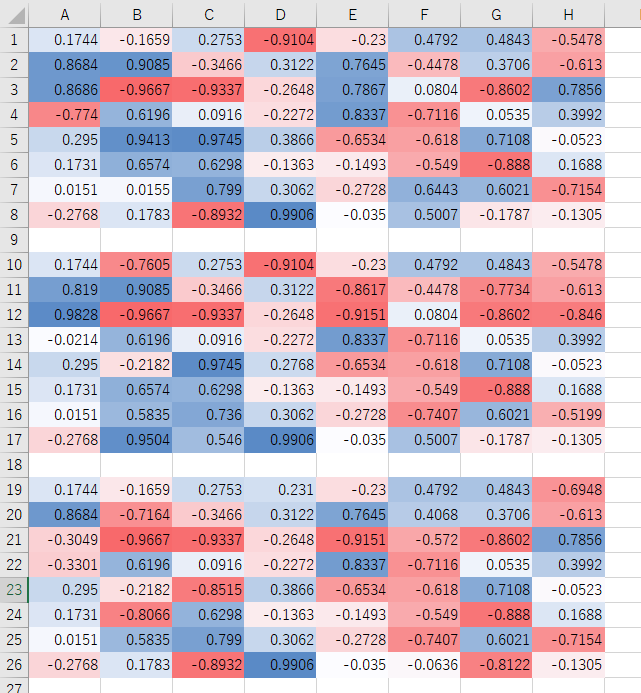
学習後の評価値も以下の通り。なお、実際には30通り出力されますが、すべては載せきれないため三つだけ表示します。また、色がついているのはExcelの機能を使っています。
初期値かな? と思うくらいにランダムな値が入っているだけでした。
改善1 run_2hand_rand
1handでダメなら2handを試します。
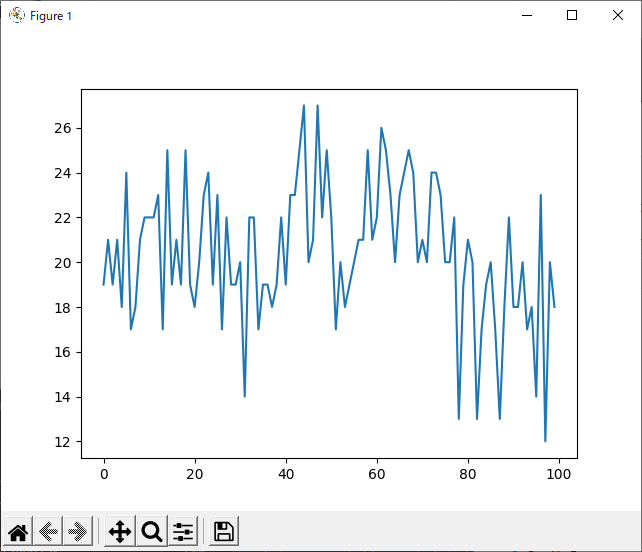
実行に時間がかかったため100世代しかしておりません。
ほとんど学習しておりませんでした。
改善案2 run_1hand_1hand
では、コンピュータが評価値に従った1hand、プレイヤーが1handで打ち合った場合どうなるかを試しました。
勝率は向上しています。
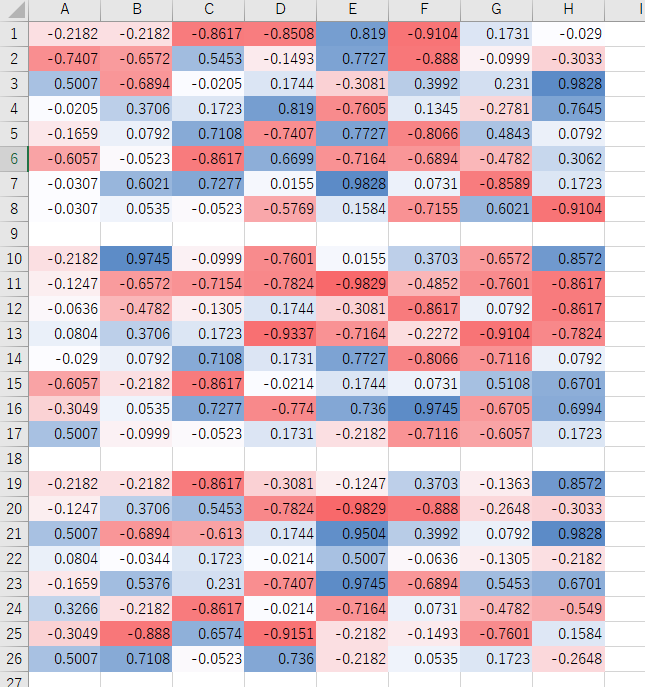
一方の評価値は・・・
ほとんど学習しておりません。
フルバージョン
geneticフォルダに入っています。
実際にやってみた
やってません。
次回は
遺伝的アルゴリズムの改良または今回の考察を行いたいと思います。