コンピュータとオセロ対戦37 ～新AIの準備～

今回の目標

今後予定しているAI作成のため、まずは4層の深層学習モデルを完成させる。

ここから本編

まず、「今後予定しているAI」について説明します。「34 ～性能評価～」にて、nleast、つまり相手の手数を減らしていく考え方が非常に有用であることが示されました。
また「32　～深層学習で勝敗予測、実験2～」の結果から、深層学習モデルはRidge回帰と比べ高い精度が期待できることがわかりました。記事として書いてはいませんが、Ridge回帰モデルは数回の予測結果の平均を用いるため思考に時間がかかりますが、深層学習ならあまり時間がかかりませんでした。

以上のことから、深層学習による最終結果の予測値(ゲーム終了時点での自分の石数-相手の石数)と、次のターンなどでの相手の手数を総合的に考えれば強いAIが作れるのではないかと考えました。
具体的には、予測値と手数に対し適した重みをかけ、その合計値を「予想される勝利確率」とし、それが最も高くなる位置に石を置くというAIを作成したいと思います。

そのためにまず、ミスを見つけたまま修正していなかった4層の深層学習モデルについてミスを修正し、よく学習できるハイパーパラメータを探します。

ファイル構造

ファイル構造についてはこれまでとあまり変わりません。
具体的には以下の通りです(アルファベット順に並んでいないのはわざとです)。

.
├── fig
│   └── 実験結果のグラフを格納
├── BitBoard.py　　　　・・・オセロ実行のためのクラス
├── osero_learn.py　　 ・・・データ集めのためのクラス
├── Net.py　　　　　　 ・・・ニューラルネットワーク
├── deep_learn.py　　　・・・データ集めや学習を行うクラス
├── run.ipynb　　　　　・・・実行プログラム
└── analyse.ipynb　　　・・・csvファイル分析プログラム

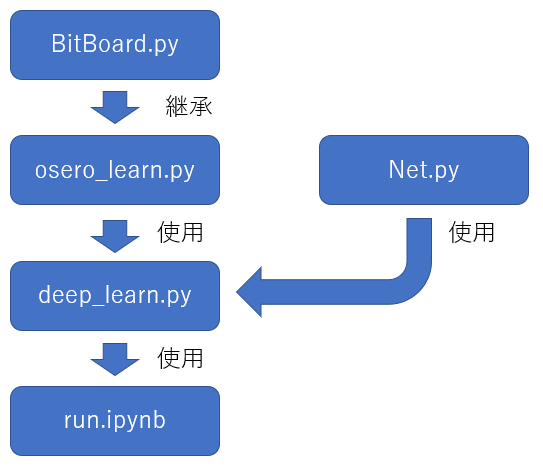
クラスの関係を図で表すと以下のようになっています。なお、クラス名とファイル名は一致しません。

BitBoard.py

オセロをプレイするためのクラスを格納しています。
変更はありません。

osero_learn.py

データ集めのためのクラスを格納しています。
これまでは、自分の石の配置及び相手の石配置が説明変数で、最終的な黒の石数-白の石数が目的変数でした。ですが、学習のためには黒のターンなら「最終的な黒の石数-白の石数」、白のターンなら「最終的な白の石数-黒の石数」とすべきでした。
そのため、試合を行うplayメソッド及びデータを追加するdata_setメソッドを変更し、それぞれのターンでその時のプレイヤー目線での最終結果が得られるようにしました。また、何も置かれていない場所はそれが明記されるようにしました。

    def play(self) -> list:
        can, old_can = True, True
        turn_num = 0
        data = []
        turn_arr = []

        can = self.check_all()
        while can or old_can:
            if can:
                turn_num += 1
                if self.turn:
                    self.think[self.black_method]()
                else:
                    self.think[self.white_method]()
                if turn_num in self.check_point:
                    self.data_set(data, turn_num)
                    turn_arr.append([self.turn])
            self.turn = not self.turn
            old_can = can
            can = self.check_all()

        self.count_last()

        turn_arr = np.array(turn_arr)
        last_score = self.score * (-1) ** turn_arr

        return data, last_score.tolist()

    def data_set(self, data: list, turn_num: int) -> None:
        data.append([])
        if self.turn:
            my = ["b_u", "b_d"]
            opp = ["w_u", "w_d"]
        else:
            my = ["w_u", "w_d"]
            opp = ["b_u", "b_d"]
        for i in range(32):
            if self.bw[my[0]] & 1 << i:
                data[-1].append(1)
                data[-1].append(0)
                data[-1].append(0)
            elif self.bw[opp[0]] & 1 << i:
                data[-1].append(0)
                data[-1].append(1)
                data[-1].append(0)
            else:
                data[-1].append(0)
                data[-1].append(0)
                data[-1].append(1)
        for i in range(32):
            if self.bw[my[1]] & 1 << i:
                data[-1].append(1)
                data[-1].append(0)
                data[-1].append(0)
            elif self.bw[opp[1]] & 1 << i:
                data[-1].append(0)
                data[-1].append(1)
                data[-1].append(0)
            else:
                data[-1].append(0)
                data[-1].append(0)
                data[-1].append(1)

deep_learn.py

deep_learnについても、大幅に変更した箇所のみ記載します。
いままで、各条件ごとにグラフを作成していましたが、グラフ数が非常に多くなり手間が増えてしまうため一つにまとめるようにplotメソッドを変更しました。

    def plot(self, row: int) -> None:
        self.ax[row-1][0].plot(self.results_train["MSE"], label="train")
        self.ax[row-1][0].plot(self.results_valid["MSE"], label="valid")
        self.ax[row-1][0].legend()
        self.ax[row-1][0].set_xlabel(self.xlabel1)
        self.ax[row-1][0].set_ylabel(self.ylabel1)
        self.ax[row-1][0].set_title(self.fig_name1)

        self.ax[row-1][1].plot(self.results_train["MAE"], label="train")
        self.ax[row-1][1].plot(self.results_valid["MAE"], label="valid")
        self.ax[row-1][1].legend()
        self.ax[row-1][1].set_xlabel(self.xlabel2)
        self.ax[row-1][1].set_ylabel(self.ylabel2)
        self.ax[row-1][1].set_title(self.fig_name2)

run.ipynb

準備

import matplotlib.pyplot as plt

from deep_learn import *

実験

以下、ハイパーパラメータなどを変えながら実験を行います。

データ量

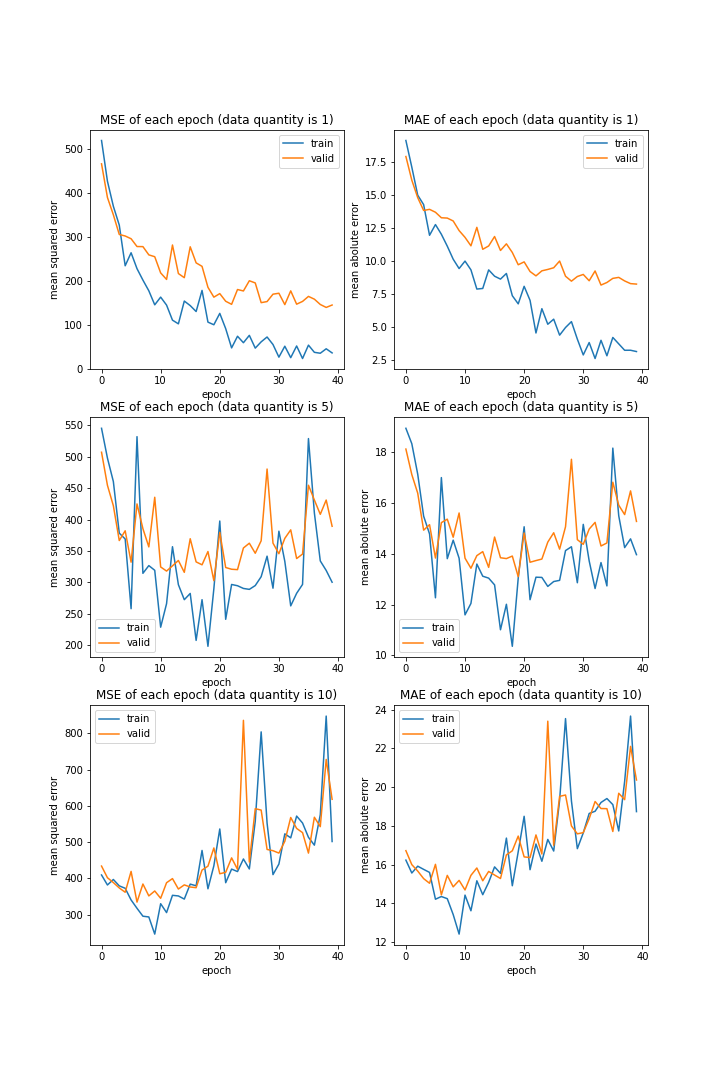
データ量を変更しながら学習をするのは今までの実験と同じですが、条件ごとのグラフを別々に出力せずにまとめました。

run = deep_learn()

num_arr = [1, 5, 10]
run.fig, run.ax = plt.subplots(ncols=2, nrows=len(num_arr), figsize=(10, len(num_arr)*5))
plt.subplots_adjust(wspace=None, hspace=0.2)
i = 1
MSE_test = []
MAE_test = []

for num in num_arr:
    print("\r%d/%d" % (i, len(num_arr)), end="")
    run.num = num
    run.fig_name1 = "MSE of each epoch (data quantity is %d)" % num
    run.fig_name2 = "MAE of each epoch (data quantity is %d)" % num
    run.set_data()
    run.fit()
    run.plot(i)
    test_error = run.cal_test_error()
    MSE_test.append(test_error[0])
    MAE_test.append(test_error[1])
    i += 1

run.fig.savefig("fig/data_quantity.png")
run.fig.clf()

実行結果はこちら。

number:  [1, 5, 10]
MSE:  [variable(152.81169), variable(372.01184), variable(643.15546)]
MAE:  [variable(8.03122), variable(15.009193), variable(20.94951)]

これまでと同様、データ量が多すぎるとうまく学習しませんでした。

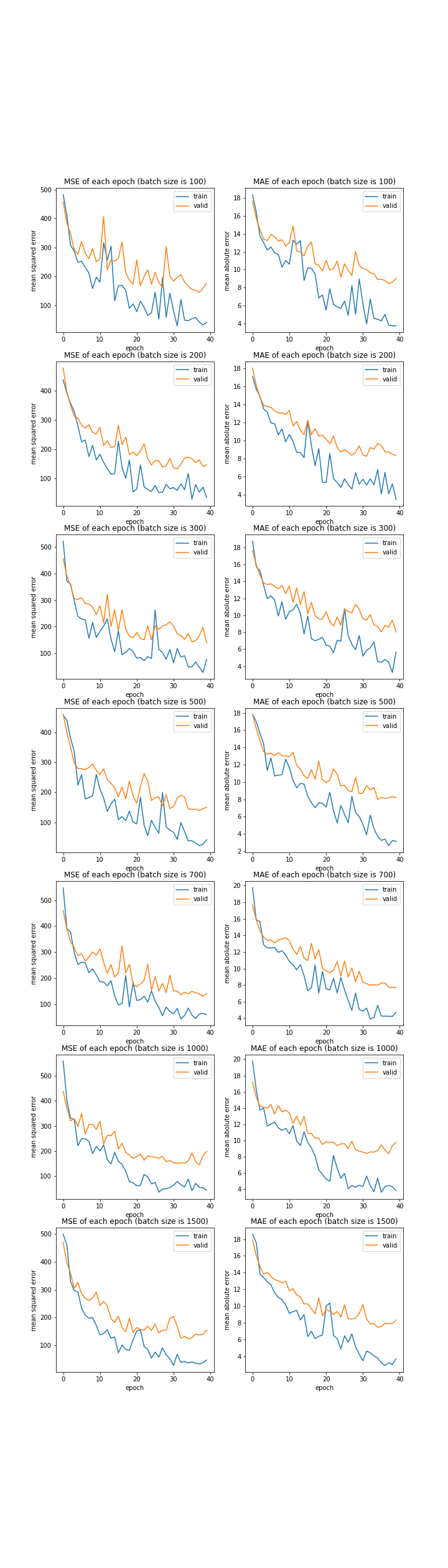
バッチサイズ

プログラムはデータ量の時のものとほぼ同じですので省略します。

batch size:  [100, 200, 300, 500, 700, 1000, 1500]
MSE:  [variable(162.9739), variable(152.05502), variable(153.27628), variable(162.2756), variable(145.58446), variable(204.26527), variable(167.85017)]
MAE:  [variable(8.527661), variable(8.186351), variable(8.13009), variable(8.399555), variable(7.9057674), variable(9.92684), variable(8.66958)]

こちらもこれまでと同様、変更しても結果はあまり変わりませんでした。
バッチサイズは大きいほど学習が早く進みますが、大きすぎても怖いので今回は1000を採用することにします。

活性化関数の種類

f_name = [
    "clipped_relu",
    "elu",
    "leaky_relu",
    # "log_softmax",
    "rrelu",
    "relu",
    "sigmoid",
    "softmax",
    # "softplus",
    "tanh"
]

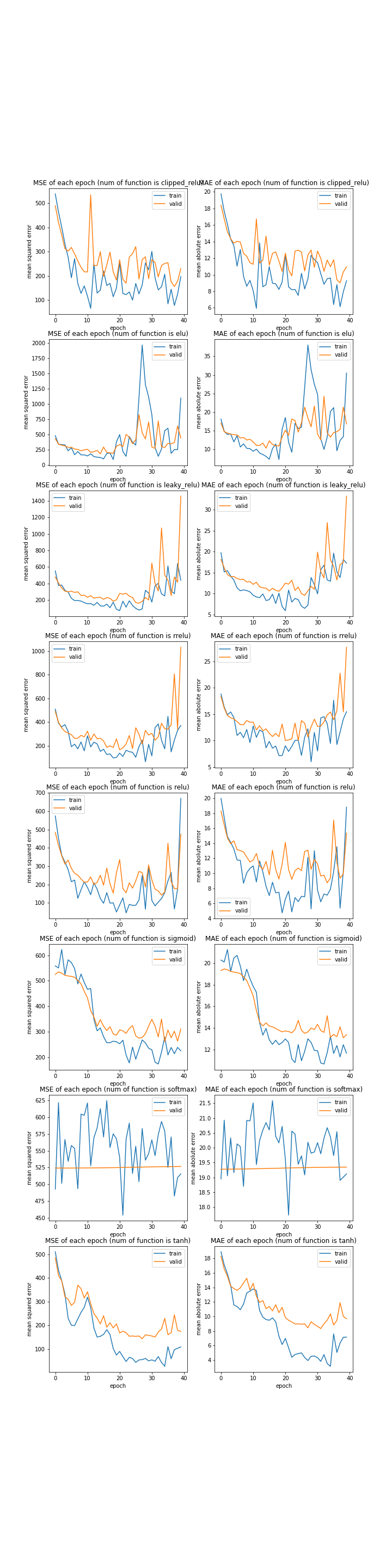
上に示す活性化関数について調べました。今回は四層しかないため勾配消失の心配はないと判断し、sigmoid関数なども入れています。コメントアウトしている関数は、候補ではあったものの学習途中でオーバーフローしたという理由で除外したものです。
結果はこちら。

function:  ['clipped_relu', 'elu', 'leaky_relu', 'rrelu', 'relu', 'sigmoid', 'softmax', 'tanh']
MSE:  [variable(234.85422), variable(435.0493), variable(1528.1886), variable(1051.0135), variable(451.09824), variable(294.6485), variable(571.89453), variable(171.02132)]
MAE:  [variable(10.507885), variable(16.28336), variable(33.503345), variable(28.046625), variable(15.27029), variable(13.055871), variable(20.325909), variable(9.534906)]

やはりrelu系列は全体的にうまく学習しませんでした。優秀だったのはsigmoidとtanhでした。
負の数が存在しない関数が学習しにくいのは今までの実験でも示されていましたが、softmaxは極端な結果になりました。負の数がないだけでなく上限の値が決められていることが大きな枷になったのだと考えられます。

最適化関数

opt_name = [
    "SGD",
    "MomentumSGD",
    "AdaGrad",
    "RmSprop",
    "AdaDelta",
    "Adam",
    "RMSpropGraves",
    "SMORMS3",
    "AMSGrad",
    "AdaBound",
    "AMSBound"
]

上に示す最適化関数について調べました。

opt name:  ['SGD', 'MomentumSGD', 'AdaGrad', 'RmSprop', 'AdaDelta', 'Adam', 'RMSpropGraves', 'SMORMS3', 'AMSGrad', 'AdaBound', 'AMSBound']
MSE:  [variable(220.08337), variable(576.7117), variable(251.20909), variable(569.64264), variable(184.31363), variable(162.6182), variable(156.20638), variable(161.93105), variable(169.1945), variable(150.75018), variable(139.02298)]
MAE:  [variable(10.743682), variable(20.432753), variable(12.183864), variable(20.282295), variable(9.238301), variable(9.405695), variable(8.508823), variable(9.181299), variable(8.943705), variable(8.068955), variable(7.9657555)]

思っていたより多くの最適化関数で収束が見られました。
収束が見られたのはSGD、AdaGrad、AdaDelta、Adam、RMSpropGraves、SMORMS3、AMSGrad、AdaBound、AMSBoundで、見られなかったのはMomentumSGDとRmSpropのみでした。
SGDで収束し、MomentumSGDで収束しなかったということは、振動抑制の必要がなかった、むしろ悪手であったのではないかと最初は考えました。しかしSGDの最終的な誤差は、AdaGradを除く収束した最適化関数のすべてに劣っています。つまりSGDが今回たどり着いたのは局所解であり、MomentumSGDは局所解から抜け出そうとしたものの一歩足りなかったのではないかと考えます。
こういった理由から、MomentumSGD及びSGDはこの先除外したいと思います。
収束はしたものの精度の高くないAdaGrad、収束しなかったRMSpropから、パラメータごとの勾配にはあまり差がないのではないかと考えました。なおこれまでの実験でも、この二つはいい結果を残せていません(31　～深層学習で勝敗予測、実験～、36　～10層のハイパーパラメータ～)。
よって、残りの七つの最適化関数を後ほど再実験したいと思います。

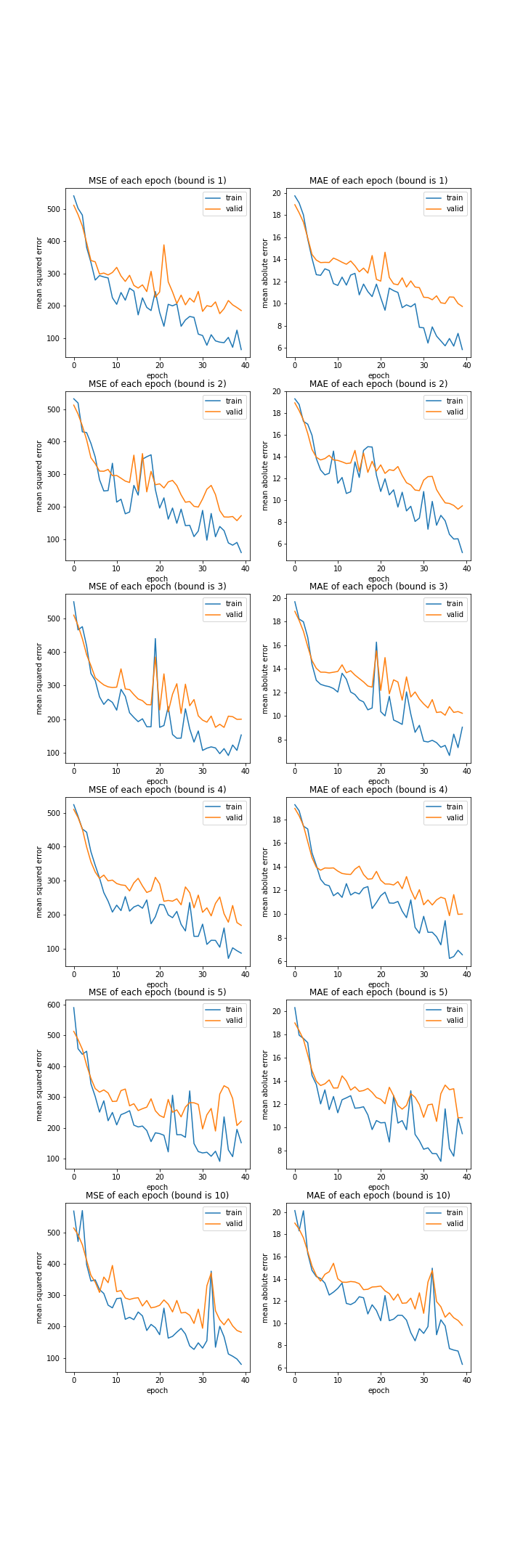
bound

現在、学習の安定のためGradientHardClippingを用いていますが、その引数であるbound変数を変更し実験してみます。

bound : [1, 2, 3, 4, 5, 10]
MSE:  [variable(208.39401), variable(195.04422), variable(211.6011), variable(189.95116), variable(244.27588), variable(212.02213)]
MAE:  [variable(10.187112), variable(9.844666), variable(10.383668), variable(10.060881), variable(11.47002), variable(10.53158)]

どれも大して変わらない結果でした。
なんでもよさそうです。

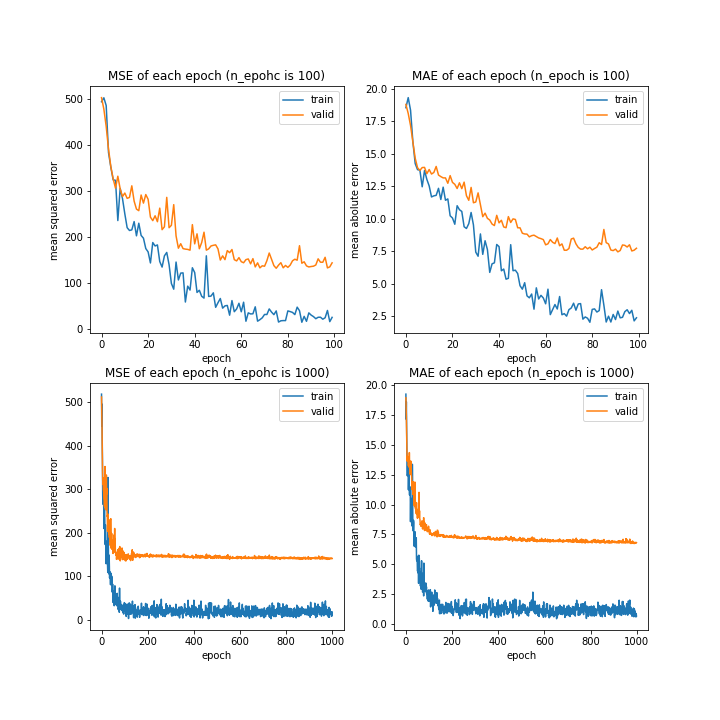
更新回数

更新回数を極端に増やして実験してみました。

n_epoch:  [100, 1000]
MSE:  [variable(152.18834), variable(144.9502)]
MAE:  [variable(7.6830935), variable(7.124355)]

10層の時のような上昇はなく、4層の時のように一度誤差が下がりきるとそこからの更新はなくなりました。
150回程度更新させれば十分でしょう。

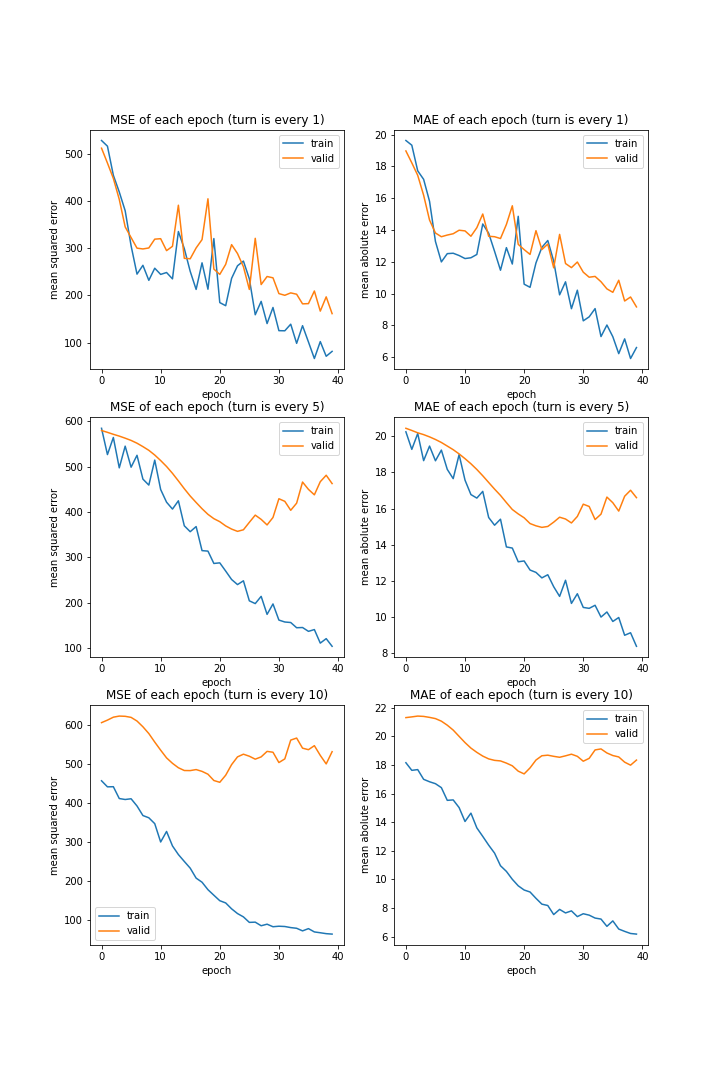
調査ターン

データ集めをする際、何ターンごとにデータを集めるかを変更して学習させてみました。

['every 1', 'every 5', 'every 10']
MSE:  [variable(194.50024), variable(512.78925), variable(447.7704)]
MAE:  [variable(9.789661), variable(17.579159), variable(16.539795)]

これまでの実験と同様、データ量が少ないほど過学習しやすい結果になりました。

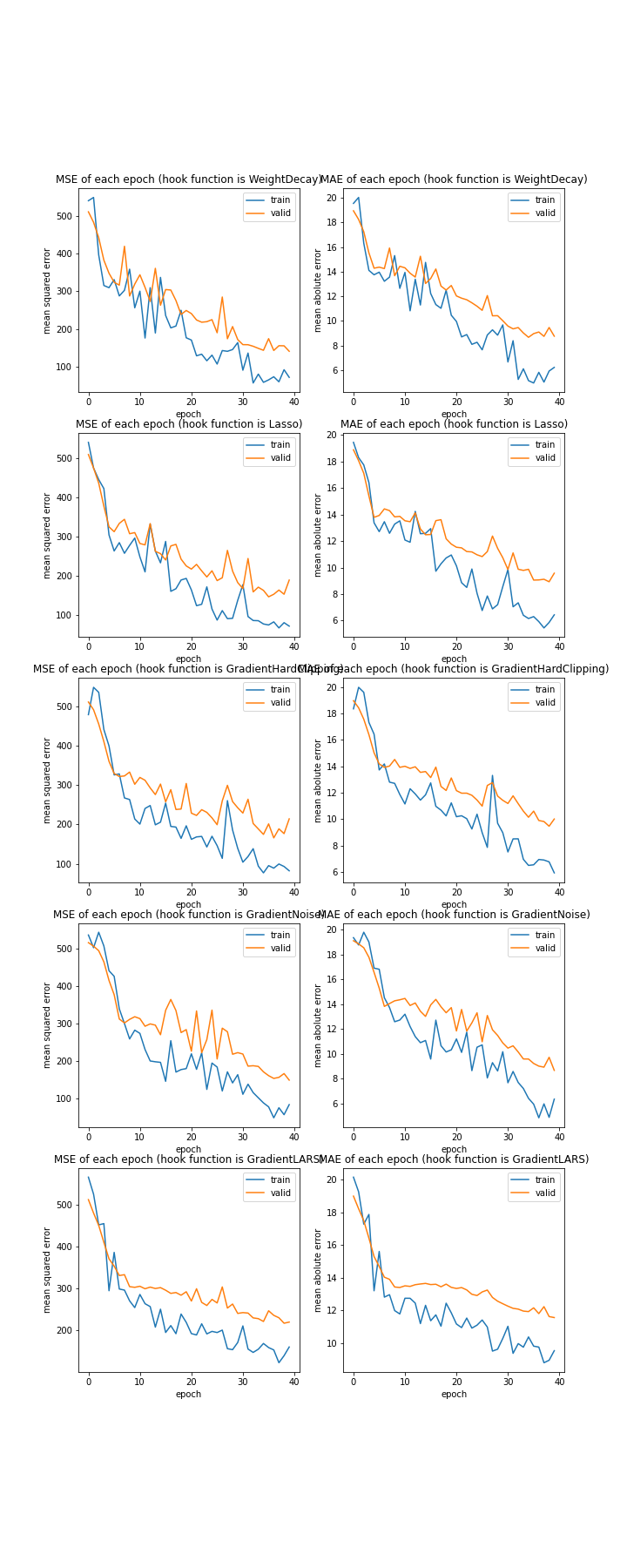
hook function

['WeightDecay', 'Lasso', 'GradientHardClipping', 'GradientNoise', 'GradientLARS']
MSE:  [variable(162.75676), variable(200.36641), variable(209.13129), variable(156.30049), variable(235.34283)]
MAE:  [variable(9.0745125), variable(10.085787), variable(9.9866905), variable(8.721768), variable(11.526583)]

どれも収束していました。また、全て似たような結果となっておりどれが適しているかをここで判断することは難しそうです。

組み合わせ実験

上述した実験はパラメータの種類ごとで行いましたが、ここでは条件を絞ったうえで総当たりで調べます。
具体的な条件は以下の通りです。

• データ量　1
• バッチサイズ　1000
• 活性化関数　sigmoid、tanh
• 最適化関数　AdaDelta、Adam、RMSpropGraves、SMORMS3、AMSGrad、AdaBound、AMSBound
• 更新回数　40回
• 調査ターン　every 1
• hook function WeightDecay、Lasso、GradientHardClipping、GradientNoise、GradientLARS

なおboundなど、追加関数のパラメータについては一般的なものを使います。
更新回数が40回なのは、実験時間を短くするためです。
プログラムはこちら。

import chainer.functions as F
import chainer.optimizers as opt
import chainer.optimizer_hooks as hf
import pandas as pd

import Net
import deep_learn

################################

num = 1
batch_size = 1000
f_arr = [
    F.sigmoid,
    F.tanh
]
f_name = [
    "sigmoid",
    "tanh"
]
opt_arr = [
    opt.AdaDelta(),
    opt.Adam(),
    opt.RMSpropGraves(),
    opt.SMORMS3(),
    opt.AMSGrad(),
    opt.AdaBound(),
    opt.AMSBound()
]
opt_name = [
    "AdaDelta",
    "Adam",
    "RMSpropGraves",
    "SMORMS3",
    "AMSGrad",
    "AdaBound",
    "AMSBound"
]
hf_arr = [
    hf.WeightDecay(0.00001),
    hf.Lasso(0.00001),
    hf.GradientHardClipping(-2, 2),
    hf.GradientNoise(0.3),
    hf.GradientLARS()
]
hf_name = [
    "WeightDecay",
    "Lasso",
    "GradientHardClipping",
    "GradientNoise",
    "GradientLARS"
]

################################

data = {}

data["function"] = []
data["optimizer"] = []
data["hook_function"] = []
data["test_MSE"] = []
data["test_MAE"] = []

################################

run = deep_learn.deep_learn()
run.num = num
run.batch_size = batch_size
run.set_data()
i, j, k = 0, 0, 0

for function in f_arr:
    Net.func = function
    run.Net = Net.Net
    j = 0
    for optimizer in opt_arr:
        run.optimizer = optimizer
        k = 0
        for hook_function in hf_arr:
            loading = "%d/%d" % (i+1, len(f_arr))\
                    + "#" * (j + 1)\
                    + "." * (k + 1)
            print("\r" + loading, end="")
            run.hook_f = hook_function
            run.fit()
            test_error = run.cal_test_error()
            data["function"].append(f_name[i])
            data["optimizer"].append(opt_name[j])
            data["hook_function"].append(hf_name[k])
            data["test_MSE"].append(float(test_error[0].array))
            data["test_MAE"].append(float(test_error[1].array))
            k += 1
        j += 1
    i += 1

################################

data_df = pd.DataFrame(data)
data_df.to_csv("data.csv")

結果を確認します。

import pandas as pd

df = pd.read_csv("data.csv")

################################

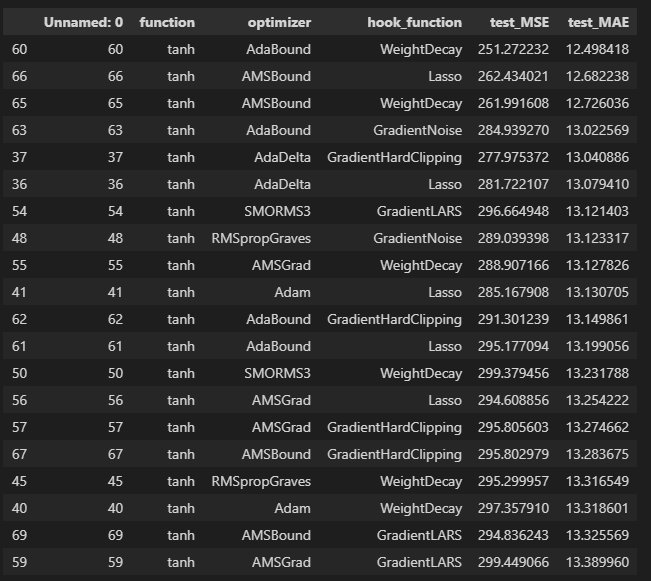
df_sorted = df.sort_values(by="test_MAE", inplace=False)
df_sorted.head(20)

ひどい結果でした。
理由として考えられるのは、バッチサイズが大きすぎたことでしょうか。
バッチサイズをもともとの設定である200、今回の1000、ついでに間をとって600の三種類にして再実験しようと思います。

また、ついでに望みの薄そうなパラメータについても実行時間短縮のためこの時点で除外しておこうと思います。まず、活性化関数について、明らかにtanhの方がよい結果となっているのでこれを使います。
次に、誤差が小さくなりやすいまたは大きくなりやすい最適化関数を調べてみます。

optimizers = df["optimizer"].unique()
df_top = df.sort_values(by="test_MSE", inplace=False).head(25)
df_worst = df.sort_values(by="test_MSE", inplace=False, ascending=False).head(25)

print("top")
for opt in optimizers:
    num = 0
    num += len(df_top.query("optimizer=='%s'" % opt))

    print("%s:\t%d" % (opt, num))

print("\nworst")
for opt in optimizers:
    num = 0
    num += len(df_worst.query("optimizer=='%s'" % opt))

    print("%s:\t%d" % (opt, num))

top
AdaDelta:   3
Adam:   4
RMSpropGraves:  3
SMORMS3:    2
AMSGrad:    4
AdaBound:   4
AMSBound:   5

worst
AdaDelta:   1
Adam:   5
RMSpropGraves:  4
SMORMS3:    3
AMSGrad:    5
AdaBound:   2
AMSBound:   5

AdaDelataは非常に有用そうですが、ほかのパラメータは特に偏りがありませんでした。
同様に追加関数についても調べました。

top
WeightDecay:    6
Lasso:  6
GradientHardClipping:   5
GradientNoise:  4
GradientLARS:   4

worst
WeightDecay:    5
Lasso:  5
GradientHardClipping:   4
GradientNoise:  7
GradientLARS:   4

GradientNoiseは誤差が大きくなりやすい結果となりましたので、これのみ除外しようと思います。他は特に偏りありませんでした。

組み合わせ実験2

今度は以下のパラメータで実験します。

• データ量　1
• バッチサイズ　200、600、1000
• 活性化関数　tanh
• 最適化関数　AdaDelta、Adam、RMSpropGraves、SMORMS3、AMSGrad、AdaBound、AMSBound
• 更新回数　40回
• 調査ターン　every 1
• hook function WeightDecay、Lasso、GradientHardClipping、GradientLARS

num = 1
batch_arr = [200, 600, 1000]
func = F.tanh
opt_arr = [
    opt.AdaDelta(),
    opt.Adam(),
    opt.RMSpropGraves(),
    opt.SMORMS3(),
    opt.AMSGrad(),
    opt.AdaBound(),
    opt.AMSBound()
]
opt_name = [
    "AdaDelta",
    "Adam",
    "RMSpropGraves",
    "SMORMS3",
    "AMSGrad",
    "AdaBound",
    "AMSBound"
]
hf_arr = [
    hf.WeightDecay(0.00001),
    hf.Lasso(0.00001),
    hf.GradientHardClipping(-2, 2),
    hf.GradientLARS()
]
hf_name = [
    "WeightDecay",
    "Lasso",
    "GradientHardClipping",
    "GradientLARS"
]

一度目の実験と同様、誤差の小さくなりやすいまたは大きくなりやすいパラメータを探しました。
結果はこちら。

batch_size:
top
200:    11
600:    7
1000:   7

worst
200:    7
600:    8
1000:   10

optimizer: 
top
AdaDelta:   6
Adam:   1
RMSpropGraves:  0
SMORMS3:    0
AMSGrad:    1
AdaBound:   8
AMSBound:   9

worst
AdaDelta:   4
Adam:   8
RMSpropGraves:  2
SMORMS3:    3
AMSGrad:    6
AdaBound:   1
AMSBound:   1

hook_function:
top
WeightDecay:    8
Lasso:  9
GradientHardClipping:   7
GradientLARS:   1

worst
WeightDecay:    5
Lasso:  5
GradientHardClipping:   5
GradientLARS:   10

結果をまとめると、以下のことが言えそうです。

• バッチサイズは、この中では200が最も適しており1000は適さない。ただし、思っていたほどの差はなかった。
• 最適化関数は、AdaBoundまたはAMSBoundが最も適する。Adam及びAMSGradは適さない。
• 追加関数は、WeightDecayまたはLassoが最も適する。GradientLARSは適さない。

一回目の実験と比べ数字にばらつきが出たのは、バッチサイズを変更したからだと思われます。バッチサイズを大きくしすぎると、ほかのパラメータを変えても等しく学習しにくくなるのかもしれません。

モデル作成

バッチサイズ、最適化関数、追加関数、そして各関数に与えるパラメータについてはまだ完全に検証できていませんが、キリがないこと、これは本題ではないという理由で、ここでいったん終了したいと思います。
ここまでで求めたパラメータを使い学習済みモデルを作成します。
具体的には、

• データ量　1
• バッチサイズ　200
• 活性化関数　tanh
• 最適化関数　AMSBound
• 更新回数　150回
• 調査ターン　every 1
• hook function Lasso

です。
まず、これらの条件で学習を行います。

import chainer.functions as F
from chainer.optimizers import AMSBound
from chainer.optimizer_hooks import Lasso
import matplotlib.pyplot as plt
from chainer.serializers import save_npz

import deep_learn
import Net

########################################

run = deep_learn.deep_learn()

run.num = 1
run.batch_size = 200
Net.func = F.tanh
run.Net = Net.Net
run.optimizer = AMSBound()
run.n_epoch = 150
run.hook_f = Lasso(0.00001)

########################################

run.set_data()
run.fit()

次に、きちんと学習できているか確認します。
まずはテスト用データでの精度を見てみます。

error = run.cal_test_error()
error

(variable(140.72816), variable(7.2066855))

控えめに言って最高ですね、Ridgeでの平均絶対誤差の最高記録が全ターン平均して約13ですので、非常に良い結果です。
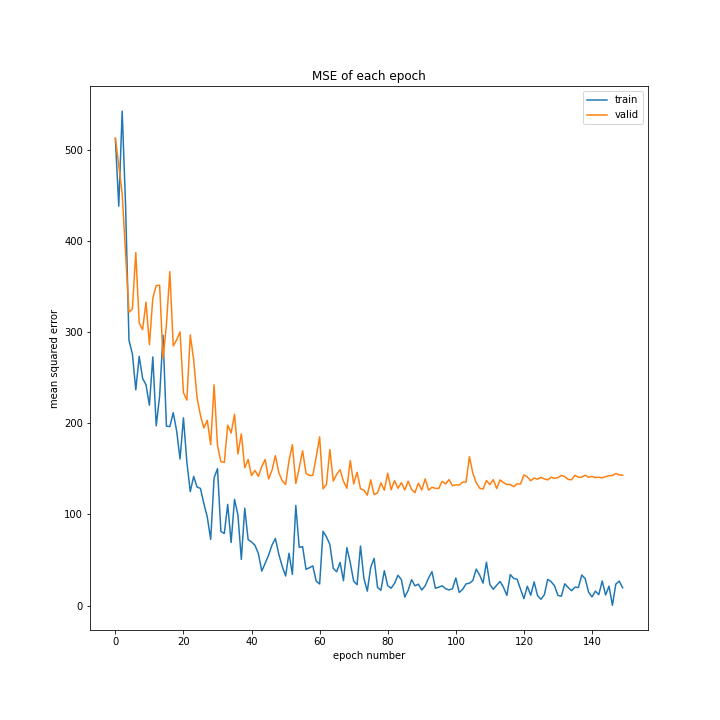
次に学習の様子を見てみます。

fig = plt.figure(figsize=(10, 10))
plt.plot(run.results_train["MSE"], label="train")
plt.plot(run.results_valid["MSE"], label="valid")
plt.legend()
plt.xlabel("epoch number")
plt.ylabel("mean squared error")
plt.title("MSE of each epoch")
plt.savefig("fig/model_MSE")
plt.clf()
plt.close()

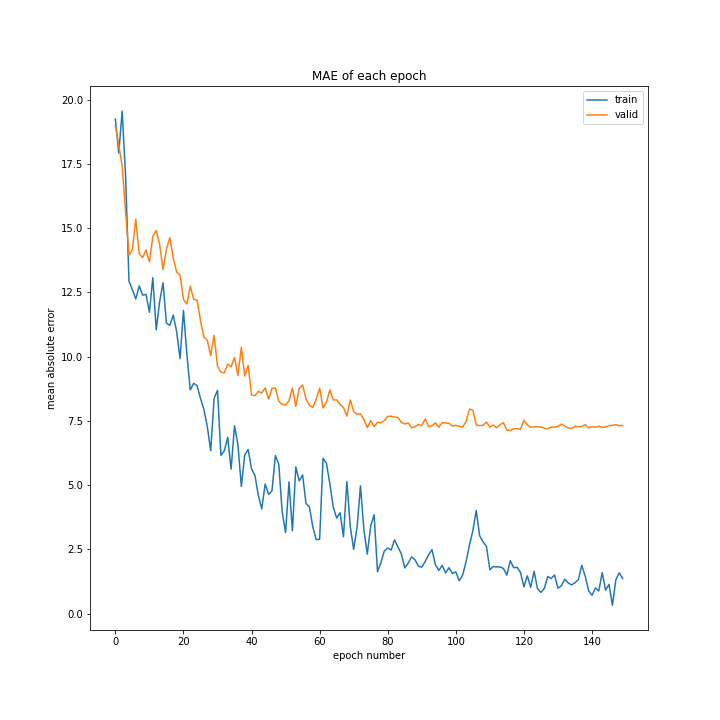
記載はしませんが、絶対平均誤差についてもほぼ同じプログラムを使用しエポック数毎の誤差をグラフ化しました。
結果はこちら。

とてもいい結果になりました。
最後にモデルを保存します。

save_npz("model.net", run.net)

フルバージョン

参考文献

深層学習の最適化アルゴリズム

次回は

今回作成したモデルを用いて、冒頭で構想を記したAIを作成したいと思います。

次回