今回の目標
前回の機械学習を改善する
ここから本編
具体的に、ターン数5でも平均絶対誤差が10程度になれば有効に予想できているといえると考え、これを目標に改善をしていきます。
改善案1
前回は盤面情報のみから学習を行い、最終結果を予想しました。
今回はより精度の高い学習を目指し、以下の点を変更しました。
- 説明変数として次のターンで相手が置ける手数を追加
- 最終スコアを「黒の駒の数-白の駒の数」から「自分の駒の数-相手の駒の数」に変更、それに伴い「黒の盤面」を「自分の盤面」に、「白の盤面」を「相手の盤面」に変更
- 学習方法を、前回良い結果を残したLinearRegression、Ridge、KNeighborsClassifierにしぼる
- ターン数を10回ごとから5回ごとに
osero_learn
プログラムを以下のように変更し、指定したターン数の時にターン数(turn_num)、相手のとれる手数(opp_put_num)、今どちらのターンか(turn)、自分の盤面(my0~my63)、相手の盤面(opp0~opp63)を記録できるようにしました。
check_point変数に配列を入れ、ターン数を指定します。
前回turnと呼んでいたものが今回はturn_numに変わっています。
from pandas import DataFrame
from BitBoard import osero
class learn(osero):
def __init__(self, black_method, white_method, check_point,\
read_goal=[1, 1], eva=None):
super().__init__(black_method, white_method, read_goal, eva)
self.check_point = check_point
def play(self) -> DataFrame:
can, old_can = True, True
turn_num = 0
data = {}
self.first_data_set(data)
can = self.check_all()
while can or old_can:
if can:
turn_num += 1
if self.turn:
self.think[self.black_method]()
else:
self.think[self.white_method]()
if turn_num in self.check_point:
self.data_set(data, turn_num)
self.turn = not self.turn
old_can = can
can = self.check_all()
self.count_last()
for i in range(len(data["turn_num"])):
if data["turn"][i]:
data["last_score"].append(self.score)
else:
data["last_score"].append(-self.score)
return DataFrame(data)
def first_data_set(self, data: DataFrame) -> None:
data["turn_num"] = []
data["opp_put_num"] = []
data["turn"] = []
data["last_score"] = []
for i in range(64):
data["my%d" % i] = []
data["opp%d" % i] = []
def count_last(self) -> None:
black = self.popcount(self.bw["b_u"])\
+ self.popcount(self.bw["b_d"])
white = self.popcount(self.bw["w_u"])\
+ self.popcount(self.bw["w_d"])
self.score = black - white
def search_put(self) -> int:
num = 0
for i in range(8):
for j in range(8):
if self.check(i, j, self.bw, not self.turn):
num += 1
return num
def data_set(self, data: DataFrame, turn_num: int) -> None:
data["turn_num"].append(turn_num)
data["opp_put_num"].append(self.search_put())
data["turn"].append(self.turn)
if self.turn:
my = ["b_u", "b_d"]
opp = ["w_u", "w_d"]
else:
my = ["w_u", "w_d"]
opp = ["b_u", "b_d"]
for i in range(32):
data["my%d" % i].append(int((self.bw[my[0]] & (1 << i)) != 0))
data["opp%d" % i].append(int((self.bw[opp[0]] & (1 << i)) != 0))
for i in range(32):
data["my%d" % (i + 32)].append(int((self.bw[my[1]] & (1 << i)) != 0))
data["opp%d" % (i + 32)].append(int((self.bw[opp[1]] & (1 << i)) != 0))
run
前回同様ipynbで作成。
前回とほぼ同じなのでプログラムは省略します。
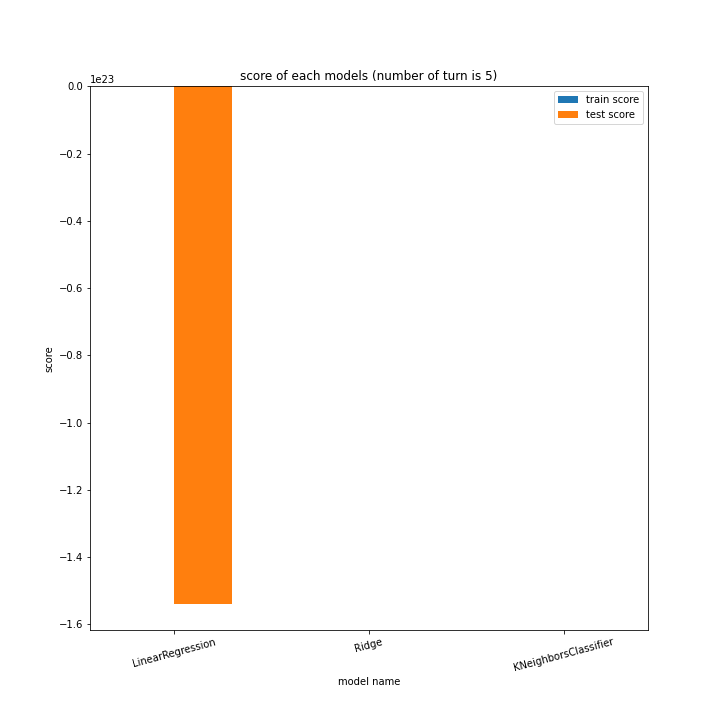
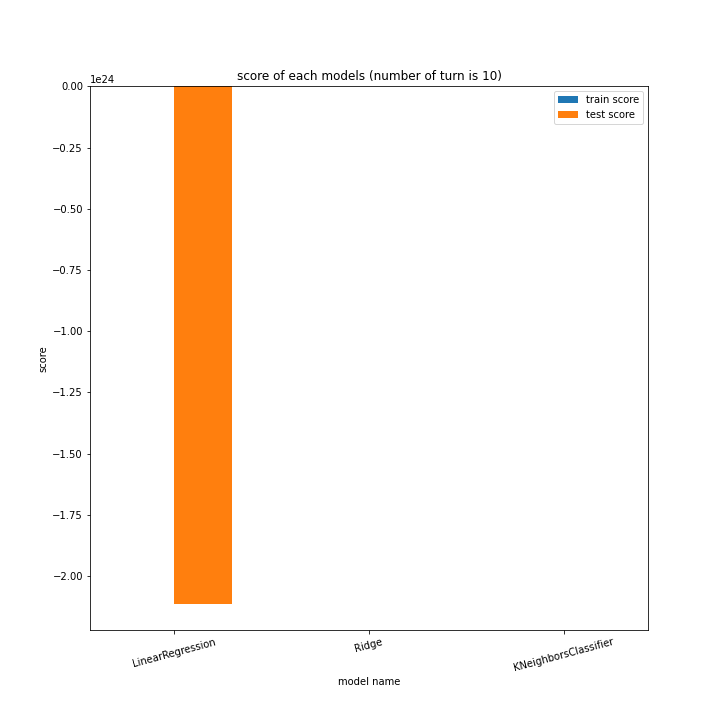
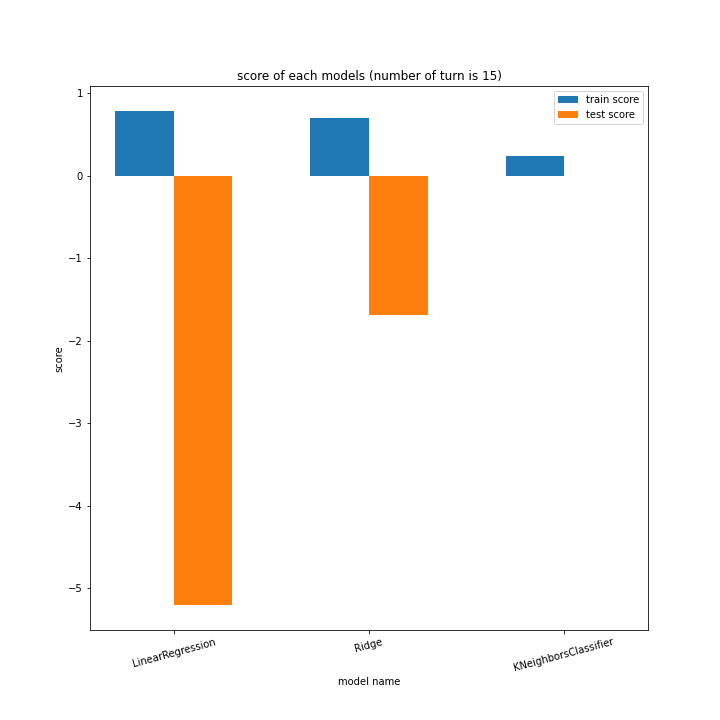
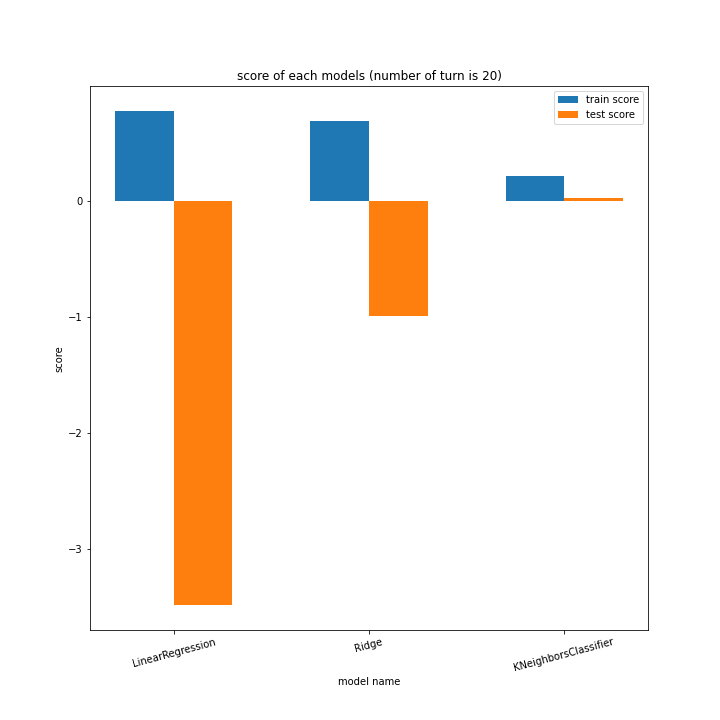
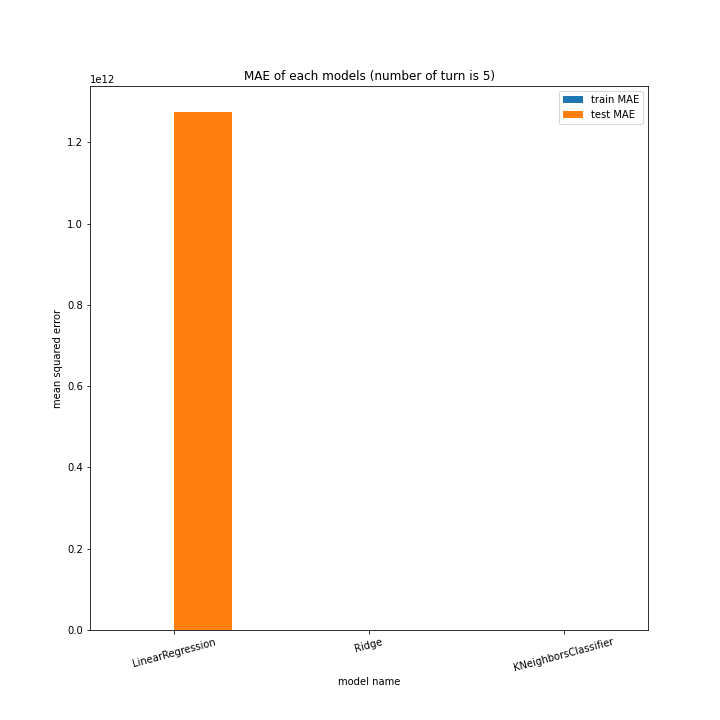
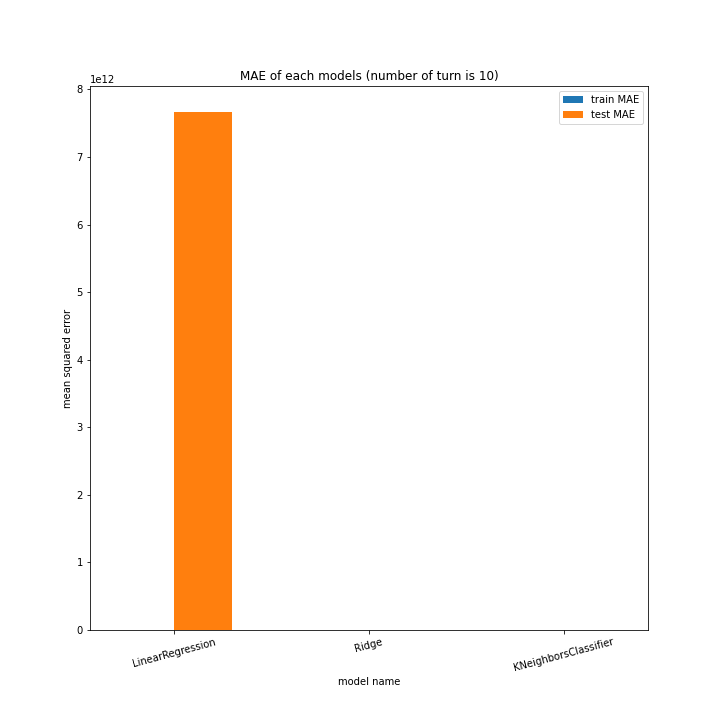
学習結果
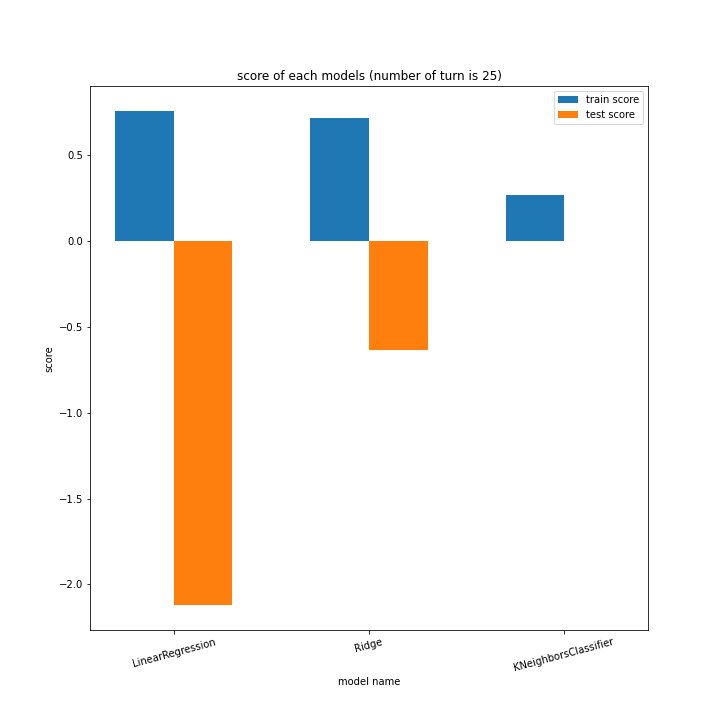
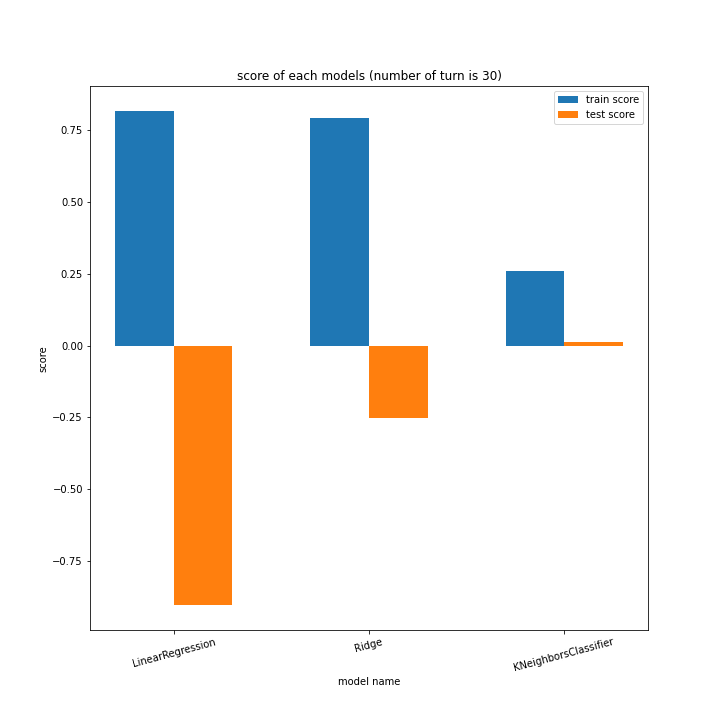
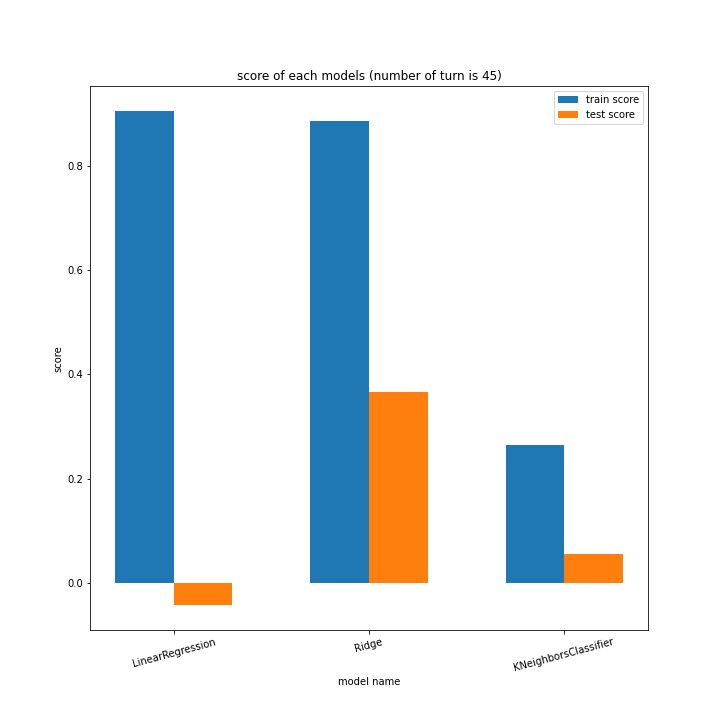
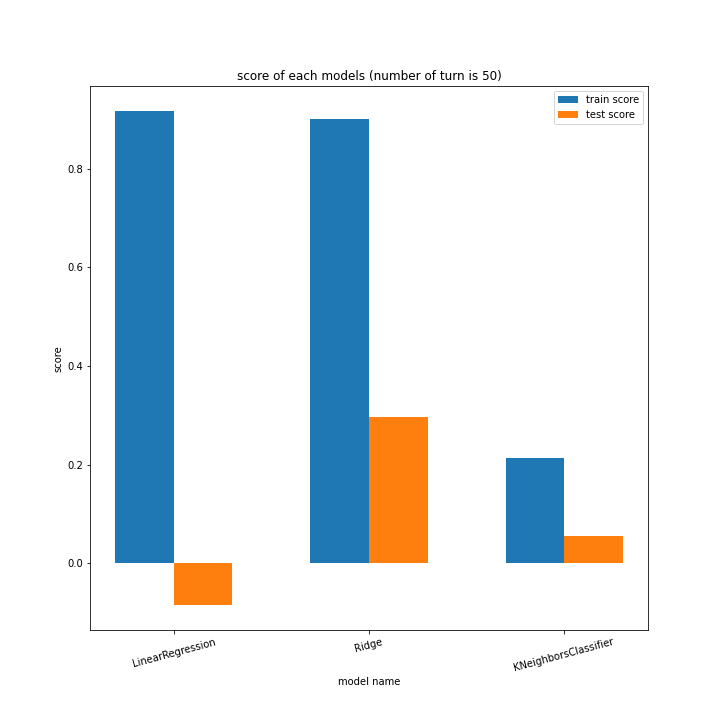
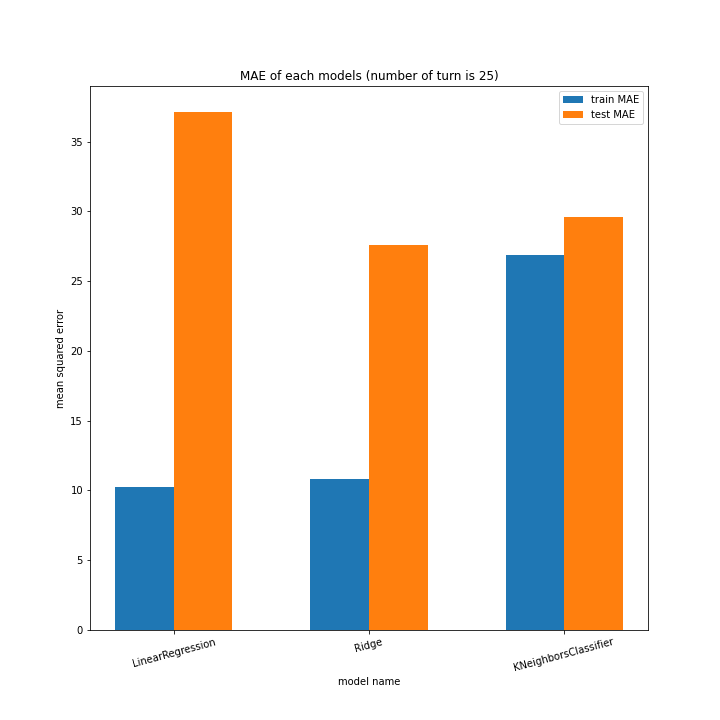
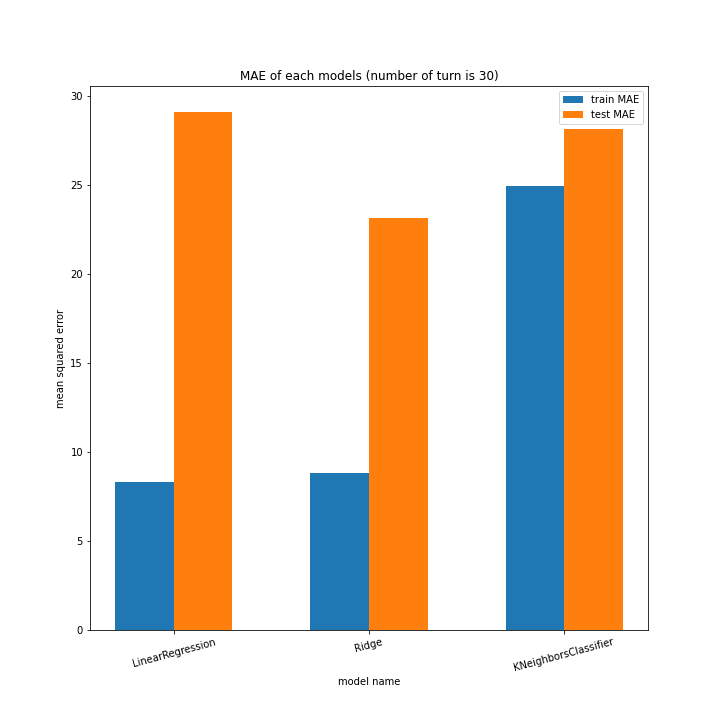
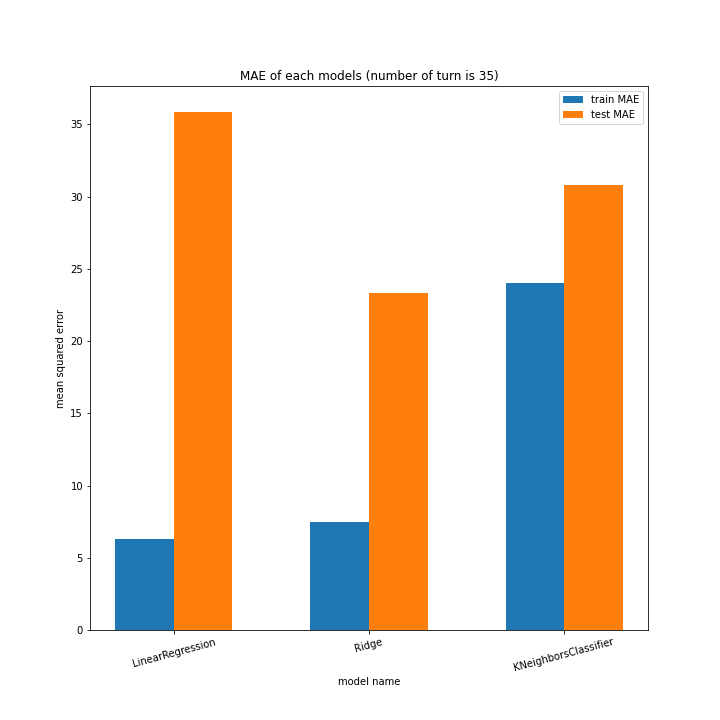
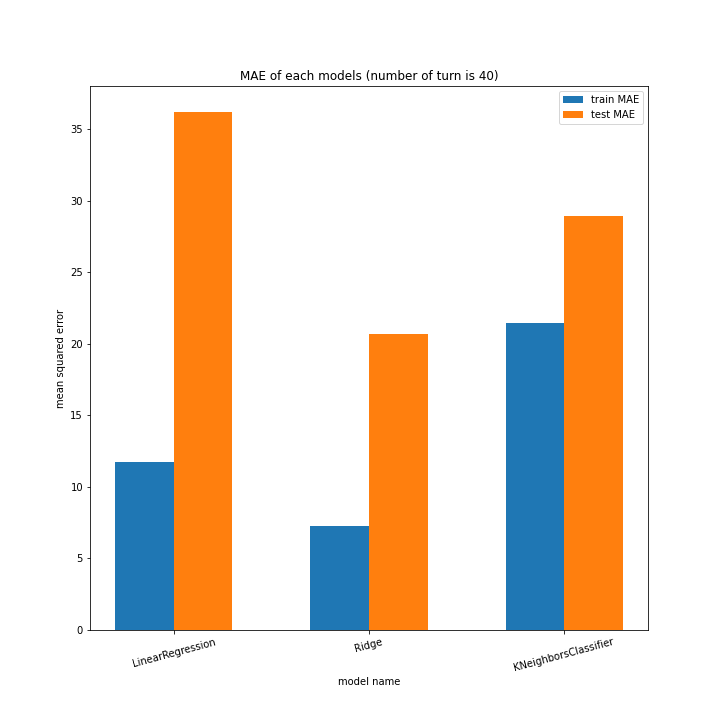
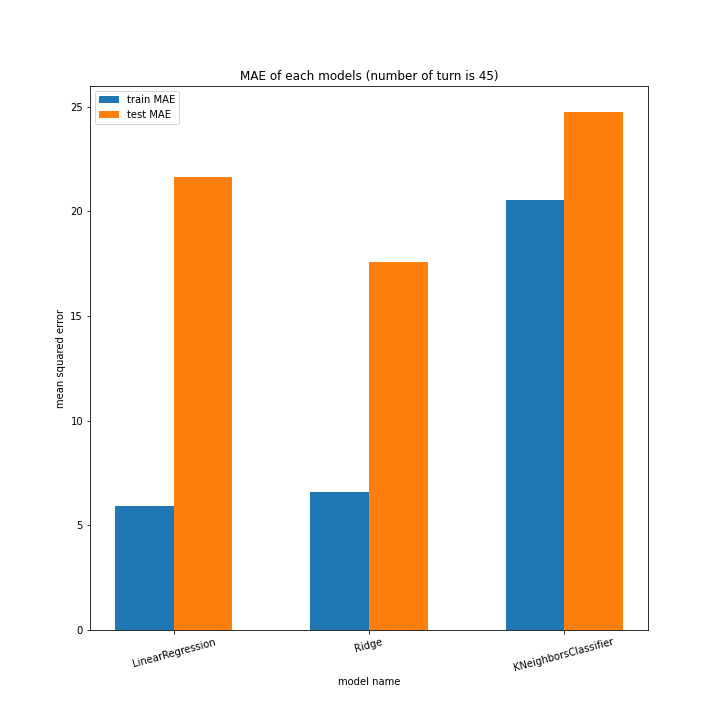
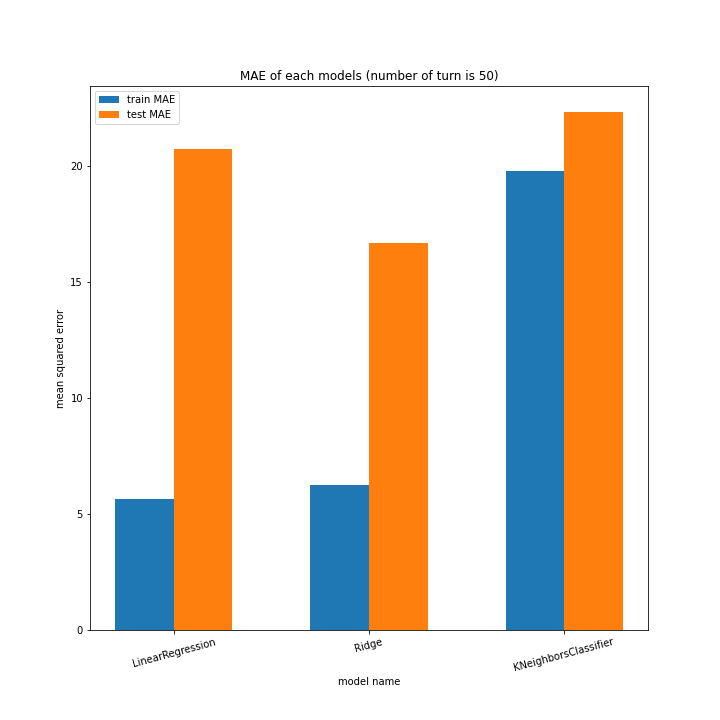
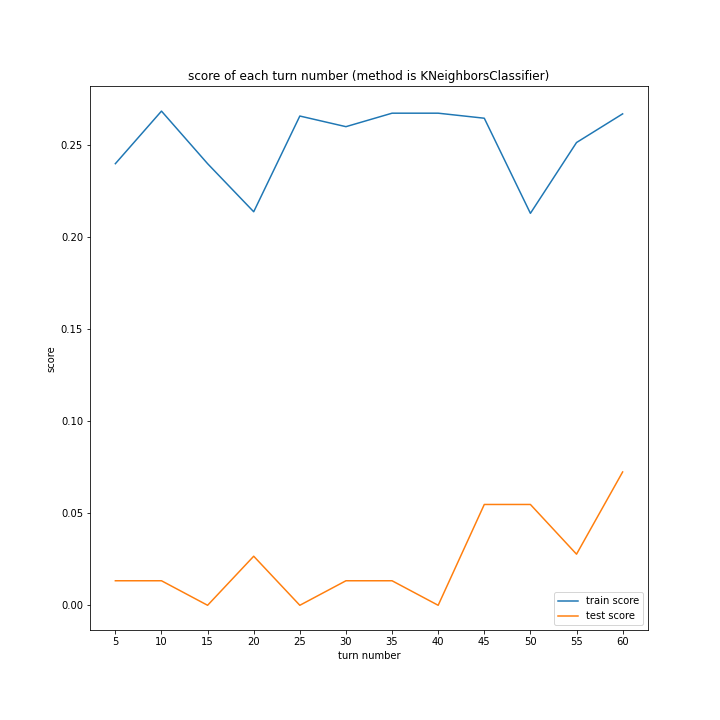
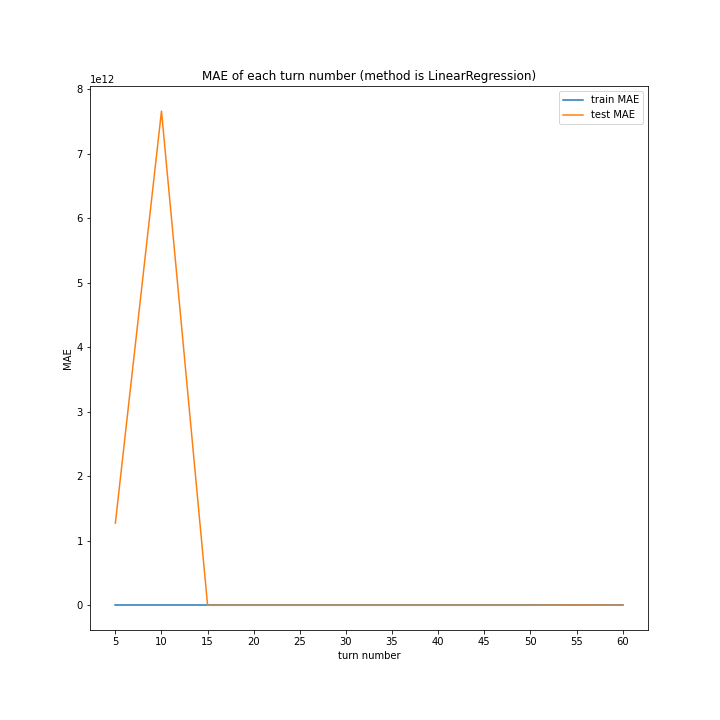
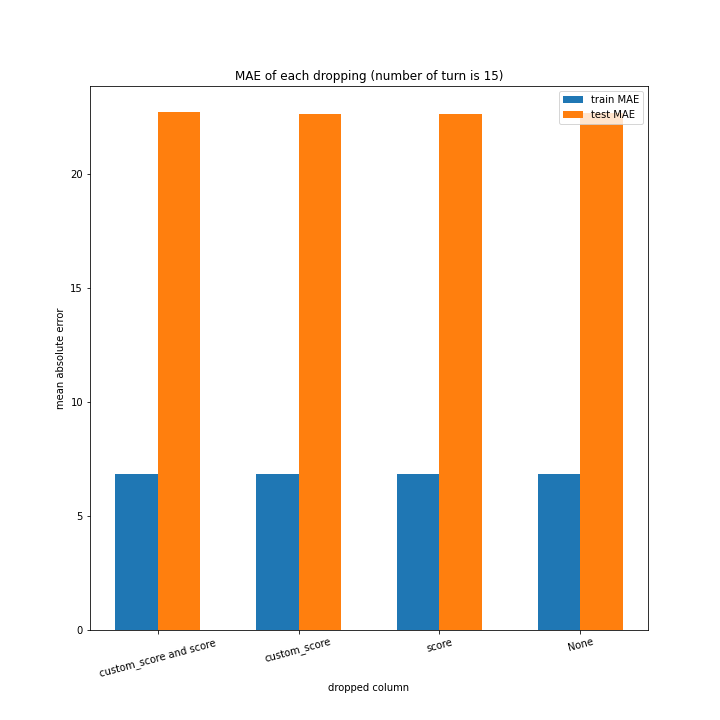
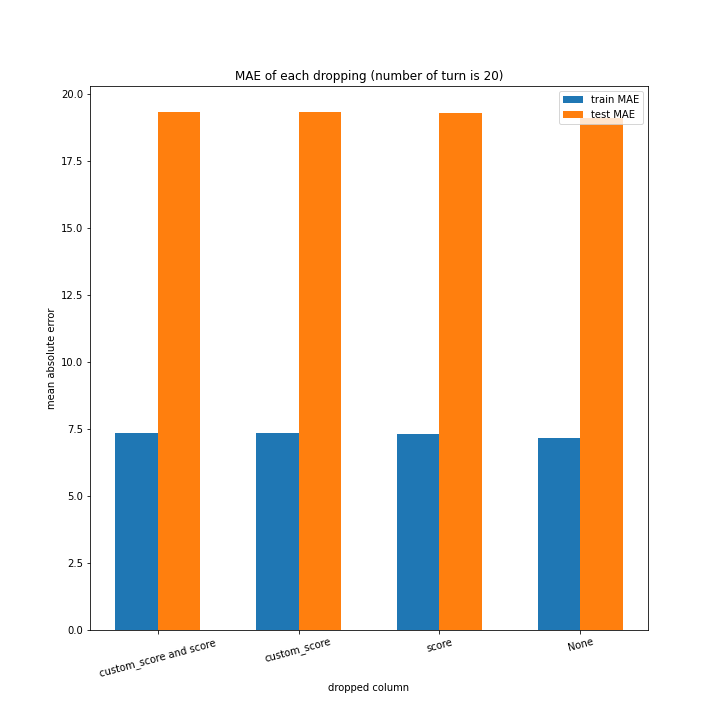
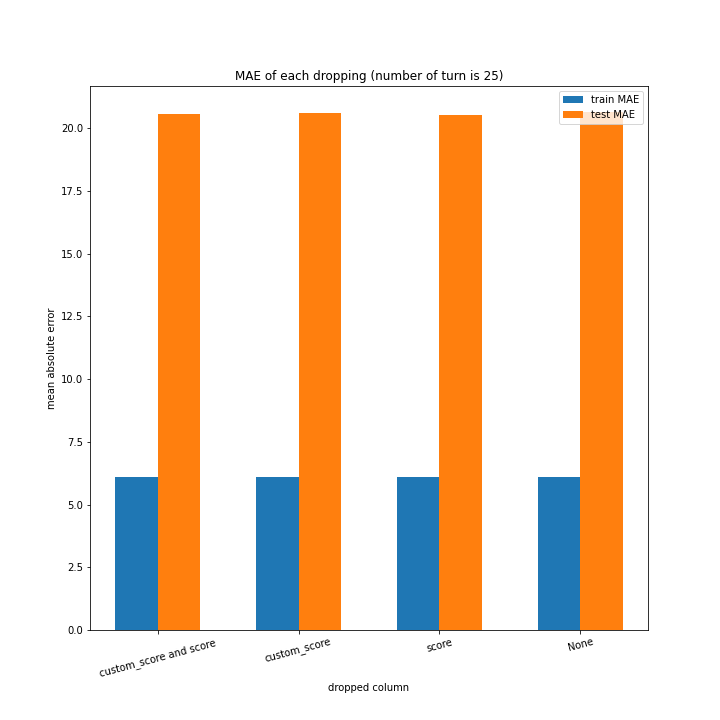
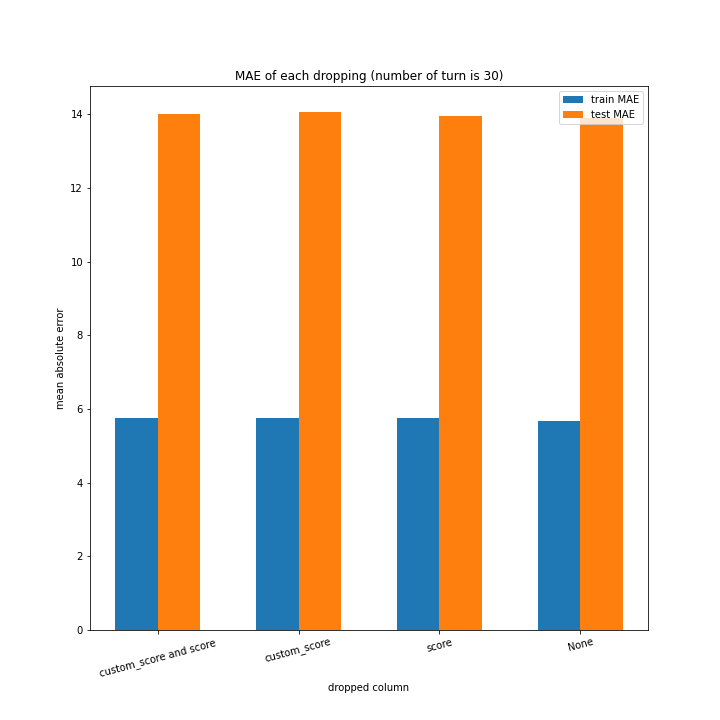
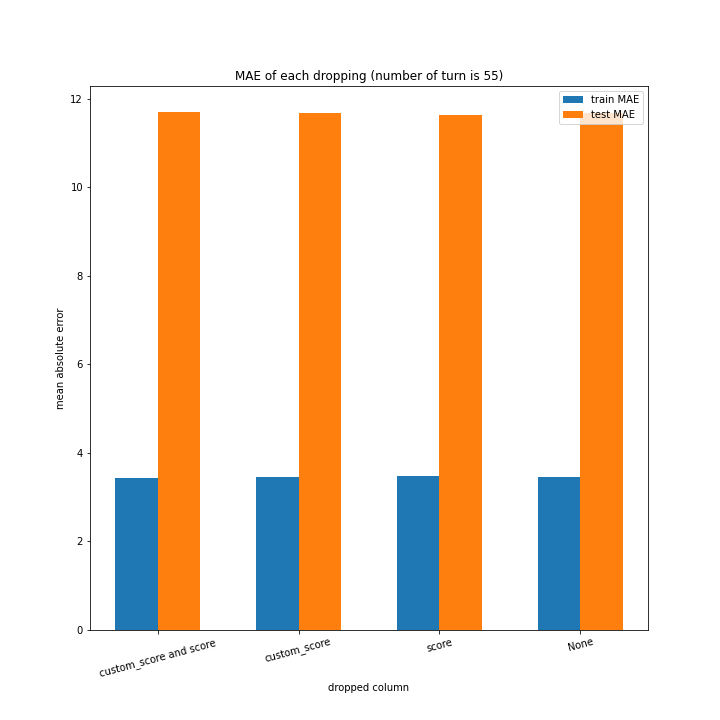
前回同様、ターン数ごとに学習方法別のスコアと平均絶対誤差、学習方法ごとにターン数別のスコアと平均絶対誤差をグラフ化しました。
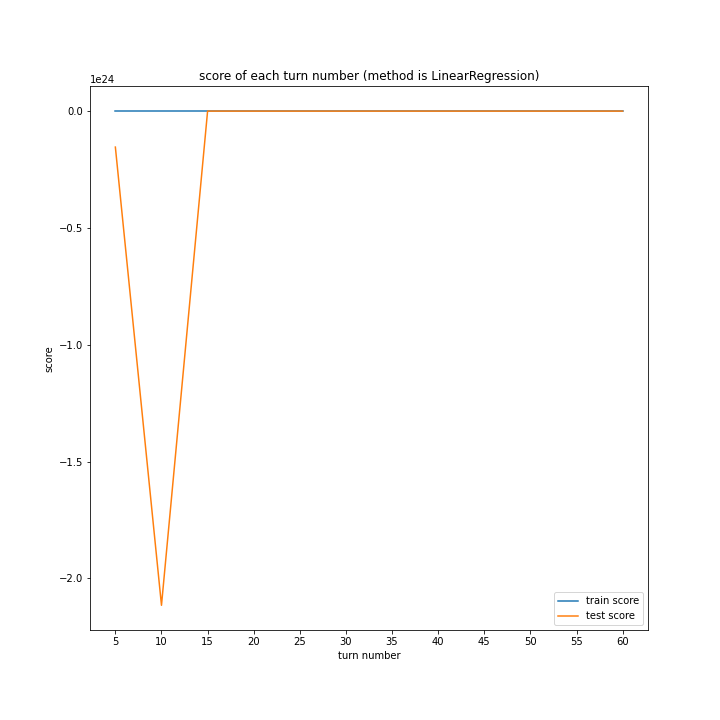
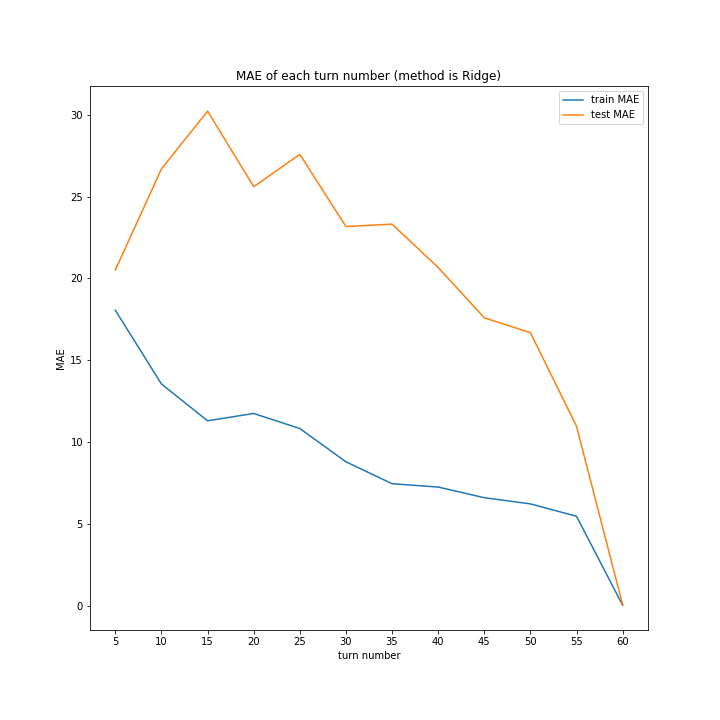
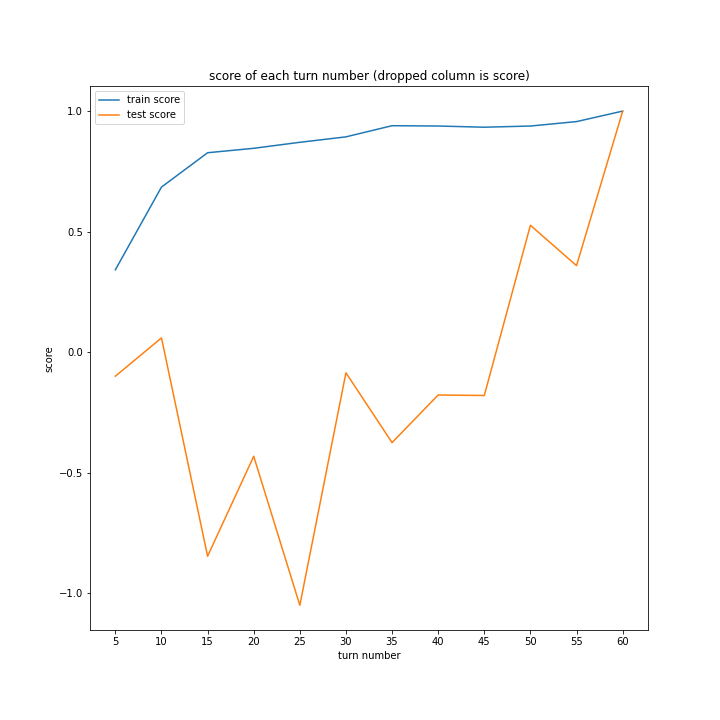
LinearRegressionがやや情緒不安定ですが、それ以外はターン数が進むごとに少しずつ良いスコアとなっていっているのが見て取れます。
今更ですがmodel nameを傾ける必要は今回なかったような・・・。
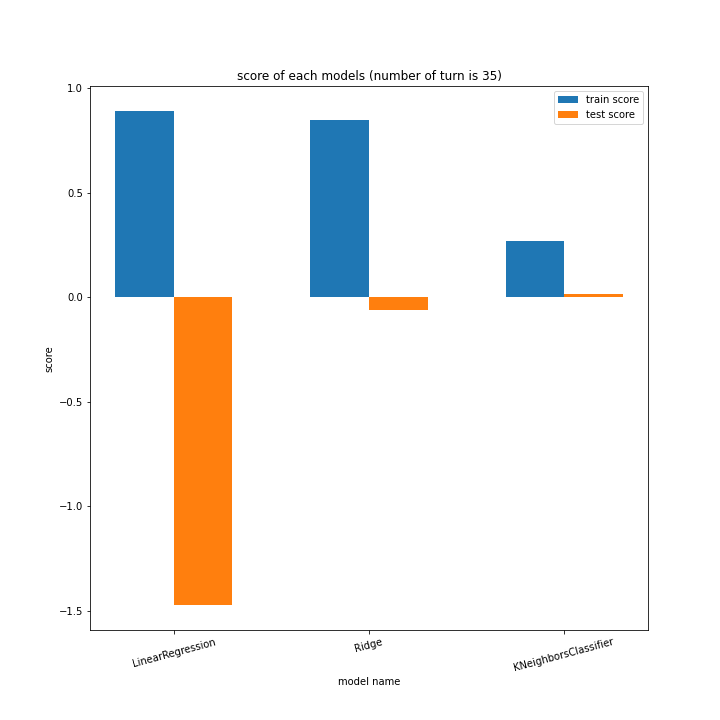
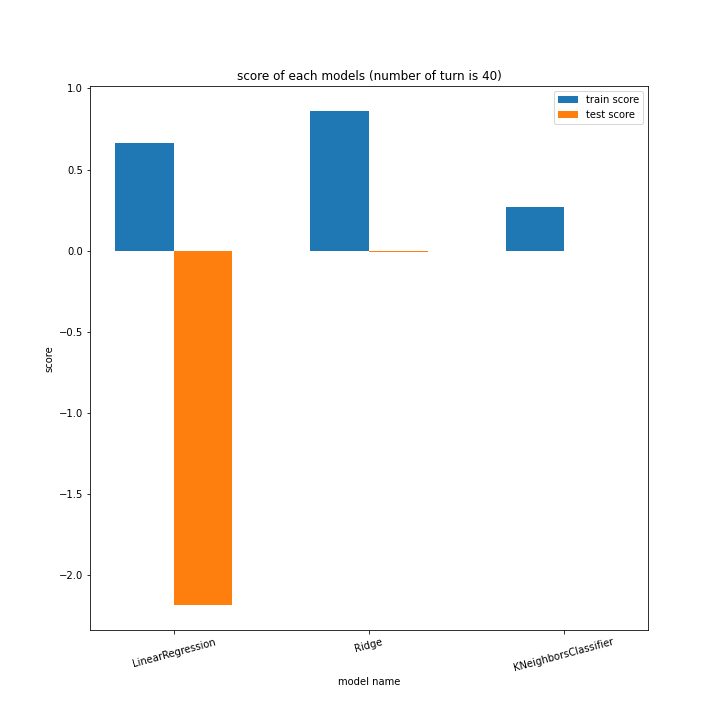
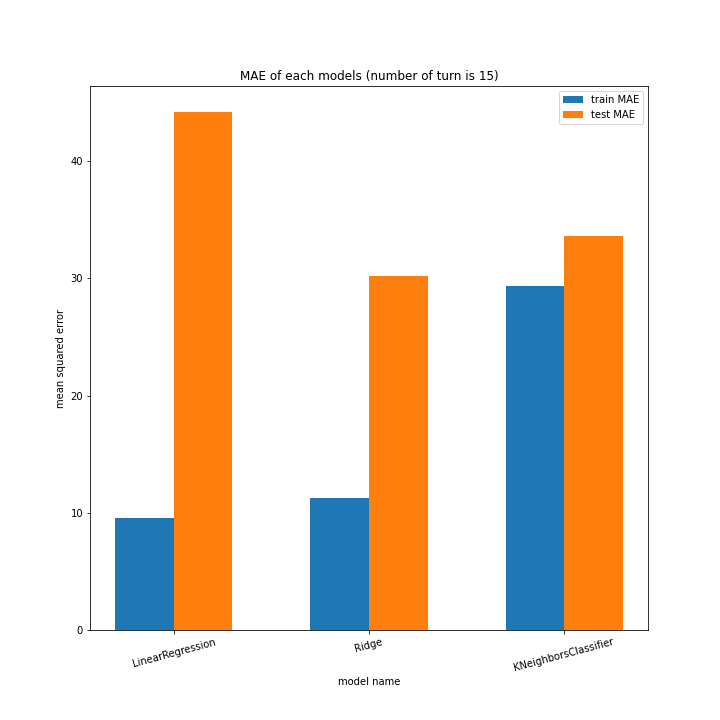
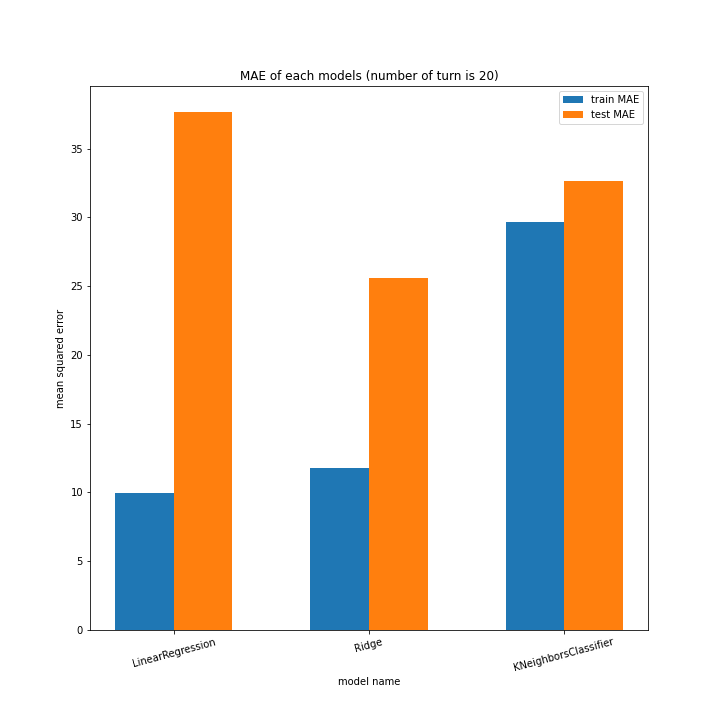
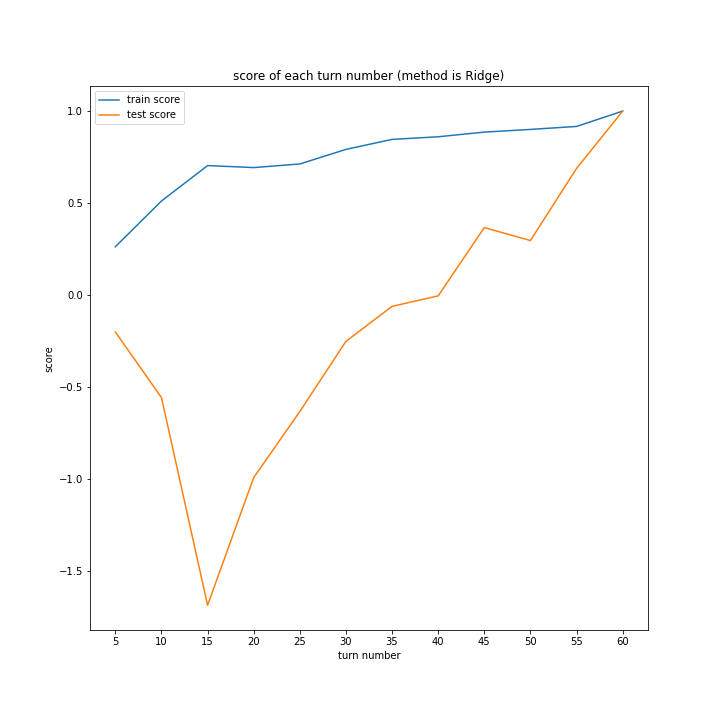
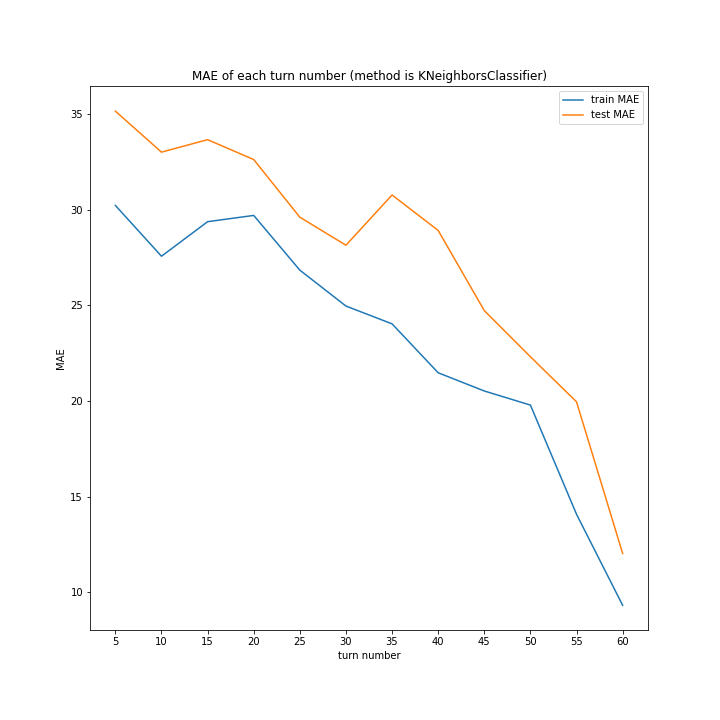
こちらもLinearRegression以外はターン数が進むごとに順調に誤差を小さくできています。
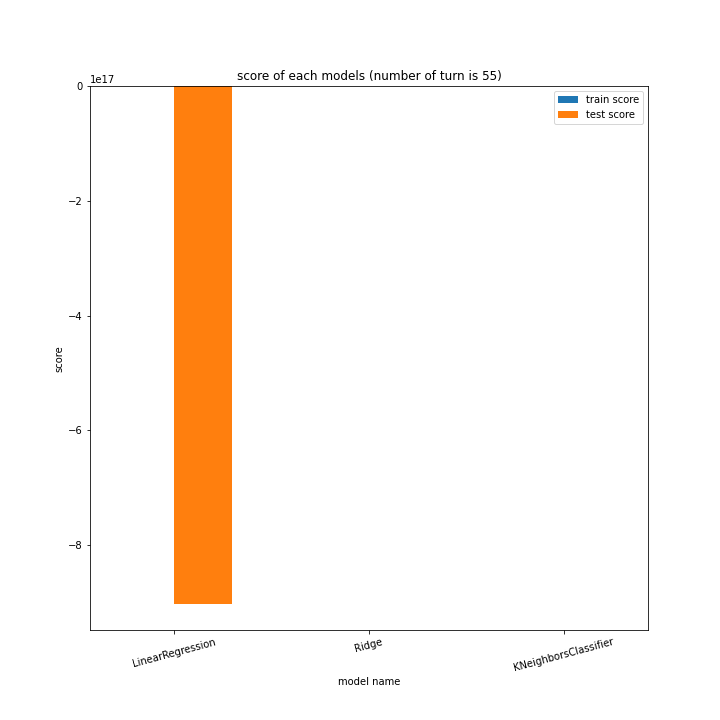
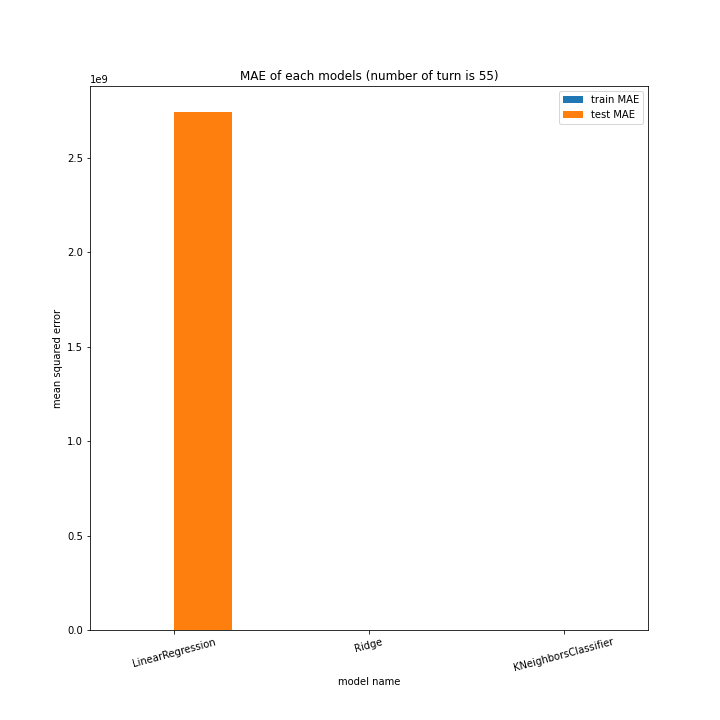
LinearRegressionは相変わらず55ターン目で過学習を起こしているようです。
理由はわかりません、今回ランダム関数のシード値を指定していないので再現性のないプログラミングをしてしまいました。もう一度実行すれば55ターンでの過学習は起きない可能性がありますが、そもそもLinearRegressionはRidgeに比べ過学習しやすいので他のターンで過学習が起きる可能性はあります。
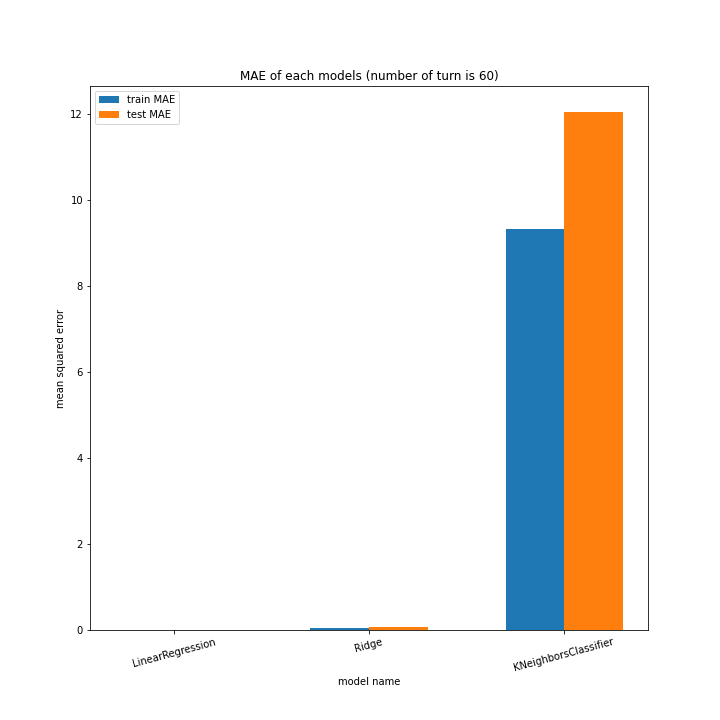
Ridgeが15ターン目で大きくテストスコアが下がっているのが気になります。15ターンの前後も下がっているので偶然ではなく理由があると思います。
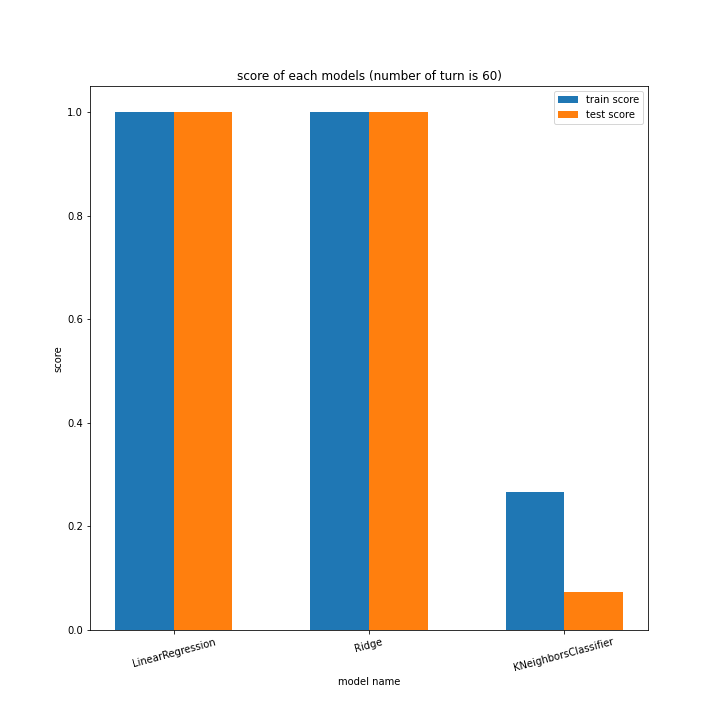
全体として、前回より向上したとは言えない誤差となりました。
まとめ
あまり改善しなかった。
理由として考えられるのは、新しく追加した「opp_put_num」が、あまり意味がなかったのでは? ということです。終盤ならまだしも、序盤であれば「次のターンで相手がとれる手数」が最終結果に響くことはそうそうないのでは? と今更ながら気づきました。そして、終盤は追加の説明変数なんてなくてもある程度正確に最終結果を予測できています。
最終スコアを「自分の駒の数-相手の駒の数」としたのは正しい判断だったと思うので一応継続させます。
改善案2
改善案1及び前回でも優秀だったRidgeに絞り学習を行いたいと思います。
また、盤面情報だけでなく現在のスコア(自分の駒の数-相手の駒の数)および現在のカスタムスコア(自分のカスタムスコア-相手のカスタムスコア)も説明変数として追加してみようと思います。ここでカスタムスコアとは、評価値の重み付きのスコアのことです。
BitBoard
オセロのためのスーパークラス。
乱数のシード値を指定できるようにしました。
def __init__(self, black_method, white_method,\
seed_num=0, read_goal=[1, 1], eva=None):
self.think = [\
self.human,
self.random,
self.nhand,
self.nhand_custom,
self.nleast,
self.nmost
]
if (black_method == osero.PLAY_WAY["nhand_custom"]\
or white_method == osero.PLAY_WAY["nhand_custom"])\
and eva is None:
raise ValueError("designate eva")
self.black_method = black_method
self.white_method = white_method
self.read_goal = read_goal
self.eva = eva
if black_method == osero.PLAY_WAY["nhand"]:
self.eva[0] = [1] * 64
if white_method == osero.PLAY_WAY["nhand"]:
self.eva[1] = [1] * 64
seed(seed_num)
self.setup()
osero_learn
学習のデータ集めのためのクラス。
dataにscoreとcustom_scoreを追加しました。
def data_set(self, data: DataFrame, turn_num: int) -> None:
if self.turn:
my = ["b_u", "b_d"]
opp = ["w_u", "w_d"]
else:
my = ["w_u", "w_d"]
opp = ["b_u", "b_d"]
data["turn_num"].append(turn_num)
data["turn"].append(self.turn)
data["score"].append(self.popcount(self.bw[my[0]])
+ self.popcount(self.bw[my[1]])
- self.popcount(self.bw[opp[0]])
- self.popcount(self.bw[opp[1]]))
data["custom_score"].append(self.count(self.bw, self.turn))
for i in range(32):
data["my%d" % i].append(int((self.bw[my[0]] & (1 << i)) != 0))
data["opp%d" % i].append(int((self.bw[opp[0]] & (1 << i)) != 0))
for i in range(32):
data["my%d" % (i + 32)].append(int((self.bw[my[1]] & (1 << i)) != 0))
data["opp%d" % (i + 32)].append(int((self.bw[opp[1]] & (1 << i)) != 0))
run
実行ファイル。
ipynbで書いています。
データ集め部分
今までと全く同じなので省略。
学習部分
盤面情報はすべての学習で使うとして、スコアとカスタムスコアについては、
- 両方使わない
- スコアのみ使う
- カスタムスコアのみ使う
- 両方使う
という四パターンで学習を行いグラフを作成しました。
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error
from sklearn.linear_model import Ridge
x_data = df.drop(["turn", "last_score"], axis=1)
y_data = df[["turn_num", "last_score"]]
turn_vari = df["turn_num"].unique()
drop_vari = ["custom_score and score", "custom_score", "score", "None"]
################################
train_score = []
test_score = []
train_MAE = []
test_MAE = []
for turn_num in turn_vari:
train_score.append([])
test_score.append([])
train_MAE.append([])
test_MAE.append([])
for drop_list in [["custom_score", "score"], ["custom_score"], ["score"], []]:
drop_list.append("turn_num")
x_train, x_test, y_train, y_test = train_test_split(\
x_data.query("turn_num==%d" % turn_num).drop(drop_list, axis=1),
y_data.query("turn_num==%d" % turn_num).drop("turn_num", axis=1),
test_size=0.3,
random_state=0
)
model = Ridge(random_state=0)
model.fit(x_train, y_train)
train_score[-1].append(model.score(x_train, y_train))
test_score[-1].append(model.score(x_test, y_test))
train_predict = model.predict(x_train)
train_MAE[-1].append(mean_absolute_error(train_predict, y_train))
test_predict = model.predict(x_test)
test_MAE[-1].append(mean_absolute_error(test_predict, y_test))
################################
width = 0.3
x_axis = np.array([i + 1 for i in range(len(drop_vari))])
for i in range(len(turn_vari)):
fig_name = "score of each dropping (number of turn is %d)" % turn_vari[i]
fig = plt.figure(figsize=(10, 10))
plt.bar(x_axis, train_score[i], label="train score", width=width)
plt.bar(x_axis + width, test_score[i], label="test score", width=width)
plt.xticks(x_axis + width/2, labels=drop_vari, rotation=15)
plt.legend()
plt.title(fig_name)
plt.xlabel("dropped column")
plt.ylabel("score")
plt.savefig("fig/" + fig_name)
# plt.show()
plt.clf()
plt.close()
fig_name = "MAE of each dropping (number of turn is %d)" % turn_vari[i]
fig = plt.figure(figsize=(10, 10))
plt.bar(x_axis, train_MAE[i], label="train MAE", width=width)
plt.bar(x_axis + width, test_MAE[i], label="test MAE", width=width)
plt.xticks(x_axis + width/2, labels=drop_vari, rotation=15)
plt.legend()
plt.title(fig_name)
plt.xlabel("dropped column")
plt.ylabel("mean absolute error")
plt.savefig("fig/" + fig_name)
# plt.show()
plt.clf()
plt.close()
################################
x_axis = np.array([i + 1 for i in range(len(turn_vari))])
x_axis_name = [str(i) for i in turn_vari]
train_score_T = np.array(train_score).T
test_score_T = np.array(test_score).T
train_MAE_T = np.array(train_MAE).T
test_MAE_T = np.array(test_MAE).T
for i in range(len(drop_vari)):
fig_name = "score of each turn number (dropped column is %s)" % drop_vari[i]
fig = plt.figure(figsize=(10, 10))
plt.plot(x_axis_name, train_score_T[i], label="train score")
plt.plot(x_axis_name, test_score_T[i], label="test score")
plt.legend()
plt.title(fig_name)
plt.xlabel("turn number")
plt.ylabel("score")
plt.savefig("fig/" + fig_name)
# plt.show()
plt.clf()
plt.close()
fig_name = "MAE of each turn number (dropped column is %s)" % drop_vari[i]
fig = plt.figure(figsize=(10, 10))
plt.plot(x_axis_name, train_MAE_T[i], label="train MAE")
plt.plot(x_axis_name, test_MAE_T[i], label="test MAE")
plt.legend()
plt.title(fig_name)
plt.xlabel("turn number")
plt.ylabel("mean absolute error")
plt.savefig("fig/" + fig_name)
# plt.show()
plt.clf()
plt.close()
学習結果
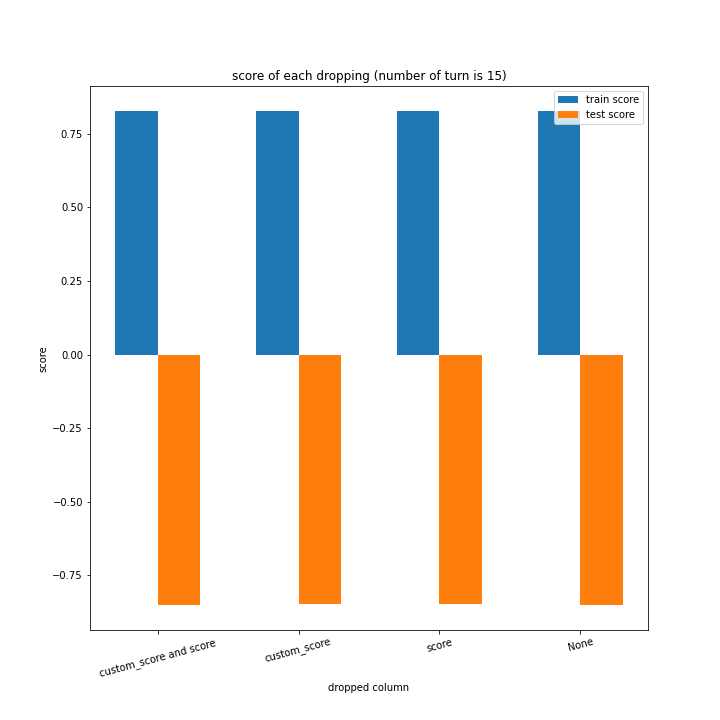
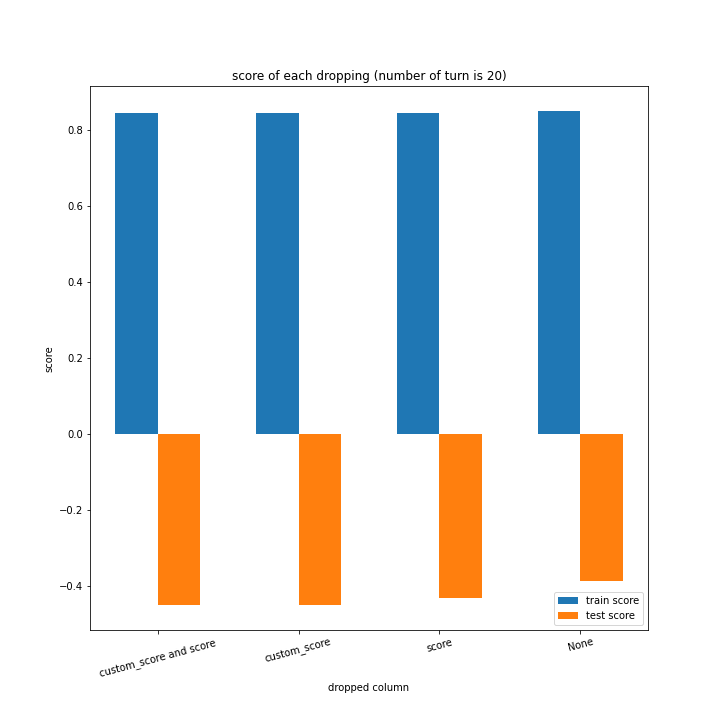
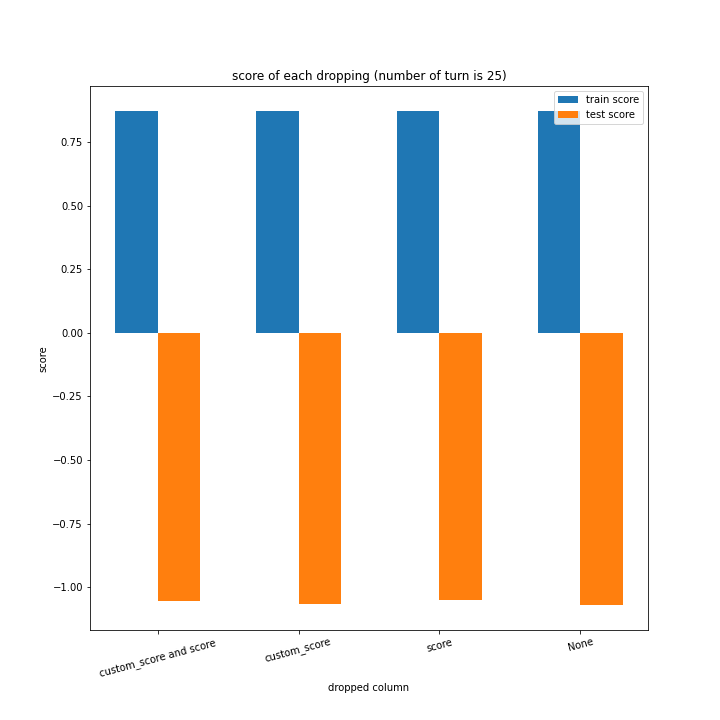
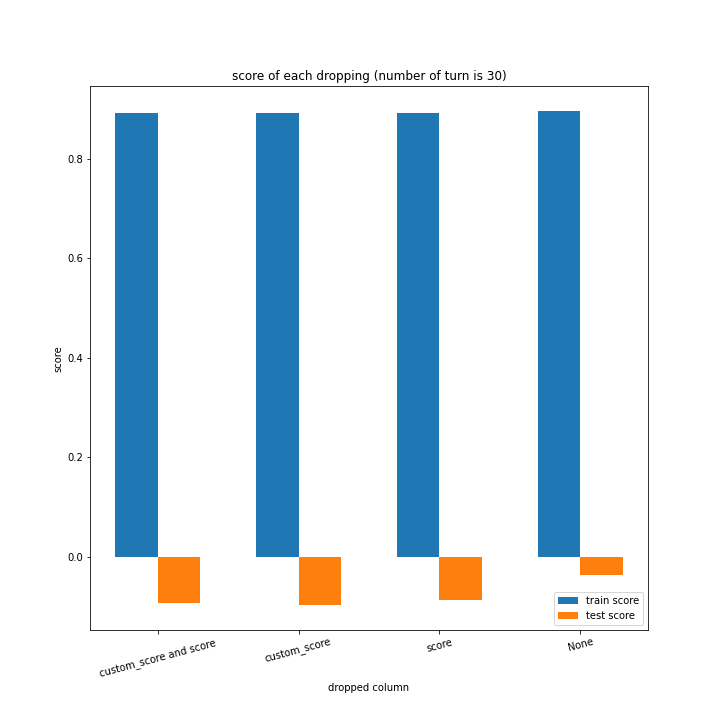
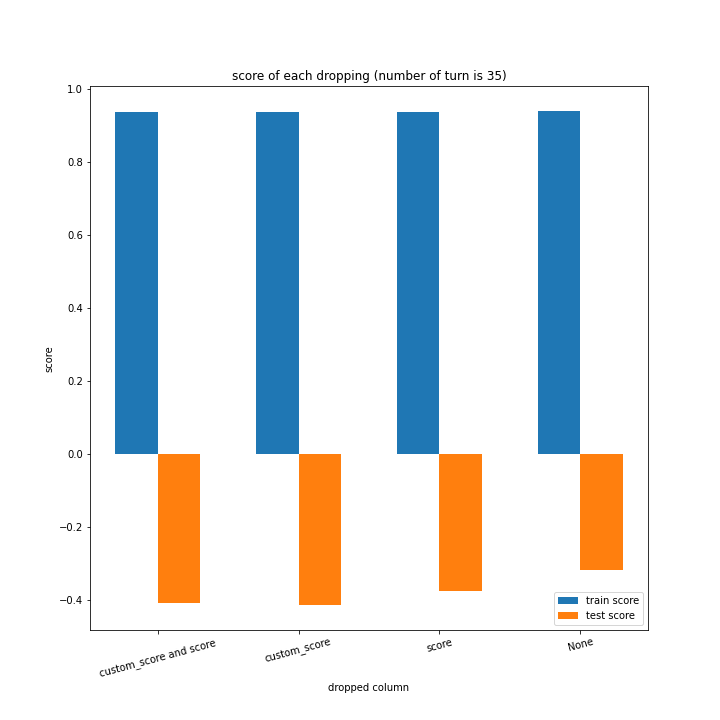
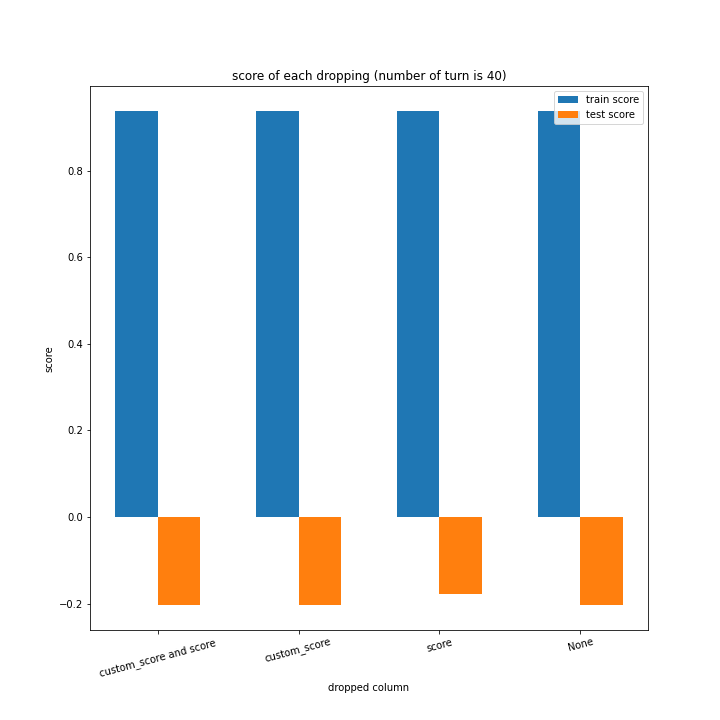
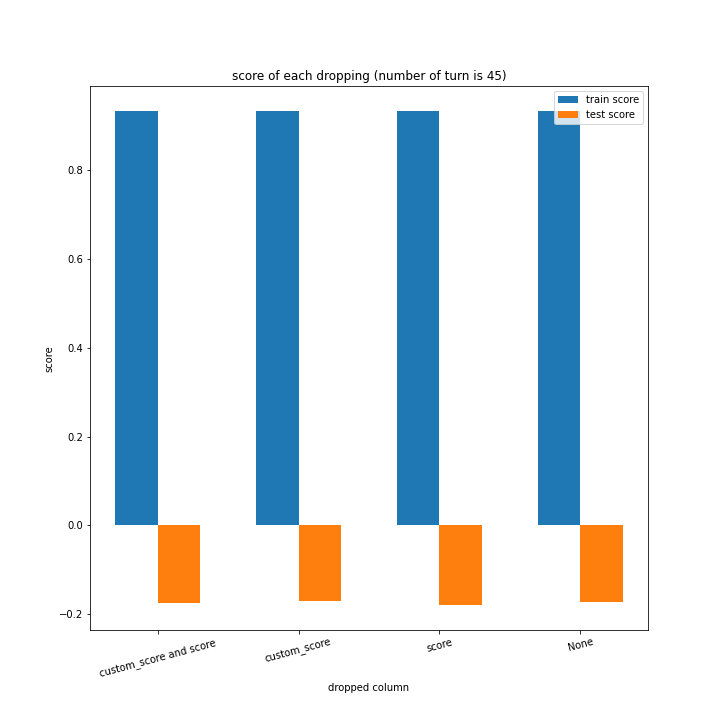
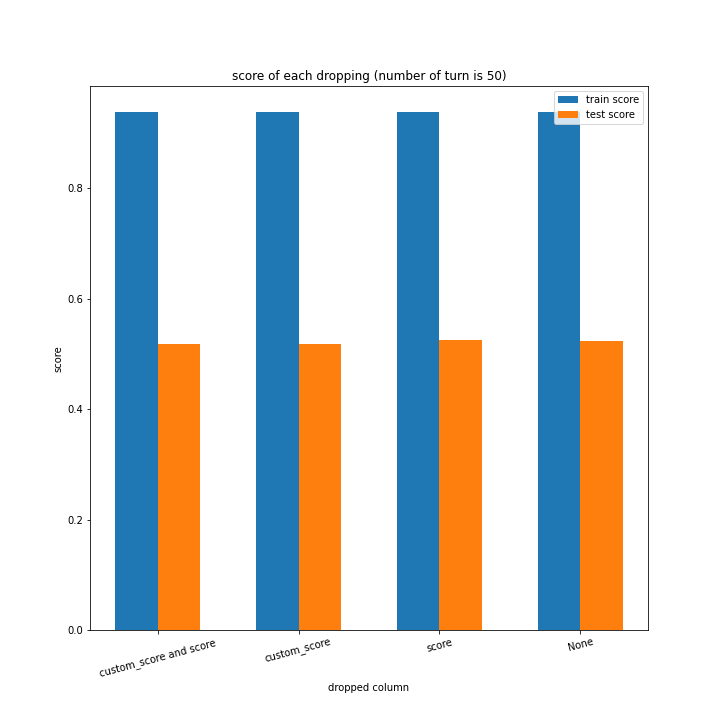
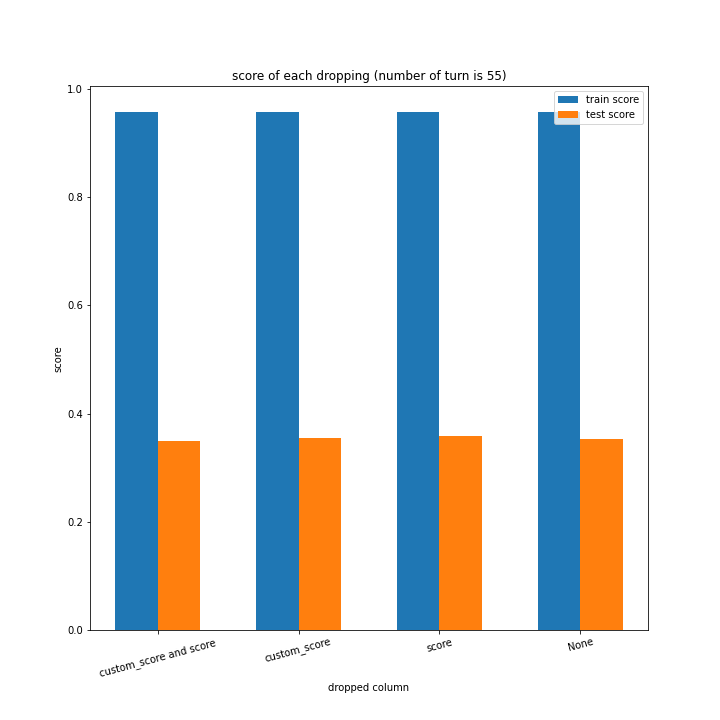
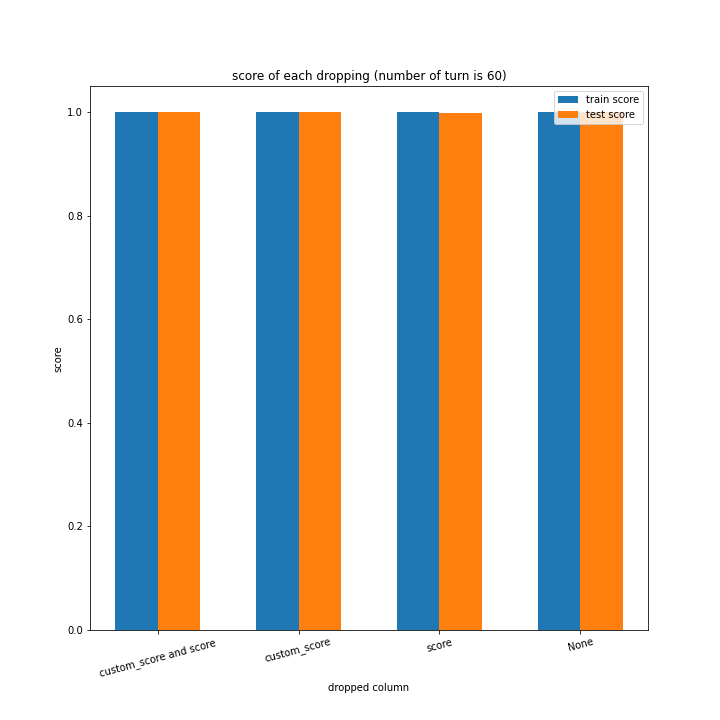
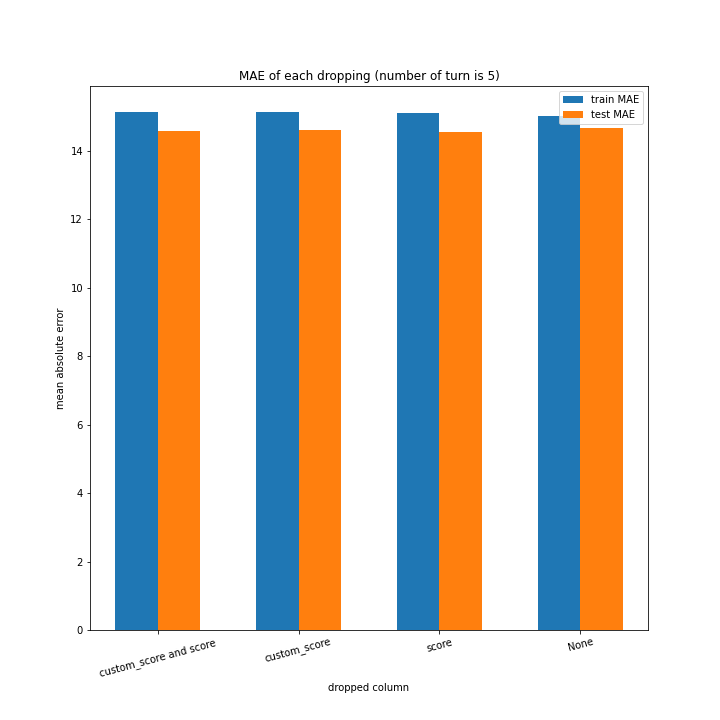
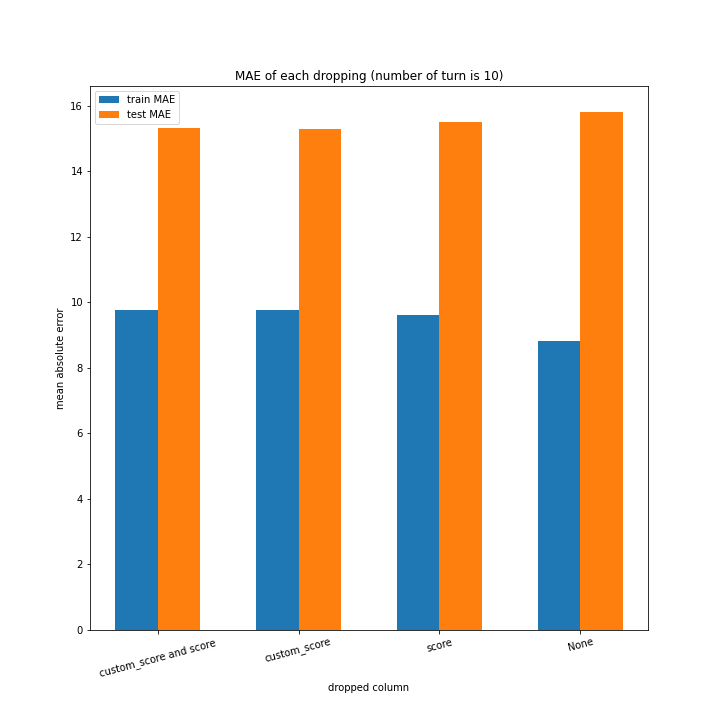
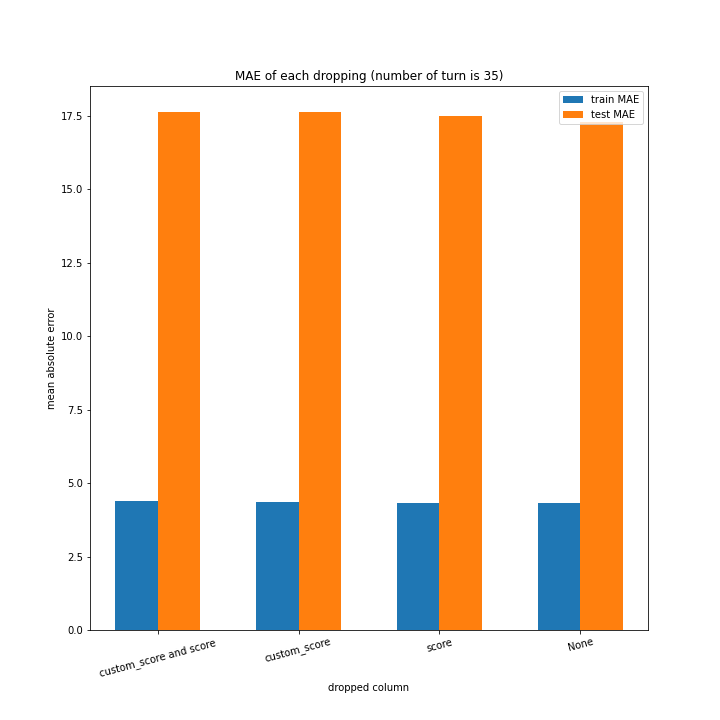
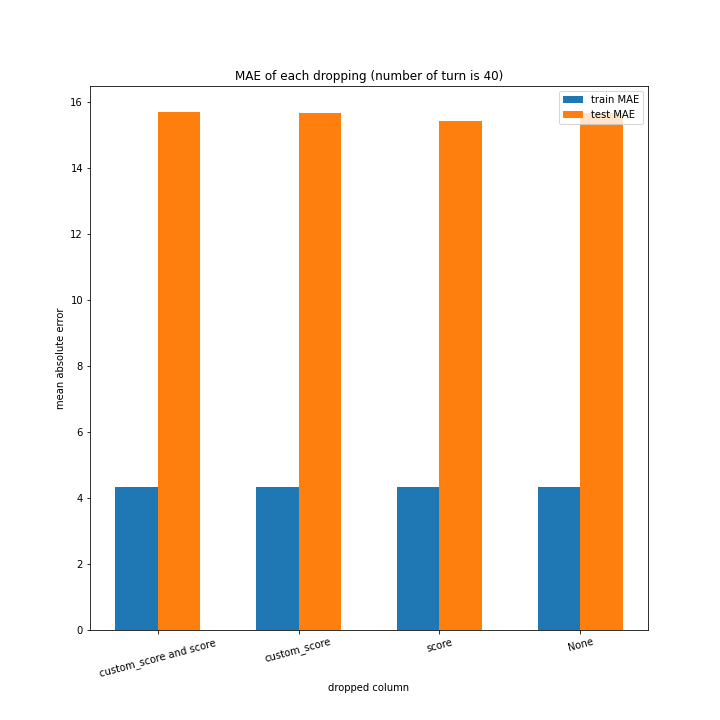
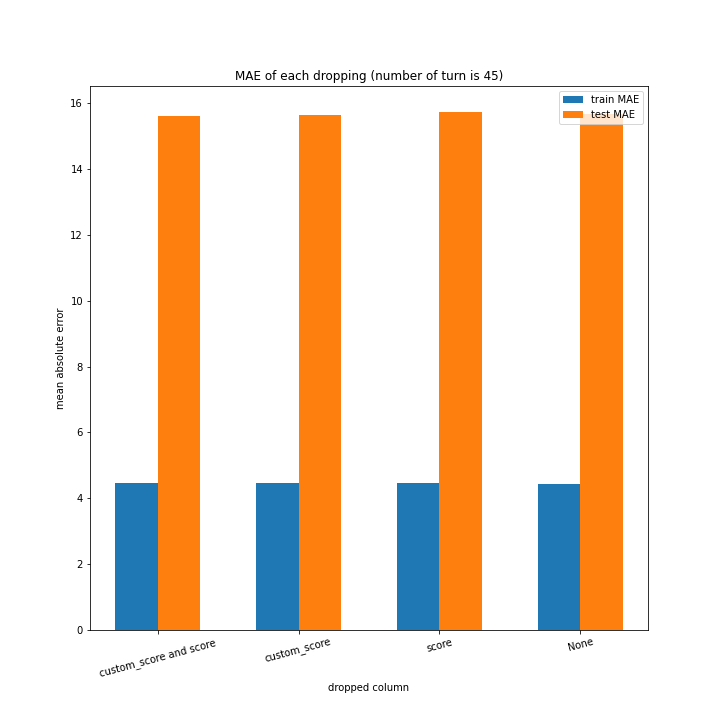
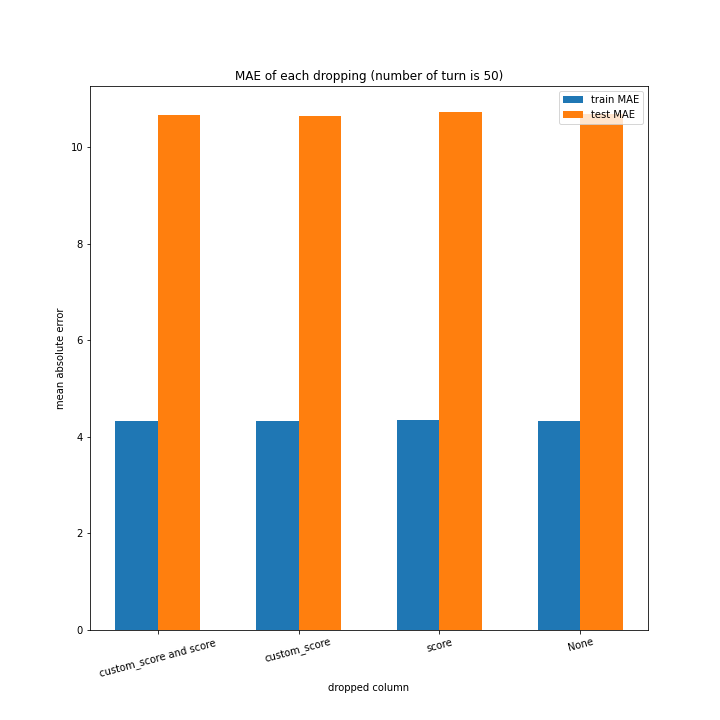
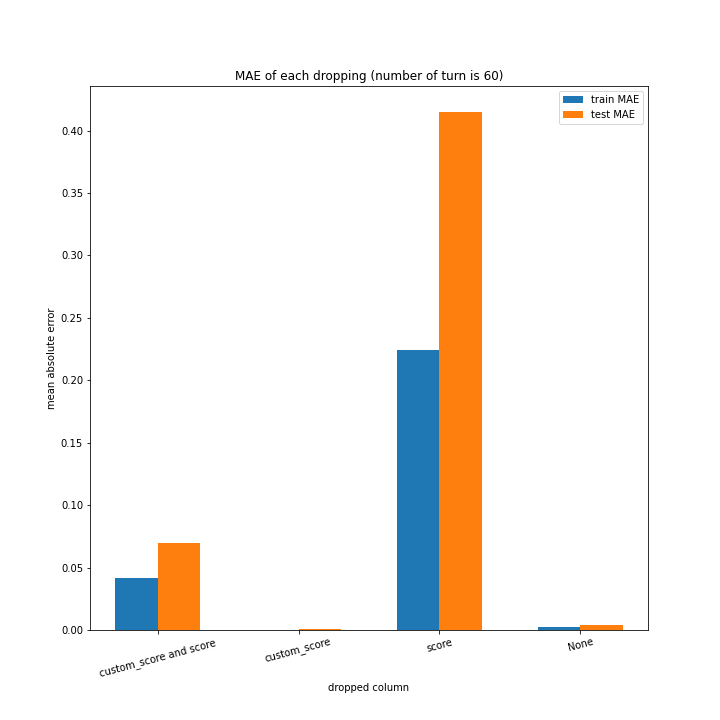
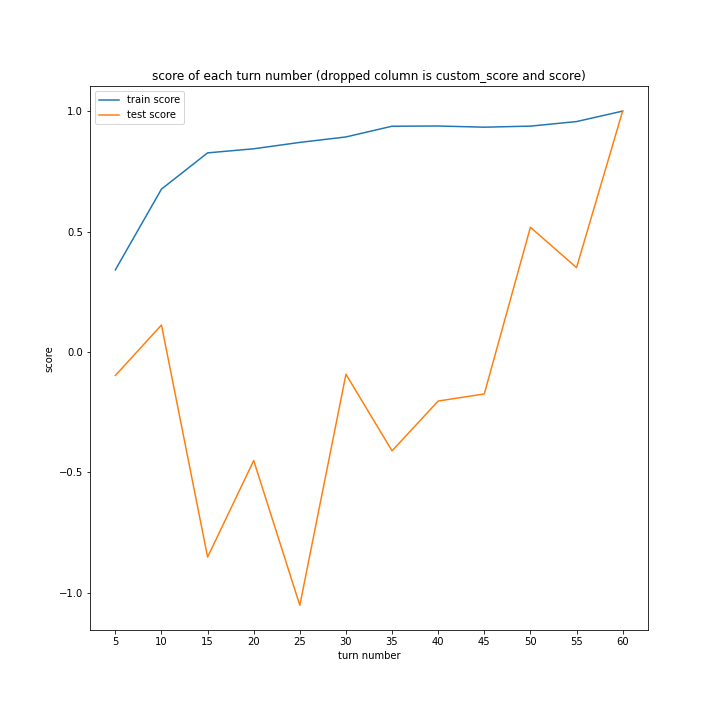
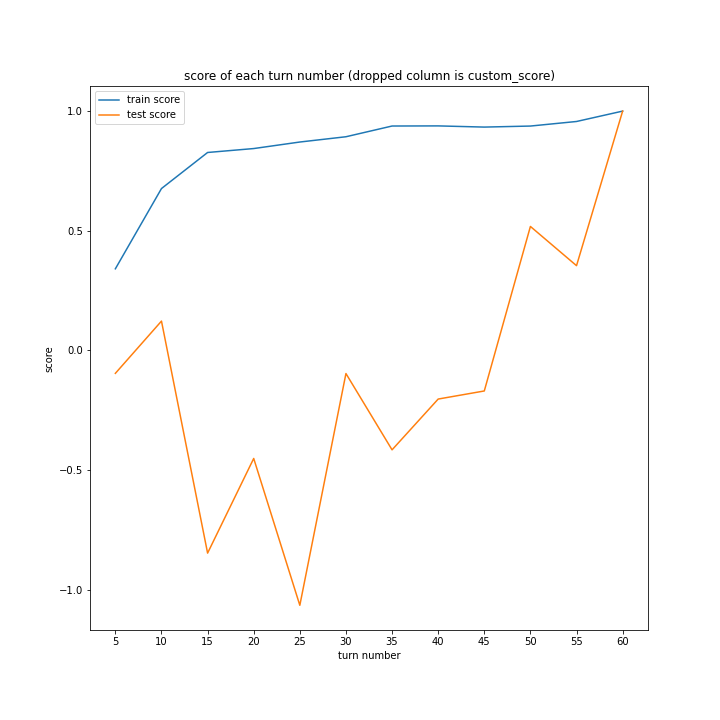
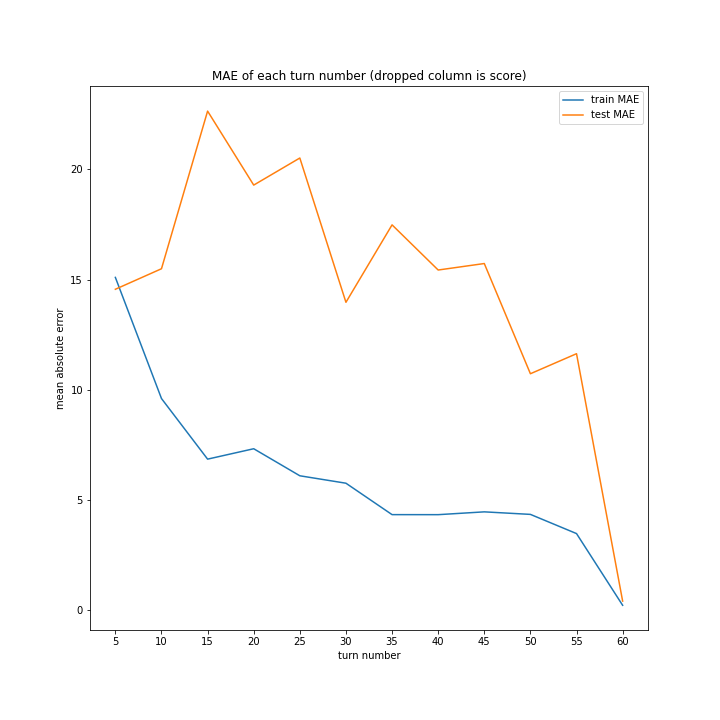
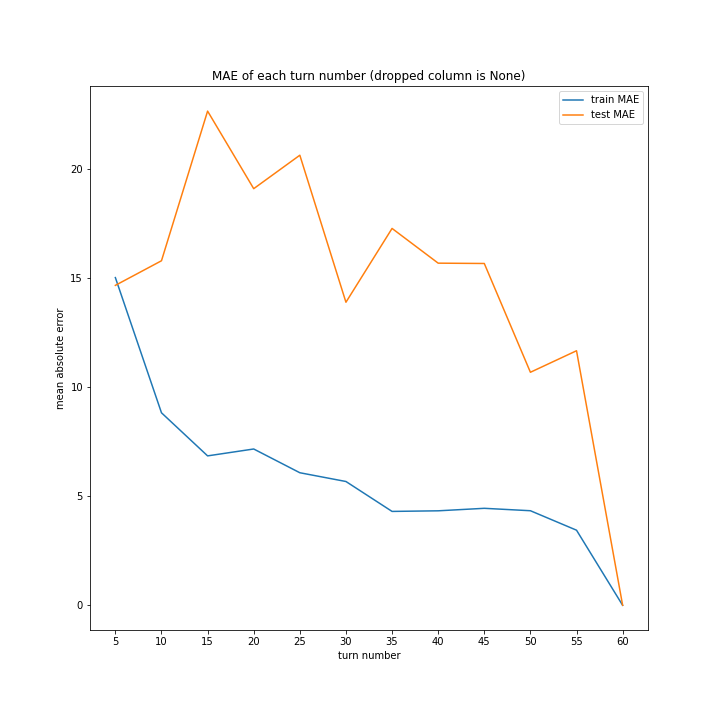
例のごとくターン数ごとの説明変数別のスコアと平均絶対誤差、説明変数ごとのターン数別のスコアと平均絶対誤差をグラフにしました。
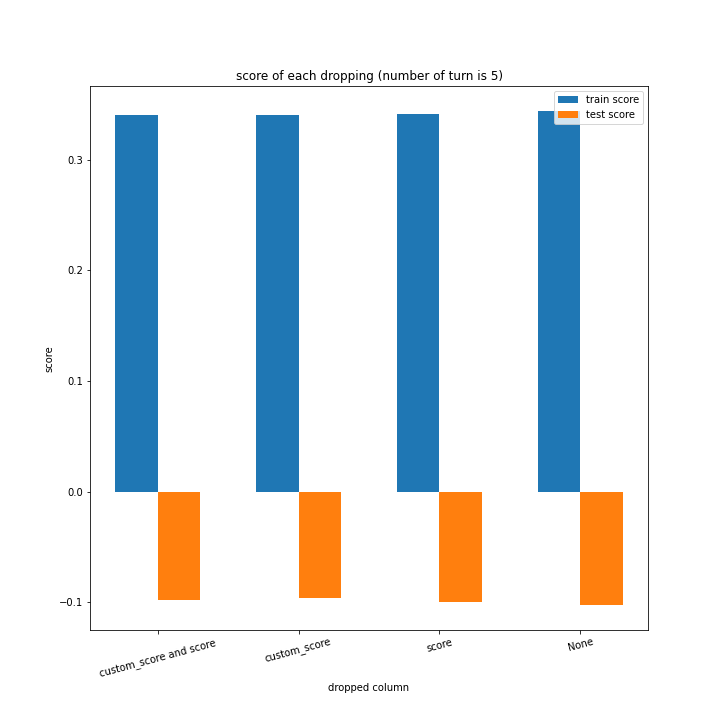
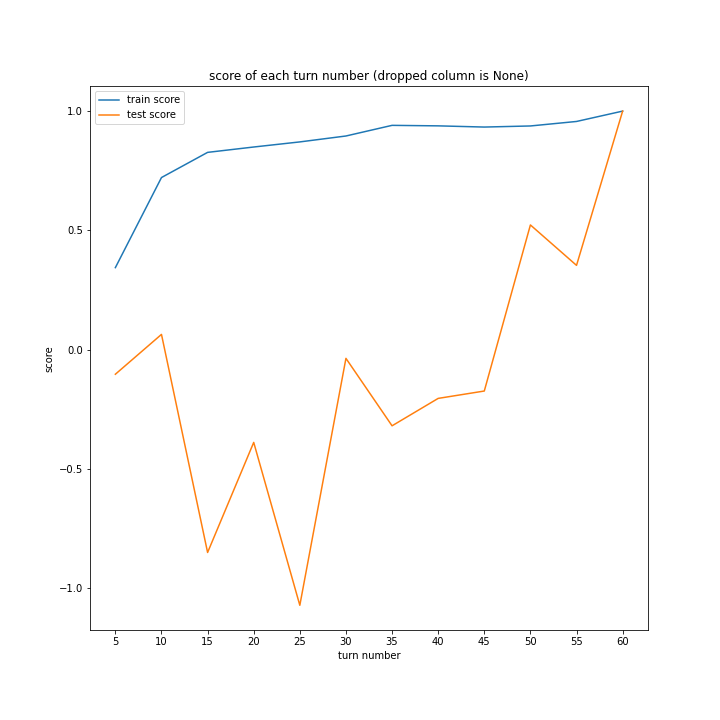
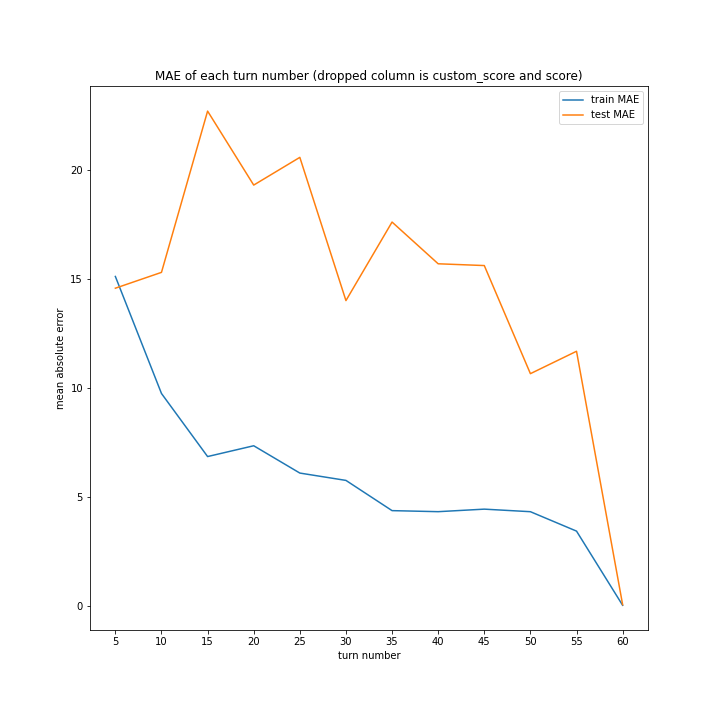
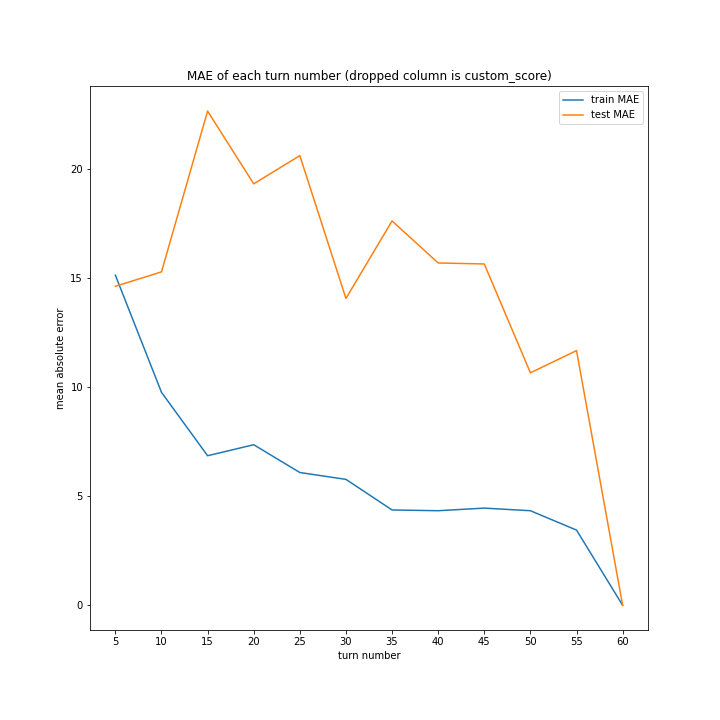
ターン数が進むごとに良くなっている、とは言えない結果になりました。
よくなったり悪くなったりを繰り返しています。
また、どの棒グラフも似たような形をしています。
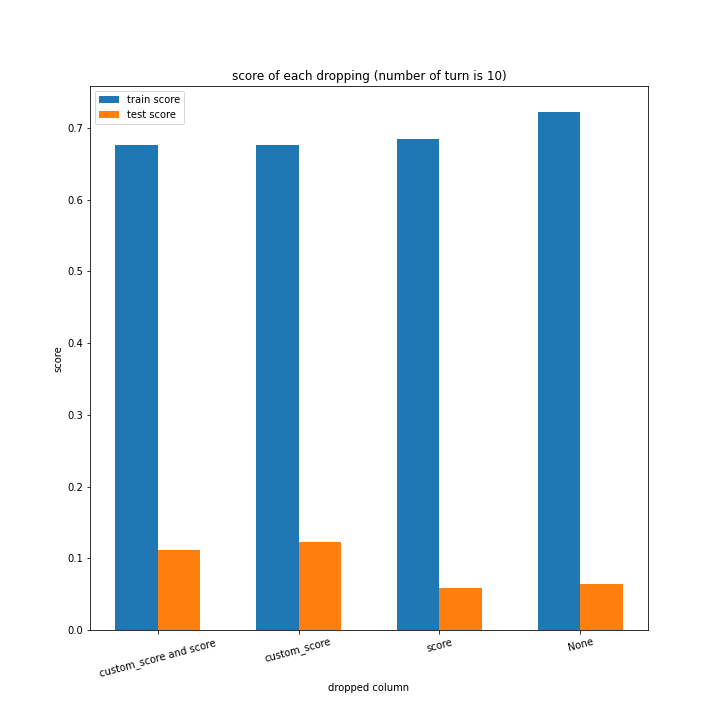
こちらもターン数が進むごとに線形に数字が変わるような結果にはなりませんでした。
しかし誤差が最大でも20程度に収まったのはこれまでの改善案などと違うところです。
60ターン目のグラフで、custom_scoreのみ除いたデータ、つまりスコアを入れたデータの正解率が高いですが、これは単純に説明変数として与えたスコアと最終スコアがほぼ同じになるからだと考えられます。
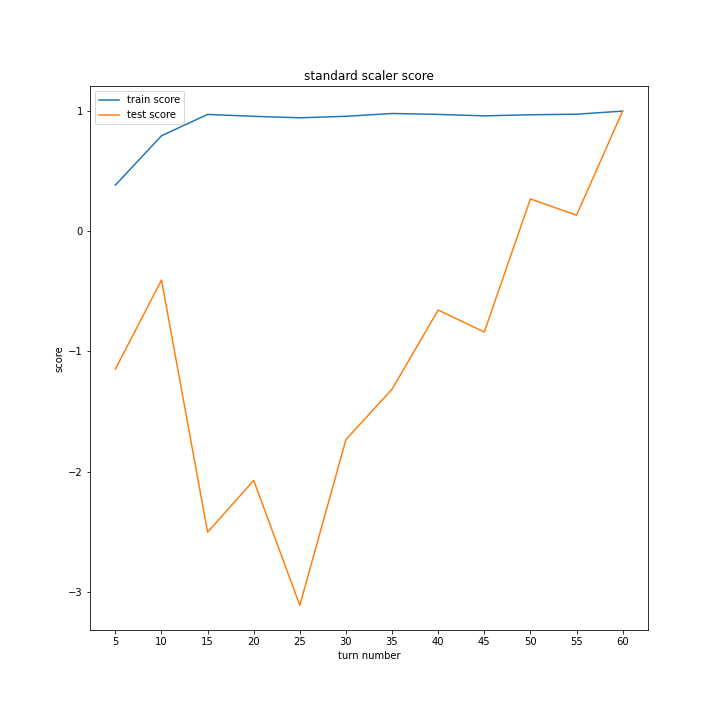
どのグラフも紆余曲折をへてスコア1に収束しています。
大きな違いはありません。
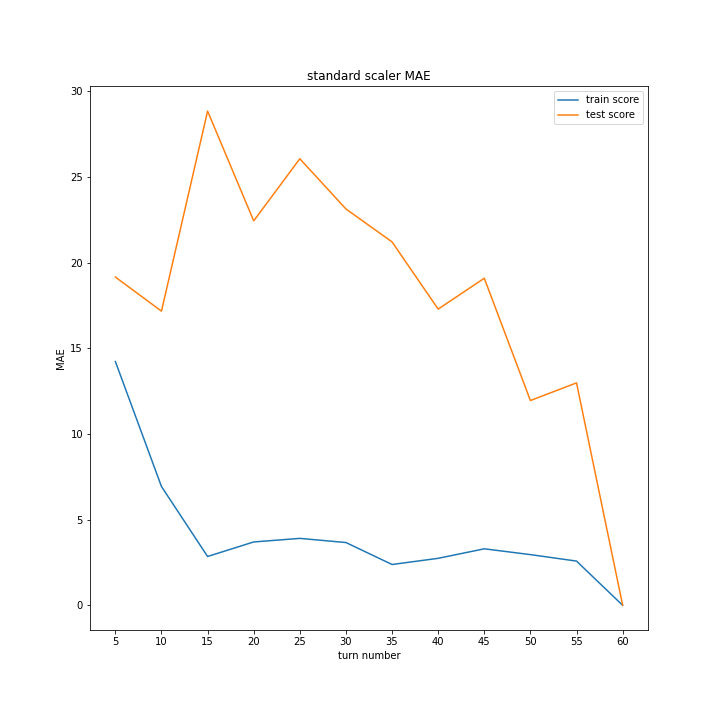
こちらも、15ターンから20ターンで誤差が大きくなるものの最大誤差は25程度にとどまっています。
まとめ
「今のスコア」や「今のカスタムスコア」を使ってもあまり結果は変わりませんでしたが、改善案1と比べ制度は上がりました。
このことから、やはり次のターンでの相手の手数はあまり関係ないこと、また目的変数を「自分のスコア-相手のスコア」にすることは有効であることがいえます。
また、15ターン付近で過学習を起こす傾向にあるともわかりました。理由は分かりません。
改善案3
今までの検証で現在のスコアなどを与えてもあまり意味はないと分かったので、ここではデータの前処理などを行い精度の向上を図ります。
osero_learn
結局data変数はこうなりました。
これらとlast_scoreのみです。
def data_set(self, data: DataFrame, turn_num: int) -> None:
if self.turn:
my = ["b_u", "b_d"]
opp = ["w_u", "w_d"]
else:
my = ["w_u", "w_d"]
opp = ["b_u", "b_d"]
data["turn_num"].append(turn_num)
data["turn"].append(self.turn)
for i in range(32):
data["my%d" % i].append(int((self.bw[my[0]] & (1 << i)) != 0))
data["opp%d" % i].append(int((self.bw[opp[0]] & (1 << i)) != 0))
for i in range(32):
data["my%d" % (i + 32)].append(int((self.bw[my[1]] & (1 << i)) != 0))
data["opp%d" % (i + 32)].append(int((self.bw[opp[1]] & (1 << i)) != 0))
run
データ集め部分
今までと全く同じなので割愛。
学習部分
二つの方法を用いて説明変数の正規化を行いました。
そのうえで学習を行い、結果をグラフ化しました。
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import PowerTransformer
from sklearn.pipeline import Pipeline
from sklearn.linear_model import Ridge
x_data = df.drop(["turn", "last_score"], axis=1)
y_data = df[["turn_num", "last_score"]]
turn_vari = df["turn_num"].unique()
################################
def two_plot(x, y, xlabel, ylabel, title, save_dir):
fig = plt.figure(figsize=(10, 10))
plt.plot(x, y[0], label="train score")
plt.plot(x, y[1], label="test score")
plt.title(title)
plt.xlabel(xlabel)
plt.ylabel(ylabel)
plt.legend()
plt.savefig(save_dir + "/" + title)
plt.clf()
plt.close()
# def two_bar(x, x_name, y, xlabel, ylabel, title, save_dir):
# fig = plt.figure(figsize=(10, 10))
# plt.bar(x, y[0], label="train score", width=0.3)
# plt.bar(x + 0.3, y[1], label="test score", width=0.3)
# plt.xticks(x + 0.15, labels=x_name)
# plt.title(title)
# plt.xlabel(xlabel)
# plt.ylabel(ylabel)
# plt.legend()
# plt.savefig(save_dir + "/" + title)
# plt.clf()
# plt.close()
################################
pipeline = Pipeline([
("scaler", StandardScaler()),
("reg", Ridge(random_state=0))
])
train_score = []
test_score = []
train_MAE = []
test_MAE = []
for turn_num in turn_vari:
x_train, x_test, y_train, y_test = train_test_split(\
x_data.query("turn_num==%d" % turn_num).drop("turn_num", axis=1),
y_data.query("turn_num==%d" % turn_num).drop("turn_num", axis=1),
test_size=0.3,
random_state=0
)
pipeline.fit(x_train, y_train)
train_score.append(pipeline.score(x_train, y_train))
test_score.append(pipeline.score(x_test, y_test))
train_predict = pipeline.predict(x_train)
train_MAE.append(mean_absolute_error(train_predict, y_train))
test_predict = pipeline.predict(x_test)
test_MAE.append(mean_absolute_error(test_predict, y_test))
x = [str(i) for i in turn_vari]
y = [train_score, test_score]
two_plot(x, y, "turn number", "score", "standard scaler score", "fig")
y = [train_MAE, test_MAE]
two_plot(x, y, "turn number", "MAE", "standard scaler MAE", "fig")
################################
pipeline = Pipeline([
("scaler", PowerTransformer()),
("reg", Ridge(random_state=0))
])
train_score = []
test_score = []
train_MAE = []
test_MAE = []
for turn_num in turn_vari:
x_train, x_test, y_train, y_test = train_test_split(\
x_data.query("turn_num==%d" % turn_num).drop("turn_num", axis=1),
y_data.query("turn_num==%d" % turn_num).drop("turn_num", axis=1),
test_size=0.3,
random_state=0
)
pipeline.fit(x_train, y_train)
train_score.append(pipeline.score(x_train, y_train))
test_score.append(pipeline.score(x_test, y_test))
train_predict = pipeline.predict(x_train)
train_MAE.append(mean_absolute_error(train_predict, y_train))
test_predict = pipeline.predict(x_test)
test_MAE.append(mean_absolute_error(test_predict, y_test))
x = [str(i) for i in turn_vari]
y = [train_score, test_score]
two_plot(x, y, "turn number", "score", "power transformed score", "fig")
y = [train_MAE, test_MAE]
two_plot(x, y, "turn number", "MAE", "power transformed MAE", "fig")
学習結果
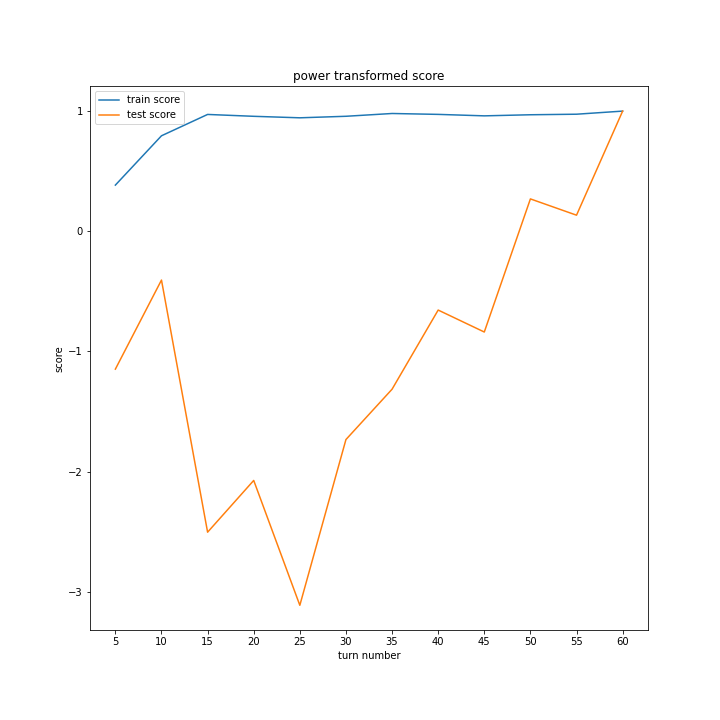
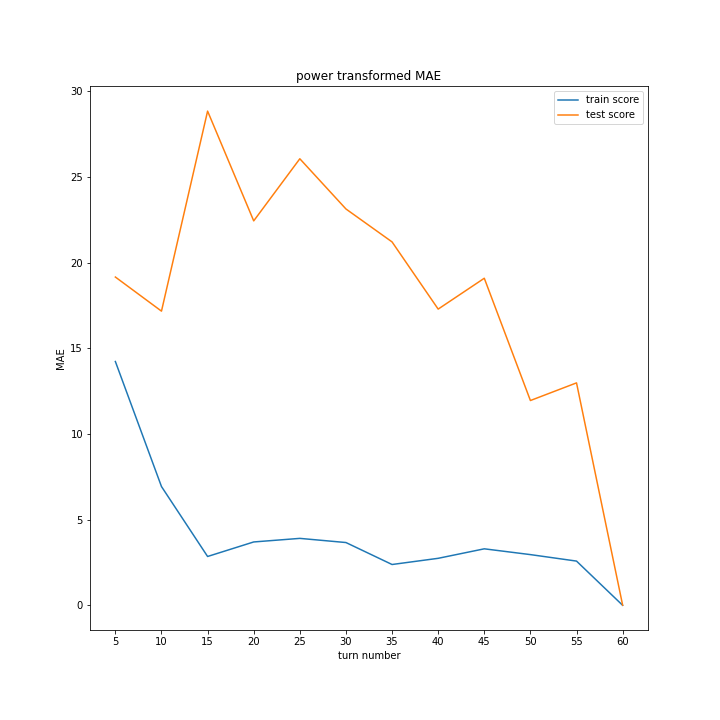
正規化方法ごとにスコアと平均絶対誤差のグラフを作りました。
同じグラフを掲載しているように見えるかもしれませんが別のグラフです。
ほとんど変わらないという結果になりました。
まとめ
改善案2の時と比べ精度が下がる結果になったため、今回の場合、正規化は逆効果であると分かりました。
改善案4
正規化を行わず、インスタンス作成時に与えるパラメータを調整することで精度の向上を図ります。
データ集めのプログラムについては例のごとく省略します。
各方法でターン数ごとに学習を行い、その平均絶対誤差を方法ごとに平均し比較します。
スコアを調べてなかったのは、今回の場合平均絶対誤差の方が直感的でわかりやすいと考えたためです。
alpha
公式サイト読んだんですがよく分かりませんでした。
とりあえず0.1~20でやってみたいと思います。
デフォルト値は1.0です。
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error
from sklearn.linear_model import Ridge
x_data = df.drop(["turn", "last_score"], axis=1)
y_data = df[["turn_num", "last_score"]]
turn_vari = df["turn_num"].unique()
################################
def two_plot(x, y, xlabel, ylabel, title, save_dir):
fig = plt.figure(figsize=(10, 10))
plt.plot(x, y[0], label="train MAE")
plt.plot(x, y[1], label="test MAE")
plt.minorticks_on()
plt.grid(which="major")
plt.grid(which="minor", linestyle="--")
plt.title(title)
plt.xlabel(xlabel)
plt.ylabel(ylabel)
plt.legend()
plt.savefig(save_dir + "/" + title)
plt.clf()
plt.close()
################################
alpha_arr = [i * 0.1 for i in range(1, 10)] + [i for i in range(1, 31)]
train_MAE = []
test_MAE = []
for alpha in alpha_arr:
train_MAE.append([])
test_MAE.append([])
for turn_num in turn_vari:
x_train, x_test, y_train, y_test = train_test_split(\
x_data.query("turn_num==%d" % turn_num).drop("turn_num", axis=1),
y_data.query("turn_num==%d" % turn_num).drop("turn_num", axis=1),
random_state=0
)
model = Ridge(alpha=alpha, random_state=0)
model.fit(x_train, y_train)
train_predict = model.predict(x_train)
train_MAE[-1].append(mean_absolute_error(train_predict, y_train))
test_predict = model.predict(x_test)
test_MAE[-1].append(mean_absolute_error(test_predict, y_test))
train_MAE = np.array(train_MAE)
test_MAE = np.array(test_MAE)
y_MAE = [[], []]
for i in range(len(train_MAE)):
y_MAE[0].append(train_MAE[i].mean())
y_MAE[1].append(test_MAE[i].mean())
two_plot(alpha_arr, y_MAE, "alpha", "MAE", "MAE each alpha", "fig")
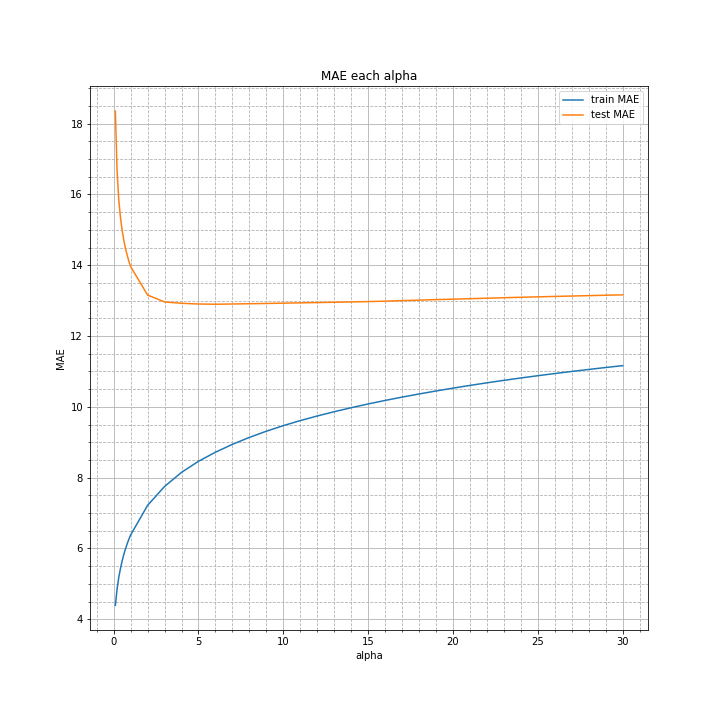
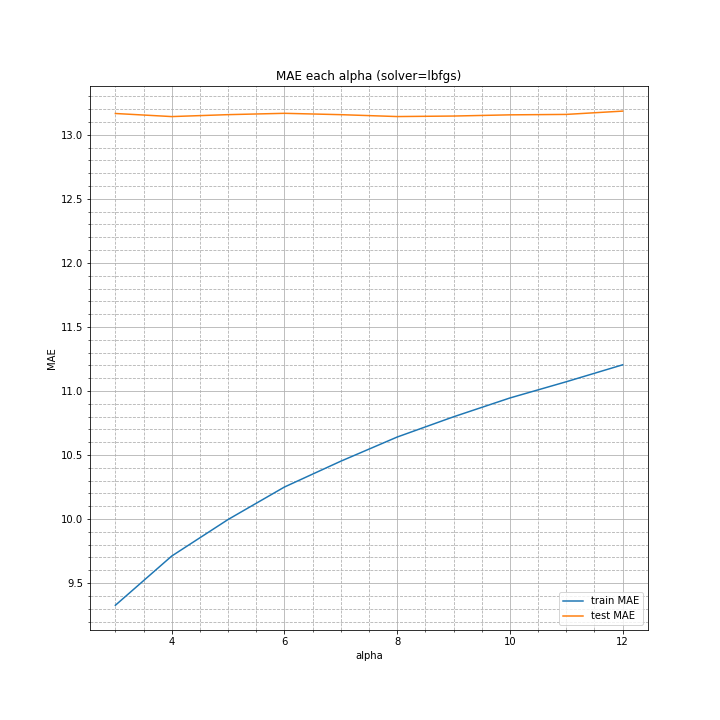
alphaが極端に小さいと過学習を起こし、大きすぎても誤差が大きくなる結果となりました。テストデータの平均絶対誤差が最も小さかったのは3~12ほどの区間でした。
max_iter
学習プログラムは上のalphaとほぼ同じなので省略します。
まさかの全く変化なしという結果に。
tol
max_iter同様全く変化なし。
solver
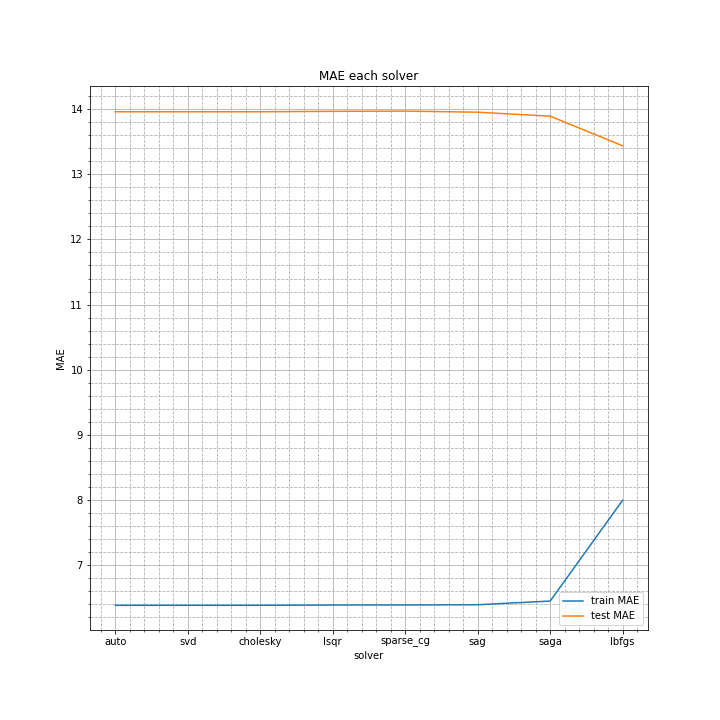
本当は棒グラフにすべきだと思ったのですが、これだけなのでサボりました。
lbfgsが最も良い結果になりましたが、そのほかはほぼ同じ。
総合
上の検証で、誤差の小さいパラメータ範囲が分かりましたので、今度はそれらを総当たりで、最も効果の高いパラメータを探します。
といってもsolverをlbfgsで固定し、alphaを3~12の範囲で調べます。
僅差ですが、テストデータの誤差の最小値はalpha=4の時となりました。
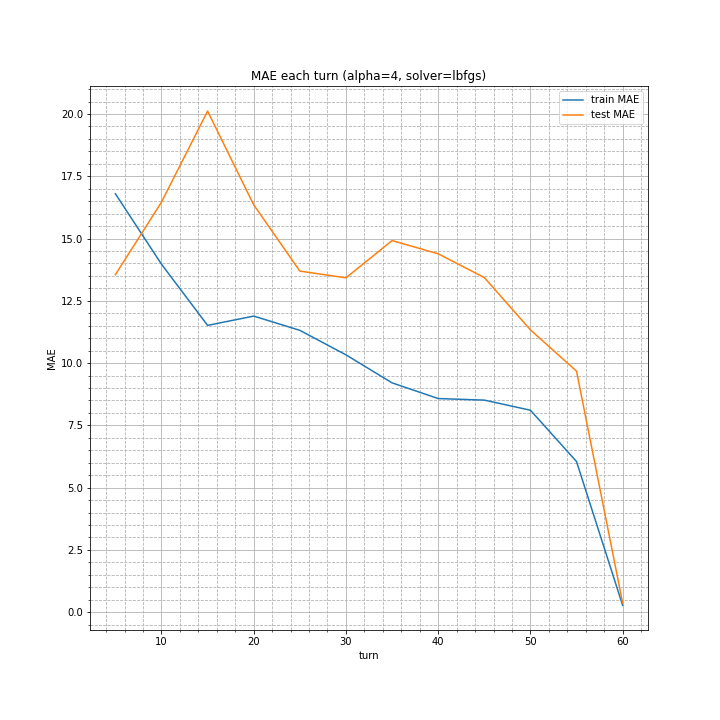
alpha=4, solver=lbfgsの条件で、各ターン数ごとの平均絶対誤差を調べました。
今までよりは改善されていますが、あと一息という感じですね。
まとめ
alpha=4, solver=lbfgsを指定することで精度は向上しました。
しかしまだあまり正確ではありません。
改善案5
ランダムフォレストから着想を得て、複数の条件で学習したRidgeから多数決をとる手法を考えました。
solverはlbfgsで固定し、alphaを3~12の範囲で調べ、その十個の予測値を用います。
データ集めのプログラムはこれまで通りです。
なおここでは、テストデータの平均絶対誤差でモデルの良し悪しを評価します。
平均案
まず、出てきた十個の数字の平均を予測値とする案を考えました。
プログラムは以下の通り。
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error
from sklearn.linear_model import Ridge
x_data = df.drop(["turn", "last_score"], axis=1)
y_data = df[["turn_num", "last_score"]]
turn_vari = df["turn_num"].unique()
################################
def two_plot(x, y, xlabel, ylabel, title, save_dir):
fig = plt.figure(figsize=(10, 10))
plt.plot(x, y[0], label="train MAE")
plt.plot(x, y[1], label="test MAE")
plt.minorticks_on()
plt.grid(which="major")
plt.grid(which="minor", linestyle="--")
plt.title(title)
plt.xlabel(xlabel)
plt.ylabel(ylabel)
plt.legend()
plt.savefig(save_dir + "/" + title)
plt.clf()
plt.close()
################################
model = []
alpha_arr = [i for i in range(3, 13)]
train_MAE = []
test_MAE = []
for turn_num in turn_vari:
model.append([])
for alpha in alpha_arr:
x_train, x_test, y_train, y_test = train_test_split(\
x_data.query("turn_num==%d" % turn_num).drop("turn_num", axis=1),
y_data.query("turn_num==%d" % turn_num).drop("turn_num", axis=1),
random_state=0
)
model[-1].append(Ridge(\
alpha=alpha,
solver="lbfgs",
positive=True,
random_state=0
))
model[-1][-1].fit(x_train, y_train)
if alpha == alpha_arr[0]:
train_predict = model[-1][-1].predict(x_train)
test_predict = model[-1][-1].predict(x_test)
else:
train_predict += model[-1][-1].predict(x_train)
test_predict += model[-1][-1].predict(x_test)
train_predict = train_predict / len(alpha_arr)
test_predict = test_predict / len(alpha_arr)
train_MAE.append(mean_absolute_error(train_predict, y_train))
test_MAE.append(mean_absolute_error(test_predict, y_test))
two_plot(turn_vari, [train_MAE, test_MAE], "turn", "MAE", "MAE of mean", "fig")
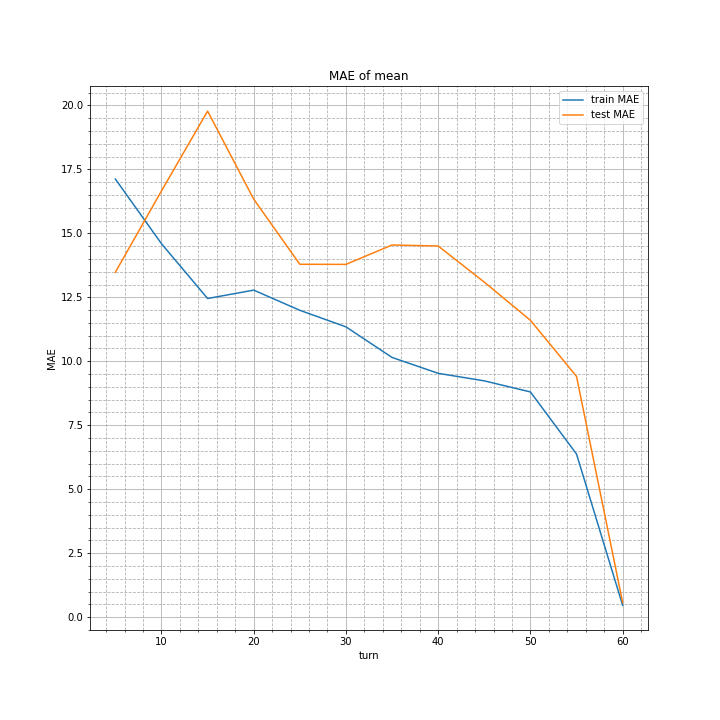
実行結果は以下の通り。
改善案4の最後に示したグラフと比べると、よく見れば1程度誤差が小さくなっているターン数があります。
しかし劇的に精度が上がったりはしていません。
最頻値案
十個の数字を四捨五入し、最頻値を予測値とする案を考えました。
model = []
alpha_arr = [i for i in range(3, 13)]
train_MAE = []
test_MAE = []
for turn_num in turn_vari:
train_predict = []
test_predict = []
model.append([])
for alpha in alpha_arr:
x_train, x_test, y_train, y_test = train_test_split(\
x_data.query("turn_num==%d" % turn_num).drop("turn_num", axis=1),
y_data.query("turn_num==%d" % turn_num).drop("turn_num", axis=1),
random_state=0
)
model[-1].append(Ridge(\
alpha=alpha,
solver="lbfgs",
positive=True,
random_state=0
))
model[-1][-1].fit(x_train, y_train)
train_predict.append(np.array(model[-1][-1].predict(x_train)))
test_predict.append(np.array(model[-1][-1].predict(x_test)))
train_predict = np.array(train_predict, dtype=np.int32).T
test_predict = np.array(test_predict, dtype=np.int32).T
for i in range(len(alpha_arr)):
for j in range(len(train_predict[0][i])):
train_predict[0][i][j] = np.round(train_predict[0][i][j])
for j in range(len(test_predict[0][i])):
test_predict[0][i][j] = np.round(test_predict[0][i][j])
train_predict_mode = []
test_predict_mode = []
for i in range(len(x_train)):
discard, unique = np.unique(train_predict[0][i], return_counts=True)
train_predict_mode.append(np.argmax(unique))
for i in range(len(x_test)):
discard, unique = np.unique(test_predict[0][i], return_counts=True)
test_predict_mode.append(np.argmax(unique))
train_MAE.append(mean_absolute_error(train_predict_mode, y_train))
test_MAE.append(mean_absolute_error(test_predict_mode, y_test))
two_plot(turn_vari, [train_MAE, test_MAE], "turn", "MAE", "MAE of mode", "fig")
プログラムの途中で「[0][i][j]」などが出てくるのは、逆行列を求めるとなぜか三次元配列で返ってくるからです。
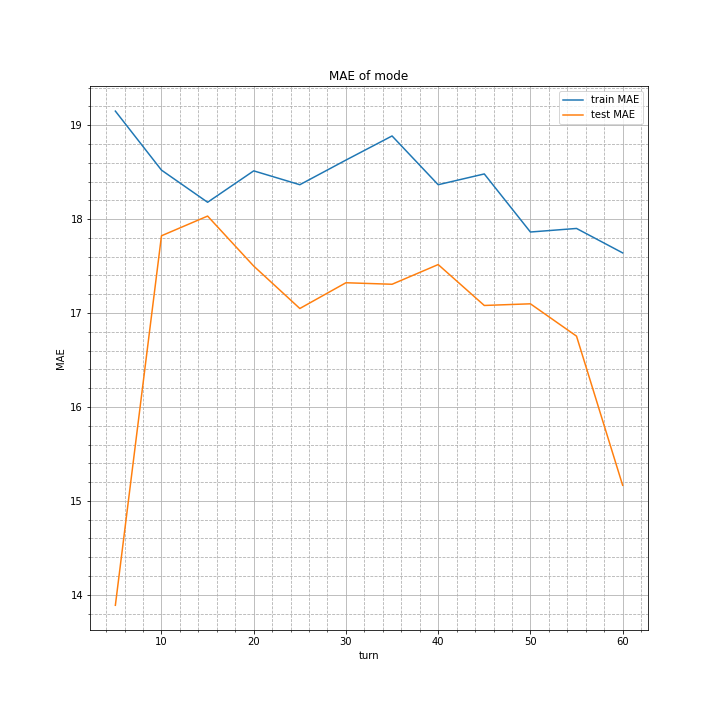
実行結果はこちら。
理由は分かりませんが、テスト時の誤差がトレーニングデータでの誤差を下回る結果に。
さらに、5ターン目での予測がなぜか正確になっており、14以下。
もっと不思議なのは60ターンでの予測の精度が非常に低いことです。
総合的に平均案と比べると、20ターン以前は最頻値の方が誤差が小さく、逆に25ターン以降は平均値の誤差が小さくなりました。
平均値案が全体的にalpha=4, solver=lbfgsの結果と変わらなかったことから、「結局alphaを変えても出てくる値はあまり変わらないのでは?」という懸念がありましたが、最頻値案が全く違う形のグラフを作ったのでそうでもないようです。
しかしalpha=4と固定した時も平均値案も60ターン目の精度が非常に高く出ていたのに、最頻値案で急に下がったのは不思議です。
トレーニングデータの誤差がテストデータの誤差を上回ったことに関してもよく分かりません。
面白いデータは取れましたが、どうしていいか分からないのが正直なところです。
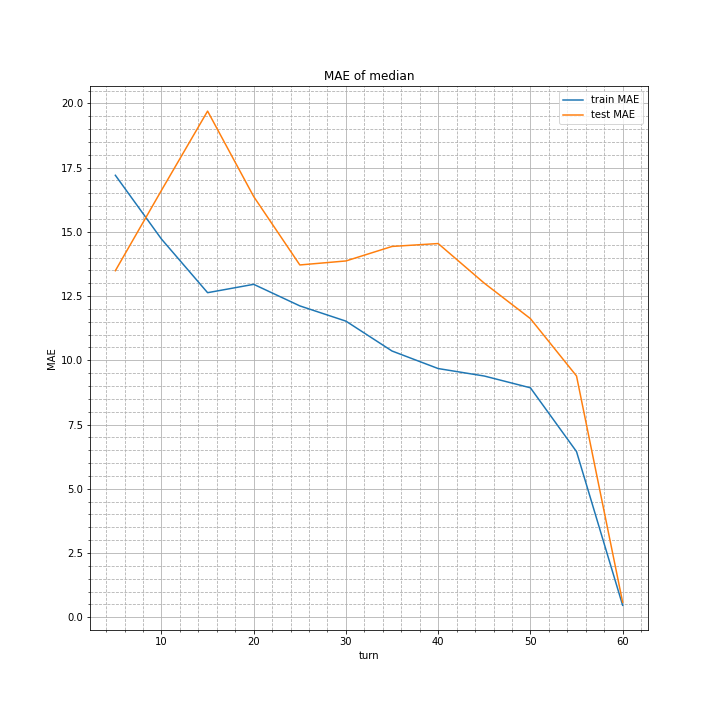
中央値案
alphaごとの結果をソートし、その中央値を予測値として誤差を計算してみました。
model = []
alpha_arr = [i for i in range(3, 13)]
center = len(alpha_arr) // 2
train_MAE = []
test_MAE = []
for turn_num in turn_vari:
train_predict = []
test_predict = []
model.append([])
for alpha in alpha_arr:
x_train, x_test, y_train, y_test = train_test_split(\
x_data.query("turn_num==%d" % turn_num).drop("turn_num", axis=1),
y_data.query("turn_num==%d" % turn_num).drop("turn_num", axis=1),
random_state=0
)
model[-1].append(Ridge(\
alpha=alpha,
solver="lbfgs",
positive=True,
random_state=0
))
model[-1][-1].fit(x_train, y_train)
train_predict.append(model[-1][-1].predict(x_train))
test_predict.append(model[-1][-1].predict(x_test))
train_predict = np.array(train_predict).T
test_predict = np.array(test_predict).T
train_predict_median = []
test_predict_median = []
for i in range(len(x_train)):
sorted = np.sort(train_predict[0][i])
train_predict_median.append(sorted[center])
for i in range(len(x_test)):
sorted = np.sort(test_predict[0][i])
test_predict_median.append(sorted[center])
train_MAE.append(mean_absolute_error(train_predict_median, y_train))
test_MAE.append(mean_absolute_error(test_predict_median, y_test))
two_plot(turn_vari, [train_MAE, test_MAE], "turn", "MAE", "MAE of median", "fig")
結果はこちら。
平均案とほぼ変わりません。
しいて言えば、ターン数30の時の誤差が0.2ほど増えています。
ここから言えるのは、平均値と中央値はほぼ一致するが、最頻値はこの限りではないということです。つまりalphaを変えた時の予測値分布は正規分布に従わず、中央値付近に谷を作るような二つの山からなっているのではないでしょうか。
目的変数(最終的な自分の駒の数-相手の駒の数)は0を中心とした分布をとるはずなので、接戦や引き分けになることは少ないということでしょうか。
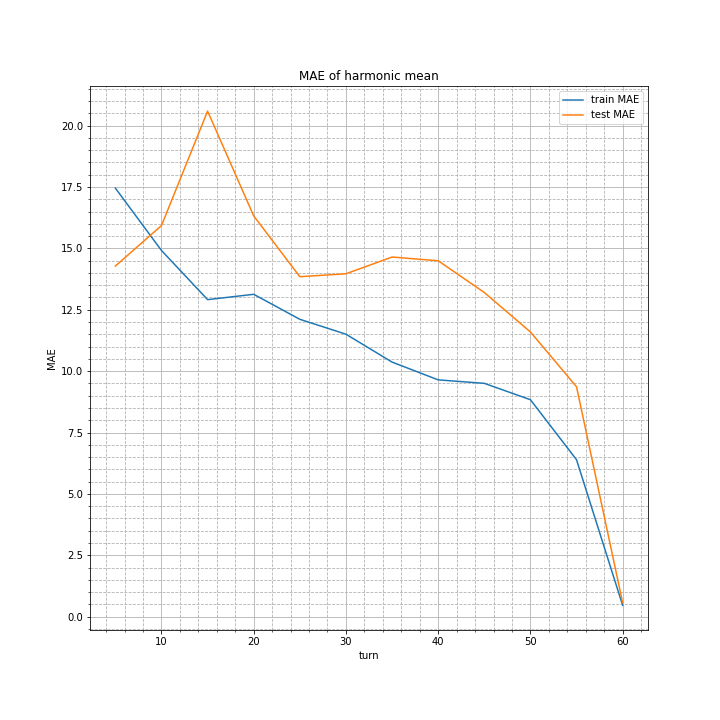
調和平均案
意味があるかどうかは分かりませんが、様々な学習で得られた値を、算術平均ではなく調和平均でまとめてそれを予測値として考えてみます。
幾何平均を用いない理由は、前述の通り目的変数が負の値をとったり正の値をとったりするため、幾何平均は明らかに有効ではないと考えられるためです。また、掛け算結果が負になれば計算できないためです。加重平均に関しては適切な荷重が分からないという理由です。
model = []
alpha_arr = [i for i in range(3, 13)]
train_MAE = []
test_MAE = []
for turn_num in turn_vari:
model.append([])
for alpha in alpha_arr:
x_train, x_test, y_train, y_test = train_test_split(\
x_data.query("turn_num==%d" % turn_num).drop("turn_num", axis=1),
y_data.query("turn_num==%d" % turn_num).drop("turn_num", axis=1),
random_state=0
)
model[-1].append(Ridge(\
alpha=alpha,
solver="lbfgs",
positive=True,
random_state=0
))
model[-1][-1].fit(x_train, y_train)
if alpha == alpha_arr[0]:
train_predict = 1 / model[-1][-1].predict(x_train)
test_predict = 1 / model[-1][-1].predict(x_test)
else:
train_predict += 1 / model[-1][-1].predict(x_train)
test_predict += 1 / model[-1][-1].predict(x_test)
train_predict = len(alpha_arr) / train_predict
test_predict = len(alpha_arr) / test_predict
train_MAE.append(mean_absolute_error(train_predict, y_train))
test_MAE.append(mean_absolute_error(test_predict, y_test))
two_plot(turn_vari, [train_MAE, test_MAE], "turn", "MAE", "MAE of harmonic mean", "fig")
学習結果はこちら。
算術平均と比較すると、10ターンでの誤差はやや小さくなっていますが、15ターンでの誤差は大きくなっています。
しかし意外にもその他に関してはほぼ変わらない結果でした。
加重平均
先ほど「加重平均は適切な加重が判断できないため行わない」と書きましたが、局所探索法を用いて誤差が小さくなる重みを探しました。
プログラムでの実装は、まず学習データとそれぞれのalphaでの学習後の予測値を保存します。その後、局所探索法を用いて最適な重みを探し更新していきます。
# weighted mean 1
# make predict data
from random import random, seed
from copy import deepcopy
alpha_arr = [i for i in range(3, 13)]
train_predict = []
test_predict = []
x_train = []
x_test = []
y_train = []
y_test = []
for turn_num in turn_vari:
train_predict.append([])
test_predict.append([])
x_train_ele, x_test_ele, y_train_ele, y_test_ele = train_test_split(\
x_data.query("turn_num==%d" % turn_num).drop("turn_num", axis=1),
y_data.query("turn_num==%d" % turn_num).drop("turn_num", axis=1),
random_state=0
)
x_train.append(x_train_ele)
x_test.append(x_test_ele)
y_train.append(y_train_ele)
y_test.append(y_test_ele)
for alpha in alpha_arr:
model = Ridge(\
alpha=alpha,
solver="lbfgs",
positive=True,
random_state=0
)
model.fit(x_train_ele, y_train_ele)
train_predict[-1].append(model.predict(x_train_ele))
test_predict[-1].append(model.predict(x_test_ele))
# weighted mean 2
# local search
GENERATION = 100
CHILDLEN = 30
seed(0)
weight = [random() for i in range(len(alpha_arr))]
min_MAE = 0xffff
for generation in range(GENERATION):
seed(generation)
print("\r%4d/%4d MAE: %d" % (generation + 1, GENERATION, min_MAE), end="")
for child in range(CHILDLEN):
train_predict_keep = []
test_predict_keep = []
train_MAE_sum = 0
test_MAE_sum = 0
weight_candi = deepcopy(weight)
for i in range(len(weight_candi)):
weight_candi[i] += (0.5 - random()) / 2
for i in range(len(turn_vari)):
for j in range(len(alpha_arr)):
train_predict_weight = np.array([0] * len(train_predict[i][j]))
test_predict_weight = np.array([0] * len(test_predict[i][j]))
for k in range(len(train_predict_weight)):
train_predict_weight[k] += train_predict[i][j][k] * weight_candi[j]
for k in range(len(test_predict_weight)):
test_predict_weight[k] += test_predict[i][j][k] * weight_candi[j]
train_predict_weight = train_predict_weight / sum(weight_candi)
test_predict_weight = test_predict_weight / sum(weight_candi)
train_predict_keep.append(train_predict_weight)
test_predict_keep.append(test_predict_weight)
train_MAE_sum += mean_absolute_error(train_predict_weight, y_train[i])
test_MAE_sum += mean_absolute_error(test_predict_weight, y_test[i])
if test_MAE_sum < min_MAE and generation != GENERATION - 1:
min_MAE = test_MAE_sum
train_predict_ans = deepcopy(train_predict_keep)
test_predict_ans = deepcopy(test_predict_keep)
weight_next = deepcopy(weight_candi)
weight = deepcopy(weight_next)
# weighted mean 3
# make diagram
train_MAE = []
test_MAE = []
for i in range(len(turn_vari)):
train_MAE.append(mean_absolute_error(train_predict_ans[i], y_train[i]))
test_MAE.append(mean_absolute_error(test_predict_ans[i], y_test[i]))
two_plot(
turn_vari,
[train_MAE, test_MAE],
"turn",
"MAE",
"MAE of weighted mean (max generation is %d)" % GENERATION,
"fig"
)
# weighted mean 4
# output result
print(weight)
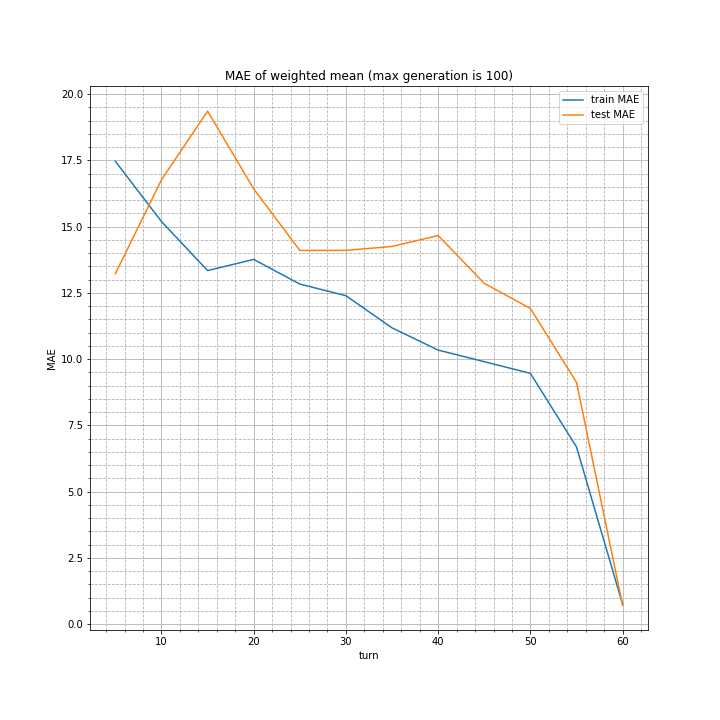
実行結果はこちら。
算術平均とほぼ変わらない結果になりました。
また、weightは以下の通り。
[-0.1064985666709149, 0.3163889075346738, -0.10411753741468255, -0.8111324426281548, 0.22063493037623882,
0.1415032823705678, -0.3051317188273051, 0.06266523938940216, 0.5196314675991498, 0.8612372013999511]
なお、毎世代で平均絶対誤差を表示させていましたが、十世代ほどで157に到達し、その後全く変わりませんでした。
つまり、そもそもこれ以上精度が出ることはないと考えられます。
まとめ
実装の際の手間と誤差の大きさを考慮すると、算術平均で予測する方法が最も適していると考えました。
また、どうしても最大平均絶対誤差は20近くになると分かりました。
フルバージョン
次回は
目標とした制度には達していませんが、今回のモデルを用いてAIオセロを実際に作りたいと思います。