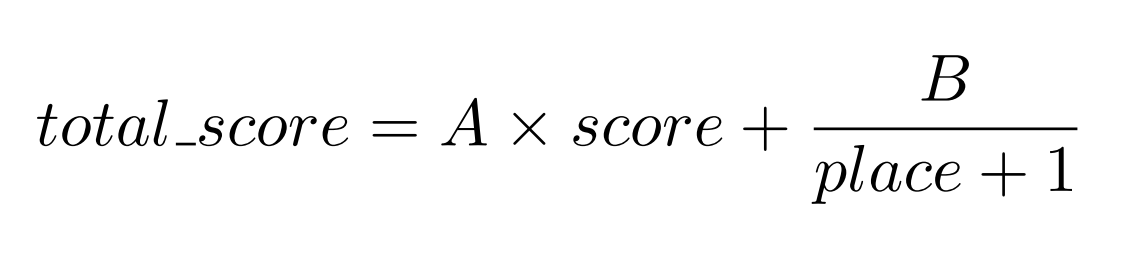今回の目標
前回作成したニューラルネットワークを用いて、新しい構想でのAIを作成する。
ここから本編
前回も説明した通り、新しく作るAIは、今までのAIの考え方とnleastを融合させます。
つまり、
- 深層学習モデルを用いて、現在の盤面から最終結果を予測する
- 深さ優先探索を用いて、先のターンで相手がとれる手数を得る
という二つの動作を行い、そして、得られた予測値と手数から総合的な「勝利係数」を計算し、その結果が最も高い位置に置くという考え方をします。
計算方法は以下の通りです。
ここで、
- total_score 計算結果(勝利係数)
- score 予測した最終結果(最終的な自分の駒の数-相手の駒の数)
- place 相手がとれる手数
- A, B 任意定数
予測した最終結果が大きいほど、また、相手がとれる手数が少ないほどより勝利しやすいと予測します。ここで、AとBの係数を適切なものに変えることで強いAIが作れると考えました。
今回はこの適切なAとBを、局所探索法を用いて求めることを目標とします。
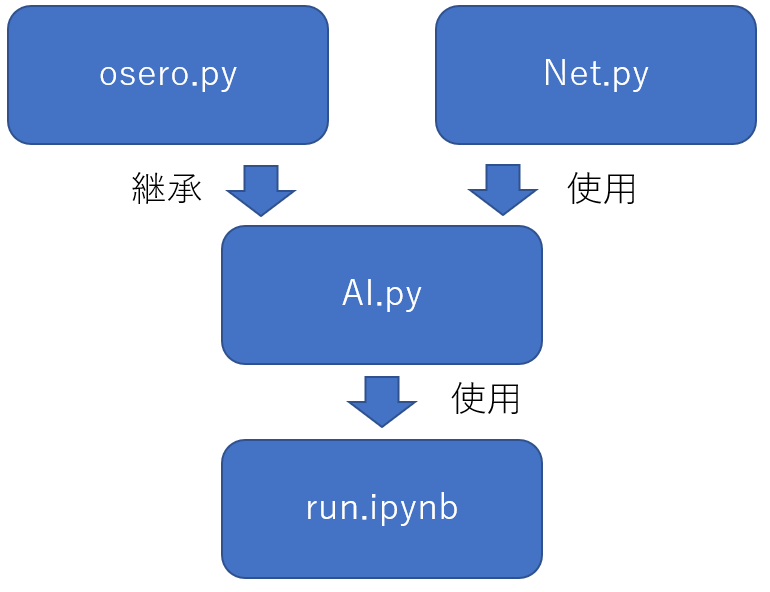
今回使用したPythonのクラス構造は以下の通りです。
- osero.py オセロをするための基本クラス
- Net.py ニューラルネットワークを定義したクラス
- AI.py 人工知能でオセロをプレイするためのクラス
- run.ipynb 実行ファイル
また、今回からファイル名とクラス名を同じにしました。
osero.py
今までのBitBoard.pyと同様です。
本質ではないのでここでは説明を省略します。
Net.py
ニューラルネットワークです。前回用いたものと全く同じです。
import chainer.links as L
import chainer.functions as F
from chainer import Chain
n_multi = 1
func = F.tanh
class Net(Chain):
def __init__(self):
n_in = 192
n_hidden = 192
n_out = 1
super().__init__()
with self.init_scope():
self.l1 = L.Linear(n_in, n_hidden)
self.l2 = L.Linear(n_hidden, n_hidden)
self.l3 = L.Linear(n_hidden, n_hidden)
self.l4 = L.Linear(n_hidden, n_out)
def __call__(self, x):
h = n_multi * func(self.l1(x))
h = n_multi * func(self.l2(h))
h = n_multi * func(self.l3(h))
h = self.l4(h)
return h
AI.py
人工知能でオセロをプレイするためのクラス。
from copy import deepcopy
from random import randint
from chainer.serializers import load_npz
import numpy as np
import osero
import Net
コンストラクタ
オセロの思考方法にAIを追加し、AとBを仮に決定しています。
model_loadメソッドは後述。
class AI(osero.osero):
def __init__(self, black_method, white_method, seed_num=0,
read_goal=[1, 1], eva=[0, 0], model_name="model.net"):
super().__init__(black_method, white_method, seed_num,
read_goal, eva)
self.PLAY_WAY["AI"] = len(self.PLAY_WAY)
self.think.append(self.AI)
self.model_name = model_name
self.A = 1
self.B = 1
self.model_load()
model_load
前回保存しておいたニューラルネットワークを呼び出します。
def model_load(self) -> None:
self.model = Net.Net()
load_npz(self.model_name, self.model)
dict_to_ndarray
現在の盤面を、ニューラルネットワークに投げられる形(numpy.ndarray)に変換します。
このメソッドは直接run.ipynbなどで使うためのものではなく、後述するメソッド内でのみ使用します。
def dict_to_ndarray(self, now: dict) -> np.array:
data = []
if self.turn:
my = ["b_u", "b_d"]
opp = ["w_u", "w_d"]
else:
opp = ["b_u", "b_d"]
my = ["w_u", "w_d"]
for i in range(2):
for j in range(32):
if self.bw[my[i]] & 1 << j:
data.append(1)
data.append(0)
data.append(0)
elif self.bw[opp[i]] & 1 << j:
data.append(0)
data.append(1)
data.append(0)
else:
data.append(0)
data.append(0)
data.append(1)
return np.array([data], dtype=np.float32)
predict
ニューラルネットワークに説明変数を投げ、結果を返すメソッド。
こちらも直接ではなく、後述するメソッド内でのみ利用しています。
def predict(self, now: dict) -> float:
now = self.dict_to_ndarray(now)
ans = self.model(now)
return float(ans.array)
AI
上述した思考を行うメソッドです。なおこのメソッドは、oseroクラスのcheckメソッドにより、最低一か所は置ける場所があることを確認したうえでしか呼び出されません。
cal_score_placeメソッドは盤面から予測値及び相手の手数をもらえるメソッドだと思ってください。
もらった予測値及び相手の手数にAとBを噛ませ、その結果が最も大きくなる位置に石を置きます。
アルゴリズムを説明すると、
- すべての場所について、置けるかどうか調べる
- すべての置ける場所について、予測値及び相手の手数をもらい、勝利係数を計算する。
- 勝利係数が最も大きい位置に石を置く。同じ値が複数出た場合はランダムでどれかに置く。
def AI(self) -> None:
min_total_score = -0xffff
line_ans, col_ans = [-1], [-1]
place_num = 0
for i in range(8):
for j in range(8):
if not self.check(i, j, self.bw, self.turn):
continue
board_leaf = deepcopy(self.bw)
self.put(i, j, board_leaf, self.turn)
score, place = self.cal_score_place(\
board_leaf,
not self.turn,
not self.turn,
1
)
total_score = self.A * score + self.B / (place + 1)
if total_score > min_total_score:
min_total_score = total_score
place_num = 0
line_ans = [i]
col_ans = [j]
elif total_score == min_total_score:
line_ans.append(i)
col_ans.append(j)
place_num += 1
if place_num:
place_num = randint(0, place_num)
line_ans[0] = line_ans[place_num]
col_ans[0] = col_ans[place_num]
self.put(line_ans[0], col_ans[0], self.bw, self.turn)
cal_score_place
盤面から予測値及び相手の手数をもらえるメソッド。
あらかじめread_goalで指定しておいたターン数だけ先まで調べ、その位置での予測値と相手の手数の平均を返します。
今回read_goalは1を指定するため、自分が置いた後に相手が置くターンで、予測値がどうなるか、また、そのときの相手の手数を返します。
簡単に関数の流れについて解説します。
def cal_score_place(self, now: dict, turn: bool,\
tar_turn: bool, num: int) -> tuple:
place_num = 0
if turn == tar_turn:
if num == self.read_goal[self.turn]:
for i in range(8):
for j in range(8):
if self.check(i, j, now, turn):
place_num += 1
score = self.predict(now)
return score, place_num
else:
score_sum = 0
place_sum = 0
for i in range(8):
for j in range(8):
if not self.check(i, j, now, turn):
continue
board_leaf = deepcopy(now)
self.put(i, j, board_leaf, turn)
score, place = self.cal_score_place(\
board_leaf,
not turn,
tar_turn,
num + 1
)
score_sum += score
place_sum += place
place_num += 1
if place_num:
return score_sum / place_num, place_sum / place_num
else:
return 0, 0
else:
score_sum = 0
place_sum = 0
for i in range(8):
for j in range(8):
if not self.check(i, j, now, turn):
continue
board_leaf = deepcopy(now)
self.put(i, j, board_leaf, turn)
score, place = self.cal_score_place(\
board_leaf,
not turn,
tar_turn,
num
)
score_sum += score
place_sum += place
place_num += 1
if place_num:
return score_sum / place_num, place_sum / place_num
else:
return self.cal_score_place(\
deepcopy(now),
not turn,
tar_turn,
num
)
count_last
最終結果を返します。
def count_last(self) -> int:
black = self.popcount(self.bw["b_u"])\
+ self.popcount(self.bw["b_d"])
white = self.popcount(self.bw["w_u"])\
+ self.popcount(self.bw["w_d"])
return black - white
play
オセロをプレイし最終結果を返します。
両プレイヤーが置ける場所がなくなった時点でゲームは終了します。こうすることで以下に示すオセロの終了条件をすべて満たします。
- 盤面がすべて埋まる
- 片陣営の石の個数が0になる
- 上のどちらの状況でもないが、両プレイヤーともに置ける場所がない
def play(self) -> int:
can, old_can = True, True
can = self.check_all()
while can or old_can:
if can:
if self.turn:
self.think[self.black_method]()
else:
self.think[self.white_method]()
self.turn = not self.turn
old_can = can
can = self.check_all()
return self.count_last()
run.ipynb
from random import random, seed
import matplotlib.pyplot as plt
import AI
01 もっともよい結果だけ次世代へつなぐ
上述したクラスを用いて最適なA、Bを探します。
そのアルゴリズムを説明します。
- 10通りのA、Bをランダムに作成する。
- そのA、Bに従うAIとnleastで二試合行う(黒側と白側をそれぞれ一回ずつ)。
- 二試合総合で、最も大差で勝利したA、Bをわずかに変化させて次世代のA、Bとする(3%の確率で突然変異)。
- 以下、指定した世代数まで繰り返し
また、ついでに各世代ごとの勝利数を記録しておきます。
run = AI.AI(0, 0)
run.read_goal = [1, 1]
play_method = {"AI": run.PLAY_WAY["AI"], "nleast": run.PLAY_WAY["nleast"]}
################################
seed(0)
generations = 50
children = 10
ab = [[random(), random()] for i in range(children)]
player = list(play_method.values())
win_result = []
score = {"AI": [0] * children, "nleast": [0] * children}
# 各世代
for g in range(generations):
print("\r%d/%d" % (g+1, generations), end="")
score = {"AI": [0] * children, "nleast": [0] * children}
next = 0
win_num = 0
# 各人
for c in range(children):
run.A = ab[c][0]
run.B = ab[c][1]
# 黒と白を入れ替えて二試合
for p in [0, 1]:
run.black_method = player[p]
run.white_method = player[not p]
run.setup()
result = run.play()
if run.black_method == play_method["AI"]:
score["AI"][c] += result
score["nleast"][c] -= result
else:
score["AI"][c] -= result
score["nleast"][c] += result
if score["AI"][c] > score["nleast"][c]:
win_num += 1
if c:
if score["AI"][c] - score["AI"][c-1] > 0:
next = c
# 次世代のA、Bを作成
for c in range(children):
if random() > 0.03:
ab[c][0] = ab[next][0] + random() / 5 - 0.1
ab[c][1] = ab[next][1] + random() / 5 - 0.1
else:
ab[c][0] = random()
ab[c][1] = random()
win_result.append(win_num)
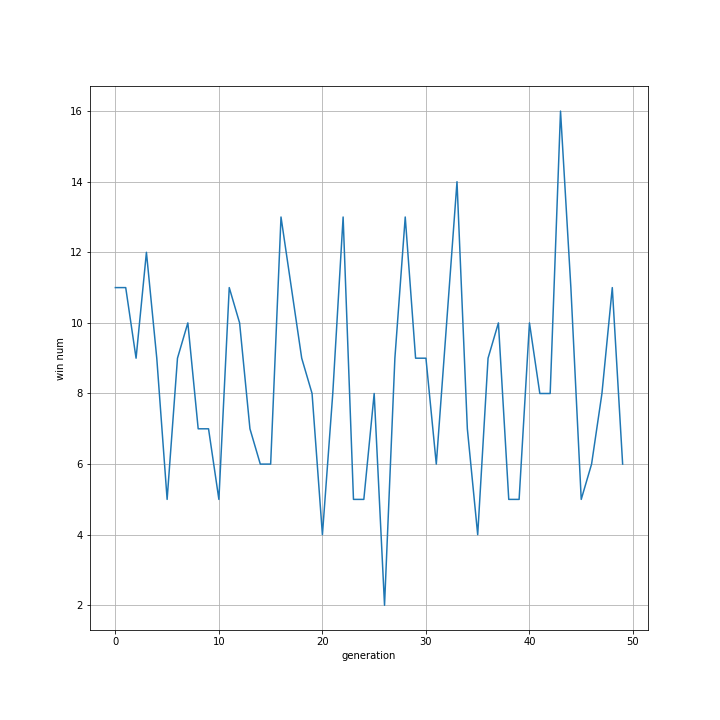
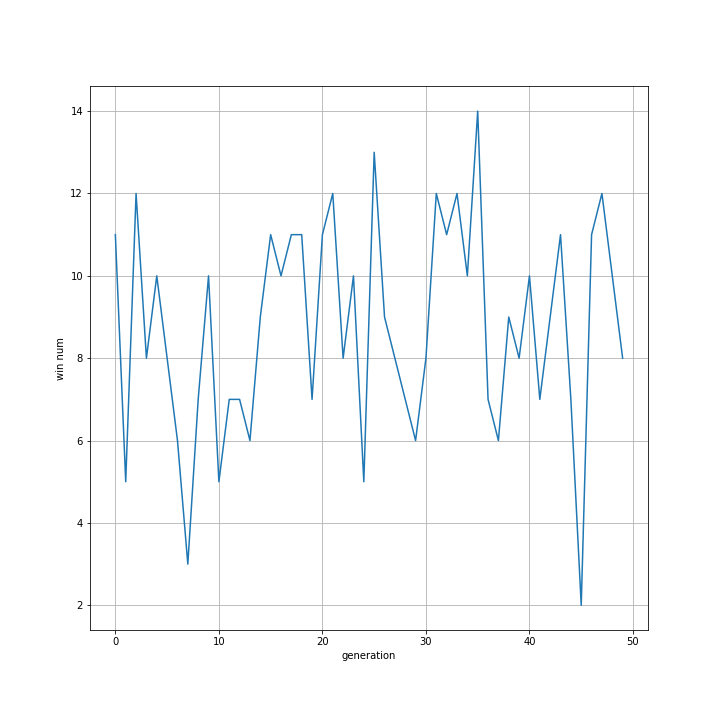
また、世代ごとの勝利回数の推移をグラフ化しました。
fig = plt.figure(figsize=(10, 10))
plt.ylabel("win num")
plt.xlabel("generation")
plt.plot(win_result)
plt.grid()
plt.savefig("fig/01")
plt.clf()
plt.close()
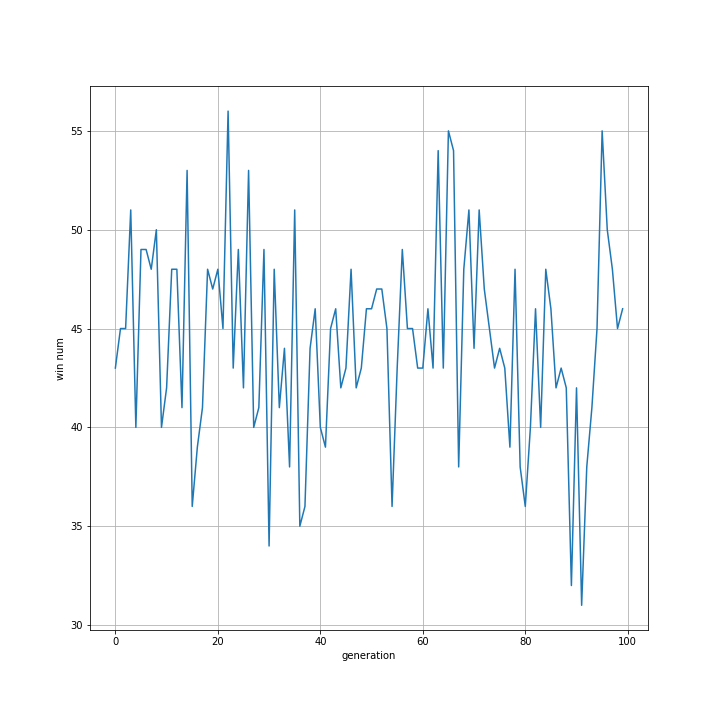
10人の子供で2試合ずつ行うため、1世代ごとの試合数は20です。
見たところ平均9程度なのでnleast相手に善戦してはいることが分かります。
しかしA、Bを少しずつ改善しているはずなので勝利数は世代ごとに高くなっていって欲しかったですが、そうはなっていません。
この方法はあまりよくないことが分かります。
なお、最終的なABは以下のようになっていました。
for ab_ele in ab:
print(ab_ele)
まず、十通りのABです。左がA、右がBです。
[0.23941609547807505, 0.35777572785685996]
[0.2983086249263909, 0.46224661956749136]
[0.1352297881214178, 0.4671043567151586]
[0.174742860019351, 0.47745183099553845]
[0.3091825692112029, 0.49155231282240563]
[0.2667506602754828, 0.5135156230949472]
[0.21879576811512422, 0.346266849934172]
[0.17725439322589046, 0.4149851951459512]
[0.29682016349473106, 0.49624233468089407]
[0.18890073904354618, 0.4371081951750502]
ab_arr = np.array(ab)
ab_arr = ab_arr.T
print(ab_arr[0].mean(), ab_arr[1].mean())
次に、ABそれぞれの平均を計算します。
必然的に前の世代での最優秀とほぼ近い値が出るはずです。
0.23054016619112122 0.4464249045988469
02 もっともよい結果と二番目の結果を次世代につなぐ
もっともよい結果のみを次世代につなぐのは局所解に陥りやすいと考え、もっともよいけっかだけでなく二番目によかった結果も次世代につないでみました。
プログラムについては01のものとほぼ同様であるため省略します。
こちらも01と同様に勝率は向上しませんでした。
最終的なABはこちら。
[0.4366761413226924, 0.363847389968887]
[0.585117759367691, 0.3411556111862247]
[0.6215485774727806, 0.3828643590646774]
[0.553811235787369, 0.2539978233561665]
[0.5499046820401436, 0.26588887637728187]
[0.41797605296436946, 0.21303874673399606]
[0.3941538926147179, 0.19443095633810717]
[0.33549869473366334, 0.2621866288286896]
[0.4232687188237969, 0.24411451234083645]
[0.41047338094411434, 0.26471724953187703]
0.4728429136071338 0.2786242153726744
01ではAよりBの方が大きくなっていましたが、こちらでは逆の結果になりました。
もちろんどちらの結果も正しくはないのですが、「一位のみ引き継ぐ」と「一位と二位を引き継ぐ」というほぼ同じ検証で全く違う結果になったことが気になります。
おそらく前世代では二位だった結果が、マイナーチェンジすることにより一位の結果を抜かしたりした結果だと思われます。また、最終結果で似たような数字が並んでいるのは、一位と二位のABが大して変わらないからだと考えられます。結局局所解のような場所から抜け出せないという状態に近そうです。
03 トーナメントで次世代へつなぐ
20 ~遺伝的アルゴリズム、改善~、21 ~データ分析~で示したように、トーナメントは遺伝的アルゴリズムにおいて優秀な選択方法です。
そのため、順位で次世代へつなぐものを決めるのではなくトーナメントで決定することにしました。
ただし、遺伝的アルゴリズムでのトーナメントとは少し異なります。具体的に、十人の子供を二列に並べ、二試合後のスコアをペアで比較します。スコアが優秀だった方はそのまま次の世代に選出、そうでなかった方は優秀だった方の数値を少しずらしたものに変更としました。
具体的には以下のプログラムのとおりです。
seed(0)
generations = 50
children = 10
ab = [[random(), random()] for i in range(children)]
player = list(play_method.values())
win_result = []
score = {"AI": [0] * children, "nleast": [0] * children}
for g in range(generations):
print("\r%d/%d" % (g+1, generations), end="")
score = {"AI": [0] * children, "nleast": [0] * children}
win_num = 0
for c in range(children):
run.A = ab[c][0]
run.B = ab[c][1]
for p in [0, 1]:
run.black_method = player[p]
run.white_method = player[not p]
run.setup()
result = run.play()
if run.black_method == play_method["AI"]:
score["AI"][c] += result
score["nleast"][c] -= result
else:
score["AI"][c] -= result
score["nleast"][c] += result
if score["AI"][c] > score["nleast"][c]:
win_num += 1
if c % 2 == 1:
if random() > 0.03:
if score["AI"][c] > score["AI"][c-1]:
ab[c-1][0] = ab[c][0] + random() / 5 - 0.1
ab[c-1][1] = ab[c][1] + random() / 5 - 0.1
else:
ab[c][0] = ab[c-1][0] + random() / 5 - 0.1
ab[c][1] = ab[c-1][1] + random() / 5 - 0.1
else:
for i in range(2):
ab[c-i][0] = random()
ab[c-i][1] = random()
win_result.append(win_num)
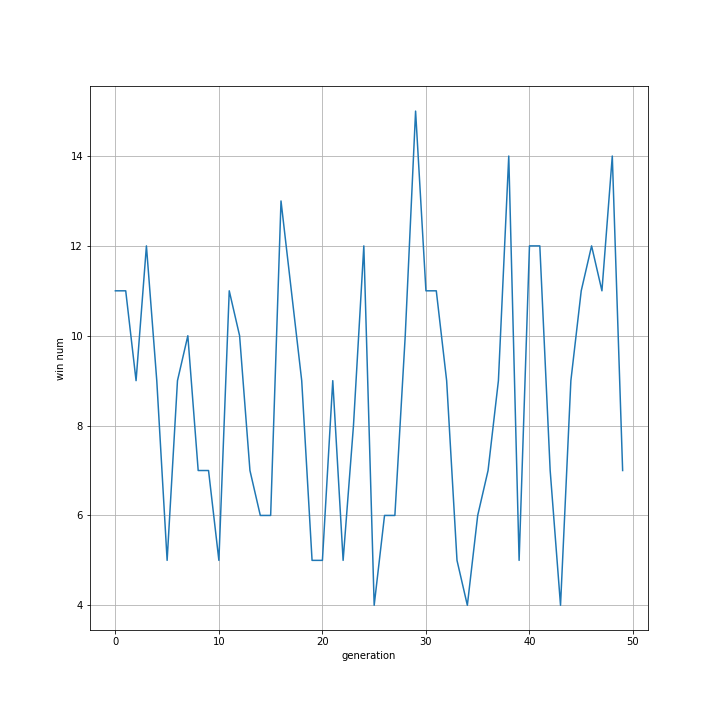
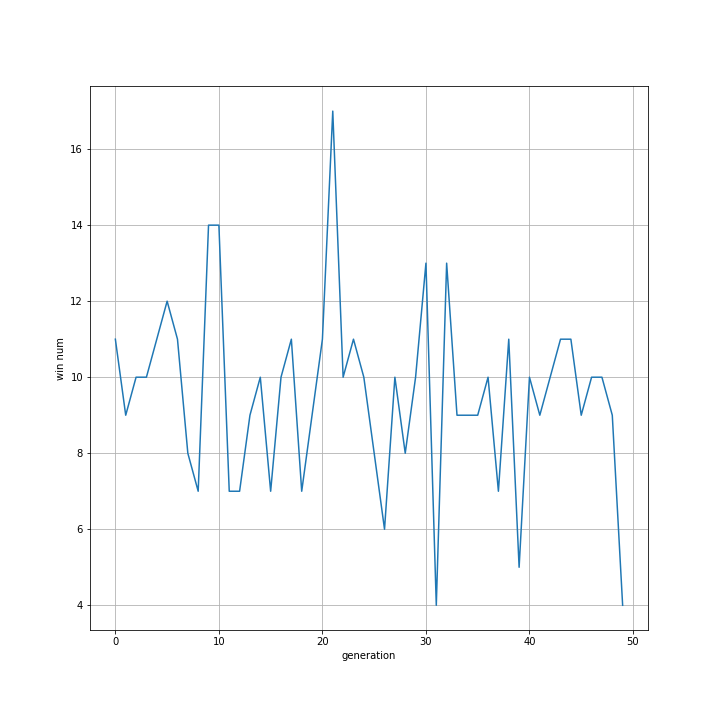
実行結果はこちら。
上二つと同様、勝率の向上は見られませんでした。
[0.1968494642692303, 0.2920115201230645]
[0.26636557320745735, 0.23529047782429022]
[0.5611248560008166, 1.0794628051551478]
[0.5522261667279165, 1.1626702364057204]
[0.3717229051582698, 0.32279192848978777]
[0.4411758976785576, 0.39212233285307596]
[0.2757179482011153, 0.6951279547710917]
[0.1816633111544517, 0.6212004434604531]
[0.49370925535099575, 1.2709043301267027]
[0.5524299023585191, 1.2077682787268995]
0.389298528010733 0.7279350307936234
ABについて、トーナメントですので多様な値が出力されましたが、全体としての勝率は向上していません。
毎回同じペアでスコアの比較・ABの更新を行っていたため、上から順にふたつずつは似たような結果になっています。具体的に、
A: 0.2程度, B: 0.25程度
A: 0.55程度, B: 1.1程度
A: 0.4程度, B: 0.35程度
A: 0.2程度, B: 0.65程度
A: 0.5程度, B: 1.2程度
でした。
この中に最適解がある可能性はありますが、どれなのかは分かりません。
また、一つの解に収束することなくそれぞれで違う進化を遂げたことは意外でした。
04 トーナメント改良
上のトーナメントでは、十人の子供を二列に並べ、常に同じ相手同士でスコアを比較していました。
しかしそれでは全体として向上しづらいことが分かりました。また、ペアを同時に突然変異させてしまうとせっかくうまくいっていたペアを初期化してしまう危険性もあります。
そこで、世代ごとにペアを変え、いろいろな相手とスコアを比較させることで全体の強さを底上げしていくことを考えました。
from random import randint
################################
run = AI.AI(0, 0)
run.read_goal = [1, 1]
play_method = {"AI": run.PLAY_WAY["AI"], "nleast": run.PLAY_WAY["nleast"]}
################################
def key_list():
global children
key = [i for i in range(children)]
key_return = []
while key:
num = randint(0, len(key)-1)
key_return.append(key[num])
del key[num]
return key_return
上に示すkey_list関数を使うことで、0~children-1までの数をランダムに並べた配列を受け取れます。
その番号順に並べてスコアを比較することで、毎回同じ相手と比較することがなくなります。
seed(0)
generations = 50
children = 10
ab = [[random(), random()] for i in range(children)]
player = list(play_method.values())
win_result = []
score = [0] * children
for g in range(generations):
print("\r%d/%d" % (g+1, generations), end="")
score = [0] * children
win_num = 0
for c in range(children):
run.A = ab[c][0]
run.B = ab[c][1]
for p in [0, 1]:
run.black_method = player[p]
run.white_method = player[not p]
run.setup()
result = run.play()
if run.black_method == play_method["AI"]:
score[c] += result
if result > 0:
win_num += 1
else:
score[c] -= result
if result < 0:
win_num += 1
key = key_list()
for i in range(int(len(key) / 2)):
if random() > 0.03:
if score[key[i]] > score[key[(i<<1)+1]]:
ab[key[(i<<1)+1]][0] = ab[key[i<<1]][0] + random() / 5 - 0.1
ab[key[(i<<1)+1]][1] = ab[key[i<<1]][1] + random() / 5 - 0.1
else:
ab[key[i<<1]][0] = ab[key[(i<<1)+1]][0] + random() / 5 - 0.1
ab[key[i<<1]][1] = ab[key[(i<<1)+1]][1] + random() / 5 - 0.1
else:
for j in range(2):
ab[key[i<<1]][j] = random()
ab[key[(i<<1)+1]][j] = random()
win_result.append(win_num)
上に示すプログラムを用いることで、毎回ペアを変えながらトーナメントを行うことができます。
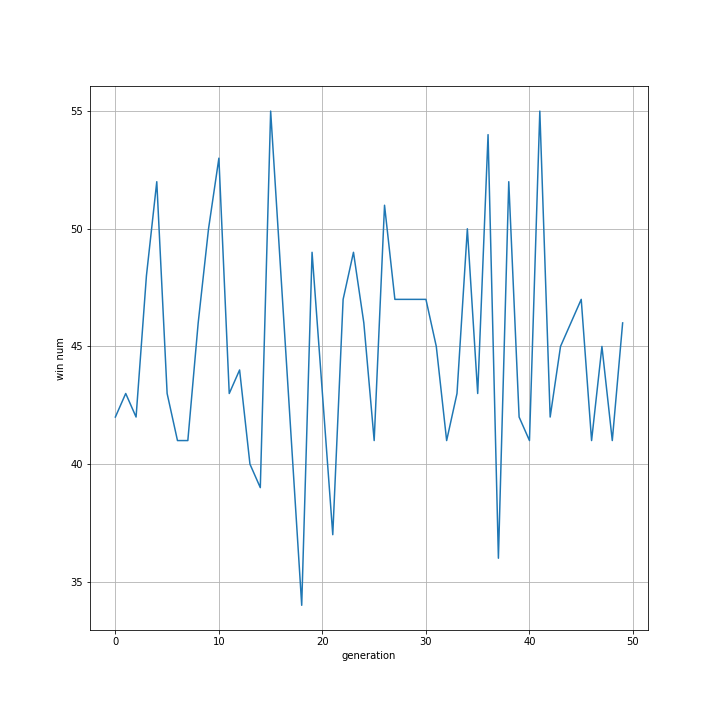
これを実行したときの各世代ごとの勝利数は以下の通りです。
今までよりも平均としての勝率は上がったような気はしますが、それでも向上はしませんでした。
[0.7845317965203, 0.7282481006185132]
[0.887998591216725, 0.7798613691517554]
[0.7539896409299109, 0.5864060138323008]
[0.7994245226477315, 0.6976976619352092]
[0.8580297286849564, 0.7568389384151408]
[0.7436182363961433, 0.64724601430552]
[0.15306714563572918, 0.43333188307689097]
[0.12307210319871517, 0.5095366112833001]
[0.12901552090490803, 0.44081907902404904]
[0.0866980084219135, 0.534229302808782]
0.5319445294557033 0.6114214974451462
ABは想像よりバラエティーに富んだ結果でした。
おおまかに
A: 0.8程度, B: 0.7程度
A: 0.1程度, B: 0.5程度
という二つの結果に分かれているように見えます。
これらは01、02の結果と合わず、また03の五通りの結果のどれとも合致しません。
完全に独自の進化を遂げましたが、これも最適解ではなさそうに見えます。
05 対戦数を増やす
上に示した方法で勝率が改善しなかったのは、ABの適切さを判断するための試合数が2つしかなく、少ない試料で決定していたことが原因だと考えました。
そのため、ABに従うAIを、random、nhand、nmost、nleastと対戦させ、その後白黒反転してもう一度対戦の計8試合行います。そしてその結果でABの適切さを判断することを考えました。
nhand_customと対戦させることも考えましたが、おそらく膨大な実行時間になってしまうこと、またプログラムが複雑になってしまうという懸念があったためやめました。
また、改良後のトーナメントを用いて次世代へつなぐことも考えましたが、対照実験のためまずは最初に行ったトーナメント方法を採用しました。
seed(0)
generations = 50
children = 10
ab = [[random(), random()] for i in range(children)]
ai = run.PLAY_WAY["AI"]
other = [run.PLAY_WAY["random"], run.PLAY_WAY["nhand"], run.PLAY_WAY["nmost"], run.PLAY_WAY["nleast"]]
win_result = []
score = [0] * children
for g in range(generations):
print("\r%d/%d" % (g+1, generations), end="")
score = [0] * children
win_num = 0
for c in range(children):
run.A = ab[c][0]
run.B = ab[c][1]
for p in [0, 1]:
for o in other:
if p:
run.black_method = ai
run.white_method = o
else:
run.black_method = o
run.white_method = ai
run.setup()
result = run.play()
if run.black_method == run.PLAY_WAY["AI"]:
score[c] += result
if result > 0:
win_num += 1
else:
score[c] -= result
if result < 0:
win_num += 1
if c % 2 == 1:
if random() > 0.03:
if score[c] > score[c-1]:
ab[c-1][0] = ab[c][0] + random() / 5 - 0.1
ab[c-1][1] = ab[c][1] + random() / 5 - 0.1
else:
ab[c][0] = ab[c-1][0] + random() / 5 - 0.1
ab[c][1] = ab[c-1][1] + random() / 5 - 0.1
else:
for i in range(2):
ab[c-i][0] = random()
ab[c-i][1] = random()
win_result.append(win_num)
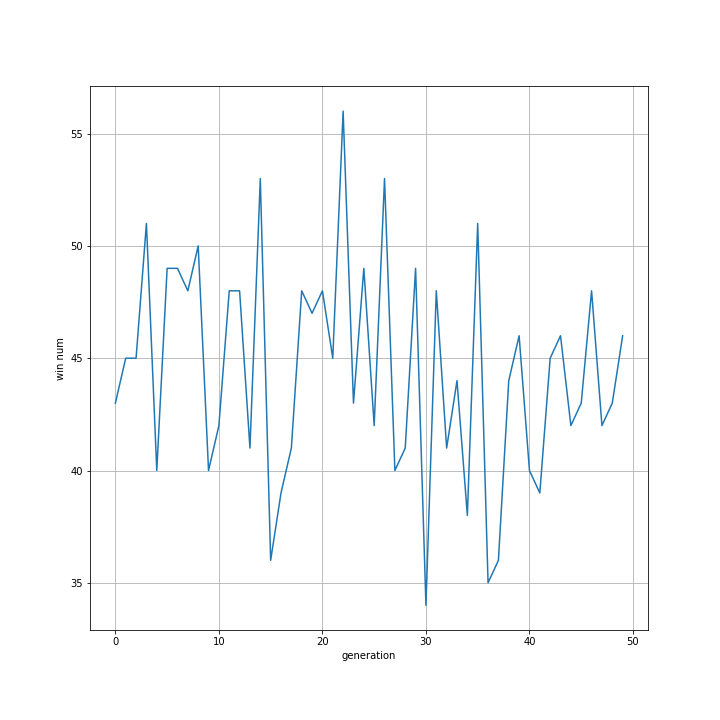
実行結果はこちら。
1人8試合x10人いるので一世代の総合数は先ほどの4倍の80試合です。また、対戦相手はnleastだけでなくrandomなども含むためこれまでの実験と比べ勝率は上がっていますが、世代間での向上は見られません。
また、試合数が増えたことにより相応に実行時間も倍増しました。Javaを早く習得したいです。
[1.02724256462233, 0.26337275542624516]
[1.009950479397224, 0.2159791032577633]
[0.22922242678565338, 0.9734637632138236]
[0.13223405592320084, 0.9543661981037578]
[-0.06376729223249714, 0.8300427714479159]
[-0.15341627116082962, 0.7539450770368438]
[0.24111965717074832, 0.5558870178965837]
[0.17822858286954305, 0.49821795165496663]
[0.02748397669100308, 0.015100622809889594]
[-0.06205959166701412, 0.01733021427322594]
0.25662385883993616 0.5077705475121015
A: 1.0程度, B: 0.25程度
A: 0.2程度, B: 1.0程度
A: -0.1程度, B: 0.8程度
A: 0.2程度, B: 0.5程度
A: 0.0程度, B: 0.0程度
今までにない曲者がそろいました。
対戦相手の種類が増えたことで対応しなければならない戦術が増えたことが原因だと思われます。
06 対戦数を増やし、トーナメント改良
04のトーナメント改良と05の対戦数を増やすを合体させました。
プログラムは継ぎはぎですので省略します。
最初は横ばいに見えますが、35世代付近から上がっているようにも見えます。
[0.20405658462660622, 0.1680605186286642]
[0.5067586035335895, 0.2257166330359812]
[0.506989666989787, 0.39973170956614057]
[0.14497172001539446, 0.1968499870887512]
[0.43622213588550574, 0.2515135205850171]
[0.05490792986502008, 0.32594965169802903]
[0.17250523018856503, 0.34862524795583516]
[0.10559360468888276, 0.2670811780558886]
[0.10494083678931704, 0.2684445529286096]
[0.4517255898186786, 0.3276437286310824]
0.2688671902401346 0.2779616728173999
A: 0.5程度, B: 0.3程度
A: 0.15程度, B: 0.25程度
A: 0.1程度, B: 0.3程度
対戦数を増やす前のトーナメント改良(04)と比べ、いろいろな結果が出ました。
これも05と同様、対戦相手の種類が増えたことが原因ではないかと考えます。
Bがひとつも0.4を超えていないことが気になります。
07 対戦数を増やし、トーナメント改良し、世代数を増やす
06のグラフで、35世代以降勝率が向上しているように見えなくもないので追加検証してみました。
たしかに35~60世代にかけて勝率が向上しているように見えますが、偶然このような形になっただけにも見えます。
[0.33151187738915355, 0.06057437681006733]
[0.3678616364493409, 0.12723243895942166]
[0.5198915583730699, 0.04268710109725918]
[0.44061206459599045, 0.051610048696537625]
[0.46808837087950583, 0.7329708184903793]
[0.5073052040093725, 0.1718749134495976]
[0.3635208255702669, 0.08699886357653655]
[0.40261513162926466, 0.04176901447947265]
[0.2642246747320115, 0.23195360857080813]
[0.1696507008061556, 0.1759563678482843]
0.38352820444341323 0.17236275519783642
一定の特徴はあまり見られず、
A:0.5程度, B: 0.0程度
A:0.4程度, B: 0.0程度
の二つだけでした。
世代数を増やした結果、かなり迷走することになってしまったようです。
フルバージョン
次回は
現在の方法ではうまくいきませんでしたので、別の方法を考え最適なABを求めます。