今回の目標
前回作成したプログラムの実行結果について分析します。
ここから本編
pnadasとmatplotlibを使い、いろいろな条件でのデータを見てみます。
今回、ipynbでやってみたところpandasとの相性抜群に感じましたのでこれからはipynbでやっていきたいと思います。
まずこんなプログラムを書きました。拡張子が「.py」になっていますが実際は「.ipynb」で、二つのセルに分けて書かれています。
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv("data.csv")
generation = df["generation"].nunique()
game_num = 32
dir_name = "fig/%s"
def bar(directory, fig_name, xlabel):
global x, y, game_num
fig = plt.figure(figsize=(10, 10))
plt.bar(x, y)
plt.title(fig_name)
plt.xlabel(xlabel)
plt.ylabel("win count (max: %d)" % game_num)
plt.savefig(directory + fig_name)
plt.clf()
plt.close()
def plot(directory, fig_name):
global x, y, game_num
fig = plt.figure(figsize=(10, 10))
plt.plot(x, y)
plt.title(fig_name)
plt.xlabel("generation")
plt.ylabel("win count (max: %d)" % game_num)
plt.savefig(directory + fig_name)
plt.clf()
plt.close()
データ選択方法
以下のプログラムでグラフを作りました。
なお他の方法についても似たようなプログラムなので、これ以外は省略します。
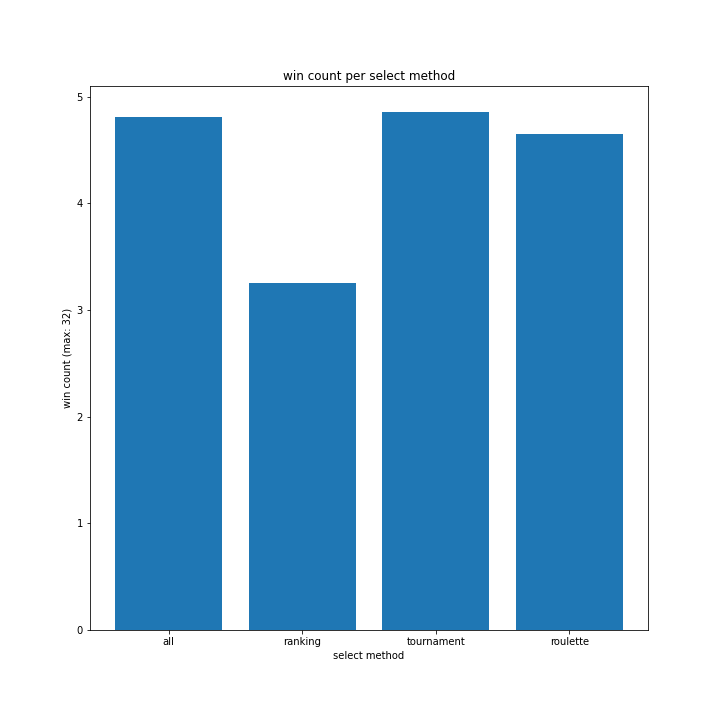
fig_name = "win count per select method"
num = df["select_method"].nunique()
x = ["all", "ranking", "tournament", "roulette"]
y = []
for i in range(num):
df_ele = df[df.select_method == i]
y.append(df_ele["win_per"].mean())
bar(dir_name % "sele_method/", fig_name, "select method")
勝率が異常に低いですね。
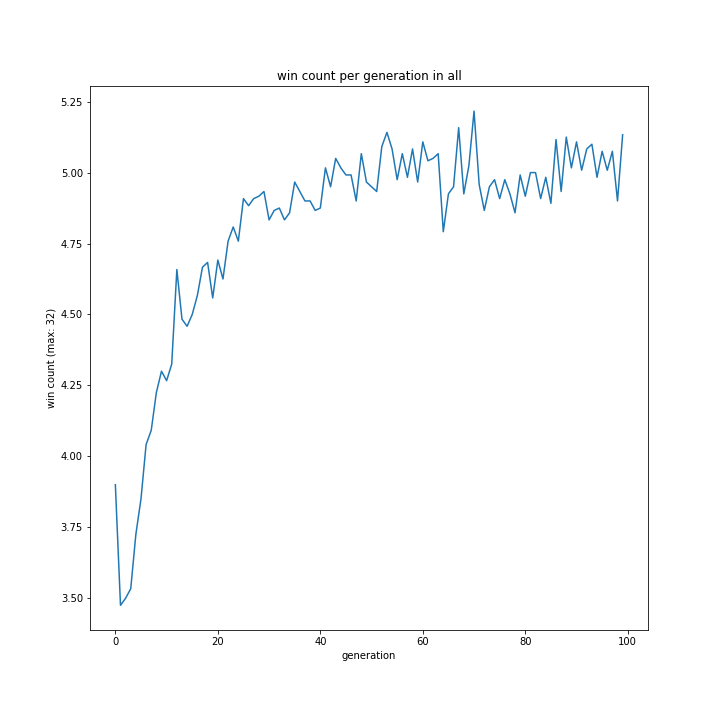
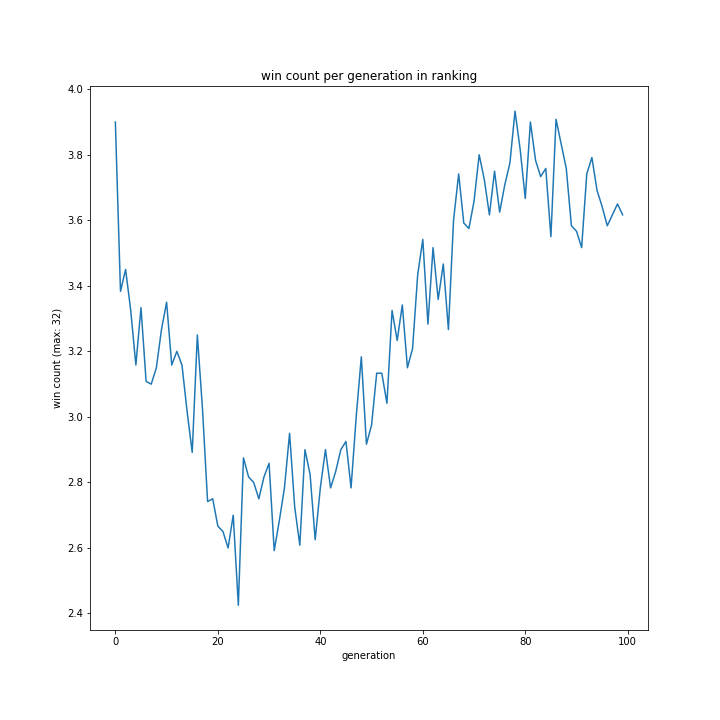
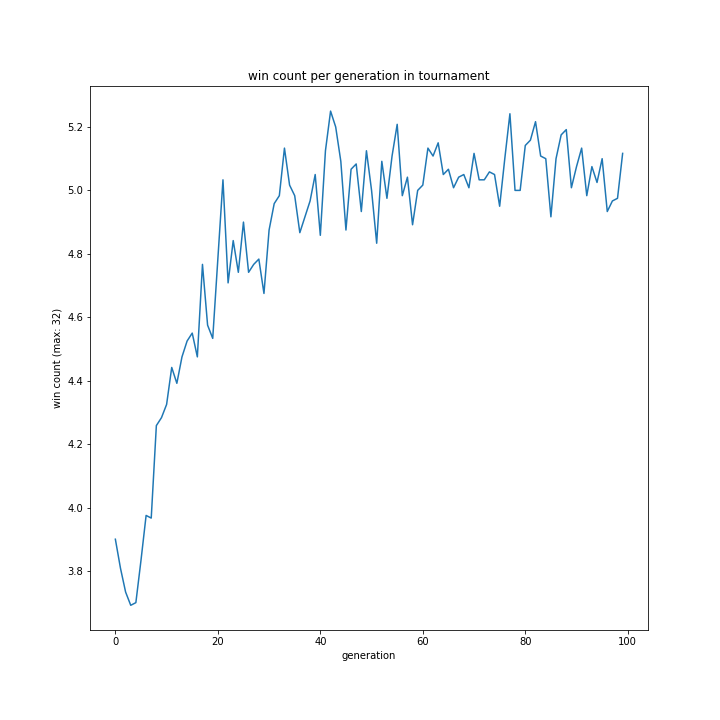
fig_name = "win count per generation in %s"
sele_name = x
x = [i for i in range(generation)]
for i in range(num):
df_ele = df[df.select_method == i]
y = []
for j in range(generation):
df_per_gene = df_ele[df_ele.generation == j]
y.append(df_per_gene["win_per"].mean())
plot(dir_name % "sele_method/", fig_name % sele_name[i])
明らかに勝率がおかしいですが、ひとまず続けます。
交叉方法
やっぱり変ですね。
コンピュータの思考方法
以外にも二手先まで読む方が一手先まで読むよりも低い結果に。
プレイヤー役の思考方法
問題はここにありました。
おそらくプログラムミスですね。
省略しましたが「p one hand」、「p two hand」、「my one hand」、「my two hand」いずれもすべての世代において勝利数0のグラフとなっていました。
プログラム修正
コンストラクタにて、メンバ変数であるmodeを0にしていたことに気づきました。
これが原因で勝利数が0になっていたようです。
修正し実行しました。
また、ついでに世代数も1000まで増やして実行してみました。
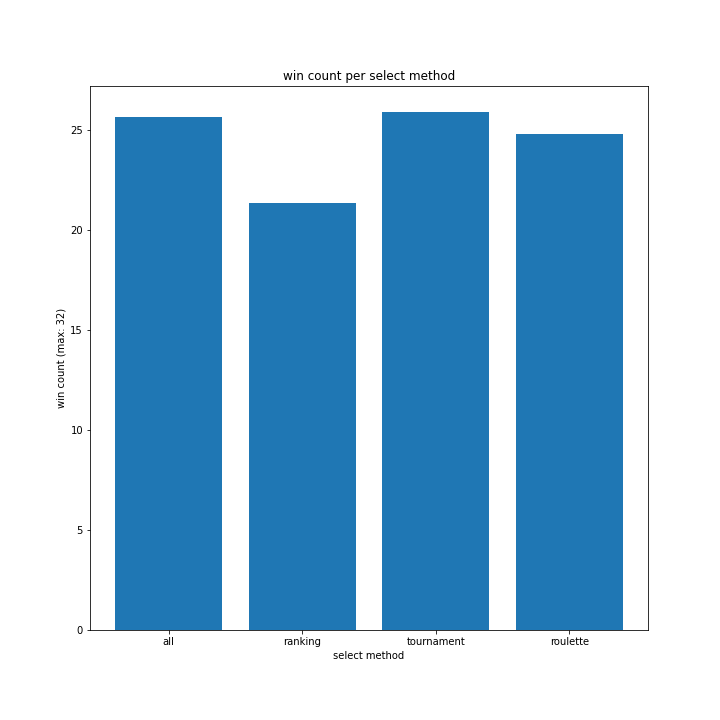
データ選択方法
グラフ作成プログラムは上に示したものと全く同じです。
意外にも全選択の勝率が高くまとまり、ランキングが最下位であとはあまり変わらない結果となりました。
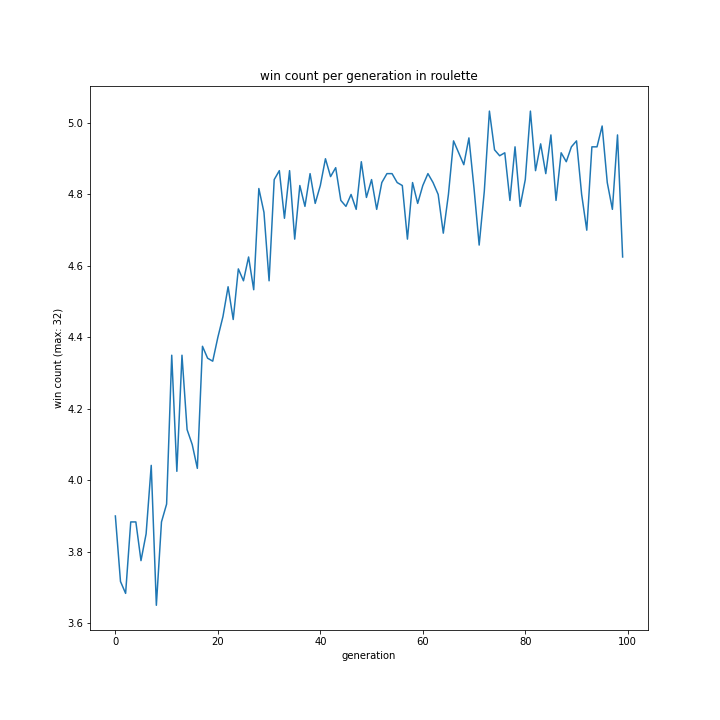
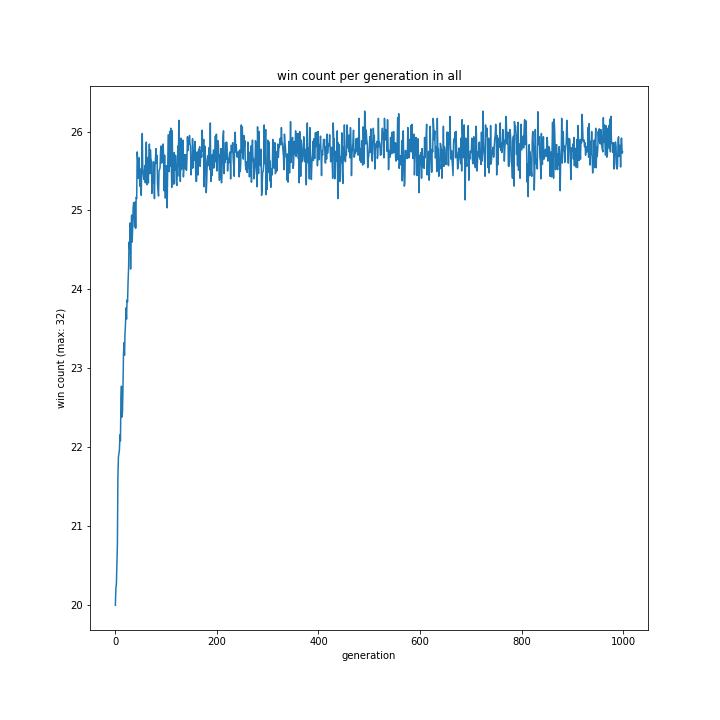
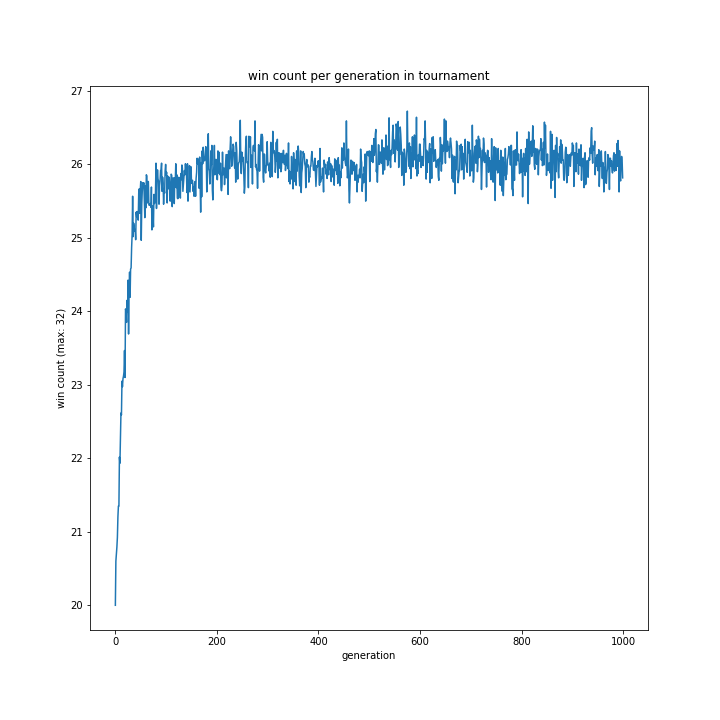
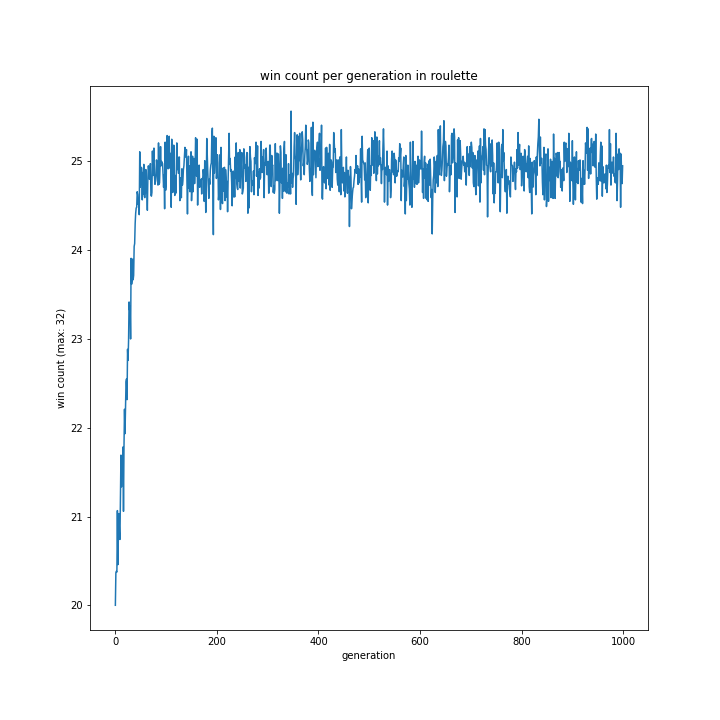
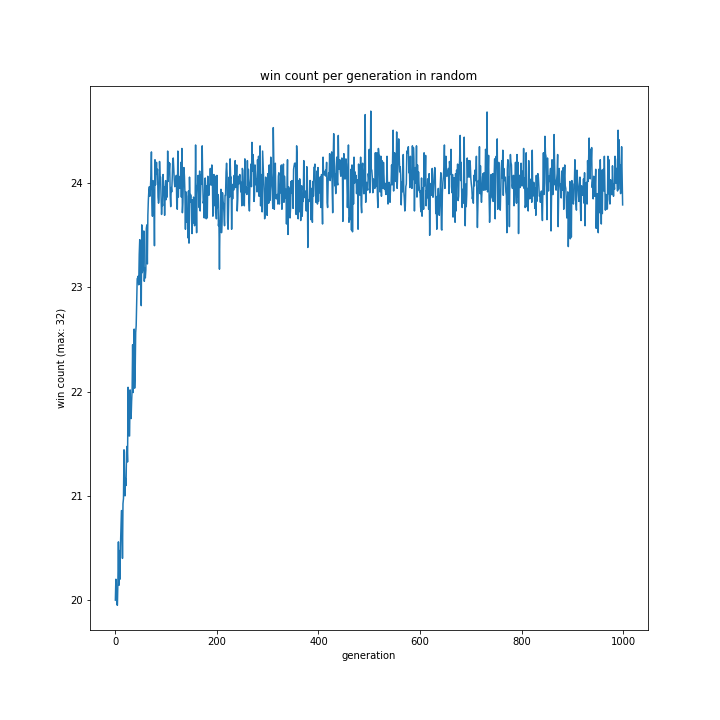
選択方法別の、世代による勝率の移り変わりは以下のグラフです。
allとtournamentはほぼ同じ形をとり、rouletteは二つを縮小したような結果でした。
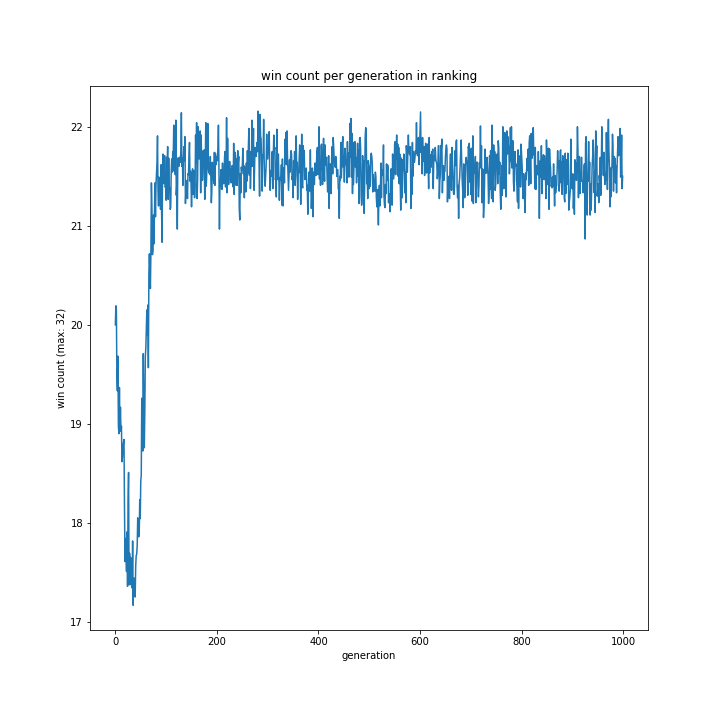
特徴的なのはrankingです。上の、100世代でやっていた時と同様に一度大きく勝率が落ち込み、その後学習し回復するものの最高記録は22程度で止まっています。
ランキングの設定がそもそも雑であったことは可能性として考えられると思います。今回、プログラムの実行時間を減らすため1位の採用確率を99%としていましたが、それによって局所解からなかなか抜けられなかった可能性はあります。
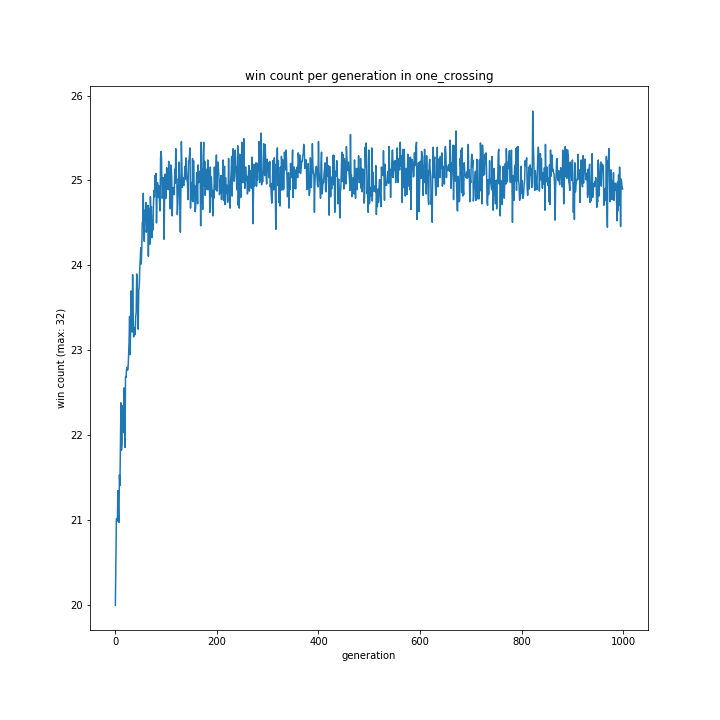
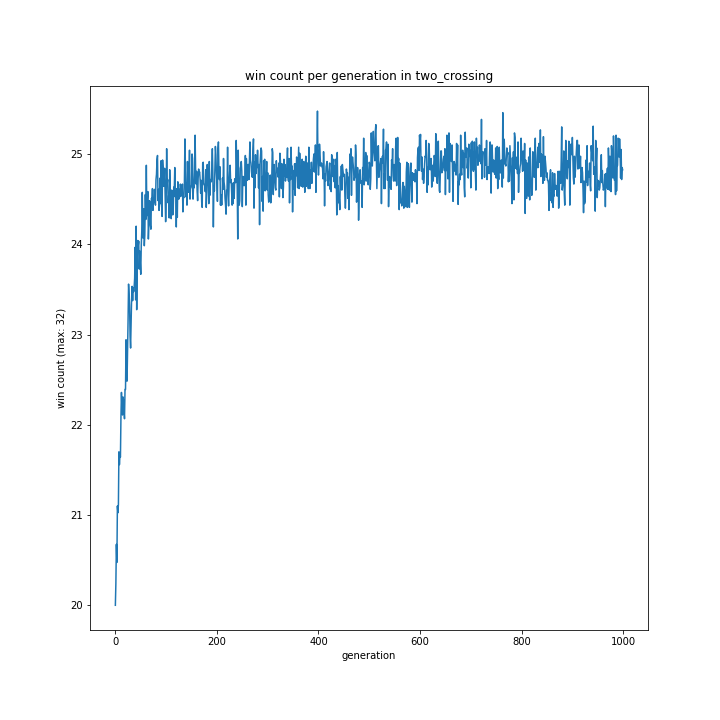
交叉方法
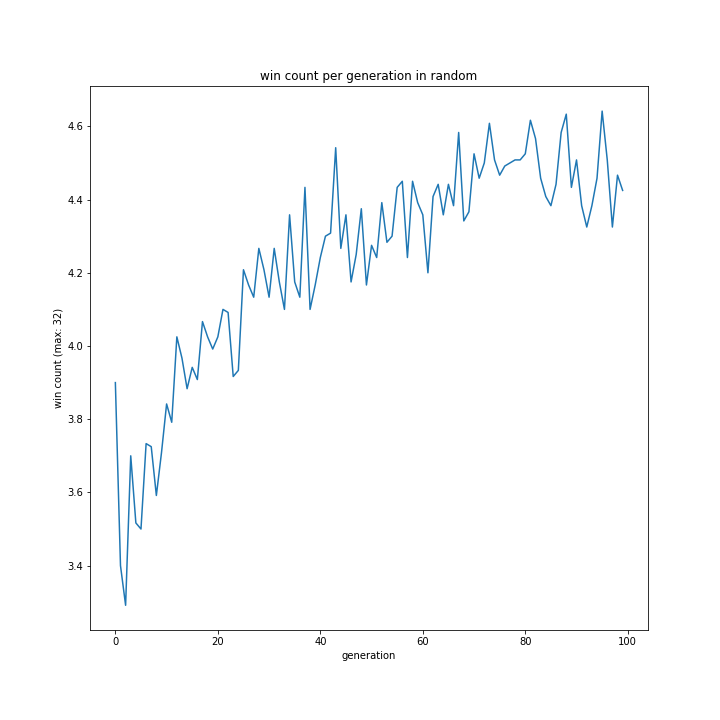
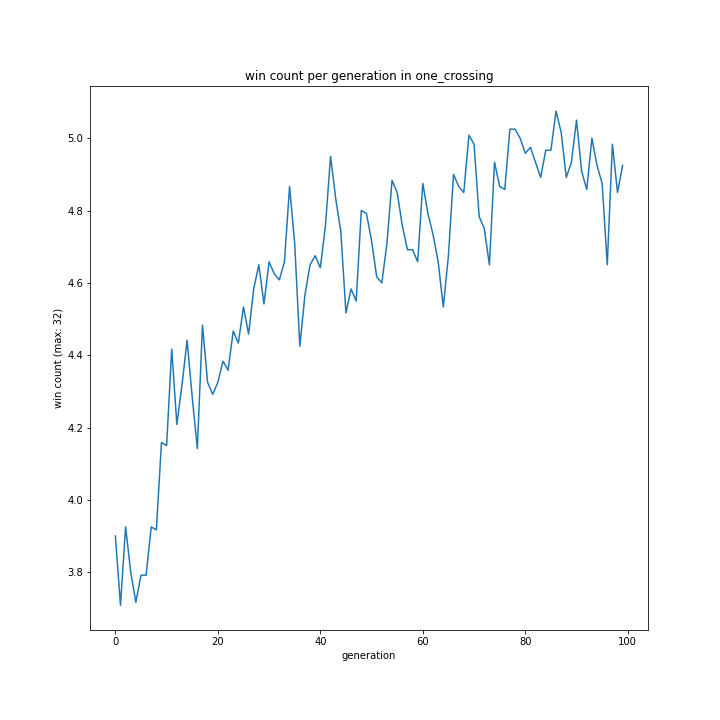
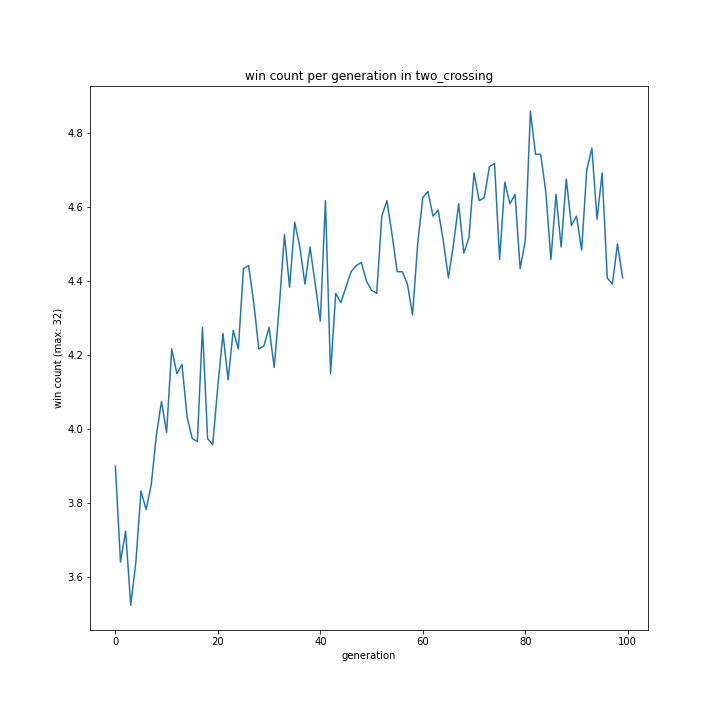
これに関してはどれも同じような形となり、最優秀は一点交叉でした。
以前予想した通りランダム交叉でも大きな問題はなさそうですが、より精度を求めるなら他の方法が適しているようです。
コンピュータの思考方法
一手先まで読む方が勝率が高い結果になりました。
最初は意外に感じましたが、よく考えれば評価値はすべて1ではないので、今回のようなカスタム評価値を用いるなら一手先まで読むような単純な思考に用いる方が合っているのではないでしょうか。
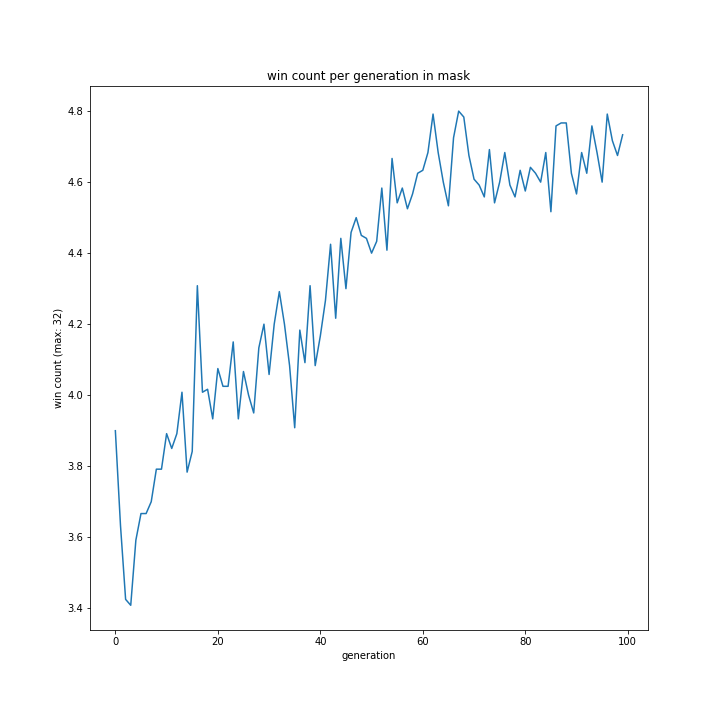
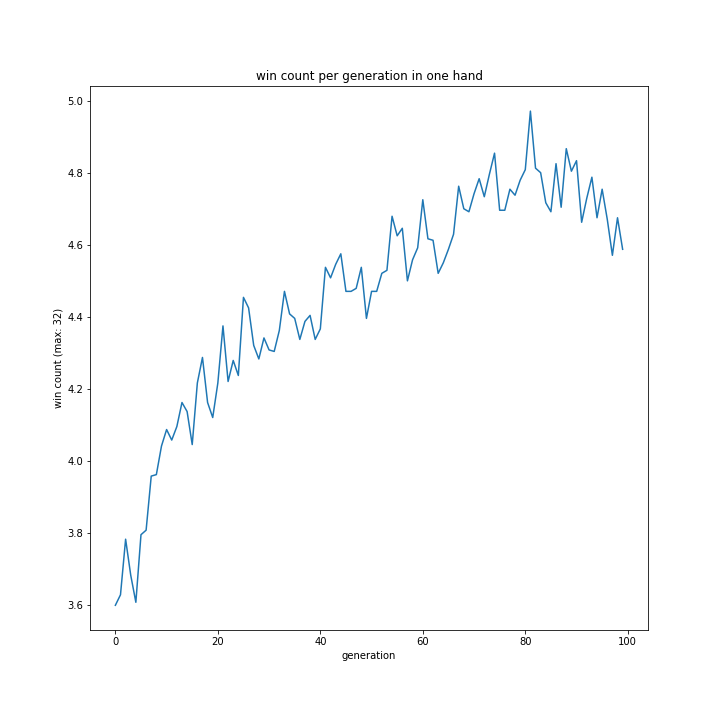
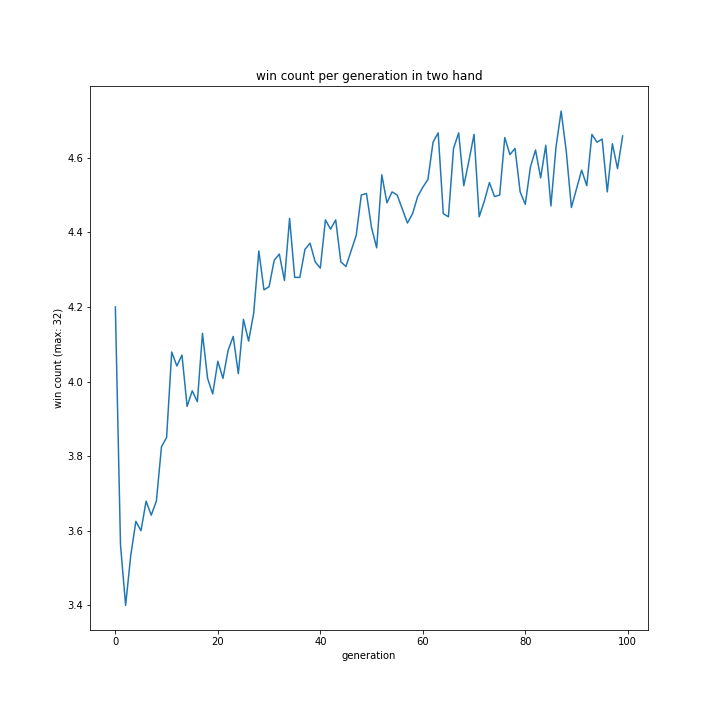
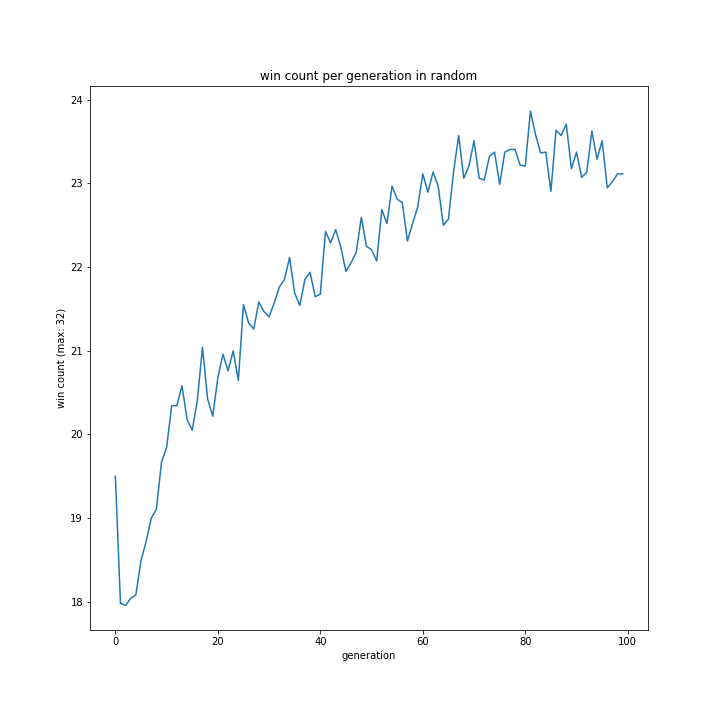
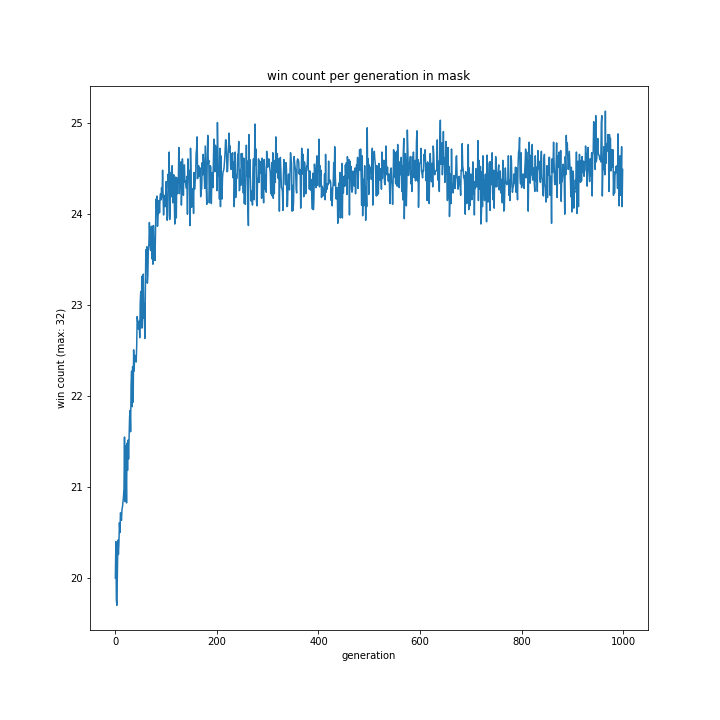
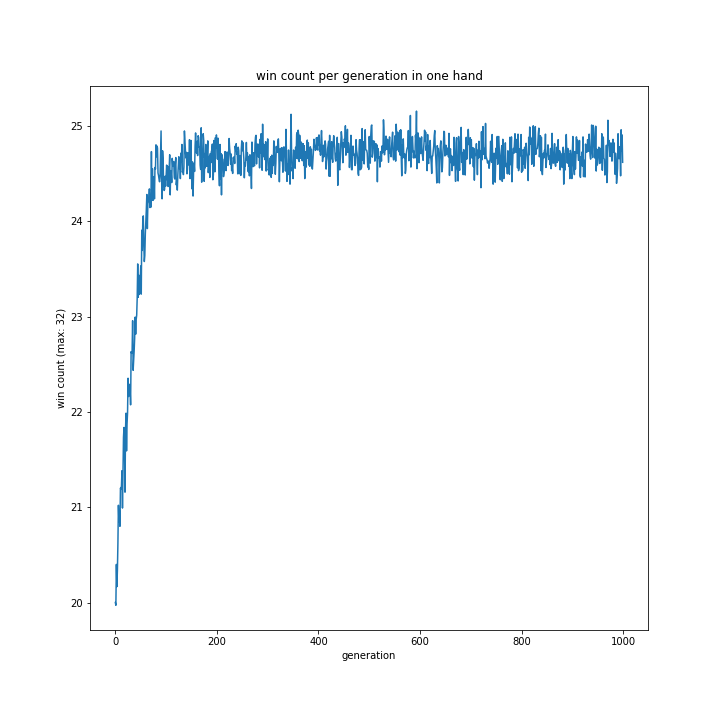
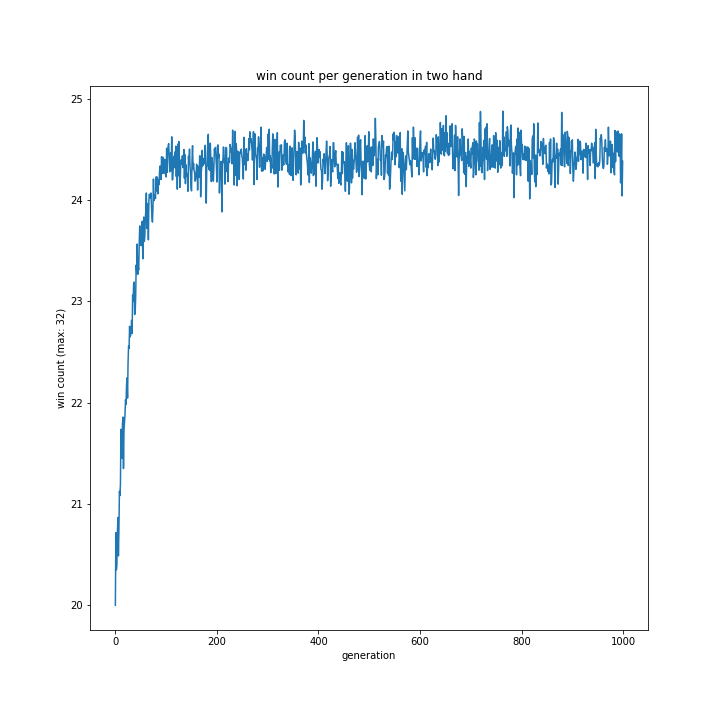
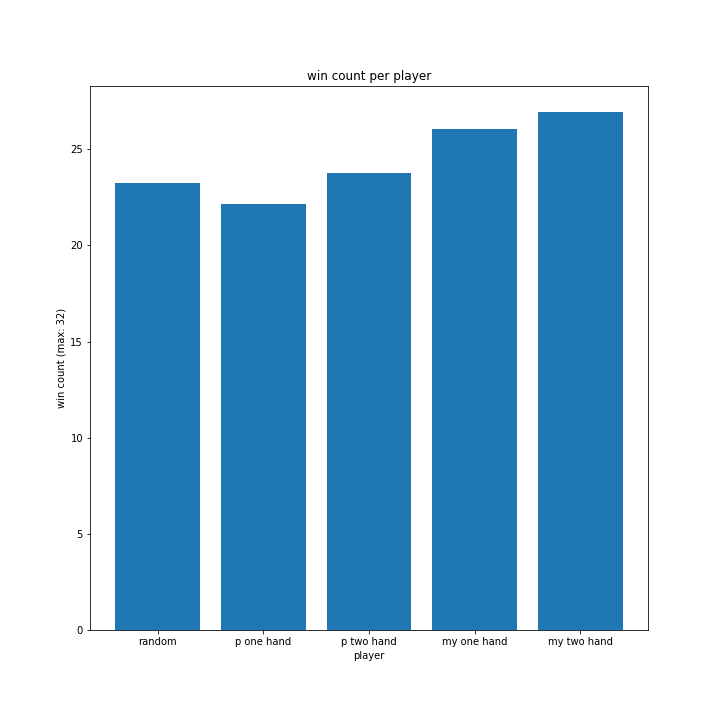
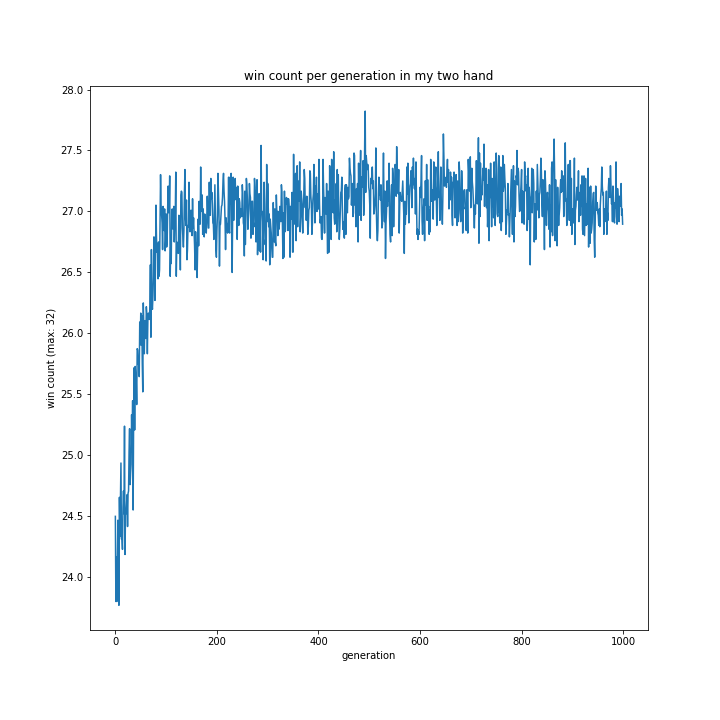
プレイヤー役の思考方法
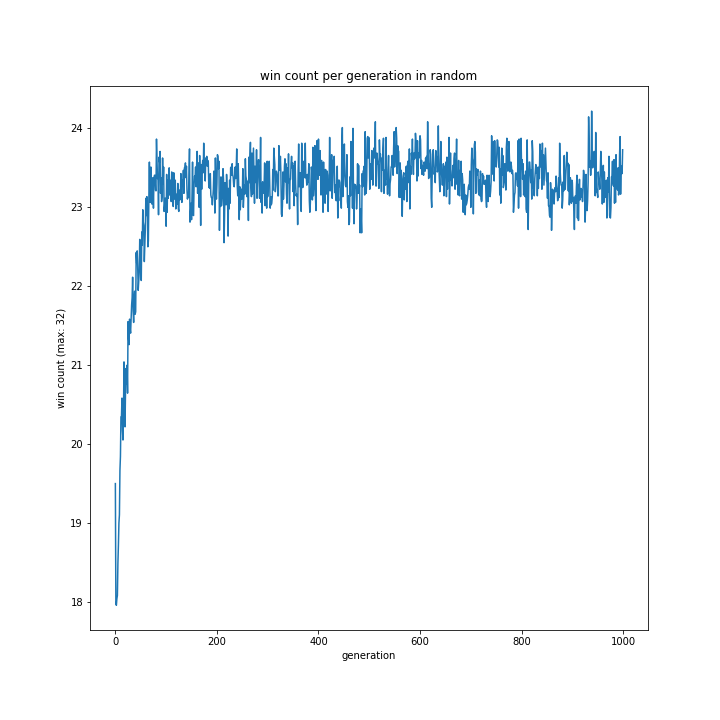
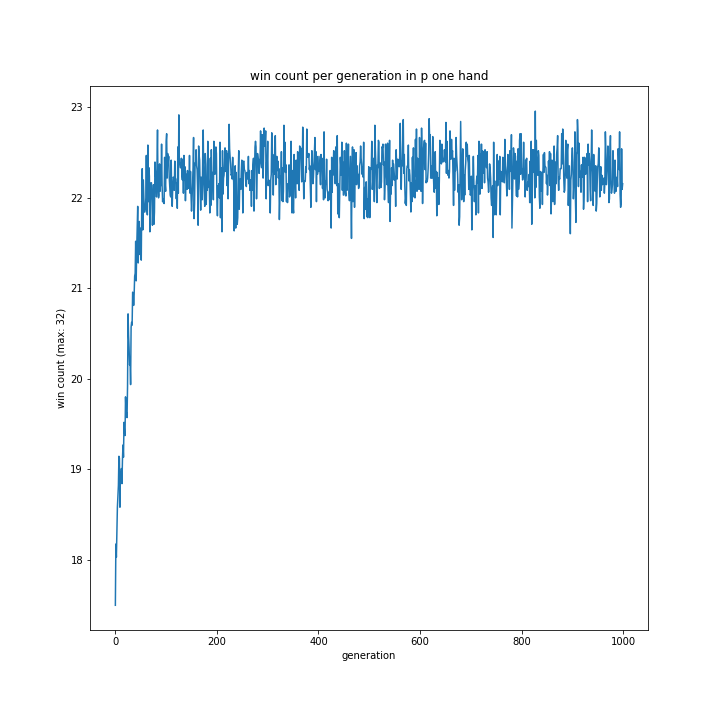
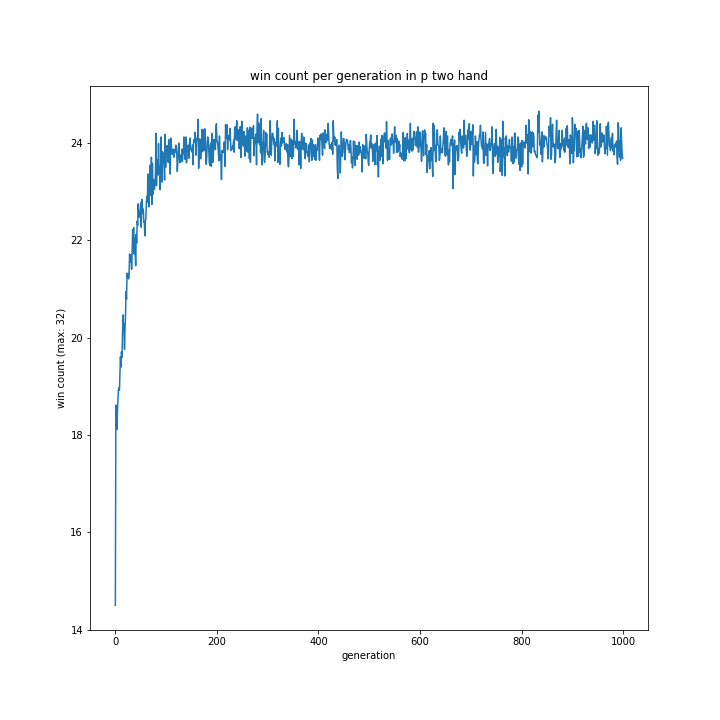
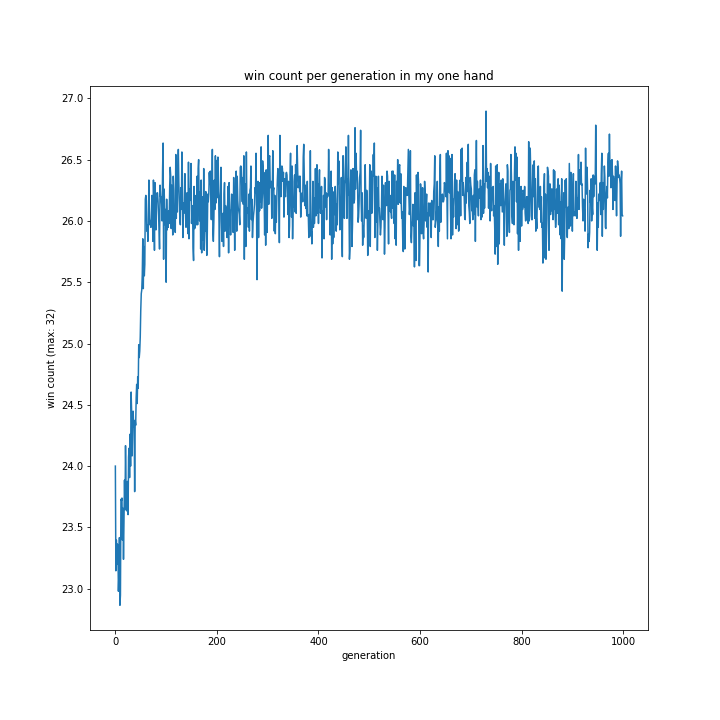
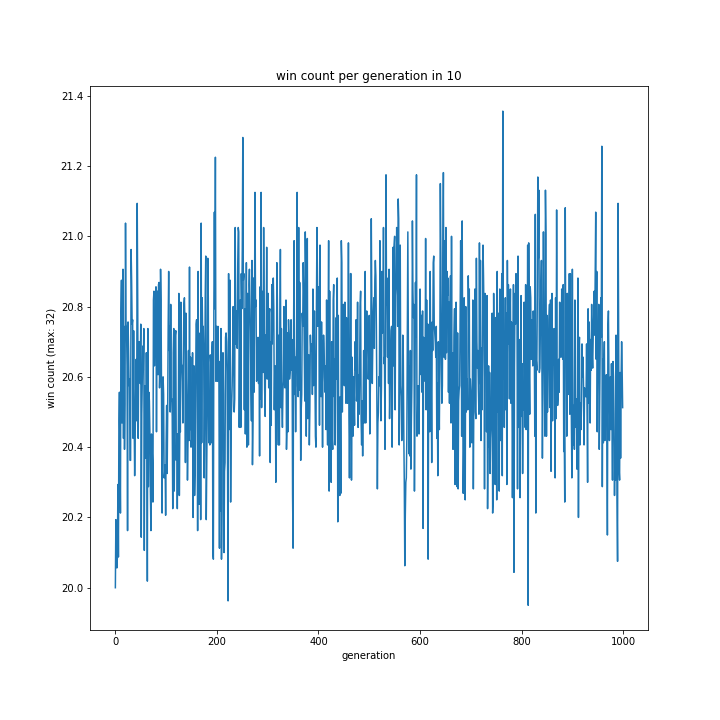
意外にも1hand相手の勝率が最も低く、my2hand相手だと最も高い結果に。random相手の勝率は相変わらず低い傾向にあるようです。
このグラフだけではよく分かりません。
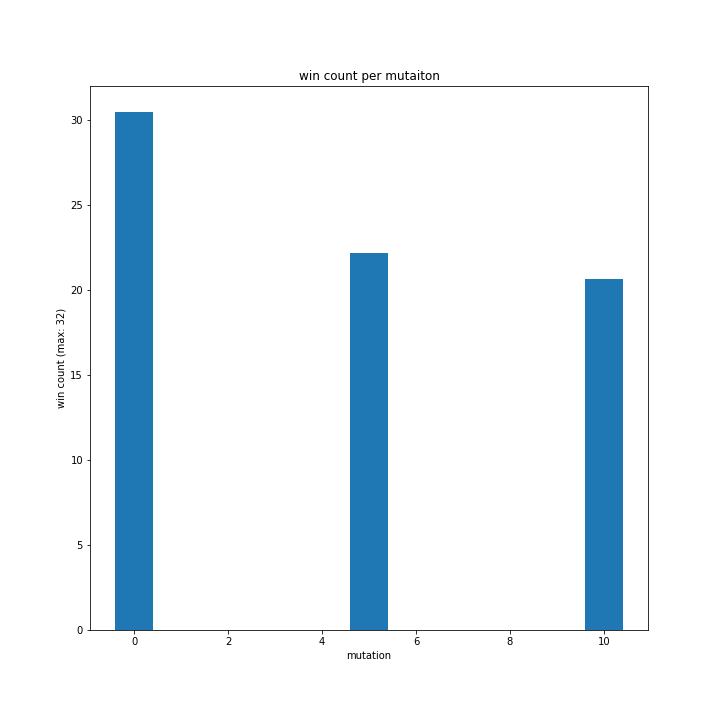
突然変異の確率
完全に失念していました。
0%、5%、10%と変えながら実験したやつです。
0%が最も高く階段状になりました。
0%はほぼ完勝クラスの勝率を100世代付近で既にたたき出しています。
5%と10%は面白い結果になりました。10%は変異しすぎのようです。
とはいえ0%はさすがに非常識なので、0~5%の間が適切ではないでしょうか。
複合条件
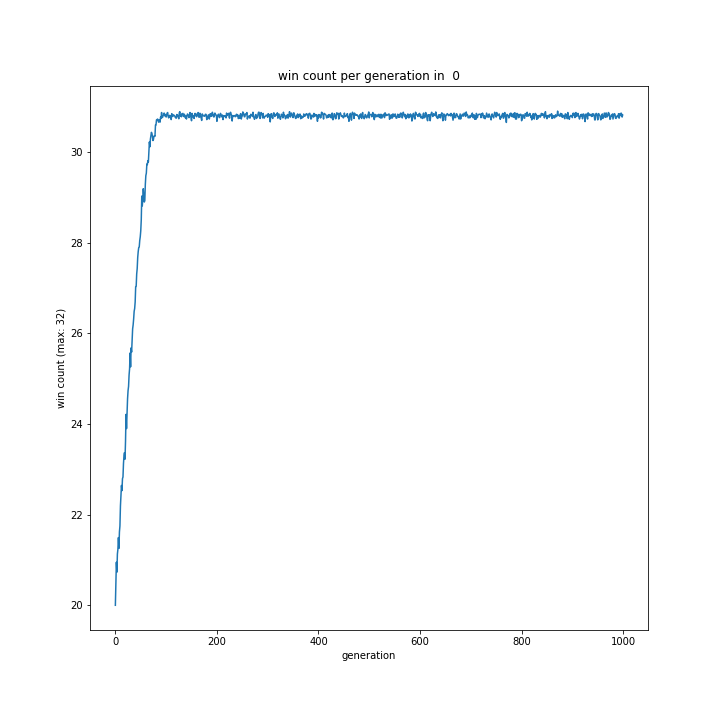
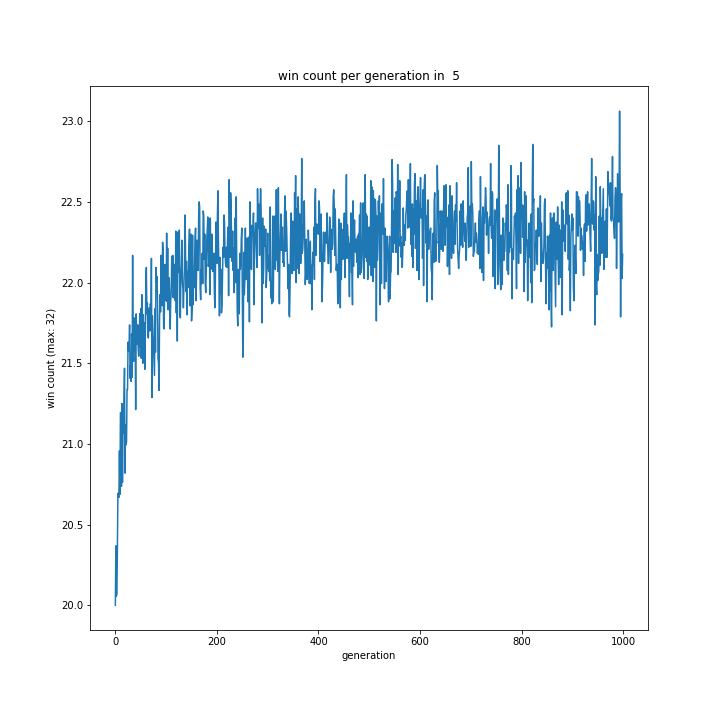
突然変異0% + プレイヤー役の思考方法
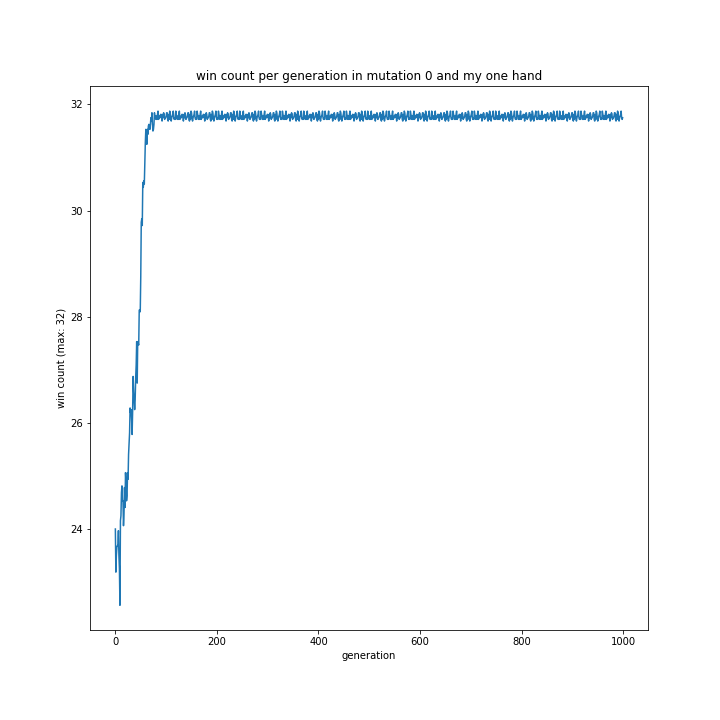
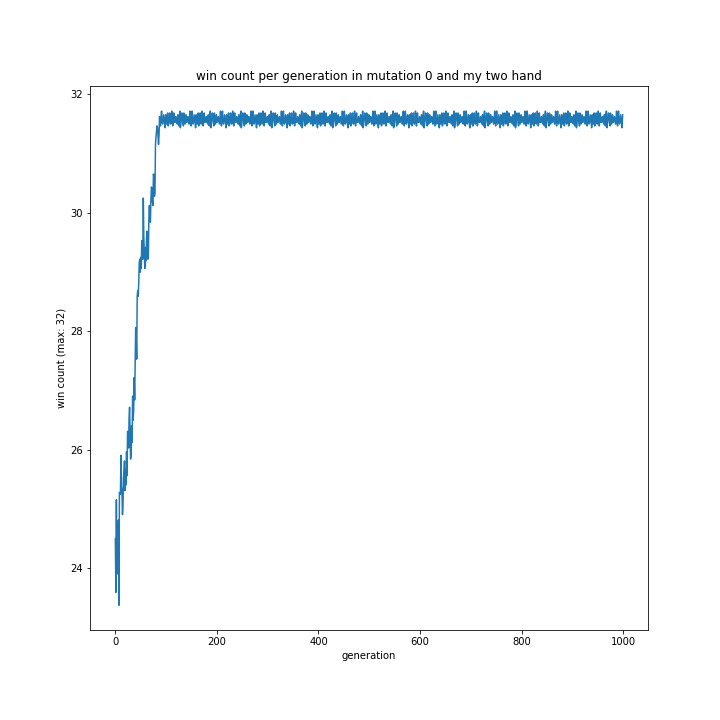
普通にグラフを見てもよく分からなかったプレイヤー役の思考方法について、突然変異0%なら見やすいグラフが作れるのではないかと思い作成してみました。
以下が作成プログラムと出来上がったグラフたちです。
fig_name = "win count per generation in mutation 0 and %s"
df_ele = df[df.per_mutation == 0]
player_name = ["random", "p one hand", "p two hand", "my one hand", "my two hand"]
player = df_ele["player"].unique()
x = [i for i in range(generation)]
for i in player:
df_sur = df_ele[df_ele.player == i]
y = []
for j in range(generation):
df_per_gene = df_sur[df_sur.generation == j]
y.append(df_per_gene["win_per"].mean())
plot(dir_name % "composite/mutation0_player/", fig_name % player_name[i])
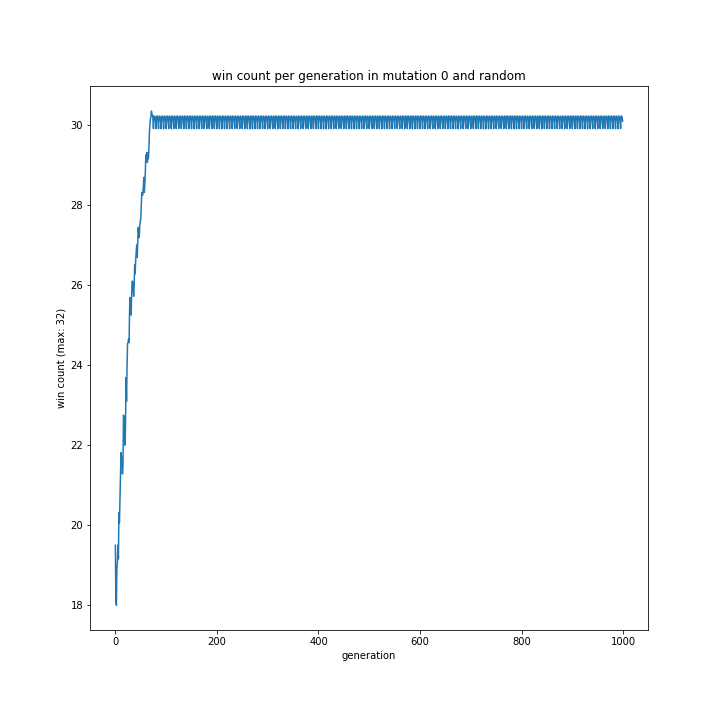
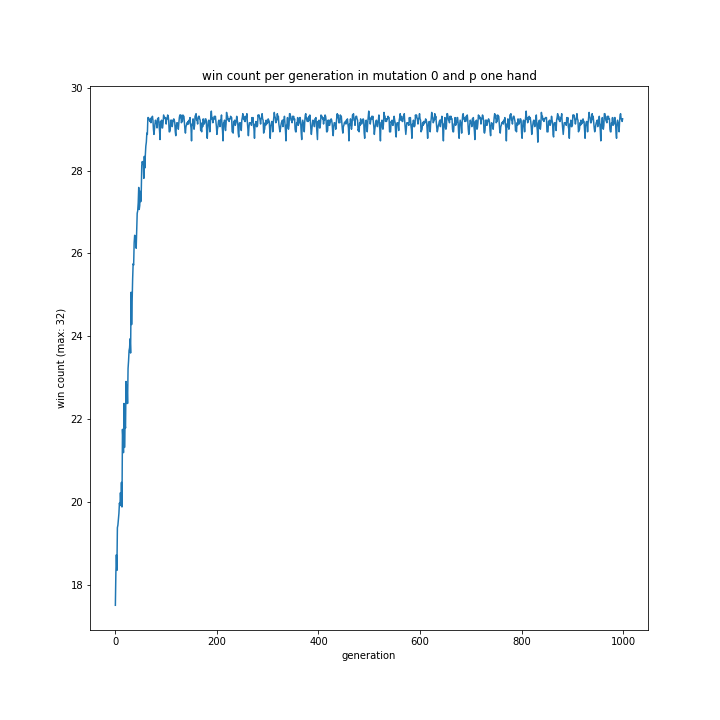
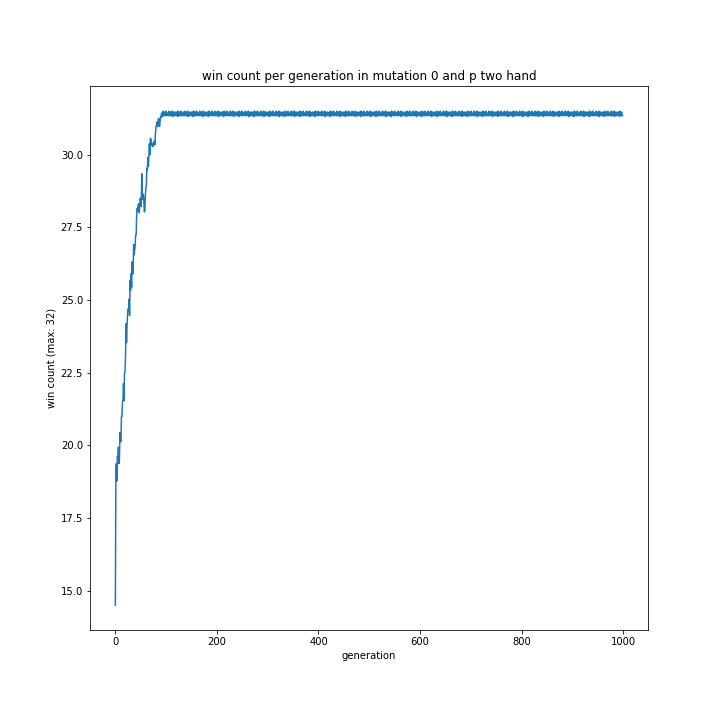
my相手ならほぼ完勝していました。
pよりmyのほうが強いと予想していましたが、全くそんなことはないという結果に。
無理やり理由を探るなら、myの方がコンピュータの思考により近かったからでしょうか?
全く分かりません。
最高記録は?
もともと調べたかったのは遺伝的アルゴリズムではなく評価値です。
ということで、最も強い、つまり理にかなっている評価値を調べたいと思います。
まず、勝利回数のパターンを調べました。
# high score 以降
win_per = df["win_per"].unique()
win_per.sort()
print(win_per)
実行結果は以下の通り。
[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
24 25 26 27 28 29 30 31 32]
全敗している世代もありますが、全勝している世代もありました。
次に、全勝した世代の数を調べました。
df_win_max = df[df.win_per == 32]
print(len(df_win_max))
print(len(df_win_max) / len(df) * 100)
135739
28.278958333333332
実行結果はなんと135739世代で、全世代の訳3割でした。
さすがにこんな数の評価値すべてをチェックするわけにはいかないので、ここではより早い段階で全勝した評価値を調べることにします。
gene_lim = [100, 50, 40, 30, 20, 14, 13, 12, 10]
for i in gene_lim:
df_win_max_top = df_win_max[df_win_max.generation < i]
print("data num smaller than %d generation: %d" % (i, len(df_win_max_top)))
data num smaller than 100 generation: 8487
data num smaller than 50 generation: 1900
data num smaller than 40 generation: 971
data num smaller than 30 generation: 371
data num smaller than 20 generation: 75
data num smaller than 14 generation: 15
data num smaller than 13 generation: 9
data num smaller than 12 generation: 6
data num smaller than 10 generation: 2
100世代未満で全勝した世代は8487ありました。
数こそ少ないですが10世代未満で全勝したデータもありました。
15個の評価値を見るのは大変なので、9個の評価値について詳しく見ていきたいと思います。
# check eva 以降
df_sur = df_win_max[df_win_max.generation < 13]
df_eva = pd.read_csv("eva.csv")
colum = df_sur.columns
################################################
eva = []
for i in range(len(df_sur)):
df_eva_ele = df_eva[df_eva.indi == 0]
eva.append([])
for j in colum:
if j != "generation" and j != "win_per":
df_eva_ele = df_eva_ele.query("%s == %d" % (j, df_sur[i:i + 1][j]))
for j in range(64):
eva[i].append(df_eva_ele[str(j)])
################################################
evap = open("eva_view.csv", "w")
for i in range(len(eva)):
for j in range(len(eva[i])):
evap.write("%f" % eva[i][j])
if j % 8 == 7:
evap.write("\n")
else:
evap.write(",")
evap.write("\n")
evap.close()
前回の調査同様、予想とは大きく違う形になりました。
ここで、調べたデータの情報を調べてみたところ、面白いことが分かりました。
print(df_sur)
evolution_method select_method per_mutation computer player \
120010 1 0 0 1 0
120012 1 0 0 1 0
184009 1 2 0 1 4
184011 1 2 0 1 4
184012 1 2 0 1 4
189011 1 2 0 2 4
189012 1 2 0 2 4
213005 1 3 0 1 3
464011 3 3 5 1 4
generation win_per
120010 10 32
120012 12 32
184009 9 32
184011 11 32
184012 12 32
189011 11 32
189012 12 32
213005 5 32
464011 11 32
見事に突然変異していないデータばかりですね。
しかも、5世代で全勝に到達しているデータがあるうえ、プレイヤー役のほとんどは「my two hand」です。
早く全勝にたどり着いたデータを見るという方法はどうやら上手く行かないようです。
ということで、最も評価値が熟成? されているであろう終盤の全勝に着目してみたいと思います。
# last eva 以降
df_sur = df[df.win_per == game_num]
################################################
df_sur = df_sur.sort_values(by=["generation"], ascending=False)
print(df_sur)
print(len(df_sur[df_sur.generation == generation - 1]))
evolution_method select_method per_mutation computer player \
458999 3 3 0 2 3
8999 0 0 0 2 3
330999 2 3 0 1 0
300999 2 2 0 1 0
360999 3 0 0 1 0
... ... ... ... ... ...
189011 1 2 0 2 4
464011 3 3 5 1 4
120010 1 0 0 1 0
184009 1 2 0 1 4
213005 1 3 0 1 3
generation win_per
458999 999 32
8999 999 32
330999 999 32
300999 999 32
360999 999 32
... ... ...
189011 11 32
464011 11 32
120010 10 32
184009 9 32
213005 5 32
[135739 rows x 7 columns]
141
最終世代で全勝したのは141家庭x32子でした。
そんなにたくさんは見れないので大雑把に平均してみたいと思います。
df_sur = df_sur[df_sur.generation == generation - 1]
df_eva = pd.read_csv("eva.csv")
colum = df_sur.columns
################################################
eva = []
for i in range(64):
eva_ele = []
for j in range(len(df_sur)):
df_eva_ele = df_eva
for k in colum:
if k != "generation" and k != "win_per":
df_eva_ele = df_eva_ele.query("%s == %d" % (k, int(df_sur[j:j + 1][k])))
eva_ele.append(df_eva_ele[str(i)].mean())
eva.append(sum(eva_ele) / len(df_sur))
################################################
evap = open("eva_last_view.csv", "w")
for i in range(64):
evap.write("%f" % eva[i])
if i % 8 == 7:
evap.write("\n")
else:
evap.write(",")
evap.write("\n")
evap.close()
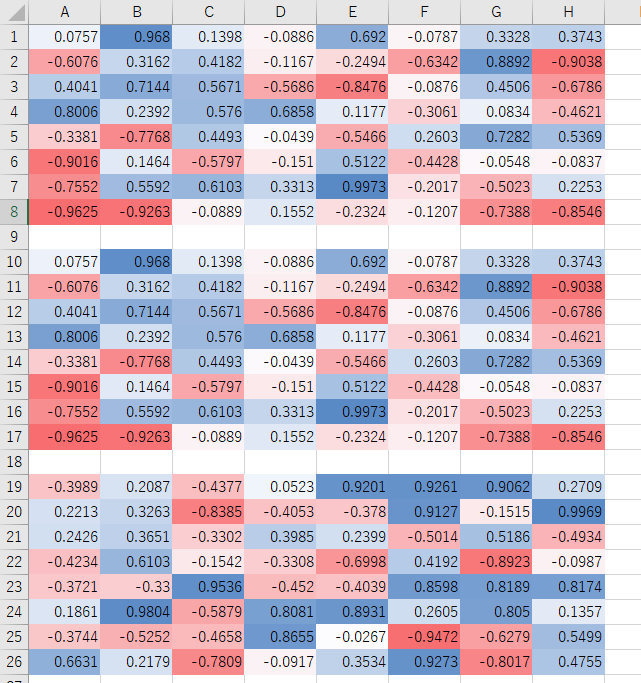
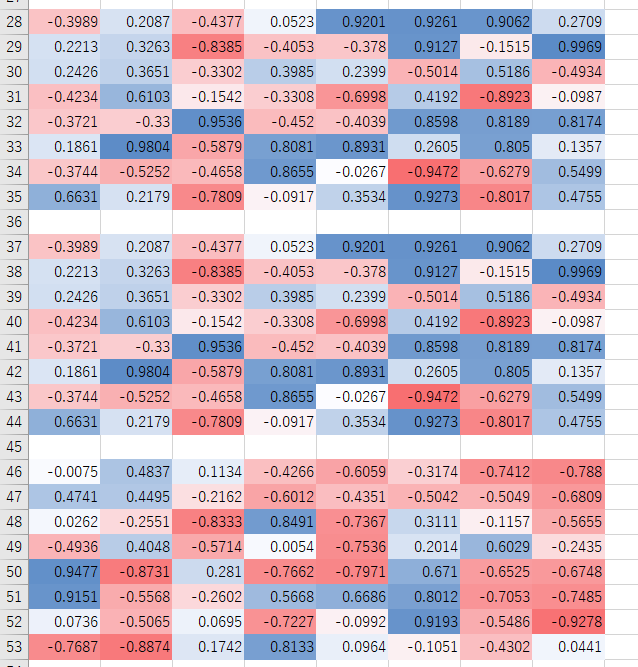
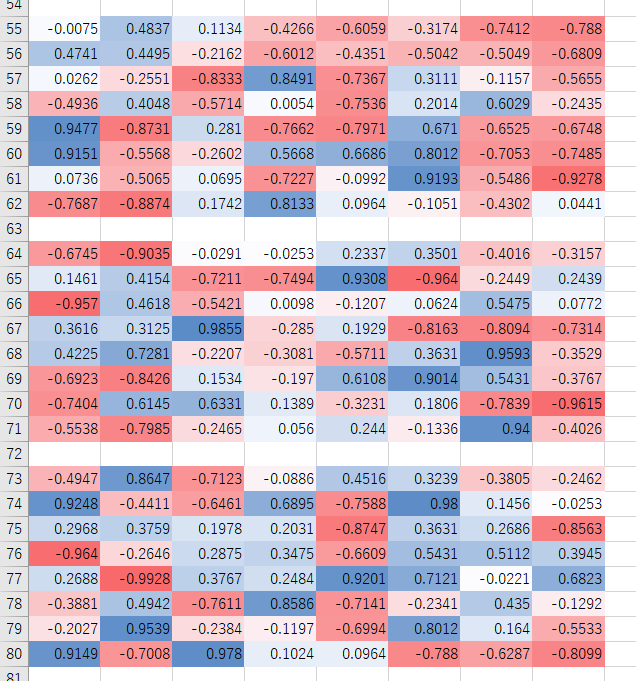
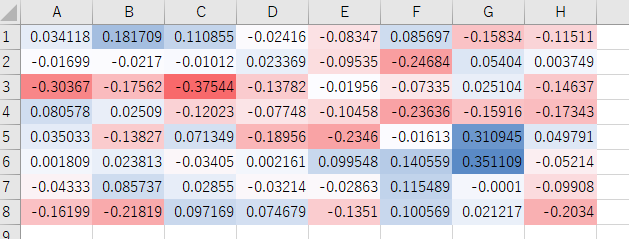
結果がこちら。
どの位置でも0に近い値となりました。
つまり様々な条件で学習を行いましたが、条件によってそれぞれの位置で異なる値がランダム的に得られたことになります(評価値はどの位置でも-1~1の範囲をとります)。
ここで、先の9つの評価値と、その下の詳細データを見比べてみると面白いことが分かります。
1つめと2つめは世代が違うだけで他の条件は同じ、3、4、5および6、7も同様です。世代が違うだけのデータは、似たような形の評価値を形成しているのが見て取れます。
ここから考察できるのは、各条件での学習で得られたのはその条件でのみ強い評価値であり、いわば特化型でしかないということです。
つまりどんな状況でも普遍的に有効な評価値を作るのは現方針では不可能であると考えました。
今考えれば当たり前のことでしたが、気づきませんでした。
フルバージョン
kaizenフォルダ内に入っています。
次回は
今回の考察でわかったように、一つの条件の中で評価値を求める方法はあまりよくないようなので、様々な相手と戦う方式で学習させてみます。