今さら聞けないGAN（4） WGAN

はじめに

前回までの記事で、DCGANへの拡張および、現状のGANの問題点について述べました。今回は、それを解決するための方法としてWGANおよびその改良版（WGAN-gp）について説明します。前回までの記事は以下

今さら聞けないGAN (1)　基本構造の理解
今さら聞けないGAN (2)　DCGANによる画像生成
今さら聞けないGAN (3)　潜在変数と生成画像

WGANについて参考になったリンク
Wasserstein GAN [arXiv:1701.07875] ご注文は機械学習ですか？
Wasserstein GAN（WGAN）でいらすとや画像を生成してみる
Wasserstein GAN と Kantorovich-Rubinstein 双対性

#GANの問題点

• 学習が難しい
  • 勾配消失問題が起こる
• 生成結果のクオリティを損失関数から判断しにくい
• モード崩壊が起こる

改良方法

• Wasserstein GANの導入
  • Wasserstein距離により損失関数を設計
    • 要請を満たすために重みをクリッピング（WGAN）
    • 学習が不安定化する問題
  • 別の方法としてGrgdient penalityを導入（WGAN-gp）

基本構造からの変更点

• 損失関数（binary cross entropyからWasserstein lossに）
• discriminator の構造

損失関数

まず損失関数について説明します。通常のGAN では以下の価値関数の最適化を行いました。

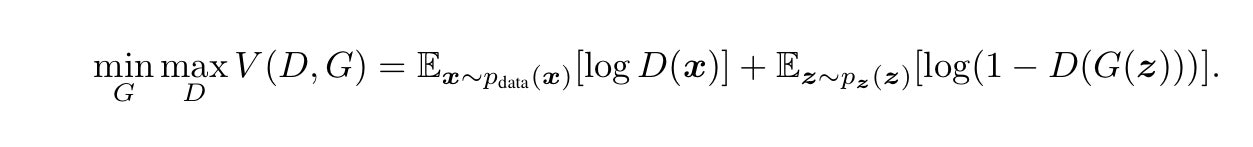
Discriminatorの最適化の際は、右辺を最大化させれば良いわけですから、右辺第1項はなるべく大きくなるよう、本物データ（label=1）に対して、識別結果を本物（1）と返し、なおかつ偽物データ（0）を偽物（0）と返せばよいことがわかります。結果的にこれに対応するのがbinary cross関数ということを説明しました。

　なお、本物データの確率密度分布$p_{data}(x)$と生成データの確率密度分布$p_g(z)$が固定されている場合、最適な識別関数D*は以下になります。

D^*(x) = \frac{p_{data}(x)}{p_{data}(x)+p_g(x)}

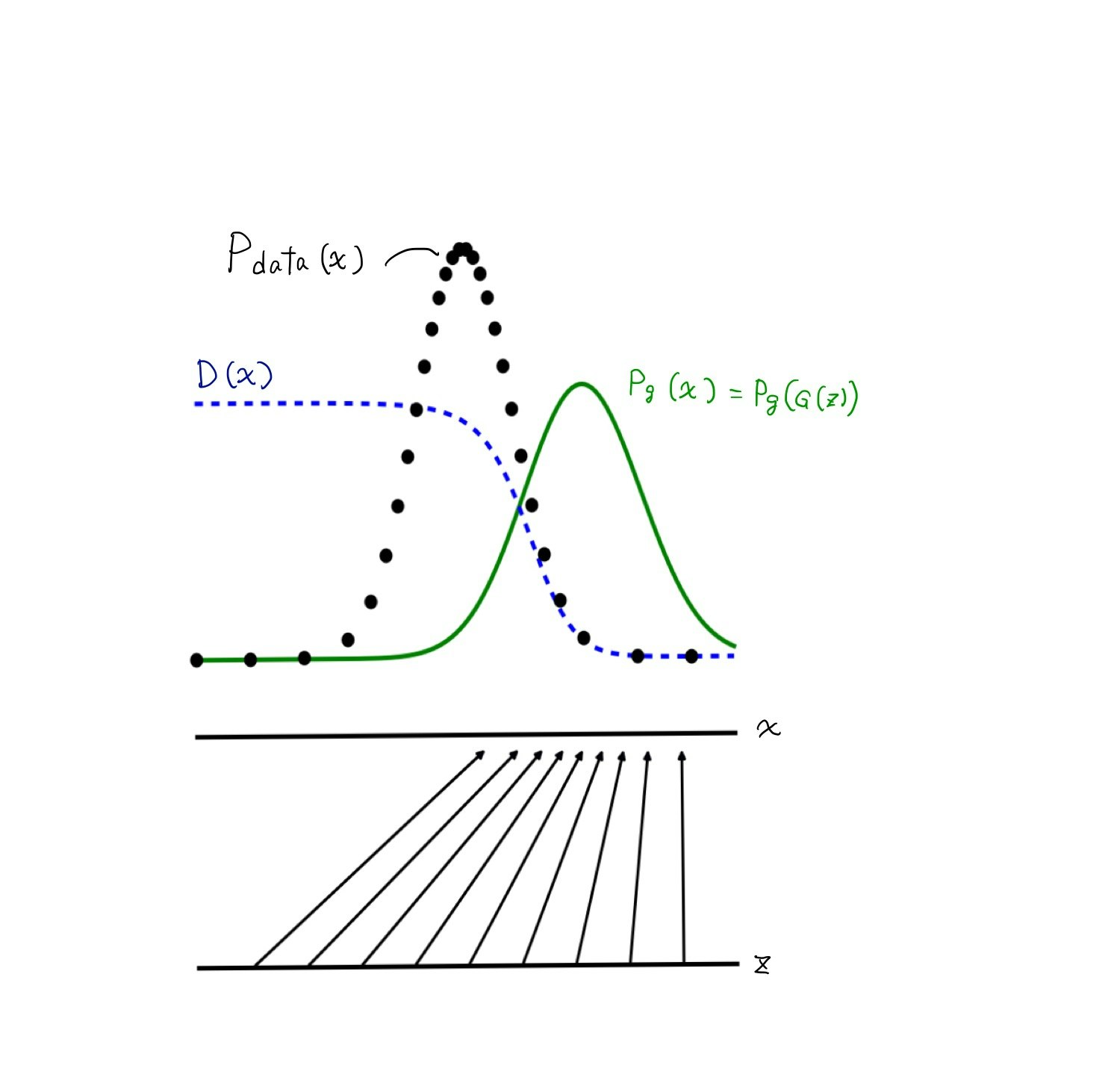
arXiv:1406.2661から引用。一部改変

この式は、$p_{data}(x)$の周り（つまり$p_g(x)$がほぼ0の領域）では、$D^*=1$に、逆に$p_g(x)$の周りでは$D^*=0$に。二つの分布の交点では$D^*=0.5$になります。

Jensen-Shannon ダイバージェンス

さらに、最適なDiscriminator下でのGeneratorの価値関数は

C(G) = -log(4) + 2\times JSD(p_{data}||p_g)

と表されます。

JSDはJensen-Shannon divergenceという、二つの確率密度間の距離を表す関数です。JSDが0になる時は、$p_{data}(x)$と$p_z(x)$が（全てのxで）完全に一致する時です。言い換えると通常のGANはJensen-Shannonダイバージェンスを指標に、二つの確率密度間の距離を学習によって近づけていく作業と見なせます。

　 Jensen-Shannonダイバージェンスを用いることの欠点は、勾配消失問題にあります。Generatorのパラメータ$\theta$の最適値周りで勾配が0になってしまい、学習がうまくいかなくなることが知られており、WGANの論文でそれが指摘されています。

そこで、Jensen-Shannonダイバージェンスの代わりに別の指標（距離）を用いてGANを作ってしまおう、というアイデアがでてきます。確率分布間の距離はいろいろありますが、Wasserstein距離を用いるコンセプトがWasserstein GAN (WGAN)です。

この距離を用いるメリットは、パラメータの最適点付近で勾配が消失せず、学習が安定して進む点にあります。

WGAN では、Jensen-Shanonダイバージェンスの代わりにWasserstein距離を用いた損失関数を定義します。いろいろ飛ばしてしまいますが、二つの確率密度間のWasserstein距離Wは以下のように表されます。

Kerasのフレームワークでは、損失関数の最小化をおこなうので、上記の式にマイナスをかけて最小化問題に定式化します。その結果、最小化すべき損失関数Lは

になります。$\tilde{x}$は、zより生成した画像を、xは本物の画像を示します。

JSDを用いた通常のGANに対するWasserstein距離の特徴は、

• 損失関数にlogを用いない

ことが上げられます。さらに、D(x)はもはや、識別結果としての意味をもたないため、出力をsigmoid関数によって[0,1]に押し込める必要もありません。WGANではD(x)をf(x)と表したり、Discriminatorの代わりにCriticと呼んだりします。

Discriminatorの制約条件

　さて、D(x)がWasserstein距離として意味を持つためには、一つの制約条件があります。それはD(x)がリプシッツな関数である（との）ことです。もはやこの辺りから、訳がわからなくなってきますが、一番初めに提唱されたWGANでは、この制約条件を満たすために、重みパラメータの最小、最大値をclipしています。

ただし、このclipという作業も、結構力技のようで学習が不安定になるそうな。そこで改良型のWGANでは、パラメータのclipの代わりに、損失関数にペナルティ項を与えることで学習の最適化を達成しています。

　以下、天下り式ですが説明します。最適化されたDiscriminatorにおいては、生成データと本物データ間の任意の点でDiscriminatorの生成データおよび本物データ間の任意の点$\hat{x}$に対する勾配のL2ノルムが1になるという性質があるそうです。この性質を逆手にとって、損失関数に勾配のL2ノルムが1以外のときにペナルティを課すことによって、Discriminatorの最適化を行っています。すなわち以下の損失関数を最小化することが改良型WGANすなわちWGAN-gp (gradient penalty)に他なりません。

ここで、$\hat{x}$は生成データと本物データを結んだ直線上の任意の点です。

Discriminatorの構造

WGAN-gpのDiscriminatorの構造を示します。まずは通常のGANのDiscriminatorの構造を示します。説明は以下

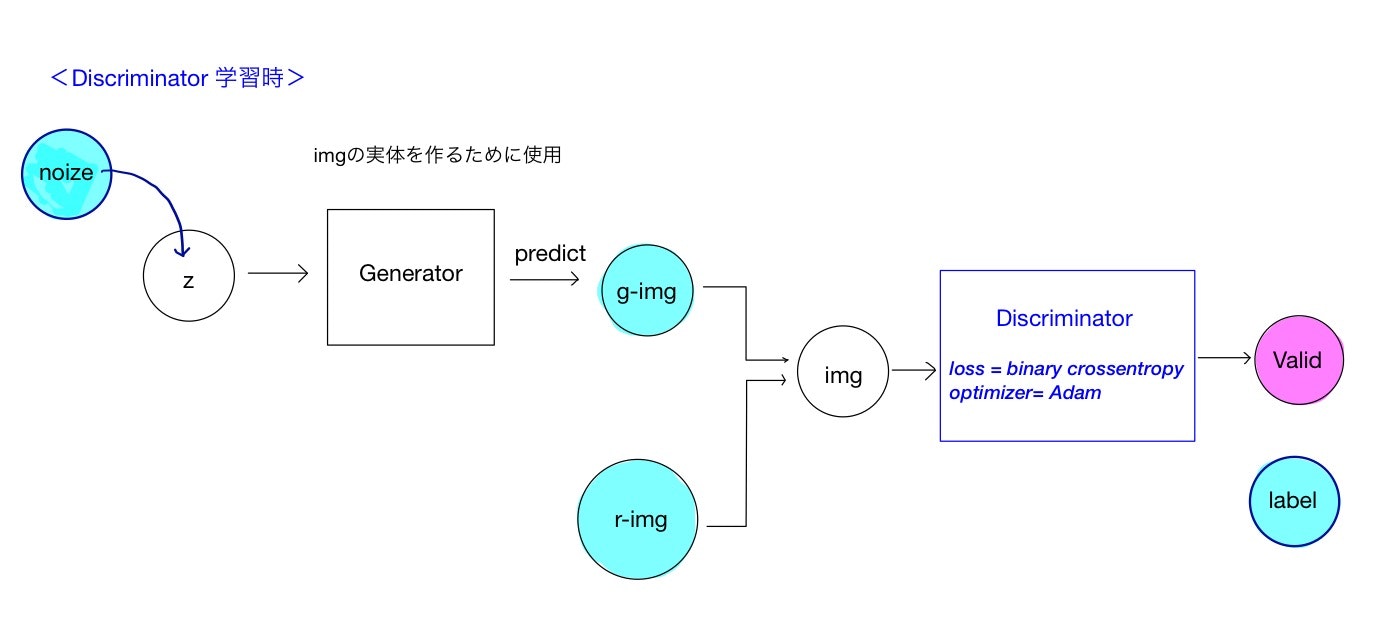
GeneratorとDiscriminatorを完全に切り離し、Discriminatorだけを考えました。本物データと、生成（偽物）データは別々に学習させています。

次に、WGAN-gpのDiscriminatorの構造を以下に示します。

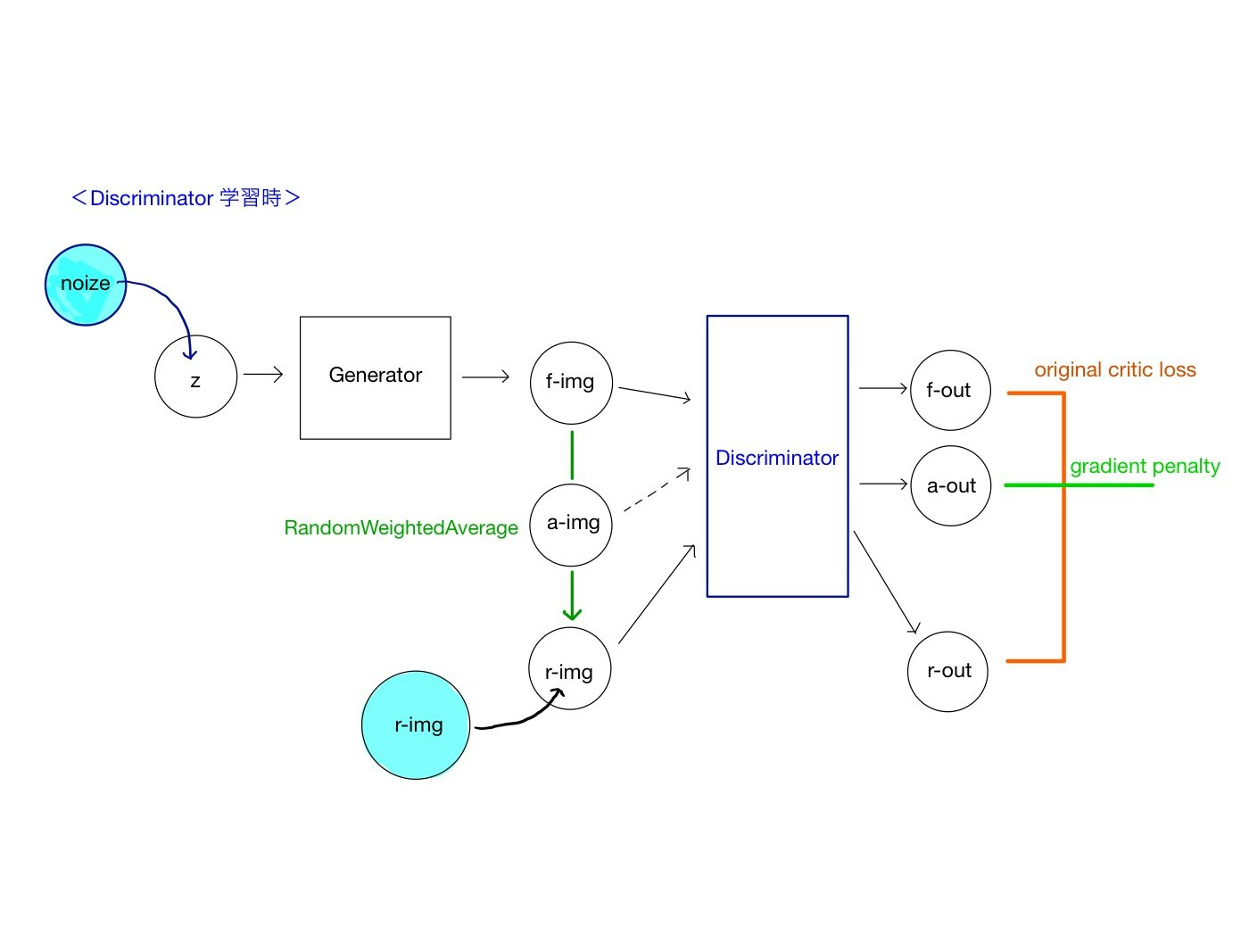
　WGAN-gpでは、本物データと生成データを同時に学習させる必要があるので、Generatorは切り離さず、入力データとして、noizeとr-imgを用いる構造とします。ただし、Discriminatorに対する実質的な入力はnoizeによって生成されたデータf-img（fはfakeの意）と、r-img（rはrealの意）に加え、二つのサンプル間の任意の点であるa-img（aはaverageの意）を用います。二つの入力値から、各入力を直線で繋いだ任意の点を用います。そのための関数としてRandomWeightedAverageを実装します。

　Discriminatorからの出力も、これに対応して3つです。f-outとr-outを用いてOriginal critic lossを、a-outを用いてgradient penaltyを記述して、損失関数を定義します。最終的にOptimizerを定義することによってDiscriminatorの学習を進めます。

生成画像

左が通常のGANの識別関数、右がWasserstein距離を用いたWGANです。ネットワークはどちらもDCGANを使用しています。

WGANの方は、学習初期黒い画面から段々もやもやっとあぶり出されてきます。ちょっと怖いですね笑
WGANの方がボヤッとした画像になることが知られていますが、この結果でもそうなっています。
mnistだとWGANの恩恵を感じにくいのかもしれませんね。

長くなったので、一度この辺りで切ります。次回は今回のコンセプトをKerasのコードを解説します。

180311 追記
アルゴリズムを見直したら改善しました。ぼやけない綺麗な画像が生成されています。

###次の記事
今さら聞けないGAN (5) WGAN-gpの実装