はじめに
引き続きGANについての考察をおこないます。
前々回の記事でGANについての基本構造を説明し、前回の記事でgenerator, discriminatorのネットワークをCNNに置き換えたDCGANを実装しました。
今回は画像を生成するうえでの種となる潜在変数zと、生成される画像、そして画像の識別結果について深堀りしていきます。コードはgithubに上げています。
生成モデル
mnist画像を元に生成モデルについて考えてみましょう。mnistは2次元の画像データなのですが、実際は縦28ピクセル、横28ピクセル、計784ピクセルのそれぞれに画素値が入っています。つまり、2次元画像なのですが、取り扱い的には784次元のデータとなることに注意してください。
さて、この784次元のキャンパスに画像を生成する意味について考えてみましょう。1つの画像データimgは784個の値の羅列で表せます。つまり、i番目のピクセル値を$x_i$とすると
img =(x_1, x_2, x_3, .., x_{784})
で表せます。
さて、生成モデル$P_{gen}$とは、各ピクセル値が任意の値をとった時の同時確率分布を求めることに他なりません。つまり
P_{gen} = p(x_1, x_2, x_3, .., x_{784})
これにより、例えば各ピクセルが全て0の時の確率とか、全て1の時の確率とか、もっと中間的な値とか、784次元のすべての値の分布についての確率を出せるようになります。つまり、全てのxの分布についての密度分布がわかるようになります。確率密度分布がわかることの最大のメリットは、その確率密度に基づいてデータを人工的に生成できることにあります。
サイコロを例にするとわかりやすいでしょう。あるサイコロを振る現象を観測したとき、多数の試行の結果、サイコロの目を表す一次元変数xの値が1,2,3,4,5,6のどれかをとり、かつその確率が全て等しいことがわかったとします。その場合、xの確率密度分布は
P(x) = 1/6\,(x = \{1,2,3,4,5,6\})
になります。一度生成モデルが決定されたら、確率密度分布からxの値をサンプリングすることができます。確率分布に従ってサイコロを振ればいいのです。
GANの生成モデル
この確率密度分布P(x)をニューラルネットワークで近似してやろうと言うのがGANのgeneratorの考え方です。潜在変数zが与えられた時に、zの条件付き確率分布D(x|z)を求めます。求めた確率分布からサンプリングを行うことでxつまり画像を生成します。
実際は、generatorは潜在変数から画像データの確率密度分布ではなく、画像データそのものを直接出力する関数です。本来確率分布からサンプリングするときは、その分布に従った揺らぎを持って確率論的に値を生成します。しかし、generatorの場合は同じzからは、常に(決定論的に)同じ値が出力されます。
生成画像の揺らぎは、zを乱数から決めることで再現する、という考え方なのでしょうか。このあたり、論文で論じられている確率密度関数と、実装上の決定論的な関数の理論的な関係性がイマイチよくわかっていません。お分かりの方いらっしゃったら教えていただけると幸いです。
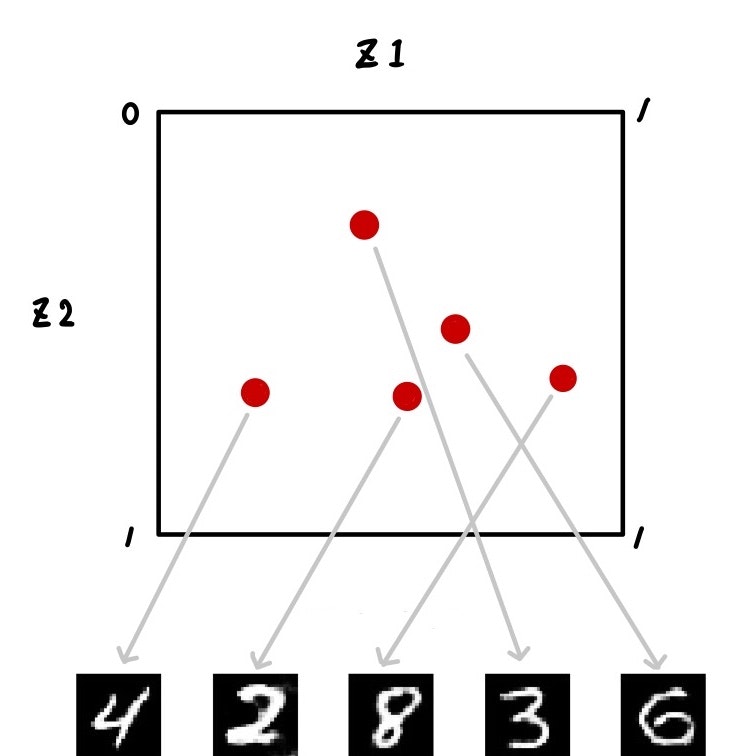
ともかく、潜在変数zから画像を生成するイメージを下図に示します。
潜在変数空間上zのある値に対して、決まった画像が出力されます。ここでは図示するためにzを2次元にしています。ランダムにサンプリングした各zから、それに対応した画像が生成されるイメージです。
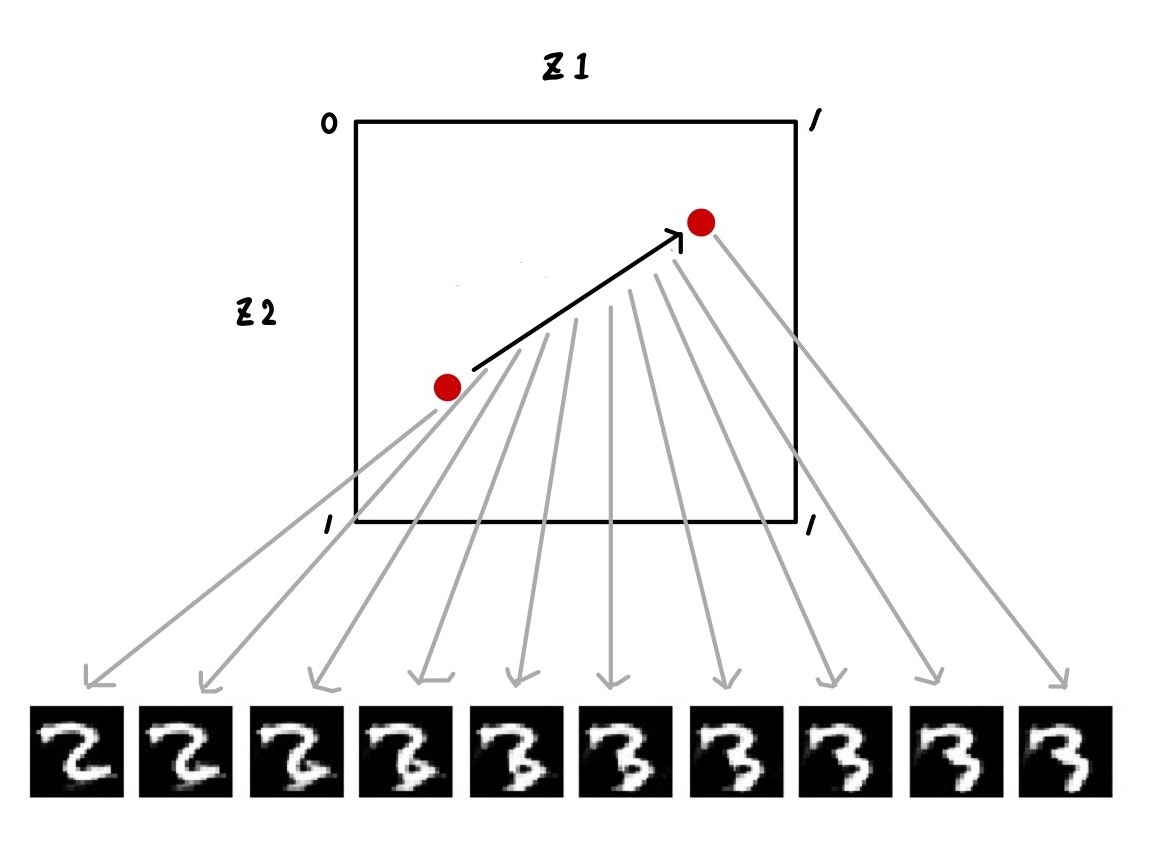
また、任意の2点間を連続的に変化させることで、生成する画像も連続的に変化させることができます。
潜在変数の次元
さて、discriminatorを迷わせるほど本物に近いデータを生成するにはzの次元をどれくらいに設定すれば良いでしょう。データの次元(784)くらい必要でしょうか。おそらくそんなことはないですね。言ってしまえば高々10種類の数字を表現するのですから、mnistデータの分布はそれよりも低い次元に集約されているはずです。
もし画素を縦横2倍にしたmnist改データがあったとき、22784=3136次元の潜在変数が必要になるとは思えないですよね。解像度が大きくなっても、そこに集約されている情報量は基本的に変わらないはずです。
それでは実際にzの次元数を変化させて、それぞれの生成画像を見てみましょう。
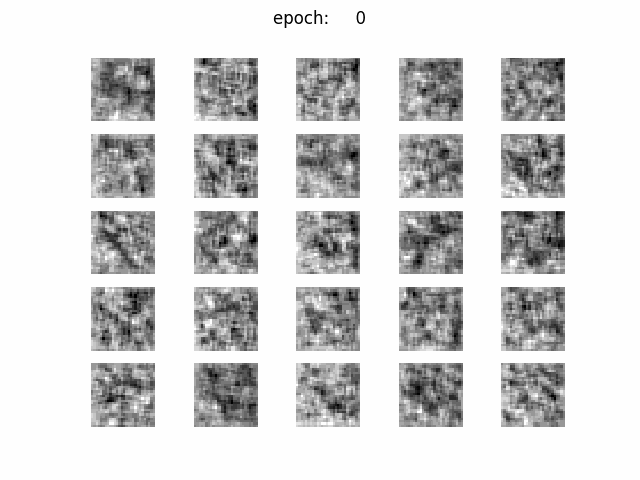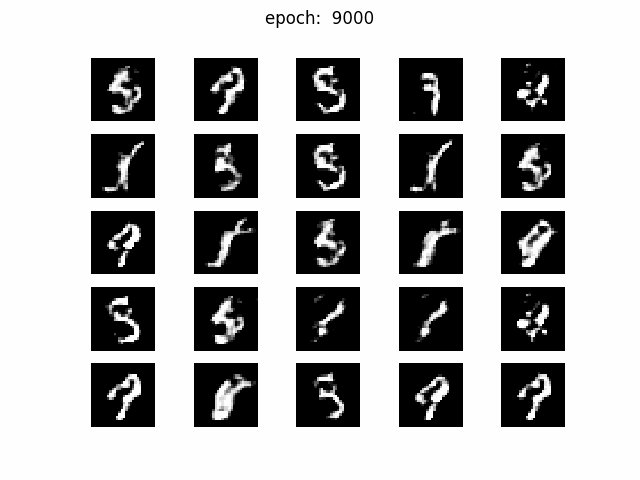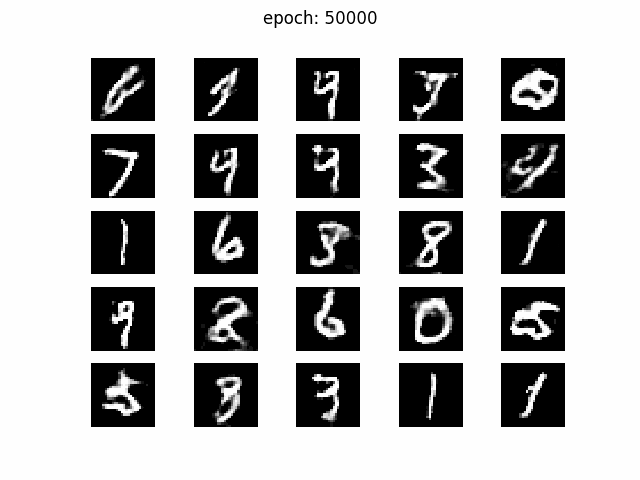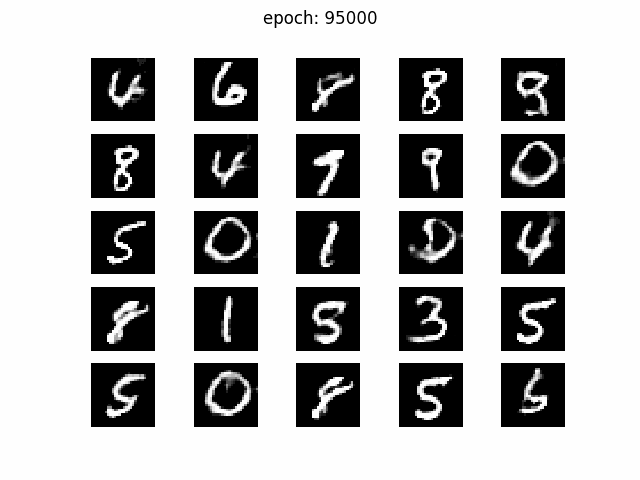
乱数は固定して、各iterationごとに同じzから画像を出力させています。
注: 図にepochと書かれていますが、実際はiterationの間違いです。
綺麗な画像が生成されていますね。乱数は固定されていますので30000 iteration辺りから
zのマッピングが収束して、各マスで同じような数字が生成されつづけています。
4が9になったり、3が8になったり、微妙に揺れていますね。
zの次元を段々小さくしていきます。
次はz_dim= 50
画像の質自体はz_dim= 100とそう変わりませんが、iterationを経てもそれぞれのマスで生成される数字が定まっている感じがしないですね。数字がパタパタと変わっていて、落ち着きがない感じです。学習のたびにgenerator関数が書き換わっていて、zのマッピングが収束していない気がします。あと、よく見ると5x5の25マスの中に同じような画像が多い気がします。
次はz=10

安定して生成されていますね。100より画質がクリアかも。
z=2
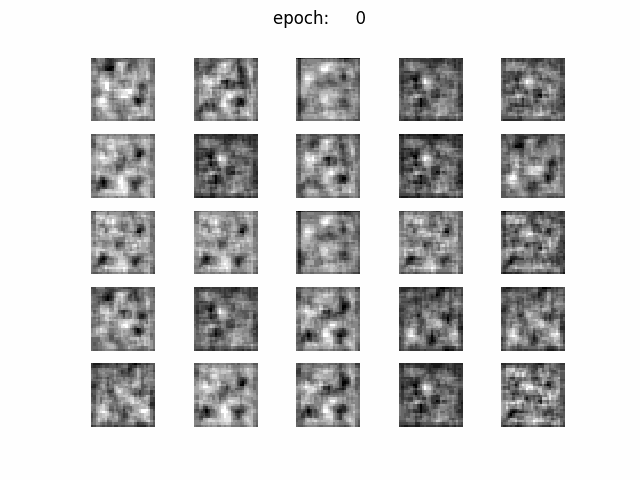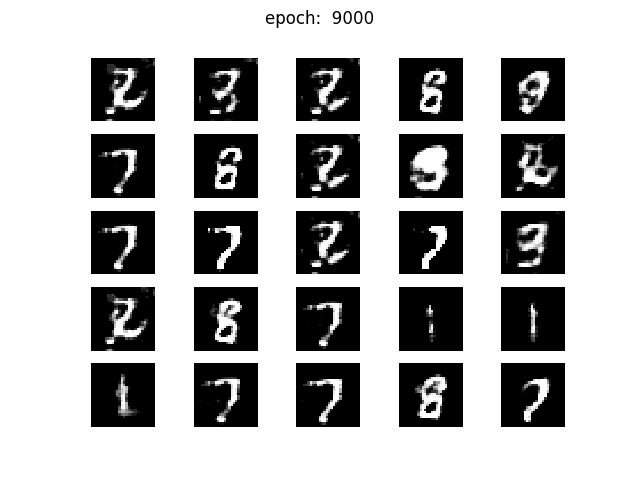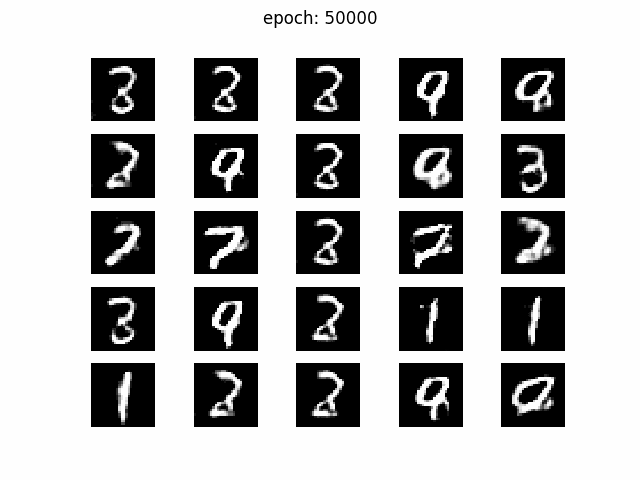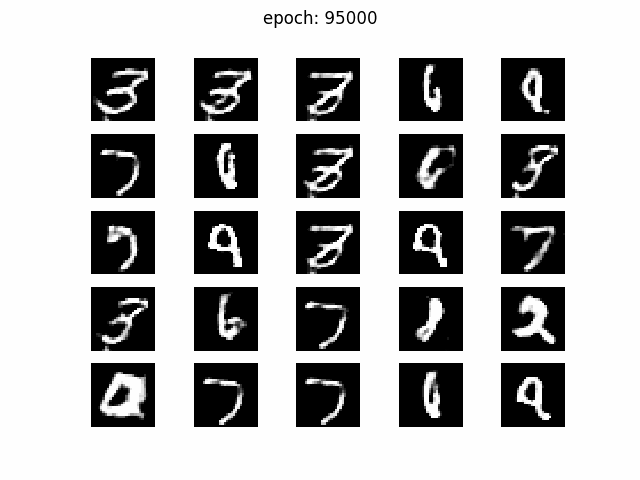
z_dim=50で見られた現象が顕著ですね。パタパタと画像が変わりますし、3なら3ばっかりとか、明らかに同じ画像が生成されています。
z=1

z_dim=2と同じです。画像自体はクリアなので、ここまでくると訓練データの分布を再現するような生成モデルを学習すると言うよりも、単に訓練データを模倣しているように思えます。
これはモード崩壊(mode collapse)と呼ばれる現象で、generatorの学習に失敗して、訓練データの(しばしば多峰性の)分布全体を表現できずに訓練データの最頻値(mode)のみを学習してしまいます。全国民の期待に応える能力がなく、とりあえず多数派のための政策をつくる、みたいなイメージですかね。
z_dim=2,1の時は、潜在変数の次元が不十分で、generatorが訓練データの分布を表現しきれず、苦肉の策として特定の画像に集中することで、discriminatorを騙す策をとったと言えます。
z_dim=50の時もモード崩壊の現象が見られました。z_dim=10で画像生成に成功していますので、次元が足りないという理由ではなさそうです。おそらく、generatorとdiscriminatorの学習係数のバランスが適切でなく、generatorの出力が特定の分布に集中したと考えられます。このあたりがGANのパラメータチューニングが難しい一因だと思っています。(間違っていたら教えてください)
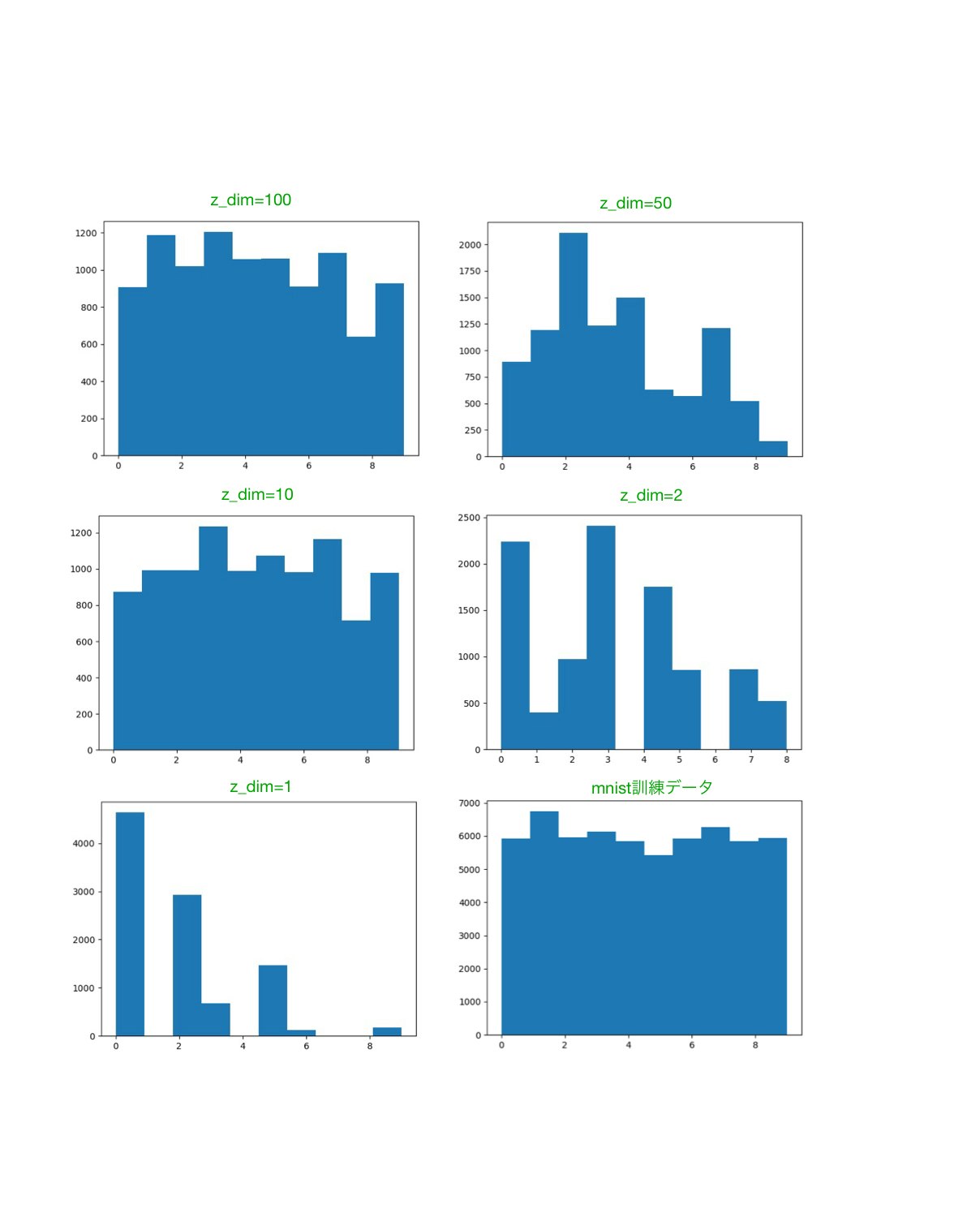
各次元数の生成モデルで、99000 iteration後に10000サンプル生成させたときの、各数字の頻度をヒストグラムにしたものが下図になります。といっても、実際にどの数字をGANが作ったかについてはわからないので、その代わりに数字を識別するモデルをCNN_classifierとして構築して(Kerasのexampleにあったものをそのままつかいました)、その識別結果を用いました。従って、あくまでCNN_classifierが考えたヒストグラムです。これをみてもサンプルを満遍なく生成しているのはz_dim=100, 10のときだとわかります。
さて、せっかくGANでサンプルを生成したいのにモード崩壊によって生成サンプルが偏ることは避けたいですね。モード崩壊が起きている、もしくは起きていないことを確認するにはどうすればよいでしょうか。PCに張り付いて生成サンプルを眺めるのは苦痛ですし、視角化できないサンプルには使えません。生成データを見ずに、学習時の損失関数から学習がうまくいっているかを判断することは可能でしょうか。
まとめ
dcganにより高精細な画像を生成することに成功しても、モード崩壊により望む出力を得られない問題があることがわかった
課題
- 生成結果を確認せずに学習の正否を判断する方法
- そもそもモード崩壊させない方法
次回
上記の課題に対応するために新しいGANにトライしてみます。(一応ストーリー仕立てになってます)Wesserstein GANなる手法を使えば、これらを解決できるとのことなので、実装して次回の記事にしたいと思います。