この文章は,英語の勉強を兼ねた
https://vincentherrmann.github.io/blog/wasserstein/
の和訳です.
twitter:@UMU____
私が見るに,最近提案されたWasserstein GAN(WGANs)はとても興味深いものである.この投稿では,WGANsについての背景や構造や利点については説明しない.WGANについての構造等については,元論文やこの素晴らしい要約(英語)を参照することをオススメする.その代わり,この投稿では主にKantorovich-Rubinstein 双対性とその特殊なケースの詳細について言及する.この双対性はある意味WGANsの中心的な役割を果たしていると考えられる.もちろん,この双対性についての研究は最近になって新しく示されたものではないが,WGANsという応用先としては魅力的な手法である.
元論文は,フィールズ賞受賞者のフランスの奇人Cedric Villaniによる“Optimal Transport - Old and New”を引用しており,これはVillaniのホームページからダウンロードできる.この文献は約千ページにも及ぶ数学博士や数学研究者向けに書かれたものである.楽しみながら読んでみてほしい.Villaniはここで取り上げる話題についても,このレクチャー動画でアクセスできる形で取り上げている(28分頃).原著に関する本質的な説明をしていて,かつ私の知らない膨大あな定義や定理の参照を含んでいない資料を見つけることにとても苦労した.この投稿によって,行間を埋める作業が多少は楽になるだろう.この投稿では基本的な線形代数,確率論,最適化の理論のみを用いている.厳密な証明はせずに,おおまかに理論を追っていくこととするが,理論の流れはできうる限り完全かつ明白になるようにしたので,この話題について何かを得られるのに十分なはずである.
WGANsのために必要となるKantorovich-Rubinstein双対性についての議論は,実はそれほど複雑すぎるものではなく,それ単体で理解できるものである.しかしながら,この理論はとても抽象的である,このため,私はこの抽象的な議論を結論まで先送りにして,まず理解しやすい離散的なケースと,線形計画法に関する問題から始めようと決めた.
もし興味があるなら,以降に使用されている図を作るために使用したJupyter notebookファイルを見ることができる.
Earth-Mover距離
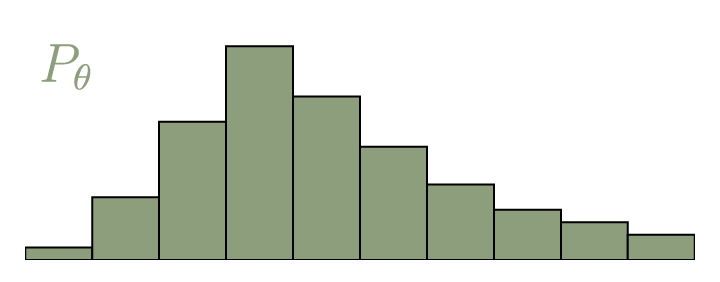
離散確率分布のみを考えれば,Wasserstein距離はEarth-Mover距離(EMD)ともよばれている.図1のような分布の違う確率密度分布を考え,これを土の山としてみると,EMDは,片方の確率分布の山をもう片方の確率分布の山に,土を輸送して変形させるための最小の労力である.ここで,輸送する労力とは,輸送する土の量と輸送する距離との積で定義される.2つある確率分布をそれぞれ $P_r$と $P_\theta$とし,それぞれから起きうる事象の変数を$x$,$y$,事象の数を$l$個とする.
EMDの上述の定義からわかるように,EMDを計算することそれ自体が最適化問題となっている.土を輸送して目的の形に変形する方法は無限の方法があるが,今ほしいのは最適な方法である.適切な土の輸送方法を求めるために,$\gamma(x,y)$を定義する.これは,$P_r$を $P_\theta$に変形するためにxからyへ土を輸送する量である(逆も然り).
訳注:ここでは輸送しない土は$\gamma(x,y=x)$で表すこととする.
輸送方法$\gamma(x,y)$を有効な方法とするために, $\sum_x \gamma(x,y) = P_r(y)$ と$\sum_y \gamma(x,y) = P_\theta(x)$が当然ながら制約されている必要がある.$\gamma$は,同時確率として考えることができ,この場合制約は$\gamma \in \Pi(P_r, P_\theta)$となる.$\Pi(P_r, P_\theta)$は$x$,$y$による周辺分布がそれぞれ$P_r$と$P_\theta$になるような同時確率分布の集合である.EMDを得るために,この同時確率$\gamma(x,y)$と,$x$と$y$との距離の積のすべての組み合わせの総和を計算する必要がある.これに基づき,EMDの定義は,次のようになる:
$$ \mathrm{EMD}(P_r, P_\theta) = \inf_{\gamma \in \Pi} , \sum\limits_{x,y} \Vert x - y \Vert \gamma (x,y) = \inf_{\gamma \in \Pi} \ \mathbb{E}_{(x,y) \sim \gamma} \Vert x - y \Vert $$
$\inf$という記号に不慣れである方へ説明すると,$\inf$はinfimum(最大の下界,下限)のことである.これは最小値とほぼ同じ意味である.infimumの逆はsupremum(上限)であり,後程この表記が出てくることになる.ここで,$\mathbf{\Gamma} = \gamma(x,y)$ , $\mathbf{D} = \Vert x - y \Vert$, $\mathbf{\Gamma}, \mathbf{D} \in \mathbb{R}^{l \times l}$とすれば,EMDは次のようにも表せる.
$$ \mathrm{EMD}(P_r, P_\theta) = \inf_{\gamma \in \Pi} , \langle \mathbf{D}, \mathbf{\Gamma} \rangle_\mathrm{F} $$
$\langle , \rangle_\mathrm{F}$は,フロベニウス積(対応する要素の積の総和)である.
図2 最適輸送方法$\mathbf{\Gamma}$と輸送距離$\mathbf{D}$
線形計画法
図2は,図1に示された$P_r$ から $P_\theta$への,最適輸送方法$\mathbf{\Gamma}$と輸送距離$\mathbf{D}$を示したものである.この最適輸送方法は,一般的な線形計画法(LP,Linear Programming)の手法を使って解くことができる.LPでは,次のような形式の問題を解くことができる:
$z = \mathbf{c}^T \mathbf{x}, \ \mathbf{c} \in \mathbb{R}^n$を最小化するようななベクトル$\mathbf{x} \in \mathbb{R}^n$は何か.ただし,
$\mathbf{x}$ は次のような制約を満たしているとする. $\mathbf{A} \mathbf{x} = \mathbf{b}, \ \mathbf{A} \in \mathbb{R}^{m \times n}, \mathbf{b} \in \mathbb{R}^m$ and $\mathbf{x} \geq \mathbf{0}$.
EMDを線形計画法で計算するために,まず$\mathbf{\Gamma}$ と $\mathbf{D}$をベクトル化する.
\begin{align}
\mathbf{x} &= \mathrm{vec}(\mathbf{\Gamma}) \\
\mathbf{c} &= \mathrm{vec}(\mathbf{D}) \\
\end{align}
これは $n = l^2$となることを意味する.また制約については,まず2つの活率分布を合体させて次のようにする.これにより $m=2l$となる.
\mathbf{b} = \begin{bmatrix} P_r \\ P_\theta\end{bmatrix}
$\mathbf{A}$については前述した制約を作るために大きい疎な0か1の行列を作成し,$\mathbf{x}$からいくつかの値をとって$\mathbf{b}$にするといったような計算を行う. 次式を見るとわかりやすい.
% <![CDATA[
\newcommand\FixWidth[1]{ \hspace{2.2em} \llap{#1}}
\begin{array}{rc}
& \left. \left[ \begin{array} {rrrr|rrrr}
\FixWidth{P_r(x_1)} & \FixWidth{P_r(x_2)} & \FixWidth{\dots} & \FixWidth{P_r(x_n)} & \FixWidth{P_\theta(y_1)} & \FixWidth{P_\theta(y_2)} & \FixWidth{\dots} & \FixWidth{P_\theta(y_n)}
\end{array} \right] \, \right\} \; \mathbf{b}^T \\ \\
\mathbf{x} \left\{ \begin{bmatrix}
\gamma(x_1, y_1) \\
\gamma(x_1, y_2) \\
\vdots \\ \hline
\gamma(x_2, y_1) \\
\gamma(x_2, y_2) \\
\vdots \\ \hline
\vdots \\ \hline
\gamma(x_n, y_1) \\
\gamma(x_n, y_2) \\
\vdots \\
\end{bmatrix} \right.
& \left. \left[ \begin{array}{rrrr|rrrr}
1 & 0 & \dots & 0 & 1 & 0 & \dots & 0 \cr
1 & 0 & \dots & 0 & 0 & 1 & \dots & 0 \cr
\vdots & \vdots & \dots & \vdots & \vdots & \vdots & \ddots & \vdots \cr \hline
0 & 1 & \dots & 0 & 1 & 0 & \dots & 0 \cr
0 & 1 & \dots & 0 & 0 & 1 & \dots & 0 \cr
\vdots & \vdots & \dots & \vdots & \vdots & \vdots & \ddots & \vdots \cr \hline
\FixWidth{\vdots} & \FixWidth{\vdots} & \FixWidth{\vdots} & \FixWidth{\vdots} & \FixWidth{\vdots} &
\FixWidth{\vdots} & \FixWidth{\vdots} & \FixWidth{\vdots} \cr \hline
0 & 0 & \dots & 1 & 1 & 0 & \dots & 0 \cr
0 & 0 & \dots & 1 & 0 & 1 & \dots & 0 \cr
\vdots & \vdots & \dots & \vdots & \vdots & \vdots & \ddots & \vdots \cr
\end{array} \right] \right\} \mathbf{A}^T
\end{array} %]]>
このように構築した線形計画問題に対して,線形計画問題を解くスタンダードなライブラリを使って解く.
import numpy as np
from scipy.optimize import linprog
# We construct our A matrix by creating two 3-way tensors,
# and then reshaping and concatenating them
A_r = np.zeros((l, l, l))
A_t = np.zeros((l, l, l))
for i in range(l):
for j in range(l):
A_r[i, i, j] = 1
A_t[i, j, i] = 1
A = np.concatenate((A_r.reshape((l, l**2)), A_t.reshape((l, l**2))), axis=0)
b = np.concatenate((P_r, P_t), axis=0)
c = D.reshape((l**2))
opt_res = linprog(c, A_eq=A, b_eq=b)
emd = opt_res.fun
gamma = opt_res.x.reshape((l, l))
すると図3のように最適輸送方法を計算することができた.
図3:最適輸送方法
双対形式
残念なことに,この手法を使った最適化はたくさんのケースで非現実的で,GANsが通常用いられるような分野においても同様に非現実的である.前述の例では,1次元で10個の事象をとりうる確率変数を扱った.確率変数がとりうる事象の数は,確率変数の次元の数が増えるにしたがって指数関数的に増大する.たとえば画像を取り扱いたければ,次元は優に数千次元を超えることになる.これでは,$\gamma$は次元が大きいので近似すらできない.
しかしながら,実際には我々は最適輸送方法$\gamma$を知りたいわけではない.知りたいのはただ1つの量,EMDのみである.同様に,WGANsにてgeneratorを学習するために必要となるのは,generatorが出力する分布$P_\theta$を正しい分布$P_r$にするためのEMDのみである.学習を行うためには,$P_r$ と $P_\theta$のみから計算される,EMDの勾配$\nabla_{P_\theta} \mathrm{EMD}(P_r, P_\theta)$が計算可能である必要がある.しかし直接的な方法では(次元が多いため,$\gamma$を計算するのが大変で)難しい.
結論から言えば,EMDをより簡便に計算するほかの方法がある.あらゆる線形計画問題は,その問題を定式化する2つの方法がある.主形式(primal form)と,それに対応する双対形式(dual form)である.
% <![CDATA[
\begin{array}{c|c}
\mathbf{primal \ form:} & \mathbf{dual \ form:}\\
\begin{array}{rrcl}
\mathrm{minimize} \ & z & = & \ \mathbf{c}^T \mathbf{x}, \\
\mathrm{so \ that} \ & \mathbf{A} \mathbf{x} & = & \ \mathbf{b} \\
\mathrm{and}\ & \mathbf{x} & \geq &\ \mathbf{0}
\end{array} &
\begin{array}{rrcl}
\mathrm{maximize} \ & \tilde{z} & = & \ \mathbf{b}^T \mathbf{y}, \\
\mathrm{so \ that} \ & \mathbf{A}^T \mathbf{y} & \leq & \ \mathbf{c} \\ \\
\end{array}
\end{array} %]]>
変数間の関係式を変えることによって,最小化問題を最大化問題へと変形することができる.双対形式では,目的関数$\tilde{z}$は$\mathbf{b}$に直接依存している.$\mathbf{b}$は$P_r$ と $P_\theta$を含んだものであるので,これがまさに我々が欲していたものである.この$\tilde{z}$が(主形式の方の)$z$の下界になることは,容易に示される.
$$ z = \mathbf{c}^T \mathbf{x} \geq \mathbf{y}^T \mathbf{A} \mathbf{x} = \mathbf{y}^T \mathbf{b} = \tilde{z} $$
これは弱双対定理と呼ばれている.定理の名前から推察できるように,強双対定理というのも存在し,強双対定理は,双対問題に最適値$\tilde{z}$が存在するならば,それは主問題の最適値$z$と等しい($z=\tilde{z}$)ということを主張する.強双対定理を証明するのは少し複雑で,Farkasの補題を示す必要がある.
Farkasの補題
行列$\hat{\mathbf{A}} \in \mathbb{R}^{d \times n}$の列をベクトル$\mathbf{a}_{1}$$\mathbf{a}_{2}, ..., \mathbf{a}_{n} \in \mathbb{R}^{d}$とみなすことにする.これらのベクトルの線形非負結合で表される領域は,原点を頂点とする凸錘になる(もちろん全空間 $\mathbb{R}^{d}$となりうる).この領域を非負結合の係数$\mathbf{x} \in \mathbb{R}^{n}_{\geq 0}$であらわす.
ここで,ベクトル$\hat{\mathbf{b}} \in \mathbb{R}^{d}$を考えると,2つの可能性がある.$\hat{\mathbf{b}}$が凸錘の領域に含まれるか,含まれないかである.仮に$\hat{\mathbf{b}}$が凸錘に含まれないとすると,$\hat{\mathbf{b}}$と凸錘の間に超平面$h$を作ることができ,超平面の$\hat{\mathbf{b}}$側の法線$\hat{\mathbf{y}} \in \mathbb{R}^{d}$を定義できる.この超平面$h$上のベクトル$\mathbf{v} \in \mathbb{R}^{d}$に関して,内積$\mathbf{v}^T \hat{\mathbf{y}}$は,$\mathbf{v}$が$\mathbf{b}$側にあれば正,その逆側にあれば負,超平面上なら零となる.よって,図4のように,超平面$h$が存在すれば,どの$\mathbf{a}_i$をとっても$\mathbf{b}$とは超平面$h$を境にして逆側に存在する.(存在しなければそのようにできない.)
図4: Frakasの補題の幾何学的なイメージ.$\mathbf{b}$が青い凸錘の外側にあれば,$h$を$\mathbf{b}$と凸錘の間にひくことができる.
すなわち,次の2つの条件のうち,常に片方のみが正しいといえる.
- $(1)$ $\hat{\mathbf{A}} \mathbf{x} = \hat{\mathbf{b}}$ かつ $\mathbf{x} \geq \mathbf{0}$となるような$\mathbf{x} \in \mathbb{R}^{n}$が存在する.
- $(2)$ $\hat{\mathbf{A}}^T \hat{\mathbf{y}} \leq \mathbf{0}$ かつ $\hat{\mathbf{b}}^T \hat{\mathbf{y}} > 0$となるような $\hat{\mathbf{y}} \in \mathbb{R}^{d}$が存在する.
この定理をFarkasの補題と呼ぶ.Farkasの補題には微妙に違うバージョンや違う証明があるが,今ここで必要なものは上記に示したもので十分である.
強双対性
強双対定理の証明のつづきは,元の線形計画問題に1つの新しい次元を導入して,$\hat{\mathbf{b}}$が凸錘のほんの近くにいるような問題を考える.そして,Frakasの補題より,ある$\hat{\mathbf{y}}$において,それに基づく超平面は$\hat{\mathbf{b}}$に任意に近づくことができる.これに弱双対定理を加えて,強双対性定理を証明する.
主問題の最適値(最小値)を${z^* } = \mathbf{c}^T \mathbf{x}^{* }$とする.さらに次を定義する.
\hat{\mathbf{A}} = \begin{bmatrix} \mathbf{A} \\ -\mathbf{c}^T \end{bmatrix}, \ \ \
\hat{\mathbf{b}}_\epsilon = \begin{bmatrix} \mathbf{b} \\ -z^* + \epsilon \end{bmatrix}, \ \ \
\hat{\mathbf{y}} = \begin{bmatrix} \mathbf{y} \\ \alpha \end{bmatrix}
ただし $\epsilon, \alpha \in \mathbb{R}$である. $\epsilon = 0$の場合を考えると, これはFrakasの補題の$(1)$の場合である.これは$\hat{\mathbf{A}} \mathbf{x}^* = \hat{\mathbf{b}}_0$であるからである. $\epsilon > 0$の場合を考えると, 非負の解は存在せず, ($z^{* }$ がすでに最適値であるから) Farkasの補題の$(2)$に相当する. これはすなわち,次式を満たす$\mathbf{y}$ and $\alpha$が存在するということである.
\begin{bmatrix} \mathbf{A} \\ -\mathbf{c}^T \end{bmatrix}^T
\begin{bmatrix} \mathbf{y} \\ \alpha \end{bmatrix} \leq \mathbf{0}, \ \ \ \
\begin{bmatrix} \mathbf{b} \\ -z^* + \epsilon \end{bmatrix}
\begin{bmatrix} \mathbf{y} \\ \alpha \end{bmatrix} > 0
または次のようにも表せる.
$$\mathbf{A}^T \mathbf{y} \leq \alpha \mathbf{c}, \ \ \mathbf{b}^T \mathbf{y} > \alpha(z^* - \epsilon).$$
先ほど構築したような方法で,$\hat{\mathbf{b}}_0 \hat{\mathbf{y}} = 0$となるような$\hat{\mathbf{y}}$を見つけることができる.また,$\epsilon$を0より大きい数にすると,$\hat{\mathbf{b}}_0 \hat{\mathbf{y}} > 0$となる.我々が考えている問題では,$z^* > 0$であるので,これは$\alpha > 0$が成立しているときのみ可能である.先ほど示したように$\hat{\mathbf{y}}$は超平面の法線であるから,正ならば大きさを自由に変えることができる.よって,$\alpha = 1$としても一般性を失わない.これは次式を満たす$\mathbf{y}$が存在することを示している.
$$
\mathbf{A}^T \mathbf{y} \leq \mathbf{c}, \ \ \mathbf{b}^T \mathbf{y} > z^* - \epsilon.$$
よって,主問題と双対問題の関係において,あらゆる$\epsilon > 0$について$\tilde{z} := z^* - \epsilon$であることがわかる.弱双対定理より,$\tilde{z} \leq z^{* }$であるから,すなわちこれは主問題の最適値と双対問題の最適値が(存在すれば)一致することを意味する.
双対形式化
これでやっと自信をもってEMDを計算するための双対形式への変換をすることができる.双対形式のところで示したように,$\tilde{z}^* = \mathbf{b}^T \mathbf{y}^{* }$(双対形式の最適値)が求めるEMDになる.次式を定義する.
\mathbf{y}^* = \begin{bmatrix} \mathbf{f} \\ \mathbf{g} \end{bmatrix}
ただし, $\mathbf{f}, \mathbf{g} \in \mathbb{R}^d$.これは$\mathrm{EMD}(P_r, P_\theta) = \mathbf{f}^T P_r + \mathbf{g}^T P_\theta$を意味する. 双対形式の制約$\mathbf{A}^T \mathbf{y} \leq \mathbf{c}$を考える:
% <![CDATA[
\newcommand\FixWidth[1]{ \hspace{1.6em} \llap{#1}}
\begin{array}{rc}
& \left. \left[ \begin{array} {rrr|rrr|r|rrr}
\FixWidth{\mathbf{D}_{1,1}} & \FixWidth{\mathbf{D}_{1,2}} & \FixWidth{\dots} & \FixWidth{\mathbf{D}_{2,1}} & \FixWidth{\mathbf{D}_{2,2}} & \FixWidth{\dots} & \FixWidth{\dots} & \FixWidth{\mathbf{D}_{n,1}} & \FixWidth{\mathbf{D}_{ n,2}} & \FixWidth{\dots}
\end{array} \right] \, \right\} \; \mathbf{c}^T \\ \\
\mathbf{y} \left\{ \begin{bmatrix}
f(x_1) \\
f(x_2) \\
\vdots \\
f(x_n) \\ \hline
g(x_1) \\
g(x_2) \\
\vdots \\
g(x_n) \\
\end{bmatrix} \right.
& \left. \;\; \left[ \begin{array} {rrr|rrr|r|rrr}
1 & 1 & \dots & 0 & 0 & \dots & \dots & 0 & 0 & \dots \cr
0 & 0 & \dots & 1 & 1 & \dots & \dots & 0 & 0 & \dots \cr
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \dots & \vdots & \vdots & \vdots \cr
0 & 0 & \dots & 0 & 0 & \dots & \dots & 1 & 1 & \dots \cr \hline
1 & 0 & \dots & 1 & 0 & \dots & \dots & 1 & 0 & \dots \cr
0 & 1 & \dots & 0 & 1 & \dots & \dots & 0 & 1 & \dots \cr
\vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \dots & \vdots & \vdots & \ddots \cr
\FixWidth{0} & \FixWidth{0} & \FixWidth{\dots} & \FixWidth{0} & \FixWidth{0} & \FixWidth{\dots} & \FixWidth{\dots} & \FixWidth{0} & \FixWidth{0} & \FixWidth{\dots}
\end{array} \right] \right\} \mathbf{A}\phantom{^T ;}
\end{array} %]]>
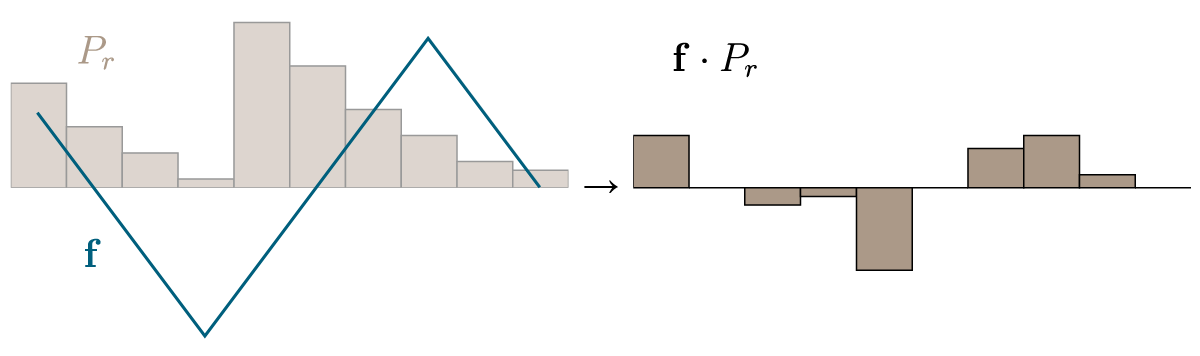
ベクトル$\mathbf{f}$ and $\mathbf{g}$の値は関数 $f$ and $g$として表現することができる.この表記を道いると,上記の制約は,すべての$i$について,$f(x_i) + g(x_j) \leq \mathbf{D}_{i,j}$と書ける. $i=j$の場合は$\mathbf{D}_{i,i} = 0$であるから$g(x_i) \leq -f(x_i)$となる.ここで, $P_r$ and $P_\theta$は非負であるから,目的関数(EMD)を最大化するには,$\sum_i \mathbf{f}_i + \mathbf{g}_i $が可能な限り大きい必要がある.そしてこの和は最大で0となり,このとき$g = - f$である.これは、ほかの制約に影響を与えず真のままである.よって,$g(x_{i}) < - f(x_{i})$を選ぶことは,図5を見ればわかる通り,ほかの制約に影響を与えずに,$g = - f$を与えることで目的関数の値を増加させることができるので,意味がない.
図5 双対問題の制約条件.青と赤の線は$\mathbf{f}$ and $\mathbf{g}$の上限を表している.$\mathbf{f} \neq -\mathbf{g}$となるすべての解は,目的関数をよくする余地を残している.
よって,$g = - f$となり,制約条件は,$f(x_i) - f(x_j) \leq \mathbf{D}_{i,j}$ and $f(x_i) - f(x_j) \geq -\mathbf{D}_{i,j}$と書き換えられる.この制約は, $f(x_i)$ を連続関数としてみると,上下方向の勾配が制限されていることになる.ここではユークリッド距離を用いており,勾配は $1$ and $-1$で制限されていることになるだろう.この制約のことを(1-)リプシッツ連続とよび,$\lVert f \lVert_{L \leq 1}$とかく.よって,双対形式化したEMDは,次のように表せる.
$$ \mathrm{EMD}(P_r, P_\theta) = \sup_{\lVert f \lVert_{L \leq 1}} \ \mathbb{E}_{x \sim P_r} f(x) - \mathbb{E}_{x \sim P_\theta} f(x). $$
実装は次のようになる(簡単).結果は図6.
# linprog() can only minimize the cost, because of that
# we optimize the negative of the objective. Also, we are
# not constrained to nonnegative values.
opt_res = linprog(-b, A, c, bounds=(None, None))
emd = -opt_res.fun
f = opt_res.x[0:l]
g = opt_res.x[l:]
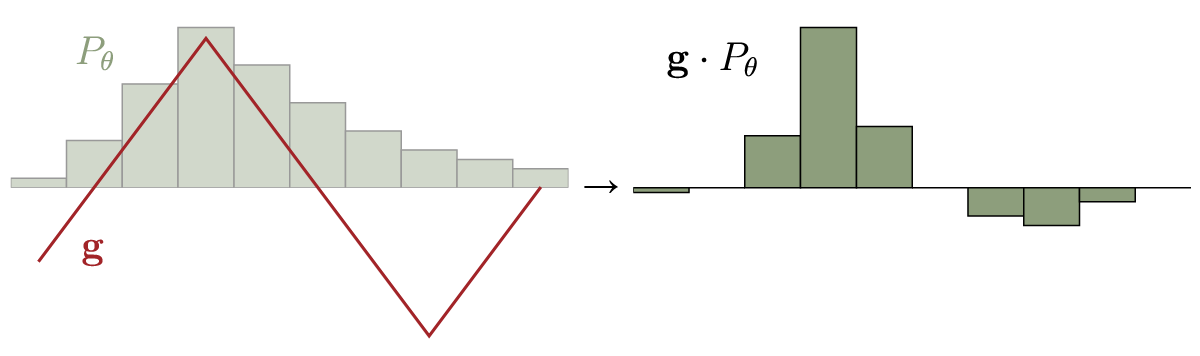
図6 $\mathbf{f}$と$P_r$の要素積,ならびに$\mathbf{g} = -\mathbf{f}$と$P_\theta$の要素積
みてわかるように,最適戦略はもちろん$P_r(x) > P_\theta(x)$であるときに$f(x)$を高い値に,逆に $P_\theta > P_r$であるときは,低い値にすることである.
Wasserstein距離
最後に,確率分布が連続的であるときを考える.もちろん,直感的には,前述の離散的なものを無限に状態があると考え,同様なやりかたを行えば,同じようなことが言える.しかしながら,初めに言ったように,もっときれいな方法に挑戦する.連続分布$p_r$,$p_\theta$および同時分布$\pi(p_r, p_\theta)$を考える.するとWasserstein距離は次のようになる.
$$W(p_r, p_\theta) = \inf_{\gamma \in \pi} \iint\limits_{x,y} \lVert x - y \lVert \gamma (x,y) , \mathrm{d} x , \mathrm{d} y = \inf_{\gamma \in \pi} \mathbb{E}_{x,y \sim \gamma} \left[ \lVert x - y \lVert \right]. $$
ここに適切な項を付けると,$\gamma$についての分布の制約を除くことができる.この場合適切な項とは,関数$f: x \mapsto k \in \mathbb{R}$に関する新たな最適化項を追加することである:
% <![CDATA[
\begin{array}{rl}
W(p_r, p_\theta) & = \inf\limits_{\gamma \in \pi} \mathbb{E}_{x,y \sim \gamma} [ \lVert x - y \lVert ] \\
&\begin{array}{cc}
= \inf\limits_{\gamma } \mathbb{E}_{x,y \sim \gamma} [ \lVert x - y \lVert & + \; \underbrace{\sup\limits_{f} \mathbb{E}_{s \sim p_r}[f(s)] - \mathbb{E}_{t \sim p_\theta}[f(t)] - \left( f(x) - f(y) \right)} ] \\
&= \cases{\begin{align} 0, & \ \ \ \mathrm{if \ \gamma \in \mathrm{\pi}} \\ + \infty & \ \ \ \mathrm{else} \end{align}} \end{array}\\
& = \inf\limits_{\gamma} \ \sup\limits_{f} \ \mathbb{E}_{x,y \sim \gamma} [ \lVert x - y \lVert + \mathbb{E}_{s \sim p_r}[f(s)] - \mathbb{E}_{t \sim p_\theta}[f(t)] - \left( f(x) - f(y) \right) ]
\end{array} %]]>
このようにすることによって,変わりに2段階計画問題を得た.これは外側の最適化($\inf_\gamma$)を行うためのすべての値について,内側の最適化($\sup_f$)を行う必要があるということである.次に,特定の場合において $\inf$と$\sup$を入れ替えられるミニマックス原理を利用する.その前に,我々が考えている問題がそのような特殊ケースであるかどうかを示す.
関数$g: A, B \rightarrow \mathbb{R}$を考える.$g(\hat{a}, \hat{b}) = \inf_{a \in A} \sup_{\ b \in B} g(a,b)$(最大のうちで最も低い)と$g(\hat{a}’, \hat{b}’) = \sup_{\ b \in B} \inf_{a \in A} g(a,b)$(最小のうちで最も高い)とする.$g(\hat{a}, \hat{b}) \geq g(\hat{a}’, \hat{b}’)$は,$g(\hat{a}, \hat{b})$が自動的に$\sup_{\ b \in B} \inf_{a \in A} g(a,b)$の下限の候補になることからわかる.その逆は成り立たない.
$g(\hat{a}, \hat{b}) > g(\hat{a}’, \hat{b}’)$が成り立つとき,少なくとも次の二つは成り立つ.
- $g(\hat{a}+t, \hat{b}) < g(\hat{a}, \hat{b})$が t \neq 0$でないときに成り立つ. これは$a$について$\sup_{\ b \in B} g(a,b)$が凸出ないときにのみ成り立つ.なぜなら,$\hat{a}$について$g(\hat{a}, \hat{b})$がすでに下限となているからである.
- $g(\hat{a}’, \hat{b}’+t) > g(\hat{a}’, \hat{b}’)$が$t \neq 0$出ないときに成り立つ. これは$\inf_{\ a \in A} g(a,b)$が$b$について凹出ないときにのに成り立つ.なぜなら, $\hat{b}’$について$g(\hat{a}’, \hat{b}’)$がすでに上限となっているからである.
これは,すなわち,$\sup_{\ b \in B} g(a,b)$が凸でかつ$\inf_{\ a \in A} g(a,b)$が凹であるとき,ミニマックス原理が適用てきて$g(\hat{a}, \hat{b}) = g(\hat{a}’, \hat{b}’)$がいえるということである.我々の場合では,この条件はすでに下括弧から凸条件が満たされていることがわかる.よって$\sup \inf$を交換できます.交換すると,次のようになる.
\begin{array}{ll}
&\phantom{= , } \sup\limits_{f} \ \inf\limits_{\gamma} \ \mathbb{E}_{x,y \sim \gamma} [ \lVert x - y \lVert + \mathbb{E}_{s \sim p_r}[f(s)] - \mathbb{E}_{t \sim p_\theta}[f(t)] - (f(x) - f(y)) ] \\
&\begin{array}{cc}
= \sup\limits_{f} \ \mathbb{E}_{s \sim p_r}[f(s)] - \mathbb{E}_{t \sim p_\theta}[f(t)] + & \underbrace{ \inf\limits_{\gamma} \ \mathbb{E}_{x,y \sim \gamma} [ \lVert x - y \lVert - ( f(x) - f(y))} ] \\
&= \cases{\begin{align} 0, & \ \ \ \mathrm{if} \ \| f \| {}_{L} \leq 1\\ - \infty & \ \ \ \mathrm{else} \end{align}}
\end{array}
\end{array}
加えて必要な下界の凹性も確認できた.ここで,リプシッツ連続となる関数$f$について,$\inf_\gamma$は同じ最適値となり,さらにリプシッツ連続であることが(訳注:それ以外はマイナス無限大となるため)$\sup_f$の最適値として必要であるから,この二段階計画問題を制約付き計画問題に変形することができる.よって,Wasserstein distanceの双対形式は,次のようになる.
\begin{align}
W(p_r, p_\theta) & = \sup_{f} \ \mathbb{E}_{s \sim p_r}[f(s)] - \mathbb{E}_{t \sim p_\theta}[f(t)] + \inf_{\gamma} \ \mathbb{E}_{x,y \sim \gamma} [ \lVert x - y \lVert - ( f(x) - f(y)) ] \\
& = \sup_{\lVert f \lVert_{L \leq 1}} \ \mathbb{E}_{s \sim p_r}[f(s)] - \mathbb{E}_{t \sim p_\theta}[f(t)]
\end{align}
これが,Wasserstein距離に関するKantorovich-Rubinstein双対性である.これは実は,我々が使っているユークリッド距離ではないほかの測度でも成り立つことが知られている.しかし,関数 $f$はニューラルネットワークを用いて近似するのに適しており,この方法では,リプシッツ連続性が重みを制約づけることで達成できるという利点がある.
(訳終)
一言感想
いい勾配が出る距離を使おう!