はじめに
こんにちは。株式会社エイアイ・フィールドでプロダクト開発をしている久保です。この記事はエイアイ・フィールドアドベントカレンダー2021の14日目の記事です。この記事では、多腕バンディット問題について、前回の続きで、DMEDアルゴリズムについての紹介をします。問題設定は初回記事をご覧ください。
UCBアルゴリズムの考え方の改良
前回バンディット問題の一つの方策としてUCBアルゴリズムを紹介しました。そこでは、はUCBスコアと呼ばれる
$$
\hat{\mu}_i(t) + \sqrt{\frac{\log t}{2 N_i(t)}}
$$
という量で判断し、このスコアのもっとも大きな腕$i$を選択するというものでした。ここで、$\hat{\mu}_i$はマシン$i$の結果から推定される確率。$t$は現在までに使ったコインの数。$N_i$は現在までにそのマシンに使ったコインの数です。ここをもう少し詳しく見てみると各腕に対して、
$$
\max\{\mu| 2N_i(t)(\hat{\mu}_i(t)-\mu)^2 \geq \log t \}
$$
という量を評価していることになります。ここで、$(\mu - \hat{\mu}_i(t))^2$という量に注目すると、これは期待値の二乗誤差について評価しているようです。これは、Hoeffdingの不等式による評価からきているのですが、こちらをChernoff-Hoeffdingによる評価に置き換えるとより精度の高い評価を与えることができます。つまり、
$$
\max\{\mu| 2N_i(t)d(\hat{\mu}_i(t), \mu) \geq \log t \}
$$
とすると、より精度を高くできます。ここで、$d(\mu, \mu')$はベルヌーイ分布間のKL divergenceで
$$
d(\mu, \mu') := \mu \log \frac{\mu}{\mu'} + (1 - \mu )\log \frac{1-\mu}{1-\mu'}
$$
と定義されます。これを$\mu$について解いてアルゴリズムとすれば、UCBをより改良した、KL-UCBアルゴリズムというものが得られます。
しかしながら、$\mu$について解計算がく計算が若干面倒です。このあたりの面倒な部分を近似によって解消したアルゴリズムが**DMED(Deterministic Minimum Empirical Divergence)**アルゴリズムです。
DMEDアルゴリズム
DMEDアルゴリズムでは、ループを回しながら、腕を選んでいくことになります。
より詳細に言うと現在のループで試すべき腕と次のループで試すべき腕を分けて考え、現在のループ中に
$$
N_i(t)d(\hat{\mu}_i(t), \hat{\mu}^*(t)) \leq \log t
$$
を満たす腕$i$を次のループで回します。ここで、$\hat{\mu}^*(t)$は、
$$
\hat{\mu}^*(t) = \max_i\{\hat{\mu}_i(t)\}
$$
であり、その時刻で最も値の大きい腕の期待値です。何はともあれ数値実験をしてみましょう。
import random
import math
class PlayBoard:
def __init__(self, n_machines=3, n_coins=100):
self.reset_machines(n_machines)
self.reset_history(n_coins)
def reset_machines(self, n_machines):
self.n_machines = n_machines
self.machine_mu = [random.random() for _ in range(self.n_machines)]
def set_machines(self, machine_mu):
self.n_machines = len(machine_mu)
self.machine_mu = machine_mu
def reset_history(self, n_coins):
self.n_coins = n_coins
self.history = []
self.reward = 0
def play(self, arm):
if self.n_coins < 1:
return
self.n_coins -= 1
record = {'arm': arm, 'result': None}
if random.random() < self.machine_mu[arm]:
record['result'] = 1
self.reward += 1
else:
record['result'] = 0
self.history.append(record)
return record['result']
def b_divergence(p, q):
if q == 0:
if p == 0:
return 0
return 100_000_000
if q == 1:
if p == 1:
return 0
return 100_000_000
if p == 0:
return - math.log(1-q)
if p == 1:
return - math.log(q)
return p * math.log(p/q) + (1-p) * math.log((1-p)/(1 - q))
class Score:
def __init__(self, arm):
self.arm = arm
self.n_tries = 0
self.reward = 0
def get_ucb_score(self, count):
if self.n_tries == 0:
return 100_000_000
return self.reward / self.n_tries + math.sqrt(math.log(count) / 2 / self.n_tries)
def get_mu_hat(self):
if self.n_tries == 0:
return 100_000_000
return self.reward / self.n_tries
class Scores:
def __init__(self, n_scores):
self.scores = [Score(arm) for arm in range(n_scores)]
self.max_mu_hat_arm = None
def select_score_ucb(self, count):
res_ = []
for score in self.scores:
res_.append({'arm': score.arm, 'score': score.get_ucb_score(count)})
max_arm = max(res_, key=lambda x: x['score'])
return self.scores[max_arm['arm']]
def get_max_mu_hat(self):
m_score = self.scores[self.max_mu_hat_arm]
return m_score.get_mu_hat()
def judge_dmed(self, arm, count):
score = self.scores[arm]
return score.n_tries * b_divergence(score.get_mu_hat(), self.get_max_mu_hat()) <= math.log(count)
def dmed(pb):
scores = Scores(pb.n_machines)
count = 0
n_coins = pb.n_coins
ended = False
for score in scores.scores:
res = pb.play(score.arm)
score.n_tries += 1
score.reward += res
if scores.max_mu_hat_arm is None:
scores.max_mu_hat_arm = score.arm
elif scores.get_max_mu_hat() < score.get_mu_hat():
scores.max_mu_hat_arm = score.arm
count += 1
if count == n_coins:
ended = True
break
this_loop = [arm for arm in range(pb.n_machines)]
next_loop = []
while not ended:
for arm in this_loop:
score = scores.scores[arm]
res = pb.play(arm)
score.n_tries += 1
score.reward += res
if scores.get_max_mu_hat() < score.get_mu_hat():
scores.max_mu_hat_arm = score.arm
count += 1
if count == n_coins:
ended = True
break
for arm_ in range(pb.n_machines):
if arm_ in next_loop:
continue
if scores.judge_dmed(arm_, count):
next_loop.append(arm_)
this_loop = next_loop
next_loop = []
return pb.reward
これを使って評価してみます。条件は前回と同じです。
import pandas as pd
pb = PlayBoard()
pb.set_machines([0.3, 0.5, 0.8])
results = []
for _ in range(100):
pb.reset_history(100)
results.append(dmed(pb))
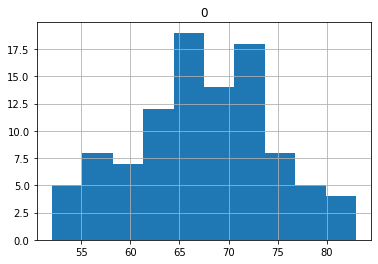
df_ = pd.DataFrame(results)
df_.hist()
こちらの平均は67.24と前回のUBCの73.75や前々回のε貪欲の70.9より悪くなってしまいました。
おわりに
今回は多腕バンディット問題の中でもDMED法について紹介しました。理論的には良くなるはずが、結果は一見悪くなってしまっています。これについては、次回どのような状況下だとどのアルゴリズムが良いパフォーマンスを出すのかということについての記事で、理由を考察したいと思います。次回がこのシリーズ最後の記事です。次回もぜひお付き合いください。